下载文档原格式
浙教版数学九年级下册《2.2 切线长定理》教学设计2一. 教材分析《2.2 切线长定理》是浙教版数学九年级下册中的一章，主要讲述了切线长定理的内容及其应用。
本章内容在学生的数学知识体系中占据重要地位，为后续学习圆的性质和方程奠定了基础。
二. 学情分析九年级的学生已经掌握了相似三角形的性质、锐角三角函数等知识，具备了一定的逻辑思维能力和空间想象能力。
但他们对切线长定理的理解还需要通过具体实例和实际操作来加深。
三. 教学目标1.理解切线长定理的定义及其内涵。
2.学会运用切线长定理解决实际问题。
3.培养学生的空间想象能力、逻辑思维能力和动手操作能力。
四. 教学重难点1.重点：切线长定理的理解和应用。
2.难点：切线长定理的证明和灵活运用。
五. 教学方法1.采用问题驱动法，引导学生探究切线长定理。
2.利用实物模型和几何画板软件，直观展示切线长定理的应用。
3.采用小组合作学习，培养学生的团队协作能力。
六. 教学准备1.准备相关的实物模型和图片，用于展示和讲解。
2.准备几何画板软件，用于动态展示切线长定理。
3.准备练习题和拓展题，用于巩固和提高学生的理解。
七. 教学过程1.导入（5分钟）通过展示生活中的实例，如自行车轮子、滑滑板等，引导学生思考这些实例中是否存在切线长定理的应用。
让学生意识到本节课的重要性，激发学生的学习兴趣。
2.呈现（10分钟）利用实物模型和几何画板软件，呈现切线长定理的定义和证明过程。
让学生直观地理解切线长定理，并学会如何应用它解决实际问题。
3.操练（10分钟）让学生分组讨论，每组选择一个实例，运用切线长定理进行解答。
教师巡回指导，解答学生的疑问。
4.巩固（10分钟）出示一组练习题，让学生独立完成。
题目要求运用切线长定理解决问题。
完成后，教师进行讲评，指出解题的关键点和易错点。
5.拓展（10分钟）出示一组拓展题，让学生小组合作，探讨解题方法。
题目要求运用切线长定理解决生活中的实际问题。
教师巡回指导，解答学生的疑问。
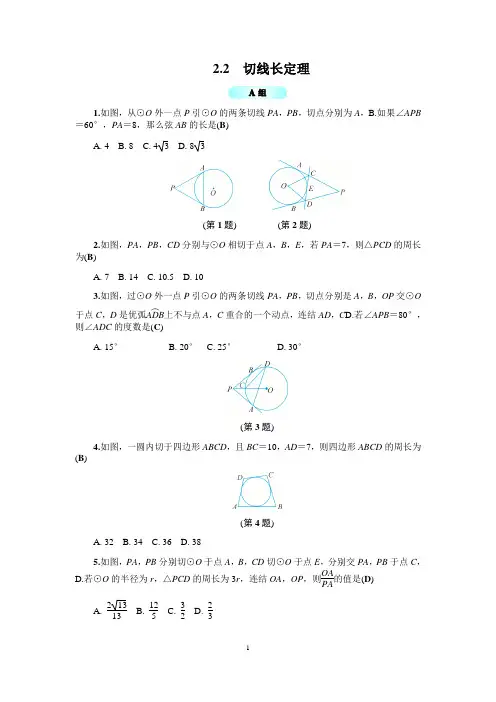
2.2 切线长定理1.如图，从⊙O 外一点P 引⊙O 的两条切线PA ，PB ，切点分别为A ，B.如果∠APB ＝60°，PA ＝8，那么弦AB 的长是(B )A. 4B. 8C. 4 3D. 8 3(第1题) (第2题)2.如图，PA ，PB ，CD 分别与⊙O 相切于点A ，B ，E ，若PA ＝7，则△PCD 的周长为(B )A. 7B. 14C. 10.5D. 103.如图，过⊙O 外一点P 引⊙O 的两条切线PA ，PB ，切点分别是A ，B ，OP 交⊙O于点C ，D 是优弧ADB ︵上不与点A ，C 重合的一个动点，连结AD ，C D.若∠APB ＝80°，则∠ADC 的度数是(C )A. 15°B. 20°C. 25°D. 30°(第3题)4.如图，一圆内切于四边形ABCD ，且BC ＝10，AD ＝7，则四边形ABCD 的周长为(B )(第4题)A. 32B. 34C. 36D. 385.如图，PA ，PB 分别切⊙O 于点A ，B ，CD 切⊙O 于点E ，分别交PA ，PB 于点C ，D.若⊙O 的半径为r ，△PCD 的周长为3r ，连结OA ，OP ，则OAPA 的值是(D )A. 21313B. 125C. 32D. 23(第5题)(第6题)6.如图，⊙O与△ABC中AB，AC的延长线及BC边相切，且∠ACB＝90°，∠A，∠B，∠C所对的边长依次为3，4，5，则⊙O的半径是2.(第7题)7.如图，PA，PB分别切⊙O于点A，B，连结OP与⊙O交于点C，连结AC，B C.求证：AC＝B C.【解】∵PA，PB分别切⊙O于点A，B，∴PA＝PB，∠APC＝∠BP C.又∵PC＝PC，∴△APC≌△BP C.∴AC＝B C.(第8题)8.如图，已知正方形ABCD的边长为2，M是BC的中点，P是线段MC上的一个动点(不与点M，C重合)，以AB为直径作⊙O，过点P作⊙O的切线交AD于点F，切点为E.求四边形CDFP的周长.【解】∵四边形ABCD是正方形，∴∠A＝∠B＝90°，即OA⊥AD，OB⊥B C.∵OA，OB是半径，∴AF，BP是⊙O的切线.又∵PF是⊙O的切线，∴FE ＝FA ，PE ＝PB ，∴四边形CDFP 的周长为DC ＋PC ＋DF ＋FP ＝DC ＋PC ＋DF ＋FE ＋PE ＝DC ＋PC ＋DF ＋FA ＋PB ＝DC ＋AD ＋CB ＝2＋2＋2＝6.9.如图，在直角梯形ABCD 中，以AD 为直径的半圆O 与BC 相切于点E ，BO 交半圆O 于点F ，DF 的延长线交AB 于点P ，连结DE .有下列结论：①DE ∥OF ；②AB ＋CD ＝BC ；③PB ＝PF ；④AD 2＝4AB ·D C.其中正确的结论是(C )(第9题)A. ①②③④B. ①②C. ①②④D. ③④ 【解】 连结AE .∵四边形ABCD 是直角梯形， ∴CD ⊥AD ，AB ⊥A D.∵AD 是半圆O 的直径，∴CD ，AB 是半圆O 的切线. ∵BC 是半圆O 的切线，∴BO 是∠ABE 的平分线，CD ＝CE ，AB ＝BE ， ∴OB ⊥AE ，AB ＋CD ＝BC ，故②正确. ∵点E 在半圆O 上，∴DE ⊥AE ，∴DE ∥OF ，故①正确. 连结O C.易得△OAB ∽△CDO ，∴OA CD ＝ABDO ，即OA ·OD ＝AB ·CD ， ∴AD 2＝4AB ·DC ，故④正确. ③无法证明，故正确的结论是①②④.(第10题)10.如图，⊙D 的半径为3，A 是⊙D 外一点，且AD ＝5，AB ，AC 分别与⊙D 相切于B ，C 两点，G 是BC ︵上任意一点，过点G 作⊙D 的切线，交AB 于点E ，交AC 于点F .(1)△AEF 的周长是 8 .(2)当G 为线段AD 与⊙D 的交点时，连结CD ，则五边形DBEFC 的面积是 9 . 【解】 (1)∵AB ，AC 分别与⊙D 相切于点B ，C ， ∴AB ＝AC ，∠ABD ＝∠ACD ＝90°. 又∵BD ＝3，AD ＝5， ∴AB ＝AD 2－BD 2＝4.∵EF 切⊙O 于点G ， ∴BE ＝EG ，FG ＝F C.∴△AEF 的周长＝AE ＋EG ＋FG ＋AF ＝AB ＋AC ＝8.(第10题解)(2)如解图，AG ＝AD －DG ＝5－3＝2. 在△AEG 和△ADB 中， ∵∠AGE ＝∠ABD ＝90°， ∠GAE ＝∠BAD ， ∴△AEG ∽△ADB ，∴S △AEG S △ADB ＝⎝⎛⎭⎫AG AB 2＝⎝⎛⎭⎫242＝14. 又∵S △ADB ＝12AB ·BD ＝12×4×3＝6， ∴S △AEG ＝32.同理，S △ACD ＝6，S △AFG ＝32.∴S 五边形DBEFC ＝S △ABD ＋S △ACD －S △AEG －S △AFG ＝6＋6－32－32＝9.11.如图，在△ABC 中，∠ACB ＝90°，以AC 为直径的⊙O 交AB 于点D ，过点D 作⊙O 的切线交BC 于点E ，EF ⊥AB ，垂足为F .(第11题)(1)求证：DE ＝12B C.(2)若AC ＝6，BC ＝8，求S △ACD ∶S △EDF 的值. 【解】 (1)由题意，得EC ，ED 都是⊙O 的切线， ∴EC ＝ED ，∠ECD ＝∠ED C.∵AC 为⊙O 的直径，∴∠ADC ＝90°， ∴∠EDC ＋∠EDB ＝90°，∠ECD ＋∠B ＝90°， ∴∠EDB ＝∠B ，∴ED ＝BE . ∴DE ＝BE ＝E C.∴DE ＝12B C.(2)在Rt △ABC 中，∵AC ＝6，BC ＝8，∴AB ＝10. 易知△ADC ∽△ACB ，∴AD AC ＝ACAB ， ∴AD ＝AC 2÷AB ＝3.6， ∴BD ＝AB －AD ＝6.4，∴S△ACD∶S△BCD＝AD∶BD＝9∶16.∵ED＝EB，EF⊥BD，∴S△EDF＝12S△EB D.同理可得S△EBD ＝12S△BCD，∴S△EDF＝14S△BCD，∴S△ACD∶S△EDF＝94.12.如图，O是△ABC内一点，⊙O与BC相交于F，G两点，且与AB，AC分别相切于点D，E，DE∥BC，连结DF，EG.(1)求证：AB＝A C.(2)若AB＝10，BC＝12，求当四边形DFGE是矩形时⊙O的半径.(第12题)【解】(1)∵⊙O与AB，AC分别相切于点D，E，∴AD＝AE，∴∠ADE＝∠AE D.∵DE∥BC，∴∠B＝∠ADE，∠C＝∠AED，∴∠B＝∠C，∴AB＝A C.(2)如解图，连结AO，交DE于点M，延长AO交BC于点N，连结OE，DG.(第12题解)设⊙O的半径为r.∵四边形DFGE是矩形，∴∠DFG＝90°.∴DG是⊙O的直径.∵⊙O与AB，AC分别相切于点D，E，∴OD ⊥AB ，OE ⊥A C.又∵OD ＝OE ，∴AN 平分∠BA C. ∵AB ＝AC ，∴AN ⊥BC ，BN ＝12BC ＝6， ∴AN ＝AB 2－BN 2＝102－62＝8.∵OD ⊥AB ，AN ⊥BC ，∴∠ADO ＝∠ANB ＝90°. 又∵∠OAD ＝∠BAN ，∴△AOD ∽△ABN ， ∴OD BN ＝AD AN ，即r 6＝AD 8.∴AD ＝43r .∴BD ＝AB －AD ＝10－43r . ∵OD ⊥AB ，∴∠GDB ＝∠ANB ＝90°. 又∵∠B ＝∠B ，∴△GBD ∽△ABN ， ∴BD BN ＝GD AN ，即10－43r6＝2r 8，∴r ＝6017.∴当四边形DFGE 是矩形时，⊙O 的半径为6017.13.如图，在△ABC 中，AC ＝BC ，∠CAB ＝α(定值)，⊙O 的圆心O 在AB 上，并分别与AC ，BC 相切于点P ，Q .(第13题)(1)求∠POQ 的度数(用含α的代数式表示).(2)设D 是CA 延长线上的一个动点，DE 与⊙O 相切于点M ，点E 在CB 的延长线上，试判断∠DOE 的度数是否保持不变，并说明理由.(3)在(2)的条件下，如果AB ＝m(m 为已知数)，cos α＝35，设AD ＝x ，DE ＝y ，求y 关于x 的函数表达式(并指出自变量x 的取值范围).【解】 (1)∵AC ＝BC ， ∴∠OBQ ＝∠OAP ＝α.∵⊙O 分别与AC ，BC 相切于点P ，Q ， ∴∠OPA ＝∠OQB ＝90°， ∴∠AOP ＝∠BOQ ＝90°－α， ∴∠POQ ＝180°－2(90°－α)＝2α. (2)∠DOE 的度数保持不变.理由如下： 连结OM .由切线长定理，得EM ＝EQ . 又∵OM ＝OQ ，OE ＝OE ， ∴△OEM ≌△OEQ . ∴∠MOE ＝∠QOE .同理，∠MOD ＝∠PO D.∴∠DOE ＝12(∠POM ＋∠QOM )＝12(360°－∠POQ )＝180°－α.∵α为定值，∴∠DOE 的度数保持不变.(3)∵OP ＝OQ ，∠APO ＝∠BQO ＝90°，∠PAO ＝∠QBO ， ∴△APO ≌△BQO .∴OA ＝O B. ∵AB ＝m ，∴OA ＝OB ＝12AB ＝m2， ∴BQ ＝AP ＝AO ·cos α＝310m ， ∴DM ＝DP ＝310m ＋x .∵∠ADO ＋∠AOD ＝∠OAP ＝α，∠BOE＋∠AOD＝180°－∠DOE＝α，∴∠ADO＝∠BOE.又∵∠DAO＝∠OBE＝180°－α，∴△ADO∽△BOE，∴ADAO＝BOBE，∴BE＝OA·OBAD＝m24x.∴ME＝QE＝BQ＋BE＝310m＋m2 4x.∴DE＝DM＋ME＝310m＋x＋310m＋m24x＝x＋m24x＋35m.因此所求的函数表达式为y＝x＋m24x＋35m(x＞0).初中数学试卷金戈铁骑制作。
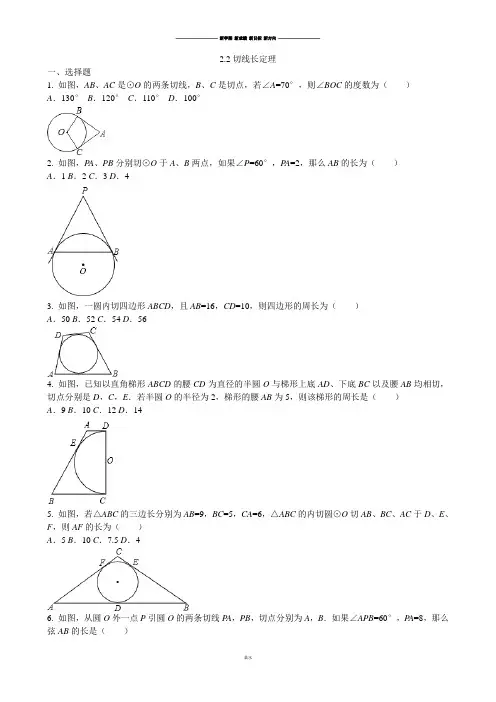
2.2切线长定理一、选择题1. 如图，AB、AC是⊙O的两条切线，B、C是切点，若∠A=70°，则∠BOC的度数为（）A．130°B．120°C．110°D．100°2. 如图，P A、PB分别切⊙O于A、B两点，如果∠P=60°，P A=2，那么AB的长为（）A．1 B．2 C．3 D．43. 如图，一圆内切四边形ABCD，且AB=16，CD=10，则四边形的周长为（）A．50 B．52 C．54 D．564. 如图，已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD、下底BC以及腰AB均相切，切点分别是D，C，E．若半圆O的半径为2，梯形的腰AB为5，则该梯形的周长是（）A．9 B．10 C．12 D．145. 如图，若△ABC的三边长分别为AB=9，BC=5，CA=6，△ABC的内切圆⊙O切AB、BC、AC于D、E、F，则AF的长为（）A．5 B．10 C．7.5 D．46. 如图，从圆O外一点P引圆O的两条切线P A，PB，切点分别为A，B．如果∠APB=60°，P A=8，那么弦AB的长是（）A ．4B ．8C ．34D ．38二、填空题7. 如图，⊙O 的半径为3cm ，点P 到圆心的距离为6cm ，经过点P 引⊙O 的两条切线，这两条切线的夹角为 .8. 如图，⊙O 与△ABC 中AB 、AC 的延长线及BC 边相切，且∠ACB =90°，∠A ，∠B ，∠C 所对的边长依次为3，4，5，则⊙O 的半径是 .9. 如图：EB 、EC 是⊙O 的两条切线，B 、C 是切点，A 、D 是⊙O 上两点，如果∠E =46°，∠DCF =32°，则∠A 的度数是 °.10. 如图，⊙O 的半径为3cm ，点P 到圆心的距离为6cm ，经过点P 引⊙O 的两条切线，则∠APO =°.11. 如图，P A 、PB 分别切⊙O 于A 、B ．P A =5，在劣弧AB 上取点C ，过C 作⊙O 的切线，分别交P A ，PB 于D ，E ，则△PDE 的周长等于 .12.如图，已知PA，PB分别切⊙O于A、B，CD切⊙O于E，PO=13，AO=5，则△PCD周长为 .三、解答题13.已知：⊙O的半径为3cm，点P和圆心O的距离为6cm，经过点P和⊙O的两条切线，求这两条切线的夹角及切线长．参考答案2.2切线长定理一、选择题1.C2.B3.B4.D5.A6.B二、填空题7.60度8.29.9910.3011.1012.24三、解答题13.初中数学试卷鼎尚图文**整理制作。
