当前位置：文档之家 › 材料科学基础第6章扩散

材料科学基础第6章扩散

  • 格式：ppt
  • 大小：631.00 KB
  • 文档页数：51

下载文档原格式

  / 51

合集下载

材料科学基础重点总结3扩散

材料科学基础重点总结3扩散

材料科学基础重点总结3扩散三材料的扩散扩散是物质中原⼦（分⼦或离⼦）的迁移现象，是物质传输的⼀种⽅式。

扩散的本质是原⼦依靠热运动从⼀个位置迁移到另⼀个位置。

是固体中原⼦迁移的唯⼀⽅式。

研究扩散⼀般有两种⽅法：表象理论—根据所测量的参数描述物质传输的速率和数量等；（宏观）原⼦理论—扩散过程中原⼦是如何迁移的。

（微观）3.1 扩散的分类1. 根据有⽆浓度变化⾃扩散：原⼦经由⾃⼰元素的晶体点阵⽽迁移的扩散。

(如纯⾦属或固溶体的晶粒长⼤-⽆浓度变化)互扩散：原⼦通过进⼊对⽅元素晶体点阵⽽导致的扩散。

（有浓度变化）2. 根据扩散⽅向下坡扩散：原⼦由⾼浓度处向低浓度处进⾏的扩散。

上坡扩散：原⼦由低浓度处向⾼浓度处进⾏的扩散。

固态扩散的条件1、温度⾜够⾼；2、时间⾜够长；3、扩散原⼦能固溶；4、具有驱动⼒：5、化学位梯度。

菲克第⼀定律稳态扩散：扩散过程中各处的浓度及浓度梯度不随时间变化（?C/?t=0，?J/?x=0）菲克第⼀定律：在稳态扩散过程中，扩散通量J与浓度梯度成正⽐J为扩散通量，表⽰单位时间内通过垂直于扩散⽅向x的单位⾯积的扩散物质质量，其单位为kg/(m2s)或kg/(cm2s)。

D为扩散系数，其单位为m2/s；ρ是扩散物质的质量浓度，其单位为kg/m3。

式中的负号表⽰物质从⾼浓度向低浓度扩散的现象，扩散的结果导致浓度梯度的减⼩，使成份趋于均匀。

菲克第⼆定律⾮稳态扩散——各处的浓度和浓度梯度随时间发⽣变化的扩散过程。

（?C/?t≠0, ?J/?x≠0）。

⼤多数扩散过程是⾮稳态扩散过程，某⼀点的浓度是随时间⽽变化的菲克第⼆定律：扩散过程中，扩散物质浓度随时间的变化率，与沿扩散⽅向上物质浓度梯度随扩散距离的变化率成正⽐。

3.2 置换式固溶体中的扩散---互扩散与柯肯达尔效应互扩散——柯肯达尔效应柯肯达尔最先发现互扩散，在α黄铜—铜扩散偶中，⽤钼丝作为标志，785℃下保温不同时间后，钼丝向黄铜内移动，移动量与保温时间的平⽅根成正⽐，Cu-黄铜分界⾯黄铜侧出现宏观疏孔。

《材料科学基础》总复习题

《材料科学基础》总复习题

《材料科学基础》复习题第1章原子结构与结合键一、选择题1、具有明显的方向性和饱和性。

A、金属键B、共价键C、离子键2、以下各种结合键中，结合键能最大的是。

A、离子键、共价键B、金属键C、分子键3、以下各种结合键中，结合键能最小的是。

A、离子键、共价键B、金属键C、分子键4、以下关于结合键的性质与材料性能的关系中，是不正确的。

A、具有同类型结合键的材料，结合键能越高，熔点也越高。

B、具有离子键和共价键的材料，塑性较差。

C、随着温度升高，金属中的正离子和原子本身振动的幅度加大，导电率和导热率都会增加。

二、填空题1、构成陶瓷化合物的两种元素的电负性差值越大，则化合物中离子键结合的比例。

2、通常把平衡距离下的原子间的相互作用能量定义为原子的。

3、材料的结合键决定其弹性模量的高低，氧化物陶瓷材料以键为主，结合键故其弹性模量；金属材料以键为主，结合键故其弹性模量；高分子材料的分子链上是键，分子链之间是键，故其弹性模量。

第2章晶体结构（原子的规则排列）一、名词解释1、点阵2、晶胞3、配位数4、同素异晶转变5、组元6、固溶体7、置换固溶体8、间隙固溶体9、金属间化合物10、间隙相二、选择题1、体心立方晶胞中四面体间隙的r B/r A和致密度分别为A 0.414，0.68B 0.225，0.68C 0.291，0.682、晶体中配位数和致密度之间的关系是。

A、配位数越大，致密度越大B、配位数越小，致密度越大C、两者之间无直接关系3、面心立方晶体结构的原子最密排晶向族为。

A <100> B、<111> C、<110>4、立方晶系中，与晶面(011)垂直的晶向是。

A [011]B [100]C [101]5、立方晶体中（110）和（211）面同属于晶带。

A [101] B[100] C [111]6、金属的典型晶体结构有面心立方、体心立方和密排六方三种，它们的晶胞中原子数分别为：A、4；2；6B、6；2；4 D、2；4；66、室温下，纯铁的晶体结构为晶格。

材料科学基础-第六章_金属及合金的回复与再结晶

材料科学基础-第六章_金属及合金的回复与再结晶


晶界凸出形核机制
在晶界处A 晶粒中的某些亚晶粒能通过 晶界迁移而凸入B 晶粒中，借消耗B 中的 具有亚晶粒组织晶粒间的凸出形核机制 亚晶而生长，从而形成再结晶的核心。
第六章 金属及合金的回复与再结晶－§6.3 再结晶
2.长大
再结晶晶核形成之后，即借界面的移动向周围畸变区域长大。 ①再结晶晶核长大（晶界迁移）的驱动力 无畸变的新晶粒与周围畸变的旧晶粒之间的畸变能差。 ②晶界的迁移方向 晶界总是背离其曲率中心，向着畸变区域推进，直至全部形成无畸变的等 轴晶粒为止，再结晶即告完成。
将后式代入前式并积分，以x0表示开始时性能增量的残留分数，则得：
t dx Q / RT x0 x c0e 0 dt x
或
x0 ln c0 te Q/RT x
回复的速度随温度升高和加热时间的延长而增大。
举例：
采用不同的温度加热冷变形金属使之回复到同样的程度（即残留分数相 同），则所需时间不同。
轴小晶粒，并随时间的延长不断长大，直至伸长的晶粒完全转变为新的等轴 晶粒为止。
3.晶粒长大阶段
再结晶过程中形成的等轴晶粒逐步相互吞并而长大，直至达到一个稳定的 尺寸。
第六章 金属及合金的回复与再结晶－§6.1 冷变形金属在加热时的组织和性能变化
二、储存能及内应力的变化
1.储存能的变化
冷变形造成的偏离平衡位置 大、能量较高的原子，在加热
冷变形后保留在金属内部的畸变 能，或称储存能。 冷变形金属在不同加热温度时 组织和性能的变化
第六章 金属及合金的回复与再结晶－§6.1 冷变形金属在加热时的组织和性能变化
一、显微组织的变化
1.回复阶段
显微组织几乎没 有发生变化，晶粒 仍保持冷变形后的 伸长状态。
上海交通大学_材料科学基础第六章

上海交通大学_材料科学基础第六章

• 可解释纯金属与二元合金结晶时的差别
纯金属结晶，液－固共存，f =0，说明结晶为恒温。 二元系金属结晶两相平衡，f =2-2+1=1，说明有一个可变因素(T)，表明 它在一定（T）范围内结晶。 二元系三相平衡，f =2-3+1=0，此时温度恒定，成分不变，各因素恒定。
Page 8
相率的应用
• 相律是检验、分析和使用相图的重要工具。利用它可以分 析和确定系统中可能存在的相数，检验和研究相图。
6.1.1 相平衡条件和相律
• 相平衡的条件：通过一些数学推导和系统平衡条件dG=0可 得：处于平衡状态下的多相(P个相)体系中，每个组元(共 有C个组元)在各相中的化学势（chemical potential）都彼此 相等。
• 相平衡(phase equilibrium)是一种动态平衡。
Page 6
第六章 单组元相图 及纯晶体的凝固
Page 1
本章要求掌握的内容
• 应掌握的内容:
– 纯金属凝固的过程和现象 – 结晶的热力学、动力学、能量、和结构条件 – 过冷度对结晶过程和结晶组织的影响；过冷度、临界过冷度、有效过
冷度、动态过冷度之间的区别。 – 几个重要概念：过冷度，临界晶核半径，临界形核功，形核率，均匀
Page 20
Page 21
6.2.2 晶体凝固的热力学条件
自由能
G H TS
dG Vdp SdT
在等压时，dp＝0， 所以可推导得：
dG S dT
由于熵S恒为正值，所以自由能是随温度增高而减小。
Page 22
在一定温度下，从一相转变为另一相的自由能变化为
G H TS
令液相转变为固相后的单位体积自由能变化为 GV ，则
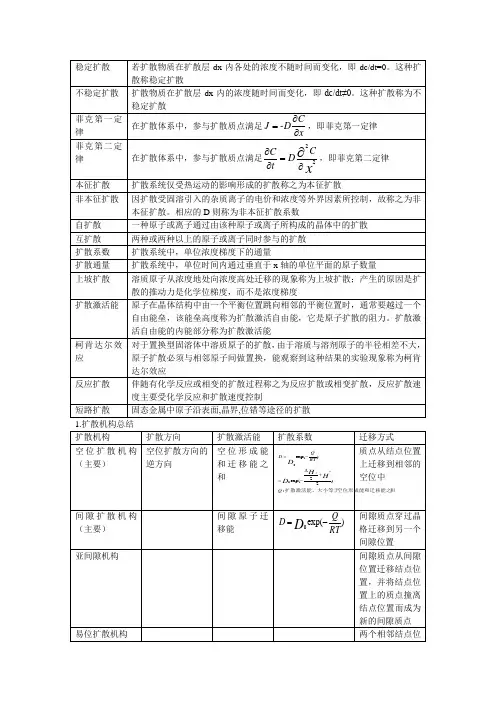
材料科学基础-扩散

材料科学基础-扩散

稳定扩散 若扩散物质在扩散层dx 内各处的浓度不随时间而变化，即dc/dt=0。

这种扩散称稳定扩散不稳定扩散 扩散物质在扩散层dx 内的浓度随时间而变化，即dc/dt≠0。

这种扩散称为不稳定扩散菲克第一定律在扩散体系中，参与扩散质点满足xC-DJ ∂∂=，即菲克第一定律 菲克第二定律 在扩散体系中，参与扩散质点满足xC D t C22∂=∂∂∂，即菲克第二定律 本征扩散 扩散系统仅受热运动的影响形成的扩散称之为本征扩散非本征扩散 因扩散受固溶引入的杂质离子的电价和浓度等外界因素所控制，故称之为非本征扩散。

相应的D 则称为非本征扩散系数自扩散 一种原子或离子通过由该种原子或离子所构成的晶体中的扩散 互扩散 两种或两种以上的原子或离子同时参与的扩散 扩散系数 扩散系统中，单位浓度梯度下的通量扩散通量 扩散系统中，单位时间内通过垂直于x 轴的单位平面的原子数量上坡扩散 溶质原子从浓度地处向浓度高处迁移的现象称为上坡扩散；产生的原因是扩散的推动力是化学位梯度，而不是浓度梯度扩散激活能原子在晶体结构中由一个平衡位置跳向相邻的平衡位置时，通常要越过一个自由能垒，该能垒高度称为扩散激活自由能，它是原子扩散的阻力。

扩散激活自由能的内能部分称为扩散激活能柯肯达尔效应 对于置换型固溶体中溶质原子的扩散，由于溶质与溶剂原子的半径相差不大，原子扩散必须与相邻原子间做置换，能观察到这种结果的实验现象称为柯肯达尔效应反应扩散 伴随有化学反应或相变的扩散过程称之为反应扩散或相变扩散，反应扩散速度主要受化学反应和扩散速度控制短路扩散 固态金属中原子沿表面,晶界,位错等途径的扩散1.扩散机构总结扩散机构扩散方向 扩散激活能 扩散系数迁移方式 空位扩散机构（主要）空位扩散方向的逆方向空位形成能和迁移能之和和空位形成能和迁移能之扩散激活能，大小等于:)22exp()(exp *00Q RTQ D HHD Df+∆-=-=质点从结点位置上迁移到相邻的空位中间隙扩散机构（主要）间隙原子迁移能 )(exp 0RT Q D D -=间隙质点穿过晶格迁移到另一个间隙位置 亚间隙机构间隙质点从间隙位置迁移结点位置，并将结点位置上的质点撞离结点位置而成为新的间隙质点 易位扩散机构两个相邻结点位置上的质点直接交换位置进行迁移环易位机构几个结点位置上的质点以封闭的环形依次交换位置进行迁移1.空位机构和间隙机构是金属体系和离子化合物体系中质点扩散的主要形式2.空位机构比间隙机构的扩散激活能大，但是扩散系数小3.固态金属中扩散方向是化学位梯度降低方向 2.扩散中常用公式)(exp 0RT Q D D -=δ261D Γ=(频率,自由程)xC -D J ∂∂=(适用于稳定扩散和非稳定扩散)x C D t C 22∂=∂∂∂（不稳定扩散） dxdc -DA JA dt dm == Dt K x =(实验测得的浓度已知) DtA t x x4),(lnI 2-=（A ：图像的截距，Dt41-为斜率；）3.扩散的结果都是使不均匀体系均匀化，不平衡逐渐达到平衡4.非稳定扩散类型①扩散质在晶体表面浓度恒定情况：)2(),(C 0Dtx erfc t x C =②定量扩散质由晶体表面向内部扩散（示踪扩散法原理）：)4exp(2),(C 221)(DtM t x xDt -=π5.本征扩散一般处于高温处，非本征扩散一般处于低温处；由杂质扩散转变为本征扩散，其T1-ln D r 曲线上会出现转折点;置换型固溶体扩散一般只能在高温进行;杂质浓度升高,转折点升高6.扩散系数测定一般使用示踪扩散方法7.扩散动力学方程式（能斯特-爱因斯坦方程）)ln ln 1)((D 211221~γγ∂∂++=D N D N①(γγ21ln ln 1∂∂+)>0:扩散系数大于0,正常扩散,高浓度向低浓度迁移,溶质趋于均匀②(γγ21ln ln 1∂∂+)<0:扩散系数小于0,反常扩散,低浓度向高浓度迁移,溶质偏聚或分相8.影响扩散系数因素①温度:影响扩散激活能和改变物质结构 ②杂质 ③气氛 ④固溶体类型:间隙性固溶体比置换型固溶体更容易扩散;在置换型固溶体中,原子间尺寸差别越小,电负性越大,亲和力越强,扩散越困难 ⑤扩散物质性质和结构 ⑥化学键类型和强度 ⑦扩散介质结构:体心立方结构大于面心立方结构的扩散系数 ⑧结构缺陷:结构缺陷活化能小,容易扩散 9.激活能越大,扩散速率对温度的敏感性越大 10.反应扩散对扩散层深度的影响过程实际上反应扩散起初由于新相层较浅,原子扩散不是主要矛盾,过程由表面扩散所支配,新相层的增加服从直线关系;随新相层深度增加,原子扩散逐步称为主要矛盾,新相层的增加服从抛物线规律。

《材料科学基础》习题

《材料科学基础》习题


1
2．固态下完全不互溶的三元共晶相图如图6-2所示，画出过Am、PQ的垂直截面。若三组元的熔点tA＞tB＞tC，请画出tB ＜t＜tA温度下的水平截面。
3．液相面投影图如图6-3，分析O合金的结晶过程，画出冷却曲线、结晶示意图、注明反应式，并计算室温下组织组成物的相对量。
4．液相面投影图如图6-4，请写出全部四相平衡转变。
4．计算面心立方结构（111）、（110）与（100）面的面密度和面间距。
5．FeAl是电子化合物，具有体心立方点阵，试画出其晶胞，计算电子浓度，画出（112）面原子排列图。
6．合金相VC、Fe3C、CuZn、ZrFe2属于何种类型，并指出其结构特点。
第二章 晶体缺陷
1．铜的空位生成能1.7×10-19J，试计算1000℃时，1cm3铜所包含的空位数，铜的密度8.9g/cm3，相对原子质量63.5，玻尔兹曼常数K=1.38×10-23J/K。
1．何为成份过冷？影响成份过冷的因素有那些？试述区域提纯的原理。
2．简述枝晶偏析形成过程和消除方法。
3．分析0.45%C，1.2%C和2.3%C 的铁碳合金的平衡结晶过程，计算室温下组织组成 物的相对量及两相相对量。
4．根据显微组织分析，一灰口铁内石墨的体积占12%，铁素体的体积占88%，试求该合金的碳含量。
如图2-1所示的位错环，说明各段位错的性质，并指出刃位错多余半原子面的位置。
2．如图2-2，某晶体滑移面上有一个 柏氏矢量为b的位错环，受到均匀切应力τ作用，试分析：
该位错环各段位错的结构类型；
求各段位错所受的力；
在τ的作用下，位错环将如何运动？
在τ的作用下，位错环稳定不动，其最小半径应该多大？
材料科学基础重点知识

材料科学基础重点知识

第5章 纯金属的凝固1、金属结晶的必要条件：过冷度-理论结晶温度与实际结晶温度的差；结构起伏-大小不一的近程有序排列的此起彼伏；能量起伏-温度不变时原子的平均能量一定，但原子的热振动能量高低起伏的现象；成分起伏-材料内微区中因原子的热运动引起瞬时偏离熔液的平均成分，出现此起彼伏的现象。

结晶过程：形核和长大过程交替重叠在一起进行2、过冷度与液态金属结晶的关系：液态金属结晶的过程是形核与晶核的长大过程。

从热力学看，没有过冷度结晶就没有趋动力。

根据T R k ∆∝1可知当过冷度T ∆=0时临界晶核半径R *为无穷大，临界形核功（21T G ∆∝∆）也为无穷大，无法形核，所以液态金属不能结晶。

晶体的长大也需要过冷度，所以液态金属结晶需要过冷度。

孕育期：过冷至实际结晶温度，晶核并未立即产生，结晶开始前的这段停留时间3、均匀形核和非均匀形核均匀形核：以液态金属本身具有的能够稳定存在的晶胚为结晶核心直接成核的过程。

非均匀形核：液态金属原子依附于固态杂质颗粒上形核的方式。

临界晶核半径：ΔG 达到最大值时的晶核半径r *=-2γ/ΔGv 物理意义：r<rc 时， ΔGs 占优势，故ΔG>0，晶核不能自动形成。

r>rc 时， ΔGv 占优势，故ΔG<0，晶核可以自动形成，并可以稳定生长。

临界形核功：ΔGv *=16πγ3/3ΔGv 3 形核率：在单位时间单位体积母相中形成的晶核数目。

受形核功因子和原子扩散机率因子控制。

4、正的温度梯度：靠近型壁处温度最低，凝固最早发生，越靠近熔液中心温度越高。

在凝固结晶前沿的过冷度随离界面距离的增加而减小。

纯金属结晶平面生长。

负的温度梯度：过冷度随离界面距离的增加而增加。

纯金属结晶树枝状生长。

5、光滑界面即小平面界面：液固两相截然分开，固相表面为基本完整的原子密排面，微观上看界面光滑，宏观上看由不同位向的小平面组成故呈折线状的界面。

粗糙界面即非小平面界面：固液两相间界面微观上看高低不平，存在很薄的过渡层，故从宏观上看界面反而平直，不出现曲折小平面的界面。

材料科学基础--第六章

材料科学基础--第六章


2012-10-16
Introduction to Materials Science
第六章－6
Materials Science
3. 合金凝固后溶质分布的数学表达式(续)
Material
3-2 凝固方程
在探讨凝固方程时，我们假设K0为常数，忽略固相中的扩散，L/S 界面平直移动，液相和固相密度相同。
2012-10-16
Introduction to Materials Science
第六章－10
Materials Science
3. 合金凝固后溶质分布的数学表达式(续)
1)溶质部分混合
Lessons
C S K e C 0 (1
Z l
)
K e 1
式中，Ke－有效分配系数
2012-10-16
液相温度梯度对成分过冷的影响
2012-10-16 Introduction to Materials Science 第六章－23
Materials Science
3. 成分过冷对晶体生长形貌的影响
晶体平面生长动画
2012-10-16 Introduction to Materials Science 第六章－24
1. 成分过冷的形成
1-1 定义
成分过冷 —— L/S界面前沿L相中的实际温度低于由溶质分 布所决定的理论凝固温度（熔点）时产生的过冷，称为成分 Definition 过冷。
如图，左上角的是一匀晶相 图，右下角是凝固过程的示 意图。
你能根据左图与 说明阐述产生成 分过冷的原因吗
？
第六章－18
2012-10-16
不平衡结晶包含如下的情况：
• • 液相内溶质完全混合（在缓慢结晶条件下）； 液相中溶质部分混合（在较快的结晶条件下）；
材料科学基础_第6章_固态相变的基本原理

材料科学基础_第6章_固态相变的基本原理

1）原子的扩散速度 ➢ 由于新旧两相的化学成分不同，相变时必须有原子的扩散 ➢ 原子扩散速度成为相变的控制因素。 ➢ 当相变温度较高时，即扩散不是决定性因素的温度范围内
，随着温度的降低，即过冷度的增大，相变驱动力增大， 相变速度加快；但是当过冷度增大到一定程度，扩散称为 决定性因素，进一步增大过冷度，反而使得相变速度减小 。
15
➢ ①共格界面：当界面上的原子所占据的位置恰好是两相点 阵的共有位置时，两相在界面上的原子可以一对一地相互 匹配 。
➢ ②半共格界面：如果一相的某一晶面上的原子排列和另一 相的某晶面的原子排列不能达到完全相同，但相近，这样 形成的界面在小区域内可以利用少量得到弹性变形来维持 共格关系，适当利用位错的半原子面来进行补偿，达到能 量较低。
9
2）. 非扩散型（位移型）： 在相变过程中没有原子的扩散运动，相变前后没有成分
的变化，原子以切变的方式，即相对周围原子发生有规律 的少量的偏移，基本维持原来的相邻关系，而发生晶体结 构的改变。
新旧相的界面有共格 马氏体相变就是属于非扩散型相变。
10
3）.过度型相变： 介于二者之间的，具有扩散型和非扩散型的综合特征Hale Waihona Puke 2T 2P
( S T
)P
CP T
CP等压热容
2 1
P 2
T
22
P 2
T
2
P2
T
V V
V ( P )T
VB
B压缩系数
2 1
TP
22
TP
2
TP
V V
( V T
)P
VA
A膨胀系数
7
二级相变
V V ,S S CP CP , B B , A A
第六章 扩散

第六章 扩散


直接应用菲克第二定律解决实际扩散问题，往往很复杂。 但是有两条由菲克第二定律推导出来的结论却十分简单、 有用：
推论 （1）对于同一扩散系统、扩散系数D与 扩散时间t的乘积为一常数。


已知Cu在Al中的扩散系数D， 在500℃和600℃时分别为 4.8×10-14 m2/s和5.3×10-13 m2/s。假如一个工件在600℃ 需要处理10小时，如果在500℃处理，要达到同样的效果 则需要多少小时？ (Dt)500 = (Dt)600
三、扩散的热力学分析
1．扩散驱动力 浓度梯度有关的扩散：顺扩散（高浓度→低浓度），逆扩散 （低浓度→高浓度） 热力学：决定组元扩散流向的是化学位 浓度梯度与化学位梯度一致，顺扩散，成分趋于均匀，如铸 锭均匀化 浓度梯度与化学位梯度不一致，逆扩散，成分区域性不均匀， 如共析分解 i, j 两组元系统，组元的体积浓度为 Ci ， ni 为组元 i 的摩尔 数，M：组元i的摩尔质量。 C i c M n 则Ci=Mni， i i ，则 n i
渗碳层按齿廓分布的渗碳齿轮
1. 概述

实际上，金属的真空冶炼、材料的提纯、 铸件的凝固和成分均匀化、变形金属的回 复再结晶、相变、化学热处理、粉末冶金 或陶瓷材料的烧结等都受扩散影响 原子或分子的迁移现象称为扩散。扩散的 本质是原子依靠热运动从一个位置迁移到 另一个位置。扩散是固体中原子迁移的唯 一方式。 扩散过程是传质过程。它是一个不可逆过 程，也是体系熵增过程。
§2.2 菲克第二定律

考虑如图所示的扩散系统， 扩散物质沿x方向通过横截面 积为A(=ΔyΔz)、长度为Δx的 微元体，假设流入微元体（x 处）和流出微元体（x+Δx处） 的扩散通量分别为Jx和Jx+Δx， 则在Δt时间内微元体中累积 的扩散物质量为
【材料科学基础】必考知识点第六章

【材料科学基础】必考知识点第六章

2020届材料科学基础期末必考知识点总结第六章固体中的扩散第一节概述1 扩散的现象与本质（1）扩散：热激活的原子通过自身的热振动克服束缚而迁移它处的过程。

（2）现象：柯肯达尔效应。

（3）本质：原子无序跃迁的统计结果。

（不是原子的定向移动）。

2 扩散的分类（1）根据有无浓度变化自扩散：原子经由自己元素的晶体点阵而迁移的扩散。

（如纯金属或固溶体的晶粒长大。

无浓度变化。

）互扩散：原子通过进入对方元素晶体点阵而导致的扩散。

（有浓度变化）（2）根据扩散方向下坡扩散：原子由高浓度处向低浓度处进行的扩散。

上坡扩散：原子由低浓度处向高浓度处进行的扩散。

（3）根据是否出现新相原子扩散：扩散过程中不出现新相。

反应扩散：由之导致形成一种新相的扩散。

3 固态扩散的条件（1）温度足够高；（2）时间足够长；（3）扩散原子能固溶；（4）具有驱动力：化学位梯度。

第二节扩散定律1 菲克第一定律（1）第一定律描述：单位时间内通过垂直于扩散方向的某一单位面积截面的扩散物质流量（扩散通量J）与浓度梯度成正比。

（2）表达式：J=-D(dc/dx)。

（C－溶质原子浓度；D-扩散系数。

）（3）适用条件：稳态扩散，dc/dt=0。

浓度及浓度梯度不随时间改变。

2 菲克第二定律一般：∂C/∂t=∂(D∂C/∂x)/ ∂x二维：（1）表达式特殊：∂C/∂t=D∂2C/∂x2三维：∂C/∂t=D(∂2/∂x2+∂2/∂y2+∂2/∂z2)C稳态扩散：∂C/∂t=0，∂J/∂x=0。

（2）适用条件：非稳态扩散：∂C/∂t≠0，∂J/∂x≠0（∂C/∂t=－∂J/∂x）。

3 扩散第二定律的应用（1）误差函数解适用条件：无限长棒和半无限长棒。

表达式：C=C1－(C1-C2)erf(x/2√Dt) (半无限长棒)。

在渗碳条件下：C:x,t处的浓度；C1:表面含碳量;C2:钢的原始含碳量。

（2）正弦解C x=Cp-A0sin(πx/λ)Cp:平均成分；A0：振幅Cmax- Cp；λ:枝晶间距的一半。

材料科学基础之金属学原理扩散习题及答案

《材料结构》习题：固体中原子及分子的运动1. 已知Zn在Cu中扩散时D0=2.1×10-5m2/s，Q=171×103J/mol。

试求815℃时Zn在Cu中的扩散系数。

2. 已知C在γ铁中扩散时D0=2.0×10-5m2/s，Q=140×103J/mol; γ铁中Fe自扩散时D0=1.8×10-5m2/s，Q=270×103J/mol。

试分别求出927℃时奥氏体铁中Fe的自扩散系数和碳的扩散系数。

若已知1％Cr可使碳在奥氏体铁中的扩散激活能增加为Q=143×103J/mol，试求其扩散系数的变化和对比分析以上计算结果。

3. 若将铁棒置于一端渗碳的介质中，其表面碳浓度达到相应温度下奥氏体的平衡浓度C S。

试求（1）结合铁－碳相图，试分别示意绘出930℃和800℃经不同保温时间（t1<t2<t3）碳浓度沿试棒纵向的分布曲线；（2）若渗碳温度低于727℃，试分析能否达到渗碳目的。

4. 含碳0.2％的低碳钢进行870℃渗碳较930℃渗碳具有晶粒细小的优点，则（1）试计算以上两种温度下碳在γ-Fe中的扩散系数；（2）试计算870℃渗碳需多少时间可达到930℃渗碳10小时的渗层厚度（忽略C在γ-Fe 中的溶解度差异）；（3）若渗层厚度测至含碳量0.4％处，计算870℃渗碳10小时后的渗层厚度及其与930℃同样时间渗层厚度的比值。

（表面碳浓度取1.2）FeDγCDγCDγ习题4答案：1．解：根据扩散激活能公式得3-5132017110e x p () 2.110e x p 1.2610m /s8.314(815273)-⎛⎫⨯=-=⨯⨯-=⨯ ⎪⨯+⎝⎭CuZn Q D D RT 2．解：根据扩散激活能公式得3γ-5172027010e x p () 1.810e x p 3.1810m /s 8.314(927273)-⎛⎫⨯=-=⨯⨯-=⨯ ⎪⨯+⎝⎭Fe Q D D RT 3γ-5112014010e x p () 2.010e x p 1.6110m /s 8.314(927273)-⎛⎫⨯=-=⨯⨯-=⨯ ⎪⨯+⎝⎭C Q D D RT 已知1％Cr 可使碳在奥氏体铁中的扩散激活能增加为Q =143×103J/mol ， 所以，3γ-51120143.310exp() 2.010exp 1.1610m /s 8.314(927273)-⎛⎫⨯'=-=⨯⨯-=⨯ ⎪⨯+⎝⎭CQ D D RT 由此可见，1％Cr 使碳在奥氏体铁中的扩散系数下降，因为Cr 是形成碳化物的元素，与碳的亲和力较大，具有降低碳原子的活度和阻碍碳原子的扩散的作用。

材料科学基础 第6章 材料的塑性变形与再结晶


两三个晶粒的拉伸试验表明：晶界处 的变形能力差，呈竹节状
2)晶界对材料的强化作用机理
晶界对材料的强化作用是通过晶界对位错 的阻塞作用实现的。塑性变形是通过位错在滑 移面上的滑移产生的，晶界可以阻止位错的滑 移，因此位错在晶界处形成阻塞，位错处阻塞 位错的数量越多，对位错源形成位错的反作用 力越大，当增大的某一数值，位错源停止形成 新的位错，因此滑移面停止进行，要使相邻晶 粒发生滑移须增大外应力，以启动其位错源动 作。这就是晶界的强化作用。
滑移方向 〈110〉 〈110〉
〈111〉
〈111〉 〈111〉 〈111〉 〈111〉 〈1120〉 〈1120〉 〈1123〉 〈1120〉 〈1120〉 〈1010〉 〈1120〉 〈1120〉 〈1120〉 〈1120〉
3.位错滑移时受到的点阵阻力
由于原子排列的周 期性，位错在滑移过程 中，位错中心的能量将 发生周期性变化，当位 错从位置1移动到位置2 时需要越过一个势垒， 即阻力，其大小如右图 所示。
切应力
2.晶体结构引起的加工硬化曲线的差异
6.1.2多晶体的塑性变形
通常使用的材料多为多晶材料，多晶材料变形 有以下特点： ①每个晶粒的变形行为方式与其单晶相同； ②每个晶粒的变形受其周围晶粒的影响；主要涉及 到晶粒之间的方位及取向关系； ③整个材料体的变形是通过各晶粒变形相互配合与 协调实现的。 因此多晶材料的屈服强度明显高于同类材料的 单晶体；并且晶粒越细，强度越高。
0 10 20 40 60 80 276 497 566 593 607 662
抗拉强度 （Mpa）
456 518 580 656 704 792
延伸率 断面收缩率 （% ） （% ）
34 20 17 16 14 7 70 65 63 60 54 26

材料科学基础(上海交大)_第6章.答案

材料与化学化工学院
第6章 单组元相图及纯晶体凝固
6.1 单元系相变的热力学与相平衡
6.2 纯晶体的凝固
6.3 气固相变与薄膜生长
重点与难点：
• • • • • 结晶的热力学、结构和能量条件； 相律的应用； 克劳修斯——克拉珀龙方程的应用； 亚稳相出现的原因； 均匀形核的临界晶核半径和形核功的推 导； 润湿角的变化范围及其含义；
• 两条斜率不同的自由能曲线必然相交于一点
• 液、固两相的自由能相等 • 两相处于平衡而共存。 事实上， Tm—既不能完全结晶，也不能完全熔化 • 要发生结晶则体系必须降至低于Tm温度， • 而发生熔化则必须高于Tm 。
(2) 热力学条件
a △T>0, △Gv<0－过冷是结晶的
必要条件（之一）。
b △T越大, △Gv越小－过冷度越
图6.4
大， 越有利于结晶。
c △Gv的绝对值为凝固过程的驱 动力。
ΔT=Tm-T，是熔点Tm与实际凝固温度T之差 Lm是熔化热，
要使 ΔGv＜0，必须使Δ T＞0，即 T＜Tm，故ΔT
称为过冷度。
晶体凝固的热力学条件——实际凝固温度应低于
熔点Tm，即需要有过冷度，其中热分析实验装置示 意图见图6.5。
如果外界压力保持恒定（例如一个标准大气 压），那么单元系相图只要一个温度轴来表示，如 水的情况见图6.1（b）。根据相律，在汽、水、冰
的各单相区内（f＝1），温度可在一定范围内变动。
在熔点和沸点处，两相共存，f＝0，故温度不能变
动，即相变为恒温过程。
在单元系中，除了可以出现气、液、固三相之
间的转变外，某些物质还可能出现固态中的同素异
构转变，见图6.2和图6.3。
• bcc • fcc

无机材料科学基础-6-扩散过程


田长安 合肥学院
4
易位扩散所需活化能最大，特别是离子晶体，正 负离子由于尺寸、电荷和配位情况的不同，直接 易位非常困难。同种粒子的环形易位在能量上虽 然是可能的，但实际可能性甚小。 空位扩散所需活化能最小，是最常见的扩散。其 次是间隙扩散和准间隙扩散。
上述粒子扩散完全是由热振动引起的无序的、 向任意方向的迁移。要形成定向的扩散，必须 有推动力，而推动力一般就是浓度梯度。
将上式两边取对数：
lnC
(x, t)
ln
Q 2 Dt

x
2
4Dt
用lnC(x,t)对x2作图 得一直线，斜率 k= -1/4Dt， 所以 D= -1/4tk。
田长安 合肥学院
29
应用续 2）制作半导体时，常先在硅表面涂覆一薄层硼，然后加热 使之扩散。利用上式可求得给定温度下扩散一定时间后硼的 分布。 例如，测得1100℃硼在硅中的扩散系数D=4 ×10 7m2.s-1，硼薄膜质量M=9.43 ×10 19，原子扩散7 ×10 7 s后，表面（x=0）硼浓度为
20
x
2
田长安 合肥学院
引入函数： u x/
t
使得C(x,t) 转化为只是u 的函数C(u)，从而可以将 上述偏微分方程化为常微分方程：
C C u dC x dC u 3/2 t u t du 2t du 2t
C
C u C u ( ) ( ) ( ) ( ) 2 C u C x u x u x 2 x x x x x u x u u x x
0
田长安 合肥学院
27
可以求得扩散方程的解为：
C (x, t)
Q 2 Dt

材料科学基础————扩散

无穷长的意义是相对于扩散区长度而言，若一维扩散物 体的长度大于，则可按一维无穷长处理。由于固体的扩散 系数D在10-2~10-12cm2s-1很大的范围内变化，因此这里 所说的无穷并不等同于表观无穷长。
求解过程
设A，B是两根成分均匀的等截面金属棒，长度符合上
述无穷长的要求。A的成分是C2，B的成分是C1。将两根
在t时间内，试样表面扩散组元I的浓度Cs被维持为常数，试 样中I组元的原始浓度为c1，厚度为4 Dt ，数学上的无限” 厚，被称为半无限长物体的扩散问题。此时，Fick’s secondlaw的初始、边界条件应为 t=0，x ＞0，c= ０ ； t ≧ 0，x=0，c= Cs ；x=∞，c= ０ 满足上述边界条件的解为
图3 扩散过程中溶质原子的分布
由扩散通量的定义，有
C J D x
（1）
上式即菲克第一定律 式中J称为扩散通量常用单位是g/(cm2.s)或 mol/(cm2.s) ； D是同一时刻沿轴的浓度梯度；是比例系数， 称为扩散系数。
图4 溶质原子流动的方向与浓度降低的方向一致
讨论：
对于菲克第一定律，有以下三点值得注意： （1）式（1）是唯象的关系式，其中并不 涉及扩散系统内部原子运动的微观过程。 （2）扩散系数反映了扩散系统的特性，并 不仅仅取决于某一种组元的特性。 （3）式（1）不仅适用于扩散系统的任何 位置，而且适用于扩散过程的任一时刻。
Dk ( P2 P 1) A F JxA l
引入金属的透气率表示单位厚度金属在单位压 差（以为单位）下、单位面积透过的气体流量 δ=DS 式中D 为扩散系数，S为气体在金属中的溶解度， 则有 F J ( p1 p2 )

在实际中，为了减少氢气的渗漏现象，多采用 球形容器、选用氢的扩散系数及溶解度较小的 金属、以及尽量增加容器壁厚等。

材料科学基础第06章--扩散


扩散方程的误差函数解
扩散方程的误差函数解
半无限长棒扩散方程的误差函数解
解为：
定义函数：
一维半无限长棒中扩 散方程误差函数解：
高斯误差函数
高斯误差函数
无限长棒中的扩散模型
实际意义：将溶质含量不同的两种材料焊接在一起，因 为浓度不同，在焊接处扩散进行后，溶质浓度随时间的 会发生相应的变化。
无限长棒扩散方程的误差函数解
为了解释上坡扩散的现象，正确分析扩散规律， 必需用热力学来讨论扩散过程的实质，因为扩散的自发 进行方向也必然是系统吉布斯自由能下降。
驱动扩散的真实动力是自由能
化学位的定义，某溶质i的化学位为
平衡条件是各处的化学位相等。如果存在一化学位 梯度，表明物质迁移 dx 距离，系统的能量将变化了。 好象有一作用力推动它移动一样，设这个力为 F，所作
菲克第二定律 引出
如图所示设为单位面积A上 取dx的单元体，体积为Adx， 在dt的时间内通过截面1流入 的物质量为
而通过截面2流出的物质量 在dt时间内，单元体中的积有量为：
菲克第二定律 微分方程
在dt时间内单元体的浓度变化量 则需要的溶质量为
菲克第二定律 微分方程标准型
在一维状态下非稳态扩散的微分方程，即为 菲克第二定律的数学表达式，又称为扩散第二方
菲克定律的表达式是正确的，用它分析可以把 问题简化。 应用那种模式要具体分析。
第四节 扩散的微观机制
• 原子热运动和扩散系数的关系 • 间隙扩散机制 • 空位扩散机制
原子热运动和扩散系数的关系
图示出晶体中两个相邻的晶面1、 2，面间距为α，截面的大小为单位面 积。假定在1、2面上的溶质原子数(面 密度)分别为 n1和 n2.。每个原子的 跃迁频率Γ是相同的，跃迁方向是随 机的，从晶面1到晶面2(或者相反)的 几率都是P。如果n1 > n2，在单位时间 从晶面1到晶面2的净流量为
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

三维情况，设在不同的方向扩散系数为相 等的常数，则扩散第二方程为：
半无限长棒中的扩散模型
实际意义：低碳钢的渗碳处理，材料的原始含碳量为C0， 热处理时外界条件保证其表面的碳含量始终维持在 CP(碳势)，经过一段时间后，求材料的表面附近碳含量 的情况。
扩散方程的误差函数解
扩散方程的误差函数解
扩散方程的误差函数解
菲克定律的表达式是正确的，用它分析可以把 问题简化。 应用那种模式要具体分析。
第四节
扩散的微观机制
• 原子热运动和扩散系数的关系 • 间隙扩散机制 • 空位扩散机制
原子热运动和扩散系数的关系
图示出晶体中两个相邻的晶面1、 2，面间距为α ，截面的大小为单位面 积。假定在1、2面上的溶质原子数(面 密度)分别为 n1和 n2.。每个原子的 跃迁频率Γ 是相同的，跃迁方向是随 机的，从晶面1到晶面2(或者相反)的 几率都是P。如果n1 > n2，在单位时间 从晶面1到晶面2的净流量为
2．其他任何对粒子运动的力也都可能影响扩散，如电磁场对代
电粒子的扩散。
影响程度：温度－成分－结构－其它
第六节
反应扩散
• 反应扩散的概念 • 反应扩散的实例 • 反应扩散的主要特征
反应扩散的概念
•反应扩散
在扩散中由于成分的变化，通过化学反应而伴随 着新相的形成(或称有相变发生)的扩散过程称为 “反应扩散”，也称为“相变扩散”。
原子热运动和扩散系数的关系
从微观分析表明，扩散系数与扩散方向相邻晶面的面 间距α 、原子的跃迁频率Γ 、跃迁几率P的关系。下面 对不同的机制进行具体分析。
间隙扩散机制
扩散机制：溶质原子存在
晶格的间隙中，如Fe中的C、 N、H等元素，扩散过程是间 隙原子从所处在的间隙，挤 过晶格原子的空隙，到达相 邻的另一个间隙。 溶质原子从一个间隙到另一个间隙的过程，在间隙中的 平衡位置的能量为G1，从晶格原子中挤过去，最高能量 达到G2，存在能垒Δ G=G2-G1，根据统计物理分析可知， 超出平均能量Δ G的原子几率为
扩散方程的误差函数解应用例二
例二：上例中处理条件不变，把碳含量达到0.4％C处 到表面的距离作为渗层深度，推出渗层深度与处理时 间之间的关系，层深达到1.0mm则需多少时间? 解：因为处理条件不变
在温度相同时，扩散系数也相同，因此渗层深度与
处理时间之间的关系：
因为x2/x1= 2，所以t2/t1= 4，这时的时间为
代替 Fick 第一定律的真实法则为：
扩散系数与化学位的关系
如果某组元的浓度提高反而可降低化学位 ( 降低其吉 布斯自由能)，则组元会进行上坡扩散。组元的集中降低 吉布斯自由能的原因和原子之间的键结合能来决定。所 以在分析扩散过程时，应该从化学位来分析，不能单从 浓度梯度来分析。
当然在很多情况下，当
菲克第二定律 引言
菲克第一定律适用于稳态扩散，即在扩散的 过程中各处的浓度不因为扩散过程的发生而随 时间的变化而改变，也就是 dc/dt = 0。当物质分 布浓度随时间变化时，由于不同时间在不同位 置的浓度不相同，浓度是时间和位置的函数 C(x,t)，扩散发生时不同位置的浓度梯度也不一 样，扩散物质的通量也不一样。在某一dt的时间 段，扩散通量是位置和时间的函数j(x,t)。
驱动扩散的真实动力是自由能
化学位的定义，某溶质i的化学位为
平衡条件是各处的化学位相等。如果存在一化学位 梯度，表明物质迁移 dx 距离，系统的能量将变化了。 好象有一作用力推动它移动一样，设这个力为 F，所作 的功为 Fdx 作为化学位的变化 。
称为扩散的驱动力，负号表示推动物质流向 化学位较低处
柯肯达尔(Kirkendall)效应
为了证实在代位扩散过程中存 在晶格数量的变化，Kirkendall在 1947做过如下实验，在Cu－30%Zn 的合金两边焊上纯铜，并在焊缝处 加入一些细的Mo丝作标记，如图所 示。 先测定标记之间的距离，放置在785℃下保温( 为加快扩散速 度 ) 。经过一天 (24hr) 后再测量，发现标记之间的距离缩短了 0.0015cm；经过56天后，标记之间的距离缩短了0.0124cm。
第一节
• • • •
菲克定律
菲克第一定律 菲克第二定律 扩散方程的误差函数解 扩散方程的误差函数解应用举例
菲克第一定律
菲克(A.Fick)在1855年总结出的，数学表达式为：
J为单位时间通过垂直于扩散方向的单位面积的扩 散物质的通量，单位是
为溶质原子的浓度梯度；
负号表示物质总是从浓度高处向浓度低的方向迁移； 比例常数D称为扩散系数，单位为
空位扩散机制（2）
晶体中空位的浓度 ： 扩散系数为 ：
扩散系数与温度之间的 关系 统称为置换扩散的激活能
第五节
影响扩散系数的因素
扩散过程引起的物质流量除了与浓度梯度(和化学位梯 度)有关外，另一个重要的因素就是扩散系数。
•温度
无论是间隙机制，还是空位机制，都遵循热激活规律， 温度提高，能超过能垒的几率越大，同时晶体的平衡空位浓度 也越高，这些都是提高扩散系数的原因。扩散系数与温度T 成 指数关系，在以下因素中这个影响最为明显。
影响扩散系数的因素
•材料的成分
原子之间的结合键力越强，通常对应材料的熔点也越高，激活能 较大，扩散系数较小。材料的成分不同，即组成材料的元素和比 例不同，不同原子之间结合键能不一样，成分的变化也影响不同 类型结合键的相对数量，所以材料的成分变化带来的影响有：
1．结合键能不同，影响到激活能不同而影响扩散系数； 2．结合键能的不同，一种元素的数量 ( 成分比例 ) 可能改变自己 或其他元素的化学位，从而影响扩散的速度，甚至方向。 3．代位扩散 (置换原子 )通量决定于互扩散系数，互扩散系数本 身就是各组元成分的函数。
空位扩散机制
扩散机制：在置换固溶体
中，由于晶格中存在空位， 空位周围的原子(包括溶剂和 溶质原子)由热运动可能进入 空位，即原子利用空位最后 达到迁移，当存在浓度梯度 (化学位梯度)时，溶质原子 就会发生定向的扩散迁移，这是置换原子扩散的主要 方式。 扩散进行有两个要求条件，一是有空位存在，二是空 位周围的原子从原来的平衡位置进入空位也要一定的 激活能。
许多相变的过程是有成分的变化，或由扩散过程 来控制的。了解反应扩散的规律对了解由成分的 变化来控制的相变有十分重要的意义。
在含有浓度梯度的置换固溶体中，埋入一个惰性 标记，由于两组元扩散能力不相等，经过扩散后会引起 标记的移动。这个现象以后就成为柯肯达尔 (Kirkendall)效应。
代位扩散的方程（Darken方程）
描述置换固溶体中的扩散方程由Darken提出。
标记移动的速度
式中的Ｄ1、Ｄ2为组元的自扩散系数（自扩散系
半无限长棒扩散方程的误差函数解
解为：
定义函数： 一维半无限长棒中扩 散方程误差函数解： 高斯误差函数
高：将溶质含量不同的两种材料焊接在一起，因 为浓度不同，在焊接处扩散进行后，溶质浓度随时间的 会发生相应的变化。
无限长棒扩散方程的误差函数解
解为：
利用高斯误差函数
数又称禀性扩散系数
N1、N2为组元的摩尔浓度(原子百分比)
代位扩散的方程（Darken方程）
扩散方程：
第三节
扩散中的热力学
• 菲克定律的局限性 • 驱动扩散的真实动力是自由能 • 扩散系数与化学位的关系
菲克定律的局限性
分析菲克定律，结论是扩散中物质的流动是从浓度 高处流向浓度低处，如果浓度梯度消失(dC/dx=0)，各处 的浓度相等，就不应该再出现物质的传输，在一般的情 况下可以解释许多现象。在固体材料中，还有些现象与 此相矛盾，物质的迁移(扩散)会出现从低浓度向高浓度 处聚集，例如过饱和固溶体的脱溶，从中析出第二相， 此外固体电解质中的带电离子在电场或磁场的作用下， 发生的扩散迁移也不一定是从高浓度处流向低浓度处， 这种反向的扩散称为“上坡扩散”。 为了解释上坡扩散的现象，正确分析扩散规律， 必需用热力学来讨论扩散过程的实质，因为扩散的自发 进行方向也必然是系统吉布斯自由能下降。
第六章
• • • • • • •
固体中的扩散
概述 菲克定律 代位扩散 扩散中的热力学 扩散的微观机制 影响扩散系数的因素 反应扩散
概述
扩散现象：大家已经在气体和液体 中知道，例如在房间的某处打开一瓶香 水，慢慢在其他地方可以闻到香味，在 清水中滴入一滴墨水，在静止的状态下 可以看到他慢慢的扩散。 扩散：由构成物质的微粒(离子、原 子、分子 ) 的热运动而产生的物质迁移 现象称为扩散。扩散的宏观表现是物质 的定向输送。
间隙扩散机制（2）
在面心立方(fcc)中延[100]方向间隙扩散：
其中A为常数，Z相邻的间隙数，ν 振动频 率。
间隙扩散中的几率P
间隙扩散机制（3）
扩散系数为 ：
D0为与晶格结构和扩散方向有关的常数，Δ G为 一个原子的扩散激活能，工程中也常用Q表示 1mol的激活能。
扩散系数与温度之间的 关系
影响扩散系数的因素
•晶体结构
1 ．原子排列越紧密，晶体结构的致密度越高，激活能 较大，扩散系数较小。
2 ．晶体结构的对称性差的材料中，不同方向上扩散系 数的差别也大，常见金属材料的晶体结构较简单，各方 向的差别大多都不明显。
影响扩散系数的因素
•晶体缺陷
1 ．点缺陷： 主要影响扩散的空位
浓度 。
2．线缺陷：线缺陷主要形式是位错，
如果将一块铜和一块锌焊接在一起，这两种材料的 成分不同，铜要向锌中扩散，铜进入锌的晶格存在于 晶格节点，形成的是置换固溶体，锌也要向铜中扩散， 也存在于铜晶格节点，形成的是置换固溶体。这种扩 散方式称为代位扩散。
代位扩散基本现象
这种扩散与间隙扩散不 相同的是，一方面一种原子 进入另一种原子的晶格要另 一种原子扩散运动离开才能 达到节点位置； 另一方面，在晶体中两种原子的大小、性质不 相同，扩散迁移的速度也不一样，一种原子离开 的个数与另一种原子进入的个数不相等时就会形 成新的晶格(或部分晶格消失)，因此代位扩散过 程中会引起某种材料晶格数量的变化。