回归分析-回归分析课件-第七章

章节 第七章 相关与回归分析 课时 10

教

学

目

的 通过本章的学习，了解相关分析的基本概念，了解定性数据的相关分析，掌握定量数据相关分析的主要方法。了解回归分析的基本概念；了解相关分析及回归分析之间的关系；掌握最小二乘估计原理及其性质；了解回归分析的简单应用。熟悉多元线性回归模型矩阵形式;掌握回归系数的估计公式;了解多元线性回归模型总体方差的估计,多元线性回归模型的检验及简单应用。熟悉几种常用的非线性回归模型;掌握这几种常用的非线性回归模型线性化的方法;了解其回归系数的估计方法.

教学

重点

及

突出

方法 1.直线相关关系的测算

2.一元线性回归模型的估计

3.多元线性回归系数的估计公式

4.非线性回归模型线性化的方法

通过实例演示以及习题练习进行突破

教学

难点

及

突破

方法 1.简单相关系数与等级相关系数的计算

2.最小二乘估计原理

3.回归参数的估计

4.多元线性回归模型的检验

5.非线性回归分析

6.非线性回归模型线性化的方法

通过实例演示以及习题练习进行突破

相关

内容

素材

教

学

过

程 教师授课思路、设问及讲解要点

第一节 相关分析的一般问题

一、相关分析的概念

1．相关关系是研究一个变量y和另一个变量x或另一组变量（x1,x2,x3……xn）之间关系密切程度和相关方向的一种统计分析方法。（考试成绩与学习时间，产量与施肥量，浇水量的关系）

2．社会经济现象之间的关系一般可分为两种：函数关系和相关关系。

函数关系是现象之间存在的完全对应的依存关系。

相关关系是现象之间存在的一种不严格的依存关系（两个要点：一，现象之间存在着依存关系；这种依存关系是一种不确定的，不严格的依存关系。）。

3自变量和因变量：作为变化根据的量叫自变量，产生对应变化的量叫因变量。有时两个变量可以互为依据。

二、相关分析的作用

1．确定现象之间有无相关关系。（根据自己的专业知识、理论水平、实践经验、逻辑推断进行判断）

第七章相关分析与回归分析

（一）单项选择题

1、相关分析研究的是( A )

A.变量之间关系的密切程度 B.变量之间的因果关系

C.变量之间严格的相互依存关系 D.变量之间的线性关系

2、相关关系是（ B ）

A、现象间客观存在的依存关系

B、现象间的一种非确定性的数量关系

C、现象间的一种确定性的数量关系

D、现象间存在的函数关系

3、下列情形中称为正相关的是( A )

A.随着一个变量的增加，另一个变量也增加

B.随着一个变量的减少，另一个变量增加

C. 随着一个变量的增加，另一个变量减少

D.两个变量无关

4、当自变量x的值增加，因变量y的值也随之增加，两变量之间存在着（ B ）

A、曲线相关 B、正相关 C、负相关 D、无相关

5、相关系数r的取值范围是( C )

A. B. C. D.

6、当自变量x的值增加，因变量y的值也随之减少，两变量之间存在着（ C ）

A、曲线相关 B、正相关 C、负相关 D、无相关

7、相关系数等于零表明两变量( C )

A.是严格的函数关系 B.不存在相关关系

C. 不存在线性相关关系 D. 存在曲线相关关系

8、相关系数r的取值范围是（ C ）

A、从0到1 B、从-1到0

C、从-1到1 D、无范围限制

9、相关分析对资料的要求是( C )

A.两变量均为随机的 B.两变量均不是随机的

C.自变量是随机的，因变量不是随机的

D.自变量不是随机的，因变量是随机的

10、相关分析与回归分析相比，对变量的性质要求是不同的，回归分析中要求（ A ）

A、自变量是给定的，因变量是随机的 B、两个变量都是随机的

第七章 相关分析与回归分析

1.从某一行业中随机抽取12个企业，各企业产量与生产费用的数据如下表：

企业编号 产量（千件） 生产费用（千元） 企业编号 产量（千件） 生产费用（千元）

1

2

3

4

5

6 40

42

49

49

50

55 130

140

155

150

154

160 7

8

9

10

11

12 84

100

110

114

125

130 165

170

167

183

175

189

试根据上表材料：

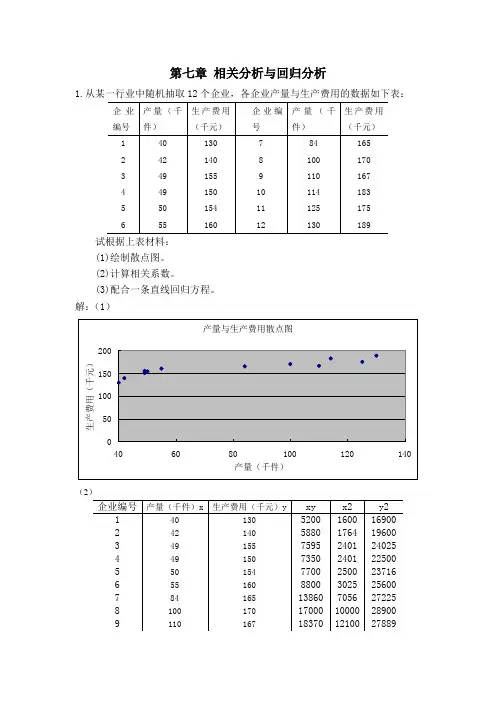
(1)绘制散点图。

(2)计算相关系数。

(3)配合一条直线回归方程。

解：（1）

产量与生产费用散点图050100150200406080100120140产量（千件）生产费用（千元）

（2）

企业编号 产量（千件）x 生产费用（千元）y xy x2 y2

1 40 130 5200 1600 16900

2 42 140 5880 1764 19600

3 49 155 7595 2401 24025

4 49 150 7350 2401 22500

5 50 154 7700 2500 23716

6 55 160 8800 3025 25600

7 84 165 13860 7056 27225

8 100 170 17000 10000 28900

9 110 167 18370 12100 27889

10 114 183 20862 12996

33489

11 125 175 21875 15625

30625

12 130 189 24570 16900 35721

合计 948 1938 159062 88368 316190

9072.084.78838715201938316190129488836812193894815906212)()())((222222yynxxnyxxynr

（3）设回归方程为ˆyabx

第七章 相关与回归分析

一、填空题：

1. 当一个变量取一定数值时，另一个变量有确定值与之相对应，这种关系称为 。

2. 相关系数的数值范围，是在-1和+1之间，即-1≤r≤+1。计算结果r>0为 ，r<0为 。

3. 当一个变量取一定数值时，与之相对应的另一变量的数值虽然不确定，但它仍按某种规律在一定的范围内变化，这种关系称为 。

4．相关关系按相关的方向分为 和 。

5. 相关关系按相关的程度分为 、不完全相关和 。

6. 回归分析是对具有相关关系的现象，根据其关系形态，选择一个合适的数学模型，用来近似地表示变量间 关系的一种统计分析方法。

7.我们把两个变量之间的线性相关关系称为 。

二、单项选择题：

1. 如果一个变量的数量变化，由另一个变量的数量变化所唯一确定，这时两个变量间的关系称为（ ）。

A、单相关 B、复相关 C、不完全相关 D、完全相关

2. 当变量x的数值增大时，变量y的数值也明显增大，相关点的分布集中呈直线状态，则表明这两个变量间是（ ）。

A、强正相关 B、弱正相关 C、强负相关 D、弱负相关

3. 判定现象之间相关关系密切程度的主要方法是（ ）。

A、绘制相关图 B、编制相关表

C、进行定性分析 D、计算相关系数

4．根据你的判断，下面的相关系数取值哪一个是错误的（ ）

A、–0.86 B、0.78 C、1.25 D、0

5．下面的关系中不是相关关系的是（ ）

A、身高与体重之间的关系 B、工资水平与工龄之间的关系

C、农作物的单位面积产量与降雨量之间的关系

D、圆的面积与半径之间的关系

6. 如果两个变量之间存在负相关关系，下列回归方程中哪个肯定有误（ ） A、y=25–0.75x B、y= –120+ 0.86x

第七章 相关分析与回归分析

例1、有10个同类企业的固定资产和总产值资料如下：

企业编号 固定资产（万元） 总产值（万元）

1

2

3

4

5

6

7

8

9

10 318

910

200

409

514

502

314

1210

1022

1225 524

1019

638

815

913

928

605

1516

1219

1624

合计 6525 9801

根据以上资料计算(1)协方差和相关系数;(2)建立以总产值为因变量的一元线性回归方程；(3)当固定资产改变200万元时，总产值平均改变多少(4)当固定资产为1300万元时，总产值为多少

解：计算表如下：

固定资产x

总产值y

2x 2y xy

318

910

200

409

514

502

314

1210

1022

1225 524

1019

638

815

913

928

605

1516

1219

1624 101124

828100

40000

167281

172225

252004

98596

1464100

1044484

1500625 274576

1038361

407044

664225

833569

861184

366025

2298256

1485961

1637376 166632

927290

127600

333335

387895

465856

189970

1834360

1245818

1989400

6525 9801 5668539 7659156

（1）协方差——用以说明两指标之间的相关方向。

22))((nyxxynnyyxxxy035.12640010098016525765915610

计算得到的协方差为正数，说明固定资产和总产值之间存在正相关关系。

（2）相关系数用以说明两指标之间的相关方向和相关的密切程度。

])(][)([2222yynxxnyxxynr95.0)98011086657710()6525566853910(9801652576591561022

第七章 岭回归

1. 岭回归估计是在什么情况下提出的？

答：当解释变量间出现严重的多重共线性时，用普通最小二乘法估计模型参数，往往 参数估计方差太大，使普通最小二乘法的效果变得很不理想，为了解决这一问题，统 计学家从模型和数据的角度考虑，采用回归诊断和自变量选择来克服多重共线性的影 响，这时，岭回归作为一种新的回归方法被提出来了。

2. 岭回归估计的定义及其统计思想是什么？ 答：一种改进最小二乘估计的方法叫做岭估计。当自变量间存在多重共线性，∣ X'X ∣≈

0 时，我们设想给 X'X 加上一个正常数矩阵 kI（k>0）, 那么 X'X+kI 接近奇异的程度小得 多，考虑到变量的量纲问题，先对数据作标准化，为了计算方便，标准化后的设计阵 仍然用 X表示，定义为 ? X 'X I X 'y ，称为 的岭回归估计，其中 k称 为岭参数。

3. 选择岭参数 k 有哪几种主要方法？ 答：选择岭参数的几种常用方法有 1. 岭迹法， 2. 方差扩大因子法， 3.由残差平方和来 确定 k 值。

4. 用岭回归方法选择自变量应遵从哪些基本原则？ 答：用岭回归方法来选择变量应遵从的原则有：

（1）在岭回归的计算中，我们假定设计矩阵 X 已经中心化和标准化了，这样可以直接

比较标准化岭回归系数的大小，我们可以剔除掉标准化岭回归系数比较稳定且绝对值 很小的自变量。

（ 2） 当 k 值较小时标准化岭回归系数的绝对值并不是很小，但是不稳定，随着

k 的增加迅速趋于零。像这样的岭回归系数不稳定 , 震动趋于零的自变量，x5

K 我们也可以予以删除。

3) 去掉标准化岭回归系数很不稳定的自变量，如果有若干个岭回归系数不稳 定，究竟去掉几个，去掉哪几个，这并无一般原则可循，这需根据去掉某 个变量后重新进行岭回归分析的效果来确定。

5. 对第 5 章习题 9 的数据，逐步回归的结果只保留了 3 个自变量 x1 ，x2 ，x5 ，用 y

《回归分析课程教案》课件

第一章：引言

1.1 课程目标

让学生了解回归分析的基本概念和应用领域。

让学生掌握回归分析的基本原理和方法。

培养学生应用回归分析解决实际问题的能力。

1.2 教学内容

回归分析的定义和分类

回归分析的应用领域

回归分析的基本原理和方法

1.3 教学方法

讲授法：讲解回归分析的基本概念和原理。

案例分析法：分析实际案例，让学生了解回归分析的应用。

1.4 教学资源

课件：介绍回归分析的基本概念和原理。

案例：提供实际案例，让学生进行分析。

1.5 教学评估

课堂讨论：学生参与课堂讨论，回答问题。

第二章：一元线性回归分析

2.1 教学目标

让学生了解一元线性回归分析的基本概念和原理。

让学生掌握一元线性回归模型的建立和估计方法。 培养学生应用一元线性回归分析解决实际问题的能力。

2.2 教学内容

一元线性回归分析的定义和特点

一元线性回归模型的建立和估计方法

一元线性回归模型的检验和预测

2.3 教学方法

讲授法：讲解一元线性回归分析的基本概念和原理。

数据分析法：分析实际数据，让学生了解一元线性回归模型的建立和估计方法。

2.4 教学资源

课件：介绍一元线性回归分析的基本概念和原理。

数据分析软件：用于一元线性回归模型的建立和估计。

2.5 教学评估

课堂练习：学生进行课堂练习，应用一元线性回归分析解决实际问题。

第三章：多元线性回归分析

3.1 教学目标

让学生了解多元线性回归分析的基本概念和原理。

让学生掌握多元线性回归模型的建立和估计方法。

培养学生应用多元线性回归分析解决实际问题的能力。

3.2 教学内容

多元线性回归分析的定义和特点

多元线性回归模型的建立和估计方法

多元线性回归模型的检验和预测 3.3 教学方法

讲授法：讲解多元线性回归分析的基本概念和原理。

数据分析法：分析实际数据，让学生了解多元线性回归模型的建立和估计方法。

3.4 教学资源

课件：介绍多元线性回归分析的基本概念和原理。

第七章相关分析与回归分析

1.从某一行业中随机抽取12个企业，各企业产量与生产费用的数据如下表:

企业

编号 产量（千

件） 生产费用

（千元） 企业编

号 产量（千

件） 生产费用

（千元）

1 40 130 7 84 165

2 42 140 8 100 170

3 49 155 9 110 167

4 49 150 10 114 183

5 50 154 11 125 175

6 55 160 12 130 189

试根据上表材料：

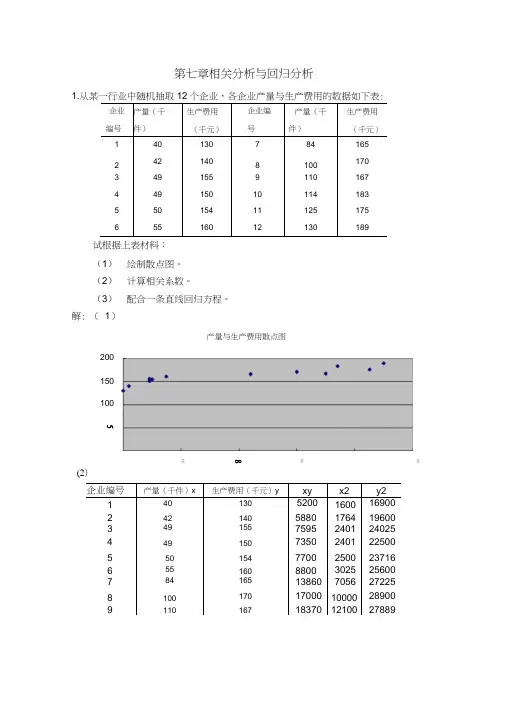
（1） 绘制散点图。

（2） 计算相关系数。

（3） 配合一条直线回归方程。

解: （ 1）

(2)

企业编号 产量（千件）x 生产费用（千元）y xy x2 y2

1 40 130 5200 1600 16900

2 42 140 5880 1764 19600

3 49 155 7595 2401 24025

4 49 150 7350 2401 22500

5 50 154 7700 2500 23716

6 55 160 8800 3025 25600

7 84 165 13860 7056 27225

8 100 170 17000 10000 28900

9 110 167 18370 12100 27889 60 800 40 200

150

100 产量与生产费用散点图

510

11

12 114

125

130 183

175

189 20862

21875

24570 12996

15625

16900 33489

30625

35721

合计 948 1938 159062| 88368 316190

12x159062 -948x1938

.12 88368 -9482、12 316190 -19382

(3)设回归方程为? = a bx

b』甞7

nZ x 一(送 x) 12 159062-948 1938 12

y -bx =1^ -0.4423 948 =126.5583

====Word行业资料分享--可编辑版本--双击可删====

源-于-网-络-收-集 第七章 相关与回归分析

一、思考题

1、回归分析中总离差平方和可以分解成哪两部分？每部分的意义是什么？

2、简述相关分析与回归分析的异同。

3、OLS方法的数学依据是什么？

4、回归方程中，回归系数的意义是什么？

5、什么是虚假相关？

二、计算题

1．某企业某种产品与单位成本的资料如下：

月 份 产量（千件） 单位成本 （元／件）

1

2

3

4

5

6 2

3

4

3

4

5 73

72

71

73

69

68

要求计算：

（1）产量与单位成本的相关系数。

（2）确定单位成本（y） 对产量（x）的直线回归方程。

（3）产量为6千件时，单位产品成本为多少？

2. 从某市抽查十家百货商店得到销售额和利润率的资料如下：

商店编号 每人月平均销售额（千元）x 利 润 率 （％）ｙ

1

2

3

4

5

6

7

8

9

10 6

5

8

1

4

7

6

3

3

7

1465,294,9.654,8.110,5022yxxyyx

要求：

（1）计算每人月平均销售额与利润率的相关系数。

（2）推断利润率对每人月平均销售额的回归直线方程。

（3）计算估计标准误差。

（4）若某商店每人月平均销售额为2千元，试估计其利润率的区间(α=5%)。

1

第七章 非参数回归模型与半参数回归模型

第一节 非参数回归与权函数法

一、非参数回归概念

前面介绍的回归模型，无论是线性回归还是非线性回归，其回归函数形式都是已知的，只是其中参数待定，所以可称为参数回归。参数回归的最大优点是回归结果可以外延，但其缺点也不可忽视，就是回归形式一旦固定，就比较呆板，往往拟合效果较差。另一类回归，非参数回归，则与参数回归正好相反。它的回归函数形式是不确定的，其结果外延困难，但拟合效果却比较好。

设Y是一维观测随机向量，X是m维随机自变量。在第四章我们曾引进过条件期望作回归函数，即称

g (X) = E (Y|X) （7.1.1）

为Y对X的回归函数。我们证明了这样的回归函数可使误差平方和最小，即

22)]([min)]|([XLYEXYEYEL （7.1.2）

这里L是关于X的一切函数类。当然，如果限定L是线性函数类，那么g (X)就是线性回归函数了。

细心的读者会在这里立即提出一个问题。既然对拟合函数类L(X)没有任何限制，那么可以使误差平方和等于0。实际上，你只要作一条折线(曲面)通过所有观测点(Yi，Xi)就可以了是的，对拟合函数类不作任何限制是完全没有意义的。正象世界上没有绝对的自由一样，我们实际上从来就没有说放弃对L(X)的一切限制。在下面要研究的具体非参数回归方法，不管是核函数法，最近邻法，样条法，小波法，实际都有参数选择问题(比如窗宽选择，平滑参数选择)。

所以我们知道，参数回归与非参数回归的区分是相对的。用一个多项式去拟合(Yi，Xi)，属于参数回归；用多个低次多项式去分段拟合(Yi，Xi)，叫样条回归，属于非参数回归。

二、权函数方法

非参数回归的基本方法有核函数法，最近邻函数法，样条函数法，小波函数法。这些方法尽管起源不一样，数学形式相距甚远，但都可以视为关于Yi的线性组合的某种权函数。也就是说，回归函数g (X)的估计gn(X)总可以表为下述形式：

§7—5 非线性回归分析（简介）

本节借用一个例子，简单介绍用Matlab软件分析和计算非线性回归问题。

非线性回归模型为

.),0(~,),...,,(221NxxxfYm

1．问题

三个自变量：氢x1、n—戊烷x2、异戊烷x3

因变量： 某物质的反应速度Y

根据数据13,...,2,1),,,,(321iyxxxiiii，建立非线性回归模型，并进行统计分析。

--------------------------------------------------------------------- i 1 2 3 …… 12 13

1ix 470 285 470 …… 285 285

2ix 300 80 300 …… 300 190

3ix 10 10 120 …… 10 120

iy 8.55 3.79 4.82 …… 11.32 3.13

---------------------------------------------------------------------

2．模型的假设和建立

假设该问题需要建立非线性回归模型。有两种情况：

（1）各因素（自变量）与指标（因变量）之间的信息“一无所知”，假设模型中的函数f是多项式形式，进一步假设为二次多项式模型（也称为：二次曲面模型），模型为

.),0(~,22333222221113223311321123322110Nxbxbxbxxbxxbxxbxbxbxbby

（2）假设由实际背景分析得经验公式：

.1/3423125321xxxxxy

下面分别对这两种模型进行参数辩识和统计分析。

3．模型的求解和结果分析

第七章虚拟变量回归

第七章 虚拟变量回归

第⼀节 虚拟变量的性质

在实际建模过程中，被解释变量不但受定量变量影响，同时还受定性变量影响。例如需要考虑性别、民族、不同历史时期、季节差异、政府的更迭（⼯党-保守党）、经济体制的改⾰、固定汇率变为浮动汇率、从战时经济转为和平时期经济等。这些因素也应该包括在模型中。

⼀、基本概念

由于定性变量通常表⽰的是某种特征的有和⽆，所以量化⽅法可采⽤取值为1或0。这种变量称作虚拟变量（dummy variable）。虚拟变量也称：哑元变量、定性变量等等。通常⽤字母D 或DUM 加以表⽰（英⽂中虚拟或者哑元Dummy 的缩写）。

⽤1表⽰具有某⼀“品质”或属性，⽤0表⽰不具有该“品质”或属性。 虚拟变量使得我们可以将那些⽆法定量化的变量引⼊回归模型中。

虚拟变量应⽤于模型中，对其回归系数的估计与检验⽅法和定量变量相同。 虚拟变量表⽰两分性质，即“是”或“否”，“男”或“⼥”等。 下⾯给出⼏个可以引⼊虚拟变量的例⼦。

例1：你在研究学历和收⼊之间的关系，在你的样本中，既有⼥性⼜有男性，你打算研究在此关系中，性别是否会导致差别。

例2：你在研究某省家庭收⼊和⽀出的关系，采集的样本中既包括农村家庭，⼜包括城镇家庭，你打算研究⼆者的差别。

例3：你在研究通货膨胀的决定因素，在你的观测期中，有些年份政府实⾏了⼀项收⼊政策。你想检验该政策是否对通货膨胀产⽣影响。

上述各例都可以⽤两种⽅法来解决，⼀种解决⽅法是分别进⾏两类情况的回归，然后看参数是否不同。另⼀种⽅法是⽤全部观测值作单⼀回归，将定性因素的影响⽤虚拟变量引⼊模型。

⼆、虚拟变量设置规则

虚拟变量的设置规则涉及三个⽅⾯: 1.“0”和“1”选取原则

虚拟变量取“1”或“0”的原则，应从分析问题的⽬的出发予以界定。

从理论上讲，虚拟变量取“0”值通常代表⽐较的基础类型；⽽虚拟变量取“1”值通常代表被⽐较的类型。“0”代表基期（⽐较的基础，参照物）；“1”代表报告期（被⽐较的效应）。

精品文档

精品文档

第七章 非参数回归模型与半参数回归模型

第一节 非参数回归与权函数法

一、非参数回归概念

前面介绍的回归模型，无论是线性回归还是非线性回归，其回归函数形式都是已知的，只是其中参数待定，所以可称为参数回归。参数回归的最大优点是回归结果可以外延，但其缺点也不可忽视，就是回归形式一旦固定，就比较呆板，往往拟合效果较差。另一类回归，非参数回归，则与参数回归正好相反。它的回归函数形式是不确定的，其结果外延困难，但拟合效果却比较好。

设Y是一维观测随机向量，X是m维随机自变量。在第四章我们曾引进过条件期望作回归函数，即称

g (X) = E (Y|X) （7.1.1）

为Y对X的回归函数。我们证明了这样的回归函数可使误差平方和最小，即

22)]([min)]|([XLYEXYEYEL （7.1.2）

这里L是关于X的一切函数类。当然，如果限定L是线性函数类，那么g (X)就是线性回归函数了。

细心的读者会在这里立即提出一个问题。既然对拟合函数类L(X)没有任何限制，那么可以使误差平方和等于0。实际上，你只要作一条折线(曲面)通过所有观测点(Yi，Xi)就可以了是的，对拟合函数类不作任何限制是完全没有意义的。正象世界上没有绝对的自由一样，我们实际上从来就没有说放弃对L(X)的一切限制。在下面要研究的具体非参数回归方法，不管是核函数法，最近邻法，样条法，小波法，实际都有参数选择问题(比如窗宽选择，平滑参数选择)。

所以我们知道，参数回归与非参数回归的区分是相对的。用一个多项式去拟合(Yi，Xi)，属于参数回归；用多个低次多项式去分段拟合(Yi，Xi)，叫样条回归，属于非参数回归。

二、权函数方法

非参数回归的基本方法有核函数法，最近邻函数法，样条函数法，小波函数法。这些方法尽管起源不一样，数学形式相距甚远，但都可以视为关于Yi的线性组合的某种权函数。也就是说，回归函数g (X)的估计gn(X)总可以表为下述形式： 精品文档

应⽤回归分析-第7章课后习题参考答案

第7章 岭回归

思考与练习参考答案7.1 岭回归估计是在什么情况下提出的？

答：当⾃变量间存在复共线性时，｜X’X ｜≈0，回归系数估计的⽅差就很⼤， 估计值就很不稳定，为解决多重共线性，并使回归得到合理的结果，70年代提出了岭回归(Ridge Regression,简记为RR)。7.2岭回归的定义及统计思想是什么？

答：岭回归法就是以引⼊偏误为代价减⼩参数估计量的⽅差的⼀种回归⽅法，其

统计思想是对于（X ’X ）-1为奇异时，给X’X 加上⼀个正常数矩阵D, 那么X’X+D

接近奇异的程度就会⽐X ′X 接近奇异的程度⼩得多，从⽽完成回归。但是这样的回归必定丢失了信息，不满⾜blue 。但这样的代价有时是值得的，因为这样可以获得与专业知识相⼀致的结果。7.3 选择岭参数k 有哪⼏种⽅法？

答：最优k 是依赖于未知参数β和2σ的，⼏种常见的选择⽅法是：○

1岭迹法：选择0k 的点能使各岭估计基本稳定，岭估计符号合理，回归系数没有不合乎经济意义的绝对值，且残差平⽅和增⼤不太多； ○

2⽅差扩⼤因⼦法：11()()()c k X X kI X X X X kI --'''=++，其对⾓线元()jj c k 是岭估计的⽅差扩⼤因⼦。要让()10jj c k ≤；

○

3残差平⽅和：满⾜()SSE k cSSE

7.4 ⽤岭回归⽅法选择⾃变量应遵循哪些基本原则？

答：岭回归选择变量通常的原则是：1. 在岭回归的计算中，我们通常假定涉及矩阵已经中⼼化和标准化了，这样可以直接⽐较标准化岭回归系数的⼤⼩。我们可以剔除掉标准化岭回归系数⽐较稳定且绝对值很⼩的⾃变量；

2. 当k 值较⼩时，标准化岭回归系数的绝对值并不很⼩，但是不稳定，随

着k的增加迅速趋近于零。像这样岭回归系数不稳定、震动趋于零的⾃

变量，我们也可以予以剔除；3.去掉标准化岭回归系数很不稳定的⾃变量。如果有若⼲个岭回归系数不

稳定，究竟去掉⼏个，去掉那⼏个，要根据去掉某个变量后重新进⾏岭

----------------------------

精选资料 第七章 相关与回归分析

（一）填空题

1、相关关系按其相关的程度不同，可分为 、 和 。

2、相关系数的正负表示相关关系的方向，r为正值，两变量是 ；r为负数，两变量是 。

3、r=0，说明两个变量之间 ；r=+1，说明两个变量之间 ；r=-1说明两个变量之间 。

4、一元线性回归方程bxayˆ 中的参数a代表 ，数学上称为 ；b代表 ，数学上称为 。

5、 分析要根据研究的目的确定哪一个为自变量，哪一个为因变量，在这一点与

分析时不同。

6、相关关系按方向不同，可分为 和 。

7、完全线性相关的相关系数r值等于 。

8、计算回归方程要注意资料中因变量是 的，自变量是 的。

9、回归方程只能用于由 推算 。

（二）单项选择题（在每小题备选答案中，选出一个正确答案）

1、相关分析研究的是( )

A. 变量之间关系的密切程度 B. 变量之间的因果关系

C. 变量之间严格的相互依存关系 D. 变量之间的线性关系

2、相关关系是（ ）

A、现象间客观存在的依存关系 B、现象间的一种非确定性的数量关系

C、现象间的一种确定性的数量关系 D、现象间存在的函数关系

3、下列情形中称为正相关的是( )

A. 随着一个变量的增加，另一个变量也增加

B. 随着一个变量的减少，另一个变量增加

C. 随着一个变量的增加，另一个变量减少

第七章 岭回归

1.岭回归估计是在什么情况下提出的？

答：当解释变量间出现严重的多重共线性时，用普通最小二乘法估计模型参数，往往参数估计方差太大，使普通最小二乘法的效果变得很不理想，为了解决这一问题，统计学家从模型和数据的角度考虑，采用回归诊断和自变量选择来克服多重共线性的影响，这时，岭回归作为一种新的回归方法被提出来了。

2.岭回归估计的定义及其统计思想是什么？

答：一种改进最小二乘估计的方法叫做岭估计。当自变量间存在多重共线性，∣X'X∣≈0时，我们设想给X'X加上一个正常数矩阵kI(k>0),那么X'X+kI 接近奇异的程度小得多，考虑到变量的量纲问题，先对数据作标准化，为了计算方便，标准化后的设计阵仍然用X表示，定义为1ˆ''XXIXy ，称为的岭回归估计，其中k称为岭参数。

3.选择岭参数k有哪几种主要方法？

答：选择岭参数的几种常用方法有1.岭迹法，2.方差扩大因子法，3.由残差平方和来确定k值。

4.用岭回归方法选择自变量应遵从哪些基本原则？

答：用岭回归方法来选择变量应遵从的原则有：

（1）在岭回归的计算中，我们假定设计矩阵X已经中心化和标准化了，这样可以直接比较标准化岭回归系数的大小，我们可以剔除掉标准化岭回归系数比较稳定且绝对值很小的自变量。

（2）当k值较小时标准化岭回归系数的绝对值并不是很小，但是不稳定，随着k的增加迅速趋于零。像这样的岭回归系数不稳定,震动趋于零的自变量，我们也可以予以删除。

（3）去掉标准化岭回归系数很不稳定的自变量，如果有若干个岭回归系数不稳定，究竟去掉几个，去掉哪几个，这并无一般原则可循，这需根据去掉某个变量后重新进行岭回归分析的效果来确定。

5.对第5章习题9的数据，逐步回归的结果只保留了3个自变量x1，x2，x5，用y对这3个自变量做岭回归分析。

答： 依题意，对逐步回归法所保留的三个自变量做岭回归分析。

程序为：

include'C:\Program Files\SPSSEVAL\Ridge regression.sps'.