小学奥数之面积1

六年级奥数练习题（圆和组合图形）1、算出圆内正方形的面积为多少2.右图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是多少平方厘米.3.一个扇形圆心角120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是多少4.右图中三角形是等腰直角三角形,阴影部分的面积是(平方厘米).5.三角形ABC是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米. AB长40厘米, BC长厘米.6.如右图,阴影部分的面积为2平方厘米,等腰直角三角形的面积为 .7.扇形的面积是平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是度.8.图中扇形的半径OA=OB=6厘米.45=∠AOB, AC垂直OB于C,那么图中阴影部分的面积是平方厘米.)14.3(=π9.右图中正方形周长是20厘米.图形的总面积是平方厘米.10.在右图中(单位:厘米),两个阴影部分面积的和是平方厘米.12.如图,半圆S1的面积是平方厘米,圆S2的面积是平方厘米.那么长方形(阴影部分的面积)是多少平方厘米13.如图,已知圆心是O,半径r=9厘米,1521=∠=∠,那么阴影部分的面积是多少平方厘米)14.3(≈π13、如图,求阴影部分的面积 .14、大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大平方厘米.212112215、在一个半径是厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是 平方厘米.(π取,结果精确到1平方厘米)16、如图所求,圆的周长是厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是 厘米.)14.3(=π17.下图中正方形部分是一个水池，其余部分是草坪，已知正方形的面积是300平方米，草坪的面积是多少平方米17、已知:ABCD 是正方形, ED =DA =AF =2厘米,阴影部分的面积是 .18、如图:阴影部分的面积是多少四分之一大圆的半径为r .(计算时圆周率取722)19、已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.求阴影部分的面积.20.如图{图在下面}两个连在一起的轮轴，已知小轮的半径是3分米，当这个小轮转3圈时，大轮正好转一圈，只蜜蜂分别沿着阴影部分的边缘飞1次，那只蜜蜂飞过的路线最长（3个正方形的边长都为4m ）23.将半径分别是3厘米和2厘米的两个半圆如图放置,求阴影部分的周长24.求阴影部分的面积25.一个圆环外直径是内直径的二分之三倍，圆环面积150cm ，求外圆的面积26.一个长方形的面积是20平方厘米，如果在这个长方DCB AGF形里画一个最大的半圆形，这个半圆形是多少平方厘米因为这个半圆的直径是长方形的长，半径是宽，说明长方形的长是宽的2倍。

平面图形的面积(一)——图形的等分例1 有一个三角形花坛，要把它平均分成两个相等的三角形，可以怎样分？练习将任一三角形分成面积相等的六个三角形，应怎么分？例2 三角形ABC中，DC=2BD，CE=3AE，阴影部分的面积是20平方厘米，求三角形ABC的面积。

练习已知AE=3AB,BD=2BC，三角形ABC的面积是6，求三角形BDE的面积。

练习如图所示，找出梯形ABCD中有几组面积相等的三角形。

例3 已知三角形ABC的面积是12平方厘米，并且BE=2EC，F是CD的中点。

求阴影部分面积。

练习AC是CD的3倍，E是BC的中点，三角形CDE的面积为2平方厘米。

求三角形ABC的面积。

练习如图，正方形ABCD的边长是4厘米，CG＝3厘米，长方形EFGD的长是5厘米，DE长几厘米？例4 在一块长方形的地里有一口长方形的水井，试画一条线把除井处的这块地平分成两块。

练习下图为5个面积为1的正方形拼成的。

试用一直线将此图形划分为面积相等的两块。

例5 将下图分成4个形状、大小完全相同的图形，且每个部分中都有一个小黑圈。

练习将下图分成4个形状相同、面积相等的小块。

作业1、三角形的面积公式：________________。

同底等高的三角形面积___________。

平行线间的距离处处___________。

2、甲、乙两个三角形的高相等，若甲的底是乙的底的5倍，则甲的面积就是乙面积的_____倍。

3、甲、乙两个三角形的底相等，若甲的高是乙的高的4倍，则甲的面积就是乙面积的______倍。

4、把一个等边三角形分成面积相等的三个三角形，有________种不同的方法。

5、如图1，该图是一个直角梯形，面积相等的三角形有_________组，请分别写出________________ __________________________________。

6、如图2，AD与BC平行，AD=5，BC=10，三角形ADC面积为10，则三角形ABC的面积是_______________。

第27讲表面积与体积（一）一、知识要点小学阶段所学的立体图形主要有四种长方体、正方体、圆柱体和圆锥体。

从平面图形到立体图形是认识上的一个飞跃，需要有更高水平的空间想象能力。

因此，要牢固掌握这些几何图形的特征和有关的计算方法，能将公式作适当的变形，养成“数、形”结合的好习惯，解题时要认真细致观察，合理大胆想象，正确灵活地计算。

在解答立体图形的表面积问题时，要注意以下几点：（1）充分利用正方体六个面的面积都相等，每个面都是正方形的特点。

（2）把一个立体图形切成两部分，新增加的表面积等于切面面积的两倍。

反之，把两个立体图形粘合到一起，减少的表面积等于粘合面积的两倍。

（3）若把几个长方体拼成一个表面积最大的长方体，应把它们最小的面拼合起来。

若把几个长方体拼成一个表面积最小的长方体，应把它们最大的面拼合起来。

二、精讲精练【例题1】从一个棱长10厘米的正方体木块上挖去一个长10厘米、宽2厘米、高2厘米的小长方体，剩下部分的表面积是多少？这是一道开放题，方法有多种：①按图27-1所示，沿着一条棱挖，剩下部分的表面积为592平方厘米。

图27--1②按图27-2所示，在某个面挖，剩下部分的表面积为632平方厘米。

图27--2③按图27-3所示，挖通某两个对面，剩下部分的表面积为672平方厘米。

图27--3练习1：1、从一个长10厘米、宽6厘米、高5厘米的长方体木块上挖去一个棱长2厘米的小正方体，剩下部分的表面积是多少？2、把一个长为12分米，宽为6分米，高为9分米的长方体木块锯成两个想同的小厂房体木块，这两个小长方体的表面积之和，比原来长方体的表面积增加了多少平方分米？3、在一个棱长是4厘米的立方体上挖一个棱长是1厘米的小正方体后，表面积会发生怎样的变化？图27—4【例题2】把19个棱长为3厘米的正方体重叠起来，如图27-4所示，拼成一个立体图形，求这个立体图形的表面积。

要求这个复杂形体的表面积，必须从整体入手，从上、左、前三个方向观察，每个方向上的小正方体各面就组合成了如下图形（如图27-5所示）。

五年级下册数学奥数知识讲解第一课《不规则图形面积的计算1》奥数练习题和答案五年级奥数下册：第一讲不规则图形面积的计算（一）
五年级奥数下册：第一讲不规则图形面积的计算习题
五年级奥数下册：第一讲不规则图形面积的计算习题解答
学生每日提醒
励志名言：
1、播下一个信念，收获一种行动；播下一个行动，收获一种习惯；播下一个习惯，收获一种性格；播下一个性格，收获一种命运。

2、人生的绚丽多彩和卑微只因是平台不同，而决定平台的恰恰是自己平时的行为和习惯。

3、如果把学习看作投资的话，它应该是一本万利的，应该是世界回报最多的投资。

4、伟人所达到并保持着的高处，并不是一飞就到的，而是他们在同伴们都睡着的时候，一步步艰辛地向上攀爬的。

5、学习只是一种状态和一种习惯而已。

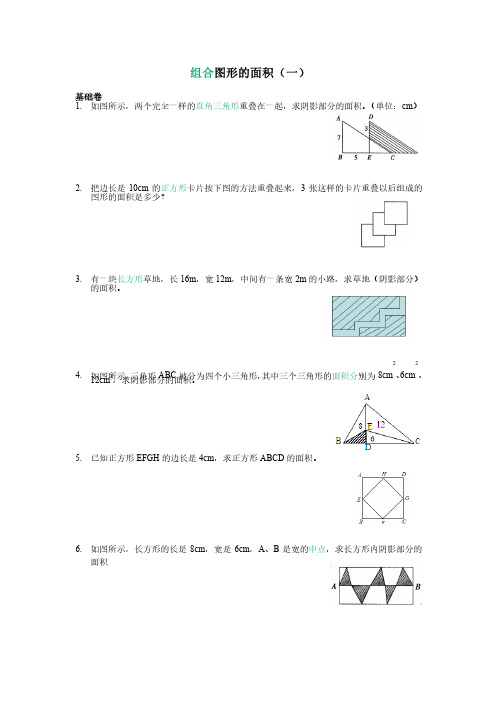
组合图形的面积（一）基础卷 1. 如图所示，两个完全一样的如图所示，两个完全一样的直角三角形直角三角形重叠在一起，求阴影部分的面积。

（单位：cm ）2. 把边长是10cm 的正方形卡片按下图的方法重叠起来，3张这样的卡片重叠以后组成的图形的面积是多少？图形的面积是多少？3. 有一块有一块长方形长方形草地，长16m ，宽12m ，中间有一条宽2m 的小路，求草地（阴影部分）的面积。

的面积。

4. 如图所示，三角形ABC 被分为四个小三角形，其中三个三角形的其中三个三角形的面积分面积分别为8cm 2、6cm 2、12cm 2，求阴影部分的面积。

，求阴影部分的面积。

5. 已知正方形EFGH 的边长是4cm ，求正方形ABCD 的面积。

的面积。

6. 如图所示，长方形的长是8cm ，宽是6cm ，A 、B 是宽的是宽的中点中点，求长方形内阴影部分的面积面积提高卷1. 在腰长为10cm ，面积为34cm 2的等腰三角形的底边上任取一点，设这个点到两腰的垂线分别长acm 、bcm ，那么a+b 的长度是多少厘米？的长度是多少厘米？2. 如图所示，ABCD 是正方形，三角形DEF 的面积比三角形ABF 的面积大6cm 2，CD 长４ｃｍ，求DE 的的长度。

的的长度。

3. 如图所示，大正方形和小正方形的边长分别是４cm ，3cm ，求，求阴影阴影部分的面积。

部分的面积。

4. 长方形ABCD 的周长是16cm ，在它的每条边上各画一个以该边为边长的正方形，已知这四个正方形的面积和是68cm 2，求长方形ABCD 的面积。

的面积。

5. 如图所示，在边长为12cm 的正方形ABCD 中，E 、F 是BC 边上的三边上的三等分等分点，M 、N 是对角线BD 上的三等分点，邱三角形EMN 的面积。

的面积。

6. 梯形ABCF 的下底BC 是12cm ，高AB 是18cm ，CE=2DE ，求DF 。

第27讲表面积与体积（一）一、知识要点小学阶段所学的立体图形主要有四种长方体、正方体、圆柱体和圆锥体。

从平面图形到立体图形是认识上的一个飞跃，需要有更高水平的空间想象能力。

因此，要牢固掌握这些几何图形的特征和有关的计算方法，能将公式作适当的变形，养成“数、形”结合的好习惯，解题时要认真细致观察，合理大胆想象，正确灵活地计算。

在解答立体图形的表面积问题时，要注意以下几点：（1）充分利用正方体六个面的面积都相等，每个面都是正方形的特点。

（2）把一个立体图形切成两部分，新增加的表面积等于切面面积的两倍。

反之，把两个立体图形粘合到一起，减少的表面积等于粘合面积的两倍。

（3）若把几个长方体拼成一个表面积最大的长方体，应把它们最小的面拼合起来。

若把几个长方体拼成一个表面积最小的长方体，应把它们最大的面拼合起来。

二、精讲精练【例题1】从一个棱长10厘米的正方体木块上挖去一个长10厘米、宽2厘米、高2厘米的小长方体，剩下部分的表面积是多少？这是一道开放题，方法有多种：①按图27-1所示，沿着一条棱挖，剩下部分的表面积为592平方厘米。

图27--1②按图27-2所示，在某个面挖，剩下部分的表面积为632平方厘米。

图27--2③按图27-3所示，挖通某两个对面，剩下部分的表面积为672平方厘米。

图27--3练习1：1、从一个长10厘米、宽6厘米、高5厘米的长方体木块上挖去一个棱长2厘米的小正方体，剩下部分的表面积是多少？2、把一个长为12分米，宽为6分米，高为9分米的长方体木块锯成两个想同的小厂房体木块，这两个小长方体的表面积之和，比原来长方体的表面积增加了多少平方分米？3、在一个棱长是4厘米的立方体上挖一个棱长是1厘米的小正方体后，表面积会发生怎样的变化？图27—4【例题2】把19个棱长为3厘米的正方体重叠起来，如图27-4所示，拼成一个立体图形，求这个立体图形的表面积。

要求这个复杂形体的表面积，必须从整体入手，从上、左、前三个方向观察，每个方向上的小正方体各面就组合成了如下图形（如图27-5所示）。

技巧例题讲学第三讲图形的面积（一）第一课时例 1 已知平行四边形的面积是 28 平方厘米，求阴影部分的面积。

【思路点拨】4 厘米既是平行四边形的高，也是阴影三角形的高，平行四边形的面积是 28 平方厘米，它的底为 28÷4=7（厘米），平行四边形的底减去5 厘米就是三角形的底，7-5=2（厘米）。

根据三角形的面积公式直接求出阴影部分的面积。

求阴影部分的面积最直接的方法是利用计算公式直接求阴影面积；还可以用总面积减去空白面积求得阴影部分面积。

这两种是最常用最简便的方法。

同步精练1.下面的梯形中，阴影部分的面积是 150 平方厘米，求梯形的面积。

15 厘米25 厘米2．已知平行四边形的面积是 483．如果用铁丝围成如下图一样的平行四边形，需要用铁丝多少厘米？（单位：厘米）一） 乙甲乙甲例题讲学第三讲图形的面积（第二课时例 2 下图中甲和乙都是正方形，求阴影部分的面积。

（单位：厘米）GACB6E4F【思路点拨】图中的阴影部分是一个三角形，它的三条边的长都不知道，三条边上的高也不知道。

所以，无法用公式计算出它的面积。

仔细观察本题的图，我们可以发现，如果延长 GA 和 FC ，它们会相交（设交点为 H ），这样就得到长方形 GBFH （如下图），它的面积很容易求，而长方形 GBFH 中除阴影部分之外的其他三部分（△AGB 、△BFC 及△AHC ）的面积都能直接求出。

GAH C6E4F同步精练1、求右图中阴影部分的面积。

（单位：厘米）12432、求右图中阴影部分的面积。

（单位：厘米）885例题讲学第三讲图形的面积（一）第三课时例 3 如图所示：，甲三角形的面积比乙三角形的面积大 6 平方厘米，求 CE 的长度。

E【思路点拨】 题目中告诉我们，甲三角形的面积比乙三角形的面积大 6 平方厘米，即甲-乙=6（平方厘米），而甲和乙分别加上四边形 ABCF 后相减的结果还是 6 平方厘米，即：甲-乙=6（平方厘米）5EE（甲+四边形 ABCF ）-（乙+四边形 ABCF ）=6（平方厘米）即：正方形 ABCD- △ABE=6（平方厘米）这就是说正方形 ABCD 的面积比三角形 ABE 的面积大 6 平方厘米。

教学过程课堂精讲一、知识梳理1、三角形的面积=底边长 高÷2;所以，两个面积相等的三角形，当底边相等时，高也相等；反之亦然。

2、当两个三角形高相等时，面积之比等于底边长之比。

3、当两个三角形的底边长相等时，面积之比等于高之比。

4、在等底等高的情况下，三角形面积是平行四边形面积的一半；5、底边之和等于平行四边形的一边，且高相等的所有三角形，面积之和是平行四边形面积的一半；例1、如图，直角三角形ABC中AB=2,BC=2，其中AE=3AB,BD=2BC,三角形BDE的面积是多少？拓展、如图，三角形ABC 的面积为1，其中AE=3AB,BD=2BC,三角形BDE 的面积是多少？例2、如下图，AD DB =，AE EF FC ==，已知阴影部分面积为6平方厘米，ABC ∆的面积是多少平方厘米？FE DCBA拓展、如图，三角形ABC 中，AB 是AD 的5倍，AC 是AE 的3倍，三角形ADE 面积为3，三角形BDE 、三角形ABC 面积分别是多少？拓展、如下图，长方形AFEB 和长方形FDCE 拼成了长方形ABCD ，长方形ABCD 的长是20，宽是12，则它内部阴影部分的面积是．F E DCBA拓展、如图,一个长方形被分成4个不同颜色的三角形,红色三角形的面积是9平方厘米,黄色三角形的面积是21平方厘米,绿色三角形的面积是10平方厘米,那么蓝色三角形的面积是多少平方厘米?例5、图中的E 、F 、G 分别是正方形ABCD 三条边的三等分点，如果正方形的边长是12，那么阴影部分的面积是多少？E D GCFBA拓展、正图长方形ABCD 的面积是32平方厘米，E 、F 都是所在边的中点，三角形AEF 的面积是多少？例6、已知正方形ABCD的边长是10厘米，正方形EFGH的面积是多少？拓展、已知大正方形的边长是12厘米，中间最小正方形的面积是多少？拓展、如图所示，正方形的边长为厘米，长方形的长为厘米，那么长方形的宽为几厘米？例7、图中两个正方形的边长分别是6厘米和4厘米，则图中阴影部分三角形的面积是多少平方厘米．拓展、右图是由大、小两个正方形组成的，大正方形的边长是6厘米，小正方形的边长是4厘米，求三角形ABC 的面积．G4AB CDEF例8、四边形ABCD 和四边形DEFG 都是正方形，已知三角形AFH 的面积是7平方厘米。

第一讲 直线型面积的计算内容概述前三讲我们将针对几何部分进一步学习提高！首先，让我们一起来回顾一些基本知识！我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形，一般称为基本图形或规则图形。

我们的面积及周长都有相应的公式直接计算。

如下表：对于不规则图形的面积及周长计算，我们大都是由规则图形转化而来的！在实际问题的研究中，我们还会常常用到以下结论：① 等底等高的两个三角形面积相等．②两个三角形高相等，面积比等于它们的底之比； 两个三角形底相等，面积比等于它们的高之比；③夹在一组平行线之间的等积变形，如下图，ACD ∆和BCD ∆夹在一组平行线之间，且有公共底边CD 那么BCD ACD S S ∆∆=；反之，如果BCD ACD S S ∆∆=则可知直线AB 平行于CD 。

这节课我们将通过例题学习到几个很重要的定理结论！同学们注意做好笔记啊！例题精讲【例1】你有多少种方法将任意一个三角形分成（1）2个面积相等的三角形；（2）3个面积相等的三角形；（3）4个面积相等的三角形。

分析：（1）如右图，D、E、F分别是对应边上的中点，这样就将三角形分成了2个面积相等的三角形；（2）如右图，D、E是BC的三等分点，F、G分别是对应线段的中点；答案不唯一；（3）如下图，答案不唯一，以下仅供参考；前四种答案学生都容易得到，在这里我们需要特别说明的是第五个答案，请看例2 。

【例2】在学习三角形时，很多同学都听说过中位线，所谓中位线就是三角形两边中点的连线。

如右图所示，D、E、F分别是AB、AC、BC边的中点，根据定义可知DE、DF、EF就是三角形ABC的中线。

那么请你说明：（1）DE与BC平行（2）DE= 1/2 BC（3）S△ADE= 1/4 S△ABC分析：（1）在解答一些几何问题时，我们常常需要添加一些辅助线帮助我们分析解决。

如右图（1），连接DC、BE。

因为D、E分别是AB、AC的中点，所以S△BDC=1/2 S△ABC= S△BEC，又因为△BDC与△BEC同用BC做底，根据“内容概述”部分常用结论③可得：DE与BC平行。

1.如图14-9所示，大圆半径为6，则其阴影部分的面积为____。

2.已知正方形ABCD的边长为10厘米，过它的四个顶点作一个大圆，过它的各边中点作一个小圆，再将对边中点用直线连接起来，得到图14-10。

那么，图中阴影部分的面积为____平方厘米（π取3计算）。

3.如图14-11所示，正方形DEOF的四分之一圆中，如果圆形的半径为1厘米，那么，阴影部分的面积是____平方厘米（π取3计算）。

4.如图11-12。

小圆的35是阴影部分，大圆的78是阴影部分，小圆阴影面积与大圆阴影面积的比是____。

5.如图14-13是三个同心圆，圆心为P，且PQ=QR=RS，S1中间圆与外圆之间的圆环面积，S2是中间圆与小圆之间的圆环面积，那么21SS=____。

6.如图14-14所示，∠AOB=90°，C为AB弧的重点，已知阴影甲的面积为16平方厘米，阴影乙的面积为____平方厘米。

7.%8.如图14-15所示，正方形ABCD的面积为200平方厘米，求内接圆的面积（π取）。

图14-159.如图14-16所示，已知圆的面积为3140平方厘米，求内接正方形ABCD的面积（π取3计算）。

、10.如图14-17所示，已知大圆的半径为20厘米，求a、b、c、d四个小圆的周长之和。

\11.如图14-18所示，将直角三角形ABC向下旋转90°。

已知BC=5厘米，AB=4厘米，AC=3厘米。

求三角形ABC扫过的面积。

）12.如图14-19所示，大圆的半径为100厘米，小圆的半径为1厘米，将小圆沿大圆周长滚动一周。

求（1）小圆的圆心经过的长度；（2）求小圆扫过的面积。

$13.如图14-20所示，已知六个圆的面积相等，而且阴影部分的面积为60平方厘米，求六个圆的面积为多少平方厘米|14.如图14-21所示，已知大正方形的面积为100平方厘米，小正方形面积为50平方厘米，求阴影部分的面积。

面积计算（一）专题简析：计算平面图形的面积时，有些问题乍一看，在已知条件与所求问题之间找不到任何联系，会使你感到无从下手。

这时，如果我们能认真观察图形，分析、研究已知条件，并加以深化，再运用我们已有的基本几何知识，适当添加辅助线，搭一座连通已知条件与所求问题的小“桥”，就会使你顺利达到目的。

有些平面图形的面积计算必须借助于图形本身的特征，添加一些辅助线，运用平移旋转、剪拼组合等方法，对图形进行恰当合理的变形，再经过分析推导，方能寻求出解题的途径。

例题1。

已知图18－1中，三角形ABC 的面积为8平方厘米，AE ＝ED ，BD=23 BC ，求阴影部分的面积。

【思路导航】阴影部分为两个三角形，但三角形AEF 的面积无法直接计算。

由于AE=ED,连接DF ，可知S △AEF =S △EDF （等底等高），采用移补的方法，将所求阴影部分转化为求三角形BDF 的面积。

因为BD=23 BC ，所以S △BDF ＝2S △DCF 。

又因为AE ＝ED ，所以S △ABF ＝S △BDF ＝2S △DCF 。

因此，S △ABC ＝5 S △DCF 。

由于S △ABC ＝8平方厘米，所以S △DCF ＝8÷5＝1.6（平方厘米），则阴影部分的面积为1.6×2＝3.2（平方厘米）。

练习11、 如图18－2所示，AE ＝ED ，BC=3BD ，S △ABC ＝30平方厘米。

求阴影部分的面积。

2、 如图18－3所示，AE=ED ，DC ＝13 BD ，S △ABC ＝21平方厘米。

求阴影部分的面积。

3、 如图18－4所示，DE ＝12AE ，BD ＝2DC ，S △EBD ＝5平方厘米。

求三角形ABC 的面积。

AB CFD E18－2ABCFE D18－1 ABCFED 18－3CB D EF 18－4例题2。

两条对角线把梯形ABCD 分割成四个三角形，如图18－5所示，已知两个三角形的面积，求另两个三角形的面积各是多少？【思路导航】已知S △BOC 是S △DOC 的2倍，且高相等，可知：BO ＝2DO ；从S △ABD 与S △ACD相等（等底等高）可知：S △ABO 等于6，而△ABO 与△AOD 的高相等，底是△AOD 的2倍。

周长和面积(一) 姓名例题精讲：1、有两个相同的长方形，长7厘米，宽5厘米，把它们按下图的样子叠在一起，这个图形的周长是多少厘米？变式练习：1、下图是一个楼梯的侧面，如果在阶梯上铺地毯，要计算地毯的长度，可以怎么样测量？8cm8cm 例题精讲：2、两个大小相同的正方形拼成一个长方形后，周长比原来两个正方形的周长的和减少了6厘米。

原来一个正方形的周长是多少厘米？变式练习：2、把一个正方形剪成两个大小相同的长方形后，两个长方形周长的和比原来正方形的周长增加28分米，原来正方形的周长是多少分米?3、把边长是48厘米的正方形剪成三个同样大小的长方形。

每个长方形的周长是多少？例题精讲：3、把长130厘米的铁丝围成一个长方形，街头处重合2厘米，要使长比宽多18厘米，这个长方形的长和宽各是多少厘米？变式练习：4、小华家给长方形的院子装上了篱笆墙，由于门宽2米，所以篱笆墙共长16米，而这个长方形的的宽是长的一半。

这个长方形的长和宽各是多少？5、一个长方形，它的长减少5厘米，宽增加5厘米，周长会怎么样变化？例题精讲:4、学校里有一个正方形的花坛，花坛的四周种了一圈绿篱，绿篱总长20米。

求花坛的面积是多少平方米？变式练习：6、公园里有一个长方形花圃和一个正方形的花圃，这两个花圃的周长相等，其中长方形花圃长40米、宽20米，求正方形花圃的面积。

例题精讲：5、求下图的面积。

（单位：厘米）变式练习：7、计算下面图形的面积。

（单位：厘米）例题精讲：6、有两个相同的长方形，长是8厘米、宽是3厘米，把它们按下图叠放。

这个图形的面积是多少平方厘米？变式练习：8、两张相同的边长为8厘米的正方形纸，一部分叠在一起放在桌上（如下图所示）。

问桌子被覆盖住的面积是多少？5 13 21 2 5 1 1 44 4 8。

本讲主要通过求一些不规则图形的面积，体会一种转化思想，重点在于把不规则图形转化为规则图形的方法，包括平移、旋转、割补、差不变原理，通过这些方法的学习，让学生体会求面积的技巧，提高学生的观察能力、动手操作能力、综合运用能力．【例 1】 你有什么好的方法计算所给图形的面积呢？(单位：厘米)3994399439943994图1 图2 图3 【考点】不规则图形的面积 【难度】1星 【题型】解答 【解析】 (方法一)采用分割法，可给原图分成两个长方形，(图1或图2)两个长方形的总面积就是所求的面积．图1的面积是： 4(93)9375⨯++⨯=(平方厘米)．图2的面积是：(94)39475+⨯+⨯=(平方厘米)．(方法二)采用补图法，如果补上一个边长是9厘米的正方形(图3)，就成了一个面积是：(49)(93)156+⨯+=(平方厘米)的大长方形．因此用这个长方形的面积减去所补正方形的面积，就是要求的图形面积(49)(93)9975+⨯+-⨯=(平方厘米)． 【答案】75平方厘米【巩固】如图是学校操场一角，请计算它的面积(单位：米)30203040例题精讲4-2-6.不规则图形的面积【解析】 这是一个不规则图形，怎样使它能转化为我们熟悉的基本图形呢？可以在图中添上一条辅助线，把多边形切割成上下两个长方形或左右两个长方形；也可以把多边形补充完整，成为一个长方形；302030403020304030203040图一 图二 图三方法一：如图一，3040203040120014002600⨯+⨯+=+=（）(平方米) 方法二：如图二，203040203060020002600⨯+⨯+=+=（）(平方米) 方法三：如图三，40302030303035009002600+⨯+-⨯=-=（）（）(平方米)【答案】2600平方米【巩固】如右图所示，图中的ABEFGD 是由一个长方形ABCD 及一个正方形CEFG 拼成的，线段的长度如图所示(单位：厘米)，求ABEFGD 的周长和面积．F【考点】不规则图形的面积 【难度】1星 【题型】解答 【解析】 方法一：如果求出长方形的宽及正方形的边长，则图形ABEFGD 的周长和面积可以求出．而正方形的边长1046GC DC DG AB DG =-=-=-=(厘米)，长方形的宽1064BE CE =-=-=(厘米)，所求图形的周长102624440=⨯+⨯++=(厘米) 面积1046676CEFG ABCD S S =+=⨯+⨯=正方形长方形(平方厘米)方法二：可以将线段GF 、DG 向外平移，得一个新的图形ABEH ，因为DG HF =，GF DH =，所以图形ABEH 的周长就是图形ABEFGD 的周长．而10AB BE ==(厘米)，所以图形ABEH 是边长为10厘米的正方形． 所求图形的周长=正方形ABEH 的周长10440=⨯=(厘米) 面积10106476ABEH DGFH S S =-=⨯-⨯=正方形长方形(平方厘米)【总结】方法一是利用基本图形的周长及面积公式求解，因此首先要知道长方形的长、宽及正方形的边长．方法二是利用转化的思想方法，将较复杂图形转化为基本图形，图形转化前后的周长不变，面积增加了，在计算时应减去增加的面积． 【答案】76【巩固】求图中五边形的面积．6453【解析】由图可见五边形为矩形切去一角得来，把切去的角补出来，它的一条直角边长633-=，斜边等于5，所以另一直角边为4，所以矩形的长为448+=，五边形面积16843422⨯-⨯⨯=．【答案】42【例 2】这是一个楼梯的截面图，高280厘米，每级台阶的宽和高都是20 厘米．问，此楼梯截面的面积是多少？【考点】不规则图形的面积【难度】2星【题型】解答【关键词】华杯赛、口试【解析】如果把楼梯截面补成右图所示的长方形，那么此长方形高280厘米．宽300厘米，它的面积恰好是所求截面的2倍．所以楼梯截面面积为280300242000⨯÷=（）(平方厘米)．【答案】42000【巩固】如图是一个楼梯的截面图，每级台阶的宽和高都是20厘米．这楼梯的截面积是多少平方厘米？【考点】不规则图形的面积【难度】2星【题型】解答【解析】先求出大三角形的两条直角边都是208160⨯=(厘米)，因此大三角形的面积为160160212800⨯÷=(平方厘米)；8个小三角形的面积为2020281600⨯÷⨯=(平方厘米)；因此这楼梯的截面积为12800160014400+=(平方厘米)．【答案】14400【例 3】有一块菜地长16米，宽8米，菜地中间留了宽2米的路，把菜地平均分成四块，每一块地的面积是多少？【考点】不规则图形的面积【难度】2星【题型】解答【解析】方法一：可以直接求出每小块菜地的长和宽，从而求出每小块菜地的面积；每一块地的面积是：[1622][822]7321-÷⨯-÷=⨯=（）（）(平方米)方法二：也可以求出这块地的总面积，再减去道路的面积，然后把剩余的面积四等分求出每小块菜地的面积；每一块地的面积是：[1682168222]412844421⨯-⨯+⨯-⨯÷=-÷=（）（）(平方米)方法三：还可以运用平移的方法，将道路移到菜地的边沿，先求出四个小长方形组成的长方形面积，再求出其中每一小块菜地的面积．如图所示：[16282]484421-⨯-÷=÷=（）（）(平方米) 【答案】21【例 4】 有10张长3厘米，宽2厘米的纸片，将它们按照下图的样子摆放在桌面上，那么这10张纸片所盖住的桌面的面积是多少平方厘米？【考点】不规则图形的面积 【难度】3星 【题型】解答 【解析】 通过操作，一张一张的添加，可以发现每多盖一张，遮住的面积增加21⨯平方厘米，所以这10张纸片盖住的面积是：3221924⨯+⨯⨯=(平方厘米)．【答案】24【例 5】 下图(单位：厘米)是两个相同的直角梯形重叠在一起，求阴影部分的面积.【考点】不规则图形的面积 【难度】3星 【题型】解答 【解析】 所求面积等于图中阴影部分的面积，为2052082140-+⨯÷=()(平方厘米)． 【答案】140【巩固】两个相同的直角三角形如下图所示(单位：厘米)重叠在一起，求阴影部分的面积.FBA【考点】不规则图形的面积 【难度】3星 【题型】解答 【解析】 阴影部分是一个高为3厘米的直角梯形，然而它的上底与下底都不知道，因而不能直接求出它的面积.因为三角形ABC 与三角形DEF 完全相同，都减去三角形DOC 后，根据差不变性质，差应相等，即阴影部分与直角梯形OEFC 面积相等，所以求阴影部分的面积就转化为求直角梯形OEFC 的面积.直角梯形OEFC 的上底为1037-=(厘米)，面积为7102217+⨯÷=()(厘米2). 所以，阴影部分的面积是17平方厘米。

年 级 五年级学 科 奥数版 本通用版课程标题 不规则图形的面积（一）我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形，一般称为基本图形或规则图形，它们的面积及周长都可由相应的公式直接计算。

实际问题中，有些图形是由一些基本图形组合、拼凑成的，它们的面积及周长可能无法应用公式直接计算。

我们一般称这样的图形为不规则图形。

组合的形式分为两种：一是拼接组合，二是重叠组合。

由于组合图形具有条件相等的特点，往往使得问题的解决无从下手。

那么，怎样去计算不规则图形的面积及周长呢？我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系，这样问题就能解决了。

本节课主要用公式法、求和差法、分割法、等量代换法解答不规则图形的面积问题。

1. 常见图形的面积公式：名称 图形面积公式长方形ab正方形 2a三角形 ah 21 平行四边形ah梯形h b a ⋅+)(212. 几个重要结论：（1）如果两个三角形的底和高分别相等，那么这两个三角形的面积相等。

（2）如果两个三角形的底（或高）相等，那么它们的面积之比等于它们的高（或底）之比。

例１ 如图所示，大正方形和小正方形的边长分别为4和2，求阴影部分的面积。

分析与解：如题图，欲求阴影部分的面积，通过分析发现它是一个底是2、高是4的三角形，可以直接利用三角形的面积公式求得阴影部分的面积为2×4÷2＝4。

本题是利用公式直接求解，这种方法是根据已知条件，从整体出发观察组合图形的特征，并与熟悉的基本图形产生联想。

例２正方形甲的边长是5厘米，正方形乙的边长是4厘米，阴影部分的面积是多少？分析与解：两个正方形的面积和：＋＝41（平方厘米）；三个空白三角形的面积和：（5＋4）×5÷2＋4×4÷2＋5×（5－4）÷2＝33（平方厘米）；阴影部分的面积：41－33＝8（平方厘米）。

四年级奥数：面积问题
面积是数学中的一个重要概念，它用来描述平面上的形状或图形所占据的空间大小。

四年级的奥数也涉及到了面积问题，下面我们来介绍一些常见的面积问题及解决方法。

正方形的面积
正方形是一个四边都相等且角均为90度的特殊矩形。

要计算正方形的面积，只需要将正方形的边长乘以它自己即可。

例如，一个边长为5厘米的正方形的面积是25平方厘米。

长方形的面积
长方形是另一种常见的图形，它有两对相等的边和四个角均为90度。

计算长方形的面积需要知道它的长和宽，然后将长乘以宽即可得到面积。

例如，一个长为7厘米，宽为4厘米的长方形的面积是28平方厘米。

三角形的面积
三角形是一个具有三条边和三个角的多边形。

计算三角形的面积需要知道底边的长度和高的长度。

将底边乘以高的一半即可得到三角形的面积。

例如，一个底边长度为6厘米，高为3厘米的三角形的面积是9平方厘米。

平行四边形的面积
平行四边形是一个具有两对平行边和四个角的四边形。

计算平行四边形的面积需要知道底边的长度和高的长度。

将底边乘以高即可得到平行四边形的面积。

例如，一个底边长度为8厘米，高为5厘米的平行四边形的面积是40平方厘米。

总结
面积是描述平面图形所占据空间大小的概念。

在四年级的奥数中，我们经常会遇到正方形、长方形、三角形和平行四边形的面积问题。

要计算这些图形的面积，只需要记住相应的公式，并将已知的值代入求解即可。

通过练习这些面积问题，我们能够更好地理解图形的特点和面积的计算方法，提高自己的数学水平。