【K12学习】七年级数学《数据的收集与整理》知识点复习北师大版
- 格式:doc
- 大小:13.50 KB
- 文档页数:2


北师大版七年级数学《数据的收集与整理》
知识要点汇总
◆◆◆数据的收集
普查:为了一定的目的而对考察对象进行的全面调查.
总体:所要考察对象的全体称为总体gt;gt;gt;精选初一数学数据的收集知识点归纳~
◆◆◆普查与抽样调查
当普查的对象很少时,普查无疑是一项非常好的调查方式,但是事实上,有些问题是不适合普查的gt;gt;gt;七年级数学《普查与抽样调查》相关内容~
◆◆◆统计图的选择
(1)条图:又称直条图,表示独立指标在不同阶段的情况,有两维或多维,图例位于右上方。
(2)百分条图和圆图:描述百分比(构成比)的大小,用颜色或各种图形将不同比例表达出来gt;gt;gt;初一数学《统计图的选择》知识点必备~
◆◆◆练习题
初一数学数据的收集与整理练习题
初一上册数学普查与抽样调查同步练习
初一上册数学《统计图的选择》课后练习
期末考试即将到来,那么作为一名学生,你是否已经为接下来的期末考试做好准备了呢?七年级数学数据的收集与整理知识要点希望对大家有所帮助!。

北师大版(2024)七年级上册第六章数据的收集与整理知识点知识点 1 简单随机抽样【举例讲解】为制定某市初中七、八、九年级学生校服的生产计划,有关部门准备对360 名初中女生的身高进行调查,现有四种调查方案:A.测量少年体校中360名篮球、排球女队员的身高;B.查阅有关外地360名女生身高的统计资料;C.在本市的市区和郊区各选三所高级中学、三所初级中学,在这12所学校有关年级的(2)班中,用抽签的方法分别选出10名女生,然后测量她们的身高;D.在本市的市区和郊区各选三所高级中学、三所初级中学,在这12所学校中,用抽签的方法分别选出10名男生,然后测量他们的身高.为了达到估计本市初中这三个年级女生身高分布的目的,你认为采用上述哪一种调查方案比较合理,为什么?这是用抽样调查进行调查的事件,抽样调查选择的样本不同,调查的结果就有可能不同,抽样调查所选取的样本要有代表性和随机性,对于方案A,如果在体校测量360名篮球、排球女队员的身高,得到的数据肯定偏高;对于方案B,查阅有关外地360名女生身高不能代表本地女生的身高;对于方案C,这个样本的选取有随机性、代表性,这样选取的学生的身高得到的数据可以代表本地学生身高情况;对于方案D,本事件是研究女生身高,测量男生身高得到的数据不具有代表性.【归纳总结】知识归纳为了获取能够客观反映问题的结果,通常按照总体中每个个体都有相同的被抽取机会的原则抽取样本,这种抽取样本的方法叫做简单随机抽样.简单随机抽样是在总体中抽取一部分个体组成总体的一个样本,抽样时要求抽取的样本要有随机性和代表性,样本中个体的个数要适中.方法归纳①抽取的样本要具有随机性;②抽取的样本要具有代表性;③抽取的样本的容量要适中.知识点2 用样本估计总体【举例讲解】为了估计养鱼池里有多少条鱼,养鱼者从池中捕上100 条鱼做上标记,然后放回池中,经过一段时间,待带标记的鱼完全混合于鱼群后,再捕第二次样品鱼120条,其中带标记的鱼有15 条,试估计鱼池中约有鱼多少条?由题意可知,对鱼池中鱼的条数不可能进行普查,所以只能抽样调查,从中抽取100 条后放回鱼池做了标记,又从中抽出120条作为样本,其中样本中有15 条做了标记,所以设鱼池约有x条鱼,则100∶15=x∶120,解得x=800.估计鱼池里约有鱼800条,得到的数据只是一个约数,是通过样本对鱼池中鱼的条数作出的估算,这就是数学中的用样本估计总体.【归纳总结】知识归纳在随机抽样时,样本容量越大,样本对于总体的代表性也就越大,但在实际调查中,为了缩小抽样误差而大量增加样本中的个体数量,同样也是花费较多的时间和费用,所以在确定样本容量时,必须正确全面地权衡调查的精确性与时间、费用支出两方面的利弊,适当地确定样本容量.方法归纳抽样调查的基本思想是用局部估计整体,这是因为局部的特征在某种程度上能反映整体的特征,要使样本具有代表性,不偏向总体中的某些个体,就要求每个个体都有均等的机会进入样本,具体步骤为:①将每个个体编号;②将写有这些编号的纸条或乒乓球全部放入一个盒子中,搅拌均匀;③用抽签的办法抽取一个编号,这个编号的个体就被选入样本,依据上述方法再抽取第二个,第三个……直到被抽取的个体的数量达到样本容量的要求.1.要了解一个城市的气温变化情况,下列观测方法中最可靠的是( )A.一年中随机选中20天进行观测B.一年中随机选中一个月进行连续观测C.一年四季各随机选中一个月进行连续观测D.一年四季各随机选中一个星期进行连续观测2.张家界市属国家珍稀动物“大鲵”保护地,科考人员某日在其中一个保护区捕捞6 只大鲵,并在它们身上都做了标记后放回,几天后,在该保护区又捕捞18 只大鲵,其中2 只身上有标记,据此估计该保护区大鲵约有( )A.54 只B.24 只C.32 只D.108 只3. (2018·安顺中考)要调查安顺市中学生了解禁毒知识的情况,下列抽样调查最适合的是( )A.在某中学抽取200名女生B.在安顺市中学生中抽取200名学生C.在某中学抽取200 名学生D.在安顺市中学生中抽取200 名男生4.为了解佛山市老人的身体健康状况,在以下抽样调查中,你认为样本选择较好的是 (填序号).①100位女性老人;②公园内100 位老人;③在城市和乡镇选 10 个点,每个点任选 10 位老人.5.某旅行社在“十一”长假期间平均每天的营业额为4万元,由此推断其10月份的总营业额约为4 4×31=124(万元).根据所学的统计知识,你认为这样的推断是否合理?答:6.下面两个抽样调查选取样本的方法是否合适,并说明理由.(1)为调查全校学生对购买正版书籍、唱片和软件的支持率,在全校所有的班级中任意抽取8个班级,调查这8个班所有学生对购买正版书籍、唱片和软件的支持率;(2)为调查一个省的环境污染情况,调查省会城市的环境污染情况.。



北师大版七年级上册第六章数据的收集与
整理复习知识点
第六章数据的收集与整理一、数据的收集
1.数据收集的方法
①直接方法:观察、调查、试验、查阅资料等,调查又分为实地调查、问卷调查和访问调查等.
②间接方法:互联网查询、查阅文献资料等.
2.统计活动的过程
(1)明确调查目的和问题(2)确定调查对象(3)选择调查方法(4)展开调查(5)收集并整理数据(6)分析数据,得出结论
二、普查和抽样调查
1.普查(为一特定目的而对所有考察对象所做的全面调查)
①总体:所考察的对象的全体
②个体:组成总体的每一个考察对象
2.抽样调查(为一特定目的而对部分考察对象所做的调查)
①样本:从总体中所抽取的一部分个体。
只有抽样调查里,才有样本
②样本容量:从总体中抽取的个体的数量
③为了使样本能较好地反映总体情况,除了有合适的样
本容量外,抽取时还要尽量使每一个个体有相等的机会被抽到.。

初一数学第十章数据的收集与整理实验版【本讲教育信息】一. 教学内容:第十章数据的收集与整理(一)数据的收集、整理与表示(二)平均数、众数、中位数[教学要求]1. 了解总体与样本以及数据的收集与整理的意义和步骤。
2. 掌握利用条形统计图、折线统计图和扇形统计图表示数据的方法。
3. 会求一组数据的平均数、众数和中位数。
二. 重点、难点:1. 重点:(1)数据的收集、整理的方法、步骤以及表示的方法。
(2)平均数、众数和中位数的有关计算。
2. 难点:数据的收集与整理的步骤。
[知识要点]1. 全面调查(也称普查)与抽样调查(1)全面调查:如:某校七年级(1)班共有50名同学,现打算对每人最喜欢的体育项进行统计,由于被调查的人数不是很多,我们可以对50人逐一进行问卷调查,然后加以整理,这种方法叫做全面调查(也称普查)。
特点:被调查的对象数量不太多,逐一进行调查,结果真实可靠。
又如:全班同学的睡眠情况、饮食习惯、喜欢的电视节目等。
(2)抽样调查(也称抽查)如1:为了了解某地区50000余户家庭年人均收入的情况,如果将每个家庭的年收入和人口数据搜集起来计算,由于数据太多,将是十分麻烦的,通常是从中抽取部分家庭(例如1000户)的年收入和人口数进行计算,用计算出来的这部分家庭年人均收入,去估计这个地区所有家庭的年人均收入。
又如2:要了解某工厂的某种产品的质量(如:灯泡的寿命、轮胎的质量),由于通常产品的产量很大或检测具有一定的破坏性,通常从中抽取部分产品(如100件)的质量进行检测,然后用这部分产品的质量状况去估计这个工厂所有这类产品的质量。
以上两种方法就是抽样调查(也称抽查)。
又如:对全国人口中易患感冒的年龄段,大气污染状况,玻璃耐压程度都只能采取抽查。
特点:被调查的对象数量太多或必须进行“破坏性”试验。
2. 总体和样本、个体、样本容量在数据进行统计时,我们把所要考察的对象的全体叫做总体。
其中的每一个考查对象叫做个体,从总体中所抽取的一部分个体叫总体的一个样本,样本中个体的数量叫样本的容量。

七年级数学第六章复习复习内容:第六章及期末小综合上周检测:1、 如果7a —5与3 —5a 互为相反数,那么a 的值为( ) A. 0 B. 1 C. -1 D. 22、 小明从家里骑自行车到学校,每小时骑\5而,可早到10分钟,每小时骑12如7就会迟到5 的路程是多少七〃?设他家到学校的路程是才勿〃,那么据题意列出的方程是( )4^己知关于x 的方程3%—2//7=4的解是x=m 那么〃7的值是 _____ ・5、随着电子技术的开展, 价格不断降低,某品牌 按原价降低〃7元后,又降低2096,此时售价为〃元,那么该原价为 _______ 元. 6、解方程7、某校七年级学生到某风景区郊游,1班学生组成前队,速度4千米/小时,2班学生组成后队,速度6千米/小时, 前队出发1小时后,后队才出发,同时后队一名联络员骑自行车在两队之间不间断进行联络,他骑自行车的速度为 12千米/小时,① 后队追上前队时,用了多少时间? ②后队追上前队时,联络员行了多少路程?第六章数据的收集与整理一、本单元知识点总结: 1、 普查与抽样调查为了特定目的对全部考察对象进行的全面调查,叫做普查。
其中被考察对象的全体叫做总体,组成总体的每一 个被考察对象称为个体。
从总体中抽取局部个体进行调查,这种调查称为抽样调查,其中从总体抽取的一局部个体叫做总体的一个样本。
2、 扇形统计图扇形统计图:利用圆与扇形来表示总体与局部的关系,扇形的大小反映局部占总体的百分比的大小,这样的统 计图叫做扇形统计图。
(各个扇形所占的百分比之和为1)圆心角度数= 360° X 该项所占的百分比。
(各个局部的圆心角度数之和为360° )画法:(1) 计算不同局部占总体的百分比(在扇形中,每局部占总体的百分比等于该局部所对应的扇形圆心角的度数 与360的比)。
(2) 计算各个扇形的圆心角(顶点在圆心的角叫做圆心角)的度数。
3、% 10 x15 丁 60 12560B 、 x 10 x 5 =—+ — 60 15 60 12C 、15 60 12 60± + 10 = —-515 12某种商品的进价为800元, 低于5%,那么最多可打( A. 6折 B. 7折 出售标价为1200元,C. 8折 后来由于该商品积压,商店准备打折销售,但要保证利润率不D. 9折x-210 2x-53+3=05x + 1 9x + 1 \ -x(3)在圆中画出各个扇形,并标上百分比。
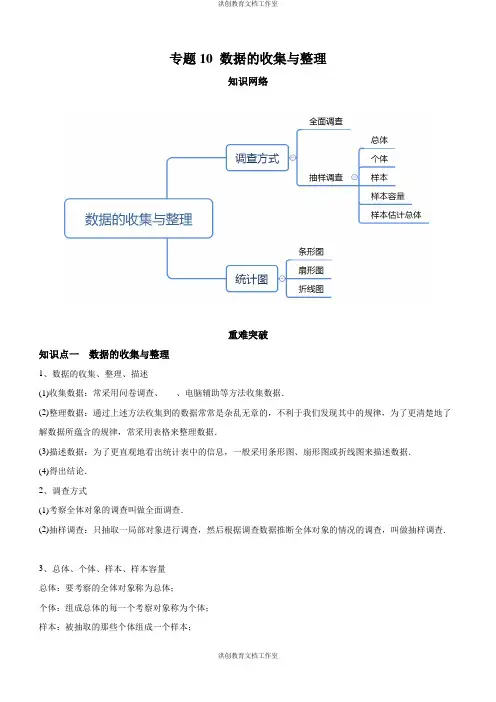
专题10 数据的收集与整理知识网络重难突破知识点一数据的收集与整理1、数据的收集、整理、描述(1)收集数据:常采用问卷调查、、电脑辅助等方法收集数据.(2)整理数据:通过上述方法收集到的数据常常是杂乱无章的,不利于我们发现其中的规律,为了更清楚地了解数据所蕴含的规律,常采用表格来整理数据.(3)描述数据:为了更直观地看出统计表中的信息,一般采用条形图、扇形图或折线图来描述数据.(4)得出结论.2、调查方式(1)考察全体对象的调查叫做全面调查.(2)抽样调查:只抽取一局部对象进行调查,然后根据调查数据推断全体对象的情况的调查,叫做抽样调查.3、总体、个体、样本、样本容量总体:要考察的全体对象称为总体;个体:组成总体的每一个考察对象称为个体;样本:被抽取的那些个体组成一个样本;样本容量:样本中个体的数目称为样本容量.在抽取样本的过程中,总体中的每一个个体都有相等的时机被抽到,这样的抽样方法叫做简单随机抽样.用样本估计总体是归纳法在统计中的一种运用,统计的根本思想就是由总体中抽取一个样本,通过研究样本的特性,去估计总体的相应特性.抽样调查方法就是利用了用样本估计总体的思想.典例1(2020•承德二模)北京海淀区某中学经过食堂装修后重新营业,同学们很快乐品尝各种美食菜品,某同学想要得到本校食堂最受同学欢送的菜品,以下是排乱的统计步骤:①从扇形图中分析出最受学生欢送的菜品;②去食堂收集同学吃饭时选择的菜品名称和人数;③绘制扇形图来表示各个种类产品所占的百分比;④整理所收集的数据,并绘制频数分布表;正确统计步骤的顺序是()A.②→③→①→④B.③→④→①→②C.①→②→④→③D.②→④→③→①【解答】解:统计的一般步骤为:收集数据,整理数据,绘制统计图表,分析图表得出结论,从正确的步骤为②④③①,应选:D.典例2(2019秋•龙岗区校级期末)以下调查中不适合抽样调查的是()A.调查某景区一年内的客流量B.了解全国食盐加碘情况C.调查某小麦新品种的发芽率D.调查某班学生骑自行车上学情况【解答】解:A、调查某景区一年内的客流量,所费人力、物力和时间较多,适合抽样调查,故本选项不合题意;B、了解全国食盐加碘情况,所费人力、物力和时间较多,适合抽样调查,故本选项不合题意;C、调查某小麦新品种的发芽率,适合抽样调查,故本选项不合题意;D、调查某班学生骑自行车上学情况,适合全面调查,故本选项符合题意.应选:D.典例3(2019春•天台县期末)为了调查某校学生的视力情况,在全校的800名学生中随机抽取了80名学生,以下说法正确的选项是()A.此次调查属于全面调查B.样本容量是80C.800名学生是总体D.被抽取的每一名学生称为个体【解答】解:A.此次调查属于抽样调查,故本选项不合题意;B.样本容量是80,正确;C名学生的视力情况是总体,故本选项不合题意;.800D.被抽取的每一名学生的视力情况称为个体.故本选项不合题意.应选:B.知识点二统计图1、统计图(1)条形统计图的特点:①能够使人们一眼看出各个数据的大小。
七年级数学《数据的收集与整理》知识点复
习北师大版
总体:所有考察对象的全体叫做总体。
个体:总体中每一个考察对象叫做个体。
样本:从总体中所抽取的一部分个体叫做总体的一个样本。
普查:为某一特定目的而对所有考察对象进行的全面调查。
抽样调查:从总体中抽取部分个体进行调查。
样本容量:样本中个体的数目叫做样本容量。
样本平均数:样本中所有个体的平均数叫做样本平均数。
总体平均数:总体中所有个体的平均数叫做总体平均数,在统计中,通常用样本平均数估计总体平均数。
众数:在一组数据中,出现次数最多的数据叫做这组数据的众数。
0、中位数:将一组数据按大小依次排列,把处在最中间位置的一个数据叫做这组数据的中位数。
1、频率分布的意义:在许多问题中,只知道平均数和方差还不够,还需要知道样本中数据在各个小范围所占的比例的大小,这就需要研究如何对一组数据进行整理,以便得
到它的频率分布。
研究频率分布的一般步骤及有关概念
研究样本的频率分布的一般步骤是:计算极差决定组距与组数决定分点列频率分布表画频率分布直方图
频率分布的有关概念
极差:最大值与最小值的差
频数:落在各个小组内的数据的个数
频率:每一小组的频数与数据总数的比值叫做这一小组的频率。
扇形统计图:利用圆与扇形来表示总体与部分的关系,即圆代表总体,圆中的各个扇形分别代表总体中的不同部分,扇形的大小反映部分占总体的百分比的大小,这样的统计图叫做扇形统计图。
3、统计图对统计的作用:
可以清晰有效地表达数据。
可以对数据进行分析。
可以获得许多的信息。
可以帮助人们作出合理的决策。
各种统计图的优缺点:
条形统计图:能清楚地表示出每个项目的具体数目。
折线统计图:能清楚地反映事物的变化情况。
扇形统计图:能清楚地表示出各部分在总体中所占的百分比。