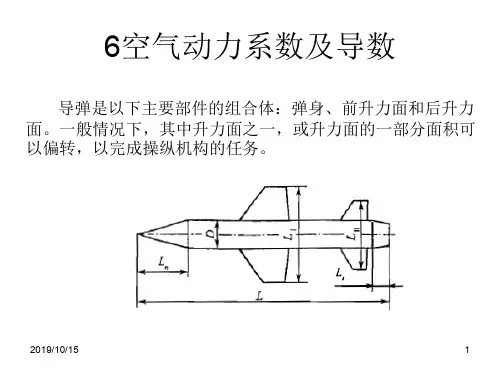
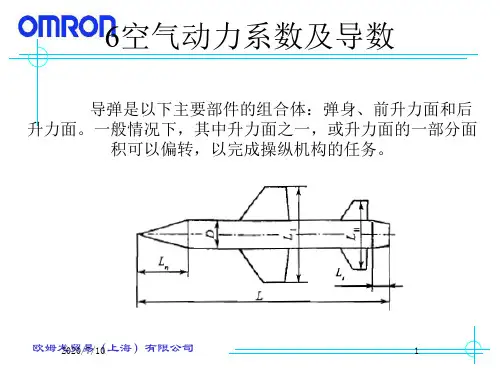
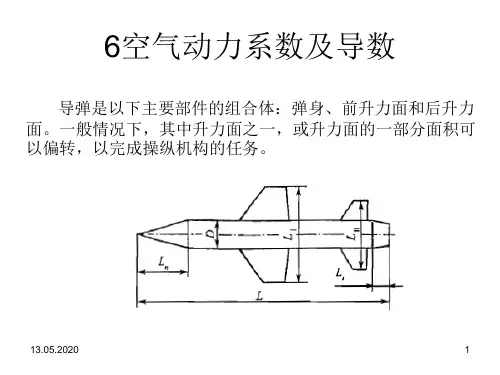
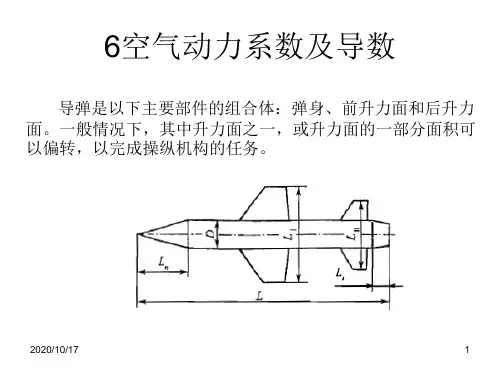
空气的动力粘滞系数空气的动力粘滞系数是一个描述空气流动阻力的物理量。
它反映了空气对物体的阻碍力大小，也是流体力学中一个重要的参数。
本文将从不同角度介绍空气的动力粘滞系数，并探讨其在科学研究和工程应用中的重要性。
一、什么是动力粘滞系数动力粘滞系数（η）是描述流体内部粘滞阻力大小的一个物理量。
在空气中，动力粘滞系数表示了空气分子间相互作用的强度和空气流动阻力的大小。
其数值大小与空气温度、压力等因素有关，通常在常温常压下的空气中，动力粘滞系数约为1.8×10^-5 kg/(m·s)。
二、动力粘滞系数的计算方法动力粘滞系数的计算是通过实验或模拟方法得到的。
实验方法一般采用流体力学实验设备，通过测量流体在不同条件下的流动速度和施加的力来计算动力粘滞系数。
模拟方法则是通过建立数学模型和计算机模拟，利用流体力学方程来计算动力粘滞系数。
无论是实验方法还是模拟方法，都需要考虑到流体的物性参数、流动条件等因素。
三、动力粘滞系数的作用1. 空气动力学研究：在飞行器、汽车、火箭等工程领域，研究空气动力学是非常重要的。
动力粘滞系数是计算空气动力学力学性能的重要参数，可以帮助工程师设计更加流线型和低阻力的飞行器，提高其性能和燃油利用率。
2. 空气流体传热：在热工学和传热学中，动力粘滞系数是计算流体传热性能的重要参数。
通过研究动力粘滞系数，可以优化热交换设备的结构，提高传热效率，降低能源消耗。
3. 涂层材料工程：动力粘滞系数在涂层材料工程中也有重要应用。
通过研究涂层材料的动力粘滞系数，可以选择合适的涂层材料，提高涂层的附着力和耐久性。
四、动力粘滞系数的影响因素动力粘滞系数的数值大小受到多种因素的影响，主要包括温度、压力和气体的组成等。
一般来说，温度升高会使动力粘滞系数减小，而压力升高会使动力粘滞系数增大。
此外，气体的组成也会对动力粘滞系数产生影响，不同气体的动力粘滞系数是不同的。
五、动力粘滞系数的实际应用动力粘滞系数在科学研究和工程应用中有着广泛的应用。
