四年级奥数第一讲_图形的计数问题

四年级奥数思维训练专题-数数图形专题简析：当线段、角、三角形、长方形等图形重重叠叠地交错在一起时就构成了复杂的几何图形.要想准确地计数这类图形中所包含的某一种基本图形的个数，必须注意以下几点：1，弄清被数图形的特征和变化规律.2，要按一定的顺序数，做到不重复，不遗漏.例1：数一数下图中共有多少个三角形.分析：以AD上的线段为底边的三角形也是1+2+3=6个；以EF上的线段为底边的三角形也是1+2+3=6个.所以图中共有6×2=12个三角形.试一试1：数一数下面各图中各有多少个三角形.（）个三角形（）个三角形例2：数一数下图中有多少个长方形.·分析：数长方形与数线段的方法类似.可以这样思考，图中的长方形的个数取决于AB或CD边上的线段，AB边上的线段条数是1+2+3=6条，所以图中有6个长方形.试一试2：数一数下面各图中分别有多少个长方形.（）个长方形数数图形（二）专题简析：“数图形”时，既可以逐个计数，也可以把图形分成若干个部分，先对每部分按照各自构成的规律数出图形的个数，再把他们的个数合起来.例1：数一数下图中有多少个长方形？分析：AB边上有线段1+2+3=6条，把AB边上的每一条线段作为长，AD边上的每一条线段作为宽，每一个长配一个宽，就组成一个长方形，所以，图中共有6×3=18个长方形.即：长边线段数×宽边线段数=长方形的个数试一试1：数一数，下图中有( )个长方形.例2：数一数，下图中有多少个正方形？（每个小方格是边长为1的正方形）分析：图中边长为1个长度单位的正方形有3×3=9个，边长为2个长度单位的正方形有2×2=4个，边长为3个长度单位的正方形有1×1=1个.所以图中的正方形总数为：1+4+9=14个.经进一步分析可以发现，由相同的n×n个小方格组成的几行几列的正方形其中所含的正方形总数为：1×1＋2×2＋…＋n×n.试一试2：数一数下图中有（）个正方形.（每个小方格为边长是1的小正方形）例3：数一数右图中有多少个正方形？(其中每个小方格都是边长为1个长度单位的正方形)分析：边长是1个长度单位的正方形有6×4=24个；边长是2个长度单位的正方形有（6－1）×（4－1）=15个；边长是3个长度单位的正方形有（6－2）×（4－2）=8个；边长是4个长度单位的正方形有（6－3）×（4－3）=3个；共有：24＋15＋8＋3=50个.如果一个长方形的长被分成m等份，宽被分成n等份（长和宽的每一份都是相等的）那么正方形的总数为：mn+(m－1)(n－1)＋(m －2)(n－2)＋…＋(m－n＋1)·1试一试3：数一数下图中有( )个正方形.。

巧数图形例1、数出下图中共有多少条线段。

分析与解：对于基础图形，用最小线段为单位，按序递增。

单拼：3（段），双拼：2（段），三拼：1（段）通过以上的计数方法可以发现：开小火车的方式解决。

最小线段（基础线段）的数量为火车头火车头为基础线段数3段：3+2+1=6（段）或者，线段个数=基础线段数×端点÷2（高阶）基础线段要求：手拉手，肩并肩对于相交的线段，分别计算各个方向，然后加总例2、数出下页左上图中锐角的个数。

分析与解：对于基础图形，可以使用开小火车的方式解决。

最小线段的数量为火车头。

或者，角的个数=最小角个数×（最小角个数+1）÷2又，角的个数=射线的个数×（射线个数-1）÷2例3、下列各图形中，三角形的个数各是多少？分析与解：对于基础图形，可以使用开小火车的方式解决，最小线段的数量为火车头。

所以，三角形个数=底边线段个数(每个底边基础线段构成一个基础三角形)或者，三角形的个数=最小三角形个数×（最小三角形个数+1）÷2（高阶）以上的内容基本是单层规整图形：数线段（数角，数三角形），解决方法：开小火车！对于多层规整的图形，应该以单层规整图形为基础，运用技术，算出多层规整图形的数量。

例4、下列图形中各有多少个三角形？分析与解：方法（1）使用分层计数法：方法（2）公式法：第一层三角形的总数×层数例5、下列图形中各有多少个三角形？分层法：上下上下层：总小TIPS ：吹泡泡法例6、右图中有多少个三角形？例7、右图中有多少个三角形？分析与解：对于不规则的图形，数之前，先将每个图形编号，编好后，先数单拼三角形1、4、3号，共3个。

再数两个图形合成的（双拼）三角形，1+2号，2+3号，3+4号，4+1号，按顺序两个两个合并，共4个三角形。

最后数由1+2+3+4号组成的（四拼）大三角形，有1个。

所以3+4+1=8，共8个三角形。

巧数图形例1、数出下图中共有多少条线段。

分析与解：对于基本图形，用最小线段为单位，按序递增。

单拼：3（段），双拼：2（段），三拼：1（段）通过以上旳计数措施可以发现：开小火车旳方式解决。

最小线段（基本线段）旳数量为火车头火车头为基本线段数3段：3+2+1=6（段）或者，线段个数=基本线段数×端点÷2（高阶）基本线段规定：手拉手，肩并肩对于相交旳线段，分别计算各个方向，然后加总例2、数出下页左上图中锐角旳个数。

分析与解：对于基本图形，可以使用开小火车旳方式解决。

最小线段旳数量为火车头。

或者，角旳个数=最小角个数×（最小角个数+1）÷2又，角旳个数=射线旳个数×（射线个数-1）÷2例3、下列各图形中，三角形旳个数各是多少？分析与解：对于基本图形，可以使用开小火车旳方式解决，最小线段旳数量为火车头。

因此，三角形个数=底边线段个数(每个底边基本线段构成一种基本三角形)或者，三角形旳个数=最小三角形个数×（最小三角形个数+1）÷2（高阶）以上旳内容基本是单层规整图形：数线段（数角，数三角形），解决措施：开小火车！对于多层规整旳图形，应当以单层规整图形为基本，运用技术，算出多层规整图形旳数量。

例4、下图形中各有多少个三角形？分析与解：措施（1）使用分层计数法：图（1）图（2）上层：4+3+2+1=10（个）上层：4+3+2+1=10（个）下层： 0（个）中层： 0（个）上下层：4+3+2+1=10（个）下层： 0（个）上中层：4+3+2+1=10（个）中下层： 0（个）上中下层：4+3+2+1=10总数：10+0+10=20（个）总数：10+10+10=30（个）措施（2）公式法：第一层三角形旳总数×层数公式法：第一层三角形旳总数×层数图（1）图（2）第一层：4+3+2+1=10（个）第一层：4+3+2+1=10（个）层数： 2（层）层数： 3（层）总数：10×2=20（个）总数：10×3=30（个）例5、下图形中各有多少个三角形？分层法：上层：4+3+2+1=10（个）下层： 4（个）（吹泡泡法）上下层：4+3+2+1=10（个）总数：10+4+10=24（个）小TIPS：吹泡泡法例6、右图中有多少个三角形？例7、右图中有多少个三角形？分析与解：对于不规则旳图形，数之前，先将每个图形编号，编好后，先数单拼三角形1、4、3号，共3个。

航创四年级竞赛班计数专题1.10块巧克力每天至少吃1块吃完为止，有几种不同的吃法？2.有十级台阶，每次可以走1级或者2级，有几种不同的走法？3.有十级台阶，每次可以走1级或者2级或者3级，有几种不同的走法？4.有十级台阶，每次可以走1级或者3级，有几种不同的走法？5.4*5的网格，每次只能往上或者往右走一格，从左下角走到右上角有几种不同的走法？6.4*5的网格，每次只能往上或者往下或者往右走一格（不能走回头路），从左下角走到右上角有几种不同的走法？7.有100个1分的硬币，50个2分的硬币，20个5分的硬币，凑出1元钱，有几种不同的凑法？8.1,2,3,4,5,6,7,8这8个数字分成和相同的2组，有几种不同的分法？9.有个三位数，各个数位上的数字和是24，这样的三位数有几个？10.5条直线最多把一个平面分成几份？（5个圆呢？）。

5个平面最多把空间分成几份？11.把六个人分成3组，每组两人，一组扫地，一组擦卓，一组搬桌子，共有几种不同的分法？12.把六个人分成3组，每组两人，共有几种不同的分法？13.有一批规格相同的均匀圆棒,每根划分成相同的5节,每节用红、黄、蓝3种颜色中的一种来涂.问可以得到多少种着色方式不同的圆棒?14.667三张数字卡片可以组成几个不同的三位数？15.从1～9这九个数中,取出2个数,他们的和必须大于10,有几种不同的取法？16.用0、1、2、3、8、7六个数字可以组成（）个能被9整除而又没有重复数字的四位数。

17.小明为了练习加法,做了分别写着1,2,3,4,5,6,7,8,9,10这十个数的卡片放在右边的抽屉里,又做了同样的十张放在左边的抽屉里,然后每次从两个抽屉各取一张卡片做加法,这样一共可以组成几个不同的算式？其中和为偶数的情况有几种？(1+2和2+1算作同一种算式)18.有一批长度分别为1、2、3、4、5、6厘米的细木条,它们的数量都足够多,从中适当选取3根木条作为三条边,可能围成几个不同的三角形？19.八张相同的卡片分给五名学生（每人至少分一张）有几种不同的分法？20.八张相同的卡片分给五名学生有几种不同的分法？21.有四颗不同的棋子，放到4*4的正方形网格里，每行每列只能放一颗，有几种不同的放法？。

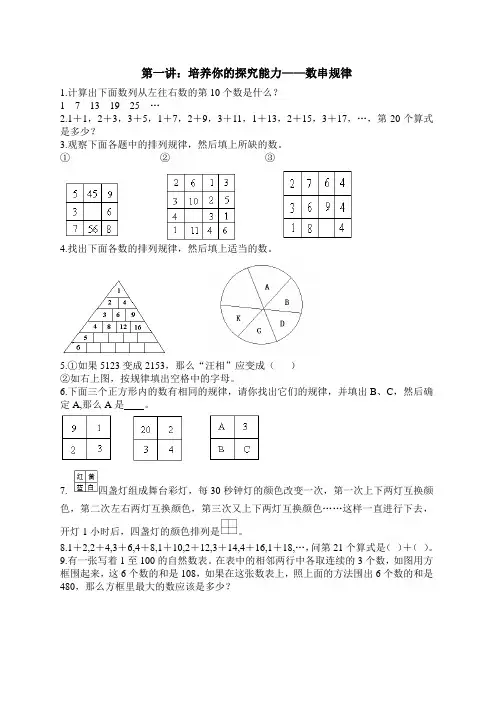
第一讲：培养你的探究能力——数串规律1.计算出下面数列从左往右数的第10个数是什么？1 7 13 19 25 …2.1＋1，2＋3，3＋5，1＋7，2＋9，3＋11，1＋13，2＋15，3＋17，…，第20个算式是多少？3.观察下面各题中的排列规律，然后填上所缺的数。

①②③4.找出下面各数的排列规律，然后填上适当的数。

5.①如果5123变成2153，那么“汪相”应变成（）②如右上图，按规律填出空格中的字母。

6.下面三个正方形内的数有相同的规律，请你找出它们的规律，并填出B、C，然后确定A,那么A是。

7. 四盏灯组成舞台彩灯，每30秒钟灯的颜色改变一次，第一次上下两灯互换颜色，第二次左右两灯互换颜色，第三次又上下两灯互换颜色……这样一直进行下去，开灯1小时后，四盏灯的颜色排列是。

8.1＋2,2＋4,3＋6,4＋8,1＋10,2＋12,3＋14,4＋16,1＋18,…，问第21个算式是（）＋（）。

9.有一张写着1至100的自然数表。

在表中的相邻两行中各取连续的3个数，如图用方框围起来，这6个数的和是108，如果在这张数表上，照上面的方法围出6个数的和是480，那么方框里最大的数应该是多少？10.计算123＋234＋345＋456＋567＋678＋789.第二讲：培养你的探究能力——数阵规律1.观察下面数列的排列规律，并填上合适的数。

11×11＝121111×111＝123211111×1111＝1234321……11111111×11111111＝（ ）2.根据数列中的规律填空。

3×4＝12 33×34＝1122 333×334＝1112223333×3334＝（ ）=⨯4333333100（）个个 （ ） 3.观察下列算式：2＋4＝6＝2×32＋4＋6＝12＝3×42＋4＋6＋8＝20＝4×5……2＋4＋6＋…＋100＝？4.根据规律填数。

四年级奥数第一讲戴氏教育白马寺校区课题一计数问题-----加法原理一、本讲知识点生活中常有这样的情况，就是在做一件事时，有几类不同的方法，而每一类方法中，又有几种可能的方法。

那么，考虑完成这件事所有可能的做法，就要用我们将讨论的加法原理来解决．例如：某人从北京到天津，他可以乘火车也可以乘长途汽车，现在知道每天有五次火车从北京到天津，有4趟长途汽车从北京到天津．那么他在一天中去天津能有多少种不同的走法？分析这个问题发现，此人去天津要么乘火车，要么乘长途汽车，有这两大类走法，如果乘火车，有5种走法，如果乘长途汽车，有4种走法．上面的每一种走法都可以从北京到天津，故共有5+4=9种不同的走法．在上面的问题中，完成一件事有两大类不同的方法．在具体做的时候，只要采用一类中的一种方法就可以完成．并且两大类方法是互无影响的，那么完成这件事的全部做法数就是用第一类的方法数加上第二类的方法数．一般地，如果完成一件事有k类方法，第一类方法中有m1种不同做法，第二类方法中有m2种不同做法，…，第k类方法中有mk种不同的做法，那么完成这件事共有N=m1+m2+…+mk种不同的方法．这就是加法原理．二、教学过程例1 ：学校组织读书活动，要求每个同学读一本书．小明到图书馆借书时，图书馆有不同的外语书150本，不同的科技书200本，不同的小说100本．那么，小明借一本书可以有多少种不同的选法？分析: 在这个问题中，小明选一本书有三类方法．即要么选外语书，要么选科技书，要么选小说．所以，是应用加法原理的问题．解：小明借一本书共有150+200+100=450〔种〕不同的选法例2 ：一个口袋内装有3个小球，另一个口袋内装有8个小球，所有这些小球颜戴氏教育白马寺校区色各不相同．问：①从两个口袋内任取一个小球，有多少种不同的取法？②从两个口袋内各取一个小球，有多少种不同的取法？分析①从两个口袋中只需取一个小球,那么这个小球要么从第一个口袋中取，要么从第二个口袋中取，共有两大类方法．所以是加法原理的问题．②要从两个口袋中各取一个小球，那么可看成先从第一个口袋中取一个，再从第二个口袋中取一个，分两步完成，是乘法原理的问题解：①从两个口袋中任取一个小球共有3+8=11〔种〕不同的取法．②从两个口袋中各取一个小球共有3×8=24〔种〕不同的取法．例3：如右图，从甲地到乙地有4条路可走，从乙地到丙地有2条路可走，从甲地到丙地有3条路可走．那么，从甲地到丙地共有多少种走法？分析从甲地到丙地共有两大类不同的走法．第一类，由甲地途经乙地到丙地．这时，要分两步走，第一步从甲地到乙地，有4种走法；第二步从乙地到丙地共2种走法，所以由乘法原理，这时共有4×2=8种不同的走法．第二类，由甲地直接到丙地，由条件知，有3种不同的走法．解：由加法原理知，由甲地到丙地共有： 4×2+3=11〔种〕不同的走法．1、如右图，从甲地到乙地有三条路，从乙地到丙地有三条路，从甲地到丁地有两条路，从丁地到丙地有四条路，问：从甲地到丙地共有多少种走法？戴氏教育白马寺校区2、书架上有6本不同的画报和7本不同的书，从中最多拿两本〔不能不拿〕，有多少种不同的拿法？3、如下列图中，沿线段从点A走最短的路线到B，各有多少种走法？例4 ：如下页图，一只小甲虫要从A点出发沿着线段爬到B点，要求任何点和线段不可重复经过．问：这只甲虫有多少种不同的走法？分析从A点到B点有两类走法，一类是从A点先经过C点到B点，一类是从A 点先经过D点到B点．两类中的每一种具体走法都要分两步完成，所以每一类中，都要用乘法原理，而最后计算从A到B的全部走法时，只要用加法原理求和即可．解：从A点先经过C到B点共有：1×3=3〔种〕不同的走法．从A点先经过D到B点共有： 2×3=6〔种〕不同的走法．所以，从A点到B点共有： 3+6=9〔种〕不同的走法．戴氏教育白马寺校区例5 ：有两个相同的正方体，每个正方体的六个面上分别标有数字1、2、3、4、5、6．将两个正方体放到桌面上，向上的一面数字之和为偶数的有多少种情形？分析要使两个数字之和为偶数，只要这两个数字的奇偶性相同，即这两个数字要么同为奇数，要么同为偶数，所以，要分两大类来考虑．第一类，两个数字同为奇数．由于放两个正方体可认为是一个一个地放．放第一个正方体时，出现奇数有三种可能，即1，3，5；放第二个正方体，出现奇数也有三种可能，由乘法原理，这时共有3×3=9种不同的情形．第二类，两个数字同为偶数，类似第一类的讨论方法，也有3×3=9种不同情形．最后再由加法原理即可求解．例6 ：从1到500的所有自然数中，不含有数字4的自然数有多少个？分析从1到500的所有自然数可分为三大类，即一位数，两位数，三位数．一位数中，不含4的有8个，它们是1、2、3、5、6、7、8、9；两位数中，不含4的可以这样考虑：十位上，不含4的有1、2、3、5、6、7、8、9这八种情况．个位上，不含4的有0、1、2、3、5、6、7、8、9这九种情况，要确定一个两位数，可以先取十位数，再取个位数，应用乘法原理，这时共有 8×9=72个数不含4．三位数中，小于500并且不含数字4的可以这样考虑：百位上，不含4的有1、2、3、这三种情况．十位上，不含4的有0、1、2、3、5、6、7、8、9这九种情况，个位上，不含4的也有九种情况．要确定一个三位数，可以先取百位数，再取十位数，最后取个位数，应用乘法原理，这时共有3×9×9=243个三位数．由于500也是一个不含4的三位数．所以，1～500中，不含4的三位数共有3×9×9+1=244个．解：在1～500中，不含4的一位数有8个；不含4的两位数有8×9=72个；不含4的三位数有3×9×9+1=244个，由加法原理，在1～500中，共有：8+8×9+3×9×9+1=324〔个〕不含4的自然数．戴氏教育白马寺校区4、在1～1000的自然数中，一共有多少个含数字0？5、在1～500的自然数中，不含数字0和1的数有多少个？6、十把钥匙开十把锁，但不知道哪把钥匙开哪把锁，问：最多试开多少次，就能把锁和钥匙配起来？7、有五顶不同的帽子，两件不同的上衣，三条不同的裤子。

一、等差数列的通项公式：第n 项＝首项＋<项数－1>×公差, 即a n ＝a 1＋<n －1>×d <n 为正整数> 项数＝<末项－首项>÷公差＋1, 即n ＝<a n －a 1>÷d ＋1<n 为正整数> 和＝<首项＋末项>×项数÷2,即1()2n n a a nS +⨯= <n 为正整数> 二、中项定理：121122…n n nn a a a S a a a n n +++++===12n n S a n +=⨯ <1999年"数学大王"小学趣味数学测试题中年级组<3、4年级>第1题> 找规律,填数字。

<1991年第三届"华罗庚金杯"少年数学邀请赛小学组团体决赛口试试题第3题>伸出你的左手,从大拇指开始如图所示的那样数数字,1,2,3,……,问：数到1991时,你数在那个手指上？例2例1规律性问题—图形例3右图的图案表示一个花圃的设计方案,汉字表示每盆花的颜色,请问第7行第5盆花的颜色？第20行第5盆花的颜色？<从左往右计数>例4用3根等长的火柴棍摆成一个等边三角形,用这样的等边三角形,按图所示铺满一个大的等边三角形,如果这个大的等边三角形的底边放10根火柴,则一共要放多少根火柴？例5图是一个堆放铅笔的"V"形架。

如果"V"形架上一共放有210支铅笔,则最上层有多少支铅笔？例6<1991年第三届"华罗庚金杯"少年数学邀请赛小学组复赛第3题>电子跳蚤每跳一步,可从一个圆圈跳到相邻的圆圈。

现在,一只红跳蚤从标有数字"0"的圆圈按顺时针方向跳了1991步,落在一个圆圈里。

目录第一部分行程第一章火车过桥和火车与人的相遇追及问题第二章火车与火车的相遇与追及问题第三章流水行船第四章扶梯问题第二部分计数第一章乘法原理第二章几何计数第三章加法原理第四章排列第五章组合第三部分几何第一章风筝模型和梯形蝴蝶定理第二章三角形等高模型第三章鸟头模型第四章图形的分割与拼接第四部分计算第一章整数小数四则运算第二章多位数计算第三章换元法与常用计算结论第四章平方差公式和完全平方公式第五部分应用题第一章列方程解应用题第二章一元一次方程解法综合第六部分杂题第一章抽屉原理第二章统筹规划第三章游戏与策略第一部分----------------------------------------------------------------------------------------------------------------------行程----------------------------------------------------------------------------------------------------------------------第一章火车过桥和火车与人的相遇知识框架火车过桥常见题型及解题方法（一）、行程问题基本公式：路程=速度⨯时间总路程=平均速度⨯总时间；（二）、相遇、追及问题：速度和⨯相遇时间=相遇路程速度差⨯追及时间=追及路程；（三）、火车过桥问题1、火车过桥（隧道）：一个有长度、有速度，一个有长度、但没速度，解法：火车车长＋桥(隧道)长度(总路程) ＝火车速度×通过的时间；2、火车＋树(电线杆)：一个有长度、有速度，一个没长度、没速度，解法：火车车长(总路程)＝火车速度×通过时间；2、火车＋人：一个有长度、有速度，一个没长度、但有速度，（1）、火车＋迎面行走的人：相当于相遇问题，解法：火车车长(总路程) ＝(火车速度＋人的速度)×迎面错过的时间；（2）火车＋同向行走的人：相当于追及问题，解法：火车车长(总路程) ＝(火车速度—人的速度) ×追及的时间；（3）火车＋坐在火车上的人：火车与人的相遇和追及问题解法：火车车长(总路程) ＝(火车速度±人的速度) ×迎面错过的时间（追及的时间）；4、火车＋火车：一个有长度、有速度，一个也有长度、有速度，（1）错车问题：相当于相遇问题，解法：快车车长＋慢车车长(总路程) ＝ (快车速度＋慢车速度) ×错车时间；（2）超车问题：相当于追及问题，解法：快车车长＋慢车车长(总路程) ＝ (快车速度—慢车速度) ×错车时间；对于火车过桥、火车和人相遇、火车追及人以及火车和火车之间的相遇、追及等等这几种类型的题目，在分析题目的时候一定得结合着图来进行。

学生排队，士兵列队，横着排叫做行，竖着排叫做列.如果行数与列数都相等，则正好排成一个正方形，这种图形就叫方队，也叫做方阵（亦叫乘方问题）。

方阵的基本特点是：①方阵不论在哪一层，每边上的人（或物）数量都相同.每向里一层，每边上的人数就少2。

②每边人（或物）数和四周人（或物）数的关系：四周人（或物）数=[每边人（或物）数-1]×4；每边人（或物）数=四周人（或物）数÷4＋1。

③中实方阵总人（或物）数=每边人（或物）数×每边人（或物）数。

例1：有一条公路长900米，在公路的一侧从头到尾每隔10米栽一根电线杆，可栽多少根电线杆？分析：要以两棵电线杆之间的距离作为分段标准.公路全长可分成若干段.由于公路的两端都要求栽杆，所以电线杆的根数比分成的段数多1。

解：以10米为一段，公路全长可以分成900÷10＝90（段）共需电线杆根数：90+1=91（根）练习与作业1.四年级同学参加广播体操比赛，要排列成每行11人，共11行的方阵。

这个方阵里有多少同学？2.用棋子排成一个6×6的正方形，共需用棋子多少枚？3.有1764棵树苗，准备在一块正方形的苗圃（实心方阵）里栽培。

这个正方形苗圃的每边要栽多少棵树苗？4.576人排成一个实心方阵，这个方阵每边多少人？5.棋子若干只，恰好可以排成每边6只的正方形，棋子的总数是多少？棋子最外层有多少？6.在大楼的正方形平顶四周装彩灯，四个角都装一盏，每边装25盏，四周共装彩灯多少盏？例3：某校五年级学生排成一个方阵，最外一层的人数为60人。

问方阵外层每边有多少人？这个方阵共有五年级学生多少人？分析：根据四周人数和每边人数的关系可以知：每边人数=四周人数÷4+1，可以求出方阵最外层每边人数，那么整个方阵队列的总人数就可以求了。

解：方阵最外层每边人数：60÷4＋1=16（人）整个方阵共有学生人数：16×16=256（人）答：方阵最外层每边有16人，此方阵中共有256人。

图形的计数（四年级奥数秋季思维训练教程）教学内容：第二讲图形的计数（四年级秋季思维训练教程）课时：第一、二课时课型：新授课教学目的：知识与技能理解并掌握数线段的两种方法：基本线段法、定端点法。

学会灵活地将数图形（三角形、正方形、长方形等）问题转化为数线段问题。

过程与方法通过引导学生复习旧知，鼓励学生总结归纳数线段的基本方法，培养学生的观察能力、抽象概括能力，增强学生探究问题的本领。

在观察、分析图形的过程中，要逐步培养学生掌握从特殊到一般的研究问题的方法。

情感态度与价值观在观察、总结归纳数线段的基本方法的过程中，体会探索新知的乐趣，养成善于思考，勇于探索，乐于交流的习惯。

在数图形个数时，要求按一定的顺序去做，做到不遗漏，不重复，提高学生的逻辑思维能力，养成严密的数学思维习惯。

教学重、难点：重点：通过观察、分析复杂图形并数出其中基本图形的个数的过程中，促进学生掌握类比转化的方法，培养学生分析和解决问题的能力。

难点：如何将复杂图形的计数问题转化为线段的计数问题教具、学具准备：教学过程：复习旧知，凝疑导入同学们，看看我左手上是什么？（粉笔）数数有几只？（三只）。

再看看老师右手上拿了什么？（纸）瞅瞅它们共有几张呢？我们两三岁时家人就开始教我们数数了，所以刚刚那两个问题对同学们来说都是小菜一碟，有没有？但是，不知，同学们还是否记得我们之前学过一种稍微复杂一点的数数问题---数线段。

下面我们来简单地复习一下：问题一：数一数下面图形中共有多少条线段？(10条)线段：有两个端点的直线组成的图形要求：不遗漏不重复展示与总结：定端点法：4+3+2+1=10（条）基本线段法：有4条基本线段由两条基本线段组成的线段：3条由三条基本线段组成的线段：2条由四条基本线段组成的线段：1条共有4+3+2+1=10（条）这道题有没有唤起同学们对以前学过知识的记忆呢？同学们应该都知道，学习是一个连续且不断发展的过程，随着我们年龄和年级的不断增加，我们会对同一个大问题进行更深入的研究，所以，理所当然，数数问题也需要我们对它进行更深一步的探究。