线性规划在炼油厂的优化问题中的应用

炼油企业生产计划的优化炼油企业生产计划的优化加强炼油企业的生产计划优化工作，能更好地为炼油生产提供科学性指导和控制，根据市场及装置运行情况确定生产方案及生产方向，避免无计划生产偏离企业经营方向，能对企业的原油加工品种、生产流程、产品结构做出最优设计，保证企业按预期方向运行，大幅提高企业经济效益。

那么如何实现炼油企业生产计划的优化呢？一、炼油生产计划的重要性炼油生产计划管理是炼油生产管理的首要环节，炼油生产计划的制定主要是根据产品的市场需求、原料的供应情况、企业的生产能力等，在保证安全生产前提下，利用企业现有生产能力以经济效益最大化为目标，优化组织生产。

二、生产计划的编制方法炼油企业生产计划的编制方法主要有以下几种：经验编制方法、线性规划方法和流程模拟编制方法。

1.经验方法计划人员在多年生产实践的基础上，按企业当前原(料)油资源及装置实际运行情况，根据原油及产品市场情况制定计划。

经验方法做出的生产计划准确性及时效性差，受计划编制人员业务水平及主观判断能力影响较大，对当今规模大、复杂性高的大型炼厂而言，手工编制生产计划显然已经无法满足生产要求。

2.线性规划方法炼油厂生产流程基本符合线性规划模型，通过建立原油及装置相关数据库，采用线性规划与递归(如PIMS软件)，以整体效益最大化为原则，可以实现原油品种选择、中间物料流向、产品产量的自动优化，特别适合大型炼厂使用。

缺点是不能反映装置机理模型，当装置工艺条件发生重大变化时测算会出现误差。

3.流程模拟方法通过对炼油厂生产的全流程模拟来编制生产计划(如RSIM软件)，准确度高，能准确反映装置操作条件变化影响，但需操作人员具备相当水平的全厂各装置相关知识。

其软件涉及变量多、范围广、复杂程度高、运算时间长，多数软件不能进行物料及产品的自动优化，一般用于对单个装置进行优化。

三、生产计划优化应用生产计划优化主要从加工原油品种、中间物料流向、产品结构调整等三个方面进行，目的是实现经济效益最大化。

【精品】运筹学建模炼油厂生产计划安排炼油厂生产计划安排是一个重要的运筹学问题，具有重大的经济意义。

在全球石油市场竞争日益激烈，高效而稳定的生产计划安排尤为重要。

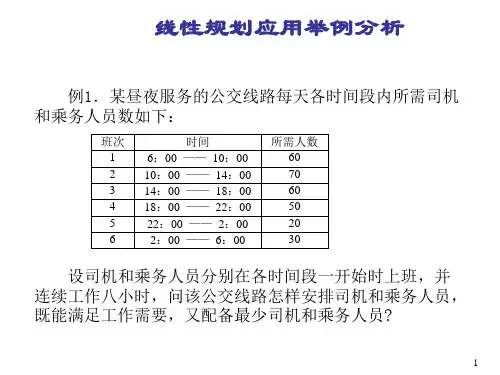
本文将从炼油厂生产计划安排的目标、限制条件、决策变量等方面进行建模，提出一种基于整数线性规划的求解方法。

1.目标炼油厂生产计划安排的主要目标是在满足市场需求和质量要求的前提下，最大化利润。

炼油厂的产量、品质和价格都受到全球油价、市场需求和竞争压力等因素的影响。

因此，生产计划需要考虑这些因素，并调整产量、产品质量和价格以实现最优利润。

2.限制条件炼油厂生产计划安排面临的限制条件主要包括炼油过程的技术、能源和环保要求，以及市场需求和产品品质等方面的限制。

具体包括以下内容：（1）技术限制：炼油厂生产过程中需要考虑到不同原油的处理和混合要求、反应温度、反应时间、催化剂的使用和修复、设备维修等一系列技术问题，其过程为一个复杂的非线性系统。

（2）能源限制：炼油过程需要消耗大量的能源，包括燃料油、天然气、蒸汽和电力等。

因此，生产计划需要考虑到能源的供应和利用效率。

（3）环保限制：炼油厂需要遵守国家和地方的环保要求，如废气排放标准、各类废物处理等。

（4）市场需求限制：生产计划需要考虑到市场需求的波动和变化，满足市场需求也是炼油厂生产计划安排中的一个重要限制条件。

（5）产品品质限制：生产计划需要考虑到产品品质的要求，如硫含量、密度、粘度、凝点、闪点、车用油或航空燃油等不同产品的规格要求。

3.决策变量炼油厂生产计划安排的决策变量主要包括各种原油的混合比例、各种产品的产量、产品价格、设备的维修和更换等。

具体分为：（1）原油混合比例：生产计划需要确定各种原油的混合比例，以达到生产要求。

（2）产品产量：生产计划需要确定不同产品的产量，包括各种汽油、润滑油、航空燃油等。

（3）产品价格：生产计划需要确定产品的价格，以最大化利润。

（4）设备维修和更换：生产计划需要考虑设备的维修和更换，以确保生产的连续性和稳定性。

线性规划在生产调度中的应用随着现代化生产工艺的不断发展，生产调度的难度和复杂度不断提高。

如何在不影响产品质量和生产效率的前提下，合理安排生产计划和资源分配成为了生产调度的重要问题。

线性规划是一种优化方法，广泛应用于生产调度问题的解决中。

它是优化问题中的一种数学模型，通过对不同生产环节的收益和成本进行数量化，进行资源分配的最优化设计与调度。

线性规划方法可以考虑各种限制条件和约束条件，从而实现对生产调度过程的最优化控制。

一般来说，线性规划方法适用于那些可流程化、重复性强的生产过程。

具体来说，它展现强大的适用性是在那些需要确定并管理复杂的原材料、半成品和最终产品流程的项目上。

在某些情况下，线性规划还可以用于改善生产过程中的现有方法和系统。

通过引入智能算法和预测模型，使得在线性规划模型中考虑到现有的实施、检测和反馈环节，可以达到更好的生产调度效果。

在生产调度中，线性规划方法的应用主要包括以下几个方面：1. 生产线优化生产线优化是线性规划最主要的应用领域之一。

它旨在通过有效的生产线管理，最大化生产效率和产量，同时降低生产成本。

利用线性规划算法，可以建立智能化的生产线管理模型。

该模型可以针对各种生产调度条件，快速合理安排生产计划和资源分配。

同时，该模型还可以预测生产线瓶颈点，及时进行调整和优化，最大化生产效率。

2. 物流调度物流调度是另一个重要的领域，它主要涉及到货物的快速分配和交付。

通过在物流调度中应用线性规划，可以针对不同的物流环节，建立最优化的调度模型。

例如，在货运运输中，线性规划可以用来优化装货和卸货的顺序，以提高卡车的利用率。

该模型可以考虑到货物的体积、重量、装卸时间、运输距离等各种因素，制定最优的运输计划。

3. 库存管理库存管理是另一个与线性规划密切相关的领域。

在库存管理中，线性规划可以应用于控制物料和成品的库存水平。

通过建立一个有效的库存管理模型，可以避免因过多库存或过少库存导致的资源浪费和生产滞涨的问题。

运筹学案例分析报告—炼油厂生产计划安排班级：1516122组号：6姓名、学号（组长、分工）：吴锴楠151612219、建立数学模型（组员、分工）：张灿龙151612220、编写报告（组员、分工）：游泽锋151612222、编写lingo程序一.案例描述某炼油厂的工艺流程图如下图1。

炼油厂输入两种原油（原油1和原油2）。

原油先进入蒸馏装置，每桶原油经蒸馏后的产品份额见表1，其中轻、中、重石脑油的辛烷值分别为90、80和70。

表1轻石脑油中石脑油重石脑油轻油重油渣油原油1 0.1 0.2 0.2 0.12 0.2 0.13原油2 0.15 0.25 0.18 0.08 0.19 0.12 石脑油部分直接用于发动机油混合，部分输入重整装置，得辛烷值为115的重整汽油。

1桶轻、中、重石脑油经重整后得到的重整汽油分别为0.6、0.52、0.45桶。

蒸馏得到的轻油和重油，一部分直接用于煤油和燃料油的混合，一部分经裂解装置得到裂解汽油和裂解油。

裂解汽油的辛烷值为105。

1桶轻油经裂解后得到0.28桶裂解汽油和0.68桶裂解油；1桶重油裂解后得到0.2桶裂解汽油和0.75桶裂解油。

其中裂解汽油用于发动机油混合，裂解油用于煤油和燃料油的混合。

渣油可直接用于煤油和燃料油的混合，或用于生产润滑油。

1桶渣油经处理后可得0.5桶润滑油。

混合成的发动机油高档的辛烷值应不低于94，普通的辛烷值不低于84。

混合物的辛烷值按混合前各油料辛烷值和所占比例线性加权计算。

规定煤油的气压不准超过1kg/cm2，而轻油、重油、裂解油和渣油的气压分别为1.0、0.6、1.5和0.05kg/cm2。

而气压的计算按各混合成分的气压和比例线性加权计算。

燃料油中，轻油、重油、渣油和裂解油的比例应为10：3：1：4。

已知每天可供原油1为20000桶，原油2为30000桶。

蒸馏装置能力每天最大为45000桶，重整装置每天最多重整10000桶石脑油，裂解装置能力每天最大为8000桶。

线性规划的应用引言概述：线性规划是一种数学优化方法，用于解决线性约束条件下的最优化问题。

它在许多领域都有广泛的应用，包括生产计划、资源分配、运输问题等。

本文将详细介绍线性规划的应用，并分为五个部分进行阐述。

一、生产计划的优化1.1 生产成本最小化：线性规划可用于确定生产计划，以最小化生产成本。

通过设定生产量的变量和成本的约束条件，可以得到最优的生产计划。

1.2 资源分配优化：线性规划可以帮助确定资源的最优分配，以满足生产需求。

通过考虑资源的供应量和需求量，可以得出最佳的资源分配方案。

1.3 生产效率提升：线性规划可以优化生产过程，提高生产效率。

通过考虑生产线上的各个环节和资源的利用率，可以得出最佳的生产安排，从而提升生产效率。

二、运输问题的解决2.1 最优运输方案：线性规划可用于解决运输问题，以确定最佳的运输方案。

通过考虑运输成本、运输量和运输距离等因素，可以得出最优的运输方案。

2.2 供应链优化：线性规划可以优化供应链的运作，以提高运输效率和降低成本。

通过考虑供应商、生产商和分销商之间的关系和需求，可以得出最佳的供应链优化方案。

2.3 库存管理：线性规划可用于优化库存管理，以最小化库存成本和满足需求。

通过考虑库存量、订购量和供应量等因素，可以得出最佳的库存管理方案。

三、资源分配问题的解决3.1 人力资源优化：线性规划可以优化人力资源的分配，以满足不同部门和项目的需求。

通过考虑人员的技能、工作量和工作时间等因素，可以得出最佳的人力资源分配方案。

3.2 资金分配优化：线性规划可用于优化资金的分配，以最大化利润或最小化成本。

通过考虑不同项目的收益和成本，可以得出最佳的资金分配方案。

3.3 能源利用优化：线性规划可以优化能源的利用，以提高能源效率和降低能源成本。

通过考虑不同能源的供应量和需求量，可以得出最佳的能源利用方案。

四、市场营销策略的制定4.1 定价策略优化：线性规划可用于优化产品定价策略，以最大化利润或市场份额。

线性规划在决策优化中的应用随着社会和经济的快速发展，各行各业都在不断地尝试优化自身的业务过程，以达到最高效、最优化的发展状态。

而决策优化则是实现这一目标的重要手段之一。

在决策优化中，线性规划是一种非常常见的方法。

线性规划，简称LP，是一种基于数学优化的方法，可以用来求解最大或最小值的问题。

LP问题的主要特点是目标函数和限制条件均为线性函数。

在实际应用中，LP问题经常出现在各种不同的领域，例如生产计划、运输与物流、金融投资、市场营销等。

一、LP的概述LP问题可以用下列形式进行表示：Max/minimize Z = c1x1 + c2x2 + … + cnxnSubject toa11x1 + a12x2 + … + a1nxn ≤ b1a21x1 + a22x2 + … + a2nxn ≤ b2am1x1 + am2x2 + … + amnxn ≤ bmwhere x1,x2, … , xn are the decision variables;c1,c2, … , cn are the coefficients of the objective function;a11,a12,…,a1n , a21,a22,…,a2n , … , am1,am2,…,amn are the coefficients of the constraints;b1,b2,… , bm are the right-hand side values of the constraints.LP问题的主要目标是求解使得目标函数最大（或最小）的决策变量的值，同时满足系统中的约束条件。

在LP问题中，所有的目标函数和约束条件均为线性函数，因此可以用数学方法求解这一问题。

通常情况下，LP问题可以使用单纯形法、对偶理论、内点法等方法求解，这些方法都是比较成熟的线性规划求解方法。

二、LP在生产计划中的应用生产计划是一个复杂的过程，需要深入分析不同因素的影响和相互关系，以实现生产过程的最优化。

线性规划的应用标题：线性规划的应用引言概述：线性规划是一种数学优化方法，用于求解线性约束条件下的最优解。

在现代社会中，线性规划被广泛应用于各个领域，如生产计划、资源分配、运输问题等。

本文将探讨线性规划在实际应用中的重要性和具体应用案例。

一、生产计划1.1 生产成本最小化：企业在生产过程中需要考虑成本问题，通过线性规划可以优化生产计划，使得成本最小化。

1.2 生产效率最大化：线性规划可以匡助企业合理安排生产资源，提高生产效率，实现生产效益最大化。

1.3 生产排程优化：通过线性规划可以制定合理的生产排程，避免生产过程中的资源浪费，提高生产效率。

二、资源分配2.1 人力资源优化：企业在进行人力资源分配时，可以利用线性规划方法，合理配置人员，提高工作效率。

2.2 资金分配优化：线性规划可以匡助企业合理分配资金，确保各项投资得到最大回报。

2.3 物资调配优化：在物资调配过程中，线性规划可以匡助企业合理安排物资的采购和使用，避免资源浪费。

三、运输问题3.1 最优运输路径：线性规划可以匡助企业确定最优的运输路径，降低运输成本，提高运输效率。

3.2 货物分配优化：在货物分配过程中，线性规划可以匡助企业合理分配货物，避免货物积压或者短缺情况。

3.3 运输成本最小化：通过线性规划可以优化运输计划，使得运输成本最小化，提高企业运输效益。

四、市场营销4.1 产品定价优化：线性规划可以匡助企业确定最优的产品定价策略，提高产品市场竞争力。

4.2 推广策略优化：在市场推广过程中，线性规划可以匡助企业制定合理的推广策略，提高市场覆盖率。

4.3 销售计划优化：通过线性规划可以优化销售计划，提高销售额，实现销售目标。

五、金融投资5.1 投资组合优化：线性规划可以匡助投资者优化投资组合，降低风险，提高回报率。

5.2 资产配置优化：在资产配置过程中，线性规划可以匡助投资者合理配置资产，实现资产增值。

5.3 风险控制优化：通过线性规划可以制定有效的风险控制策略，保护投资者的资产安全。

Vol.28No.4Apr.2012赤峰学院学报（自然科学版）Journal of Chifeng University （Natural Science Edition ）第28卷第4期（下）2012年4月1引言线性规划是运筹学的一个重要分支，它辅助人们进行科学管理，是国际应用数学、经济、管理、计算机科学界所关注的重要研究领域.线性规划主要研究有限资源的最佳分配问题，即如何对有限的资源进行最佳地调配和最有利地使用，以便于最充分发挥资源的效能来获取最佳的经济效益.线性规划运用数学语言描述某些经济活动的过程，形成数学模型，以一定的算法对模型进行计算，为制定最优计划方案提供依据[1].其解决问题的关键是建立符合实际情况的数学模型，即线性规划模型.在各种经济活动中，常采用线性规划模型进行科学、定量分析，安排生产组织与计划，实现人力物力资源的最优配置，获得最佳的经济效益.目前，线性规划模型被广泛应用于经济管理、交通运输、工农业生产等领域.石化企业是我国国民经济的支柱产业，因此，对企业资源的优化配置尤为重要.石化企业以石油和天然气为原材料，进行深加工和精加工，生产不同的石化产品，其生产过程具有原材料单一、生产流程稳定、工艺复杂和产品多样等特点，适合采用线性规划模型进行优化配置.本文根据石化企业生产经营过程的特点，应用线性规划方法，建立反映石化企业实际情况的线性规划模型，辅助决策者及时找到最优的决策方案，获得最大的经济效益.2线性规划的数学模型线性规划问题是求线性目标函数在线性约束条件下的最大值或最小值的问题.这类问题的数学表达式称为线性规划模型.线性规划模型的一般形式包括决策变量、约束条件和目标函数三部分.决策变量都是非负的，其值代表待解决问题的一个具体方案，形式如下：x 1,x 2,……，x n ≥0约束条件都是线性等式或线性不等式，它们反映了待解决问题对资源的客观限制及对所要完成的任务的各类要求，形式如下：a 11x 1+a 12x 2+……+a 1n x n =(>,<)b 1a 21x 1+a 22x 2+……+a 2n x n =(>,<)b 2………a m 1x 1+a m 2x 2+……+a m n x n =(>,<)b m其中，a ij 为第i 个约束条件中对应第j 个变量的约束条件系数，b i 是第i 个约束条件的右边常数，它表示必须满足的某种要求.目标函数是决策变量的线性函数，根据待解决问题的不同，可要求目标函数Z 实现最大值或最小值，形式如下：max(min)Z=c 1x x +c 2x x +…+c n x n其中，c 1，c 2，…，c n 是目标函数系数或价值系数.3线性规划模型在石化企业的应用3.1问题定义石化企业是由一系列的生产装置组成的复杂生产系统，其生产核心是各种生产装置.装置输入和输出的是源源不断的化学物质，包括工艺中生产装置处理的原料、半成品、添加剂和成品.装置的输入和输出都通过管线完成，管线起到连接各种生产装置和传递化学物质的作用.在实际生产过程中，每个生产装置可以采用多种不同的生产方案，根据不同的生产方案来生产满足市场需求的各种产品.通过分析，石化企业的生产经营过程的优化是一个线性规划问题，可以分解为目标函数、决策变量和约束条件三部分，通过在目标函数和约束条件下对决策变量进行求解，来获得最优的生产经营决策，产生最大的经济效益，从而保证所形成的生产计划更具有指导意义，为石化企业的生产经营管理提供更准确的依据.3.2线性规划模型的建立3.2.1选取决策变量根据石化企业生产经营过程优化的需要，选取原料量、各方案的进料量、侧线产品产量、实际销售的各成品的产量作为决策变量.例如：彩石原油、进口原油等原料用量，石脑油、拔头油、轻脱油、重脱油等侧线产品的产量，实际销售的90#汽油、93#汽油、0#柴油、－10#柴油等各成品产量.决策变量分别设为x 1，x 2，x 3，…，x n ，用x i （1≤i ≤n ）来表示.3.2.2确定目标函数石化企业的目标是实现经济效益最大化，即总利润最大.确定总利润时，不仅要考虑成品的总收入和原料成本，还线性规划模型的应用研究秦晓薇（赤峰学院，内蒙古赤峰024000）摘要：线性规划模型是科学与工程领域广泛应用的数学模型.本文应用线性规划模型，以石化企业为研究对象，以实现利润最大为目标，根据石化企业的特点和实际生产情况，分析了其生产经营过程线性规划模型的建立方法，并建立了能够正确反映石化企业的实际情况的线性规划模型.关键词：线性规划；数学模型；石化企业中图分类号：TP391文献标识码：A 文章编号：1673-260X （2012）04-0030-0230--需要考虑生产装置的各种加工费用，这里包括固定加工费用和可变加工费用.目标函数如下：maxF=∑r c r x r-∑iv i y i-∑k(a k+u k z k)r＝1，2，…，m；i＝1，2，…，n；k＝1，2，…，s其中，m表示成品的种类数，n表示原料的种类数，s表示生产装置的个数，cr 表示第r种成品的单价，xr表示第种成品的产量，vj 表示第j种原料的单价，yj表示第j种原料的消耗量，ak 表示第k个生产装置的固定加工费，uk表示第k个生产装置的单位可变加工费，z k表示第k个生产装置的加工量.3.2.3确定约束条件约束条件是由石化企业生产经营的特点和生产装置的性能决定的，它反映了决策变量与生产工艺流程参数之间必须遵循的关系.如果在建立模型时忽略了重要的约束条件，则求得的解不可信；但如果过于细微，约束条件数目增加，计算时间也将增加；同时由于变量多，关系复杂，比较容易给出互为矛盾的约束条件，造成模型无解.通过对石化企业生产工艺流程进行分析，根据其生产经营特点和装置性能，确定如下约束条件：（1）原料总量约束.石化企业的原料总量是有限的，在生产过程中，每种原料的加工量不能超过它的总量，否则会影响其他产品的产量.∑fx if≤d i，i＝1，2，…，n其中，n表示原料的种类，xif表示第i种原料在生产方案f中的加工量，ai表示第i种原料的总量.（2）侧线产品的产量约束.侧线定义为生产装置和管道中的出料，即中间产品.每个装置在一种方案下所生产的侧线产品总量与其所用的进料量必须平衡，如果相差太多，会影响模型最终结果的正确性.e jm in∑i x fi≤x jj≤e jm ax∑ix fj,f＝1，2，…，p；j＝1，2，…，q其中，p表示生产方案的个数，a表示侧线产品的种类，e jm in表示第j种侧线产品的收率下限，x jm ax表示第j种侧线产品的收率上限，xfi 表示生产方案f第i种进料的输入量，xfj表示生产方案f第j种侧线产品的输出量.（3）装置的最大处理能力约束.装置是石化企业的生产核心，每种产品都是通过不同的生产装置在不同的生产方案下生产加工而成，因此，要正确反映石化企业实际的生产经营情况，需要考虑装置的最大处理能力.生产过程中，每个装置的进料总量不能超过该装置的最大处理能力.∑i x i≤b其中，xi表示装置第i种进料的输入量，b表示装置的最大处理能力.（4）侧线产品的产用平衡约束.各个生产装置在不同温度、压力等条件下精炼出的产品，既可以去其它生产装置进行精加工，又可以去调合装置调和成品油，因此每个侧线产品的产量和其用量应满足物料平衡.∑ix li=∑jx lj，l＝1，2，…，e其中，e表示侧线产品的个数，xli表示第l个侧线产品的第i个产量，xlj表示第l个侧线产品的第j个用量.（5）生产装置投入产出平衡约束.生产装置在可行的生产方案下进行生产时，要保证生产装置的进料总量与侧线产量之间的平衡，否则就可能导致侧线产量和进料总量相差太多，影响结果的正确性.这个平衡方程通过生产方案的总收率来表示.e jm in∑ix fi≤x fj≤e jm ax∑ix fi，f＝1，2，…，m其中，m代表方案的个数，efm in代表方案f的总收率下限，efm ax代表方案l的总收率上限，xfi代表方案f第i种进料的输入量，xfj代表方案f第j种侧线产品的输出量.（6）成品平衡约束.成品有多种调合组分，成品是由各个组分调合而成，调合是由多种进料产生一种出料的过程，成品本身就是这种出料.成品的总量应该与所有的调合组分总量保持一致.∑jx rj≤x r，r＝1，2，…，m其中，m表示成品的种类，xr表示第r种成品的产量，xrj表示第r种成品的第j种组分的输入量.4结论线性规划模型必须能够准确直观的反映企业的生产状况，通过对所建立模型进行求解，可以获得最大经济效益，能够正确反映石化企业的实际情况，快速准确的找到最优方案，满足企业的生产能力和市场要求.线性规划模型通过科学、定量地分析各种因素，可以制定出经济效益最优的生产计划，实现石化企业的优化配置.———————————————————参考文献：〔1〕L.N.,Vasertein.Introduction of Linear Program-ming[M].北京：机械工业出版设，2006.1－99.〔2〕张国光，李朋辉.石化企业资源优化配置系统[J].石油化工自动化，2005（3）：51-53.〔3〕成孟金，李朋辉，赵振东，等.用线性规划模型解决石化企业产品结构优化[J].沈阳化工学院学报，2001，15（4）：278－281.31--。

浅谈线性规划在项目管理中对工期成本优化的应用作者：李鹏来源：《科技资讯》 2013年第25期李鹏(中国航空油料集团公司北京 100088)摘要:本论文以某油库增容工程项目进度管理为研究对象,将理论与实践相结合运用相关技术手段解决实际工作中的工期-成优化问题。

首先对项目进行了工作范围定义及工作结构分解,制定了各工作先后关系并估算出了工作持续时间,然后根据上述成果编制了项目网络图确定了各工作的时间参数并确定了关键路径。

接下来利用线性规划方法对本工程进行了工期-成本的优化,借用这些方法与技术为解决未来项目管理中类似问题提供了科学指导。

关键词:线性规划工期－成本项目管理中图分类号:C93 文献标识码:A 文章编号:1672-3791(2013)09(a)-0164-04本文以某油库扩建工程建设项目为例,该工程新建2座2000 m3的储油罐,1间油泵房、2间油车库,一座600 m3消防水池,并新建油罐区及其配套设施。

利用线性规划方法对工期压缩方案进行优化必选,从而选择出最节省费用的工期压缩方案。

1 工作分解结构首先对整个项目进行WBS分解,它是各类计划、预算与项目控制的基础,在此一号油罐工作分解结构为例,其他单项工程工作分解结构省略(图1、2）。

2 绘制单代号网络图根据项目工作先后关系及持续时间估算(此处省略)编制单代号网络图,得出单代号网络图为如(图3)所示。

3 确定各项工作时间参数和关键路径线路参数主要包括计算工期和计划工期,根据项目网络图可知网络计划的起点为施工准备阶段编码为12000。

根据公式计算最早开始时间、最早完成时间、最晚开始时间、最晚完成时间。

根据总时差＝LF－EF,总时差为“0”的活动为关键活动,因此关键路径如(表1)所示。

4 工期优化(1)根据本工程关键路线计算工期为TC＝101天,而合同工期TP＝91天。

根据实际情况得出每道工序的正常持续时间,合理持续时间和可压缩时间,如表2所示。

(2）合同工期为:△D=TC-TP=(101-91)=10天对关键路径上的各工作,计算得最大限度可压缩工期为101-28=73天。

线性规划应用线性规划解决实际问题线性规划应用：线性规划解决实际问题线性规划是一种数学优化方法，广泛应用于解决各种实际问题。

通过对线性函数和线性不等式进行约束，线性规划能够找到最佳解，使得目标函数在约束条件下达到最大或最小值。

在本文中，将探讨线性规划在解决实际问题方面的应用。

一、生产问题的线性规划在生产过程中，线性规划可以帮助企业制定最佳的生产方案。

例如，某家制造公司生产两种产品A和B，每天的生产时间有限。

产品A每单位可以获得100元的利润，产品B每单位可以获得80元的利润。

根据市场需求，每天销售量的上限是200个单位的A和150个单位的B。

此外，生产一个单位的产品A需要2小时，而生产一个单位的产品B需要3小时。

企业想要最大化每天的利润，应该如何分配生产时间？这个问题可以用线性规划来解决。

假设$x$代表生产的产品A数量，$y$代表生产的产品B数量。

则目标函数为$100x+80y$，约束条件为$2x+3y \leq T$，其中$T$为每天的生产时间（以小时为单位）。

另外还有约束条件$x \leq 200$（销售上限）和$y \leq 150$（销售上限），以及$x,y \geq 0$（生产数量非负）。

通过求解这个线性规划问题，可以得到最佳的生产方案，从而实现最大的利润。

二、资源分配问题的线性规划线性规划还可以应用于资源分配问题。

例如，某社区有一定数量的土地可供开发，而开发商希望在这块土地上建造住宅和商业用地，以获得最大的利润。

由于土地有限，住宅和商业面积的总和不能超过土地面积。

此外，开发商希望确保住宅面积至少是商业面积的2倍。

在给定土地面积和其他约束条件的情况下，该如何确定住宅和商业面积的最佳分配？这个问题可以建模为一个线性规划问题。

假设$x$代表住宅面积，$y$代表商业面积。

则目标函数为$x+y$，约束条件为$x+y \leq A$，其中$A$表示土地面积。

另外还有约束条件$x \geq 2y$（住宅面积至少是商业面积的2倍），以及$x,y \geq 0$（面积非负）。

线性规划模型在生产运营管理中的应用1.引言线性规划（linear programming, LP）是运筹学中一种常见的优化问题求解方法，它能够利用数学模型描述复杂的经济、工程、管理等问题，并在满足约束条件的前提下，寻求最优的决策方案。

在现代生产运营管理中，线性规划广泛应用于资源配置、生产计划、库存管理、物流配送等方面，为企业求得优化的决策提供了支持。

本文将重点介绍线性规划模型在生产运营管理中的应用。

2.资源配置资源配置是一个典型的线性规划问题，它涉及到如何根据企业的需求最优地分配资源，以实现成本最小化或利润最大化。

在生产运营管理中，资源配置问题主要包括机器、人力、时间、原料等资源的分配。

为了更好地理解线性规划模型在资源配置中的应用，我们以一个简单的例子作为说明。

假设某企业需要生产两种产品 A 和 B，其中 A 的利润为 10 元/件，B 的利润为 20 元/件。

该企业有两台机器 M1 和 M2，生产一件 A 需要机器 M1 工作 2小时，机器 M2 工作 1 小时；而生产一件 B 则需要 M1 工作 1 小时和 M2 工作 3 小时。

同时，该企业拥有员工若干，每小时的工作费用为 5 元，生产一件 A 和 B 分别需要 1 个和 2 个小时的人力资源。

现在该企业想要最大化每小时利润，那么该如何分配资源呢？为了解决这个问题，我们可以采用线性规划模型。

将目标函数设置为每小时利润的最大化，约束条件包括机器和人力资源的限制，即：max z = 10 x1 + 20 x2s.t.2 x1 + x2 <= 12 (M1 工作时间不能超过 12 小时)x1 + 3 x2 <= 24 (M2 工作时间不能超过 24 小时)x1 + 2 x2 <= n (人力资源不能超过 n 个小时）其中，x1 和 x2 分别表示生产 A 和 B 的产量，n 为企业拥有的人力资源总量。

根据线性规划模型求得的最优解即为每小时利润的最大值，以及相应的资源分配方案。

运筹学建模-炼油厂生产计划安排炼油厂生产计划安排摘要本文主要论述了炼油厂生产计划的优化问题，在该厂的生产能力和市场条件的限制下，通过对炼油厂生产流程的分析，得到了总利润与成品油产量的函数关系，以及成品油产量所需满足的约束条件，从而将问题转化为线性规划问题，然后转换建立了一个模型。

模型将总利润作为目标函数，将炼油厂生产所受到的生产能力、原料供应和市场需求方面的限制条件转化为目标函数的约束条件，最后利用lindo 软件编程实现求解。

一、问题的提出炼油厂通过不同渠道购买原油1和原油2，原油经过分馏、重整、裂解和调和处理，所得到油和煤油可以直接用于销售。

（1）分馏分馏是将每一种原油根据沸点不同分解为轻石脑油、中石脑油、重石脑油、轻油、重油和残油。

每桶原油可以产生的各种油分馏见表1。

油原油1 0.10 0.20 0.20 0.12 0.20 0.13（石脑油进入重整过程产生辛烷值为115的重整汽油，经过重整得到的重整汽油见表2。

表2 石脑油经过重整后提到的重整汽油(桶/桶)轻石脑油中石脑油重石脑油重整汽油0.6 0.52 0.45（3）裂解轻油和重油经过催化裂解过程而产生裂化油和裂化汽油，轻油和重油裂解产生的产品见表3。

表3 轻油重油裂解产生的产品(桶/桶)裂解油裂解汽油轻油0.68 0.28重油0.75 0.20（4）调合汽油、航空煤油和煤油都可以利用石脑油、轻油、重油和裂解油等调合而成，而航空煤油的蒸汽压必须不超过每平方厘米1公斤，而轻油、重油、裂解油和残油的蒸汽压见表4。

表4 各种油品的蒸汽压（公斤／平方厘米）轻油重油裂解油渣油蒸汽压1.0 0.6 1.5 0.05煤油的相关数据如下：假定煤油由轻油、裂解油、重油和渣油按10:4:3:1调合而成。

①每天原油1的可供应量为20,000桶；②每天原油2的可供应量为30,000桶；③每天最多可分馏45,000桶原油；④每天最多可重整10,000桶石脑油；⑤每天最多可裂解处理8,000桶；⑥每天生产的润滑油必须在500桶到1,000桶之间；⑦高档发动机油的产量必须是普通发动机油产量的40％。

线性规划在工业生产中的应用近年来，随着工业生产的不断发展，工业生产管理问题也不断复杂化。

在对工业生产进行优化管理的过程中，线性规划技术因其较为成熟的理论基础和实用性，成为了众多企业优化管理的首选方法之一。

本文将就线性规划技术在工业生产中的应用进行深入探讨。

一、线性规划的概念及其与生产管理的关联线性规划是运筹学中的一种重要方法，主要用于解决各种实际问题中的优化问题。

它的基本思想是将一个复杂的问题转化成一个数学模型，然后应用线性规划方法求解最优解。

线性规划的数学模型分为目标函数和约束条件两个部分，其中，目标函数描述了需要最小化或最大化的量，而约束条件则描述了模型中可能存在的各种限制条件。

在工业生产管理中，线性规划技术的应用十分广泛。

通过将生产量、成本、材料、设备等因素作为线性规划模型中的变量，将现有的生产资源进行有效的利用，并优化生产过程，提高生产效率，降低生产成本，从而增强企业的竞争优势。

因此，线性规划和生产管理之间存在着密切的联系。

二、线性规划在生产计划中的应用在企业的生产管理中，生产计划是一个至关重要的环节。

合理的生产计划可以帮助企业提高生产效率，降低成本，增加利润。

而线性规划技术的应用可以帮助企业设计出更为合理的生产计划。

假设一家制造企业需要在每月生产产品 A、B、C 三个品种，已知生产 A 产品需要 2 个单位的生产资源，生产 B 产品需要 3 个单位的生产资源，生产 C 产品需要 4 个单位的生产资源。

该企业目前拥有的生产资源一共有 180 个单位，同时假设 A、B、C 三个品种的生产利润分别是 5 元/个、6 元/个、8 元/个，那么该企业应该如何安排生产计划，以达到最大利润？假设该企业在月末决定生产 x 个 A 产品、y 个 B 产品和 z 个 C 产品，且满足以下约束条件：2x + 3y + 4z <= 180，表示生产 A、B、C 三种产品所需的总资源不应该超过企业现有的总生产资源。

线性规划的应用引言概述：线性规划是一种数学优化方法，广泛应用于各个领域。

它通过建立数学模型，寻觅最优解来解决实际问题。

本文将介绍线性规划的应用，并分析其在经济、物流、生产、资源分配和运筹学等领域的具体应用。

一、经济领域的应用1.1 产量最大化：线性规划可以用于匡助企业确定最佳生产方案，以最大化产量。

通过考虑生产成本、资源限制和市场需求等因素，线性规划可以确定最优的生产数量和产品组合。

1.2 资源分配：线性规划可以匡助企业合理分配资源，以最大化利润。

通过考虑各种资源的供应和需求关系，线性规划可以确定最优的资源分配方案，提高资源利用效率。

1.3 价格优化：线性规划可以用于确定最佳定价策略，以最大化利润。

通过考虑市场需求、成本和竞争等因素，线性规划可以确定最优的价格水平，提高企业的竞争力。

二、物流领域的应用2.1 运输成本最小化：线性规划可以用于确定最佳的物流方案，以最小化运输成本。

通过考虑物流网络、货物流量和运输成本等因素，线性规划可以确定最优的运输路线和运输量，提高物流效率。

2.2 仓储优化：线性规划可以匡助企业优化仓储管理，以最小化仓储成本。

通过考虑仓库容量、货物存储需求和仓储成本等因素，线性规划可以确定最优的仓储方案，提高仓储效率。

2.3 供应链优化：线性规划可以用于优化供应链管理，以提高整体供应链效率。

通过考虑供应商、生产商和分销商之间的关系，线性规划可以确定最优的供应链方案，减少库存和运输成本。

三、生产领域的应用3.1 生产计划：线性规划可以用于匡助企业制定最佳的生产计划，以满足市场需求。

通过考虑生产能力、原材料供应和市场需求等因素，线性规划可以确定最优的生产计划，提高生产效率。

3.2 产能利用率优化：线性规划可以匡助企业提高产能利用率，以降低成本。

通过考虑设备利用率、工人数量和生产效率等因素，线性规划可以确定最优的产能利用方案，提高生产效率。

3.3 品质控制：线性规划可以用于优化品质控制过程，以提高产品质量。

２.某市柴油机厂年度产品生产计划的优化研究1）问题的提出某市柴油机厂是我国生产中小功率柴油机的重点骨干企业之一，主要产品有2105柴油机、X２105柴油机、X４105柴油机、X4110柴油机、Ｘ６105柴油机、Ｘ611０柴油机，产品市场占有率大,覆盖面广,广泛用于农业机械、工程机械、林业机械、船舶、发电机组等。

在同行业中占有一定的优势。

但另一方面,也确实存在管理方法陈旧、管理手段落后的实际问题,尤其是随着经济体制改革的深入，以前在计划经济体制下生存的国营企业越来越不适应市场经济的要求。

为改变这种不利局面，厂领导决定实行科学管理，其中努力提高企业编制产品生产计划的科学性是一个重要的目标。

２）生产现状及资料分析柴油机的主要生产过程为原材料经过锻造、铸造或下料,再进行热处理、机加工工序,进入总装，最后试车、装箱、入成品库。

该厂将毛坯生产工艺，即锻造、铸造或下料过程渐渐向外扩散，形成专业化生产，以达到规模效益，故该厂柴油机生产过程主要可以分三大类:热处理、机加工、总装。

与产品生产有关的数据资料如下：每种产品的单位产值如下表:每件产品所需的热处理、机加工、总装工时及全厂能提供的三种总工时如下表：产品原材料主要是生铁、焦碳、废钢、钢材四大类资源,供应科根据历年的统计资料及当年的原材料市场情况,给出了各种原材料的最大供应量如下表：油机今年的市场需求量如下表:根据以上情况,该企业应如何制定当年销售收入最大的生产计划方案?根据题设,可以获得约束方程如下：Ｍax Ｚ＝540０X１+6５0０X2+12０00X３+14000X4+1850０Ｘ5+2０000X610.58X１+1１。

０３X2+20.11X3+32。

２6X４+３7。

68X5+40。

84X6〈＝1200０0 14。

58X1＋7.05Ｘ２+23。

96Ｘ3+27．7X４+29。

36X５+４0。

43X6<=９５000１7.08X1+1５０Ｘ2＋2９．３７X3+３3．3８X4+55。