机器人运动学(培训教材)
- 格式:doc
- 大小:2.18 MB
- 文档页数:66


第三章机器人运动学机器人运动学是研究机器人如何在二维或三维空间中进行运动的学科。
它涉及到机器人的轨迹规划、运动控制和路径规划等重要内容。
本章将介绍机器人运动学的基本概念和常用模型,帮助读者全面了解机器人的运动规律和控制原理。
1. 机器人运动学的基本概念机器人运动学是研究机器人位置和姿态变化的学科,包括正运动学和逆运动学两个方面。
正运动学研究机器人的末端执行器的位置和姿态如何由关节变量确定;逆运动学则研究机器人如何通过末端执行器的位置和姿态来确定关节变量的值。
机器人的运动学建模一般采用DH(Denavit-Hartenberg)参数表示方法。
DH 参数是由Denavit和Hartenberg提出的一种机器人坐标系的选择和旋转轴的确定方法。
通过定义一系列关节坐标系,建立起机器人的坐标系链,并确定各个关节的旋转轴和约定的方向,可以方便地描述机器人的运动学特性。
2. 机器人正运动学机器人正运动学是研究机器人末端执行器位置和姿态如何由关节变量确定的问题。
在机器人的正运动学中,常用的方法有几何法和代数法。
2.1 几何法几何法是一种较为直观的方法,通过对机器人各个关节坐标系的位置和旋转进行推导,得到机器人末端执行器的位置和姿态。
几何法适用于无约束和无外力干扰的情况,可以简单快速地推导出机器人的正运动学方程。
2.2 代数法代数法是一种基于运动学链的代数运算的方法,通过DH参数建立起机器人的坐标系链,并通过矩阵运算推导出机器人的正运动学方程。
代数法在机器人正运动学的推导和计算过程中更具有普适性和灵活性。
3. 机器人逆运动学机器人逆运动学是研究机器人如何通过末端执行器的位置和姿态来确定关节变量的值的问题。
机器人逆运动学在机器人运动规划和路径控制中起到重要的作用。
机器人逆运动学的求解一般采用迭代方法,通过迭代计算来逼近解析解,实现对机器人关节变量的求解。
逆运动学的求解过程中可能会出现奇异点和多解的情况,需要通过约束条件和优化方法来处理。

Fanuc_Robot_Basic_Trning FANUC培训教材(基本) Fanuc_Robot_Basic_Trning FANUC培训教材(基本)
第一章: 介绍
1.1 FANUC的背景和发展历史
1.2 FANUC的应用领域
1.3 FANUC的工作原理和基本组成
第二章: 安全
2.1 安全标准和规定
2.2 安全防护装置的使用和维护
第三章: 控制系统
3.1 控制系统的组成
3.2 控制器的操作和编程
3.3 编程语言的基本语法和常用指令
第四章: 运动学
4.1 的坐标系和姿态表示
4.2 的运动学原理和运动控制
第五章: 传感器和视觉
5.1 传感器的种类和功能
5.2 视觉系统的原理和应用第六章: 操作与维护
6.1 操作界面和操作流程
6.2 的日常维护和故障排除6.3 的保养和维修
第七章: 编程实例
7.1 基本动作的编程实例
7.2 应用案例分析
第八章: 安全操作规程
8.1 操作安全规程和注意事项8.2 事故的预防和应急处理附件:
1.FANUC操作手册
2.FANUC编程实例
3.FANUC故障排除手册
法律名词及注释:
1.安全标准和规定:指相关法律法规中对于安全的要求和规范。
2.控制器:控制系统中的核心部件,用于控制的动作和运行。
3.编程语言:用于编写控制程序的计算机语言,包括指令和语法规则。
4.传感器:用于获取周围环境信息的装置,如力传感器和视觉传感器。
5.操作界面:用于人机交互和操作的界面,通常包括触摸屏和按键等设备。




机器人运动学入门书籍
以下是一些机器人运动学入门书籍:
Howie Choset,Kevin M. Lynch,etc的《Principles of Robot Motion Theory, Algorithms, and Implementations》。
这本书被认为是一本学习机器人运动规划入门的优秀教材,涵盖了经典的运动、路径规划算法,同时还有针对各种场景的应用示例。
Mark W. Johnson的《Robot Mechanisms and Mechanical Devices Illustrated》。
这本书提供了对机器人运动学的全面概述,包括各种机构和装置的详细说明,以及运动学和动力学的基本原理。
John J. Canny的《The Robotics Primer》。
这本书是一个机器人学的入门教程,其中包括机器人运动学的基础知识,以及如何使用Python进行机器人编程。
以上书籍仅供参考,建议咨询图书馆工作人员,获取适合的入门书籍。


第2章 机器人位置运动学2.1 引言本章将研究机器人正逆运动学。
当已知所有的关节变量时,可用正运动学来确定机器人末端手的位姿。
如果要使机器人末端手放在特定的点上并且具有特定的姿态,可用逆运动学来计算出每一关节变量的值。
首先利用矩阵建立物体、位置、姿态以及运动的表示方法,然后研究直角坐标型、圆柱坐标型以及球坐标型等不同构型机器人的正逆运动学,最后利用Denavit-Hartenberg(D-H)表示法来推导机器人所有可能构型的正逆运动学方程。
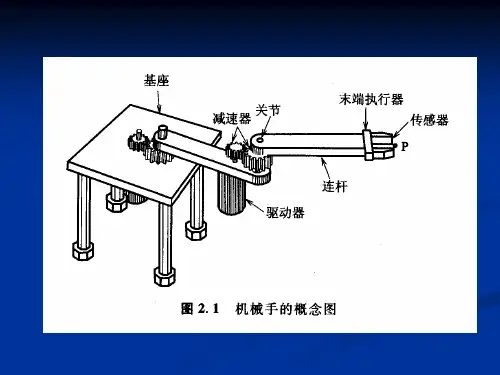
实际上,机器手型的机器人没有末端执行器,多数情况下,机器人上附有一个抓持器。
根据实际应用,用户可为机器人附加不同的末端执行器。
显然,末端执行器的大小和长度决定了机器人的末端位置,即如果末端执行器的长短不同,那么机器人的末端位置也不同。
在这一章中,假设机器人的末端是一个平板面,如有必要可在其上附加末端执行器,以后便称该平板面为机器人的“手”或“端面”。
如有必要,还可以将末端执行器的长度加到机器人的末端来确定末端执行器的位姿。
2.2 机器人机构机器手型的机器人具有多个自由度(DOF ),并有三维开环链式机构。
在具有单自由度的系统中,当变量设定为特定值时,机器人机构就完全确定了,所有其他变量也就随之而定。
如图2.1所示的四杆机构,当曲柄转角设定为120°时,则连杆与摇杆的角度也就确定了。
然而在一个多自由度机构中,必须独立设定所有的输入变量才能知道其余的参数。
机器人就是这样的多自由度机构,必须知道每一关节变量才能知道机器人的手处在什么位置。
图2.1 具有单自由度闭环的四杆机构如果机器人要在空间运动,那么机器人就需要具有三维的结构。
虽然也可能有二维多自由度的机器人,但它们并不常见。
机器人是开环机构,它与闭环机构不同(例如四杆机构),即使设定所有的关节变量,也不能确保机器人的手准确地处于给定的位置。
这是因为如果关节或连杆有丝毫的偏差,该关节之后的所有关节的位置都会改变且没有反馈。
第2章机器人位置运动学2.1 引言本章将研究机器人正逆运动学。
当已知所有的关节变量时,可用正运动学来确定机器人末端手的位姿。
如果要使机器人末端手放在特定的点上并且具有特定的姿态,可用逆运动学来计算出每一关节变量的值。
首先利用矩阵建立物体、位置、姿态以及运动的表示方法,然后研究直角坐标型、圆柱坐标型以及球坐标型等不同构型机器人的正逆运动学,最后利用Denavit-Hartenberg(D-H)表示法来推导机器人所有可能构型的正逆运动学方程。
实际上,机器手型的机器人没有末端执行器,多数情况下,机器人上附有一个抓持器。
根据实际应用,用户可为机器人附加不同的末端执行器。
显然,末端执行器的大小和长度决定了机器人的末端位置,即如果末端执行器的长短不同,那么机器人的末端位置也不同。
在这一章中,假设机器人的末端是一个平板面,如有必要可在其上附加末端执行器,以后便称该平板面为机器人的“手”或“端面”。
如有必要,还可以将末端执行器的长度加到机器人的末端来确定末端执行器的位姿。
2.2 机器人机构机器手型的机器人具有多个自由度(DOF),并有三维开环链式机构。
在具有单自由度的系统中,当变量设定为特定值时,机器人机构就完全确定了,所有其他变量也就随之而定。
如图2.1所示的四杆机构,当曲柄转角设定为120°时,则连杆与摇杆的角度也就确定了。
然而在一个多自由度机构中,必须独立设定所有的输入变量才能知道其余的参数。
机器人就是这样的多自由度机构,必须知道每一关节变量才能知道机器人的手处在什么位置。
图2.1 具有单自由度闭环的四杆机构如果机器人要在空间运动,那么机器人就需要具有三维的结构。
虽然也可能有二维多自由度的机器人,但它们并不常见。
机器人是开环机构,它与闭环机构不同(例如四杆机构),即使设定所有的关节变量,也不能确保机器人的手准确地处于给定的位置。
这是因为如果关节或连杆有丝毫的偏差,该关节之后的所有关节的位置都会改变且没有反馈。
例如,在图2.2所示的四杆机构中,如果连杆AB 偏移,它将影响2O B 杆。
而在开环系统中(例如机器人),由于没有反馈,之后的所有构件都会发生偏移。
于是,在开环系统中,必须不断测量所有关节和连杆的参数,或者监控系统的末端,以便知道机器的运动位置。
通过比较如下的两个连杆机构的向量方程,可以表示出这种差别,该向量方程表示了不同连杆之间的关系。
1122O A AB OO O B +=+(2.1)11O A AB BC OC ++=(2.2) 可见,如果连杆AB 偏移,连杆2O B 也会相应地移动,式(2.1)的两边随连杆的变化而改变。
而另一方面,如果机器人的连杆AB 偏移,所有的后续连杆也会移动,除非1O C 有其他方法测量,否则这种变化是未知的。
为了弥补开环机器人的这一缺陷,机器人手的位置可由类似摄像机的装置来进行不断测量,于是机器人需借助外部手段(比如辅助手臂或激光束)来构成闭环系统。
或者按照常规做法,也可通过增加机器人连杆和关节强度来减少偏移,采用这种方法将导致机器人重量重、体积大、动作慢,而且它的额定负载与实际负载相比非常小。
图2.2 (a)闭环机构;(b)开环机构2.3 机器人运动学的矩阵表示矩阵可用来表示点、向量、坐标系、平移、旋转以及变换,还可以表示坐标系中的物体和其他运动元件。
2.3.1 空间点的表示空间点P (如图2.3所示)可以用它的相对于参考坐标系的三个坐标来表示:x y z P a i b j c k =++ (2.3)其中,,,x y z a b c 是参考坐标系中表示该点的坐标。
显然,也可以用其他坐标来表示空间点的 位置。
图2.3 空间点的表示2.3.2 空间向量的表示向量可以由三个起始和终止的坐标来表示。
如果一个向量起始于点A ,终止于点B ,那么它可以表示为()()()AB x x y y z z P B A i B A j B A k =-+-+-。
特殊情况下,如果一个向量起始于原点(如图2.4所示),则有:x y z P a i b j c k=++(2.4)其中,,x y z a b c 是该向量在参考坐标系中的三个分量。
实际上,前一节的点P 就是用连接到该点的向量来表示的,具体地说,也就是用该向量的三个坐标来表示。
图2.4 空间向量的表示向量的三个分量也可以写成矩阵的形式,如式(2.5)所示。
在本书中将用这种形式来表示运动分量:x y z a P b c ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦(2.5)这种表示法也可以稍做变化:加入一个比例因子w,如果x, y, z 各除以w,则得到,,x y za b c 。
于是,这时向量可以写为:x y P z w ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦,其中,,x y x ya b w w ==等等 (2.6)变量w 可以为任意数,而且随着它的变化,向量的大小也会发生变化,这与在计算机图形学中缩放一张图片十分类似。
随着w 值的改变,向量的大小也相应地变化。
如果w 大于1,向量的所有分量都变大;如果w 小于1,向量的所有分量都变小。
这种方法也用于计算机图形学中改变图形与画片的大小。
如果w 是1,各分量的大小保持不变。
但是,如果w=0,,,x y z a b c 则为无穷大。
在这种情况下,x ,y 和z (以及,,x y z a b c )表示一个长度为无穷大的向量,它的方向即为该向量所表示的方向。
这就意味着方向向量可以由比例因子w=0的向量来表示,这里向量的长度并不重要,而其方向由该向量的三个分量来表示。
例2.1 有一个向量P=3i+5j+2k,按如下要求将其表示成矩阵形式:(1)比例因子为2(2)将它表示为方向的单位向量 解:该向量可以表示为比例因子为2的矩阵形式,当比例因子为0时,则可以表示为方向向量,结果如下:61042P ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦ 和 3520P ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦然而,为了将方向向量变为单位向量,须将该向量归一化使之长度等于1。
这样,向量的每一个分量都要除以三个分量平方和的开方:356.16,0.487,6.16 6.16x y P P λ=====其中,等等和0.4870.8110.3240unitP ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦2.3.3 坐标系在固定参考坐标系原点的表示一个中心位于参考坐标系原点的坐标系由三个向量表示,通常着三个向量相互垂直,称为单位向量,,n o a ,分别表示法线(normal )、指向(orientation )和接近(approach )向量(如图2.5所示)。
正如2.3.3节所述,每一个单位向量都由它们所在参考坐标系着的三个分量表示。
这样,坐标系F 可以由三个向量以矩阵的形式表示为:xx x y y y zzz n o a F n o a n o a ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦(2.7)图2.5 坐标系在参考坐标系原点的表示2.3.4 坐标系在固定参考坐标系中的表示如果一个坐标系不再固定参考坐标系的原点(实际上也可包括在原点的情况),那么该坐标系的原点相对于参考坐标系的位置也必须表示出来。
为此,在该坐标系原点与参考坐标系原点之间做一个向量来表示该坐标系的位置(如图2.6所示)。
这个向量由相对于参考坐标系的三个向量来表示。
这样,这个坐标系就可以由三个表示方向的单位向量以及第四个位置向量来表示。
1xx x x yy y y z z z z n o a p n o a p F n o a p ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦(2.8)图2.6 一个坐标系在另一个坐标系中的表示如式(2.8)所示,前三个向量是w=0的方向向量,表示该坐标系的三个单位向量,,n o a 的方向,而第四个w=1的向量表示该坐标系原点相对于参考坐标系的位置。
与单位向量不同,向量P 的长度十分重要,因而使用比例因子为1。
坐标系也可以由一个没有比例因子的3⨯4矩阵表示,但不常用。
例2.2 如图2.7所示的F 坐标系位于参考坐标系中3,5,7的位置,它的n 轴与x 轴平行,o 轴相对于y 轴的角度为45°,a 轴相对于z 轴的角度为45°。
该坐标系可以表示为:100300.7070.707500.7070.70770001F ⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥⎣⎦图2.7 坐标系在空间的表示举例2.3.5 刚体的表示一个物体在空间的表示可以这样实现:通过在它上面固连一个坐标系,再将该固连的坐标系在空间表示出来。
由于这个坐标系一直固连在该物体上,所以该物体相对于坐标系的位姿是已知的。
因此,只要这个坐标系可以在空间表示出来,那么这个物体相对于固定坐标系的位姿也就已知了(如图2.8所示)。
如前所述,空间坐标系可以用矩阵表示,其中坐标原点以及相对于参考坐标系的表示该坐标系姿态的三个向量也可以由该矩阵表示出来。
于是有:1x x x x y y y y objectz z z z n o a p n o a p F n o a p ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦(2.9)如第1章所述,空间中的一个点只有三个自由度,它只能沿三条参考坐标轴移动。
但在空间的一个钢体有六个自由度,也就是说,它不仅可以沿着X,Y,Z 三轴移动,而且还可绕这三个轴转动。
因此,要全面地定义空间以物体,需要用6条独立的信息来描述物体原点在参考坐标系中相对于三个参考坐标轴的位置,以及物体关于这三个坐标轴的姿态。
而式(2.9)给出了12条信息,其中9条为姿态信息,三条为位置信息(排除矩阵中最后一行的比例因子,因为它们没有附加信息)。
显然,在该表达式中必定存在一定的约束条件将上述信息数限制为6。
因此,需要用6个约束方程将12条信息减少到6条信息。
这些约束条件来自于目前尚未利用的已知的坐标系特性,即:•三个向量,,n o a 相互垂直 •每个单位向量的长度必须为1图2.8 空间物体的表示我们可以将其转换为以下六个约束方程: (1)0n o ⋅=(2)0n a ⋅= (3)0a o ⋅=(4)1n =(向量的长度必须为1) (2.10) (5)1o =(6)1a =因此,只有前述方程成立时,坐标系的值才能用矩阵表示。
否则,坐标系将不正确。
式(2.10)中前三个方程可以换用如下的三个向量的叉积来代替:n o a⨯=(2.11)例2.3 对于下列坐标系,求解所缺元素的值,并用矩阵来表示这个坐标系。
?0?50.707??3??020001F ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦解:显然,表示坐标系原点位置的值5,3,2对约束方程无影响。
注意在三个方向向量中只有三个值是给定的,但这也已足够了。
根据式(2.10),得:0x x y y z z n o n o n o ++= 或 (0)0.707()()0x y z z n o n o ++= 0x x y y z z n a n a n a ++= 或 ()0.707()(0)0x x y z n a a n ++= 0x x y y z z a o a o a o ++= 或 (0)()0()0x y y z a a o o ++= 2221x y z n n n ++= 或 2220.7071x z n n ++= 2221x y z o o o ++= 或 22201y z o o ++= 2221x y z a a a ++= 或 22201x y a a ++=将这些方程化简得:0.7070y z z o n o += 0.7070x x y n a a +=y y a o =220.5x z n n +=221y z o o += 221x y a a +=解这六个方程得:0.707,0,0,1,0.7070.707x z y z x y n n o o a a =±====±=-和。