开普勒的三大定律典型例题(教学课资)

（答题时间：30分钟）1. 长期以来“卡戎星”被认为是冥王星唯一的卫星，它的公转轨道半径r 1≈2.0×104km ，公转周期T 1≈6天。

2006年3月，天文学家新发现两颗冥王星的小卫星，其中一颗的公转轨道半径r 2≈4.8×104km ，取7.3)4.2(23 ，则它的公转周期T 2最接近于（）A. 11天B. 23天C. 35天D. 83天2. 银河系中有两颗行星绕某恒星运行，从天文望远镜中观察到它们的运转周期之比为27:1，则它们的轨道半径的比为（）A. 3:1B. 9:1C. 27:1D. 1:93. 一颗小行星环绕太阳做匀速圆周运动，半径是地球环绕半径的4倍，则它的环绕周期是（ ）A. 2年B. 4年C. 8年D. 16年4. 设行星绕恒星的运动轨道是圆，则其运行轨道半径R 的三次方与其运行周期T 的二次方之比为常数，即R 3/T 2= k ，那么k 的大小（）A. 只与行星的质量有关B. 只与恒星的质量有关C. 与恒星和行星的质量都有关D. 与恒星的质量及行星的速率有关 5. 如图所示是行星m 绕恒星M 运动的情况示意图，则下面的说法正确的是（）A. 速度最大的点是B 点B. 速度最小的点是C 点C. m 从A 到B 做减速运动D. m 从B 到A 做减速运动6. 月球环绕地球运动的轨道半径约为地球半径的60倍，运行周期约为27天。

应用开普勒定律计算：在赤道平面内离地面多少高度，人造地球卫星可以随地球一起转动，就像停留在天空中不动一样。

7. 神舟七号沿半径为R 的圆周绕地球运动，其周期为T ，如果飞船要返回地面，可在轨道上的某一点A 处，将速率降低到适当数值，从而使飞船沿着以地心为焦点的特殊椭圆轨道运动，椭圆和地球表面在B 点相切，如图所示，如果地球半径为R 0，求飞船由A 点返回到地面B 点所需的时间。

1. B 解析：根据开普勒行星三定律的周期定律22213231T T r r =，可得233132212≈=r r T T 天，故B 正确。

1、金星的质量为M1，绕太阳的运动的椭圆轨道半长轴为R1，公转周期为T1．地球的质量为M2，绕太阳运动的椭圆轨道半长轴为R2，公转周期为T2，那么，下面判断正确的是（）
2、设行星绕恒星的运动轨道是圆，则其运行周期T的平方与其运动轨道半径R 的三次方之比为常量，即，那么k的大小（）
A．只与行星质量有关
B．只与恒星质量有关
C．与行星及恒星的质量都有关
D．与恒星质量及行星的速度都有关
3、月亮绕地球运转，周期为T1，半径为R1，登月飞船绕月球运转，周期为T2，半径为R2则( )
A.=
B.＜
C.＞
D.无法确定
4、两颗行星的质量分别为m1和m2，它们绕太阳运转轨道的半长轴分别为R1和R2，如果m1=2m2，R1=4R2。

求它们的运行周期之比T1：T2
5、某行星围绕太阳沿椭圆轨道运行.它的近日点A离开太阳的距离为a,行星经过近日点时的速度为vA,行星的远日点B离开太阳的距离为b,求它经过远日点时速度的大小.
6、请你默写出开普勒三大定律的内容与公式。

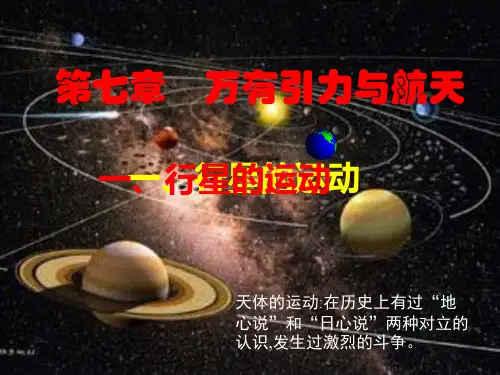
开普勒行星运动三大定律①第一定律（轨道定律）：所有行星绕太阳运动的轨道都是椭圆，太阳处在椭圆的一个焦点上。

②第二定律（面积定律）：对任意一个行星来说，它与太阳的连线在相等的时间内扫过相等的面积。

推论：近日点速度比较快，远日点速度比较慢。

③第三定律（周期定律）：所有行星的轨道的半长轴的三次方跟它的公转周期的二 次方的比值都相等。

即： 其中k 是只与中心天体的质量有关，与做圆周运动的天体的质量无关。

推广：对围绕同一中心天体运动的行星或卫星，上式均成立。

K 取决于中心天体的质量。

1、有两个人造地球卫星，它们绕地球运转的轨道半径之比是1：2，则它们绕地球运转的周期之比为 。

2．关于开普勒行星运动的公式23TR ＝k ，以下理解正确的是 （ ）A ．k 是一个与行星无关的常量B ．若地球绕太阳运转轨道的半长轴为R 地，周期为T 地；月球绕地球运转轨道的长半轴为R 月，周期为T 月，则2323月月地地T R T R =C ．T 表示行星运动的自转周期D ．T 表示行星运动的公转周期3．地球绕太阳运行的半长轴为1.5×1011 m ，周期为365 天；月球绕地球运行的轨道半长轴为3.82×108m ，周期为27.3 天，则对于绕太阳运行的行星；R 3／T 2的值为______m 3／s 2， 对于绕地球运行的物体，则R 3／T 2＝________ m 3/s 2.4.我们研究了开普勒第三定律，知道了行星绕恒星的运动轨道近似是圆形，周期T 的平方与轨道半径 R 的三次方的比为常数，则该常数的大小 ( )A .只跟恒星的质量有关B .只跟行星的质量有关C .跟行星、恒星的质量都有关D .跟行星、恒星的质量都没关5、假设行星绕太阳的轨道是圆形，火星与太阳的距离比地球与太阳的距离大53％，,试确定火星上一年是多少地球年。

6、关于开普勒第三定律下列说法中正确的是 （ ）A ．适用于所有天体B ．适用于围绕地球运行的所有卫星C ．适用于围绕太阳运行的所有行星D ．以上说法均错误7、有关开普勒关于行星运动的描述，下列说法正确的是 （ ）A.所有行星绕太阳运动的轨迹都是椭圆，太阳处在椭圆的一个焦点上B.所有行星绕太阳运动的轨迹都是圆，太阳处在圆心上C.所有行星轨道的半长轴的三次方跟公转周期的二次方的比值都相等D.不同行星绕太阳运动的椭圆轨道是相同的32a k T =1、万有引力定律的建立 ①太阳与行星间引力公式 ②月—地检验 ③卡文迪许的扭秤实验——测定引力常量2、万有引力定律①内容：自然界中任何两个物体都相互吸引，引力的大小与物体的质量1m 和2m 的乘积成正比，与它们之间的距离r 的二次方成反比。

典型例题关于开普勒的三大定律例1 月球环绕地球运动的轨道半径约为地球半径的60倍，运行周期约为27天。

应用开普勒定律计算：在赤道平面内离地面多少高度，人造地球卫星可以随地球一起转动，就像停留在无空中不动一样．分析：月球和人造地球卫星都在环绕地球运动，根据开普勒第三定律，它们运行轨道的半径的三次方跟圆周运动周期的二次方的比值都是相等的．解：设人造地球卫星运行半径为R，周期为T，根据开普勒第三定律有：同理设月球轨道半径为，周期为，也有：由以上两式可得：在赤道平面内离地面高度：km点评：随地球一起转动，就好像停留在天空中的卫星，通常称之为定点卫星．它们离地面的高度是一个确定的值，不能随意变动。

利用月相求解月球公转周期例2 若近似认为月球绕地球公转与地球绕日公转的轨道在同一平面内，且都为正圆.又知这两种转动同向，如图所示，月相变化的周期为29.5天（图是相继两次满月，月、地、日相对位置示意图）．解：月球公转（2π+）用了29.5天．故转过2π只用天．由地球公转知．所以=27.3天．例3如图所示，A、B、C是在地球大气层外的圆形轨道上运行的三颗人造地球卫星，下列说法中正确的是哪个？（）A．B、C的线速度相等，且大于A的线速度B．B、C的周期相等，且大于A的周期C．B、C的向心加速度相等，且大于A的向心加速度D．若C的速率增大可追上同一轨道上的B分析：由卫星线速度公式可以判断出，因而选项A是错误的．由卫星运行周期公式，可以判断出，故选项B是正确的．卫星的向心加速度是万有引力作用于卫星上产生的，由，可知，因而选项C是错误的．若使卫星C速率增大，则必然会导致卫星C偏离原轨道，它不可能追上卫星B，故D也是错误的．解：本题正确选项为B。

点评：由于人造地球卫星在轨道上运行时，所需要的向心力是由万有引力提供的，若由于某种原因，使卫星的速度增大。

则所需要的向心力也必然会增加，而万有引力在轨道不变的时候，是不可能增加的，这样卫星由于所需要的向心力大于外界所提供的向心力而会作离心运动。

（答题时间：30分钟）1. 长期以来“卡戎星”被认为是冥王星唯一的卫星，它的公转轨道半径r 1≈2.0×104km ，公转周期T 1≈6天。

2006年3月，天文学家新发现两颗冥王星的小卫星，其中一颗的公转轨道半径r 2≈4.8×104km ，取7.3)4.2(23 ，则它的公转周期T 2最接近于（ ）A. 11天B. 23天 C . 35天 D. 83天2. 银河系中有两颗行星绕某恒星运行，从天文望远镜中观察到它们的运转周期之比为27:1，则它们的轨道半径的比为（ ）A. 3:1B. 9:1C. 27:1D. 1:93. 一颗小行星环绕太阳做匀速圆周运动，半径是地球环绕半径的4倍，则它的环绕周期是（ ）A. 2年B. 4年 C . 8年 D . 16年4. 设行星绕恒星的运动轨道是圆，则其运行轨道半径R 的三次方与其运行周期T 的二次方之比为常数，即R 3/T 2= k ，那么k 的大小（ ）A. 只与行星的质量有关B. 只与恒星的质量有关C. 与恒星和行星的质量都有关D. 与恒星的质量及行星的速率有关5. 如图所示是行星m 绕恒星M 运动的情况示意图，则下面的说法正确的是（ ）A. 速度最大的点是B 点B. 速度最小的点是C 点C. m 从A 到B 做减速运动D. m 从B 到A 做减速运动6. 月球环绕地球运动的轨道半径约为地球半径的60倍，运行周期约为27天。

应用开普勒定律计算：在赤道平面内离地面多少高度，人造地球卫星可以随地球一起转动，就像停留在天空中不动一样。

7. 神舟七号沿半径为R 的圆周绕地球运动，其周期为T ，如果飞船要返回地面，可在轨道上的某一点A 处，将速率降低到适当数值，从而使飞船沿着以地心为焦点的特殊椭圆轨道运动，椭圆和地球表面在B 点相切，如图所示，如果地球半径为R 0，求飞船由A 点返回到地面B 点所需的时间。

1. B 解析：根据开普勒行星三定律的周期定律22213231T T r r =，可得233132212≈=r r T T 天，故B 正确。

高中物理开普勒三定律1.某行星围绕太阳做椭圆运动，如果不知太阳的位置，但经观测行星在由A到B的过程中，运行速度在变小，图中F1、F2是椭圆的两个焦点，则太阳位于（）A. F2B. AC. F1D. B2. 某一人造卫星绕地球做匀速圆周运动，其轨道半径为月球轨道半径的1/3，则此卫星运行的周期大约是（d为“天”）（）A. 1 d～4 d之间B. 4 d～8 d之间C. 8 d～16 d之间D. 16 d～20 d之间3. 在天文学上，以春分、夏至、秋分、冬至将一年分为春、夏、秋、冬四个季节。

如图所示，从地球绕太阳的运动规律入手，下列判断正确的是（）A. 在冬至日前后，地球绕太阳的运行速率较大B. 在夏至日前后，地球绕太阳的运行速率较大C. 春夏两季与秋冬两季时间相等D. 春夏两季比秋冬两季时间长4. 如图所示，对开普勒第一定律的理解，下列说法中正确的是（）A. 在行星绕太阳运动一周的时间内，它离太阳的距离是不变化的B. 在行星绕太阳运动一周的时间内，它离太阳的距离是变化的C. 某个行星绕太阳运动的轨道一定是在某一固定的平面内D. 某个行星绕太阳运动的轨道一定不在一个固定的平面内5. 长期以来，“卡戎星（Charon）”被认为是冥王星唯一的卫星，它的公转轨道半径r1＝19 600 km，公转周期T1＝6.39天.2021年3月，天文学家新发现两颗冥王星的小卫星，其中一颗的公转轨道半径r2＝48 000 km，则它的公转周期T2最接近于（）A. 15天B. 25天C. 35天D. 45天6. 第谷、开普勒等人对行星运动的研究漫长而曲折，牛顿在他们研究的基础上，得出了科学史上最伟大的定律之一——万有引力定律。

下列有关说法中正确的是（）A. 开普勒通过研究观测记录发现行星绕太阳运行的轨道是椭圆B. 太阳与行星之间引力的规律并不适用于行星与它的卫星C. 库仑利用实验较为准确地测出了引力常量G的数值D. 牛顿在发现万有引力定律的过程中应用了牛顿第三定律的知识7. 太阳系八大行星的公转轨道均可近似看作圆轨道，“行星公转周期的平方”与“行星与太阳的平均距离的三次方”成正比。

教师一对一个性化教案12定周期：T=24h; 定速度：s km V /1.3=(2) 对人造地球卫星几个速度的理解1．第一宇宙速度（环绕速度）：是指地球卫星的最小发射速度，也是卫星在地面附近环绕地球运行的速度，是卫星的最大的轨道速度．设地球半径为R ，地球质量为M ，根据G Mm R 2＝m v 2R 或mg ＝m v 2R，可得v 1＝RGM=gR ≈7.9 km/s. 2．第二宇宙速度：是使物体挣脱地球引力束缚的最小发射速度，其大小为11.2 km/s. 3．第三宇宙速度：是使物体挣脱太阳引力束缚的最小发射速度，其大小为16.7 km/s. (3) 人造地球卫星的运动问题1．人造卫星的运行规律 越高越慢(1)由G Mm r 2＝mv 2r 得v ＝ GM r ， 即v ∝ 1r ，轨道半径越大，速度越小．(2)由G Mm r 2＝mω2r 得ω＝ GM r 3， 即ω∝ 1r 3,轨道半径越大，角速度越小。

(3)由G Mm r 2＝m 4π2T 2r 得T ＝2π r 3GM， 即T ∝r 3，轨道半径越大，周期越大．(4)由n ma r GMm =2得2r GM a n =， 即21r a n ∞，轨道半径越大，向心加速度越小。

3．人造卫星的超重与失重(1)人造卫星在发射升空时，有一段加速运动；在返回地面时，有一段减速运动，这两个过程加速度方向均向上，因而都是超重状态．(2)人造卫星在沿圆轨道运行时，由于万有引力提供向心力，所以处于完全失重状态，在这种情况下凡是与重力有关的力学现象都会停止发生，因此，在卫星上的仪器，凡是制造原理与重力有关的均不能使用．同理，与重力有关的实验也将无法进行．练习题：1.把太阳系各行星运动近似看作匀速圆周运动，比较各行星周期，则太阳越远的行星（ ） A ．周期越小 B ．周期越大 C ．周期都一样 D ．无法确定2．设地球表面物体的重力加速度为g 0，某卫星在距离地心3R （R 是地球的半径）的轨道上绕地球运行，则卫星的加速度为（ ）A ．g 0B ．g 0/9C ．g 0/4D ．g 0/163．人造地球卫星A 和B,它们的质量之比为m A ：m B =1：2,它们的轨道半径之比为2:1,则下面的结论中正确的是（ ）.A. 地球的引力之比为F A ：F B =1：1B. 运行速度大小之比为v A ：v B =1：C. 运行周期之比为T A ：T B =2：1D. 角速度之比为ωA ：ωB =3：14．航天飞机绕地球做匀速圆 周运动时，机上的物体处于失重状态，是指这个物体（ ） A. 不受地球的吸引力 B. 受到地球吸引力和向心力平衡 C. 受到地球的引力提供了物体做圆周运动的向心力 D. 对支持它的物体的压力为零 5．关于宇宙速度，下列说法正确的是（ ）A ．第一宇宙速度是能使人造地球卫星绕地球飞行的最小发射速度B ．第一宇宙速度是人造地球卫星绕地球飞行的最小速度C ．第二宇宙速度是卫星在椭圆轨道上运行时近地点的速度D ．第三宇宙速度是发射人造地球卫星的最小速度6．地球半径为R ，地面重力加速度为g ，地球自转周期为T ，地球同步卫星离地面的高度为h ，则地球同步卫星的线速度大小为（ ）7．当人造卫星绕地球做匀速圆周运动时，其绕行速度（ ） A. 一定等于7.9千米/秒 B. 一定小于7.9千米/秒 C. 一定大于7.9千米/秒 D. 介于7.9～11.2千米/秒8．关于地球同步卫星，下列说法中正确的是（ ） A ．它的速度小于7.9km/s B ．它的速度大于7.9km/s C ．它的周期是24h,且轨道平面与赤道平面重合 D ．每一个地球同步卫星离开地面的高度是一样的39．人造地球卫星由于受大气阻力，其轨道半径逐渐减小，其相应的线速度和周期的变化情况是（ ）A. 速度减小，周期增大B. 速度减小，周期减小C. 速度增大，周期增大D. 速度增大，周期减小 10.以下说法正确的是（ ）A.经典力学理论普遍适用，大到天体，小到微观粒子均适用B.经典力学理论的成立具有一定的局限性C.在经典力学中，物体的质量随运动状态而改变D.相对论与量子力学否定了经典力学理论1、我们研究了开普勒第三定律，知道了行星绕恒星的运动轨道近似是圆形，周期T 的平方与轨道半径 R 的三次方的比为常数，则该常数的大小 ( )A .只跟恒星的质量有关B .只跟行星的质量有关C .跟行星、恒星的质量都有关D .跟行星、恒星的质量都没关 12、对于万有引力定律的表述式221rm m G F =，下面说法中正确的是（ ）A.公式中G 为引力常量，它是由实验测得的，而不是人为规定的B.当r 趋近于零时，万有引力趋于无穷大C. m 1与m 2受到的引力大小总是相等的，方向相反，是一对平衡力D. m 1与m 2受到的引力总是大小相等的，而与m 1、m 2是否相等无关13、下列关于地球同步卫星的说法正确的是（ ） A ．它的周期与地球自转同步，但高度和速度可以选择，高度增大，速度减小 B ．它的周期、高度、速度都是一定的 C ．我们国家发射的同步通讯卫星定点在北京上空 D ．我国发射的同步通讯卫星也定点在赤道上空14、假如一作圆周运动的人造地球卫星的轨道半径增大到原来的2倍，仍作圆周运动，则A. 根据公式v=ωr ，可知卫星的线速度将增大到原来的2倍B. 根据公式2v F m r=，可知卫星所需要的向心力将减小到原来的12C. 根据公式2Mm F G r=，可知地球提供的向心力将减小到原来的14D. 根据上述B 和C 中给出的公式，可知卫星运动的线速度将减小到原来的22、 15、两个行星各有一个卫星绕其表面运行，已知两个卫星的周期之比为1∶2，两行星半径之比为2∶1，则下列选项正确的是( )①两行星密度之比为4∶1 ②两行星质量之比为16∶1 ③两行星表面处重力加速度之比为8∶1 ④两卫星的速率之比为4∶1A ．①②B ．①②③C ．②③④D ．①③④1．2015年9月20日“长征六号”火箭搭载20颗小卫星成功发射。

典型例题关于开普勒的三大定律例1 月球环绕地球运动的轨道半径约为地球半径的60倍，运行周期约为27天。

应用开普勒定律计算：在赤道平面内离地面多少高度，人造地球卫星可以随地球一起转动，就像停留在无空中不动一样．分析：月球和人造地球卫星都在环绕地球运动，根据开普勒第三定律，它们运行轨道的半径的三次方跟圆周运动周期的二次方的比值都是相等的．解：设人造地球卫星运行半径为R，周期为T，根据开普勒第三定律有：同理设月球轨道半径为，周期为，也有：由以上两式可得：在赤道平面内离地面高度：km点评：随地球一起转动，就好像停留在天空中的卫星，通常称之为定点卫星．它们离地面的高度是一个确定的值，不能随意变动。

利用月相求解月球公转周期例2 若近似认为月球绕地球公转与地球绕日公转的轨道在同一平面内，且都为正圆.又知这两种转动同向，如图所示，月相变化的周期为29.5天（图是相继两次满月，月、地、日相对位置示意图）．解：月球公转（2π+）用了29.5天．故转过2π只用天．由地球公转知．所以=27.3天．例3如图所示，A、B、C是在地球大气层外的圆形轨道上运行的三颗人造地球卫星，下列说法中正确的是哪个？（）A．B、C的线速度相等，且大于A的线速度B．B、C的周期相等，且大于A的周期C．B、C的向心加速度相等，且大于A的向心加速度D．若C的速率增大可追上同一轨道上的B分析：由卫星线速度公式可以判断出，因而选项A是错误的．由卫星运行周期公式，可以判断出，故选项B是正确的．卫星的向心加速度是万有引力作用于卫星上产生的，由，可知，因而选项C是错误的．若使卫星C速率增大，则必然会导致卫星C偏离原轨道，它不可能追上卫星B，故D也是错误的．解：本题正确选项为B。

点评：由于人造地球卫星在轨道上运行时，所需要的向心力是由万有引力提供的，若由于某种原因，使卫星的速度增大。

则所需要的向心力也必然会增加，而万有引力在轨道不变的时候，是不可能增加的，这样卫星由于所需要的向心力大于外界所提供的向心力而会作离心运动。

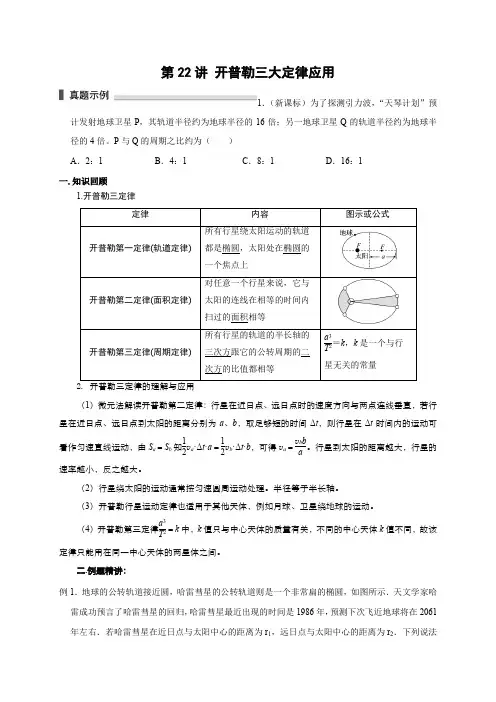
第22讲 开普勒三大定律应用1．（新课标）为了探测引力波，“天琴计划”预计发射地球卫星P ，其轨道半径约为地球半径的16倍；另一地球卫星Q 的轨道半径约为地球半径的4倍。

P 与Q 的周期之比约为（ ） A ．2：1 B ．4：1C ．8：1D ．16：1一.知识回顾1.开普勒三定律定律内容图示或公式开普勒第一定律(轨道定律)所有行星绕太阳运动的轨道都是椭圆，太阳处在椭圆的一个焦点上开普勒第二定律(面积定律)对任意一个行星来说，它与太阳的连线在相等的时间内扫过的面积相等开普勒第三定律(周期定律)所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等a 3T 2＝k ，k 是一个与行星无关的常量（1）微元法解读开普勒第二定律：行星在近日点、远日点时的速度方向与两点连线垂直，若行星在近日点、远日点到太阳的距离分别为a 、b ，取足够短的时间Δt ，则行星在Δt 时间内的运动可看作匀速直线运动，由S a ＝S b 知12v a ·Δt ·a ＝12v b ·Δt ·b ，可得v a ＝v b b a 。

行星到太阳的距离越大，行星的速率越小，反之越大。

（2）行星绕太阳的运动通常按匀速圆周运动处理。

半径等于半长轴。

（3）开普勒行星运动定律也适用于其他天体，例如月球、卫星绕地球的运动。

（4）开普勒第三定律a 3T 2＝k 中，k 值只与中心天体的质量有关，不同的中心天体k 值不同，故该定律只能用在同一中心天体的两星体之间。

二.例题精讲：例1．地球的公转轨道接近圆，哈雷彗星的公转轨道则是一个非常扁的椭圆，如图所示．天文学家哈雷成功预言了哈雷彗星的回归，哈雷彗星最近出现的时间是1986年，预测下次飞近地球将在2061年左右．若哈雷彗星在近日点与太阳中心的距离为r 1，远日点与太阳中心的距离为r 2．下列说法正确的是（ ）A ．哈雷彗星轨道的半长轴是地球公转半径的√753倍B ．哈雷彗星在近日点的速度一定大于地球的公转速度C ．哈雷彗星在近日点和远日点的速度之比为√r 2：√r 1D ．相同时间内，哈雷彗星与太阳连线扫过的面积和地球与太阳连线扫过的面积相等例2．根据开普勒定律可知，火星绕太阳运行的轨道是椭圆，太阳在椭圆的一个焦点上，如图所示，下列说法正确的是（ ）A ．火星运动到近日点时的线速度最小B ．火星运动到远日点时的加速度最小C ．太阳对火星的万有引力大小始终保持不变D ．太阳对火星的万有引力大于火星对太阳的万有引力例3．“中国天眼”是目前世界上口径最大的单天线射电望远镜（FAST ）。

开普勒三大定律和万有引力定律 一、开普勒三定律1．开普勒第一定律：所有行星绕太阳运动的轨道都是椭圆_，太阳处在椭圆的一个焦点_上．2．开普勒第二定律：对任意一个行星来说，它与太阳的连线在相同的时间内扫过相等的面积．3．开普勒第三定律：所有行星的轨道的半长轴的三次方跟它的周期的平方的比值都相等，即a 3T2＝k . 思考：开普勒第三定律中的k 值有什么特点？二、万有引力定律1．内容自然界中任何两个物体都相互吸引，引力的方向在它们的连线上，引力的大小与________________________________成正比，与它们之间____________________成反比．2．公式____________，通常取G ＝____________ N·m 2/kg 2，G 是比例系数，叫引力常量．3．适用条件公式适用于________间的相互作用．当两物体间的距离远大于物体本身的大小时，物体可视为质点；均匀的球体可视为质点，r 是__________间的距离；对一个均匀球体与球外一个质点的万有引力的求解也适用，其中r 为球心到________间的距离．考点突破考点一 天体产生的重力加速度问题考点解读星体表面及其某一高度处的重力加速度的求法：设天体表面的重力加速度为g ，天体半径为R ，则mg ＝G Mm R 2，即g ＝GM R2(或GM ＝gR 2) 若物体距星体表面高度为h ，则重力mg ′＝G Mm (R ＋h )2，即g ′＝GM (R ＋h )2＝R 2(R ＋h )2g .典例剖析例1 某星球可视为球体，其自转周期为T ，在它的两极处，用弹簧秤测得某物体重为P ，在它的赤道上，用弹簧秤测得同一物体重为0.9P ，则星球的平均密度是多少？跟踪训练1 1990年5月，紫金山天文台将他们发现的第2 752号小行星命名为吴健雄星，该小行星的半径为16 km.若将此小行星和地球均看成质量分布均匀的球体，小行星密度与地球相同．已知地球半径R ＝6 400 km ，地球表面重力加速度为g .这个小行星表面的重力加速度为 ( )A ．400g B.1400g C ．20g D.120g 考点二 天体质量和密度的计算考点解读1．利用天体表面的重力加速度g 和天体半径R .由于G Mm R 2＝mg ，故天体质量M ＝gR 2G ，天体密度ρ＝M V ＝M 43πR 3＝3g 4πGR . 2．通过观察卫星绕天体做匀速圆周运动的周期T ，轨道半径r .(1)由万有引力等于向心力，即G Mm r 2＝m 4π2T 2r ，得出中心天体质量M ＝4π2r 3GT2； (2)若已知天体的半径R ，则天体的密度ρ＝M V ＝M 43πR 3＝3πr 3GT 2R 3； (3)若天体的卫星在天体表面附近环绕天体运动，可认为其轨道半径r 等于天体半径R ，则天体密度ρ＝3πGT2.可见，只要测出卫星环绕天体表面运动的周期T ，就可估测出中心天体的密度．特别提醒 不考虑天体自转，对任何天体表面都可以认为mg ＝G Mm R2.从而得出GM ＝gR 2(通常称为黄金代换)，其中M 为该天体的质量，R 为该天体的半径，g 为相应天体表面的重力加速度．典例剖析例2 天文学家新发现了太阳系外的一颗行星，这颗行星的体积是地球的4.7倍，质量是地球的25倍．已知某一近地卫星绕地球运动的周期约为1.4小时，引力常量G ＝6.67×10－11 N·m 2/kg 2，由此估算该行星的平均密度约为 ( )A ．1.8×103 kg/m 3B ．5.6×103 kg/m 3C ．1.1×104 kg/m 3D ．2.9×104 kg/m 3跟踪训练2 为了对火星及其周围的空间环境进行探测，我国于2011年10月发射了第一颗火星探测器“萤火一号”．假设探测器在离火星表面高度分别为h 1和h 2的圆轨道上运动。

教资面试高中物理开普勒三定律题本梳理+教案题本梳理-高中物理《开普勒三定律》一、题本展示分析1.基本信息：准考证号、姓名、考场;2.正文：题目，内容(简单梳理内容，整理思路);3.基本要求：①教学内容：借助图片和演示，帮助学生直观理解开普勒定律。

②教学实施：试讲十分钟，要有适当的板书;逻辑清晰，重点突出。

二、核心素养的确立1.确立依据：文本特点：本节课是天体运动知识中的第一部分，是学习万有引力的基础，而且部分知识比较抽象，所以复杂度相对来说比较大。

学生特点:本课程是学生第一次接触天体运动的知识，对学生来说比较陌生，所以学生比较好奇，但同时学习的复杂性也很大，所以在整个教学过程中保持学生的学习兴趣是教学的关键。

2.核心素养：物理概念:掌握开普勒三定律的内容，并运用其解决实际问题。

科学思维：通过合作讨论，提升抽象思维和逻辑推理能力。

科学探究：体会科学家探索天体运动的过程，认识到科学研究一般是从最基础的观念开始不断修正，使其逐步接近真实，获得物理规律。

科学态度与责任:公认相信自然的简单与和谐是科学家研究的动力之一，尊重客观事实，坚持科学研究中实事求是的基本态度和社会责任。

三、教学重难点的确立1.确立依据教学目标：物理观念、科学思维、科学探究、科学态度与责任。

学生特点：学生很难深刻理解和运用开普勒三大定律。

2.重难点展示教学重点:开普勒行星运动三定律。

教学难点：开普勒行星运动定律的理解和应用。

四、教学思路展示讲解(一)新课导入多媒体展示漫天繁星的图片，引导学生对行星运动规律的思考之中，鼓励学生大胆说出自己的看法。

接着教师出示开普勒的人像，介绍有关他的生平事迹，尤其是在行星运动方面的研究。

激起学生对开普勒行星运动规律的求知欲，顺势引出本节新课——《开普勒定律》(二)新课讲授1.开普勒第一定律用多媒体演示太阳系八大行星绕太阳运行的动画。

请注意行星的轨道。

询问行星轨道的形状，以及太阳在轨道中的位置。

学生观察到行星的轨道是椭圆形而不是圆形，太阳在椭圆的焦点上。

个性化教学辅导教案学生姓名年级学科上课时间教师姓名课题开普勒三大定律及万有引力定律1．（2017•永州二模）河水由西向东流，河宽为800m，河中各点的水流速度大小为v水，各点到较近河岸的距离为x，v水与x的关系为v水=x（m/s），让小船船头垂直河岸由南向北渡河，小船在静水中的速度大小恒为v船=4m/s，下列说法正确的是（）A．小船渡河的轨迹为直线B．小船在河水中的最大速度是2m/sC．小船渡河的时间是200sD．小船在距南岸200m处的速度小于距北岸200m处的速度【分析】将小船的运动分解为沿河岸方向和垂直河岸方向，小船在沿河岸方向的速度随时间先均匀增大后均匀减小，结合平均速度推论，抓住等时性求出v1的大小．根据合速度与合加速度的方向是否在同一条直线上判断小船的轨迹．【解答】解：A、小船在垂直河岸方向上做匀速直线运动，在沿河岸方向上做变速运动，合加速度的方向与合速度方向不在同一条直线上，做曲线运动，故A错误．B、当小船行驶到河中央时，v水=×400=3m/s，那么小船在河水中的最大速度v max==5m/s，故B错误．C、小船船头垂直河岸由南向北渡河，那么小船渡河的时间是t===200s，故C正确；D、小船在距南岸200m处的河水速度大小与距北岸200m处的河水速度大小相等，根据矢量的合成法则，则两种情况的合速度大小相等，故D错误．故选：C．【点评】解决本题的关键知道在垂直于河岸方向上做匀速直线运动，根据河水中各点水流速大小与各点到较近河岸边的距离成正比，则水流速度随时间先均匀增大后均匀减小，从而根据矢量的合成法则，求得合速度大小．2．（2017•广陵区校级学业考试）两个物体做平抛运动的初速度之比为2：1，若它们的水平射程相等，则它们抛出点离地面的高度之比为（）A．1：2 B．2：1 C．1：4 D．4：1【分析】平抛运动在水平方向上做匀速直线运动，在竖直方向上做自由落体运动，根据水平位移和初速度求出时间之比，结合位移时间公式求出抛出点离地面的高度之比．【解答】解：根据x=v0t知，水平射程相等，初速度之比为2：1，则时间之比为1：2，根据h=得，抛出点与地面的高度之比为1：4，故C正确，A、B、D错误．故选：C．【点评】解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律，知道运动的时间由高度决定，初速度和时间共同决定水平位移．3．（2017•徐州学业考试）如图所示，小强正在荡秋千．关于绳上a点和b点的线速度和角速度，下列关系正确的是（）A．v a=v b B．v a＞v b C．ωa=ωb D．ωa＜ωb【分析】荡秋千可视为同轴转动，利用角速度相同和v=ωr判断即可．【解答】解：ABCD、荡秋千可视为同轴转动，所以a、b两点角速度相同；据v=ωr和a、b两点的半径不同，所以有：v b＞v a，故ABD错误，C 正确故选：C．【点评】明确同轴转动，角速度相同是解题的关键，灵活应用v=ωr和半径关系．4．（2017•浙江模拟）在中国南昌有世界第五高摩天轮﹣南昌之星，总建设高度为160米，横跨直径为153米．它一共悬挂有60个太空舱，每个太空舱上都配备了先进的电子设备，旋转一周的时间是30分钟，可同时容纳400人左右进行同时游览．若该摩天轮做匀速圆周运动，则乘客（）A．速度始终恒定 B．加速度始终恒定C．乘客对座椅的压力始终不变 D．乘客受到到合力不断改变【分析】转轮始终不停地匀速转动，乘客做匀速圆周运动，加速度不为零．乘客所受的合外力提供向心力，方向指向圆心，时刻在变化，是变力．乘客对座位的压力大小是变化的，在最低点最大．【解答】解：A、匀速圆周运动的速度方向沿圆周的切线方向，方向时刻在改变，故其速度是变化的．故A错误．B、做匀速圆周运动的物体，其向心加速度方向始终指向圆心，方向时刻在变化，故向心加速度是变化的，故B错误．C、乘客对座椅的压力方向始终变化，所以压力变化．故C错误．D、做匀速圆周运动的物体，其所受的合力提供向心力，其方向始终指向圆心，始终变化．故D正确．故选：D【点评】本题考查对匀速圆周运动不变量和合力方向的掌握情况，对于匀速圆周运动不变量有：角速度、周期、频率、速度和加速度的大小等等．1．（2016•新疆学业考试）关于开普勒对行星运动规律的认识，下列说法正确的是（）A．所有行星围绕太阳运动的轨道都是圆B．所有行星围绕太阳运动的轨道都是椭圆C．所有行星的轨道半径的二次方跟它的公转周期成正比D．所有行星的轨道半径跟它的公转周期的二次方成正比【分析】开普勒第一定律，所有行星绕太阳运动的轨道都是椭圆，太阳处在椭圆的一个焦点上．开普勒第三定律，所有行星的椭圆轨道的半长轴的三次方跟公转周期的平方的比值都相等．【解答】解：A、根据开普勒第一定律，所有行星绕太阳运动的轨道都是椭圆，太阳处在椭圆的一个焦点上．故A错误，B正确．C、根据开普勒第三定律，所有行星的椭圆轨道的半长轴的三次方跟公转周期的平方的比值都相等，故C错误，D错误．故选：B【点评】考查了开普勒的三个定律．第一定律，所有行星绕太阳运动的轨道都是椭圆，太阳处在椭圆的一个焦点上，第二定律，所有行星绕太阳运动，它与太阳的连线在相等的时间内扫过的面积相等，第三定律，所有行星的椭圆轨道的半长轴的三次方跟公转周期的平方的比值都相等．2．（2015•渭南一模）地球和木星绕太阳运行的轨道都可以看作是圆形的．已知木星的轨道半径约为地球轨道半径的5.2倍，则木星绕太阳运行的周期约为（）A．15.6年B．11.86年C．10.4年D．5.2年【分析】根据开普勒第三定律，有=k比较得宇宙飞船绕太阳运行的周期．【解答】解：根据开普勒第三定律，有=K知：T2=木星围绕太阳在近似圆形的轨道上运动，若轨道半径是地球轨道半径的5.2倍，木星绕太阳运行的周期是地球周期的11.86倍，即小行星绕太阳运行的周期是11.86年．故选：B．【点评】求一个物理量之比，我们应该把这个物理量先用已知的物理量表示出来，再进行作比．3．（2017•昌平区学业考试）首先通过实验的方法比较准确地测出引力常量的物理学家是（）A．开普勒B．卡文迪许 C．伽利略D．牛顿【分析】本题考查了物理学史，了解所涉及伟大科学家的重要成就，如高中所涉及到的牛顿、伽利略、开普勒、卡文迪许等重要科学家的成就要明确．【解答】解：牛顿在推出万有引力定律的同时，并没能得出引力常量G的具体值，G的数值于1789年由卡文迪许利用他所发明的扭秤得出，故ACD错误，B正确．故选：B．【点评】本题考查了学生对物理学史的掌握情况，对于物理学史部分也是高考的热点，平时训练不可忽略．4．牛顿发现的万有引力定律是科学史上最伟大的定律之一，在天体运动中起着决定性作用．万有引力定律告诉我们，两物体间的万有引力（）A．与它们间的距离成正比 B．与它们间的距离成反比C．与它们的质量乘积成正比D．与它们的质量乘积成反比【分析】依据牛顿的万有引力定律公式F=，即可知道两物体间的万有引力哪些因素有关．【解答】解：根据牛顿的万有引力定律公式知，两物体间的万有引力与它们质量的乘积成正比，与它们间距离的二次方成反比，故C正确，ABD错误．故选：C．【点评】解答本题关键掌握牛顿的万有引力定律公式，基础题．5．（2014春•道里区校级期中）关于万有引力常量G，下列说法正确的是（）A．在不同星球上，G的数值不一样B．在不同的单位制中，G的数值一样C．在国际单位制中，G的数值等于两个质量各1g的物体，相距1m时的相互吸引力D．在国际单位制中，G的单位是【分析】万有引力定律是由牛顿发现的，而万有引力恒量是由卡文迪许测定的．牛顿的万有引力定律：太阳与行星之间的引力，与它们质量的乘积成正比，与它们距离的平方成反比．其中G为一个常数，叫做引力常量．【解答】解：A、G的值是由卡文迪许通过扭秤实验测定的，在不同星球上，G的数值一样，故A 错误；B、在国际单位制中，G的单位是，在不同的单位制中，G的数值不一样，故B错误，D正确；C、G的数值等于两个质量均为1kg可看作质点的物体相距1m时的相互引力，故C错误；故选：D．【点评】对于物理学上重要实验、发现和理论，要加强记忆，这也是高考考查内容之一．万有引力定律是由牛顿发现的，不是开普勒发现的．万有引力恒量是由卡文迪许测定的．学科问题（略）教学目标1.认识开普三大定律，掌握第三定律的简单应用2.掌握万有引力定律教学过程1-1 提问学生开普勒三大定律分别是什么1-2 重点解析第三定律应用2-1 讲解万有引力现象2-2 总结出万有引力定律公式2-3 强调注意事项，如两个紧贴的小球为何万有引力不是无穷大1．（2012春•虎林市校级期中）有两颗行星环绕某恒星转动，它们的运动周期之比为27：1，由开普勒三定律可知它们的轨道半径之比为（）A．1：27 B．9：1 C．27：1 D．1：9【分析】开普勒第三定律：所有行星的椭圆轨道的半长轴的三次方与公转周期的平方比值都相等．【解答】解：根据开普勒第三定律得=k，有两颗行星环绕某恒星转动，k一定，则有：=已知T A：T B=27：1，代入上式得：R A：R B=9：1故选：B．【点评】本题是开普勒第三定律的直接运用，也可以根据万有引力提供向心力列式求解．2．（2016春•安达市期末）某行星绕太阳运行的椭圆轨道如图所示，F1和F2是椭圆轨道的两个焦点，行星在A点的速率比在B点的大，则太阳是位于（）A．B B．F1C．A D．F2【分析】开普勒第二定律的内容，对任意一个行星来说，它与太阳的连线在相等时间内扫过相等的面积．行星沿着椭圆轨道运行，太阳位于椭圆的一个焦点上．如果时间间隔相等，即t2﹣t1=t4﹣t3，那么面积A=面积B由此可知行星在远日点B的速率最小，在近日点A的速率最大．【解答】解：根据开普勒第二定律，对任意一个行星来说，它与太阳的连线在相等时间内扫过相等的面积．如果时间间隔相等，即t2﹣t1=t4﹣t3，那么面积A=面积B由此可知，弧长t1t2＞弧长t3t4则v A＞V B即行星在在近日点A的速率最大，远日点B的速率最小，故D正确，ABC错误．故选：D．【点评】考查了开普勒第二定律，再结合时间相等，面积相等，对应弧长求出平均速度．3．（2016春•开远市校级期末）有关开普勒关于行星运动的描述，下列说法中正确的是（）A．所有的行星绕太阳运动的轨道都是椭圆，太阳处在椭圆的一个焦点上B．所有的行星绕太阳运动的轨道都是圆，太阳处在圆心上C．所有的行星轨道的半长轴的二次方跟公转周期的三次方的比值都相等D．不同的行星绕太阳运动的椭圆轨道是不同的【分析】熟记理解开普勒的行星运动三定律：第一定律：所有的行星围绕太阳运动的轨道都是椭圆，太阳处在所有椭圆的一个焦点上．第二定律：对每一个行星而言，太阳行星的连线在相同时间内扫过的面积相等．第三定律：所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等【解答】解：A、B：第一定律的内容为：所有行星分别沿不同大小的椭圆轨道绕太阳运动，太阳处于椭圆的一个焦点上．故A正确，B错误．C、由第三定律：所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等．故C错误．D、由第一定律知道所有行星分别沿不同大小的椭圆轨道绕太阳运动，故D正确．故选：AD【点评】正确理解开普勒的行星运动三定律是解答本题的关键4．（2015春•新疆校级期中）关于公式=k，下列说法中正确的是（）A．围绕同一星球运行的行星或卫星，k值是相同的B．不同星球的行星或卫星，k值均相等C．公式只适用于围绕太阳运行的行星D．以上说法均错误【分析】开普勒第三定律中常数k是由中心天体决定的，与其他因素无关．【解答】解：A、开普勒第三定律中常数k是由中心天体决定的，围绕同一星球运行的行星或卫星，k值是相同的，故A正确；B、不同星球的行星或卫星，k值可能不相等，故B错误；C、开普勒定律是针对太阳系推导出来的结果，但是适用于任何天体和其周围的卫星．故C错误，D错误；故选：A．【点评】掌握开普勒三定律的内容，并能熟练应用，知道k由中心天体决定，R为轨道半长轴．5．（2015春•天水校级期中）有关开普勒关于行星运动的描述，下列说法中不正确的是（）A．所有行星绕太阳运动的轨道都是椭圆，太阳处在椭圆的一个焦点上B．所有行星均是以同样的速度绕太阳运动C．所有行星轨道的半长轴的三次方跟公转周期的二次方的比值都相等D．不同的行星绕太阳运动的椭圆轨道是不同的【分析】熟记理解开普勒的行星运动三定律：第一定律：所有的行星围绕太阳运动的轨道都是椭圆，太阳处在所有椭圆的一个焦点上．第二定律：对每一个行星而言，太阳行星的连线在相同时间内扫过的面积相等．第三定律：所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等．【解答】解：A、所有行星绕太阳运动的轨道都是椭圆，太阳处在椭圆的一个焦点上，故A正确；B、不同行星绕太阳运动的速度不同，故B错误；C、根据第三定律得所有行星轨道的半长轴的三次方跟公转周期的二次方的比值都相等，故C正确；D、不同的行星绕太阳运动的椭圆轨道是不同的，故D正确；本题选不正确的，故选：B．【点评】开普勒关于行星运动的三定律是万有引力定律得发现的基础，是行星运动的一般规律，正确理解开普勒的行星运动三定律是解答本题的关键．6．（2015春•泰州校级月考）冥王星绕太阳的公转轨道是个椭圆，公转周期为T0，如图．忽略其他行星对它的影响，则（）A．冥王星从A→B→C的过程中，速率逐渐变小B．冥王星从A→B所用的时间等于C．冥王星在B点的加速度方向指向D点D．冥王星从B→C→D的过程中，万有引力对它先做负功后做正功【分析】熟记理解开普勒的行星运动三定律：第一定律：所有的行星围绕太阳运动的轨道都是椭圆，太阳处在所有椭圆的一个焦点上．第二定律：对每一个行星而言，太阳行星的连线在相同时间内扫过的面积相等．第三定律：所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等．根据力与速度方向的夹角判断该力是做正功还是负功．【解答】解：A、根据第二定律：对每一个行星而言，太阳行星的连线在相同时间内扫过的面积相等．所以冥王星从A→B→C的过程中，冥王星与太阳的距离增大，速率逐渐变小，故A正确；B、公转周期为T0，冥王星从A→C的过程中所用的时间是T0，由于冥王星从A→B→C的过程中，速率逐渐变小，从A→B与从B→C的路程相等，所以冥王星从A→B所用的时间小于，故B错误；C、根据牛顿第二定律得冥王星在B点的加速度方向指向太阳，故C错误；D、冥王星从B→C→D的过程中，万有引力方向先与速度方向成钝角，过了C点后万有引力方向与速度方向成锐角，所以万有引力对它先做负功后做正功，故D正确；故选：AD．【点评】正确理解开普勒的行星运动三定律是解答本题的关键，会根据力与速度方向的夹角判断该力是做正功还是负功．7．（2013春•武定县校级期中）下列说法正确的是（）A．“地心说”的代表人物是哥白尼B．“日心说”的代表人物是托勒密C．第谷和开普勒通过大量的天文观测和数据分析完善了“地心说”D．第一次通过实验比较准确地测出万有引力常量的科学家是卡文迪许【分析】根据物理学史和常识解答，记住著名物理学家的主要贡献即可．【解答】解：A、“地心说”的代表人物亚里士多德和托勒密，故A错误；B、“日心说”的代表人物是哥白尼，故B错误；C、第谷和开普勒通过大量的天文观测和数据分析完善了“日心说”，故C错误；D、第一次通过实验比较准确地测出万有引力常量的科学家是卡文迪许，故D正确；故选：D．【点评】对物理学的发展史要了解，特别是一些物理学家对物理学史的贡献更应当了解，属于物理常识．8．（2015•黄冈模拟）牛顿以天体之间普遍存在着引力为依据，运用严密的逻辑推理，建立了万有引力定律．下列有关说法正确的是（）A．“月﹣地检验”表明地面物体、月球所受地球引力都遵从同样的规律B．“月﹣地检验”表明物体在地球上受到的引力是在月球上的60倍C．行星间引力与距离的平方成反比关系是根据牛顿第三定律得到的D．引力常量 G的大小是牛顿利用实验测出的【分析】万有引力定律建立后，经历过“月﹣地检验”，表明了万有引力定律的正确性；“月﹣地检验”表明物体在地球上受到的引力是在月球上的6倍；牛顿探究天体的间的作用力，证实行星间引力与距离的平方成反比；引力常量G的大小是卡文迪许测得的．【解答】解：A、万有引力定律建立后，经历过“月﹣地检验”，课本有此检验的详细描述，故A正确；B、“月﹣地检验”表明物体在地球上受到的引力是在月球上的6倍，故B错误；C、牛顿探究天体间的作用力，得到表明行星间引力与距离的平方成反比，并进一步扩展为万有引力定律，故C错误；D、牛顿发现万有引力定律，但是没有测得引力常量G的大小，G大小是卡文迪许测得的，故D错误．故选：A．【点评】该题要掌握好物理学的基本发展历史，知道各个人对物理学的贡献，其中引力常量是卡文迪许测得的这点要牢记．9．（2011春•南关区校级期末）对于万有引力定律的表达式F=G，下列说法中正确的是（）A．公式中G为引力常量，它是由实验测得的，没有单位B．当r趋近于零时，万有引力趋近于无穷大C．m1与m2受到的引力总是大小相等的，而与m1、m2是否相等无关D．m1与m2受到的引力总是大小相等、方向相反，是一对平衡力【分析】万有引力定律是在行星绕太阳做匀速圆周运动的向心力公式、开普勒第三定律及牛顿第三定律相结合得出的【解答】解：A、公式中G为引力常量，它是由卡文迪许实验测得的，单位是，故A不正确；B、式中r是两一定质量的物体间的距离，即使间距为零，但物体仍有大小，所以r达不到零，万有引力也不会趋近于无穷大，故B不正确；C、m1与m2受到的引力总是大小相等的，但与m1、m2是否相等无关，与m1、m2质量的乘积有关，故C正确；D、m1与m2受到的引力总是大小相等、方向相反的．涉及到两个物体，属于作用力与反作用力，故D不正确；故选C【点评】万有引力定律表达式不是数学公式，各量均有一定的涵义．同时突出作用力与反作用力、平衡力两者的区别．10．（2013春•富平县校级期末）对于万有引力定律的数学表达式，下列说法正确的是（）A．公式中G为引力常量，是人为规定的B．r趋近零时，万有引力趋于无穷大C．m1，m2受到的万有引力总是大小相等，与m1，m2的大小无关D．m1，m2受到的万有引力总是大小相等，方向相反，是一对平衡力【分析】引力常量G是客观存在的，不是人为规定的，由卡文迪许测出．万有引力适用于天体的大小相对其距离可以忽略不计时，当距离趋近零时此公式不在适用．万有引力作用是天体间的相互吸引，一定是等大反向．【解答】解：A、引力常量G是客观存在的，不是人为规定的，由卡文迪许测出，故A错误．B、万有引力是一种远程相互作用，在微观的距离上是不适用．故B错误．C、万有引力作用是天体间的相互吸引，一定是等大反向，m1和m2之间的引力大小总是相等，与m1和m2是否相等无关，故C正确．D、万有引力作用是天体间的相互吸引，一定是等大反向，是作用力与反作用力的关系，故D错误．故选：C．【点评】万有引力定律是一个普遍适用的定律，不管是大的物体，还是小的物体，不管是距离大，还是距离小．我们一般仅仅说它适用与宏观、低速运动的物体．微观上要结合相对论使用．11．（2015春•福州期末）两个相距为r的小物体，它们之间的万有引力为F．保持质量不变，将它们间的距离增大到3r．那么它们之间万有引力的大小将变为（）A．F B．3F C．D．【分析】根据万有引力定律的内容（万有引力是与质量乘积成正比，与距离的平方成反比）解决问题．【解答】解：根据万有引力定律得：甲、乙两个质点相距r，它们之间的万有引力为F=；若保持它们各自的质量不变，将它们之间的距离增大到3r，则甲、乙两个质点间的万有引力F′==；故选D．【点评】要求解一个物理量大小变化，我们应该把这个物理量先表示出来，再根据已知量进行判断．12．（2012春•东城区期末）在牛顿发表万有引力定律一百多年之后，卡文迪许首先精确测量了引力常量．在国际单位制中引力常量的单位是（）A．N•kg2B．N•m2C．N•kg2/m2D．N•m2/kg2【分析】根据万有引力定律F=G，由质量、距离和力三个量的单位推导出G的单位．【解答】解：万有引力定律F=G公式中，质量m的单位为kg，距离r的单位为m，引力F 的单位为N，由公式推导得出，G的单位为．故选D．【点评】物理量的单位分基本单位和导出单位，导出单位由基本单位根据公式进行推导得出．13．（2012•天心区校级模拟）卡文迪许利用如图所示的扭秤实验装置测量了引力常量G．为了测量石英丝极微小的扭转角，该实验装置中采取使“微小量放大”的主要措施是（）A ．减小石英丝的直径B ．增大T 型架横梁的长度C ．利用平面镜对光线的反射D ．增大刻度尺与平面镜的距离【分析】为测量石英丝极的扭转角，实验采取了“微小量放大”．当引进m ′时由于物体间引力作用，使石英丝极发生微小的扭转，从而带动平面镜转动，导致经平面镜反射过来的光线发生较大变化，得出转动的角度．列出石英丝极微小的扭转力矩等于引力力矩的表达式，从而求出引力常量【解答】解：当减小石英丝的直径时，会导致石英丝更容易转动，对测量石英丝极微小的扭转角却没有作用，故A 不正确；当增大T 型架横梁的长度时，会导致石英丝更容易转动，对测量石英丝极微小的扭转角却没有作用；故B 错误；为了测量石英丝极微小的扭转角，该实验装置中采取使“微小量放大”．利用平面镜对光线的反射，来体现微小形变的．当增大刻度尺与平面镜的距离时，转动的角度更明显．因此选项CD 正确．故选：CD ．【点评】本题巧妙地利用光的反射将因引力产生微小转动的角度放大，同时利用力矩平衡来解题，能拓宽学生的解题思路，提高解题能力1．[对万有引力定律的理解]关于万有引力公式F ＝G m 1m 2r 2，以下说法中正确的是 ( )A ．公式只适用于星球之间的引力计算，不适用于质量较小的物体B ．当两物体间的距离趋近于0时，万有引力趋近于无穷大C ．两物体间的万有引力也符合牛顿第三定律D ．公式中引力常量G 的值是牛顿规定的答案 C解析 万有引力公式F ＝G m 1m 2r，虽然是牛顿由天体的运动规律得出的，但牛顿又将它推广到了宇宙中的任何物体，适用于计算任何两个质点间的引力．当两个物体间的距离趋近于0时，两个物体就不能视为质点了，万有引力公式不再适用．两物体间的万有引力也符合牛顿第三定律．公式中引力常量G 的值是卡文迪许在实验室里用实验测定的，而不是人为规定的．故正确答案为C.2．[万有引力引力场与电场的类比]由于万有引力定律和库仑定律都满足平方反比定律，因此引力场和电场之间有许多相似的性质，在处理有关问题时可以将它们进行类比，例如电场中反映各点电场强弱的物理量是电场强度，其定义式为E ＝Fq，在引力场中可以用一个类似的物理量来反映各点引力场的强弱．设地球质量为M ，半径为R ，地球表面处重力加速度为g ，引力常量为G ，如果一个质量为m 的物体位于距离地心2R 处的某点，则下列表达式中能反映该点引力场强弱的是 ( )。