高中数列方法和解题技巧(学生版)

一．常见数列规律1．分子与分母分别为一个简单数列． 2．分子分母之间存在直观的简单规律．3．反约分数列：同时扩大数列中某些分数的分子与分母（分数值不变），从而时的分数的分子与分母分别形成简单数列． 二．解题技巧1．经典约分：当分子和分母含有相同因子时，应将其化成最简分数． 2．经典通分：当分数的分母很容易化成一致时，将其化为相同数． 3．分子通分：当分数的分子很容易化成一致时，将其化为相同数．重难点：分数数列找规律．题模一：求某位置的数例1.1.1观察数列： 1111111111,,,,,,,,,,1223334444…． 请问：其中的第150项是多少？例1.1.2观察数列： 1212121212,,,,,,,,,,1122334455… 请问：其中的第101项是多少？例1.1.3有这样一列数，前两个数分别是0和1，从第三个数开始，每一个数都是前两个数计算第43讲_分数数列找规律知识精讲三点剖析题模精选的和：0，1，1，2，3，5，8，13，21，34，．那么这个数列的第1000个数除以8所得的余数是=__________．例1.1.4一列数按下述规律排列：（1）第一项是101；（2）奇数项与下一项的比是3:2；（3）偶数项与下一项的比是4:3．那么，第10项与第15项的比为．例 1.1.5有一串数，13、36，59、712、915、1118、……，后一个数的分子比前一个数的分子大2，分母大3．所以第n个数为：213nn，第30个数是________，第45个数是________．例1.1.6观察数列：1121231234 ,,,,,,,,,, 1223334444…请问：其中的第150项是多少？例1.1.7观察数列：113135135720052007 ,,,,,,,,,,,, 244666888820082008…请问：其中的第2008项是多少？题模二：某数在什么位置例1.2.1观察数列：1111111111 ,,,,,,,,,, 1223334444…．请问：第一次出现的151是其中第几项？例1.2.2观察数列：1212121212,,,,,,,,,,1122334455…请问：149是其中第几项？例1.2.3观察数列：1121231234,,,,,,,,,, 1223334444…请问：4949是其中第几项？例1.2.4观察数列：113135135720052007,,,,,,,,,,,, 244666888820082008…请问：4748是其中第几项？例 1.2.5观察按下列规律排成的一列数：1121231234123451 ,,,,,,,,,,,,,,,,......, 1213214321543216在这个数列中，从左边起第m个数记为F（m），当F（m）=22001时，m=_______随练1.1观察数列：1111111111 ,,,,,,,,,, 1223334444…．请问：其中的第50项是多少？随练1.2观察数列：1212121212 ,,,,,,,,,, 1122334455…请问：其中的第100项是多少？随练1.3找规律填数：12，56，1112，1920，__________，4142，……随练1.4观察数列：1121231234 ,,,,,,,,,, 1223334444…请问：其中的第50项是多少？随堂练习随练1.5观察数列：113135135720052007 ,,,,,,,,,,,, 244666888820082008…请问：其中的第2009项是多少？随练1.6观察数列：1111111111 ,,,,,,,,,, 1223334444…．请问：第一次出现的149是其中第几项？随练1.7观察数列：1212121212,,,,,,,,,,1122334455…请问：250是其中第几项？随练1.8观察数列：113135135720052007,,,,,,,,,,,, 244666888820082008…请问：350是其中第几项？作业1观察数列：1111111111 ,,,,,,,,,, 1223334444…．请问：其中的第100项是多少？课后作业作业2观察数列：1212121212 ,,,,,,,,,, 1122334455…请问：其中的第99项是多少？作业3观察数列：1121231234 ,,,,,,,,,, 1223334444…请问：其中的第100项是多少？作业4观察数列：113135135720052007 ,,,,,,,,,,,, 244666888820082008…请问：其中的第2007项是多少？作业5有一串真分数12、13、23、14、24、34、15、25、35、45……那么按规律，第100个分数是（）．A．915B．315C．116D．316作业6观察下面一列数的规律，这列数从左往右第100个数是__________．12,35,58,711,914……．作业7观察数列：1111111111 ,,,,,,,,,, 1223334444…．请问：第一次出现的150是其中第几项？作业8观察数列：1212121212,,,,,,,,,,1122334455…请问：150是其中第几项？作业9观察数列：1121231234,,,,,,,,,, 1223334444…请问：150是其中第几项？作业10已知数列：11212312341 ,,,,,,,,,,,, 12132143215请问：（1）1130是第__________项．（2）数列第2012项是__________．。

求数列通项公式方法（1）．公式法（定义法）根据等差数列、等比数列的定义求通项 例：1已知等差数列}{n a 满足：26,7753=+=a a a ， 求n a ；2.已知数列}{n a 满足)1(1,211≥=-=-n a a a n n ，求数列}{n a 的通项公式；3.数列{}n a 满足1a =8，022124=+-=++n n n a a a a ，且 （*∈N n ），求数列{}n a 的通项公式；4.等比数列}{n a 的各项均为正数，且13221=+a a ，62239a a a =，求数列}{n a 的通项公式5.已知数列}{n a 满足)1(3,211≥===n a a a n n ，求数列}{n a 的通项公式；6.已知数列}{n a 满足2122142++=⋅==n n n a a a a a 且， （*∈N n ），求数列{}n a 的通项公式；7.已知数列}{n a 满足，21=a 且1152(5)n nn n a a ++-=-（*∈N n ），求数列{}n a 的通项公式；8.已知数列}{n a 满足，21=a 且115223(522)n n n n a a +++⨯+=+⨯+（*∈N n ），求数列{}n a 的通项公式；9.数列已知数列{}n a 满足111,41(1).2n n a a a n -==+>则数列{}n a 的通项公式= （2）累加法1、累加法 适用于：1()n n a a f n +=+21321(1)(2) ()n n a a f a a f a a f n +-=-=-= 两边分别相加得 111()nn k a a f n +=-=∑例：1.已知数列{}n a 满足141,21211-+==+n a a a n n ，求数列{}n a 的通项公式。

2. 已知数列{}n a 满足11211n n a a n a +=++=，，求数列{}n a 的通项公式。

第2讲 数列计算第一部分：知识介绍1、等差数列三个重要的公式：① 通项公式：递增数列：末项=首项+(项数1-)⨯公差，11n a a n d =+-⨯（）递减数列：末项=首项-(项数1-)⨯公差，11n a a n d =--⨯（）② 项数公式：项数=(末项-首项)÷公差+1 ③ 求和公式：和=(首项+末项)⨯项数÷22、中项定理：对于任意一个项数为奇数的等差数列，中间一项的值等于所有项的平均数，也等于首项与末项和的一半；或者换句话说，各项和等于中间项乘以项数．3、公式综合：1） 连续自然数求和(1)1232n n n ⨯+++++=L2） ()()()213572112311321n n n n n +++++-=++++-++-++++=L L L 3） N 个连续自然数的平方和 2222(1)(21)1236n n n n ⨯+⨯+++++=L4） N 个连续自然数的立方和 ()2223333(1)1231234n n n n ⨯+++++=++++=L L 5） 平方差公式：()()22a b a b a b -=+- 完全平方公式()2222a b a ab b ±=±+ 6） 122334...(1)n n ⨯+⨯+⨯++-⨯1(1)(1)3n n n =-⨯⨯+7） 1123234345...(2)(1)(2)(1)(1)4n n n n n n n ⨯⨯+⨯⨯+⨯⨯++-⨯-⨯=--+4、等比数列：如果一个数列，从第2项起，每一项与它的前一项的比等于同一个常数，这个数列就叫做等比数列，这个常数叫做等比数列的公比，公比通常用q 表示()0q ≠。

（或者从第二数开始每一个数都和前面数的倍数都是相同的，这个数列就叫做等比数列。

）一般地，等比数列求和采用“错位相减法”。

（公比不为1）其它复合型数列整数与数列本讲数表应用题找规律计算等差数列应用题求和方法初步认识等比数列第二部分：例题精讲【例 1】（试题汇编）计算11、14、17、20、……、95、98这个等差数列的项数是（）【例 1】在等差数列6，13，20，27，…中，从左向右数，第_______个数是1994．【巩固】5、8、11、14、17、20、L，这个数列有多少项？它的第201项是多少？65是其中的第几项？已知数列0、4、8、12、16、20、…… ，它的第43项是多少？【例 1】用等差数列的求和公式会计算下面各题吗？⑴3456767778L+++++++=⑵13578799L++++++=⑶471013404346L+++++++=【例 2】已知一个等差数列第8项等于50，第15项等于71.请问这个数列的第1项是（）【例 3】把210拆成7个自然数的和，使这7个数从小到大排成一行后，相邻两个数的差都是5，那么，第1个数与第6个数分别是多少？【例 4】（试题汇编）有一本50页的书，再把这本书的各页的页码累加起来时，有一张纸的页码错误的多加了一次，得到的和为1302，那么中间多加的页码为（）。

数列求和的基本方法和技巧数列求和 通项分式法 错位相减法 反序相加法 分组法 分组法 合并法一、利用常用求和公式求和利用下列常用求和公式求和是数列求和的最基本最重要的方法. 1、 等差数列求和公式：d n n na a a n S n n 2)1(2)(11-+=+=2、 等比数列求和公式：⎪⎩⎪⎨⎧≠--=--==)1(11)1()1(111q q q a a qq a q na S n nn[例] 求和1＋x 2＋x 4＋x 6＋…x 2n+4(x≠0)注：(1)利用等比数列求和公式．当公比是用字母表示时，应对其是否为1进行讨论，如本题若为“等比”的形式而并未指明其为等比数列，还应对x 是否为0进行讨论．(2)要弄清数列共有多少项，末项不一定是第n 项．对应高考考题：设数列1，（1+2），…，（1+2+1222-⋯+n ），……的前顶和为ns，则ns的值。

二、错位相减法求和错位相减法求和在高考中占有相当重要的位置，近几年来的高考题其中的数列方面都出了这方面的内容。

需要我们的学生认真掌握好这种方法。

这种方法是在推导等比数列的前n 项和公式时所用的方法，这种方法主要用于求数列{a n · b n }的前n 项和，其中{ a n }、{ b n }分别是等差数列和等比数列. 求和时一般在已知和式的两边都乘以组成这个数列的等比数列的公比q ；然后再将得到的新和式和原和式相减，转化为同倍数的等比数列求和，这种方法就是错位相减法。

[例] 求和：132)12(7531--+⋅⋅⋅++++=n n x n x x x S （1≠x ）………………………①注意、1 要考虑 当公比x 为值1时为特殊情况 2 错位相减时要注意末项 此类题的特点是所求数列是由一个等差数列与一个等比数列对应项相乘。

对应高考考题：设正项等比数列{}n a 的首项211=a ，前n 项和为n S ，且0)12(21020103010=++-S S S 。

数列求和的典型方法（学生版）※ 典型例题考点1．分组求和法求数列的前n 项和一、分组求和◎题型1：求数列{}n n a b ±的前n 项和n S思路1：1122()()()n n n S a b a b a b =±+±++±…1212()()n n a a a b b b =++⋅⋅⋅+±++⋅⋅⋅+◎题型2：求通项为()()n f n n a g n n ⎧=⎨⎩，是奇，是偶数数或(1)()n n a f n =-的数列的前n 项和n S 思路2：相邻项组合（1）当n 为偶数时，12341()()()n n n S a a a a a a -=+++++…；（2）当n 为奇数时，123421()()()n n n n S a a a a a a a --=++++++…．思路3：奇偶项组合（1）当n 为偶数时，n S =13124()()n n a a a a a a -++++++……；（2）当n 为奇数时，n S 13241()()n n a a a a a a -=++++++……．思路4：公式优化（1）当n 为偶数时，利用套路2、3其中之一；（2）当n 为奇数时，S S a =-．例3、数列{}n a 的通项公式为2cos 3n a n =⋅，其前n 项和为n S ． （Ⅰ）求32313n n n a a a --++及n S 3；（Ⅱ）若312n n n S b n -=⋅，求数列{}n b 的前n 项和n T ．考点2．倒序相加法【例2】设()442xx f x =+，求122012201320132013f f f ⎛⎫⎛⎫⎛⎫+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭的值． 变式1．求222289sin 1sin 2sin 3....sin 89S =︒+︒+︒++︒变式2．已知函数()f x 对任意的x R ∈，都有()+(1)=1f x f x -，求1231(0)()()()....()(1)n n S f f f f f f n n n n-=++++++.考点4．裂项相消法求数列的前n 项和变式2（Ⅰ）已知数列{}n a 满足：1(21)(21)n a n n =-+，求数列{}n a 的n 项和n S ． （Ⅱ）已知数列{}n a 满足：4(1)(21)(21)n n n a n n =--+，求数列{}n a 的n 项和n S ． ．考点5．数列的综合应用【例5】各项均为正数的数列{}n a 的前n 项和为n S ，n S 满足()223n n S n n S -+--()230n n +=，n N *∈. （1）求1a 的值；（2）求数列{}n a 的通项公式；（3）证明：对任意n N *∈，有1223111114n n a a a a a a ++++<. 变式1．设各项均为正数的数列{a n }的前n 项和为S n ，满足4S n ＝a 2n ＋1－4n －1，n ∈N *，且a 2，a 5，a 14构成等比数列．。

求数列通项：构造法类型1 形如n n n q k a k a 211+=+的数列的递推公式，构造)()(111nn n n Aq a k Aq a +=+++，代入递推公式求出A ，化为等比数列解决。

类型2 形如n k n k a k a n n 32211++=+的数列的递推公式，构造))1()1((21C n B n A a n ++++++)(21C Bn An a k n +++=，代入递推公式求出A ，B ，C ，化为等比数列解决。

类型3 形如n k q k a k a n n n 3211++=+的数列的递推公式，构造))1((11C n B Aq a n n ++++++)(1C Bn Aq a k nn +++=，代入递推公式求出A ，B ，C ，化为等比数列解决。

1、构造等差数列或等比数列由于等差数列与等比数列的通项公式显然，对于一些递推数列问题，若能构造等差数列或等比数列，无疑是一种行之有效的构造方法. 例1.设数列{}n a 的前n 项的和14122333n n n S a +=-⨯+，1,2,3,n =...求通项n a ； ：例2： 已知1a =2，n a a nn n ++=+321，试求n a 的通项公式.{例3： 设各项均为正数的数列{}n a 的前n 项和为n S ，对于任意正整数n ，都有等式：|例4： 数列{}n a 中前n 项的和n n a n S -=2，求数列的通项公式n a .-例5. 已知数列{}n a 中，11=a ；数列{}n b 中，01=b 。

当2≥n 时，)2(3111--+=n n n b a a ,)2(3111--+=n n n b a b ，求n a ,n b .。

2、构造差式与和式解题的基本思路就是构造出某个数列的相邻两项之差，然后采用累加的方法就可求得这一数列的通项公式.类型4 形如n n n qa pa a +=++12（其中p ，q 均为常数）的数列的递推公式。

技巧方法专题2 数列求通项问题 解析版一、数列求通项常用方法知识框架二、数列求通项方法【一】归纳法求通项1.例题【例1】由数列的前n 项，写出通项公式： (1)3,5,3,5,3,5，… (2)12，23，34，45，56，… (3)2，52，134，338，8116，…(4)12，16，112，120，130，…【例2】已知数列：，按照从小到大的顺序排列在一起，构成一个新的数列：首次出现时为数列的（ ） ()12,,,11k k N k k *⋅⋅⋅∈-k {}n a 1212381,,,,,,,213219⋅⋅⋅则{}n a 通过数列前若干项归纳出数列的一个通项公式，关键是依托基本数列如等差数列、等比数列，寻找a n 与n ，a n 与a n ＋1的联系.2. 巩固提升综合练习【练习1】由数列的前几项，写出通项公式： (1)1，－7，13，－19，25，… (2)14，37，12，713，916，… (3)1，－85，157，－249，…【练习2】如图是一个三角形数阵，满足第n 行首尾两数均为n ，(),A i j 表示第()2i i ≥行第j 个数，则()100,2A 的值为__________．【二】公式法求通项1.例题【例1】 数列满足，，则（ ） A ．B ．C ．D ．【例2】已知数列{a n }满足a 1＝4，a n ＝4－4a n －1(n >1)，记b n ＝1a n －2． 求证：数列{b n }是等差数列，并求n a ． {}n a 112a =()*1111n 11n n N a a +=-∈--10a =91010910111110等差数列：d n a a n )1(1-+=等差数列：等比数列：11-=n n qa a 等比数列：2.巩固提升综合练习【练习1】已知各项都为正数的数列{a n }满足a 1＝1，a 2n －(2a n ＋1－1)a n －2a n ＋1＝0． (1)求a 2，a 3；(2)证明数列{a n }为等比数列,并求n a ．【练习2】已知数列{}n a 和{}n b 满足111112,341,341n n n n a b a b n b a n ++=+==+-=-+()1求证：{}n n a b +是等比数列,{}n n a b -是等差数列； ()2求数列{}n a 和{}n b 的通项公式．【三】累加法求通项1.例题【例1】在数列中，，，则（ ） A ． B ． C ．D ．{}n a 12a =11ln 1n n a a n +⎛⎫=++ ⎪⎝⎭10a =2ln10+29ln10+210ln10+11ln10+型如a n ＋1＝a n ＋f (n )的递推公式求通项可以使用累加法，步骤如下： 第一步 将递推公式写成a n ＋1－a n ＝f (n )；第二步 依次写出a n －a n －1，…，a 2－a 1，并将它们累加起来； 第三步 得到a n －a 1的值，解出a n ；第四步 检验a 1是否满足所求通项公式，若成立，则合并；若不成立，则写出分段形式.累乘法类似.【例2】对于等差数列和等比数列，我国古代很早就有研究成果，北宋大科学家沈括在《梦溪笔谈》中首创的“隙积术”，就是关于高阶等差级数求和的问题.现有一货物堆，从上向下查，第一层有2个货物，第二层比第一层多3个，第三层比第二层多4个，以此类推，记第n 层货物的个数为n a ，则数列{}n a 的通项公式n a =_______，数列(2)n nn a ⎧⎫⎨⎬+⎩⎭的前n 项和n S =_______.2.巩固提升综合练习【练习1】在数列中，，则数列的通项 ________.【练习2】已知数列是首项为，公差为1的等差数列，数列满足（），且，则数列的最大值为__________．【练习3】两千多年前，古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题，他们在沙滩上画点或用小石子来表示数，按照点或小石子能排列的形状对数进行分类，如图2中的实心点个数1，5，12，22，…，被称为五角形数，其中第1个五角形数记作，第2个五角形数记作，第3个五角形数记作，第4个五角形数记作，…，若按此规律继续下去，得数列{}n a ，则1_______(2)n n a a n --=≥；对*n N ∈，_____n a =．【四】累积法求通项1.例题【例1】已知数列{a n }满足a 1＝23，a n ＋1＝nn ＋1a n ，求a n .{}n a 111,21n n a a a n +=-=+n a ={}n b 34-{}n a 12nn n a a +-=*n N ∈137a b =n n b a ⎧⎫⎨⎬⎩⎭11a =25a =312a =422a =型如)(1n f a a nn =+的递推公式求通项可以使用累积法2.巩固提升综合练习【练习1】已知数列{a n }中，a 1＝1，a n ＋1＝2n a n (n ∈N *)，则数列{a n }的通项公式为( )A.a n ＝2n －1 B.a n ＝2n C.(1)22n n n a -=D.222n n a =【五】Sn 法（项与和互化求通项）1.例题【例1】已知数列{}n a 的前n 项和n S ，且23-=nn S ，则=n a .【例2】设数列的前项和，若，，则的通项公式为_____． 【例3】设S n 是数列{a n }的前n 项和，且a 1＝－1，a n ＋1＝S n S n ＋1，则S n ＝__________. 2.巩固提升综合练习【练习1】在数列{a n }中，a 1＝1，a 1＋2a 2＋3a 3＋…＋na n ＝n ＋12a n ＋1(n ∈N *)，求数列{a n }的通项a n .【练习2】记数列的前项和为，若，则数列的通项公式为______. {}n a n n S 11a =-()*1102n n S a n N +-=∈{}n a {}n a n n S 323n n S a n =+-{}n a n a =11,(1)n n n s a s s n -⎧=⎨->⎩,（n=1)已知S n ＝f (a n )或S n ＝f (n )解题步骤：第一步 利用S n 满足条件p ，写出当n ≥2时，S n －1的表达式；第二步 利用a n ＝S n －S n －1(n ≥2)，求出a n 或者转化为a n 的递推公式的形式；第三步 若求出n ≥2时的{a n }的通项公式，则根据a 1＝S 1求出a 1，并代入{a n }的通项公式进行验证，若成立，则合并；若不成立，则写出分段形式.如果求出的是{a n }的递推公式，则问题化归为类型二.【练习3】已知数列{a n }是递增的等比数列，且a 1＋a 4＝9，a 2a 3＝8.(1)求数列{a n }的通项公式；(2)设S n 为数列{a n }的前n 项和，b n ＝a n ＋1S n S n ＋1，求数列{b n }的前n 项和T n .【练习4】设数列{}n a 满足12323...2(n N*)n na a a na ⋅⋅⋅⋅=∈．（1）求{}n a 的通项公式；（2）求数列122n n a +⎧⎫+⎨⎬⎩⎭的前n 项和n S ．【练习5】已知数列{}n a 的前n 项和为n S ，112a =，20(2)n n n n S a S a n -+=≥． （1）求证：数列1n S ⎧⎫⎨⎬⎩⎭是等差数列； （2）若1,32,nn n S n C n n -⎧⎪=+⎨⎪⎩为奇数为偶数，设数列{}n C 的前n 项和为n T ，求2n T .【六】构造法求通项1.例题【例1】已知数列{a n }中，a 1＝1，a n ＋1＝2a n ＋3，求a n .【例2】已知数列{a n }满足a n ＋1＝2a n ＋n ，a 1＝2，求数列{a n }的通项公式.【例3】已知数列{a n }满足a n ＋1＝2a n ＋3×5n ，a 1＝6，求数列{a n }的通项公式. 1.型如a n ＋1＝pa n ＋q (其中p ，q 为常数，且pq (p －1)≠0)可用待定系数法求得通项公式，步骤如下： 第一步 假设将递推公式改写为a n ＋1＋t ＝p (a n ＋t )； 第二步 由待定系数法，解得t ＝qp －1；第三步 写出数列⎭⎬⎫⎩⎨⎧-+1p q a n 的通项公式； 第四步 写出数列{a n }通项公式. 2.a n ＋1＝pa n ＋f (n )型【参考思考思路】确定()f n →设数列{}1()n a f n λ+→列关系式)]([)1(1211n f a n f a n n λλλ+=+++→比较系数求1λ，2λ→解得数列{}1()n a f n λ+的通项公式→解得数列{}n a 的通项公式【例4】 已知数列满足：，，则 （ ）A ．B ．C ．D ．2.巩固提升综合练习【练习1】已知数列{a n }满足a n ＋1＝3a n ＋2，且a 1＝1，则a n ＝________.【练习2】已知数列{a n }的首项为a 1＝1，且满足a n ＋1＝12a n ＋12n ，则此数列的通项公式a n 等于( )A.2nB.n (n ＋1)C.n2n －1D.n (n ＋1)2n【练习3】已知非零数列{}n a 的递推公式为11a =,()112n n n n a a a a n N *++=+∈.(1)求证数列11n a ⎧⎫+⎨⎬⎩⎭是等比数列； (2)若关于n 的不等式2221211152111log 1log 1log 1n m n n n a a a ++⋅⋅⋅+<-⎛⎫⎛⎫⎛⎫++++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭有解,求整数m 的最小值；(3)在数列()111n n a ⎧⎫+--⎨⎬⎩⎭中,是否一定存在首项、第r 项、第s 项()1r s <<,使得这三项依次成等差数列？若存在,请指出r s 、所满足的条件；若不存在,请说明理由. {}n a 11a =1122(2,)n n n a a n n N --=+≥∈n a =2n n a n =⋅12n n a n -=⋅(21)2n n a n =-⋅1(21)2n n a n -=-⋅【七】其他求通项方法 1.例题【例1】 已知数列满足,,则（ ） A ．B ．C ．D ．【例2】若数列{a n }中，a 1＝3且a n ＋1＝a 2n (n 是正整数)，则它的通项公式a n 为________________. 【例3】已知数列满足递推关系：，，则＝（ ） A ．B ．C ．D ．2.巩固提升综合练习【练习1】 已知数列{a n }的前n 项和是S n ，且满足a n ＋1＝11－a n (n ∈N *)，211=a ，则S 2 017＝（ ） 【练习2】 在数列中，已知，，则_______，归纳可知_______．【八】特征根和不动点法求通项（自我提升）1.例题【例1】已知数列满足，求数列的通项．{}n a 113a =111nn n a a a ++=-*()n N ∈2012391a a a a ⋯⋯⋅⋅=3-2-12-13-{}n a 11n n n a a a +=+112a =2018a 12016120171201812019{}n a 12a =()*131nn n a a n N a +=∈+2a =n a ={}n a *12212,3,32()n n n a a a a a n N ++===-∈{}n a n a 一、形如是常数）的数列形如是常数）的二阶递推数列都可用特征根法求得通项，其特征方程为…①若①有二异根，则可令是待定常数） 若①有二重根，则可令是待定常数）再利用可求得，进而求得．21(,n n n a pa qa p q ++=+112221,,(,n n n a m a m a pa qa p q ++===+n a 2x px q =+,αβ1212(,n nn a c c c c αβ=+αβ=1212()(,nn a c nc c c α=+1122,,a m a m ==12,c c n a【例2】已知数列满足，求数列的通项．2.巩固提升综合练习【练习1】设p q ，为实数，αβ，是方程20x px q -+=的两个实根，数列{}n x 满足1x p =，22x p q =-，12n n n x px qx --=-（34n =，，…）． （1）证明：p αβ+=，q αβ=； （2）求数列{}n x 的通项公式； （3）若1p =，14q =，求{}n x 的前n 项和n S ．{}n a *12211,2,44()n n n a a a a a n N ++===-∈{}n a n a1.例题【例3】已知数列满足，求数列的通项．【例4】已知数列满足，求数列的通项．{}n a 11122,(2)21n n n a a a n a --+==≥+{}n a n a {}n a *11212,()46n n n a a a n N a +-==∈+{}n a n a 二、形如的数列对于数列，是常数且）其特征方程为，变形为…②若②有二异根，则可令（其中是待定常数），代入的值可求得值．这样数列是首项为，公比为的等比数列，于是这样可求得． 若②有二重根，则可令（其中是待定常数），代入的值可求得值．这样数列是首项为，公差为的等差数列，于是这样可求得． 此方法又称不动点法． 2n n n Aa Ba Ca D++=+2n n n Aa B a Ca D++=+*1,(,,,a m n N A B C D =∈0,0C AD BC ≠-≠Ax B x Cx D+=+2()0Cx D A x B +--=,αβ11n n n n a a c a a ααββ++--=⋅--c 12,a a c n n a a αβ⎧⎫-⎨⎬-⎩⎭11a a αβ--c n a αβ=111n n c a a αα+=+--c 12,a a c 1n a α⎧⎫⎨⎬-⎩⎭1na α-c n a2.巩固提升综合练习【练习2】已知数列}{n a 满足：对于,N ∈n 都有.325131+-=+n n n a a a （1）若,51=a 求;n a （2）若,31=a 求;n a （3）若,61=a 求;n a （4）当1a 取哪些值时，无穷数列}{n a 不存在？【练习3】).1(0521681}{111≥=++-=++n a a a a a a n n n n n 且满足记).1(211≥-=n a b n n(1)求b 1、b 2、b 3、b 4的值；(2)求数列}{n b 的通项公式及数列}{n n b a 的前n 项和.n S【练习4】各项均为正数的数列{}n a 中，,,11b b a a ==且对满足q p n m +=+的正整数q p n m ,,,都有=+++)1)(1(m n m n a a a a )1)(1(q p q p a a a a +++，当时，求通项54,21==b a n a ．三、课后自我检测1．已知正项数列，则数列的通项公式为（ ） A ． B ．C ．D ．2．在数列－1，0，211298n n -，，，，…中，0.08是它的第________项． 3．在数列{a n }中，a 1＝3，a n ＋1＝a n ＋1n (n ＋1)，则通项公式a n ＝________.4．已知数列{}n a 中，1512a =-，1(1)3n n n na n a n +=+++，则该数列的通项n a =_______. 5．已知数列{}n a 中，()10a b b =>，()111n n a n N a ++=-∈+则能使n a b =的n 的数值是（ ） A ．14 B ．15 C ．16 D ．17 6．已知数列{}n a 满足112a =且131n n a a +=+． （1）证明数列12n a ⎧⎫+⎨⎬⎩⎭是等比数列； （2）设数列{}n b 满足11b =，112n n n b b a +-=+，求数列{}n b 的通项公式． {}n a *12(1)()2n n n a a a n N ++=∈{}n a n a n =2n a n =2n na =22n n a =7．已知数列{}n a 的前n 项和为n S ，12a =，1(2)3n n S n a =+． （1）求n a ； （2）求证:121111na a a ++⋯+<．8．已知f (x )＝log m x (m ＞0且m ≠1)，设f (a 1)，f (a 2)，…，f (a n )，…是首项为4，公差为2的等差数列， 求证：数列{a n }是等比数列，并求n a ．9．已知数列{}n a 满足：10a =，144n na a +=-，*n N ∈. （1）若存在常数x ，使得数列1n a x ⎧⎫⎨⎬-⎩⎭是等差数列，求x 的值；（2）设2311n n b a a a +=，证明：123n b b b +++<.10．已知数列{}n a 满足：()1231312nn a a a a +++⋅⋅⋅+=-，*n N ∈. （1）求数列{}n a 的通项公式；（2）若数列{}n b 满足31log n n b a +=，求11n n b b +⎧⎫⎨⎬⎩⎭的前n 项和n T ．11．数列{}n a ，*n N ∈各项均为正数，其前n 项和为n S ，且满足221n n n a S a -=.（1）求证数列{}2n S 为等差数列，并求数列{}n a 的通项公式；（2）设4241n n b S =-，求数列{}n b 的前n 项和n T ，并求使()2136n T m m >-对所有的*n N ∈都成立的最大正整数m 的值.12．已知数列{}n a 中，11a =，其前n 项的和为n S ，且当2n ≥时，满足21nn n S a S =-．（1）求证：数列1n S ⎧⎫⎨⎬⎩⎭是等差数列；（2）证明：2221274n S S S +++<．13．已知数列{}n a 满足：11a =，()*121n n a a n +=+∈N（1）求数列{}n a 的通项公式；（2）若数列{}n b 满足：()()n12ˆ111*4441N n b b b b n a n ---⋅⋯⋯=+∈，证明：{}nb 是等差数列.（3）证明：()*122311232n n a a a n nn a a a +-<++⋯+<∈N .14．在平面直角坐标系中，点(,)n n A n a 、(1,0)n B n -和(,)n C n t （*,n N t ∈为非零常数），满足1//n n A A +n n B C ，数列｛n a ｝的首项为1a =1，其前n 项和用n S 表示. （1）分别写出向量1n n A A +和n n B C 的坐标； （2）求数列｛n a ｝的通项公式；（3）请重新设计的n A 、n C 坐标（点n B 的坐标不变），使得在1//n n A A +n n B C 的条件下得到数列｛n b ｝，其中n b =nS n．15．已知点11,3⎛⎫ ⎪⎝⎭是函数()xf x a =（0a >且1a ≠）的图象上一点,等比数列{}n a 的前n 项和为()f n c -,数列{}()0n n b b >的首项为c ,且前n 项和n S 满足()112n n n n S S S S n -+-=+≥．(1)求数列{}n a 和{}n b 的通项公式； (2)若数列11n n b b +⎧⎫⎨⎬⎩⎭前n 项和为n T ,问使得10002015n T >成立的最小正整数n 是多少？。

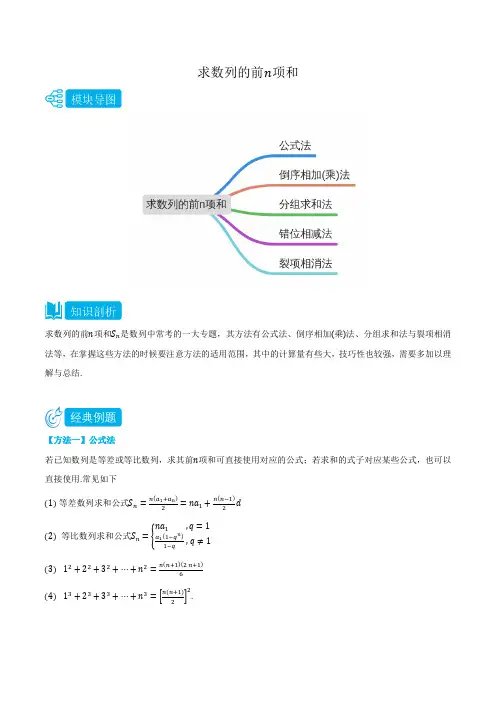
求数列的前n 项和求数列的前n 项和S n 是数列中常考的一大专题，其方法有公式法、倒序相加(乘)法、分组求和法与裂项相消法等，在掌握这些方法的时候要注意方法的适用范围，其中的计算量有些大，技巧性也较强，需要多加以理解与总结.【方法一】公式法若已知数列是等差或等比数列，求其前n 项和可直接使用对应的公式；若求和的式子对应某些公式，也可以直接使用.常见如下 (1) 等差数列求和公式S n =n (a 1+a n )2=na 1+n (n−1)2d(2) 等比数列求和公式S n ={na 1 ,q =1a 1(1−q n )1−q,q ≠1(3) 12+22+32+⋯+n 2=n (n+1)(2 n+1)6(4) 13+23+33+⋯+n 3=[n (n+1)2]2.【典题1】求和式3+6+12+⋯+3∙2n−2，先思考它是几项之和再求和.(n∈N∗)．【典题2】已知等比数列{a n}前n项和为S n，且S n=a n+1−132(1)求数列{a n}的通项公式；(2)若b n=log2a n，求数列{|b n|}的前n项和T n．巩固练习1 (★★) 求和式1+4+7+⋯+(3n+1).2 (★★) 已知{a n}是等差数列，公差d≠0，a1=1，且a1 ,a3 ,a9成等比数列，求数列{2a n}的前n项和S n．3 (★★) 已知等差数列{a n}前三项的和为－3，前三项的积为15，(1)求等差数列{a n}的通项公式；(2)若公差d>0，求数列{|a n|}的前n项和T n．4 (★★★) 设{a n}是公比大于1的等比数列，S n为数列{a n}的前n项和．已知S3=7，且a1+3，3a2，a3+4构成等差数列．(1)求数列{a n}的等差数列．(2)令b n=lna3n+1，求数列{b n}的前n项和T n．【方法二】倒序相加(乘)法1 对于某个数列{a n }，若满足a 1+a n =a 2+a n−1=⋯=a k +a n−k+1，则求前n 项和S n 可使用倒序相加法. 具体解法：设S n =a 1+a 2+⋯+a n−1+a n ① 把①反序可得S n =a n +a n−1+⋯+a 2+a 1 ②由①+②得2S n =(a 1+a n )+(a 2+a n−1)+⋯+(a n−1+a 2)+(a n +a 1)⇒S n =(a 1+a n )n2.2 对于某个数列{a n }，若满足a 1a n =a 2a n−1=⋯=a k a n−k+1，则求前n 项积T n 可使用倒序相乘法.具体解法类同倒序相加法.【典题1】 设f(x)=14x +2，利用课本中推导等差数列前n 项和的公式的方法，可求得f(－3)+f(－2)+⋯+f(0)+⋯+f(3)+f(4)的值为 ．【典题2】 求sin 21∘+sin 22∘+sin 23∘+⋯+sin 288∘+sin 289∘的值【典题3】 设函数f (x )=x2x +√2的图象上两点P 1(x 1 ,y 1)、P 2(x 2 ,y 2)，若OP ⃗⃗⃗⃗⃗ =12(OP 1⃗⃗⃗⃗⃗⃗⃗ +OP 2⃗⃗⃗⃗⃗⃗⃗ )，且点P 的横坐标为12．(1)求证：P 点的纵坐标为定值，并求出这个定值； (2)求S n =f (1n )+f (2n )+⋯+f(n−1n)+f(nn).巩固练习1 (★★) 设等差数列{a n}，公差为d，求证：{a n}的前n项和S n=(a1+a n)n2.2(★★) 设f(x)=(x−1)3+1，求f(－4)+⋯+f(0)+⋯+f(5)+f(6)的值为.3(★★) 设函数f(x)=x21+x2，求f(1)+f(2)+f(12)+f(3)+f(13)+f(4)+f(14)的值．【方法三】分组求和法1 若数列{c n}中通项公式c n=a n+b n，可分成两个数列{a n}，{b n}之和，则数列{c n}的前n项和等于两个数列{a n}，{b n}的前n项和的和.2 常见的是c n=等差+等比形式3 等比数列的通项公式形如a n=kn+b，等差数列的通项公式形如a n=A∙B n.【典题1】求数列{3n+2n−1}的前n项和S n.【典题2】已知等差数列{a n}的前n项和为S n，且a5=5a1，S3−a2=8．(2)若数列{b n }满足(n ×2n +S n )b n =a n ，求数列{1b n }的前n 项和T n ．【典题3】 设数列{a n }满足a 1=1，a n+1a n=2n (n ∈N ∗)．(1)求数列{a n }的通项公式；(2)设b n =log 2a n ，求数列b 2+b 3+⋯+b 100的值． 巩固练习1 (★★) 已知数列{a n }的通项a n =2n +n ，若数列{a n }的前n 项和为S n ，则S 8= ．2 (★★) 数列112，214，318，…，n +12n 的前n 项和为S n = ．3 (★★★) 已知数列{a n }是等比数列，公比为q ，数列{b n }是等差数列，公差为d ，且满足：a 1=b 1=1，b 2+b 3=4a 2，a 3－3b 2=－5． (1)求数列{a n }和{b n }的通项公式；(2)设c n =a n +b n ，求数列{c n }的前n 项和S n ．4(★★★) 已知公差不为0的等差数列{a n }的前9项和S 9=45，且第2项、第4项、第8项成等比数列．(2)若数列{b n }满足b n =a n +(12)n−1，求数列{b n }的前n 项和T n ．【方法四】 错位相减法当数列{a n } 的通项公式a n =b n ⋅ c n ,其中{b n } 为等差数列, {c n } 为等比数列.【典题1】 已知递增的等比数列{a n }满足a 2+a 3+a 4=28，且a 3+2是a 2 ,a 4的等差中项． ( 1)求数列{a n }的通项公式a n ；(2)令b n =a n ⋅log 12a n ，S n ＝b 1+b 2+⋯+b n ，求S n ．【典题2】 已知正项数列{a n }的前n 项和为S n ，满足a n 2+a n −2S n =0(n ∈N ∗)．(1)求数列{a n }的通项公式；(2)记数列{b n}的前n项和为T n，若b n=(2a n−7)2n，求T n；(3)求数列{T n}的最小项．巩固练习1 (★★★) 设等差数列{a n}的前n项和为S n，且S4=4S2，a2n=2a n+1．(1)求数列{a n}的通项公式；(2)设数列{b n}满足b n=2(a n−1)，求数列{b n}的前n项和R n．4n2 (★★★) 正项数列{a n}的前n项和为S n，且8S n=(a n+2)2(n∈N∗)．(1)求a1，a2的值及数列{a n}的通项公式；(2)记c n=a n，数列{c n}前n的和为T n，求证：T n<2．3n3 (★★★) 已知等比数列{a n}满足a1=2，a2=4(a3−a4)，正项数列{b n}前n项和为S n，且2√S n=b n+1．(1)求数列{a n}和{b n}的通项公式；(2)令c n=b n，求数列{c n}的前n项和T n；a n(3)若λ>0，求对所有的正整数n都有2λ2−kλ+2>a2n b n成立的k的取值范围．4(★★★) 已知数列{a n}满足：(n+1)a n+1−(n+2)a n=(n+1)(n+2)(n∈N∗)且a1=4，数列{b n}的前n 项和S n满足：S n=2b n−1(n∈N∗)．(1)证明数列{a nn+1}为等差数列，并求数列{a n}和{b n}的通项公式；(2)若c n=(√a n−1)b n+1，数列{c n}的前n项和为T n，对任意的n∈N∗，T n≤nS n+1−m−2恒成立，求实数m的取值范围．【方法五】裂项相消法常见裂项公式(1)1n(n+1)=1n−1n+1，1n(n+k)=1k(1n−1n+k)；(2)√n+1+√n =√n+1−√n，√n+k+√n=1k(√n+k−√n).【典题1】设等差数列{a n}满足a2=5，a6+a8=30，则数列{1a n2−1}的前n项的和等于．【典题2】数列{a n}的通项公式a n=√n+2+√n+3，则该数列的前n项和S n等于.【典题3】等比数列{a n}中，a1=2，q=2，数列b n=a n+1(a n+1−1)(a n−1)，{b n}的前n项和为T n，则T10的值为．【典题4】已知数列{a n}满足a n≠0，a1=13，a n−1−a n＝2a n a n−1(n≥2 ,n∈N∗)．(1)求证：{1a n }是等差数列；(2)证明：a12+a22+⋯+a n2<14．巩固练习1 (★★) 数列{a n}满足a n=1(2n+1)(2n+3),n∈N∗，其前n项和为S n．若S n<M恒成立，则M的最小值为．2 (★★★) 已知正项数列{a n}的前n项和为S n，对∀n∈N∗有2S n=a n2+a n，令b n=a√a+a√a，设{b n}的前n项和为T n，则在T1 ,T2 ,T3 ,… ,T100中有理数的个数为．3 (★★★) 已知数列{a n}的前n项和为S n，且满足a1=2，S n=a n+1−2n+2+2 ,n∈N∗．(1)求数列{a n}的通项公式；(2)设b n=2na n ，记数列{b n b n+1}的前n项和为T n，证明：12≤T n<1．4(★★★) 已知数列{a n}满足a1=1，a n+1=a na n+1．(1)证明：数列{1a n}是等差数列，并求数列{a n}的通项公式；(2)设b n=a nn+2，求数列{b n}前n项和S n．5 (★★★) 设数列{a n}的前n项和为S n，已知a n>0，a n2+2a n=4S n+3．(1)求{a n}的通项公式；(2)若数列{b n}满足b n=2n+1n2(a n+1−1)2，求{b n}的前n项和T n．6 (★★★★) 设S n为数列{a n}的前n项和，且S n+1=3S n+4n(n∈N∗)，a1=0．(1)求证：数列{a n+2}是等比数列；(2)若对任意T n 为数列{a n +2(a n +4)(a n+1+4)}的前n 项和，求证：T n <12．7(★★★★) 已知数列{a n }的前n 项和为S n ，已知a 1=2，6S n =3na n+1−2n(n +1)(n +2)，n ∈N ∗． (1)求数列{a n }的通项公式； (2)证明：1a 1+1a 2+⋯+1a n<56．。

数列专题 数列求和常用方法（学生版）一、公式法1．等差数列{a n }的前n 项和S n ＝n (a 1＋a n )2＝na 1＋n (n －1)d 2． 推导方法：倒序相加法．2．等比数列{a n }的前n 项和S n ＝⎩⎪⎨⎪⎧na 1，q ＝1，a 1(1－q n )1－q，q ≠1. 例1已知等比数列{a n }的公比q >1，a 1＝2，且a 1，a 2，a 3－8成等差数列．(1)求出数列{a n }的通项公式；(2)设数列⎩⎨⎧⎭⎬⎫1a n 的前n 项和为S n ，任意n ∈N *，S n ≤m 恒成立，求实数m 的最小值． 跟踪练习1、已知等差数列{a n }的前n 项和为S n ，a 2＝0，a 4＝1，则S 4＝( )A ．12B ．1C ．2D ．32、等差数列{a n }的首项为1，公差不为0．若a 2，a 3，a 6成等比数列，则{a n }的前6项的和为( )A ．－24B ．－3C ．3D ．83、(2022·天津模拟)设1＋2＋22＋23＋…＋2n －1>128(n ∈N *)，则n 的最小值为( )A ．6B ．7C ．8D ．94、设数列{a n }(n ∈N *)的各项均为正数，前n 项和为S n ，log 2a n ＋1＝1＋log 2a n ，且a 3＝4，则S 6＝( )A ．128B ．65C ．64D ．635、已知数列{a n }的前n 项和S n ＝4n ＋b (b 是常数，n ∈N *)，若这个数列是等比数列，则b ＝( )A ．－1B ．0C ．1D ．46、已知等比数列{a n }，a 1＝1，a 4＝18，且a 1a 2＋a 2a 3＋…＋a n a n ＋1<k ，则k 的取值范围是( ) A ．⎣⎡⎦⎤12，23 B ．⎣⎡⎭⎫12，＋∞C ．⎣⎡⎭⎫12，23D ．⎣⎡⎭⎫23，＋∞ 7、(多选)已知数列{a n }满足a 1＝1，且对任意的n ∈N *都有a n ＋1＝a 1＋a n ＋n ，则下列说法中正确的是( )A ．a n ＝n (n ＋1)2B ．数列⎩⎨⎧⎭⎬⎫1a n 的前2 020项的和为2 0202 021 C ．数列⎩⎨⎧⎭⎬⎫1a n 的前2 020项的和为4 0402 021 D ．数列{a n }的第50项为2 5508、(多选)设数列{a n }的前n 项和为S n ，若S 2n S 4n为常数，则称数列{a n }为“吉祥数列”．则下列数列{b n }为“吉祥数列”的有( )A ．b n ＝nB ．b n ＝(－1)n (n ＋1)C ．b n ＝4n －2D ．b n ＝2n9、在数列{a n }中，2a n ＝a n －1＋a n ＋1(n ≥2)，且a 2＝10，a 5＝－5．(1)求{a n }的通项公式；(2)求{a n }的前n 项和S n 的最大值．10、数列{a n }满足：a 1＝1，点(n ，a n ＋a n ＋1)在函数y ＝kx ＋1的图象上，其中k 为常数，且k ≠0．(1)若a 1，a 2，a 4成等比数列，求k 的值；(2)当k ＝3时，求数列{a n }的前2n 项的和S 2n ．11、已知等差数列{a n }和等比数列{b n }满足a 1＝b 1＝1，a 2＋a 4＝10，b 2b 4＝a 5.(1)求{a n }的通项公式；二、分组转化法一个数列的通项公式是由若干个等差数列或等比数列或可求和的数列组成的，则求和时可用分组转化法，分别求和后再相加减．例2(2022·北京模拟)已知公差不为0的等差数列{a n }的前n 项和为S n ，S 5＝20，a 3是a 2，a 5的等比中项，数列{b n }满足对任意的n ∈N *，S n ＋b n ＝2n 2．(1)求数列{a n }，{b n }的通项公式；(2)设c n ＝⎩⎪⎨⎪⎧b n －n 2，n 为偶数，2a n ，n 为奇数，求数列{c n }的前2n 项的和T 2n ．跟踪练习1、已知数列{a n }的通项公式为a n ＝2n ＋n ，若数列{a n }的前n 项和为S n ，则S 8＝( )A ．546B ．582C ．510D ．5482、(2022·珠海模拟)已知等差数列{a n }中，a 3＋a 5＝a 4＋7，a 10＝19，则数列{a n cos n π}的前2 020项和为( )A ．1 009B ．1 010C ．2 019D ．2 0203、若f (x )＋f (1－x )＝4，a n ＝f (0)＋f ⎝⎛⎭⎫1n ＋…＋f ⎝⎛⎭⎫n －1n ＋f (1)(n ∈N *)，则数列{a n }的通项公式为__ _____．4、(2022·衡水质检)已知各项都不相等的等差数列{a n }，a 6＝6，又a 1，a 2，a 4成等比数列．(1)求数列{a n }的通项公式；(2)设b n ＝2n a ＋(－1)n a n ，求数列{b n }的前2n 项和T 2n .5、已知数列{a n }满足a 1＝1，a n ＋1＝⎩⎪⎨⎪⎧a n ＋1，n 为奇数，a n ＋2，n 为偶数. (1)记b n ＝a 2n ，写出b 1，b 2，并求数列{b n }的通项公式；(2)求{a n }的前20项和．6、已知等比数列{a n }的前n 项和为S n ，且S n ＝2n ＋a ．(1)求a n ；(2)定义[x ]为取整数x 的个位数，如[1]＝1，[32]＝2，[143]＝3，求[a 1]＋[a 2]＋[a 3]＋…＋[a 100]的值．7、已知公比大于1的等比数列{a n }满足a 2＋a 4＝20，a 3＝8.(1)求{a n }的通项公式；(2)记b m 为{a n }在区间(0，m ](m ∈N *)中的项的个数，求数列{b m }的前100项和S 100.8、(2022·重庆质检)已知等差数列{a n }的前n 项和为S n ，a 5＝9，S 5＝25.(1)求数列{a n }的通项公式及S n ；(2)设b n ＝(－1)n S n ，求数列{b n }的前n 项和T n .9、已知在等差数列{a n }中，S n 为其前n 项和，且a 3＝5，S 7＝49.(1)求数列{a n }的通项公式；(2)若b n ＝2n a＋a n ，数列{b n }的前n 项和为T n ，且T n ≥1 000，求n 的取值范围．10、(2022·青岛模拟)从“①S n ＝n ⎝⎛⎭⎫n ＋a 12；②S 2＝a 3，a 4＝a 1a 2；③a 1＝2，a 4是a 2，a 8的等比中项．”三个条件中任选一个，补充到下面的横线处，并解答．已知等差数列{a n }的前n 项和为S n ，公差d ≠0，________，n ∈N *.(1)求数列{a n }的通项公式；(2)若b n ＝122n n S S ＋－，数列{b n }的前n 项和为W n ，求W n .注：如果选择多个条件分别解答，按第一个解答计分．11、(2022·株洲质检)由整数构成的等差数列{a n }满足a 3＝5，a 1a 2＝2a 4.(1)求数列{a n }的通项公式；(2)若数列{b n }的通项公式为b n ＝2n ，将数列{a n }，{b n }的所有项按照“当n 为奇数时，b n 放在前面；当n 为偶数时，a n 放在前面”的要求进行“交叉排列”，得到一个新数列{c n }，b 1，a 1，a 2，b 2，b 3，a 3，a 4，b 4，…，求数列{c n }的前(4n ＋3)项和T 4n ＋3.三、裂项相消法把数列的通项拆成两项之差，在求和时中间的一些项可以相互抵消，从而求得前n 项和．(1)1n (n ＋1)＝1n －1n ＋1； (2)1n (n ＋2)＝12⎝⎛⎭⎫1n －1n ＋2； (3)1(2n －1)(2n ＋1)＝12⎝⎛⎭⎫12n －1－12n ＋1； (4)1n ＋n ＋1＝n ＋1－n ．例3(2022·南京质检)已知数列{a n }的前n 项和为S n ，S n ＝2a n －1，数列{b n }是等差数列，且b 1＝a 1，b 6＝a 5．(1)求数列{a n }和{b n }的通项公式；(2)若c n ＝1b n b n ＋1，记数列{c n }的前n 项和为T n ，证明：3T n ＜1．跟踪练习1、(2022·北京模拟)数列{a n }的通项公式为a n ＝1n ＋n ＋1 ，若{a n }的前n 项和为9，则n的值为( )A ．576B ．99C ．624D ．625 2、(多选)已知数列{a n }满足a 1＝32，a n ＝a 2n －1＋a n －1(n ≥2，n ∈N *)．记数列{a 2n }的前n 项和为A n ，数列⎩⎨⎧⎭⎬⎫1a n ＋1的前n 项和为B n ，则下列结论正确的是( ) A ．A n ＝a n ＋1－32B ．B n ＝23－1a n ＋1C ．A n B n ＝32a nD ．A n B n <32n ＋143、在数列{a n }中，a n ＝1n (n ＋1)，若{a n }的前n 项和为2 0222 023，则项数n ＝____ ____. 4、已知数列⎩⎨⎧⎭⎬⎫1(2n －1)(2n ＋1)的前n 项和为T n ，若对任意的n ∈N *，不等式12T n <a 2－a 恒成立，则实数a 的取值范围是__ __．5、(2022·本溪模拟)已知数列{a n }的前n 项和为S n ，且2S n ＝3a n －3(n ∈N *)．(1)求数列{a n }的通项公式；(2)若b n ＝1log 3a n ·log 3a n ＋1，求数列{b n }的前n 项和T n ．6、已知数列{a n }的前n 项和为S n ，且S n ＋1＝4a n ，n ∈N *，a 1＝1．(1)在下列三个结论中选择一个进行证明，并求{a n }的通项公式； ①数列⎩⎨⎧⎭⎬⎫a n 2n 是等差数列； ②数列{}a n ＋1－2a n 是等比数列；③数列{}S n ＋1－2S n 是等比数列．(2)记b n ＝S n ＋2S n S n ＋1，求数列{b n }的前n 项和T n ． 注：如果选择多个结论分别解答，则按第一个解答计分．7、给出以下三个条件：①4a 3,3a 4,2a 5成等差数列；②∀n ∈N *，点(n ，S n )均在函数y ＝2x －a 的图象上，其中a 为常数；③S 3＝7．请从这三个条件中任选一个将下面的题目补充完整，并求解．设{a n }是一个公比为q (q >0，且q ≠1)的等比数列，且它的首项a 1＝1，________．(1)求数列{a n }的通项公式；(2)令b n ＝2log 2a n ＋1(n ∈N *)，证明：数列⎩⎨⎧⎭⎬⎫1b n b n ＋1的前n 项和T n <12． 注：如果选择多个条件分别解答，则按第一个解答计分．8、设{a n }是各项都为正数的单调递增数列，已知a 1＝4，且a n 满足关系式：a n ＋1＋a n ＝4＋2a n ＋1a n ，n ∈N *.(1)求数列{a n }的通项公式；(2)若b n ＝1a n －1，求数列{b n }的前n 项和S n .9、设数列{a n }的前n 项和为S n ，且2S n ＝3a n －1.(1)求{a n }的通项公式；(2)若b n ＝3n (a n ＋1)(a n ＋1＋1)，求{b n }的前n 项和T n ，证明：38≤T n ＜34.10、已知数列{a n }满足a 1＝4，且当n ≥2时，(n －1)a n ＝n (a n －1＋2n －2)．(1)求证：数列⎩⎨⎧⎭⎬⎫a n n 是等差数列； (2)记b n ＝2n ＋1a 2n，求数列{b n }的前n 项和S n .11、(2022·合肥模拟)已知数列{a n }满足：a 1＝2，a n ＋1＝a n ＋2n .(1)求{a n }的通项公式；(2)若b n ＝log 2a n ，T n ＝1b 1b 2＋1b 2b 3＋…＋1b n b n ＋1，求T n .12、已知数列{a n }，{b n }，{c n }满足a 1＝b 1＝c 1＝1，c n ＝a n ＋1－a n ，c n ＋1＝b n b n ＋2c n，n ∈N *. (1)若{b n }为等比数列，公比q >0，且b 1＋b 2＝6b 3，求q 的值及数列{a n }的通项公式；(2)若{b n }为等差数列，公差d >0，证明：c 1＋c 2＋c 3＋…＋c n <1＋1d，n ∈N *.13、已知数列{a n }满足a 1＝12，1a n ＋1＝1a n＋2(n ∈N *)． (1)求数列{a n }的通项公式；(2)求证：a 21＋a 22＋a 23＋…＋a 2n <12.14、若S n 是公差不为0的等差数列{a n }的前n 项和，且S 1，S 2，S 4成等比数列，S 2＝4. ①求数列{a n }的通项公式；②设b n ＝3a n a n ＋1，T n 是数列{b n }的前n 项和，求使得T n <m 20对所有n ∈N *都成立的最小正整数m .四、错位相减法如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的，那么求这个数列的前n 项和即可用错位相减法求解．例4(2022·江门模拟)已知数列{a n }满足：a 1＝1，a n ＋1＝2a n ＋n －1．(1)证明：数列{a n ＋n }是等比数列并求数列{a n }的前n 项和S n ；(2)设b n ＝(2n －1)·(a n ＋n )，求数列{b n }的前n 项和T n ．跟踪练习1、(2022·广东模拟)在数列{a n }中，a 1＝1，a n ＋1＝a n －2a n a n ＋1．(1)求{a n }的通项公式；(2)若b n ＝3na n，求数列{b n }的前n 项和S n ．2、已知数列{a n }的前n 项和为S n ，对任意正整数n ，均有S n ＋1＝3S n －2n ＋2成立，a 1＝2．(1)求证：数列{a n －1}为等比数列，并求{a n }的通项公式；(2)设b n ＝na n ，求数列{b n }的前n 项和T n ．3、(2022·湖南模拟)某同学在复习数列时，发现曾经做过的一道题目因纸张被破坏，导致一个条件看不清(即下题中“已知”后面的内容看不清)，但在(1)的后面保留了一个“答案：S 1，S 3，S 2成等差数列”的记录，具体如下：记等比数列{a n }的前n 项和为S n ，已知_____________．①判断S 1，S 2，S 3的关系；(答案：S 1，S 3，S 2成等差数列)②若a 1－a 3＝3，记b n ＝n 12|a n |，求证：b 1＋b 2＋…＋b n <43． (1)请在本题条件的“已知”后面补充等比数列{a n }的首项a 1的值或公比q 的值(只补充其中一个值)，并说明你的理由；(2)利用(1)补充的条件，完成②的证明过程．4设{a n }是公比不为1的等比数列，a 1为a 2，a 3的等差中项．(1)求{a n }的公比；(2)若a 1＝1，求数列{na n }的前n 项和．5、已知数列{a n }的前n 项和为S n ，a 1＝－94，且4S n ＋1＝3S n －9(n ∈N *)． (1)求数列{a n }的通项公式；(2)设数列{b n }满足3b n ＋(n －4)a n ＝0(n ∈N *)，记{b n }的前n 项和为T n .若T n ≤λb n ，对任意n ∈N *恒成立，求实数λ的取值范围．6、设数列{a n }满足a 1＝3，a n ＋1＝3a n －4n .(1)计算a 2，a 3，猜想{a n }的通项公式；(2)求数列{2n a n }的前n 项和S n .7、(2022·济宁模拟)已知数列{a n }是正项等比数列，满足a 3是2a 1,3a 2的等差中项，a 4＝16.(1)求数列{a n }的通项公式；(2)若b n ＝(－1)n log 2a 2n ＋1，求数列{b n }的前n 项和T n .8、(2022·重庆调研)在等差数列{a n}中，已知a6＝12，a18＝36.(1)求数列{a n}的通项公式a n；(2)若________，求数列{b n}的前n项和S n，在①b n＝4a n a n＋1，②b n ＝(－1)n·a n，③b n＝2n ana 这三个条件中任选一个补充在第(2)问中，并对其求解．9、(2022·沈阳模拟)已知正项数列{a n}的前n项和为S n，且a2n＋1＝2S n＋n＋1，a2＝2.(1)求数列{a n}的通项公式a n；(2)若b n＝a n·2n，数列{b n}的前n项和为T n，求使T n>2 022的最小的正整数n的值．。

高考数学（文）冲刺复习之——求数列的通项公式一、定义法直接利用等差数列或等比数列的定义求通项的方法叫定义法.这种方法适用于已知数列类型的题目，此题目是必须掌握的基本运算，一般有“知二求一”的方程思想.例题 等差数列{}n a 是递增数列，前n 项和为n S ，且931,,a a a 成等比数列，255a S =．求数列{}n a 的通项公式.训练【2017新课标1文】记S n 为等比数列{}n a 的前n 项和，已知S 2=2，S 3=−6．（1）求{}n a 的通项公式；（2）求S n ，并判断S n +1，S n ，S n +2是否成等差数列．二、利用n S 和n a 的关系求{}n a 的通项公式解法：巧用1112n nn S n a S S n -=⎧=⎨-≥⎩，，.使用是根据具体条件和结论，正用、逆用或同时使用，对等式退（进）一步作差. 1、形如f(S n ,n)=0型可利用公式：⎩⎨⎧-=-11S S S a n n n )1()2(=≥n n 直接求出通项n a ；（讨论1a 能否被吸收） 例题1 已知数列{a n }的前n 项和为（1）S n =2n 2-n ；（2）S n =n 2+n+1，分别求数列{a n }的通项公式；例题2 已知数列{}n a 的前n 项和n S 满足2(1), 1.n n n S a n =+-≥求数列{}n a 的通项公式；变式1 数列}{n a 的前n 项和n S 满足：n a S n n 32-=（n ∈N +），求数列}{n a 的通项公式n α；变式2 已知数列{}n a 的前n 项和为11,4n S a =且1112n n n S S a --=++，数列{}n b 满足11194b =-且13n n b b n --=(2)n n N *≥∈且．（１）求{}n a 的通项公式；（２）求证：数列{}n n b a -为等比数列；变式3 若前n 项和为S n 且满足a n =)2(1222≥-n S S n n ,且a 1=1，求数列的通项公式；2、形如f(S n ,S n+1)=0型方法（i ）.看成{S n }的递推公式，求S n 的通项公式，再由n S 求出n α.（ii ）.（逆用）利用a n =S n -S n-1转化成关于a n 和a n-1的关系式再求。

构造法求数列通项的八种技巧(三)【必备知识点】◆构造六:取对数构造法型如a n+1=ca n k,a n=ca n-1k或者a n+b=c(a n-1+b)k,b为常数.针对出现这种数列,为方便计算,两边通常取以c或首项为底的对数,就能找到突破口.什么情况取c为底,什么情况取首项为底呢?我们来看两道例题.【经典例题1】数列a n中, a1=2,a n+1=a n2,求数列a n的通项公式.【经典例题2】数列a n中,a1=1,a n+1=2a n2,求数列a n的通项公式.【经典例题3】已知a1=2,点a n,a n+1在函数f x =x2+2x的图像上,其中n∈N*,求数列a n的通项公式.【经典例题4】在数列a n中, a1=1,当n≥2时,有a n+1=a n2+4a n+2,求数列a n的通项公式.◆构造七:二阶整体构造等比简单的二阶整体等比:关于a n+1=Aa n+Ba n-1的模型,可通过构造二阶等比数列求解,大部分题型可转化为a n+1-a n=(A-1)a n-a n-1,利用a n+1-a n成等比数列,以及叠加法求出a n.还有一小部分题型可转化为a n+1+a n=(A+1)a n+a n-1,利用a n+1+a n成等比数列求出a n.【经典例题1】已知数列a n满足a1=1,a2=3,a n+2=3a n+1-2a n n∈N*,求数列a n的通项公式.【经典例题2】已知数列a n中,a1=1,a2=2,a n+2=23a n+1+13a n,求数列a n的通项公式。

【经典例题3】数列a n中,a1=1,a2=53,a n+2=53a n+1-23a n,求数列a n的通项公式。

此方法可以解决大多数的a n+1=Aa n+Ba n-1,A+B=1模型的试题.当然针对个别试题,单纯构造a n+1-a n成等比数列可能解决不了问题.我们需要学习更完整的方法来解决这种类型题.这就需要运用数列的特征方程理念来解决.当然我们不需要详细学习数列的特征方程,用高中的待定系数法也可以解决,接下来我们通过两道例题,来详细解释说明下这种方法.【经典例题4】已知数列a n满足a1=1,a2=4,a n+2=4a n+1-4a n n∈N*,求数列a n的通项公式.【经典例题5】已知数列a n满足a1=1,a2=43,a n+2=73a n+1-23a n n∈N*,求a n的通项公式.秒杀求法:a n+2=pa n+1+qa n(p,q≠0)类通项公式暴力秒杀求法a n+2=pa n+1+qa n(p,q≠0)对应的特征方程为:x2=px+q,设其两根为x1,x2当x1≠x2时, a n=Ax1n-2+Bx2n-2当x1=x2时, a n=(An+B)x1n-2其中A,B的值的求法,用a1,a2的值代入上面的通项公式中,建立方程组解之即可【秒杀例题1】已知数列a n满足a1=1,a2=43,a n+2=73a n+1-23a n n∈N*,求a n的通项公式.【秒杀例题2】已知数列a n满足a1=1,a2=4,a n+2=4a n+1-4a n n∈N*,求数列a n的通项公式.【练习1】在数列a n中,a1=1,a2=2,a n+1=3a n-2a n-1(n≥2),则a n=_______.【练习2】设数列a n的前n项和为S n,n∈N*.已知a1=1,a2=32,a3=54,且当n≥2时, 4S n+2+5S n=8S n+1+S n-1.(1)求a4的值；(2)证明：a n+1-12a n为等比数列;(3)求数列a n的通项公式.【练习3】数列a n满足a1=1,a2=2,a n+2=2a n+1-a n+2.(1)设b n=a n+1-a n,证明b n是等差数列;(2)求a n的通项公式.◆构造八：数列不动点构造求数列(较难,能力强的同学可以学习)针对x n+1=ax n+bcx n+d这类题型,考题中并不多见,难度比较大,这类题型有特定的解题方法.我们需要学习“数列不动点”的知识点.接下来我们来学习下什么是“数列不动点”,它有什么性质.当然看不懂也没关系,可以通过例题,熟记掌握解题步骤就可以.对于函数f(x),若存在实数x0,使得f x0=x0,则称x=x0是函数f(x)的不动点.在几何上，曲线y=f(x)与曲线y=x的交点的横坐标即为函数f(x)的不动点.一般地,数列x n的递推式可以由公式x n+1=f x n给出,因此可以定义递推数列的不动点:对于递推数列x n,若其递推式为x n+1=f x n,且存在实数x0,使得f x0=x0,则称x0是数列x n的不动点。

高中数学53个题型归纳与方法技巧总结篇专题23数列的基本知识与概念【考点预测】1．数列的概念（1）数列的定义：按照一定顺序排列的一列数称为数列，数列中的每一个数叫做这个数列的项．（2）数列与函数的关系：从函数观点看，数列可以看成以正整数集N *（或它的有限子集{}12n ⋯，，，）为定义域的函数()n a f n =当自变量按照从小到大的顺序依次取值时所对应的一列函数值．（3）数列有三种表示法，它们分别是列表法、图象法和通项公式法．2．数列的分类（1）按照项数有限和无限分：（2）按单调性来分：111()n n n nn n a a a a a a C +++≥⎧⎪≥⎪⎨==⎪⎪⎩递增数列：递减数列： ，常数列：常数摆动数列 3．数列的两种常用的表示方法（1）通项公式：如果数列{}n a 的第n 项与序号n 之间的关系可以用一个式子来表示，那么这个公式叫做这个数列的通项公式．（2）递推公式：如果已知数列{}n a 的第1项（或前几项），且从第二项（或某一项）开始的任一项与它的前一项（或前几项）间的关系可以用一个公式来表示，那么这个公式就叫做这个数列的递推公式．【方法技巧与总结】（1）若数列{}n a 的前n 项和为n S ，通项公式为n a ，则1112n n n S n a S S n n N*-=⎧⎪=⎨-≥∈⎪⎩ ， ， ，注意：根据n S 求n a 时，不要忽视对1n =的验证．（2）在数列{}n a 中，若n a 最大，则11n n n n a a a a -+≥⎧⎨≥⎩ ， 若n a 最小，则11.n n nn a a a a -+≤⎧⎨≤⎩【题型归纳目录】题型一：数列的周期性题型二：数列的单调性题型三：数列的最大（小）项题型四：数列中的规律问题题型五：数列的最值问题【典例例题】题型一：数列的周期性例1．已知无穷数列{}n a 满足()21N n n n a a a x *++=-∈，且11a =，2a x =()x ∈Z ，若数列{}n a 的前2020项中有100项是0，则下列哪个不能是x 的取值（）A ．1147B ．1148C ．1142-D ．1143-例2．若[]x 表示不超过x 的最大整数（如[]2.52=，[]44=，[]2.53-=-），已知2107n n a ⎡⎤=⨯⎢⎥⎣⎦，11b a =，()*110,2n n n b a a n n -=-∈≥N ，则2019b =（）A ．2B ．5C ．7D ．8例3．数列{}n a 满足12a =，111nn na a a ++=-，其前n 项积为n T ，则10T 等于（）A ．16B ．16-C ．6D ．6-例4．若数列{}n a 满足1222a a ==，且21n n n a a a ++=-，则{}n a 的前100项和为（）A ．67B ．68C ．134D ．167例5．数列{}n a 满足112,0,2121,1,2n n n n n a a a a a +⎧≤<⎪⎪=⎨⎪-≤<⎪⎩若125a =，则2021a 等于（）A ．15B ．25C ．35D ．45例6．已知数列{}n a 满足，()()111122,32n n n n n a a a a a ----⎧-+>⎪=⎨-⎪⎩ *(,1)n N n ∈>，若1(2,3)a ∈且记数列{}n a 的前n 项和为n S ，若2019=m S ，则2019S 的值为（）A ．60572B ．3028C ．60552D ．3029例7．（2022·广东汕头·三模）已知数列{}n a 中，114a =-，当1n >时，111n n a a -=-，则2022a =（）A ．14-B ．45C ．5D ．45-例8．（2022·河北·沧县中学高三阶段练习）已知数列{}n a 中，()1112n n n a a a n --=⋅+≥，12a =，则10a 等于（）A ．12-B ．12C ．-1D ．2题型二：数列的单调性例9．（2022·四川达州·二模（理））已知单调递增数列{}n a 满足9,102121,109n n m n a m n n -⎧≥⎪=⎨⎛⎫+-< ⎪⎪⎝⎭⎩，则实数m 的取值范围是（）A ．[)12,+∞B ．()1,12C ．()1,9D ．[)9,+∞例10．（2022·河南·温县第一高级中学高三阶段练习（文））已知函数()()633,7,7x a x x f x a x -⎧--≤=⎨>⎩，若数列{}n a 满足()()*n a f n n N =∈且{}n a 是递增数列，则实数a 的取值范围是（）A ．9,34⎛⎫ ⎪⎝⎭B ．9,34⎡⎫⎪⎢⎣⎭C ．()2,3D ．[)2,3例11．（2022·浙江·高三专题练习）已知数列{}n a 的首项为11a =，2a a =，且121(2,)n n a a n n n N *++=+≥∈，若数列{}n a 单调递增，则a 的取值范围为（）A ．12a <<B ．23a <<C ．3522a <<D ．1322a <<例12．（2022·全国·高三专题练习）已知等比数列{}n a 前n 项和n S 满足113n n S A +=-⋅（A R ∈），数列{}n b 是递增的，且2n b An Bn =+，则实数B 的取值范围为（）A ．2,3⎡⎫-+∞⎪⎢⎣⎭B ．[)1,-+∞C ．()1,-+∞D ．1,3⎛⎫-+∞ ⎪⎝⎭例13．（2022·全国·高三专题练习（理））已知数列{}n a 满足()712,83,8n n a n n a n a n *-⎧⎛⎫-+>⎪ ⎪=∈⎝⎭⎨⎪≤⎩N ，若对于任意n *∈N 都有1n n a a +>，则实数a 的取值范围是（）A ．10,3⎛⎫ ⎪⎝⎭B ．10,2⎛⎫ ⎪⎝⎭C ．1,12⎛⎫ ⎪⎝⎭D ．11,32⎛⎫ ⎪⎝⎭例14．（2022·全国·高三专题练习）设数列{}n a 的通项公式为2n a n bn =+，若数列{}n a 是单调递增数列，则实数b 的取值范围为（）A ．(2,)-+∞B ．[2,)-+∞C ．(3,)-+∞D ．(,3)-∞-【方法技巧与总结】解决数列的单调性问题的3种方法作差比较法根据1n n a a ＋－的符号判断数列{}n a 是递增数列、递减数列或是常数列作商比较法根据1(>0<0)n n n na a a a +或与1的大小关系进行判断数形结合法结合相应函数的图象直观判断题型三：数列的最大（小）项例15．已知数列{}n a 的首项为1，且()()*111n n n a a n n ++=∈+N ，则na的最小值是（）A ．12B ．1C ．2D ．3例16．已知数列{}n a 满足110a =，12n na a n+-=，则n a n 的最小值为（）A ．-1B ．112C ．163D ．274例17．已知数列{}n a 的前n 项和n S ，且2(1)n n S a n -=-，22na nn b S =，则数列{}n b 的最小项为（）A ．第3项B ．第4项C ．第5项D ．第6项例18．已知数列{}n a 的前n 项和2212,n S n n =-数列{||}n a 的前n 项和,n T 则nT n的最小值____例19．数列，1n =，2， ，中的最小项的值为__________．【方法技巧与总结】求数列的最大项与最小项的常用方法（1）将数列视为函数()f x 当x ∈N *时所对应的一列函数值，根据f （x ）的类型作出相应的函数图象，或利用求函数最值的方法，求出()f x 的最值，进而求出数列的最大（小）项．（2）通过通项公式n a 研究数列的单调性，利用11()2n n nn a a a n a -+≥⎧⎨≥⎩≥，确定最大项，利用11()2n n nn a a a n a -+≤⎧⎨≤⎩≥，确定最小项．（3）比较法：若有1()()10n n a a f n f n -=+->＋或0n a >时11n na a +>，则1n n a a ＋＞，则数列{}n a 是递增数列，所以数列{}n a 的最小项为1(1)a f =；若有1()()10n n a a f n f n =-+-<＋或0n a >时11n na a +<，则1n n a a <＋，则数列{}n a 是递减数列，所以数列{}n a 的最大项为1(1)a f =．题型四：数列中的规律问题例20．蜜蜂被认为是自然界中最杰出的建筑师，单个蜂巢可以近似地看作是一个正六边形，如图为一组蜂巢的截面图．其中第一个图有1个蜂巢，第二个图有7个蜂巢，第三个图有19个蜂巢，按此规律，以()f n 表示第n 幅图的蜂巢总数，则(4)f =（）；()f n =（）．A ．352331n n +-B ．362331n n -+C ．372331n n -+D ．382331n n +-例21．由正整数组成的数对按规律排列如下：()1,1，()1,2，()2,1，()1,3，()2,2，()3,1，()1,4，()2,3，()3,2，()4,1，()1,5，()2,4，⋅⋅⋅．若数对(),m n 满足()22222021m n -⋅-=，,m n N *∈，则数对(),m n 排在（）A ．第386位B ．第193位C ．第348位D ．第174位例22．已知“整数对”按如下规律排列：()()()()()1,11,22,11,32,2，，，，，()()()3,11,42,3，，()3,2，，()4,1，…，则第68个“整数对”为（）A ．()1,12B ．()3,10C ．()2,11D ．()3,9例23．将正整数排列如下：123456789101112131415……则图中数2020出现在A ．第64行3列B ．第64行4列C ．第65行3列D ．第65行4列题型五：数列的最值问题例24．（2022·北京市第十二中学高三期中）已知数列{}n a 满足32n a n n=+，则数列{}n a 的最小值为（）A ．343B ．575C ．D ．12例25．（2022·全国·高三专题练习）已知数列{}n a ，2141n n a n n -=+-，则下列说法正确的是（）A ．此数列没有最大项B ．此数列的最大项是3aC ．此数列没有最小项D ．此数列的最小项是2a 例26．（2022·河南·高三阶段练习（理））在数列{}n a 中，11a =，1n n a a n --=（N n +∈，2n ≥），则11n a n ++的最小值是（）A ．12B ．34C ．1D ．32例27．（2022·辽宁·高三阶段练习）若数列{}n a 满足24122,n nn n n a T a a a -==⋅⋅⋅，则n T 的最小值为（）A ．92-B ．102-C ．112-D ．122-例28．（2022·全国·高三专题练习）若数列{}n a 满足113a =，1n n n a a +-=，则na n的最小值为（）A ．235B ．143C 12D ．13例29．（2022·全国·高三专题练习）设221316n a n n =-+-，则数列{}n a 中最大项的值为（）A ．134B ．5C ．6D ．132例30．（2022·浙江·高三专题练习）已知数列{}n a 的通项公式为211n aa n n n=-+，5a 是数列{}n a 的最小项，则实数a 的取值范围是（）A ．[]40,25--B ．[]40,0-C ．[]25,25-D ．[]25,0-【过关测试】一、单选题1．（2022·陕西·交大附中模拟预测（理））函数()f x 定义如下表，数列{}()N n x n ∈满足02x =，且对任意的自然数n 均有()1n n x f x +=，则2022x =（）x 12345()f x 51342A ．1B ．2C ．4D ．52．（2022·内蒙古赤峰·模拟预测（理））大衍数列来源于《乾坤谱》中对易传“大衍之数五十”的推论，主要用于解释中国传统文化中的太极衍生原理．数列中的每一项，都代表太极衍生过程中曾经经历过的两仪数量总和，其中一列数如下：0，2，4，8，12，18，24，32，40，50，……．按此规律得到的数列记为{}n a ，其前n 项和为n S ，给出以下结论：①22122n a n n -=-；②182是数列{}n a 中的项；③21210a =；④当n 为偶数时，()2122n n n S S S n n *++-+=+∈N ．其中正确的序号是（）A ．①②B ．②③C ．①④D ．③④3．（2022·河南·模拟预测（理））观察数组()2,2，()3,4，()4,8，()5,16，()6,32，…，根据规律，可得第8个数组为（）A ．()9,128B ．()10,128C ．()9,256D ．()10,2564．（2022·吉林长春·模拟预测（理））已知数列{}n a 满足()()11120n n a a +-++=，112a =，则数列{}n a 的前2022项积为（）A ．16-B ．23C ．6-D ．325．（2022·江西·临川一中模拟预测（理））已知数列{}n a 满足()1112,21*+-==∈-n n n a a a n N a ，则2022=a （）A ．13B ．1C ．2D ．526．（2022·全国·高三专题练习）已知数列{}n a 的通项公式为n aa n n=+，则“21a a >”是“数列{}n a 单调递增”的（）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件7．（2022·全国·高三专题练习）已知数列{}n a 满足()2**2,5,,1,5,.n n tn n n a t n n n ⎧-+≤∈⎪=⎨->∈⎪⎩N N 且数列{}n a 是单调递增数列，则t 的取值范围是（）A ．919,24⎛⎫⎪⎝⎭B ．9,2⎛⎫+∞ ⎪⎝⎭C ．()5,+∞D ．(]1,48．（2022·全国·高三专题练习）若数列{an }的前n 项和Sn ＝n 2－10n (n ∈N *)，则数列{nan }中数值最小的项是（）A ．第2项B ．第3项C ．第4项D ．第5项9．（2022·上海普陀·二模）数列{}n a 的前n 项的和n S 满足*1(N )n n S S n n ++=∈，则下列选项中正确的是（）A ．数列{}1n n a a ++是常数列B ．若113a <，则{}n a 是递增数列C ．若11a =-，则20221013S =D ．若11a =，则{}n a 的最小项的值为1-10．（2022·北京四中三模）已知数列{n a }的通项为22n a n n λ=-，则“0λ<”是“*n ∀∈N ，1n n a a +>”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件二、多选题11．（2022·河北·衡水第一中学高三阶段练习）大衍数列，来源于《乾坤谱》中对易传“大衍之数五十”的推论．主要用于解释中国传统文化中的太极衍生原理．数列中的每一项，都代表太极衍生过程中，曾经经历过的两仪数量总和，是中国传统文化中隐藏着的世界数学史上第一道数列题．其前10项依次是0，2，4，8，12，18，24，32，40，50，…，则下列说法正确的是（）A ．此数列的第20项是200B ．此数列的第19项是180C ．此数列偶数项的通项公式为222n a n=D ．此数列的前n 项和为(1)n S n n =⋅-12．（2022·全国·高三专题练习）若数列{}n a 满足1112,012,1321,12n n n n n a a a a a a +⎧⎪⎪==⎨⎪-<<⎪⎩ ，则数列{}n a 中的项的值可能为（）A ．13B ．2C ．23D ．4513．（2022·全国·高三专题练习）下列四个选项中，不正确的是（）A ．数列2345,,,3456，⋯的一个通项公式是1n n a n =+B ．数列的图象是一群孤立的点C ．数列1，1-，1，1-，⋯与数列1-，1，1-，1，⋯是同一数列D ．数列11,24，⋯，12n是递增数列14．（2022·全国·高三专题练习）已知n S 是{}n a 的前n 项和，12a =，()1112n n a n a -=-≥，则下列选项错误的是（）A ．20212a =B ．20211012S =C ．331321n n n a a a ++⋅⋅=D ．{}n a 是以3为周期的周期数列15．（2022·全国·高三专题练习）若数列{an }满足112,2712,62n n n n n a a a a a +⎧≤⎪⎪=⎨⎪->⎪⎩，123a =，则数列{an }中的项的值可能为（）A ．19B ．16C ．13D ．4316．（2022·全国·高三专题练习）已知数列{}n a 满足112a =-，111n n a a +=-，则下列各数是{}n a 的项的有（）A ．2-B ．23C ．32D ．317．（2022·全国·高三专题练习（文））南宋杨辉在他1261年所著的《详解九章算术》一书中记录了一种三角形数表，称之为“开方作法本源”图，即现在著名的“杨辉三角”.如图是一种变异的杨辉三角，它是将数列{}n a 各项按照上小下大，左小右大的原则写成的，其中{}n a 是集合{}220,,s ts t s t Z +≤<∈且中所有的数从小到大排列的数列，即13a =，25a =，36a =，49a =，510a =，…，则下列结论正确的是（）A ．第四行的数是17，18，20，24B ．()11232-+=⋅n n n a C ．()11221n n a n +=+D ．10016640a =18．（2022·全国·高三专题练习）如图所示的数表中，第1行是从1开始的正奇数，从第2行开始每个数是它肩上两个数之和．则下列说法正确的是（）A ．第6行第1个数为192B ．第10行的数从左到右构成公差为102的等差数列C ．第10行前10个数的和为9952⨯D ．数表中第2021行第2021个数为202060612⨯19．（2022·河北·石家庄实验中学高三开学考试）大衍数列，来源于《乾坤谱》中对易传“大衍之数五十”的推论.主要用于解释中国传统文化中的太极衍生原理.数列中的每一项，都代表太极衍生过程中，曾经经历过的两仪数量总和，是中国传统文化中隐藏着的世界数学史上第一道数列题.其前10项依次是0，2，4，8，12，18，24，32，40，50，…，则下列说法正确的是（）A ．此数列的第20项是200B ．此数列的第19项是182C ．此数列偶数项的通项公式为222n a n=D ．此数列的前n 项和为(1)n S n n =⋅-20．（2022·福建漳州·三模）已知数列{n a }的前n 项和为211n S n n =-，则下列说法正确的是（）．A ．{}n a 是递增数列B ．{}n a 是递减数列C ．122n a n=-D ．数列{}n S 的最大项为5S 和6S 21．（2022·湖南·长沙一中高三阶段练习）对于正整数n ，()n ϕ是小于或等于n 的正整数中与n 互质的数的数目．函数()n ϕ以其首名研究者欧拉命名，称为欧拉函数，例如()96ϕ=（1，2，4，5，7，8与9互质），则（）A ．若n 为质数，则()1n n ϕ=-B ．数列(){}n ϕ单调递增C ．数列()2n n ϕ⎧⎫⎪⎪⎨⎬⎪⎪⎩⎭的前5项和等于72D ．数列(){}3nϕ为等比数列三、填空题22．（2022·北京·人大附中模拟预测）能说明命题“若无穷数列{}n a 满足()111,2,3,n na n a +>= ，则{}n a 为递增数列”为假命题的数列{}n a 的通项公式可以为n a =__________．23．（2022·陕西·宝鸡中学模拟预测）写出一个符合下列要求的数列{}n a 的通项公式：①{}n a 是无穷数列；②{}n a 是单调递减数列；③20n a -<<.这个数列的通项可以是__________.24．（2022·海南·模拟预测）写出一个同时具有下列性质①②③的数列{}n a 的通项公式：n a =__________．①10n n a a +<；②数列{}n a 是单调递减数列；③数列{}2nn a 是一个等比数列．25．（2022·江西·临川一中模拟预测（文））已知23n a n n =+，若2nn a λ≤对于任意*n ∈N 恒成立，则实数λ的取值范围是_______．26．（2022·天津市新华中学高三期末）在数列{}n a 中，()71()8n n a n =+，则数列{}n a 中的最大项的n =________.27．（2022·山西·模拟预测（理））数列{}n a 中，已知11a =，20a >，()*21n n n a a a n ++=-∈N ，则2022a 的取值范围是___________.28．（2022·四川成都·三模（理））已知数列{}n a 满足13a =，122n n n a a a ++=，则2022a 的值为______．29．（2022·全国·模拟预测）在数列{}na 中，11a =，1,231,nn n n n a a a a a +⎧⎪=⎨⎪+⎩为偶数为奇数，则1232021a a a a ++++= ___．。

求数列的通项公式1、数列的通项公式如果数列{a n }的第n 项a n 与n 之间的函数关系可以用一个式子a n ＝f (n )来表示，那么这个公式叫做这个数列的通项公式．2、数列的递推公式若一个数列首项确定，其余各项用a n 与a n －1或a n +1的关系式表示(如a n ＝2a n －1＋1)，则这个关系式就称为数列的递推公式．3、由数列的递推公式求数列的通项公式的常见方法(1)待定系数法：①形如a n ＋1＝ka n ＋b 的数列求通项；②形如a n ＋1＝ka n ＋r ∙b n 的数列求通项；(2)倒数法：形如a n ＋1＝pa n qa n ＋r的数列求通项可用倒数法； (3)累加法：形如a n ＋1－a n ＝f (n )的数列求通项可用累加法；(4)累乘法：形如a n ＋1a n＝f (n )的数列求通项可用累乘法； (5) “S n ”法：数列的通项a n 与前n 项和S n 的关系：a n ＝⎩⎪⎨⎪⎧S 1， n ＝1，S n －S n －1， n ≥2.；S n 与a n 的混合关系式有两个思路： ①消去S n ，转化为a n 的递推关系式，再求a n ；②消去a n ，转化为S n 的递推关系式，求出S n 后，再求a n . 考向一 待定系数法例1—1 已知数列{a n }中，a 1＝1，a n ＋1＝2a n ＋3，求数列{a n }的通项公式。

例1—2 在数列{a n }中，a 1＝－1，a n ＋1＝2a n ＋4·3n ，数列{a n }的通项公式。

可用待定系数法求通项的主要有三种：①形如a n ＋1＝ka n ＋b 的数列求通项，方法是：令a n ＋1＋λ＝k (a n ＋λ)，整理后与a n ＋1＝ka n ＋b 对比可求出λ的值，得出数列 是公比为 的等比数列；②形如a n ＋1＝ka n ＋r ∙b n 的数列求通项，方法是：令a n ＋1＋λ∙b n +1＝k (a n ＋λ∙b n )，整理后与a n ＋1＝ka n ＋r ∙b n 对比可求出λ的值，得出数列 是公比为 的等比数列；③形如a n ＋2＝ka n ＋1＋ba n 的数列求通项，方法是：a n ＋2＋λa n ＋1＝μ(a n ＋1＋λa n )，整理后与a n ＋2＝ka n ＋1＋ba n 对比可求出λ、μ的值，得出数列 是公比为 的等比数列．变式1 已知数列{a n }的前n 项和为S n ，若S 1＝1，S n ＋1＝3S n ＋2，求数列的通项公式a n .例2—1 已知数列{a n }中，其中a 1＝1，且当n ≥2时，a n ＝a n －12a n －1＋1，求数列{a n }的通项公式。

数列求和的基本方法和技巧一、利用常用求和公式求和利用下列常用求和公式求和是数列求和的最基本最重要的方法.1、 等差数列求和公式：d n n na a a n S n n 2)1(2)(11-+=+= 2、等比数列求和公式：⎪⎩⎪⎨⎧≠--=--==)1(11)1()1(111q q q a a qq a q na S n n n 3、 ()11232n n n +++++=4、 4、()()222211231216n n n n ++++=++ 5、 ()233332112314n n n ++++=+ [例1] 已知21=x ，求⋅⋅⋅++⋅⋅⋅+++n x x x x 32的前n 项和. 解：[例2]求2222222212345699100-+-+-+--+ 的和。

解：练习：1.已知数列{}n a 的通项公式为()1+=n n a n ，求前n 项和n S二、错位相减法求和这种方法是在推导等比数列的前n 项和公式时所用的方法，这种方法主要用于求数列{a n ·b n }的前n 项和，其中{ a n }、{ b n }分别是等差数列和等比数列.[例3] 求和：132)12(7531--+⋅⋅⋅++++=n n xn x x x S 解：[例4] 求数列⋅⋅⋅⋅⋅⋅,22,,26,24,2232n n 前n 项的和. 解：练习：1.求：S n =1+5x+9x 2+······+(4n -3)x n-12. 求数列13521,,,,,2482n n - 的前n 项的和。

三、倒序相加法求和这是推导等差数列的前n 项和公式时所用的方法，就是将一个数列倒过来排列，再把它与原数列相加，就可以得到n 个)(1n a a +.[例5] 求 89sin 88sin 3sin 2sin 1sin 22222++⋅⋅⋅+++的值解：练习：1. 已知lg(xy)=a ，122221lg lg()lg()lg()lg()lg n n n n n n S x x y x y x y xy y ----=++++++ ，求S.2.设()244-=x x x f ，求⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=199919981999219991f f f S 的值四、分组法求和有一类数列，既不是等差数列，也不是等比数列，若将这类数列适当拆开，可分为几个等差、等比或常见的数列，然后分别求和，再将其合并即可.[例6] 求数列的前n 项和：)23(1,,71,41,1112-+⋅⋅⋅+++-n aa a n ，… 解：[例7] 求数列{n(n+1)(2n+1)}的前n 项和.解：练习：1.求数列1111123424816、、、、的前n 项的和。

高考专题复习：数列求和一、教学目标：1．熟练掌握等差数列与等比数列的求和公式；2．能运用倒序相加、错位相减、拆项相消等重要的数学方法进行求和运算； 3．熟记一些常用的数列的和的公式． 二、教学重点：特殊数列求和的方法． 三、教学过程： （一）主要知识：1．直接法：即直接用等差、等比数列的求和公式求和。

（1）等差数列的求和公式：d n n na a a n S n n 2)1(2)(11-+=+=（2）等比数列的求和公式⎪⎩⎪⎨⎧≠--==)1(1)1()1(11q qq a q na S nn （切记：公比含字母时一定要讨论）2．分组求和法：把数列的每一项分成若干项，使其转化为等差或等比数列，再求和。

3．裂项相消法：把数列的通项拆成两项之差、正负相消剩下首尾若干项。

4．错位相减法：比如{}{}.,,2211的和求等比等差n n n n b a b a b a b a +++ 5．并项求和法：如求22222212979899100-++-+- 的和。

（二）主要方法：1．求数列的和注意方法的选取：关键是看数列的通项公式； 2．求和过程中注意分类讨论思想的运用； 3．转化思想的运用； （三）例题分析：考点1 直接运用公式求和1.在等比数列{}n a 中，如果27S =，691S =，那么4S 为( ) A ．28 B ．32 C ．35 D ．492.在等比数列{}n a 中，如果,8,44231=+=+a a a a 那么该数列的前8项和为( ) A ．12 B ．24 C ．48 D ．2043．设等差数列{}n a 的前n 项和为n S ，246a a +=，则5S 等于 ( )（A ）10 （B ）12 （C ）15 (D) 304.数列{a n }、{b n }都是公差为1的等差数列，若其首项满足a 1＋b 1＝5，a 1＞b 1，且a 1，b 1∈N *，则数列{n b a }前10项的和等于 ( )A ．100B ．85C ．70D ．555.（广东）已知等比数列}{n a 的公比为正数，且3a ·9a =225a ，2a =1，则1a =A.21B. 22C. 2D.26.（2012广东）若等比数列}{n a 满足2142=a a ，则=5231a a a _______________．考点2 分组求和 1.求和：101111123102482++++= 101562-2.已知数列{a n }的通项公式为a n =12-n +3n ，求这个数列的前n 项和。

考点05 数列的新定义问题数列的新定义问题，是近几年高考的新题型，主要北京卷考查比较多。

例如：2020年北京高考[21],2020年江苏高考[20],2021年北京高考[21]，2022年北京高考[21]等都对数列的新定义问题进行了考查。

〔1〕新定义数列问题的特点：通过给出一个新的数列的概论，或约定一种新运算，或给出几个新模型来创设全新的问题情境，要求考生在阅读理解的基础上，依据题目提供的信息，联系所学的知识和方法，实现信息的迁移，达到灵活解题的目的。

〔2〕新定义问题的解题思路：遇到新定义问题，应耐心读题，分析新定义的特点，弄清新定义的性质，按新定义的要求，逐条分析、运算、验证，使问题得以解决。

例1．（2022·北京·高考真题）已知12:,,,k Q a a a 为有穷整数数列．给定正整数m ，若对任意的{1,2,,}n m ∈，在Q中存在12,,,,(0)i i i i j a a a a j +++≥，使得12i i i i j a a a a n +++++++=，则称Q 为m -连续可表数列．(1)判断:2,1,4Q 是否为5-连续可表数列？是否为6-连续可表数列？说明理由； (2)若12:,,,k Q a a a 为8-连续可表数列，求证：k 的最小值为4；(3)若12:,,,k Q a a a 为20-连续可表数列，且1220k a a a +++<，求证：7k ≥．例2．（2021·北京·高考真题）设p 为实数.若无穷数列{}n a 满足如下三个性质，则称{}n a 为p ℜ数列： ①10a p +≥，且20a p +=； ①414,1,2,n n a a n -<=⋅⋅⋅()；①{},1m n m n m n a a a p a a p +∈+++++，(),1,2,m n =⋅⋅⋅．（1）如果数列{}n a 的前4项为2，-2，-2，-1，那么{}n a 是否可能为2ℜ数列？说明理由； （2）若数列{}n a 是0ℜ数列，求5a ；（3）设数列{}n a 的前n 项和为n S .是否存在p ℜ数列{}n a ，使得10n S S ≥恒成立？如果存在，求出所有的p ；如果不存在，说明理由．1．设n *∈N ，若无穷数列{}n a 满足以下性质，则称{}n a 为k C 数列：①()()110n n n n a a a a +--->，（n *∈N 且2n ≥）．①1n n a a +-的最大值为k ．(1)若数列{}n a 为公比为q 的等比数列，求q 的取值范围，使得{}n a 为k C 数列． (2)若k C 数列{}n a 满足：n *∀∈N ，使得21,,n n n a a a ++成等差数列， ①数列{}n a 是否可能为等比数列？并说明理由；①记数列{}n b 满足21n n b a -=，数列{}n c 满足2n n c a =，且12a a >，判断{}n b 与{}n c 的单调性，并求出1n n a a k +-=时，n 的值．2．已知等比数列{}n a 为递增数列，11a =，12a +是2a 与3a 的等差中项. (1)求数列{}n a 的通项公式；(2)若项数为n 的数列{}n b 满足：1i n i b b +-=（1i =，2，3，…，n ）我们称其为n 项的“对称数列”.例如：数列1，2，2，1为4项的“对称数列”；数列1，2，3，2，1为5项的“对称数列”.设数列{}n c 为()212k k -≥项的“对称数列”，其中1c ，2c ，3c ，…，n c 是公差为2的等差数列，数列{}n c 的最大项等于4a .记数列{}n c 的前21k -项和为21k S -，若2132k S -=，求k . 3．已知集合（Z 是整数集，m 是大于3的正整数）．若含有m 项的数列{}n a 满足：任意的,i j M ∈，都有i a M ∈，且当i j ≠时有i j a a ≠，当i m <时有12i i a a +-=或13i i a a +-=，则称该数列为P 数列． (1)写出所有满足5m =且11a =的P 数列；(2)若数列{}n a 为P 数列，证明：{}n a 不可能是等差数列； (3)已知含有100项的P 数列{}n a 满足5105100,,,,,(1,2,3,,20)k a a a a k =是公差为(0)d d >等差数列，求d 所有可能的值4．定义：对于任意一个有穷数列，第一次在其每相邻的两项间都插人这两项的和，得到的新数列称之为一阶和数列，如果在一阶和数列的基础上再在其相邻的两项间插入这两项的和称之为二阶和数列，以此类推可以得到n 阶和数列，如{1,5}的一阶和数列是{1,6,5}，设它的n 阶和数列各项和为n S ．(1)试求{1,5}的二阶和数列各项和2S 与三阶和数列各项和3S ，并猜想n S 的通项公式（无需证明）； (2)若()()311log 3log 33n n n c S S +=--⋅-，求{}n c 的前n 项和n T ，并证明：1126n T -<≤-．5．已知无穷数列12:A a a ，，满足：①*N (12)i a i ∈=，，；①1i j i j i j a a a a a ++≤≤++（12i =，，；12j =，，；3i j +≥）.设*i a 为(12)i a i =，，所能取到的最大值，并记数列***12:A a a ，，.(1)若11a =，写出一个符合条件的数列A 的通项公式；(2)若121a a ==，求*4a 的值；(3)若1212a a ==，，求数列*A 的前100项和. 6．已知数列{}n a 为无穷递增数列，且11a =．定义： 数列{}k b ：k b 表示满足i a k ≤的所有i 中最大的一个．数列{}k B ：k B 表示满足i a k ≥的所有i 中最小的一个（1i =，2，3…）(1)若数列{}n a 是斐波那契数列，即121a a ==，21n n n a a a ++=+，（1n =，2，3，…），请直接写出10b ，10B 的值； (2)若数列{}n a 是公比为整数的等比数列，且满足345b b b <=且34B B =，求公比q ，并求出此时3b ，4b 的值； (3)若数列{}n a 是公差为d 的等差数列，求所有可能的d ，使得{}n b ，{}n B 都是等差数列． 7．已知数列{}n a ，给出两个性质：①对于任意的*i N ∈，存在i k R ∈，当*,j i j >∈N 时，都有()j i i a a k j i -≥-成立；①对于任意的*,2i i ∈≥N ，存在i k R ∈，当*,j i j <∈N 时，都有()j i i a a k j i -≥-成立．(1)已知数列{}n a 满足性质①，且()*2i k i N =∈，141,7a a ==，试写出23,a a 的值； (2)已知数列{}n b 的通项公式为132n n b -=⨯，证明：数列{}n b 满足性质①；(3)若数列{}n c 满足性质①①，且当*,2i N i ∈≥时，同时满足性质①①的i k 存在且唯一.证明：数列{}n c 是等差数列． 8．设数列()12:,,,2n A a a a n ≥.如果{}()1,2,,1,2,,i a n i n ∈=，且当i j ≠时，()1,i j a a i j n ≠≤≤，则称数列A 具有性质P .对于具有性质P 的数列A ，定义数列()121:,,,n T A t t t -，其中()111,,1,2,,10,k k k k k a a t k n a a ++⎧==-⎨⎩＜＞.(1)对():0,1,1T A ，写出所有具有性质P 的数列A ； (2)对数列()121:,,,2n E e e e n -≥，其中{}()0,11,2,,1i e i n ∈=-，证明：存在具有性质P 的数列A ，使得()T A 与E 为同一个数列；(3)对具有性质P 的数列A ，若()115n a a n -=≥且数列()T A 满足()0,,1,2,,11,i i t i n i ⎧==-⎨⎩为奇数为偶数，证明：这样的数列A 有偶数个.9．如果无穷数列{}n a 是等差数列，且满足：①i ∀、*j ∈N ，*k ∃∈N ，使得i j k a a a =；①*k ∀∈N ，i ∃、*j ∈N ，使得i j k a a a =，则称数列{}n a 是“H 数列”.(1)下列无穷等差数列中，是“H 数列”的为___________；（直接写出结论）{}:1n a 、3、5、{}:0n b 、2、4、{}:0n c 、0、0、{}:1n d -、0、1、(2)证明：若数列{}n a 是“H 数列”，则1a ∈Z 且公差d ∈N ；(3)若数列{}n a 是“H 数列”且其公差*d ∈N 为常数，求{}n a 的所有通项公式.10．给定数列{}n a ，若数列{}n a 中任意（不同）两项之和仍是该数列中的一项，则称该数列是“封闭数列”.（1）已知数列{}n a 的通项公式为3nn a =，试判断{}n a 是否为封闭数列，并说明理由；（2）已知数列{}n a 满足212n n n a a a +++=且212a a -=，设n S 是该数列{}n a 的前n 项和，试问：是否存在这样的“封闭数列”{}n a ，使得对任意*n ∈N 都有0n S ≠，且12111111818n S S S <+++<，若存在，求数列{}n a 的首项1a 的所有取值；若不存在，说明理由；（3）证明等差数列{}n a 成为“封闭数列”的充要条件是：存在整数1m ≥-，使1a md =． 12．若数列{}n a 同时满足下列两个条件，则称数列{}n a 具有“性质A ”. ①212n n n a a a +++>(n *∈N )；①存在实数A ，使得对任意*n ∈N ，有n a A ≥成立. (1)设245,sin4n n n a n n b π=-+=，试判断{},{}n n a b 是否具有“性质A ”；(2)设递增的等比数列{}n c 的前n 项和为n S ，若2371,2c S =-=-，证明：数列{}n S 具有“性质A ”，并求出A 的取值范围；(3)设数列{}n d 的通项公式()122*222n n nt n nt t d n ++++=∈N ，若数列{}n d 具有“性质A ”，其满足条件的A 的最大值010A =，求t 的值.。