5-5 驻波

机械波的驻波与共振机械波是一种传递能量的波动现象，广泛应用于机械、声学等领域。

其中，驻波和共振是机械波研究中的两个重要概念。

本文将探讨机械波的驻波与共振的原理和应用。

一、驻波的概念及特点驻波是一种在空间中呈现固定形态的波动现象。

它是由相同频率、相同振幅的两个波在相同介质中相互干涉形成的。

在驻波中，存在着一些特点：1. 节点和腹点：两波叠加后，在某些位置上会形成振幅为零的节点，而在其他位置上形成振幅最大的腹点。

2. 振幅不变：整个驻波系统中，波的振幅保持恒定，不随时间和空间的变化而变化。

3. 波动不传播：驻波中的能量不传递，而是呈现固定形态，并在介质中来回反射。

二、驻波的形成条件驻波的形成需要满足一定的条件：1. 两个相同频率的波在相同介质中传播，并沿相反方向传播。

2. 波的振幅和频率相同。

3. 波的传播速度相同。

三、驻波的应用驻波在实际应用中有着广泛的用途，以下是其中几个例子：1. 物理教学实验：驻波实验是许多物理实验中常见的一种，通过声波或水波在实验装置中形成驻波，直观地展示波动的特性和干涉现象。

2. 乐器制作：驻波的概念也可以应用于乐器的制作和改良中。

比如，弦乐器中的驻波现象决定了乐器的音调和音质。

3. 通信技术：驻波的特性在微波通信中有着重要的应用。

例如，微波天线中的驻波比可以用来描述天线的工作状态和匹配程度。

四、共振的概念及特点共振是指当外界激励频率与系统的固有频率相同时，系统会发生共振现象。

在机械波中，也存在共振现象，并具有以下特点：1. 能量传递：共振现象下，能量会从外界传递到系统中，使系统的振幅不断增大。

2. 振幅最大化：共振频率下，系统的振幅会不断增大，直到达到最大值。

3. 导致破坏：如果外界激励持续存在，振幅可能超过系统的承受范围，导致系统的破坏。

五、共振的应用共振在实际应用中也有着重要的作用：1. 振动工程：共振现象的控制和利用在振动工程中具有重要意义。

例如，振动台可以通过调整频率和振幅，实现对被测物体的共振激励。

水声材料驻波管测量方法驻波管法是一种测量水声材料声速和衰减系数的重要方法。

其原理是利用驻波管中声波的干涉现象，根据驻波的波长和波腹波谷间的幅度差，推导出水声材料的声学特性。

实验装置驻波管法测量所需的装置包括驻波管、声源、接收器、频率发生器和数据采集系统。

驻波管：通常为圆柱形或矩形管，内衬被测水声材料。

声源：产生声波，激发驻波管内的驻波。

接收器：测量声波的声压，确定驻波的波形。

频率发生器：控制声波的频率，以获得不同频率下的驻波特性。

数据采集系统：记录接收器输出的声压信号，并进行分析处理。

测量步骤1. 选择合适的频率范围：根据被测水声材料的特性，选择合适的频率范围，确保在该范围内能激发清晰的驻波。

2. 激发驻波：通过声源向驻波管中输入声波，调整频率至出现驻波。

3. 移动接收器：沿驻波管轴线移动接收器，测量声压，记录驻波的波形。

4. 采集数据：使用数据采集系统记录接收器输出的声压信号，并进行数字化处理。

5. 分析数据：利用傅里叶变换或其他信号处理方法，分析声压信号，提取驻波的波长和波峰值。

计算声学特性根据驻波的波长和波峰值，可以计算水声材料的声速和衰减系数。

声速（c）：c = 2L / n，其中L为驻波管长度，n为驻波波长。

衰减系数（α）：α = (1/2) (InA1 - InA2) / L，其中A1和A2分别为驻波波峰和波谷处的声压幅度。

注意事项驻波管尺寸：驻波管的长度和直径应与被测频率相匹配，以确保能激发清晰的驻波。

声源功率：声源功率应足够大，以产生足够的声压，但又不会造成非线性失真。

接收器灵敏度：接收器灵敏度应足够高，以检测驻波的细微变化。

环境噪声：测量环境应尽量减少噪声干扰，以提高测量精度。

数据处理：数据处理应使用经过验证的算法和方法，以确保结果的准确性。

驻波比的计算公式驻波是在传播介质中发生的波动现象，其计算公式主要涉及到波长、波速和传播介质的特性。

驻波的计算公式主要有两个方面：波长和节点位置的计算。

1.波长的计算：波长是指同相位波之间的空间距离。

在一个驻波系统中，波长通常由以下公式给出：λ=2L/n其中，λ表示波长，L表示传播介质的长度，n表示节点数。

驻波系统中的节点是指波波动幅度为零的位置。

例如，当一条绳子两端固定且在上面产生驻波时，绳子上的节点数量为n=1,2,3,...，依此类推。

2.节点位置的计算：节点是指波动幅度为零的位置。

在一个简单的驻波系统中，可以使用以下公式计算节点位置：x=(2m+1)L/4n其中，x表示节点位置，L表示传播介质的长度，m表示节点序号（从0开始计算），n表示节点数。

例如，在一个固定两端的弦上产生的驻波系统中，第一个节点的位置为x=L/4，第二个节点的位置为x=3L/4，依此类推。

需要注意的是，以上的计算公式适用于基本的驻波系统。

但在实际情况中，还有其他一些因素需要考虑，比如边界条件、波速等。

3.边界条件：在实践中，边界条件对驻波的形成和位置起着重要作用。

例如，在固定两端的弦上形成驻波时，两端固定的条件限制了节点的位置。

当一个驻波系统在两端固定条件下形成时，节点位置的计算公式如下：x=(2m)L/2(n+1)其中，x表示节点位置，L表示传播介质的长度，m表示节点序号（从0开始计算），n表示节点数。

例如，在一个固定两端的弦上产生的驻波系统中，第一个节点的位置为x=L/(n+1)，第二个节点的位置为x=2L/(n+1)，依此类推。

4.波速的计算：波速是指波的传播速度。

在一个波动系统中，波速通常由以下公式给出：v=λf其中，v表示波速，λ表示波长，f表示波的频率。

在一个驻波系统中，波速也可以通过节点位置的计算进行估算。

根据节点位置的计算公式，在一个固定两端的弦上形成驻波时，节点之间的距离为λ/2、因此，波速可以通过以下公式计算：v=2f(x2-x1)其中，v表示波速，f表示波的频率，x2和x1表示两个相邻节点的位置。

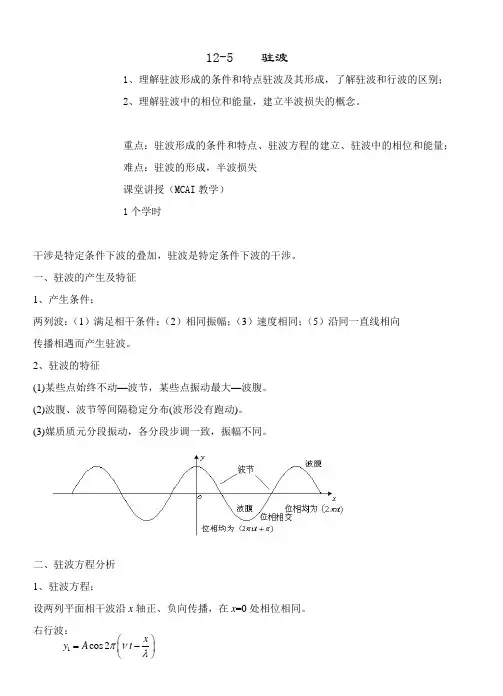
12-5 驻波1、理解驻波形成的条件和特点驻波及其形成，了解驻波和行波的区别；2、理解驻波中的相位和能量，建立半波损失的概念。

重点：驻波形成的条件和特点、驻波方程的建立、驻波中的相位和能量；难点：驻波的形成，半波损失课堂讲授（MCAI教学）1个学时干涉是特定条件下波的叠加，驻波是特定条件下波的干涉。

一、驻波的产生及特征1、产生条件：两列波：（1）满足相干条件；（2）相同振幅；（3）速度相同；（5）沿同一直线相向传播相遇而产生驻波。

2、驻波的特征(1)某些点始终不动—波节，某些点振动最大—波腹。

(2)波腹、波节等间隔稳定分布(波形没有跑动)。

(3)媒质质元分段振动，各分段步调一致，振幅不同。

二、驻波方程分析1、驻波方程：设两列平面相干波沿x轴正、负向传播，在x=0处相位相同。

右行波：1cos2πνλ⎛⎫=-⎪⎝⎭xy A t左行波：x 轴上的合振动为：122cos 2cos 2ππνλ=+=x y y y A t 2、驻波的振幅 由驻波方程2cos 2cos 2ππνλ=x y A t 与时间无关的因子为振幅分布因子，与时间有关的为谐振动因子。

振幅为：2cos 2πλxA(1) 驻波的振幅沿x 轴周期变化。

(2) 波腹——振幅最大最大振幅为2A 由22cos 22πππλλ=⇒=±xxA A k 相邻两波腹间距12λ+∆=-=k k x x x 波腹处坐标：2λ=±⋅x k （k = 0，1，2，…）(3) 波节——振幅为零 由22cos 20(21)2πππλλ=⇒=±+x x A k (21)4λ=±+x k 相邻两波节的间距12λ+∆=-=k k x x x3、驻波的相位 2cos 2πνλ⎛⎫=+ ⎪⎝⎭x y A t驻波方程2cos 2cos 2ππνλ=xy A t 可写为： 2c o s 2c o s 2(c o s 20)ππνπλλ=>x x y A t 2cos 2cos(2)(cos 20)ππνππλλ=+<x xy A t驻波的相位与坐标无关，说明不象行波随位置依次落后，即驻波的相位不向前传播。

驻波比取值范围
驻波是一种在介质中传播的波，其振动方向与传播方向垂直。

在某些情况下，驻波会在介质中形成定态，此时波的振幅为定值，这种现象被称为驻波。

驻波的形成需要两个波源，它们之间的距离必须是波长的整数倍。

当两个波源发射的波完全相位相反时，它们会产生波的叠加，形成一个节点。

当两个波源发射的波相位相同时，它们会产生波的加强，形成一个波峰。

在驻波中，波的振幅是不同的，它们的取值范围可以通过以下公式计算：A = Amax * sin(n * π * x / L)，其中A表示振幅，Amax 表示波的最大振幅，n表示节点的数量，x表示距离节点的距离，L
表示波长。

从公式中可以看出，节点处振幅为0，而波峰处振幅为Amax。

在节点和波峰之间，振幅的取值范围是[-Amax, Amax]。

这个范围是不
断重复的，因为驻波是在介质中周期性地重复出现的。

- 1 -。

驻波检测理论分析驻波检测理论分析电压驻波⽐介绍电压驻波⽐（VSWR）为英⽂Voltage Standing Wave Ratio 的简写。

电压驻波⽐产⽣的原因主要是由于在系统或者电路中存在阻抗不匹配，在⽆线电通信中，由于天线与馈线的阻抗不匹配或天线与发信机的阻抗不匹配，⾼频能量就会产⽣反射折回，并与前进的部分⼲扰汇合发⽣驻波。

为了表⽰和测量天线系统中的驻波特性，也就是天线中正向波与反射波的情况，⼈们建⽴了“驻波⽐”(Standing Wave Ratio)这⼀概念，驻波⽐的全称是电压驻波⽐。

当两个阻抗数值⼀样时，即达到完全匹配，反射系数Γ等于0，驻波⽐为1。

这是⼀种理想的状况，实际上总存在反射，所以驻波⽐总是⼤于1 的。

理想的⽐例为1:1 ，即输⼊阻抗相等于传输线的特性阻抗,但⼏乎不可能达到，如果当VSWR 1.25:1 时，反射功率⼤概为1.14 %，当VSWR 1.5:1 反射功率为4.06 %，当VSWR 1.75:1时，反射功率为7.53 %，由这个数字我们可以知道, 驻波⽐越⼤, 反射功率越⾼。

在射频系统阻抗匹配中,特别要注意要使电压驻波⽐达到⼀定要求，在移动通信系统中，⼀般要求驻波⽐⼩于1.5，⼀样⼀般可以保证通信系统的良好⼯作。

同时，因为在宽带运⽤时频率范围很⼴，驻波⽐会随着频率⽽变，所以应使阻抗在宽范围内尽量匹配。

电压驻波⽐对系统性能的影响随着驻波⽐的恶化，有效传输的功率将会减少，这是由于理想的阻抗匹配(VSWR=1:1)可以使功率⽆损传输，⽽严重的阻抗失配(⾼VSWR)将导致传输到负载的功率减少。

⾼的VSWR可能引起多种系统问题，其中对VSWR最为敏感的器件是功率放⼤器，因为其输出功率较⼤可能达到200 ⽡左右，导致很⼤的功率反射，从⽽造成⽆线电装置的⼯作范围缩⼩、发射信号使接收部分饱和。

更为严重的影响是损坏发射机并且击穿传输电介质。

同时由于天线上反射回的信号在功率放⼤器处再次反射，然后重新发射出去，导致了类似多径现象，因此⾼VSWR可能引起基站系统的遮蔽衰落VSWR 值很⾼也有可能会损坏天馈系统，反射波在天线和发射机之间来回反复时会丧失⼀部分能量⽽转化为热能损耗了，这⼀部分热量增加了馈线对热损耗的承受能⼒，会产⽣破坏作⽤。

驻波实验报告篇一：驻波实验报告实验目的：1、观察弦振动及驻波的形成；3、在振动源频率不变时，用实验确定驻波波长与张力的关系；4、在弦线张力不变时，用实验确定驻波波长与振动频率的关系；4、定量测定某一恒定波源的振动频率；5、学习对数作图法。

实验仪器：弦线上驻波实验仪（FD-FEW-II型）包括：可调频率的数显机械振动源、平台、固定滑轮、可动刀口、可动卡口、米尺、弦线、砝码等；分析天平，米尺。

实验原理：如果有两列波满足：振幅相等、振动方向相同、频率相同、有固定相位差的条件，当它们相向传播时，两列波便产生干涉。

一些相隔半波长的点，振动减弱最大，振幅为零，称为波节。

两相邻波节的中间一点振幅最大，称为波腹。

其它各点的振幅各不相同，但振动步调却完全一致，所以波动就显得没有传播，这种波叫做驻波。

驻波相邻波节间的距离等于波长λ的一半。

如果把弦线一端固定在振动簧片上，并将弦线张紧，簧片振动时带动弦线由左向右振动，形成沿弦线传播的横波。

若此波前进过程中遇到阻碍，便会反射回来，当弦线两固定端间距为半波长整数倍时，反射波与前进波便形成稳定的驻波。

波长λ、频率 f和波速V满足关系：V = f λ(1)又因在张紧的弦线上，波的传播速度V 与弦线张力T及弦的线密度μ有如下关系：(2)比较(1)、(2)式得：(3) 为了用实验证明公式(3)成立，将该式两边取自然对数，得：(4)若固定频率f 及线密度μ，而改变张力T，并测出各相应波长λ，作lnT -lnλ图，若直线的斜率值近似为，则证明了的关系成立。

同理，固定线密度μ及张力T，改变振动频率f，测出各相应波长λ，作ln f - lnλ图，如得一斜率为的直线就验证了。

将公式(3)变形，可得：(5) 实验中测出λ、T、μ的值，利用公式（5）可以定量计算出 f 的值。

实验时，测得多个(n个)半波长的距离l，可求得波长λ为：(6)为砝码盘和盘上所挂砝码的总重量；用米尺测出弦线的长度L，用分析天平测其质量，求出弦的线密度（单位长度的质量）：(7)实验内容：1、验证横波的波长λ与弦线中的张力T 的关系（f 不变）固定波源振动的频率，在砝码盘上添加不同质量的砝码，以改变同一弦上的张力。

习题五5-1 振动和波动有什么区别和联系?平面简谐波动方程和简谐振动方程有什么不同?又有什么联系?振动曲线和波形曲线有什么不同?解: (1)振动是指一个孤立的系统(也可是介质中的一个质元)在某固定平衡位置附近所做的往复运动，系统离开平衡位置的位移是时间的周期性函数，即可表示为)(t f y =；波动是振动在连续介质中的传播过程，此时介质中所有质元都在各自的平衡位置附近作振动，因此介质中任一质元离开平衡位置的位移既是坐标位置x ，又是时间t 的函数，即),(t x f y =． (2)在谐振动方程)(t f y =中只有一个独立的变量时间t ，它描述的是介质中一个质元偏离平衡位置的位移随时间变化的规律；平面谐波方程),(t x f y =中有两个独立变量，即坐标位置x 和时间t ，它描述的是介质中所有质元偏离平衡位置的位移随坐标和时间变化的规律．当谐波方程)(cos ux t A y -=ω中的坐标位置给定后，即可得到该点的振动方程，而波源持续不断地振动又是产生波动的必要条件之一．(3)振动曲线)(t f y =描述的是一个质点的位移随时间变化的规律，因此，其纵轴为y ，横轴为t ；波动曲线),(t x f y =描述的是介质中所有质元的位移随位置，随时间变化的规律，其纵轴为y ，横轴为x ．每一幅图只能给出某一时刻质元的位移随坐标位置x 变化的规律，即只能给出某一时刻的波形图，不同时刻的波动曲线就是不同时刻的波形图．5-2 波动方程y =A cos ［ω(u x t -)+0ϕ］中的ux表示什么?如果改写为y =A cos (0ϕωω+-u x t )，u x ω又是什么意思?如果t 和x 均增加，但相应的［ω(ux t -)+0ϕ］的值不变，由此能从波动方程说明什么?解: 波动方程中的u x /表示了介质中坐标位置为x 的质元的振动落后于原点的时间；uxω则表示x 处质元比原点落后的振动位相；设t 时刻的波动方程为 )cos(0φωω+-=uxt A y t则t t ∆+时刻的波动方程为])()(cos[0φωω+∆+-∆+=∆+ux x t t A y t t其表示在时刻t ，位置x 处的振动状态，经过t ∆后传播到t u x ∆+处．所以在)(uxt ωω-中，当t ，x 均增加时，)(uxt ωω-的值不会变化，而这正好说明了经过时间t ∆，波形即向前传播了t u x ∆=∆的距离，说明)cos(0φωω+-=uxt A y 描述的是一列行进中的波，故谓之行波方程．5-3 波在介质中传播时，为什么介质元的动能和势能具有相同的位相，而弹簧振子的动能和势能却没有这样的特点?解: 我们在讨论波动能量时，实际上讨论的是介质中某个小体积元dV 内所有质元的能量．波动动能当然是指质元振动动能，其与振动速度平方成正比，波动势能则是指介质的形变势能．形变势能由介质的相对形变量(即应变量)决定．如果取波动方程为),(t x f y =，则相对形变量(即应变量)为x y ∂∂/.波动势能则是与x y ∂∂/的平方成正比．由波动曲线图(题5-3图)可知，在波峰，波谷处，波动动能有极小(此处振动速度为零)，而在该处的应变也为极小(该处0/=∂∂x y )，所以在波峰，波谷处波动势能也为极小；在平衡位置处波动动能为极大(该处振动速度的极大)，而在该处的应变也是最大(该处是曲线的拐点)，当然波动势能也为最大．这就说明了在介质中波动动能与波动势能是同步变化的，即具有相同的量值．题5-3图对于一个孤立的谐振动系统，是一个孤立的保守系统，机械能守恒，即振子的动能与势能之和保持为一个常数，而动能与势能在不断地转换，所以动能和势能不可能同步变化． 5-4 波动方程中，坐标轴原点是否一定要选在波源处? t =0时刻是否一定是波源开始振动的时刻? 波动方程写成y =A cos ω(uxt -)时，波源一定在坐标原点处吗?在什么前提下波动方程才能写成这种形式?解: 由于坐标原点和开始计时时刻的选全完取是一种主观行为，所以在波动方程中，坐标原点不一定要选在波源处，同样，0=t 的时刻也不一定是波源开始振动的时刻；当波动方程写成)(cos ux t A y -=ω时，坐标原点也不一定是选在波源所在处的．因为在此处对于波源的含义已做了拓展，即在写波动方程时，我们可以把介质中某一已知点的振动视为波源，只要把振动方程为已知的点选为坐标原点，即可得题示的波动方程．5-5 在驻波的两相邻波节间的同一半波长上，描述各质点振动的什么物理量不同，什么物理量相同?解: 取驻波方程为vt x A y απλπcos 2cos2=，则可知，在相邻两波节中的同一半波长上，描述各质点的振幅是不相同的，各质点的振幅是随位置按余弦规律变化的，即振幅变化规律可表示为x A λπ2cos2．而在这同一半波长上，各质点的振动位相则是相同的，即以相邻两波节的介质为一段，同一段介质内各质点都有相同的振动位相，而相邻两段介质内的质点振动位相则相反．5-6 波源向着观察者运动和观察者向波源运动都会产生频率增高的多普勒效应，这两种情况有何区别?解: 波源向着观察者运动时，波面将被挤压，波在介质中的波长，将被压缩变短，(如题5-6图所示)，因而观察者在单位时间内接收到的完整数目(λ'/u )会增多，所以接收频率增高；而观察者向着波源运动时，波面形状不变，但观察者测到的波速增大，即B v u u +='，因而单位时间内通过观察者完整波的数目λu '也会增多，即接收频率也将增高．简单地说，前者是通过压缩波面(缩短波长)使频率增高，后者则是观察者的运动使得单位时间内通过的波面数增加而升高频率．题5-6 图多普勒效应5-7 一平面简谐波沿x 轴负向传播，波长λ=1.0 m ，原点处质点的振动频率为ν=2. 0 Hz ，振幅A ＝0.1m ，且在t =0时恰好通过平衡位置向y 轴负向运动，求此平面波的波动方程． 解: 由题知0=t 时原点处质点的振动状态为0,000<=v y ，故知原点的振动初相为2π,取波动方程为])(2cos[0φλπ++=xT t A y 则有 ]2)12(2cos[1.0ππ++=x t y)224cos(1.0πππ++=x t m5-8 已知波源在原点的一列平面简谐波，波动方程为y =A cos(Cx Bt -)，其中A ，B ，C 为正值恒量．求：(1)波的振幅、波速、频率、周期与波长；(2)写出传播方向上距离波源为l 处一点的振动方程；(3)任一时刻，在波的传播方向上相距为d 的两点的位相差． 解: (1)已知平面简谐波的波动方程)cos(Cx Bt A y -= (0≥x )将上式与波动方程的标准形式)22cos(λππυxt A y -=比较，可知： 波振幅为A ，频率πυ2B =， 波长C πλ2=，波速CB u ==λυ， 波动周期BT πυ21==．(2)将l x =代入波动方程即可得到该点的振动方程)cos(Cl Bt A y -=(3)因任一时刻t 同一波线上两点之间的位相差为 )(212x x -=∆λπφ将d x x =-12，及Cπλ2=代入上式，即得 Cd =∆φ．5-9 沿绳子传播的平面简谐波的波动方程为y =0.05cos(10x t ππ4-)，式中x ,y 以米计，t 以秒计．求：(1)波的波速、频率和波长；(2)绳子上各质点振动时的最大速度和最大加速度； (3)求x =0.2m t =1s 时的位相，它是原点在哪一时刻的位相?这一位相所代表的运动状态在t =1.25s 时刻到达哪一点? 解: (1)将题给方程与标准式)22cos(x t A y λππυ-=相比，得振幅05.0=A m ，频率5=υ1-s ，波长5.0=λm ，波速5.2==λυu 1s m -⋅．(2)绳上各点的最大振速，最大加速度分别为ππω5.005.010max =⨯==A v 1s m -⋅222max 505.0)10(ππω=⨯==A a 2s m -⋅(3)2.0=x m 处的振动比原点落后的时间为08.05.22.0==u x s 故2.0=x m ,1=t s 时的位相就是原点(0=x )，在92.008.010=-=t s 时的位相， 即 2.9=φπ． 设这一位相所代表的运动状态在25.1=t s 时刻到达x 点，则825.0)0.125.1(5.22.0)(11=-+=-+=t t u x x m5-10 如题5-10图是沿x 轴传播的平面余弦波在t 时刻的波形曲线．(1)若波沿x 轴正向传播，该时刻O ，A ，B ，C 各点的振动位相是多少?(2)若波沿x 轴负向传播，上述各点的振动 位相又是多少?解: (1)波沿x 轴正向传播，则在t 时刻，有题5-10图对于O 点：∵0,0<=O O v y ，∴2πφ=O对于A 点：∵0,=+=A A v A y ，∴0=A φ 对于B 点：∵0,0>=B B v y ，∴2πφ-=B对于C 点：∵0,0<=C C v y ，∴23πφ-=C(取负值：表示C B A 、、点位相，应落后于O 点的位相)(2)波沿x 轴负向传播，则在t 时刻，有对于O 点：∵0,0>'='O Ov y ，∴2πφ-='O对于A 点：∵0,='+='A A v A y ，∴0='A φ对于B 点：∵0,0<'='B B v y ，∴2πφ=B 对于C 点：∵0,0>'='C C v y ，∴23πφ='C(此处取正值表示C B A 、、点位相超前于O 点的位相)5-11 一列平面余弦波沿x 轴正向传播，波速为5m ·s -1，波长为2m ，原点处质点的振动曲线如题5-11图所示． (1)写出波动方程；(2)作出t =0时的波形图及距离波源0.5m 处质点的振动曲线．解: (1)由题5-11(a)图知，1.0=A m ，且0=t 时，0,000>=v y ，∴230πφ=，又5.225===λυuHz ，则ππυω52==题5-11图(a)取 ])(cos[0φω+-=ux t A y ， 则波动方程为]23)5(5cos[1.0ππ+-=x t y m(2) 0=t 时的波形如题5-11(b)图题5-11图(b) 题5-11图(c)将5.0=x m 代入波动方程，得该点处的振动方程为)5cos(1.0)235.05.055cos(1.0πππππ+=+⨯-=t t y m 如题5-11(c)图所示．5-12 如题5-12图所示，已知t =0时和t =0.5s 时的波形曲线分别为图中曲线(a)和(b) ，波沿x 轴正向传播，试根据图中绘出的条件求： (1)波动方程；(2)P 点的振动方程．解: (1)由题5-12图可知，1.0=A m ，4=λm ，又，0=t 时，0,000<=v y ，∴20πφ=，而25.01==∆∆=t x u 1s m -⋅，5.042===λυu Hz ，∴ππυω==2 故波动方程为]2)2(cos[1.0ππ+-=x t y m(2)将1=P x m 代入上式，即得P 点振动方程为t t y ππππcos 1.0)]22cos[(1.0=+-= m题5-12图5-13 一列机械波沿x 轴正向传播，t =0时的波形如题5-13图所示，已知波速为10 m ·s -1，波长为2m ，求： (1)波动方程；(2) P 点的振动方程及振动曲线； (3) P 点的坐标；(4) P 点回到平衡位置所需的最短时间．解: 由题5-13图可知1.0=A m ，0=t 时，0,200<=v A y ，∴30πφ=，由题知2=λm ， 10=u 1s m -⋅，则5210===λυuHz∴ ππυω102==(1)波动方程为]3)10(10cos[.01ππ+-=x t y m题5-13图(2)由图知，0=t 时，0,2<-=P P v A y ，∴34πφ-=P (P 点的位相应落后于0点，故取负值)∴P 点振动方程为)3410cos(1.0ππ-=t y p (3)∵ πππ34|3)10(100-=+-=t x t ∴解得 67.135==x m(4)根据(2)的结果可作出旋转矢量图如题5-13图(a)，则由P 点回到平衡位置应经历的位相角题5-13图(a)πππφ6523=+=∆ ∴所属最短时间为121106/5==∆=∆ππωφt s5-14 如题5-14图所示，有一平面简谐波在空间传播，已知P 点的振动方程为P y =A cos(0ϕω+t )．(1)分别就图中给出的两种坐标写出其波动方程； (2)写出距P 点距离为b 的Q 点的振动方程． 解: (1)如题5-14图(a)，则波动方程为])(cos[0φω+-+=uxu l t A y 如图(b)，则波动方程为题5-14图])(cos[0φω++=uxt A y (2) 如题5-14图(a)，则Q 点的振动方程为 ])(cos[0φω+-=ubt A A Q 如题5-14图(b)，则Q 点的振动方程为])(cos[0φω++=ubt A A Q5-15 已知平面简谐波的波动方程为)24(cos x t A y +=π(SI)．(1)写出t =4.2 s 时各波峰位置的坐标式，并求此时离原点最近一个波峰的位置，该波峰何时通过原点?(2)画出t =4.2 s 时的波形曲线． 解:(1)波峰位置坐标应满足ππk x t 2)24(=+ 解得 )4.8(-=k x m (,2,1,0±±=k …) 所以离原点最近的波峰位置为4.0-m ． ∵uxt t t ωωππ+=+24 故知2=u 1s m -⋅,∴ 2.024.0=-='∆t s ，这就是说该波峰在2.0s 前通过原点，那么从计时时刻算起，则应是42.02.4=-s ，即该波峰是在4s 时通过原点的．题5-15图(2)∵2,4==u πω1s m -⋅，∴12===ωπλuuT m ，又0=x 处，2.4=t s 时，ππφ8.1642.40=⨯=A A y 8.02.44cos 0-=⨯=π又，当A y -=时，πφ17=x ，则应有πππ1728.16=+x 解得 1.0=x m ，故2.4=t s 时的波形图如题5-15图所示5-16 题5-16图中(a)表示t =0时刻的波形图，(b)表示原点(x =0)处质元的振动曲线，试求此波的波动方程，并画出x =2m 处质元的振动曲线．解: 由题5-16(b)图所示振动曲线可知2=T s ,2.0=A m ，且0=t 时，0,000>=v y ， 故知20πφ-=,再结合题5-16(a)图所示波动曲线可知，该列波沿x 轴负向传播，且4=λm ，若取])(2cos[0φλπ++=xT t A y题5-16图则波动方程为]2)42(2cos[2.0ππ-+=x t y 5-17 一平面余弦波，沿直径为14cm 的圆柱形管传播，波的强度为18.0×10-3J ·m -2·s -1，频率为300 Hz ，波速为300m ·s -1，求 ： (1)波的平均能量密度和最大能量密度? (2)两个相邻同相面之间有多少波的能量?解: (1)∵ u w I =∴ 53106300100.18--⨯=⨯==u I w 3m J -⋅ 4max 102.12-⨯==w w 3m J -⋅(2) νπλπωu d w d wV W 224141=== 7251024.9300300)14.0(41106--⨯=⨯⨯⨯⨯=πJ5-18 如题5-18图所示，1S 和2S 为两相干波源，振幅均为1A ，相距4λ，1S 较2S 位相超前2π，求： (1) 1S 外侧各点的合振幅和强度； (2) 2S 外侧各点的合振幅和强度解：（1）在1S 外侧，距离1S 为1r 的点，1S 2S 传到该P 点引起的位相差为πλλππφ=⎥⎦⎤⎢⎣⎡+--=∆)4(2211r r 0,0211===-=A I A A A（2）在2S 外侧.距离2S 为1r 的点，1S 2S 传到该点引起的位相差.0)4(2222=-+-=∆r r λλππφ2121114,2A A I A A A A ===+=5-19 如题5-19图所示，设B 点发出的平面横波沿BP 方向传播，它在B 点的振动方程为t y π2cos 10231-⨯=;C 点发出的平面横波沿CP 方向传播，它在C 点的振动方程为)2cos(10232ππ+⨯=-t y ，本题中y 以m 计，t 以s 计．设BP ＝0.4m ，CP ＝0.5m ，波速u =0.2m ·s -1，求：(1)两波传到P 点时的位相差；(2)当这两列波的振动方向相同时，P 处合振动的振幅；*(3)当这两列波的振动方向互相垂直时，P 处合振动的振幅． 解: (1) )(2)(12BP CP ---=∆λπϕφφ)(BP CP u --=ωπ0)4.05.0(2.02=--=ππ题5-19图(2)P 点是相长干涉，且振动方向相同，所以321104-⨯=+=A A A P m(3)若两振动方向垂直，又两分振动位相差为0，这时合振动轨迹是通过Ⅱ，Ⅳ象限的直线，所以合振幅为33122211083.210222--⨯=⨯==+=A A A A m5-20 一平面简谐波沿x 轴正向传播，如题5-20图所示．已知振幅为A ，频率为ν 波速为u ．(1)若t =0时，原点O 处质元正好由平衡位置向位移正方向运动，写出此波的波动方程；(2)若从分界面反射的波的振幅与入射波振幅相等，试写出反射波的波动方程，并求x 轴上 因入射波与反射波干涉而静止的各点的位置．解: (1)∵0=t 时，0,000>=v y ，∴20πφ-=故波动方程为]2)(2cos[ππ--=u x t v A y m题5-20图(2)入射波传到反射面时的振动位相为(即将λ43=x 代入)2432πλλπ-⨯-，再考虑到波由波疏入射而在波密界面上反射，存在半波损失，所以反射波在界面处的位相为πππλλπ-=+-⨯-2432 若仍以O 点为原点，则反射波在O 点处的位相为ππλλπ25432-=-⨯-，因只考虑π2以内的位相角，∴反射波在O 点的位相为2π-，故反射波的波动方程为 ]2)(2cos[ππυ-+=u x t A y 反 此时驻波方程为 ]2)(2cos[ππυ--=u x t A y ]2)(2cos[ππυ-++u x t A )22cos(2cos2ππυπυ-=t u x A 故波节位置为2)12(22πλππυ+==k x u x 故 4)12(λ+=k x (,2,1,0±±=k …)根据题意，k 只能取1,0，即λλ43,41=x 5-20 一驻波方程为y =0.02cos20x cos750t (SI)，求：(1)形成此驻波的两列行波的振幅和波速；(2)相邻两波节间距离．解: (1)取驻波方程为 t u x A y πυπυ2cos 2cos2= 故知 01.0202.0==A m 7502=πυ，则πυ2750=， 202=uπυ ∴ 5.37202/7502202=⨯==πππυu 1s m -⋅ (2)∵314.01.020/2====πυπυυλu m 所以相邻两波节间距离 157.02==∆λx m5-22 在弦上传播的横波，它的波动方程为1y =0.1cos(13t +0.0079x ) (SI)试写出一个波动方程，使它表示的波能与这列已知的横波叠加形成驻波，并在x =0处为波 节．解: 为使合成驻波在0=x 处形成波节，则要反射波在0=x 处与入射波有π的位相差，故反射波的波动方程为)0079.013cos(1.02π--=x t y5-23 两列波在一根很长的细绳上传播，它们的波动方程分别为1y =0.06cos(t x ππ4-)(SI), 2y =0.06cos(t x ππ4+)(SI)．(1)试证明绳子将作驻波式振动，并求波节、波腹的位置；(2)波腹处的振幅多大?x =1.2m 处振幅多大?解: (1)它们的合成波为)4cos(06.0)4cos(06.0t x x y ππππ++-=t x ππ4cos cos 12.0=出现了变量的分离，符合驻波方程特征，故绳子在作驻波振动．令ππk x =，则k x =，k=0,±1，±2…此即波腹的位置； 令2)12(ππ+=k x ,则21)12(+=k x ，,2,1,0±±=k …，此即波节的位置． (2)波腹处振幅最大，即为12.0m ；2.1=x m 处的振幅由下式决定，即 097.0)2.1cos(12.0=⨯=π驻A m5-24 汽车驶过车站时，车站上的观测者测得汽笛声频率由1200Hz 变到了1000 Hz ，设空气中声速为330m ·s -1，求汽车的速率．解: 设汽车的速度为s v ，汽车在驶近车站时，车站收到的频率为 01υυsv u u -= 汽车驶离车站时，车站收到的频率为02υυs v u u +=联立以上两式，得3010012001000120030021211=+-⨯=+-=υυυυυu 1s m -⋅ 5-25 两列火车分别以72km ·h -1和54 km ·h -1的速度相向而行，第一 列火车发出一个600 Hz的汽笛声，若声速为340 m ·s -1，求第二列火车上的观测者听见该声音的频率在相遇前和相遇后分别是多少?解: 设鸣笛火车的车速为201=v 1s m -⋅，接收鸣笛的火车车速为152=v 1s m -⋅，则两者相遇前收到的频率为 66560020340153400121=⨯-+=-+=υυv u v u Hz 两车相遇之后收到的频率为54160020340153400121=⨯+-=+-=υυv u v u Hz。