2018年北京市初三数学各区一模27题汇编(共11个区)

尺规作图 东城区16．已知正方形ABCD .求作：正方形ABCD 的外接圆. 作法：如图，（1）分别连接AC ，BD ，交于点O ;(2) 以点O 为圆心，OA 长为半径作O .O 即为所求作的圆.请回答：该作图的依据是_____________________________________. 16. 正方形的对角线相等且互相平分，圆的定义西城区16．阅读下面材料：在复习课上，围绕一道作图题，老师让同学们尝试应用学过的知识设计多种不同的作图方法，并交流其中蕴含的数学原理．已知：直线和直线外的一点P ．求作：过点P 且与直线垂直的直线PQ ，垂足为点Q P 某同学的作图步骤如下：请你根据该同学的作图方法完成以下推理: ∵PA PB =，APQ ∠=∠__________， ∴PQ l ⊥．（依据：__________）．【答案】BPQ ，等腰三角形三线合一 【解析】BPQ ，等腰三角形三线合一．海淀区16．下面是“过圆上一点作圆的切线”的尺规作图过程.请回答尺规作图的依据是．16．与一条线段两个端点距离相等的点，在这条线段的垂直平分线上；经过半径的外端并且垂直于这条半径的直线是圆的切线；两点确定一条直线.丰台区16．下面是“作一个角等于已知角”的尺规作图过程．16．在同圆或等圆中，如果两个圆心角、两条弧、两条弦中的一组量相等，那么它们所对应的其余各组量都分别相等．或：同圆半径相等，三条边对应相等的两个三角形全等，全等三角形的对应角相等．石景山区16．小林在没有量角器和圆规的情况下，利用刻度尺和一副三角板画出了一个角的平分线，他的做法是这样的：如图，（1）利用刻度尺在AOB ∠的两边OA ，OB 上分别取OM ON =；（2）利用两个三角板，分别过点M ，N 画OM ，ON 的垂线，交点为P ； （3）画射线OP ．则射线OP 为AOB ∠的平分线．请写出小林的画法的依据 ． 16．（1）斜边和一条直角边分别相等的两个直角三角形全等； （2）全等三角形的对应角相等．朝阳区16.下面是“经过已知直线外一点作这条直线的垂线”的尺规作图过程.请回答：该尺规作图的依据是 ．16. 与一条线段两个端点距离相等的点，在这条线段的垂直平分线上；直径所对的圆周角是直角燕山区16． 在数学课上，老师提出如下问题：曈曈的作法如下：老师说：“曈曈的作法正确．”请你回答：曈曈的作图依据是________________________．16．①线段垂直平分线上的点到线段两端点的距离相等②圆的定义（到定点的距离等于定长的点的轨迹是圆）门头沟区请回答：该尺规作图的依据是__________．等圆的半径相等，直径所对的圆周角是直角，三角形定义平谷区16．下面是“作已知角的角平分线”的尺规作图过程．请回答：该尺规作图的依据是．16．答案不唯一：到线段两端点距离相等的点在线段的垂直平分线上；等腰三角形三线合一．怀柔区16. 阅读下面材料：请回答：该尺规作图的依据是16. 到角两边距离相等的点在角平分上；两点确定一条直线；角平分上的点到角两边的距离相等；圆的定义；经过半径的外端，并且垂直于这条半径的直线是圆的切线.延庆区15．如图，在平面直角坐标系xOy中，△DEF可以看作是△ABC经过若干次图形的变化（平移、轴对称、旋转）得到的，写出一种由△ABC得到△DEF的过程：．15．△ABC沿y轴翻折后，再向上平移4个单位得到△DEF顺义区16．在数学课上，老师提出一个问题“用直尺和圆规作一个矩形”．小华的做法如下：老师说：“小华的作法正确” ．请回答：小华的作图依据是．16．同圆半径相等，对角线相等且互相平分的四边形是矩形．（或直径所对的圆周角是直角，三个角是直角的四边形是矩形．等等）。

解四边形专题东城区21．如图，已知四边形ABCD是平行四边形，延长BA至点E，使AE= AB，连接DE，AC. （1）求证：四边形ACDE为平行四边形;1cos B ，求线段CE的长. （2）连接CE交AD于点O. 若AC=AB=3，321.(1) 证明：∵平行四边形ABCD，∴AB=DC，A B∥DC.∵AB=AE，∴AE=DC，AE∥DC.∴四边形ACDE为平行四边形. -------------------2分(2) ∵AB=AC，∴AE=AC. ∴平行四边形ACDE为菱形.∴AD⊥CE.∵AD∥BC，∴BC⊥CE.在Rt△EBC中，BE=6,∴BC=2 .cos BBC 1,BE 3根据勾股定理，求得BC=4 2 .----------------------5分西城区21．如图，在△ABD中，ABDADB，分别以点B，D为圆心，AB长为半径在BD的右侧作弧，两弧交于点C，分别连接BC，DC，AC，记AC与BD的交点为O．（1）补全图形，求AOB的度数并说明理由;3（2）若AB 5 ，cos ABD，求BD 的长．51BAD【解析】（1）补全的图形如图所示．AOB90．证明：由题意可知BC AB，DC AB，∵在△ABD中，ABD ADB，∴AB AD，∴BC DC AD AB，∴四边形ABCD为菱形，∴AC BD，∴AOB90．（2）∵四边形ABCD为菱形，∴OB OD．3在Rt△ABO中，AOB90，AB 5 ，ABD，cos5∴OB AB cos ABD 3 ，∴BD2OB 6 ．BCOAD海淀区221．如图，□ABCD的对角线AC, BD相交于点O，且AE∥BD，BE∥AC，OE = CD.（1）求证：四边形ABCD是菱形；（2）若AD=2，则当四边形ABCD的形状是__________时，四边形AOBE的面积取得最大值是_______.C BO ED A21．（1）证明：∵AE∥BD，BE∥AC，∴四边形AEBO是平行四边形. ………………1分∵四边形ABCD是平行四边形，∴DC AB.∵OE CD,∴OE AB.∴平行四边形AEBO是矩形. ………………2分∴BOA 90. ∴AC BD.∴平行四边形ABCD是菱形. ………………3分(2) 正方形；………………4分2. ………………5分丰台区21．已知：如图，菱形ABCD，分别延长AB，CB到点F，E，使得BF = BA，BE = BC，连接AE，EF，FC，CA．（1）求证：四边形AEFC为矩形；（2）连接DE交AB于点O，如果DE⊥AB，AB = 4，求DE的长．DA CBE F21．（1）证明：∵BF=BA，BE=BC，∴四边形AEFC为平行四边形. ………………………1分D ∵四边形ABCD为菱形，∴BA=BC.∴BE=BF.∴BA + BF = BC + BE，即AF=EC.AGBC∴四边形AEFC为矩形. ………………………2分（2）解：连接DB.E F由（1）知，AD∥EB，且AD=EB.∴四边形AEBD为平行四边形∵DE⊥AB，3∴四边形AEBD为菱形.∴AE EB，AB2AG，ED2EG. ………………………4分∵矩形ABCD中，EB AB，AB=4，∴AG2，AE 4.∴Rt△AEG中，EG=2 3 .∴ED=4 3 . ………………………5分（其他证法相应给分）石景山区21．如图，在四边形ABCD中，A BCD90°，BC CD 2 10 ，CE AD于点E．（1）求证：AE CE；（2）若tan D3，求AB的长．CBA E D21．（1）证明：（法一）过点B作BH⊥CE于H，如图1．∵CE⊥AD，∴∠BHC＝∠CED＝90°，1D90．∵∠BCD＝90°，∴1 290，∴ 2D．又BC＝CD∴△BHC≌△CED．∴BH CE．∵BH⊥CE，CE⊥AD，∠A＝90°，∴四边形ABHE是矩形，∴AE BH．∴AE CE．………………3分（法二）过点C作CH⊥AB交AB的延长线于H．图略，证明略．（2）解：∵四边形ABHE是矩形，∴AB HE．CE∵在Rt△CED中，tan D3,DE设DE x,CE3x，∴CD10x 2 10 ．4∴x 2 ．∴DE 2,CE 6．………………4分∵CH DE 2 ．∴AB HE 6 2 4 ．………………5分朝阳区21. 如图，在△ABC中，D是AB边上任意一点，E是BC边中点，过点C作AB的平行线，交DE的延长线于点F，连接BF，CD．（1）求证：四边形CDBF是平行四边形；（2）若∠FDB=30°，∠ABC=45°，BC=42，求DF的长．21.（1）证明：∵CF∥AB，∴∠ECF＝∠EBD.∵E是BC中点，∴CE＝BE.∵∠CEF＝∠BED，∴△CEF≌△BED.∴CF＝BD.∴四边形CDBF是平行四边形. ………………………2分C （2）解：如图，作EM⊥DB于点M，FE ∵四边形CDBF是平行四边形，BC＝4 2 ，1∴ 2 2BE BC，DF 2DE. AD2在Rt△EMB中，EM BE sin ABC 2. (3)分M B在Rt△EMD中，DE 2EM 4 . …………………4分∴DF＝8. ………………………………………………………5分燕山区23．如图，在△ABC中，D,E分别是AB,AC的中点，BE=2DE,延长DEA到点F，使得EF=BE,连接CF．（1）求证：四边形BCFE是菱形；（2）若∠BCF=120°，CE=4，求菱形BCFE的面积．D E F23. （1）证明：∵点D,E, 是AB,AC 中点1∴DE∥BC, DE= BC……………………….1′2B C5又 BE=2DE,即 DE=12 B E∴BC=BE 又 EF=BE ∴EF ∥BC, EF=BC∴四边形 BCFE 是平行四边形……………………….2′ 又 EF=BE∴四边形 BCFE 是菱形 ……………………….3′（2）∵四边形 BCFE 是菱形∴BC=BE 又∠BCF =120° ∴∠BCE=60°∴△BCE 是等边三角形∴连结 BF 交 EC 于点 O ．∴BF ⊥EC在 Rt △BOC 中，BO= BC 2OC 2 4 2 2 2 2 3 ……………………….4′11 SBO OC2 23BOC22 2 3S菱形BCFE42 3 8 3∴∴……………………….5′门头沟区21.在矩形 ABCD 中，连接 AC ,AC 的垂直平分线交 AC 于点 O ,分别交 AD 、BC 于点 E 、F ，连接 CE 和 AF ．EAD（1）求证：四边形 AECF 为菱形；（2）若 AB =4，BC =8，求菱形 AECF 的周长．OBCF21. （1）证明：∵EF 是 AC 的垂直平分线，∴AO =OC ，∠AOE =∠COF =90°，……………………1分 ∵四边形 ABCD 是矩形， ∴AD ∥BC ，∴∠EAO =∠FCO ，在△AEO 和△CFO 中， ∵∠EAO =∠FCO ，AO =CO ，∠AOE =∠COF ，EAD∴△AEO ≌△CFO （ASA ），∴OE =OF ． ……………2分 又∵OA =OC ，∴四边形 AECF 是平行四边形，O又∵EF ⊥AC ，∴平行四边形 AECF 是菱形；……………3分 （2）设 AF =x ，∵EF 是 AC 的垂直平分线，BCF∴AF =CF =x ，BF =8﹣x ， ………………………………………4分在Rt△ABF中，由勾股定理得：AB2+BF2=AF2，42+（8﹣x）2=x2，解得x=5，∴AF=5，∴菱形AECF的周长为20．…………………5分6大兴区21. 如图，矩形 ABCD 的对角线 AC 、BD 交于点 O ，且 DE=O C ，CE=O D ． （1）求证：四边形 OCED 是菱形；（2）若∠BAC ＝30°，AC ＝4，求菱形 OCED 的面积． 21.（1）证明：∵DE =OC ，CE =OD ，∴四边形 OCED 是平行四边形 ………………………………1分∵矩形 ABCD ，∴AC =BD ，OC = ∴OC =OD .12 AC ，OD = 1 2BD .∴平行四边形 OCED 是菱形………………………………2分 （2）解：在矩形 ABCD 中，∠ABC =90°，∠BAC =30°，AC ＝4， ∴BC =2.∴AB =DC =2 3 .…………………………………………………3分 连接 OE ，交 CD 于点 F .∵四边形 OCED 为菱形，∴F 为 CD 中点. ∵O 为 BD 中点，∴OF = 12BC =1.∴OE ＝2OF ＝2 …………………………………………………4分∴S 菱形 OCED ＝ 12 O E·CD = 1 2×2×2 3＝ 2 3 …………………………………………………5分平谷区k21．如图，在平面直角坐标系 xOy 中，函数y k的图象与直线 y =x +1交于点 A （1，a ）．x（1）求 a ，k 的值；k（2）连结 OA ，点 P 是函数y k上一点，且满足 OP=OA ，直接写出点 P 的坐标（点 Ax除外）．721．解：（1）∵直线 y =x +1经过点 A （1，a ），∴a =2． ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1 ∴A （1,2）．k∵函数yk的图象经过点 A （1，2），x∴k =2． ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2（2）点 P 的坐标（2,1），（-1，-2），（-2，-1）．∙∙∙∙∙∙∙∙∙∙∙∙∙5怀柔区21.直角三角形 ABC 中，∠BAC=90°，D 是斜边 BC 上一点，且 AB=AD ，过点 C 作 CE⊥AD ，交 AD 的延长线于点 E ，交 AB 延长线于点 F. (1)求证：∠ACB=∠DCE ； (2)若∠BAD=45°， AF 2+ 2 ，过点 B 作 BG⊥FC 于点 G ，连接 DG ．依题意补全图形，并求四边形 ABGD 的面积．21.(1)∵AB=AD ，∴∠ABD=∠ADB ，………………………………1分 ∵∠ADB=∠CDE ，∴∠ABD=∠CDE.A∵∠BAC=90°，∴∠ABD+∠ACB=90°. ∵CE⊥AE ，∴∠DCE+∠CDE=90°.∴∠ACB=∠DCE. …………………………………2分BDC（2）补全图形,如图所示: …………………………3分 E∵∠BAD=45°, ∠BAC=90°,G ∴∠BAE=∠CAE=45°, ∠F=∠ACF=45°,AF∵AE⊥CF, BG⊥CF,∴AD∥BG.∵BG⊥CF, ∠BAC=90°，且∠ACB=∠DCE, ∴AB=BG.BH DC∵AB=AD ，∴BG=AD.∴四边形 ABGD 是平行四边形. ∵AB=ADFGE∴平行四边形 ABGD 是菱形.………………4分设 AB=BG=GD=AD=x ，∴BF= 2BG= 2x.∴AB+BF=x+ 2x=2+ 2.∴x=2，过点B作BH⊥AD于H.8∴BH=22A B=1.∴S四边形ABDG=AD×BH=2. ……………………………………………………………………5分延庆区21．如图，Rt△ABC中，∠ABC=90°，点D，F分别是AC，AB的中点，CE∥DB，BE∥DC．（1）求证：四边形DBEC是菱形；（2）若AD=3，DF=1，求四边形DBEC面积.CD EBA F21．（1）在Rt△ABC中，∵CE//DC，BE//DC∴四边形DBEC是平行四边形∵D是AC的中点，∠ABC=90°∴BD=DC ……1分∴四边形DBEC是菱形……2分（2）∵F是AB的中点∴BC=2DF=2,∠AFD=∠ABC=90°在Rt△AFD中,AF = 퐴퐷2 ―퐷퐹2 = 32 ―1 = 2 2 ……3分1 1∴푆∆퐷퐵퐶= 2BC × BF = 2 × 2 × 2 2 = 2 2 ……4分∴푆菱形DBEC = 2푆∆퐷퐵퐶= 4 2……5分顺义区21．如图，四边形ABCD中，AD∥BC，∠A=90°，BD=BC，点E为CD的中点，射线BE交AD的延长线于点F，连接CF．（1）求证：四边形BCFD是菱形；A DF（2）若AD=1，BC=2，求BF的长．EB C 21．（1）证明：∵BD=BC，点E是CD的中点，∴∠1=∠2．…………………………………………………… 1分∵AD∥BC，∴∠2=∠3．DA F3E9 12B C∴∠1=∠3．……………………………2分∴BD=DF．∵BD=BC，∴DF=BC．又∵DF∥BC，∴四边形BCFD是平行四边形．∵BD=BC，∴□BCFD是菱形．…………………………………………………… 3分（2）解：∵∠A =90，AD=1，BD=BC=2，∴AB BD2 AD2 3 ．∵四边形BCFD是菱形，∴DF=BC=2．………………………………………………………… 4分∴AF=AD+DF=3．∴BF AB2 AF2 39 2 3 ．………………………………5分10。

--------------2 分
② △ MNE 是等边三角形，点 E 的坐标为 3，1 ； --------------5 分
③ 直线 y
3 x 2 交 y 轴于点 K （ 0， 2），交 x 轴于点 T 2 3， 0 .
3
∴ OK 2 ， OT 2 3 .
∴ OKT 60 . 作 OG⊥ KT于点 G, 连接 MG.
在平面直角坐标系 xOy 中，⊙ O 的半径为 1.
22
22
（ 1）如图 2， M
, 22
，N
, 2
2 .在 A（ 1， 0），B（ 1，1）， C
20,
三点中 , 是线段 MN 关于点 O 的关联点的是
；
31
（ 2）如图 3， M （ 0， 1），N
,
，点 D 是线段 MN 关于点 O 的关联点 .
3 / 21
y
M
O
Q
C
x 2
∵ Q( 1,0) ， C(1,0) ， r 1， ∴ CQ 2 ， CM 1，
∴ MQ 3 ，
2MQ
此时 k CQ
3，
②如图，若直线 QM 与⊙ C 不相切，设直线 QM 与⊙ C 的另一个交点为 N （不妨设
QN QM ，点 N ， M 在 x 轴下方时同理） ，
作 CD QM 于点 D ，则 MD ND ，
2 / 21
点，记为点 A ， B ，设 k
AQ BQ CQ ，则称点 A （或点 B ）是⊙ C 的 “k 相关依附点 ”，
2AQ
2BQ
特别地，当点 A 和点 B 重合时，规定 AQ BQ ， k
（或
）．
CQ
CQ
已知在平面直角坐标系 xOy 中， Q ( 1,0) ， C(1,0) ，⊙ C 的半径为 r ．

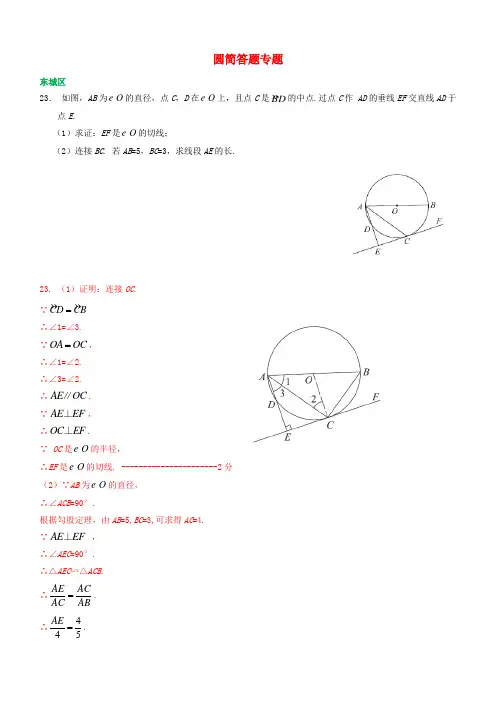
圆简答题专题东城区23．如图，AB为O的直径，点C，D在O上，且点C是BD的中点.过点C作AD的垂线EF交直线AD于点E.（1）求证：EF是O的切线；（2）连接BC. 若AB=5，BC=3，求线段AE的长.23. （1）证明：连接OC.∵CD CB=∴∠1=∠3.∵OA OC=，∴∠1=∠2.∴∠3=∠2.∴AE OC∥.∵AE EF⊥，∴OC EF⊥.∵OC是O的半径，∴EF是O的切线. ----------------------2分（2）∵AB为O的直径，∴∠ACB=90°.根据勾股定理，由AB=5,BC=3,可求得AC=4.∵AE EF⊥，∴∠AEC=90°.∴△AEC∽△ACB.∴AE AC AC AB=.∴4 45 AE=.∴165AE =. ----------------------5分 西城区24．如图，⊙O 的半径为r ，ABC △内接于⊙O ，15BAC ∠=︒，30ACB ∠=︒，D 为CB 延长线上一点，AD 与⊙O 相切，切点为A ．（1）求点B 到半径OC 的距离（用含r 的式子表示）． （2）作DH OC ⊥于点H ，求ADH ∠的度数及CBCD的值． AB C【解析】（1）如图4，作BE OC ⊥于点E ． ∵在⊙O 的内接ABC △中，15BAC ∠=︒， ∴230BOC BAC ∠=∠=︒．在Rt BOE △中，90OEB ∠=︒，30BOE ∠=︒，OB r =， ∴22OB rBE ==， ∴点B 到半径OC 的距离为2r． （2）如图4，连接OA ．由BE OC ⊥，DH OC ⊥，可得BE DH ∥． ∵AD 于⊙O 相切，切点为A ， ∴AD OA ⊥， ∴90OAD ∠=︒． ∵DH OC ⊥于点H ， ∴90OHD ∠=︒．∵在OBC △中，OB OC =，30BOC ∠=︒， ∴180752BOCOCB ︒-∠∠==︒．∵30ACB ∠=︒，∴45OCA OCB ACB ∠=∠-∠=︒． ∵OA OC =，∴45OAC OCE ∠=∠=︒， ∴180290AOC OCA ∠=︒-∠=︒， ∴四边形AOHD 为矩形，90ADH ∠=︒， ∴DH AO r ==．∵2r BE =， ∴2DHBE =．∵BE DH ∥， ∴CBE CDH ∽△△， ∴12CB BE CD DH ==． 图4CB A海淀区23．如图，AB 是O 的直径，弦EF AB ⊥于点C ，过点F 作O 的切线交AB 的延长线于点D .（1）已知A α∠=，求D ∠的大小（用含α的式子表示）；（2）取BE 的中点M ，连接MF ，请补全图形；若30A ∠=︒，MF =，求O 的半径.DA23．解：（1）连接OE ，OF ．∵EF AB ⊥，AB 是O 的直径，∴DOF DOE =∠∠． ∵2DOE A =∠∠，A α=∠，∴2DOF α=∠． ………………1分 ∵FD 为O 的切线， ∴OF FD ⊥.∴90OFD ︒=∠.∴+90D DOF ︒=∠∠. 902D α∴∠=︒-． ………………2分（2）图形如图所示.连接OM .∵AB 为O 的直径，∴O 为AB 中点， 90AEB ∠=︒． ∵M 为BE 的中点，∴OM AE ∥，1=2OM AE . ………………3分∵30A ∠=︒，∴30MOB A ∠=∠=︒． ∵260DOF A ∠=∠=︒ ，∴90MOF ∠=︒. ………………4分 ∴222+OM OF MF =．设O 的半径为r ．∵90AEB ∠=︒，30A ∠=︒，∴cos30AE AB ︒=⋅=.∴OM ． ………………5分∵FM∴222)+r =.解得=2r ．（舍去负根）∴O 的半径为2． ………………6分 丰台区DADA23．如图，A ，B ，C 三点在⊙O 上，直径BD 平分∠ABC ，过点D 作DE ∥AB 交弦BC 于点E ，过点D 作⊙O 的切线交BC 的延长线于点F ． （1）求证：EF =ED ；（2）如果半径为5，cos∠ABC =35，求DF 的长．23．（1）证明：∵BD 平分∠ABC ，∴∠1＝∠2.∵DE ∥AB ，∴∠2＝∠3.∴∠1＝∠3. ∵BC 是⊙O 的切线，∴∠BDF ＝90°. ∴∠1+∠F ＝90°，∠3+∠EDF ＝90°.∴∠F ＝∠EDF .∴EF =DE . …….…….……………2分 （2）解：连接CD .∵BD 为⊙O 的直径，∴∠BCD ＝90°. ∵DE ∥AB ，∴∠DEF ＝∠ABC . ∵cos∠ABC =35，∴在Rt△ECD 中，cos∠DEC =CE DE =35. 设CE =3x ，则DE =5x .由（1）可知，BE = EF =5x .∴BF =10x ，CF =2x. 在Rt△CFD 中，由勾股定理得DF =． ∵半径为5，∴BD =10. ∵BF ×DC = FD ×BD ， ∴1041025x x x =，解得2x =∴DF ==5. …….…….……………5分 （其他证法或解法相应给分.）石景山区23．如图，AB 是⊙O 的直径，BE 是弦，点D 是弦BE 上一点，连接OD 并延长交⊙O 于点C ，连接BC ，过点D 作FD ⊥OC 交⊙O 的切线EF 于点F ．（1）求证：12CBE F ∠=∠；（2）若⊙O的半径是，点D 是OC 中点，15CBE ∠=°，求线段EF 的长．23．（1）证明：连接OE 交DF 于点H ，∵EF 是⊙O 的切线，OE 是⊙O 的半径， ∴OE ⊥EF . ∴190F ∠+∠=°. ∵FD ⊥OC ， ∴3290∠+∠=︒. ∵12∠=∠，∴3F ∠=∠. ………………1分 ∵132CBE ∠=∠，∴12CBE F ∠=∠. ………………2分（2）解：∵15CBE ∠=°，∴3230F CBE ∠=∠=∠=°.∵⊙O 的半径是D 是OC 中点， ∴OD = 在Rt ODH ∆中，cos 3OD OH∠=，∴2OH =. ………………3分 ∴2HE =. 在Rt FEH ∆中，tan EHF EF∠=. (4)分∴6EF ==-………………5分 朝阳区23. 如图，在⊙O 中，C ，D 分别为半径OB ，弦AB 的中点，连接CD 并延长，交过点A 的切线于点E ． （1）求证：AE ⊥CE ． （2）若AE =，sin ∠ADE =31，求⊙O 半径的长．23. （1）证明：连接OA ，∵OA 是⊙O 的切线，∴∠OAE ＝90º. ………………………………1分 ∵ C ，D 分别为半径OB ，弦AB 的中点， ∴CD 为△AOB 的中位线. ∴CD ∥OA ． ∴∠E ＝90º.∴AE ⊥CE . …………………………………2分（2）解：连接OD ，∴∠ODB ＝90º. ……………………………………………………3分 ∵AE =，sin ∠ADE =31， 在Rt △AED 中，23sin =∠=ADEAEAD .∵CD ∥OA ， ∴∠1＝∠ADE . 在Rt △OAD 中，311sin ==∠OA OD .…………………………………4分 设OD ＝x ，则OA ＝3x ， ∵222OA AD OD =+， ∴()()222323x x =+.解得 231=x ，232-=x （舍）. ∴293==x OA . ……………………………………………5分即⊙O 的半径长为29.燕山区25．如图，在△ABC 中,AB=AC ,AE 是BC 边上的高线，BM 平分∠ABC 交 AE 于点M ，经过 B ，M 两点的⊙O 交 BC 于点G ，交AB 于点F ，FB 为⊙O 的直径． （1）求证：AM 是⊙O 的切线 （2）当BE =3，cosC=52时，求⊙O 的半径．25.解： (1)连结OM. ∵BM 平分∠ABC∴∠1 = ∠2 又OM=OB ∴∠2 = ∠3∴ OM ∥ BC …………………………………2′ AE 是BC 边上的高线∴AE ⊥BC,∴AM ⊥OM∴AM 是⊙O 的切线…………………………………3′ （2）∵AB=AC∴∠ABC = ∠C AE ⊥BC, ∴E 是BC 中点 ∴EC=BE=3 ∵cosC=52=AC EC ∴AC=25EC= 215…………………………………4′∵OM ∥ BC ，∠AOM =∠ABE∴△AOM ∽△ABE ∴ABAOBE OM =又∠ABC = ∠C ∴∠AOM =∠C 在Rt △AOM 中cos ∠AOM = cosC=52 52=AO OM ∴AO=OM 25AB=OM 25+OB=OM 27而AB= AC= 215门头沟区23. 如图，AB 为⊙O 直径，过⊙O 外的点D 作DE ⊥OA 于点E ，射线DC 切⊙O 于点C 、交AB 的延长线于点P ，连接AC 交DE 于点F ，作CH ⊥AB 于点H ． （1）求证：∠D =2∠A ；（2）若HB =2，cos D =35，请求出AC 的长．（1）证明：连接OC ，∵射线DC 切⊙O 于点C ， ∴∠OCP =90° ∵DE ⊥AP ，∴∠DEP =90° ∴∠P +∠D =90°，∠P +∠COB =90°∴∠COB =∠D …………………1分 ∵OA =OC , ∴∠A =∠OCA∵∠COB=∠A +∠OCA ∴∠COB =2∠A∴∠D =2∠A …………………2分 （2）解：由（1）可知：∠OCP =90°，∠COP =∠D ，∴cos ∠COP =cos ∠D =35， …………………3分 ∵CH ⊥OP ，∴∠CHO =90°， 设⊙O 的半径为r ，则OH =r ﹣2． 在Rt △CHO 中，cos ∠HOC =OH OC =2r r-=35，A∴r =5， …………………4分 ∴OH =5﹣2=3，∴由勾股定理可知：CH =4，∴AH =AB ﹣HB =10﹣2=8．在Rt △AHC 中，∠CHA =90°，∴由勾股定理可知：AC =…………………5分 大兴区23.已知：如图，在△OAB 中，OA OB =，⊙O 经过AB 的中点C ，与OB 交于点D,且与BO 的延长线交于点E ，连接EC CD ，．（1）试判断AB 与⊙O 的位置关系，并加以证明； （2）若1tan 2E =，⊙O 的半径为3，求OA 的长．23. （1）AB 与⊙O 的位置关系是相切 ···················· 1分证明：如图，连接OC ．OA OB =，C 为AB 的中点，OC AB ∴⊥．∴AB 是⊙O 的切线． （2）ED 是直径，90ECD ∴∠=．∴90E ODC ∠+∠=．又90BCD OCD ∠+∠=，OCD ODC ∠=∠， ∴BCD E ∠=∠． 又CBD EBC ∠=∠， ∴BCD BEC △∽△．BC BDBE BC∴=． ∴2BC BD BE =⋅． ························· 3分1tan 2E ∠=， ∴12CD EC =． BCD BEC △∽△，∴12BD CD BC EC ==．·························· 4分 设BD x =，则2BC x =． 又2BC BD BE =⋅， ∴2(2)(6)x x x =+． 解得10x =，22x =．0BD x =>，∴2BD =．235OA OB BD OD ∴==+=+=． ··················· 5分 平谷区24．如图，以AB 为直径作⊙O ，过点A 作⊙O 的切线AC ，连结BC ，交⊙O 于点D ，点E 是BC 边的中点，连结AE ．（1）求证：∠AEB =2∠C ； （2）若AB =6，3cos 5B =，求DE 的长．24．（1）证明：∵AC 是⊙O 的切线，∴∠BAC =90°． ······················· 1 ∵点E 是BC 边的中点， ∴AE=EC ．∴∠C =∠EAC ， ······················· 2 ∵∠AEB =∠C +∠EAC ，∴∠AEB =2∠C ． (3)（2）解：连结AD ． ∵AB 为直径作⊙O ， ∴∠ABD =90°．∵AB= 6，3 cos5B=，∴BD=185． (4)在Rt△ABC中，AB=6，3 cos5B=，∴BC=10．∵点E是BC边的中点，∴BE=5． (5)∴75DE=． (6)怀柔区23.如图，AC是⊙O的直径，点B是⊙O内一点，且BA=BC，连结BO并延长线交⊙O于点D，过点C作⊙O的切线CE，且BC平分∠DBE.(1)求证：BE=CE；(2)若⊙O的直径长8，sin∠BCE=45，求BE的长.23.(1)∵BA=BC，AO=CO,∴BD⊥AC.∵CE是⊙O的切线,∴CE⊥AC.∴CE∥BD. ……………………………………1分∴∠ECB=∠CBD.∵BC平分∠DBE,∴∠CBE=∠CBD.∴∠ECB=∠CBE.∴BE=CE. …………………………………………2分(2)解：作EF⊥BC于F. …………………………3分E∵⊙O 的直径长8，∴CO=4.∴sin∠CBD= sin∠BCE= 45=OCBC. …………………………………………………………4分∴BC=5，OB=3. ∵BE=CE,∴BF=15 22 BC=.∵∠BOC=∠BFE=90°，∠CBO=∠EBF, ∴△CBO∽△EBF.∴BE BF BC OB=.∴BE=256. ……………………………………………………………………………………5分延庆区23．如图，AB是⊙O的直径，D是⊙O上一点，点E是弧AD的中点，过点A作⊙O的切线交BD的延长线于点F．连接AE并延长交BF于点C．（1）求证：AB BC=；（2）如果AB=5，1tan2FAC∠=，求FC的长．A23．证明：（1）连接BE．∵AB是直径，∴∠AEB=90°．∴∠CBE+∠ECB=90°∠EBA +∠EAB=90°．∵点E是AD的中点，∴∠CBE =∠EBA．∴∠ECB =∠EAB．……1分∴AB=BC．……2分（2）∵FA作⊙O的切线，A BCDEFO∴FA⊥AB．∴∠FAC+∠EAB=90°．∵∠EBA+∠EAB=90°，∴∠FAC=∠EBA．∵1tan2FAC∠=AB=5，∴AE=BE=．……4分过C点作CH⊥AF于点H，∵AB=BC∠AEB=90°，∴AC=2AE=25．∵1 tan2FAC∠=，∴CH=2．……5分∵CH∥AB AB=BC=5，∴255FCFC=+．∴FC=310．…6分顺义区24．如图，等腰△ABC是⊙O的内接三角形，AB=AC，过点A作BC的平行线AD交BO的延长线于点D．（1）求证：AD是⊙O的切线；（2）若⊙O的半径为15，sin∠D＝35，求AB的长．24．（1）证明：连接AO，并延长交⊙O于点E，交BC于点F．∵AB=AC，∴=AB AC．∴AE⊥BC．∵AD∥BC，∴AE⊥AD．∴AD是⊙O的切线．…………… 2分（2）解法1：∵AD∥BC，∴∠D=∠1．HA BCDEFO∵sin∠D=35，∴sin∠1=35．∵AE⊥BC，∴OFOB=35．∵⊙O的半径OB=15，∴OF=9，BF=12．∴AF=24．∴AB= 5分3解法2：过B作BH⊥DA交DA延长线于H．∵AE⊥AD，sin∠D=35，∴OAOD=35．∵⊙O的半径OA=15，∴OD=25，AD=20．∴BD=40．∴BH=24，DH=32．∴AH=12．∴AB= 5分。

几何证明东城区19. 如图，在△ABC 中，∠BAC =90°，AD ⊥BC 于点D . BF 平分∠ABC 交AD 于点E ，交AC 于点F . 求证：AE =AF .19.证明： ∵∠BAC =90°，∴∠FBA +∠AFB =90°. -------------------1分 ∵AD ⊥BC ，∴∠DBE +∠DEB =90°．---------------- 2分 ∵BE 平分∠ABC ,∴∠DBE =∠FBA . -------------------3分 ∴∠AFB =∠DEB . -------------------4分 ∵∠DEB =∠FEA ， ∴∠AFB =∠FEA .∴AE =AF . -------------------5分 西城区19．如图，AD 平分BAC ∠，BD AD ⊥于点D ，AB 的中点为E ，AE AC <． （1）求证：DE AC ∥．（2）点F 在线段AC 上运动，当AF AE =时，图中与ADF △全等的三角形是__________．EDCBA【解析】（1）证明：∵AD 平分BAC ∠， ∴12∠=∠， ∵BD AD ⊥于点D ， ∴90ADB ∠=︒， ∴ABD △为直角三角形． ∵AB 的中点为E ， ∴2AB AE =，2ABDE =， ∴DE AE =， ∴13∠=∠， ∴23∠=∠， ∴DE AC ∥． （2）ADE △．321EDCBA海淀区19．如图，△ABC 中，90ACB ∠=︒，D 为AB 的中点，连接CD ，过点B 作CD 的平行线EF ，求证：BC 平分ABF ∠．FE DCB A19. 证明：∵90ACB ∠=︒，D 为AB 的中点， ∴12CD AB BD ==. ∴ABC DCB ∠=∠. …………… ∵DC EF ∥，∴CBF DCB ∠=∠.∴CBF ABC ∠=∠. ∴BC 平分ABF ∠. 丰台区19．如图，在△ABC 中，AB = AC ，D 是BC 边上的中点，DE ⊥AB 于点E ，DF ⊥AC 于点F ．求证：DE = DF ．F E CBA19．证明：连接AD .∵AB ＝BC ，D 是BC 边上的中点，∴∠BAD =∠CAD . ………………………3分 ∵DE ⊥AB 于点E ，DF ⊥AC 于点F ，∴DE ＝DF ． ………………………5分 （其他证法相应给分）石景山区19．问题:将菱形的面积五等分．小红发现只要将菱形周长五等分，再将各分点与菱形的对角线交点连接即可解决问题．如图，点O 是菱形ABCD 的对角线交点，5AB =，下面是小红将菱形ABCD 面积五等分的操作与证明思路，请补充完整.O H GFE DCB A（1）在AB 边上取点E ，使4AE =，连接OA ，OE ； （2）在BC 边上取点F ，使BF = ，连接OF ； （3）在CD 边上取点G ，使CG = ，连接OG ； （4）在DA 边上取点H ，使DH = ，连接OH ．由于AE = ＋ = ＋ = ＋ = . 可证S △AOE ==EOFB FOGC GOHD S S S ==四边形四边形四边形S △HOA .19．解：3，2，1； ………………2分EB 、BF ；FC 、CG ；GD 、DH ；HA. ………………4分朝阳区19. 如图，在△ACB 中，AC =BC ，AD 为△ACB 的高线，CE 为△ACB 的中线.求证：∠DAB =∠ACE.ABCEF19. 证明：∵AC＝BC，CE为△ACB的中线，∴∠CAB＝∠B，CE⊥AB. ……………………………………………2分∴∠CAB＋∠ACE＝90°. ………………………………………………3分∵AD为△ACB的高线，∴∠D＝90°.∴∠DAB＋∠B＝90°. ……………………………………………………4分∴∠DAB＝∠ACE. ………………………………………………………5分燕山区19．文艺复兴时期，意大利艺术大师达．芬奇研究过用圆弧围成的部分图形的面积问题。

(3) 4.2，点 P 是 AD 与 CE 的交点. --------------------6 分
西城区
» 25．如图，P 为⊙O的直径 AB 上的一个动点，点C 在 AB 上，连接 PC ，过点 A作 PC 的垂
线交⊙O 于点 Q ．已知 AB 5cm ， AC 3cm ．设 A 、 P 两点间的距离为 xcm ， A 、 Q 两 点间的距离为 ycm ．
A
C O P
Q B
某同学根据学习函数的经验，对函数 y 随自变量 x 的变化而变化的规律进行探究． 下面是该同学的探究过程，请补充完整： （1）通过取点、画图、测量及分析，得到了 x 与 y 的几组值，如下表：
2
x
0
(cm)
2.5
3.5
4
5
y
4.0
4.7
5.0
4.8
(cm)
4.1
3.7
（说明：补全表格对的相关数值保留一位小数） （2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象． （3）结合画出的函数图象，解决问题：当 AQ 2 AP 时， AP 的长度均为__________cm ．
y
1
O1
x
（1）请沿此思路在图 2 中完善函数图象的草图并标出此函数图象上横坐标为 0 的点 A ；（画
出网格区域内的部分即可）
（2）观察图象，写出该函数的一条性质：____________________；
（3）若关于 x 的方程 1
a(x 1) 有两个不相等的实数根，结合图象，直接写出实数 a 的
1cm ，点 P 是半圆 O 上的动点，
过点 B 作 BQ PM 交 PM （或 PM 的延长线）于点 Q .设 PM x cm ， BQ y cm .（当点

2017——2018学年度北京初三各区一模26题汇总（东城区2017-2018学年度第一次模拟检测）26．在平面直角坐标系xOy 中，抛物线()02342≠-+-=a a ax ax y 与x 轴交于A ，B 两点（点A 在点B 左侧）．（1）当抛物线过原点时，求实数a 的值；（2）①求抛物线的对称轴；②求抛物线的顶点的纵坐标（用含a 的代数式表示）；（3）当AB ≤4时，求实数a 的取值范围．（西城区2017-2018学年度第一次模拟检测）6. 在平面直角坐标系xOy 中，抛物线G ：221y mx mx m =++- (m ≠0)与y 轴交于点C ，抛物线G 的顶点为D ，直线l ：1y mx m =+-(m ≠0) ．（1）当1m =时，画出直线l 和抛物线G ，并直接写出直线l 被抛物线G 截得的线段长；（2）随着m 取值的变化，判断点C ，D 是否都在直线l 上并说明理由；（3）若直线l 被抛物线G 截得的线段长不小于．．．2．，结合函数的图象，直接写出m 的 取值范围.（朝阳区2017-2018学年度第一次模拟检测）26. 在平面直角坐标系xOy 中，抛物线()2440y ax ax a =--≠与y 轴交于点A ，其对称轴与x 轴交于点B . （1）求点A ，B 的坐标；（2）若方程有两个不相等的实数根，且两根都在1，3之间（包括1，3），结合函数的图象，求a 的取值范围.（房山区2017-2018学年度第一次模拟检测）26. 23y ax bx 分别交x 轴于点A （－1,0），C （3，0），交y 轴于点B ，抛物线的对称轴与x轴相交于点D . 点P 为线段OB 上的点，点E 为线段AB 上的点，且PE ⊥AB.（1）求抛物线的表达式；（2）计算的值；()244=00ax ax a --≠（3）请直接写出的最小值为.（丰台区2017-2018学年度第一次模拟检测）26．在平面直角坐标系xOy中，抛物线的最高点的纵坐标是2．（1）求抛物线的对称轴及抛物线的表达式；（2）将抛物线在1≤x≤4之间的部分记为图象G1，将图象G1沿直线x = 1翻折，翻折后的图象记为G2，图象G1和G2组成图象G．过(0，b)作与y轴垂直的直线l，当直线l和图象G只有两个公共点时，将这两个公共点分别记为P1(x1，y1)，P2(x2，y2)，求b的取值范围和x1+ x2的值．（海淀区2017-2018学年度第一次模拟检测）26．在平面直角坐标系xOy中，已知抛物线22y x ax b=-+的顶点在x轴上，1(,)P x m，2(,)Q x m（12x x<）是此抛物线上的两点．（1）若1a=，①当m b=时，求1x，2x的值；②将抛物线沿y轴平移，使得它与x轴的两个交点间的距离为4，试描述出这一变化过程；（2）若存在实数c，使得11x c≤-，且27x c≥+成立，则m的取值范围是．（怀柔区2017-2018学年度第一次模拟检测）26.在平面直角坐标系xOy 中，抛物线y=nx 2-4nx+4n-1(n ≠0)，与x轴交于点C ，D(点C 在点D 的左侧)，与y 轴交于点A ．(1)求抛物线顶点M 的坐标；(2)若点A 的坐标为（0，3），AB ∥x 轴，交抛物线于点B ，求点B的坐标；(3)在(2)的条件下，将抛物线在B ，C 两点之间的部分沿y 轴翻折，翻折后的图象记为G ，若直线与图象G 有一个交点，结合函数的图象，求m 的取值范围． （平谷区2017-2018学年度第一次模拟检测） 26．在平面直角坐标系xOy 中，抛物线223y x bx =-+-的对称轴为直线x =2． （1）求b 的值；（2）在y 轴上有一动点P （0，m ），过点P 作垂直y 轴的直线交抛物线于点A （x 1，y 1），B （x 2 ，y 2），其中 12x x <．①当213x x -=时，结合函数图象，求出m 的值；②把直线PB 下方的函数图象，沿直线PB 向上翻折，图象的其余部分保持不变，得到一个新的图象W ，新图象W 在0≤x ≤5 时，44y -≤≤，求m 的取值范围．（石景山区2017-2018学年度第一次模拟检测）26．在平面直角坐标系中，将抛物线（）向右平移个单位长度后得到抛物线，点是抛物线的顶点． （1）直接写出点的坐标；（2）过点且平行于x 轴的直线l 与抛物线交于，两点．①当时，求抛物线的表达式；②若，直接写出m的取值范围．（延庆区2017-2018学年度第一次模拟检测）26．在平面直角坐标系xOy中，抛物线y=ax2-4ax+3a(a＞0) 与x轴交于A，B两点（A在B的左侧）．（1）求抛物线的对称轴及点A，B的坐标；（2）点C（t，3）是抛物线上一点，（点C在对称轴的右侧），过点C作x轴的垂线，垂足为点D．①当时，求此时抛物线的表达式；②当时，求t的取值范围．（顺义区2017-2018学年度第一次模拟检测）26．在平面直角坐标系xOy中，若抛物线2y x bx c=++顶点A的横坐标是-1，且与y轴交于点B（0，-1），点P为抛物线上一点．（1）求抛物线的表达式；（2）若将抛物线2y x bx c=++向下平移4个单位，点P平移后的对应点为Q．如果OP=OQ，求点Q的坐标．（通州区2017-2018学年度第一次模拟检测）。

函数操作专题东城区25. 如图，在等腰△ABC 中，AB =AC ,点D ,E 分别为BC ，AB 的中点，连接AD .在线段AD 上任取一点P ,连接PB ,PE .若BC =4,AD =6，设PD =x （当点P 与点D 重合时，x 的值为0），PB +PE =y .小明根据学习函数的经验，对函数y 随自变量x 的变换而变化的规律进行了探究. 下面是小明的探究过程，请补充完整：（1）通过取点、画图、计算，得到了x 与y 的几组值，如下表： （说明：补全表格时，相关数值保留一位小数）. （参考数据：1.414≈1.732≈2.236≈）(2) 建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；（3）函数y 的最小值为______________(保留一位小数)，此时点P 在图1中的位置为________________________.25.解：（1）4.5 . --------------------2分 （2）--------------------4分(3) 4.2，点P 是AD 与CE 的交点. --------------------6分 西城区25．如图，P 为⊙O 的直径AB 上的一个动点，点C 在»AB 上，连接PC ，过点A 作PC 的垂线交⊙O 于点Q ．已知5cm AB =，3cm AC =．设A 、P 两点间的距离为cm x ，A 、Q 两点间的距离为cm y ．BA某同学根据学习函数的经验，对函数y 随自变量x 的变化而变化的规律进行探究． 下面是该同学的探究过程，请补充完整：（1）通过取点、画图、测量及分析，得到了x 与y 的几组值，如下表：（说明：补全表格对的相关数值保留一位小数）（2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象．（3）结合画出的函数图象，解决问题：当2AQ AP =时，AP 的长度均为__________cm ．【解析】（1）（2）如图5图5（3）2.42． 海淀区25．在研究反比例函数1y x=的图象与性质时，我们对函数解析式进行了深入分析. 首先，确定自变量x 的取值范围是全体非零实数，因此函数图象会被y 轴分成两部分；其次，分析解析式，得到y 随x 的变化趋势：当0x >时，随着x 值的增大，1x的值减小，且逐渐接近于零，随着x 值的减小，1x的值会越来越大，由此，可以大致画出1y x=在0x >时的部分图象，如图1所示：利用同样的方法，我们可以研究函数y=的图象与性质. 通过分析解析式画出部分函数图象如图2所示.（1）请沿此思路在图2中完善函数图象的草图并标出此函数图象上横坐标为0的点A；（画出网格区域内的部分即可）（2）观察图象，写出该函数的一条性质：____________________；（3）若关于x(1)a x=-有两个不相等的实数根，结合图象，直接写出实数a的取值范围：__________.25．（1）如图：………………2分x>时，y随着x的增大而减小；（答案不唯一）………………4分（2）当1a≥. ………………6分（3）1丰台区25．如图，Rt△ABC中，∠ACB = 90°，点D为AB边上的动点（点D不与点A，点B重合），过点D作ED⊥CD交直线AC于点E．已知∠A = 30°，AB = 4cm，在点D由点A到点B运动的过程中，设AD = x cm，AE = y cm.CED小东根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．下面是小东的探究过程，请补充完整：（1）通过取点、画图、测量，得到了x与y的几组值，如下表：（说明：补全表格时相关数值保留一位小数）（2）在下面的平面直角坐标系xOy 中，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；（3）结合画出的函数图象，解决问题：当AE =12AD 时，AD 的长度约为 cm ． 25．解：（1）1.2； ………………………2分 （2）如右图； ………………………4分 （3）2.4或3.3 ………………………6分 石景山区25．如图，半圆O 的直径5cm AB =，点M 在AB 上且1cm AM =，点P 是半圆O 上的动点，过点B 作BQ PM ⊥交PM （或PM 的延长线）于点Q .设cm PM x =，cm BQ y =.（当点P与点A或点B重合时，y的值为0）小石根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究.下面是小石的探究过程，请补充完整：（1）通过取点、画图、测量，得到了x与y的几组值，如下表：（2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；（3）结合画出的函数图象，解决问题：当BQ与直径AB所夹的锐角为60 时，PM的长度约为cm.25.解：（1）4； 0. ………………2分（2）………………4分（3）1.1或3.7 . ………………6分朝阳区25.如图，AB是⊙O的直径，AB=4cm，C为AB上一动点，过点C的直线交⊙O于D、E两点，且∠ACD=60°，DF⊥AB于点F，EG⊥AB于点G，当点C在AB上运动时，设AF=x cm，DE=y cm （当x的值为0或3时，y的值为2），探究函数y随自变量x的变化而变化的规律.（1）通过取点、画图、测量，得到了x与y的几组对应值，如下表：（2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；（3）结合画出的函数图象，解决问题：点F与点O重合时，DE长度约为 cm （结果保留一位小数）．25. 解：本题答案不唯一，如：（1）………………………………………………1分（2）…………………………………………4分（3）3.5．……………………… 6分燕山区26．已知y是x的函数，自变量x的取值范围是x≠0的全体实数，下表是y与x的几组对应值．小华根据学习函数的经验，利用上述表格所反映出的y与x之间的变化规律，对该函数的图象与性质进行了探究．下面是小华的探究过程，请补充完整：(1)从表格中读出，当自变量是-2时，函数值是；（2）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；(3)在画出的函数图象上标出x=2时所对应的点，并写出m = (4)结合函数的图象，写出该函数的一条性质：____________ ．26.解：(1)当自变量是-2时，函数值是 32…………………………………1′（2）如图,该函数的图象； (略) …………………………………3′(3)标出x=2时所对应的点 …………………………………4′ 且m= …………………………………5′(4)写出该函数的性质(一条即可)：_____ ． …………………………………7′ 门头沟区25.在正方形ABCD 中,4AB cm = AC 为对角线，AC 上有一动点P ,M 是AB 边的中点，连接PM 、PB , 设A 、P 两点间的距离为xcm ，PM PB +长度为ycm .D A小东根据学习函数的经验，对函数y 随自变量x 的变化而变化的规律进行了探究． 下面是小东的探究过程，请补充完整：（1）通过取点、画图、测量，得到了x 与y 的几组值，如下表：（说明：补全表格时相关数值保留一位小数）（2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象．（3）结合画出的函数图象，解决问题：PM PB 的长度最小值约为__________cm ．25.（本小题满分6分）（1）5 ……………………………………………………………………1分（2）坐标系正确……………………………………………………3分描点正确……………………………………………………4分连线正确……………………………………………………5分（3）4.5 ……………………………………………………………………6分大兴区25.如图，在△ABC中，AB=4.41cm,BC=8.83cm，P是BC上一动点，连接AP，设P，C两点间的距离为x cm，P，A两点间的距离为y cm．（当点P与点C重合时，x的值为0）小东根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．下面是小东的探究过程，请补充完整:（1）通过取点、画图、测量，得到了x与y的几组值，如下表：（说明：补全表格时相关数值保留一位小数）（2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；（3）结合画出的函数图象，解决问题：当PA=PC时，PC的长度约为cm．（结果保留一位小数）25.（1）4.6 ………………………………………………………………1分（答案不唯一）（2）………………………………………………………………4分(3) 4.4 ………………………………………………………………6分（答案不唯一）平谷区25．如图，在△ABC中，∠C=60°，BC=3厘米，AC=4厘米，点P从点B出发，沿B→C→A 以每秒1厘米的速度匀速运动到点A．设点P的运动时间为x秒，B、P两点间的距离为y 厘米．B小新根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．下面是小新的探究过程，请补充完整：（1）通过取点、画图、测量，得到了x与y的几组值，如下表：经测量m的值是（保留一位小数）．（2）建立平面直角坐标系，描出表格中所有各对对应值为坐标的点，画出该函数的图象；（3）结合画出的函数图象，解决问题：在曲线部分的最低点时，在△ABC中画出点P所在的位置．25．解：（1）3.0； (1)（2）如图所示；··························4（3）如图 (5)怀柔区25、如图，在等边△ABC中， BC=5cm，点D是线段BC上的一动点，连接AD，过点D作DE⊥AD，垂足为D，交射线AC与点E．设BD为x cm，CE为y cm．小聪根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究.下面是小聪的探究过程，请补充完整：(1)通过取点、画图、测量，得到了与y的几组值，如下表：(说明：补全表格上相关数值保留一位小数)(2)建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；(3)结合画出的函数图象，解决问题：当线段BD是线段CE长的2倍时，BD的长度约为________cm.25.(1)约 1.1； (1)分(2)如图：xy –1123456–1123456O ……………………………………………………………4分(3)约 1.7. ………………………………………………………………………………………5分 延庆区25．如图，点P 是以O 为圆心，AB 为直径的半圆上的动点，AB =6cm ，设弦AP 的长为x cm ，△APO 的面积为y cm 2，（当点P 与点A 或点B 重合时，y 的值为0）．A B小明根据学习函数的经验，对函数y 随 自变量x 的变化而变化的规律进行了探究． 下面是小明的探究过程，请补充完整；（1）通过取点、画图、测量、计算，得到了x 与y 的几组值，如下表：那么m = ；（保留一位小数）（2）建立平面直角坐标系，描出以表中各组对应值为坐标的点，画出该函数图象．（3）结合函数图象说明，当△APO 的面积是4时，则AP 的值约为 ．（保留一位小数）25．(1)m = 约4.3 ； ……1分(2)（画此函数图象时要体现出x 约为4.2时，y 有最大值，为4.5） ……4分 (3) 3.1或是5.1 ……6分-16123454321O顺义区25．如图，P是半圆弧AB上一动点，连接PA、PB，过圆心O作OC∥BP交PA于点C，连接CB．已知AB=6cm，设O，C两点间的距离为x cm，B，C两点间的距离为y cm．A小东根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行探究．下面是小东的探究过程，请补充完整：(1)通过取点、画图、测量，得到了x与y的几组值，如下表：(说明：补全表格时相关数据保留一位小数)(2)建立直角坐标系，描出以补全后的表中各对应值为坐标的点，画出该函数的图象；(3)结合画出的函数图象，解决问题：直接写出△OBC周长C的取值范围是．25．(1)4.6．……………………………………………………………………… 1分12(2)…………………………………………………………………………… 3分(3)6＜C ＜12． …………………………………………………………… 5分。

解不等式组专题东城区18． 解不等式组4+6,23x x x x ⎧⎪+⎨⎪⎩＞≥， 并写出它的所有整数解.18. 解：4+6,23x x x x ⎧⎪⎨+⎪⎩①②＞≥，由①得，-x ＞2，------------------1分 由②得，1x ≤， ------------------2分 ∴不等式组的解集为-1x 2＜≤.所有整数解为-1, 0, 1. ---------------------5分西城区18．解不等式组3(2)4112x x x ++⎧⎪⎨-<⎪⎩≥，并求该不等式组的非负整数解．【解析】解①得，364x x ++≥，22x -≥，1x -≥， 解②得，12x -<，3x <， ∴原不等式解集为13x -<≤， ∴原不等式的非负整数解为0，，2．海淀区18．解不等式组：()5331,263.2x x x x +>-⎧⎪⎨-<-⎪⎩18.解：() 5331, 263. 2x x x x +>-⎧⎪⎨-<-⎪⎩①②解不等式①，得3x >-. …2分解不等式②，得2x <. ………4分 所以 原不等式组的解集为32x -<<. ………5分丰台区18．解不等式组：341,51 2.2x x x x ≥-⎧⎪⎨->-⎪⎩18．解：解不等式①，得1x ≤， ……………………2分解不等式②，得1x >-. ……………………4分∴原不等式组的解集是11x -<≤．………5分石景山区18．解不等式组：3(1)45622x x x x +>++<⎧⎪⎨⎪⎩，． 18．解：原不等式组为3(1)45,62.2x x x x +>++<⎧⎪⎨⎪⎩解不等式①，得2x <-． ………………2分 解不等式②，得2x <． ………………4分 ∴原不等式组的解集为<2x -． ………………5分朝阳区18. 解不等式组 ：⎪⎩⎪⎨⎧>-->-.2216),3(21x x x x18. 解：原不等式组为⎪⎩⎪⎨⎧>-->-.2216),3(21x x x x① ②解不等式①，得 5<x . ………………………………………2分解不等式②，得 21>x .………………………………………………4分 ∴ 原不等式组的解集为521<<x . …………………………………5分 燕山区18．解不等式组：⎩⎪⎨⎪⎧x －32<1，2（x ＋1）≥x－1.18．解：由（1）得，x-3<2X<5 ……………………….2′（2） 得 2x+2≥x-1x ≥-3 ……………………….4′所以不等式组的解是-3≤x ＜5……………………….5′门头沟区18. 解不等式组：1031+1.xx x ⎧-<⎪⎨⎪-⎩，≤3(）18．（本小题满分5分）解不等式①得，x ＜3， …………………………………………2分 解不等式②得，x ≥﹣2， ………………………………4分 所以，不等式组的解集是﹣2≤x ＜3． ………………5分大兴区17.解不等式组：⎪⎩⎪⎨⎧>++≤+x x x x 2274)3(2 并写出它的所有整数解.17. 解：⎪⎩⎪⎨⎧>++≤+xx x x 2274)3(2 由①，得21-≥x . ………………………………………………………1分由②，得2<x . …………………………………………………………2分 ∴原不等式组的解集为221<≤-x . ………………………………………4分它的所有整数解为0，1. …………………………………………………5分平谷区18．解不等式组3(1)45,513x x x x -≥-⎧⎪-⎨->⎪⎩，并写出它的所有整数解．．．． 18．解：3(1)4553 1x x x x -≥-⎧⎪⎨-->⎪⎩①② 解不等式①，得 x≤2． ....................... 1 解不等式②，得 x ＞-1． ...................... 3 ∴原不等式组的解集为12x -<≤． ................. 4 ∴适合原不等式组的整数解为0,1,2．.. (5)怀柔区18.解不等式组:()⎪⎩⎪⎨⎧<+-<-.1213,213x x x x18.解：由①得：3x < . ………………………………………………………………………2分由②得：9x >- …………………………………………………………………………4分 原不等式组的解集为93x -<< ………………………………………………………5分延庆区① ②18．解不等式组：523(2)53.2x x x x -<+⎧⎪⎨+≤⎪⎩， 并写出它的所有整数解．18．解：由①得，x<4． ……1分 由②得，x≥1 ． ……3分∴ 原不等式组的解集为1≤x<4． ……4分 ∴ 原不等式组的所有整数解为1，2，3． ……5分顺义区18．解不等式组：()7+1,2315 1.x x x x +⎧≥-⎪⎨⎪+<-⎩18．解不等式组：()7+12315x x x x +⎧≥-⎪⎨⎪+<-⎩解：解不等式①得 x ≥3- ……………………………………………………………2分 解不等式②得 2x > ………………………………………………………………4分 不等式组的解集是 2x > …………………………………………………………5分。

目录类型1：函数图像与运动变化过程 (2)类型2：坐标系与图形变换 (6)类型3：函数探究 (8)类型4：二次函数 (21)（1）二次函数图像与性质基础 (21)（2）二次函数综合 (22)类型5：一次函数、反比例函数 (27)（1）反比例、一次函数基础 (27)（2）反比例、一次函数综合 (28)类型1：函数图像与运动变化过程1. （18通州一模10）如图是我区某一天内的气温变化图，结合该图给出的信息写出一个正确的结论：__________________________________________________2.（18平谷一模7）“龟兔赛跑”是同学们熟悉的寓言故事．如图所示，表示了寓言中的龟、兔的路程S和时间t的关系（其中直线段表示乌龟，折线段表示兔子）．下列叙述正确的是A．赛跑中，兔子共休息了50分钟B．乌龟在这次比赛中的平均速度是0.1米/分钟C．兔子比乌龟早到达终点10分钟D．乌龟追上兔子用了20分钟3.（18延庆一模8）某游泳池长25米，小林和小明两个人分别在游泳池的A，B两边，同时朝着另一边游泳，他们游泳的时间为（秒），其中0180t≤≤，到A边距离为y（米），图中的实线和虚线分别表示小林和小明在游泳过程中y与t的对应关系．下面有四个推断：①小明游泳的平均速度小于小林游泳的平均速度；②小明游泳的距离大于小林游泳的距离；③小明游75米时小林游了90米游泳；④小明与小林共相遇5次；25mA B小林小明25小林小明180150120906030y/米t/秒其中正确的是A．①②B．①③ C.③④D．②④4. （18石景山一模7）甲、乙两地相距300千米，一辆货车和一辆轿车分别从甲地开往乙地（轿车的平均速度大于货车的平均速度），如图线段OA和折线BCD分别表示两车离甲地的距离y（单位：千米）与时间x（单位：小时）之间的函数关系．则下列说法正确的是（）B．轿车在行驶过程中进行了提速C．货车出发3小时后，轿车追上货车D．两车在前80千米的速度相等5.（18房山一模8）小宇在周日上午8：00从家出发，乘车1小时到达某活动中心参加实践活动．11：00时他在活动中心接到爸爸的电话，因急事要求他在12：00前回到家，他即刻按照来活动中心时的路线，以5千米/时的平均速度快步返回．同时，爸爸从家沿同一路线开车接他，在距家20千米处接上了小宇，立即保持原来的车速原路返回．设小宇离家 x 小时后，到达离家y 千米的地方，图中折线OABCD 表示 y 与 x 之间的函数关系．下列叙述错误．．的是（ ） A ．活动中心与小宇家相距22千米 B.小宇在活动中心活动时间为2小时 C.他从活动中心返家时，步行用了0.4小时 D.小宇不能在12：00前回到家6.（18东城一模8）如图1是一座立交桥的示意图（道路宽度忽略不计）， A 为入口， F ，G 为出口，其中直行道为AB ，CG ，EF ，且AB =CG =EF ；弯道为以点O 为圆心的一段弧，且»BC ， »CD ，»DE所对的圆心角均为90°．甲、乙两车由A 口同时驶入立交桥，均以10m/s 的速度行驶，从不同出口驶出. 其间两车到点O 的距离y （m ）与时间x (s)的对应关系如图2所示．结合题目信息，下列说法错误．．的是（ ）A. 甲车在立交桥上共行驶8sB. 从F 口出比从G 口出多行驶40mC. 甲车从F 口出，乙车从G 口出D. 立交桥总长为150m7.（18丰台一模8）如图1，荧光屏上的甲、乙两个光斑（可看作点）分别从相距8cm 的A ，B 两点同时开始沿线段AB 运动，运动过程中甲光斑与点A 的距离S 1(cm)与时间t (s)的函数关系图象如图2，乙光斑与点B 的距离S 2(cm)与时间t (s)的函数关系图象如图3，已知甲光斑全程的平均速度为1.5cm/s ，且两图象中△P 1O 1Q 1≌△P 2Q 2O 2．下列叙述正确的是（ ）B A乙 甲8cmA.甲光斑从点A 到点B 的运动速度是从点B 到点A 的运动速度的4倍B.乙光斑从点A 到B 的运动速度小于1.5cm/sC.甲乙两光斑全程的平均速度一样D.甲乙两光斑在运动过程中共相遇3次图1图3图28.（18门头沟一模8）甲、乙两人约好步行沿同一路线同一方向在某景点集合，已知甲乙二人相距660米，二人同时出发，走了24分钟时，由于乙距离景点近，先到达等候甲，甲共走了30分钟也到达了景点与乙相遇.在整个行走过程中，甲、乙两人均保持各自的速度匀速行走，甲、乙两人相距的路程y （米）与甲出发的时间x （分钟）之间的关系如图所示，下列说法错误的是（ ）A ．甲的速度是70米/分；B ．乙的速度是60米/分；C ．甲距离景点2100米；D ．乙距离景点420米.9.（18通州一模8）如图， 点O 为正六边形对角线的交点，机器人置于该正六边形的某顶点处.柱柱同学操控机器人以每秒1个单位长度的速度在图1中给出的线段路径上运行，柱柱同学将机器人运行时间设为t 秒，机器人到点A 距离设为y ，得到函数图象如图2.通过观察函数图象，可以得到下列推断：①该正六边形的边长为1； ②当3t =时，机器人一定位于点O ； ③机器人一定经过点D ； ④机器人一定经过点E ； 其中正确的有（ ）.A ．①④B. ①③C. ①②③D. ②③④10. （18燕山一模8）小带和小路两个人开车从 A 城出发匀速行驶至 B 城.在整个行驶过程中，小带和小路两人的车离开 A 城的距离 y （千米）与行驶的时间 t (小时)之间的函数关系如图所示。

解四边形专题东城区21．如图，已知四边形ABCD 是平行四边形，延长BA 至点E ，使AE = AB ，连接DE ，AC . （1）求证：四边形ACDE 为平行四边形; （2）连接CE 交AD 于点O . 若AC=AB =3，1cos 3B =，求线段CE 的长.21.(1) 证明：∵平行四边形ABCD ， ∴=AB DC ，AB DC ∥.∵AB =AE ，∴=AE DC ，AE DC ∥.∴四边形ACDE 为平行四边形. -------------------2分 (2) ∵=AB AC ， ∴=AE AC .∴平行四边形ACDE 为菱形. ∴AD ⊥CE .∵AD BC ∥， ∴BC ⊥CE.在Rt △EBC 中，BE =6, 1cos 3BC B BE ==, ∴=2BC .根据勾股定理，求得BC 分 西城区21．如图，在ABD △中，ABD ADB ∠=∠，分别以点B ，D 为圆心，AB 长为半径在BD 的右侧作弧，两弧交于点C ，分别连接BC ，DC ，AC ，记AC 与BD 的交点为O ． （1）补全图形，求AOB ∠的度数并说明理由;（2）若5AB =，3cos 5ABD ∠=，求BD 的长．BDA【解析】（1）补全的图形如图所示．90AOB ∠=︒． 证明：由题意可知BC AB =，DC AB =， ∵在ABD △中，ABD ADB ∠=∠， ∴AB AD =，∴BC DC AD AB ===， ∴四边形ABCD 为菱形， ∴AC BD ⊥， ∴90AOB ∠=︒．（2）∵四边形ABCD 为菱形， ∴OB OD =．在Rt ABO △中，90AOB ∠=︒，5AB =，3cos 5ABD ∠=，∴cos 3OB AB ABD =⋅∠=， ∴26BD OB ==．ABCDO海淀区21．如图，□ABCD 的对角线,AC BD 相交于点O ，且AE∥BD ，BE∥AC ，OE = CD . （1）求证：四边形ABCD 是菱形；（2）若AD = 2，则当四边形ABCD 的形状是__________时，四边形AOBE 的面积取得最大值是_______.C B EOAD21．（1）证明：∵AE BD ∥，BE AC ∥，∴四边形AEBO 是平行四边形. ………………1分 ∵四边形ABCD 是平行四边形，∴DC AB =. ∵OE CD =, ∴OE AB =.∴平行四边形AEBO 是矩形. ………………2分 ∴90BOA ∠=︒. ∴AC BD ⊥.∴平行四边形ABCD 是菱形. ………………3分 (2) 正方形； ………………4分2. ………………5分丰台区21．已知：如图，菱形ABCD ，分别延长AB ，CB 到点F ，E ，使得BF = BA ，BE = BC ，连接AE ，EF ，FC ，CA ．（1）求证：四边形AEFC 为矩形；（2）连接DE 交AB 于点O ，如果DE ⊥AB ，AB = 4，求DE 的长．ABCEDF21．（1）证明：∵BF =BA ，BE =BC ，∴四边形AEFC 为平行四边形. ………………………1分 ∵四边形ABCD 为菱形， ∴BA =BC .∴BE =BF .∴BA + BF = BC + BE ，即AF =EC .∴四边形AEFC 为矩形. ………………………2分（2）解：连接DB .由（1）知，AD ∥EB ，且AD =EB . ∴四边形AEBD 为平行四边形∵DE ⊥AB ，∴四边形AEBD 为菱形.∴AE =EB ，AB =2AG ，ED =2EG . ………………………4分 ∵矩形ABCD 中，EB =AB ，AB=4， ∴AG =2，AE =4. ∴Rt△AEG 中，EG=∴ED=分 （其他证法相应给分）石景山区21．如图，在四边形ABCD 中，90A BCD ∠=∠=°，BC CD ==，CE AD ⊥于点E ． （1）求证：AE CE =；（2）若tan 3D =，求AB 的长．21．（1）证明：（法一）过点B 作BH ⊥CE 于H ，如图1． ∵CE ⊥AD ，∴∠BHC ＝∠CED ＝90°，190D ∠+∠=︒． ∵∠BCD ＝90°， ∴1290∠+∠=︒， ∴2D ∠=∠． 又BC ＝CD∴BHC △≌CED △． ∴BH CE =．∵BH ⊥CE ，CE ⊥AD ，∠A ＝90°， ∴四边形ABHE 是矩形， ∴AE BH =．∴AE CE =． ………………3分 （法二）过点C 作CH ⊥AB 交AB 的延长线于H ．图略，证明略． （2）解： ∵四边形ABHE 是矩形， ∴AB HE =．∵在Rt CED △中，tan 3CE D DE==,设,3DE x CE x ==，∴CD ==． ∴2x =．∴2DE =,6CE =． ………………4分 ∵2CH DE ==．∴624AB HE ==-=． ………………5分 朝阳区21. 如图，在△ABC 中，D 是AB 边上任意一点，E 是BC 边中点，过点C作AB 的平行线，交DE 的延长线于点F ，连接BF ，CD ． （1）求证：四边形CDBF 是平行四边形； （2）若∠FDB =30°，∠ABC =45°，BC =，求DF 的长．21.（1）证明：∵CF ∥AB ，∴∠ECF ＝∠EBD . ∵E 是BC 中点， ∴CE ＝BE .∵∠CEF ＝∠BED ， ∴△CEF ≌△BED . ∴CF ＝BD .∴四边形CDBF 是平行四边形. ………………………2分（2）解：如图，作EM ⊥DB 于点M ，∵四边形CDBF 是平行四边形，BC ＝24，∴2221==BC BE ，DE DF 2=. 在Rt △EMB 中，2sin =∠⋅=ABC BE EM . ……………………3分在Rt △EMD 中，42==EM DE . …………………4分∴DF ＝8. ………………………………………………………5分燕山区23． 如图，在△ABC 中，D,E 分别是AB,AC 的中点，BE=2DE ,延长DE 到点F ，使得EF=BE,连接CF ． （1）求证：四边形BCFE 是菱形；（2）若∠BCF =120°，CE=4，求菱形BCFE 的面积．23. （1）证明：∵点 D,E, 是 AB,AC 中点∴DE ∥BC, DE=12BC ……………………….1′A ABCD E F又BE=2DE,即DE=12BE ∴BC=BE 又EF=BE ∴EF ∥BC, EF=BC∴四边形BCFE 是平行四边形……………………….2′ 又EF=BE∴四边形BCFE 是菱形 ……………………….3′ （2）∵四边形BCFE 是菱形 ∴BC=BE 又∠BCF =120° ∴∠BCE=60°∴△BCE 是等边三角形∴连结BF 交EC 于点O ．∴BF ⊥EC在Rt △BOC 中，BO=32242222=-=-OC BC ……………………….4′322322121=⨯⨯=⋅⋅=∆OC BO S BOC∴∴ ……………………….5′门头沟区21.在矩形ABCD 中，连接AC ,AC 的垂直平分线交AC 于点O ,分别交AD 、BC 于点E 、F ，连接CE 和AF ．（1）求证：四边形AECF 为菱形；（2）若AB =4，BC =8，求菱形AECF 的周长．21. （1）证明：∵EF 是AC 的垂直平分线，∴AO =OC ，∠AOE =∠COF =90°，……………………1分 ∵四边形ABCD 是矩形， ∴AD ∥BC ，∴∠EAO =∠FCO ， 在△AEO 和△CFO 中，∵∠EAO =∠FCO ，AO =CO ，∠AOE =∠COF ， ∴△AEO ≌△CFO （ASA ），∴OE =OF ． ……………2分 又∵OA =OC ，∴四边形AECF 是平行四边形，又∵EF ⊥AC ，∴平行四边形AECF 是菱形；……………3分（2）设AF =x ，∵EF 是AC 的垂直平分线，∴AF =CF =x ，BF =8﹣x ， ………………………………………4分在Rt △ABF 中，由勾股定理得：AB 2+BF 2=AF 2，42+（8﹣x ）2=x 2，38324=⨯=BCFE S 菱形AB解得 x =5，∴AF =5，∴菱形AECF 的周长为20．…………………5分大兴区21. 如图，矩形ABCD 的对角线AC 、BD 交于点O ，且DE=O C ，CE=O D ． （1）求证：四边形OCED 是菱形；（2）若∠BAC ＝30°，AC ＝4，求菱形OCED 的面积． 21.（1）证明：∵DE =OC ，CE =OD ，∴四边形OCED 是平行四边形 ………………………………1分∵矩形ABCD ，∴AC =BD ，OC =12AC ，OD =12BD .∴OC =OD .∴平行四边形OCED 是菱形 ………………………………2分（2）解：在矩形ABCD 中，∠ABC =90°，∠BAC =30°，AC ＝4，∴BC =2.∴AB =DC =.…………………………………………………3分 连接OE ，交CD 于点F . ∵四边形OCED 为菱形， ∴F 为CD 中点. ∵O 为BD 中点，∴OF =12BC =1.∴OE ＝2OF ＝2 …………………………………………………4分∴S 菱形OCED ＝12OE ·CD =12×2×＝…………………………………………………5分平谷区21．如图，在平面直角坐标系xOy 中，函数()0ky k x=≠的图象与直线y =x +1交于点A （1，a ）．（1）求a ，k 的值； （2）连结OA ，点P 是函数()0ky k x=≠上一点，且满足OP=OA ，直接写出点P 的坐标（点A 除外）．21．解：（1）∵直线y =x +1经过点A （1，a ），∴a =2． ···························· 1 ∴A （1,2）．∵函数()0ky k x=≠的图象经过点A （1，2）， ∴k =2． (2)（2）点P 的坐标（2,1），（-1，-2），（-2，-1）． (5)怀柔区21.直角三角形ABC 中，∠BAC=90°，D 是斜边BC 上一点，且AB=AD ，过点C 作CE⊥AD，交AD 的延长线于点E ，交AB 延长线于点F. (1)求证：∠ACB=∠DCE；(2)若∠BAD=45°，AF =，过点B 作BG⊥FC 于点G ，连接DG ．依题意补全图形，并求四边形ABGD 的面积．21.(1)∵AB=AD，∴∠ABD=∠ADB，………………………………1分 ∵∠ADB=∠CDE，∴∠ABD=∠CDE. ∵∠BAC=90°，∴∠ABD+∠ACB=90°. ∵CE⊥AE，∴∠DCE+∠CDE=90°.∴∠ACB=∠DCE. …………………………………2分 （2）补全图形,如图所示: …………………………3分 ∵∠BAD=45°, ∠BAC=90°,∴∠BAE=∠CAE=45°, ∠F=∠ACF=45°, ∵AE⊥CF, BG⊥CF,∴AD∥BG.∵BG⊥CF, ∠BAC=90°，且∠ACB=∠DCE, ∴AB=BG.∵AB=AD，∴BG=AD.∴四边形ABGD 是平行四边形. ∵AB=AD∴平行四边形ABGD 是菱形.………………4分设AB=BG=GD=AD=x ，∴BF=2BG=2x.∴AB+BF=x+2x=2+2. ∴x=2， 过点B 作BH⊥AD 于H.∴BH=22AB=1. ∴S 四边形ABDG =AD×BH=2. ……………………………………………………………………5分 延庆区21．如图，Rt△ABC 中，∠ABC =90°，点D ，F 分别是AC ，AB 的中点，CE ∥DB ，BE ∥DC ． （1）求证：四边形DBEC 是菱形；（2）若AD =3， DF =1，求四边形DBEC 面积.FEDCBA21．（1）在Rt△ABC 中，∵CE //DC ，BE //DC∴四边形DBEC 是平行四边形∵D 是AC 的中点，∠ABC =90°∴BD =DC ……1分 ∴四边形DBEC 是菱形 ……2分 （2）∵F 是AB 的中点∴BC =2DF =2,∠AFD =∠ABC =90° 在Rt△AFD 中,……3分 ∴……4分……5分顺义区21．如图，四边形ABCD 中，AD ∥BC ，∠A =90°，BD =BC ，点E 为CD 的中点，射线BE 交AD的延长线于点F ，连接CF ．（1）求证：四边形BCFD 是菱形；（2）若AD =1，BC =2，求BF 的长．21．（1）证明：∵BD=BC ，点E 是CD 的中点，F EA BCD∴∠1=∠2． …………………………………………………… 1分 ∵AD ∥BC ， ∴∠2=∠3．∴∠1=∠3．…………………………… 2分 ∴BD=DF ． ∵BD=BC ， ∴DF=BC ． 又∵DF ∥BC ，∴四边形BCFD 是平行四边形． ∵BD=BC ，∴□BCFD 是菱形． …………………………………………………… 3分 （2）解：∵∠A =90︒，AD =1，BD =BC =2，∴AB == ∵四边形BCFD 是菱形，∴DF =BC =2． ………………………………………………………… 4分 ∴AF =AD+DF =3．∴BF == 5分321FEABCD。

二次函数（含代数综合题）（1）二次函数图像与性质基础1.（18朝阳毕业9）在平面直角坐标系xOy 中，二次函数172++=x x y 的图象如图所示，则方程0172=++x x 的根的情况是A.有两个相等的实数根B.有两个不相等的实数根C.没有实数根D.无法判断2.（18朝阳毕业13）抛物线y =x 2-6x +5的顶点坐标为 ．3.（18大兴一模11）请写出一个开口向下，并且对称轴为直线x =1的抛物线的表达式y =4.（18东城一模2） 当函数()212y x =--的函数值y 随着x 的增大而减小时，x 的取值范围是A ．x ＞0B ．x ＜1C ．1x ＞D ．x 为任意实数5. （18燕山一模12）写出经过点（0，0），（-2，0）的一个二次函数的解析式（写一个即可） 6.（18顺义一模15）如图，在边长为6cm 的正方形ABCD 中，点E 、F 、G 、H 分别从点A 、B 、C 、D 同时出发，均以1cm/s 的速度向点B 、C 、D 、A 匀速运动，当点E 到达点B 时，四个点同时停止运动，在运动过程中，当运动时间为 s 时，四边形EFGH 的面积最小，其最小值是 cm 2．（2）二次函数综合1.（18平谷一模26）在平面直角坐标系xOy 中，抛物线223y x bx =-+-的对称轴为直线x =2．（1）求b 的值；（2）在y 轴上有一动点P （0，m ），过点P 作垂直y 轴的直线交抛物线于点A （x 1，y 1），B （x 2 ，y 2），其中 12x x <．①当213x x -=时，结合函数图象，求出m 的值；②把直线PB 下方的函数图象，沿直线PB 向上翻折，图象的其余部分保持不变，得到一个新的图象W ，新图象W 在0≤x ≤5 时，44y -≤≤，求m 的取值范围．HG FE D CB A2.（18延庆一模26）在平面直角坐标系xOy 中，抛物线y =ax 2-4ax +3a (a ＞0)与x 轴交于A ，B 两点（A 在B的左侧）．（1）求抛物线的对称轴及点A ，B 的坐标；（2）点C （t ，3）是抛物线243(0)y ax ax a a =-+>上一点，（点C 在对称轴的右侧），过点C 作x轴的垂线，垂足为点D ．①当CD AD =时，求此时抛物线的表达式； ②当CD AD >时，求t 的取值范围．3. （18石景山一模26）在平面直角坐标系xOy 中，将抛物线21G y mx =+：0m ≠）单位长度后得到抛物线2G ，点A 是抛物线2G 的顶点． （1）直接写出点A 的坐标；（2）过点0（且平行于x 轴的直线l 与抛物线2G 交于B ，C 两点． ①当=90BAC ∠°时，求抛物线2G 的表达式；②若60120BAC <∠<°°，直接写出m 的取值范围．4.（18房山一模26）抛物线2y ax bx =+-x 轴于点A （－1,0），C （3，0），交y 轴于点B ，抛物线的对称轴与x 轴相交于点D . 点P 为线段OB 上的点，点E 为线段AB 上的点，且PE ⊥AB.（1）求抛物线的表达式；（2）计算PEPB的值；（3）请直接写出12PB +PD 的最小值为 .5. （18西城一模26）在平面直角坐标系xOy 中，抛物线G ：221(0)y mx mx m m =++-≠与y 轴交于点C ，抛物线G 的顶点为D ，直线l ：1(0)y mx m m =+-≠．（1）当1m =时，画出直线l 和抛物线G ，并直接写出直线l 被抛物线G 截得的线段长． （2）随着m 取值的变化，判断点C ，D 是否都在直线l 上并说明理由．（3）若直线l 被抛物线G 截得的线段长不小于2，结合函数的图象，直接写出m 的取值范围．x6.（18朝阳毕业26）抛物线c bx x y ++=2的对称轴为直线x =1，该抛物线与x 轴的两个交点分别为A 和B ，与 y 轴的交点为C ，其中A （-1，0）.（1）写出B 点的坐标 ；（2）若抛物线上存在一点P ，使得△POC 的面积是△BOC 的面积的2倍，求点P 的坐标；（3）点M 是线段BC 上一点，过点M 作x 轴的垂线交抛物线于点D ，求线段MD 长度的最大值.7.（18怀柔一模26）在平面直角坐标系xOy 中，抛物线y=nx 2-4nx+4n-1(n ≠0)，与x 轴交于点C ，D(点C在点D 的左侧)，与y 轴交于点A ． （1）求抛物线顶点M 的坐标； （2）若点A 的坐标为（0，3），AB ∥x 轴，交抛物线于点B ，求点B 的坐标；（3）在（2）的条件下，将抛物线在B ，C 两点之间的部分沿y 轴翻折，翻折后的图象记为G ，若直线与图象G 有一个交点，结合函数的图象，求m 的取值范围．m x y +=218.（18海淀一模26）在平面直角坐标系xOy 中，已知抛物线22y x ax b =-+的顶点在 x 轴上，1(,)P x m ，2(,)Q x m （12x x <）是此抛物线上的两点．（1）若1a =，①当m b =时，求1x ，2x 的值；②将抛物线沿y 轴平移，使得它与x 轴的两个交点间的距离为4，试描述出这一变化过程； （2）若存在实数c ，使得11x c ≤-，且27x c ≥+成立，则m 的取值范围是 ．9.（18朝阳一模26）在平面直角坐标系xOy 中，抛物线()2440y ax ax a =--≠与y 轴交于点A ，其对称轴与x 轴交于点B .（1）求点A ，B 的坐标；（2）若方程有两个不相等的实数根，且两根都在1，3之间（包括1，3），结合函数的图象，求a 的取值范围.()244=00ax ax a --≠10.（18东城一模26）在平面直角坐标系xOy 中，抛物线()02342≠-+-=a a ax ax y 与x 轴交于A ，B两点（点A 在点B 左侧）．（1）当抛物线过原点时，求实数a 的值； （2）①求抛物线的对称轴；②求抛物线的顶点的纵坐标（用含a 的代数式表示）； （3）当AB ≤4时，求实数a 的取值范围．11.（18丰台一模26）在平面直角坐标系xOy 中，抛物线243y ax ax a =-+的最高点的纵坐标是2．（1）求抛物线的对称轴及抛物线的表达式； （2）将抛物线在1≤x ≤4之间的部分记为图象G 1，将图象G 1沿直线x = 1翻折，翻折后的图象记为G 2，图象G 1和G 2组成图象G ．过(0，b )作与y 轴垂直的直线l ，当直线l 和图象G 只有两个公共点时，将这两个公共点分别记为P 1(x 1，y 1)，P 2(x 2，y 2)，求b 的取值范围和x 1 + x 2的值．12.（18门头沟一模26）有一个二次函数满足以下条件：①函数图象与x 轴的交点坐标分别为(1,0)A ，22(,)B x y (点B 在点A 的右侧)；②对称轴是3x =； ③该函数有最小值是-2.（1）请根据以上信息求出二次函数表达式；（2）将该函数图象2x x ＞的部分图象向下翻折与原图象未翻折的部分组成图象“G ”，平行于x 轴的直线与图象“G ”相交于点33(,)C x y 、44(,)D x y 、55(,)E x y （345x x x <<），结合画出的函数图象求345x x x ++的取值范围.13.（18大兴一模26）在平面直角坐标系xOy 中,抛物线22(31)2(0)y x m x m m m =-+++>，与y 轴交于点C ，与x 轴交于点A 1(,0)x ,B 2(,0)x ，且12x x <. （1）求1223-+x x 的值；（2）当m=1223-+x x 时，将此抛物线沿对称轴向上平移n 个单位，使平移后得到的抛物线顶点落在△ABC 的内部（不包括△ABC 的边），求n 的取值范围（直接写出答案即可）．14.（18顺义一模26）在平面直角坐标系xOy 中，若抛物线2y x bx c =++顶点A 的横坐标是-1，且与y轴交于点B （0，-1），点P 为抛物线上一点． （1）求抛物线的表达式；（2）若将抛物线2y x bx c =++向下平移4个单位，点P 平移后的对应点为Q ．如果OP =OQ ，求点Q 的坐标．15.（18通州一模26）在平面直角坐标系xOy 中，点C 是二次函数2441y mx mx m =+++的图象的顶点，一次函数4+=x y 的图象与x 轴、y 轴分别交于点A ，B . （1）请你求出点A ,B ,C 的坐标；（2）若二次函数2441y mx mx m =+++与线段AB 恰有一个公共点，求m 的取值范围.。

新定义问题1.（18海淀一模8）如图1，矩形的一条边长为x ，周长的一半为y .定义(,)x y 为这个矩形的坐标. 如图2，在平面直角坐标系中，直线1,3x y ==将第一象限划分成4个区域. 已知矩形1的坐标的对应点A 落在如图所示的双曲线上，矩形2的坐标的对应点落在区域④中.图1 图2则下面叙述中正确的是（ ）A. 点A 的横坐标有可能大于3B. 矩形1是正方形时，点A 位于区域②C. 当点A 沿双曲线向上移动时，矩形1的面积减小D. 当点A 位于区域①时，矩形1可能和矩形2全等2.（18海淀一模15）定义：圆中有公共端点的两条弦组成的折线称为圆的一条折弦．阿基米德折弦定理：如图1，AB 和BC 组成圆的折弦，AB BC >，M 是弧ABC 的中点，MF AB ⊥于F ，则AF FB BC =+．如图2，△ABC 中，60ABC ∠=︒，8AB =，6BC =，D 是AB 上一点，1BD =，作DE AB ⊥交△ABC 的外接圆于E ，连接EA ，则EAC ∠=________°．x图2图1E A3.（18平谷一模28）在平面直角坐标系xOy 中，点M 的坐标为()11,x y ，点N 的坐标为()22,x y ，且12x x ≠，12y y ≠，以MN 为边构造菱形，若该菱形的两条对角线分别平行于x 轴，y 轴，则称该菱形为边的“坐标菱形”.（1）已知点A （2，0），B （0，2，则以AB 为边的“坐标菱形”的最小内角为_______； （2）若点C （1，2），点D 在直线y =5上，以CD 为边的“坐标菱形”为正方形，求直线CD 表达式；（3）⊙O P 的坐标为(3，m ) .若在⊙O 上存在一点Q ，使得以QP 为边的“坐标菱形”为正方形，求m 的取值范围．2. （18延庆一模28）平面直角坐标系xOy 中，点1(A x ，1)y 与2(B x ，2)y ，如果满足120x x +=，120y y -=，其中12x x ≠，则称点A 与点B 互为反等点．已知：点C (3，4)（1）下列各点中， 与点C 互为反等点；D (-3，-4)，E （3，4），F （-3，4） （2）已知点G （-5，4），连接线段CG ，若在线段CG 上存在两点P ，Q 互为反等点，求点P 的横坐标p x 的取值范围； （3）已知⊙O 的半径为r ，若⊙O 与（2）中线段CG 的两个交点互为反等点，求r 的取值范围．3.（18石景山一模28）对于平面上两点A，B，给出如下定义：以点A或B为圆心，AB长为半径的圆称为点A，B的“确定圆”．如图为点A，B 的“确定圆”的示意图．．．．（1）已知点A的坐标为(1,0)-，点B的坐标为(3,3)，则点A，B的“确定圆”的面积为_________；（2）已知点A的坐标为(0,0)，若直线y x b=+上只存在一个点B，使得点A，B的“确定圆”的面积为9π，求点B的坐标；（3）已知点A在以(0)P m，为圆心，以1为半径的圆上，点B在直线y=+要使所有点A，B的“确定圆”的面积都不小于9π，直接写出m的取值范围．4.（18房山一模28）在平面直角坐标系xOy 中，当图形W 上的点P 的横坐标和纵坐标相等时，则称点P 为图形W 的“梦之点”. （1）已知⊙O 的半径为1.①在点E （1，1），F （－22 ，－22 ），M (－2，－2)中，⊙O 的“梦之点”为 ；②若点P 位于⊙O 内部，且为双曲线ky x =（k ≠0）的“梦之点”，求k 的取值范围.（2）已知点C 的坐标为（1，t ），⊙C 的半径为 2 ，若在⊙C 上存在“梦之点”P ，直接写出t 的取值范围.（3）若二次函数21y ax ax =-+的图象上存在两个“梦之点”()11A x ,y ，()22B x ,y ，且122x x -=，求二次函数图象的顶点坐标.5.（18西城一模28）对于平面内的⊙C 和⊙C 外一点Q ，给出如下定义：若过点Q 的直线与⊙C 存在公共点，记为点A ，B ，设AQ BQk CQ+=，则称点A （或点B ）是⊙C 的“k 相关依附点”，特别地，当点A 和点B 重合时，规定AQ BQ =，2AQk CQ =（或2BQCQ ）． 已知在平面直角坐标系xOy 中，(1,0)Q -，(1,0)C ，⊙C 的半径为r ．（1）如图1，当r =①若1(0,1)A 是⊙C 的“k 相关依附点”，则k 的值为__________．②2(1A 是否为⊙C 的“2相关依附点”．答：__________（填“是”或“否”）． （2）若⊙C 上存在“k 相关依附点”点M ，①当1r =，直线QM 与⊙C 相切时，求k 的值．②当k =r 的取值范围．（3）若存在r的值使得直线y b =+与⊙C 有公共点，且公共点是⊙C 的点”，直接写出b 的取值范围．x6.（18怀柔一模28）P 是⊙C 外一点，若射线．．PC 交⊙C 于点A ，B 两点，则给出如下定义：若0＜P A PB ≤3，则点P 为⊙C 的“特征点”．（1）当⊙O 的半径为1时．①在点P 1（,0）、P 2（0,2）、P 3（4，0）中，⊙O 的“特征点”是 ； ②点P 在直线y =x +b 上，若点P 为⊙O 的“特征点”．求b 的取值范围；（2）⊙C 的圆心在x 轴上，半径为1，直线y =x +1与x 轴，y 轴分别交于点M ，N ，若线段MN 上的所有点都不是．．．⊙C 的“特征点”，直接写出点C 的横坐标的取值范围．27.（18海淀一模28）在平面直角坐标系xOy 中，对于点P 和⊙C ，给出如下定义：若⊙C 上存在一点T 不与O 重合，使点P 关于直线OT 的对称点'P 在⊙C 上，则称P 为⊙C 的反射点．下图为⊙C 的反射点P 的示意图．（1）已知点A 的坐标为(1,0)，⊙A 的半径为2，①在点(0,0)O ，(1,2)M ，(0,3)N -中，⊙A 的反射点是____________； ②点P 在直线y x =-上，若P 为⊙A 的反射点，求点P 的横坐标的取值范围； （2）⊙C 的圆心在x 轴上，半径为2，y 轴上存在点P 是⊙C 的反射点，直接写出圆心C 的横坐标x 的取值范围．8.（18朝阳一模28）对于平面直角坐标系xOy中点P和线段AB，其中A(t，0)、B(t+2，0)两点，给出如下定义：若在线段AB上存在一点Q，使得P，Q两点间的距离小于或等于1，则称P为线段AB的伴随点．（1）当t=-3时，①在点P1（1，1），P2（0，0），P3（-2，-1）中，线段AB的伴随点是；②在直线y=2x+b上存在线段AB的伴随点M、N，且MN=b的取值范围；（2）线段AB的中点关于点（2，0）的对称点是C，将射线CO以点C为中心，顺时针旋转30°得到射线l，若射线l上存在线段AB的伴随点，直接写出t的取值范围．9.（18东城一模28）给出如下定义：对于⊙O 的弦MN 和⊙O 外一点P （M ，O ，N 三点不共线，且P ，O 在直线MN 的异侧），当∠MPN ＋∠MON=180°时，则称点 P 是线段MN 关于点O 的关联点．图1是点P 为线段MN 关于点O 的关联点的示意图.在平面直角坐标系xOy 中，⊙O 的半径为1.（1）如图2，22M ⎛ ⎝⎭，22N ⎛- ⎝⎭.在A （1，0），B （1，1），)C 三点中，是线段MN 关于点O 的关联点的是 ；（2）如图3， M （0，1），N 12⎫-⎪⎪⎝⎭，点D 是线段 MN 关于点O 的关联点.①∠MDN 的大小为 °；②在第一象限内有一点E),m ，点E 是线段MN 关于点O 的关联点，判断△MNE 的形状，并直接写出点E 的坐标；③点F 在直线23y x =-+上，当∠MFN ≥∠MDN 时，求点F 横坐标x F 的取值范围．10.（18丰台一模28）对于平面直角坐标系xOy 中的点M 和图形1W ，2W 给出如下定义：点P为图形1W 上一点，点Q 为图形2W 上一点，当点M 是线段PQ 的中点时，称点M 是图形1W ，2W 的“中立点”．如果点P (x 1，y 1)，Q (x 2，y 2)，那么“中立点”M 的坐标为⎪⎭⎫ ⎝⎛++2,22121y y x x ．已知，点A (-3，0)，B (0，4)，C (4，0)．（1）连接BC ，在点D (12，0)，E (0，1)，F (0，12)中，可以成为点A 和线段BC 的“中立点”的是____________；（2）已知点G (3，0)，⊙G 的半径为2．如果直线y = - x + 1上存在点K 可以成为点A 和⊙G 的“中立点”，求点K 的坐标；（3）以点C 为圆心，半径为2作圆．点N 为直线y = 2x + 4上的一点，如果存在点N ，使得y 轴上的一点可以成为点N 与⊙C 的“中立点”，直接写出点N 的横坐标的取值范围．11.（18门头沟一模28）在平面直角坐标系xOy 中，点M 的坐标为11(,)x y ，点N 的坐标为22(,)x y ，且12x x ≠，12y y =,我们规定：如果存在点P ，使MNP ∆是以线段MN 为直角边的等腰直角三角形，那么称点P 为点M 、N 的 “和谐点”.（1）已知点A 的坐标为)3,1(，①若点B 的坐标为)3,3(，在直线AB 的上方，存在点A ，B 的“和谐点”C ，直接写出点C 的坐标；②点C 在直线x =5上，且点C 为点A ，B 的“和谐点”，求直线AC 的表达式.（2）⊙O 的半径为r ，点D (1,4)为点E (1,2)、F ),(n m 的“和谐点”，若使得△DEF 与⊙O 有交点，画出示意图直接．．．．．写出半径r 的取值范围.备用图1 备用图212.（18大兴一模28）在平面直角坐标系xOy中，过y轴上一点A作平行于x轴的直线交某函数图象于点D，点P是x轴上一动点，连接D P，过点P作DP的垂线交y轴于点E（E 在线段OA上，E不与点O重合），则称 DPE为点D，P,E的“平横纵直角”.图1为点D，P，E的“平横纵直角”的示意图.图113.如图2，在平面直角坐标系xOy 中，已知二次函数图象与y 轴交于点(0,)F m ，与x 轴分别交于点B （3-，0），C （12，0）. 若过点F 作平行于x 轴的直线交抛物线于点N . （1）点N 的横坐标为 ； （2）已知一直角为点,,N M K 的“平横纵直角”，若在线段OC 上存在不同的两点1M 、2M ，使相应的点1K 、2K 都与点F 重合，试求m 的取值范围； （3）设抛物线的顶点为点Q ，连接BQ 与FN 交于点H ,当4560QHN ︒≤≤︒∠时，求m 的取值范围．图213.（18顺义一模28）如图1，对于平面内的点P 和两条曲线1L 、2L 给出如下定义：若从点P 任意引出一条射线分别与1L 、2L 交于1Q 、2Q ，总有12PQ PQ 是定值，我们称曲线1L 与2L “曲似”，定值12PQ PQ 为“曲似比”，点P 为“曲心”．例如：如图2，以点O'为圆心，半径分别为1r 、2r （都是常数）的两个同心圆1C 、2C ，从点O'任意引出一条射线分别与两圆交于点M 、N ，因为总有12''r O M O N r =是定值，所以同心圆1C 与2C 曲似，曲似比为12r r ，“曲心”为O'．（1）在平面直角坐标系xOy 中，直线y kx =与抛物线2y x =、212y x =分别交于点A 、B ，如图3所示，试判断两抛物线是否曲似，并说明理由；（2）在（1）的条件下，以O 为圆心，OA 为半径作圆，过点B 作x 轴的垂线，垂足为C ，是否存在k 值，使⊙O 与直线BC 相切？若存在，求出k 的值；若不存在，说明理由；（3）在（1）、（2）的条件下，若将“212y x =”改为“21y x m=”，其他条件不变，当存在⊙O与直线BC 相切时，直接写出m 的取值范围及k 与m 之间的关系式．图12L 1图214.（18通州一模）.在平面直角坐标系xOy 中有不重合的两个点()11,y x Q 与()22y x P ，.若Q ，P 为某个直角三角形的两个锐角顶点，且该直角三角形的直角边均与x 或y 轴平行(或重合)，则我们将该直角三角形的两条直角边的边长之和定义为点Q 与点P 之间的“直距PQ D ”.例如在下图中，点()1,1P ，()3,2Q ，则该直角三角形的两条直角边长为1和2，此时点Q 与点P 之间的“直距”=3PQ D .特别地，当PQ 与某条坐标轴平行(或重合)时，线段PQ 的长即为点Q 与点P 之间的“直距”. （1）①已知O 为坐标原点，点()2,1A -，()2,0B -，则_______=AO D ，_______=BO D ；② 点C 在直线3y x =-+上，请你求出CO D 的最小值；（2）点E 是以原点O 为圆心，1为半径的圆上的一个动点；点F 是直线24y x =+上一动点.请你直接写出点E 与点F 之间“直距EF D ”的最小值.15.（18燕山一模27）如图，抛物线)0(2>++=a c bx ax y 的顶点为M ，直线y=m 与抛物线交于点A ，B ，若△AMB 为等腰直角三角形，我们把抛物线上A ，B 两点之间的部分与线段AB 围成的图形称为该抛物线对应的准蝶形，线段AB 称为碟宽，顶点M 称为碟顶．（1）由定义知，取AB 中点N ，连结MN ，MN 与AB 的关系是（2）抛物线221x y =对应的准蝶形必经过B (m ，m ),则m = ，对应的碟宽AB 是（3）抛物线)0(3542>--=a a ax y 对应的碟宽在x 轴上，且AB =6.①求抛物线的解析式；②在此抛物线的对称轴上是否有这样的点P （p x ，p y ），使得∠APB 为锐角，若有，请求出p y 的取值范围.若没有，请说明理由. , 备用图准蝶形AMBABM。