阿基米德三角形与三道高考试题

第27讲 阿基米德三角形知识与方法1.如图1所示，不妨设抛物线为()220x py p =>，抛物线上A 、B 两点处的切线交于点P ，则：（1）设AB 中点为M ，则PM 平行于（或重合）抛物线的对称轴；（2）PM 的中点S 在抛物线上，且抛物线在点S 处的切线平行于弦AB .2．如图2所示，不妨设抛物线为()220x py p =>，抛物线上A 、B 两点处的切线交于点P ，则：（1）若弦AB 过抛物线内的定点Q ，则点P 的轨迹是直线；特别地，若弦AB 过定点()0,m ()0m >，则点P 的轨迹是直线y m =−；（2）若弦AB 过抛物线内的定点Q ，则以Q 为中点的弦与（1）中点P 的轨迹平行. 3．如图3所示，不妨设抛物线为()220x py p =>，抛物线上A 、B 两点处的切线交于点P ，若AB 过焦点F ，则点P 的轨迹为抛物线准线，PA PB ⊥，PF AB ⊥，且PAB 的面积的最小值为2p .4．如图4所示，不妨设抛物线为()220x py p =>，抛物线上A 、B 两点处的切线交于点P ，则：（1）PFA PFB ∠=∠；（2）2AF BF PF ⋅=提醒：阿基米德三角形在小题和大题中都可能涉及，小题可以直接用性质速解，大题则必须给出详细的求解过程.典型例题【例1】己知点()1,1P −在抛物线()220y px p =>的准线上，过点P 作抛物线的切线，切点为A 、B ，则直线AB 的斜率k =_______.【解析】点()1,1P −在抛物线()220y px p =>的准线上⇒抛物线的准线为1x =−⇒抛物线的焦点为()1,0F ，由阿基米德三角形性质，直线AB 过F 且PF AB ⊥，而101112PF k −==−−−，所以直线AB 的斜率为2.【答案】2变式1 已知点()2,1M −和抛物线2:4C x y =，过C 的焦点F 且斜率为k 的直线与C 交于A 、B 两点，若90AMB ∠=︒，则k =_______.【解析】由题意，M 在抛物线C 的准线上，直线AB 过点F 且90AMB ∠=︒，所以MAB 是阿基米德三角形，如图，由阿基米德三角形性质，MF AB ⊥，而11120MF k −−==−−，所以直线AB 的斜率为1.【答案】1变式2 已知抛物线2:4C x y =，过点()1,1P −作抛物线C 的两条切线，切点分别为A 和B ，则经过P 、A 、B 三点的圆的方程为______.【解析】由题意，点P 在抛物线C 的准线上，则PA PB ⊥，PF AB ⊥，且直线AB 过焦点()0,1F ，所以经过P 、A 、B 三点的圆就是以AB 为直径的圆，直线PF 的斜率为11210−−=−−， 所以直线AB 的斜率为12，其方程为112y x =+，设()11,A x y ，()22,B x y ， 联立21124y x x y ⎧=+⎪⎨⎪=⎩消去y 整理得：2240x x −−=， 故122x x +=，()12121232y y x x +=++=，从而AB 中点为31,2⎛⎫ ⎪⎝⎭，1225AB y y =++=，所以经过P 、A 、B 三点的圆的方程为()22325124x y ⎛⎫−+−= ⎪⎝⎭.【答案】()22325124x y ⎛⎫−+−= ⎪⎝⎭变式3 已知过抛物线22x y =焦点F 的直线与抛物线交于A 、B 两点，抛物线在A 、B 处的切线交于点C ，则ABC 面积的最小值为______.【解析】由阿基米德三角形性质，当直线AB 过焦点F 时，ABC 面积的最小值为21p =. 【答案】1变式4 已知抛物线2:4C y x =的焦点为F ，过F 的直线与抛物线C 交于A 、B 两点，抛物线C 在A 、B 两点处的切线相交于点P ，若3AF =，则PF =_______. 【解析】设AFO α∠=，则231cos AF α==+，所以1cos 3α=−，故()2231cos 1cos 2BF παα===+−−， 由阿基米德三角形性质，2AF BF PF ⋅=所以2PF ==.【答案】2【例2】抛物线2:2C x py =()0p >的焦点为F ，且F 与圆()22:21I x y ++=上的点的距离的最大值为4. （1）求p 的值；（2）若点Q 在圆I 上，QA 、QB 是抛物线C 的两条切线，A 、B 是切点，当IQ AB ∥时，求直线AB 与y 轴交点的坐标. 【解析】解：（1）由题意，342p+=，所以2p =. （2）显然直线AB 斜率存在，可设其方程为y kx m =+，由（1）知抛物线C 的方程为24x y =，联立24y kx m x y=+⎧⎨=⎩消去y 整理得：2440x kx m −−=，由韦达定理，124x x k +=，124x x m =−，设211,4x A x ⎛⎫ ⎪⎝⎭，222,4x B x ⎛⎫ ⎪⎝⎭，由24x y =可得24x y =，所以2x y '=，故直线QA 的方程为()211142x x y x x −=−，整理得：21124x x y x =−，同理，直线QB 的方程为22224x x y x =−，联立2112222424x x y x x xy x ⎧=−⎪⎪⎨⎪=−⎪⎩解得：1222x x x k +==，124x x y m ==−，所以点Q 的坐标Wie ()2,k m −， 因为点Q 在圆I 上，所以()22421k m +−+=①， 因为IQ AB ∥，所以22mk k−=，从而222k m =−， 代入式①可得()()22221m m −+−+=解得：3m =，又2220k m =−≥，所以2m ≤，故3m =， 从而直线AB 与y轴的交点的坐标为(0,3.【反思】对于开口向上（或向下）的抛物线的阿基米德三角形大题，通常采用设两个切点，写出切线方程并联立求出交点坐标，同时将切点弦所在直线与抛物线联立，结合韦达定理计算的方法来处理.强化训练1.（★★★）已知点()2,1P −在抛物线()2:20C y px p =>的准线上，过P 作抛物线C 的切线，切点分别为A 和B ，则直线AB 的方程为______.【解析】()2,1P −在准线上4p ⇒=⇒抛物线的焦点为()2,0F，由阿基米德三角形性质，直线AB 过F ，且PF AB ⊥，而101224PF k −==−−−，所以直线AB 的斜率为4， 故直线AB 的方程为()42y x =−【答案】()42y x =−2.（★★★）已知抛物线2:4C x y =的焦点为F ，过点F 的直线l 交抛物线C 于A 、B 两点，抛物线在A 、B 两点处的切线相交于点P ，则PAB 面积的最小值为_______. 【解析】当AB 过焦点时，阿基米德三角形面积的最小值为24p =. 【答案】43.（★★★）已知抛物线2:2C y x =和点1,12P ⎛⎫− ⎪⎝⎭，过C 的焦点F 且斜率为k 的直线l 与抛物线C 交于A 、B 两点，若0PA PB ⋅=，则k =_______.【解析】由题意，1,02F ⎛⎫⎪⎝⎭，点P 在抛物线的准线上，且PA PB ⊥，所以PAB 是阿基米德三角形，从而PF PB ⊥，直线PF 的斜率1011122PF k −==−−−，故直线AB 的斜率为1. 【答案】14.（★★★）已知抛物线2:4C x y =，过点()0,1P x −作抛物线C 的两条切线，切点分别为A 和B ，若经过P 、A 、B 三点的圆被x 轴截得的弦长为4，则0x =______.【解析】由题意，点P 在抛物线C 的准线上，则PA PB ⊥，PF AB ⊥，且AB 过焦点()0,1F ，直线PF 的斜率为001120x x −−=−−，所以直线AB 的斜率为02x ，其方程为012x y x =+，设()11,A x y ，()22,B x y 联立02124x y x x y ⎧=+⎪⎨⎪=⎩消去y 整理得：20240x x x −−=，所以1202x x x +=，()201212022x y y x x x +=+=+， 从而AB 中点为200,12x x ⎛⎫+ ⎪⎝⎭，212024AB y y x =++=+， 因为PA PB ⊥，所以经过P 、A 、B 三点的圆就是以AB 为直径的圆，该圆的半22220014222x x ⎛⎫⎛⎫++=+ ⎪ ⎪⎝⎭⎝⎭，解得：01x =±.【答案】1±5.（★★★★）已知抛物线2y x =和点()0,1P ，若过某点C 可作抛物线的两条切线，切点分别为A 和B ，且满足1233CP CA CB =+，则ABC 的面积为______.【解析】()()12123333CP CA CB CP CP PA CP PB PA PB =+⇒=+++⇒=−⇒P 、A 、B 三点共线，设直线AB 的方程为1y kx =+，设()11,A x y ，()22,B x y ，不妨设0k >, 联立21y kx y x=+⎧⎨=⎩消去y 整理得：210x kx −−=，判别式240k =+>， 由韦达定理12x x k +=，121x x =−，又2PA PB =−，所以122x x =−，联立12121212x x kx x x x+=⎧⎪=−⎨⎪=−⎩可解得：k =，所以12x x +，设AB 中点为D ，则122D x x x +==， 代入1y kx =+得51244D y =⨯+=， 由阿基米德三角形性质知CD x ⊥轴且点C 在直线1y =−上， 所以()59144CD =−−=，故121199922418216ABCSCD x x =⋅−=⨯⨯=⨯=.6.（★★★★★）已知动圆过点()0,1F ，且与直线:1l y =−相切.（l ）求动圆圆心的轨迹E 的方程； （2）设P 为一动点，过P 作曲线E 的两条切线PA 、PB ，切点分别为A 和B ，且PA PB ⊥，直线AB 与圆224x y +=相交于C 、D 两点，设点P 到直线AB 的距离为d ，是否存在点P ，使得24AB CD d ⋅=?若存在，求出点P 的坐标；若不存在，说明理由. 【解析】（1）由题意，动圆圆心到点F 的距离和到定直线l 的距离相等, 所以动圆圆心的轨迹是以F 为焦点，l 为准线的抛物线，其方程为24x y =.（2）显然直线AB 的斜率存在，故可设其方程为y kx m =+，设211,4x A x ⎛⎫ ⎪⎝⎭，222,4x B x ⎛⎫⎪⎝⎭，联立24y kx mx y=+⎧⎨=⎩消去y 整理得：2440x kx m −−=，由韦达定理，124x x k +=，124x x m =−，由24x y =得24x y =，所以2xy '=，故直线PA 的方程为()211142x x y x x −=−，整理得：21124x x y =−，同理，直线PB 的方程为22224x x y =−，联立2112222424x x y x x y ⎧=−⎪⎪⎨⎪=−⎪⎩解得：1222x x x k +==，124x x y m ==−，所以点P 的坐标为()2,k m −，因为PA PB ⊥， 所以12122x x m ⋅=−=−，故1m =，从而AB 过点F ， 所以()212122444AB y y k x x k =++=++=+， 原点到直线AB，故CD =点P 到直线AB 的距离d ==所以24AB CD d ⋅=等价于()()2244161k k +⋅=+， 化简得：2101k =+，无解，故不存在点P ，使得|24AB CD d ⋅=.。

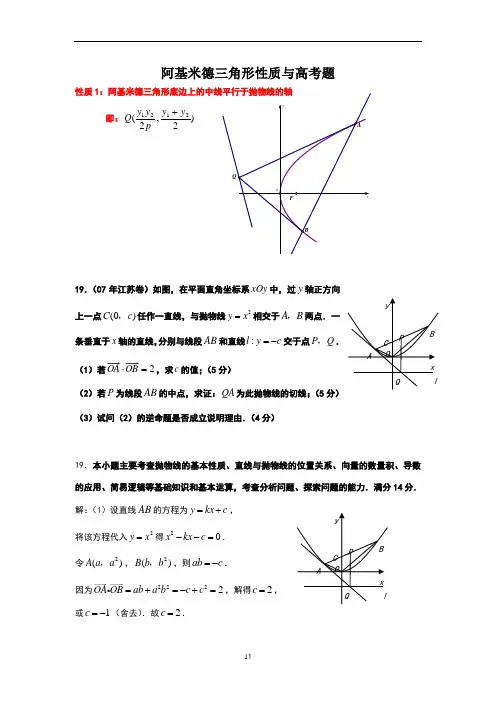
阿基米德三角形性质与高考题性质1即：)2,2(2121y y p y y Q +19．（07年江苏卷）如图，在平面直角坐标系xOy 中，过y 轴正方向上一点(0)C c ，任作一直线，与抛物线2y x =相交于A B ，两点．一条垂直于x 轴的直线，分别与线段AB 和直线:l y c =-交于点P Q ，．（1）若2=⋅，求c 的值；（5分）（2）若P 为线段AB 的中点，求证：QA 为此抛物线的切线；（5分） （3）试问（2）的逆命题是否成立说明理由．（4分）19．本小题主要考查抛物线的基本性质、直线与抛物线的位置关系、向量的数量积、导数的应用、简易逻辑等基础知识和基本运算，考查分析问题、探索问题的能力．满分14分． 解：（1）设直线AB 的方程为y kx c =+，将该方程代入2y x =得20x kx c --=．令2()A a a ，，2()B b b ，，则ab c =-．因为2222OA OB ab a b c c =+=-+=，解得2c =， 或1c =-（舍去）．故2c =．（2）由题意知2a b Q c +⎛⎫-⎪⎝⎭，，直线AQ 的斜率为22222AQ a c a ab k a a b a b a +-===+--． 又2y x =的导数为2y x '=，所以点A 处切线的斜率为2a ， 因此，AQ 为该抛物线的切线． （3）（2）的逆命题成立，证明如下：设0()Q x c -，． 若AQ 为该抛物线的切线，则2AQ k a =， 又直线AQ 的斜率为2200AQa c a ab k a x a x +-==--，所以202a aba a x -=-，得202ax a ab =+，因0a ≠，有02a bx +=． 故点P 的横坐标为2a b+，即P 点是线段AB 的中点．性质2：2||||||QF BF AF =⋅例7．（13广东）已知抛物线C 的顶点为原点,其焦点()()0,0F c c >到直线l :20x y --=的距离为2.设P 为直线l 上的点,过点P 作抛物线C 的两条切线,PA PB ,其中,A B 为切点.(Ⅰ) 求抛物线C 的方程；(Ⅱ) 当点()00,P x y 为直线l 上的定点时,求直线AB 的方程； (Ⅲ) 当点P 在直线l 上移动时,求AF BF ⋅的最小值.性质3：QFB QFA ∠=∠22．（05江西）如图，设抛物线上运动，过P 作抛物线C 的两条切线PA 、PB ，且与抛物线C 分别相切于A 、B 两点.（1）求△APB 的重心G 的轨迹方程. （2）证明∠PFA=∠PFB.22．解：（1）设切点A 、B 坐标分别为))((,(),(0121120x x x x x x ≠和，∴切线AP 的方程为：;02200=--x y x x切线BP 的方程为：;02211=--x y x x 解得P 点的坐标为：1010,2x x y x x x P P =+=所以△APB 的重心G 的坐标为 P PG x x x x x =++=310，,343)(3321021010212010pP P G y x x x x x x x x x y y y y -=-+=++=++=所以243G G p x y y +-=，由点P 在直线l 上运动，从而得到重心G 的轨迹方程为：).24(31,02)43(22+-==-+--x x y x y x 即（2）因为).41,(),41,2(),41,(2111010200-=-+=-=x x FB x x x x FP x x FA 由于P 点在抛物线外，则.0||≠∴||41)1)(1(||||cos 102010010FP x x x x x x x x FA FP AFP +=--+⋅+==∠同理有||41)1)(1(||||cos 102110110FP x x x x x x x x FB FP BFP +=--+⋅+==∠ ∴∠AFP=∠PFB.性质4：过焦点的阿基米德三角形面积的最小值为2p（21）（06年全国卷2）已知抛物线24x y =的焦点为F ，A 、B 是热线上的两动点，且(0).AF FB λλ=>过A 、B 两点分别作抛物线的切线，设其交点为M 。

专题4 阿基米德三角形专题3 阿基米德三角形 微点1 阿基米德三角形 【微点综述】在近几年全国各地高考的解析几何试题中可以发现许多试题涉及到与一个特殊的三角形——由抛物线的弦及过弦的端点的两条切线所围成的三角形有关的问题，这个三角形常被称为阿基米德三角形. 阿基米德三角形包含了直线与圆锥曲线相交、相切两种位置关系，聚焦了轨迹方程、定值、定点、弦长、面积等解析几何的核心问题，“坐标法”的解题思想和数形结合方法的优势体现得淋漓尽致，能很好的提升学生解决圆锥曲线问题的能力，落实逻辑推理、数学抽象、数学运算等核心素养.鉴于此，微点研究阿基米德三角形。

一、预备知识——抛物线上一点的切线方程（1）过抛物线()220y px p =>上一点()00,M x y 的切线方程为：()00y y p x x =+；（2）过抛物线()220y px p =−>上一点()00,M x y 的切线方程为：()00y y p x x =−+；（3）过抛物线()220x py p =>上一点()00,M x y 的切线方程为：()00x x p y y =+； （4）过抛物线()220x py p =−>上一点()00,M x y 的切线方程为：()00x x p y y =−+．下面仅以情形（3）为例给出证明，同理可证其余三种情形。

证法1：设抛物线()220x py p =>上一点()00,M x y 的切线方程为：()00y y k x x −=−，代入22x py =，整理得2002220x pkx py pkx −−+=，由0x ∆=，得()222000044220,220,p k py pkx pk x k y +−=∴−+=抛物线上一点处的切线唯一，∴ 关于k 的一元二次方程200220pk x k y −+=有两个相等的实数根，0,x k p∴=∴所求的切线方程为()000x y y x x p−=−，即2000x x x py py =+−，又2002x py =，∴过抛物线()220x py p =>上一点()00,M x y 的切线方程为：()00x x p y y =+。

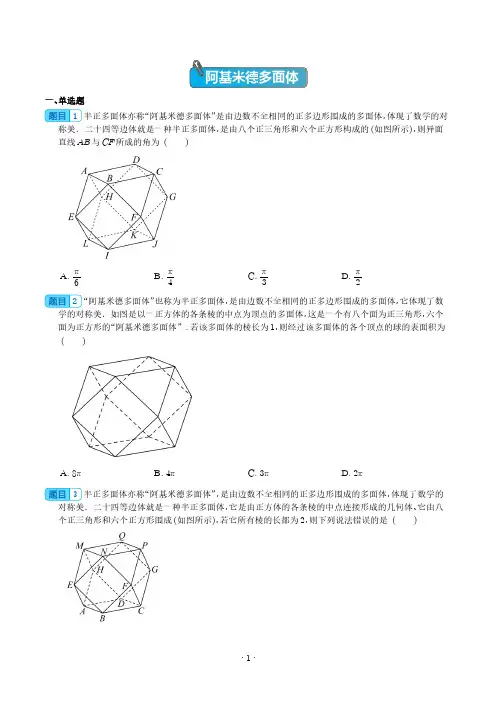
阿基米德多面体一、单选题1半正多面体亦称“阿基米德多面体”是由边数不全相同的正多边形围成的多面体，体现了数学的对称美．二十四等边体就是一种半正多面体，是由八个正三角形和六个正方形构成的(如图所示)，则异面直线AB 与CF 所成的角为()A.π6B.π4C.π3D.π22“阿基米德多面体”也称为半正多面体，是由边数不全相同的正多边形围成的多面体，它体现了数学的对称美．如图是以一正方体的各条棱的中点为顶点的多面体，这是一个有八个面为正三角形，六个面为正方形的“阿基米德多面体”.若该多面体的棱长为1，则经过该多面体的各个顶点的球的表面积为()A.8πB.4πC.3πD.2π3半正多面体亦称“阿基米德多面体”，是由边数不全相同的正多边形围成的多面体，体现了数学的对称美．二十四等边体就是一种半正多面体，它是由正方体的各条棱的中点连接形成的几何体、它由八个正三角形和六个正方形围成(如图所示)，若它所有棱的长都为2，则下列说法错误的是()A.该二十四等边体的表面积为24+83B.QH⊥平面ABEC.直线AH与PN的夹角为60°D.该半正多面体的顶点数V、面数F、棱数E，满足关系式V+F-E=24“阿基米德多面体”也称为半正多面体，半正多面体是由两种或多种正多边形面组成，而又不属于正多面体的凸多面体．如图，某广场的一张石凳就是一个阿基米德多面体，它是由正方体截去八个一样的四面体得到的．若被截正方体的棱长为40cm，则该阿基米德多面体的表面积为()A.4800+16003cm2 B.4800+48003cm2C.3600+36003cm2 D.3600+12003cm25“阿基米德多面体”也称为半正多面体，是由边数不全相同的正多边形为面围成的多面体，它体现了数学的对称美.如图，将一个正方体沿交于一顶点的三条棱的中点截去一个三棱锥，共可截去八个三棱锥，得到八个面为正三角形，六个面为正方形的“阿基米德多面体”，则该多面体中具有公共顶点的两个正三角形所在平面的夹角正切值为()A.22B.1C.2D.226如图，将正方体沿交于同一顶点的三条棱的中点截去一个三棱锥，如此共可截去八个三棱锥，截取后的剩余部分称为“阿基米德多面体”，它是一个24等边半正多面体．从它的棱中任取两条，则这两条棱所在的直线为异面直线的概率为()A.1023B.1223C.2969D.50697半正多面体(semiregular solid)亦称“阿基米德多面体”，是由边数不全相同的正多边形围成的多面体，体现了数学的对称美．下图是棱长为2的正方体截去八个一样的四面体，得到的一个半正多面体，则下列说法错误的是()A.该半正多面体是十四面体B.该几何体外接球的体积为4π3C.该几何体的体积与原正方体的体积比为5∶6D.原正方体的表面积比该几何体的表面积小8“阿基米德多面体”这称为半正多面体(semi-regularsolid)，是由边数不全相同的正多边形为面围成的多面体，它体现了数学的对称美.如图所示，将正方体沿交于一顶点的三条棱的中点截去一个三棱锥，共可截去八个三棱锥，得到八个面为正三角形、六个面为正方形的一种半正多面体.已知AB=32 2，则该半正多面体外接球的表面积为()A.18πB.16πC.14πD.12π9中国有悠久的金石文化，印信是金石文化代表之一，印信的形状多为长方体､正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”.半正多面体是由两种或两种以上的正多边形围成的多面体，古希腊著名数学家阿基米德研究过此类多面体的性质，故半正多面体又被称为“阿基米德多面体”.半正多面体体现了数学的对称美，如图，是一个棱数为24的半正多面体，它的所有顶点都在同一个正方体的棱上，且此正方体的棱长为1.则下列关于该多面体的说法中错误的是()A.多面体有12个顶点，14个面B.多面体的表面积为3C.多面体的体积为56D.多面体有外接球(即经过多面体所有顶点的球)10半正多面体亦称“阿基米德多面体”，是由边数不全相同的正多边形围成的多面体，体现了数学的对称美．二十四等边体就是一种半正多面体，是由正方体切截而成的，它由八个正三角形和六个正方形围成(如图所示)，若它所有棱的长都为2，则()A.BC ⊥平面ABEB.该二十四等边体的体积为3223C.ME 与PN 所成的角为45°D.该二十四等边体的外接球的表面积为16π11有很多立体图形都体现了数学的对称美，其中半正多面体是由两种或两种以上的正多边形围成的多面体，半正多面体因其最早由阿基米德研究发现，故也被称作阿基米德体.如图，这是一个棱数为24，棱长为2的半正多面体，它的所有顶点都在同一个正方体的表面上，可以看成是由一个正方体截去八个一样的四面体所得.若点E 为线段BC 上的动点，则直线DE 与直线AF 所成角的余弦值的取值范围为()A.13,22B.13,32C.12,22D.12,3212半正多面体亦称“阿基米德多面体”，是由边数不全相同的正多边形围成的多面体，体现了数学的对称美.二十四等边体就是一种半正多面体，它是由正方体的各条棱的中点连接形成的几何体.它由八个正三角形和六个正方形围成(如图所示)，若它的棱长为2，则下列说法错误的是()A.该二十四等边体的外接球的表面积为16πB.该半正多面体的顶点数V 、面数F 、棱数E ，满足关系式V +F -E =2C.直线AH 与PN 的夹角为60°D.QH ⊥平面ABE13“阿基米德多面体”是由边数不全相同的正多边形为面围成的多面体，它体现了数学的对称美.如图，将正方体沿交于一顶点的三条棱的中点截去一个三棱锥，共可截去八个三棱锥，得到八个面为正三角形，六个面为正方形的“阿基米德多面体”.若该多面体的棱长为2，则其外接球的表面积为()A.16πB.8πC.16π3D.32π314“阿基米德多面体”也称半正多面体，是由边数不全相同的正多边形围成的多面体，它体现了数学的对称美.如图是以一正方体的各条棱的中点为顶点的多面体，这是一个有八个面为正三角形，六个面为正方形的“阿基米德多面体”，若该多面体的棱长为1，则经过该多面体的各个顶点的球的体积为()A.43π B.82π3C.4πD.8π15有很多立体图形都体现了数学的对称美，其中半正多面体是由两种或两种以上的正多边形围成的多面体，半正多面体因其最早由阿基米德研究发现，故也被称作阿基米德体.如图，这是一个棱数为24，棱长为2的半正多面体，它的所有顶点都在同一个正方体的表面上，可以看成是由一个正方体截去八个一样的四面体所得.若点E为线段BC上的动点，则下列结论不正确的是()A.存在点E、使得A、F、D、E四点共面；B.存在点E，使DE⊥DF；C.存在点E，使得直线DE与平面CDF所成角为π3；D.存在点E，使得直线DE与直线AF所成角的余弦值3510.二、多选题16半正多面体(semiregular solid)亦称“阿基米德多面体”，是由边数不全相同的正多边形围成的多面体，半正多面体有且只有13种．最早用于1970年世界杯比赛的足球就可以近似看作是由12个正五边形和20个正六边形组成的半正面体，半正多面体体现了数学的对称美．如图所示的二十四等边体就是一种半正多面体，它由8个正三角形和6个正方形围成，它是通过对正方体进行八次切截而得到的．若这个二十四等边体的棱长都为2，则下列结论正确的是()A.MQ与平面AEMH不可能垂直B.异面直线BC和EA所成角为60°C.该二十四等边体的体积为402D.该二十四等边体外接球的表面积为18π317“阿基米德多面体”也称为半正多面体，是由边数不全相同的正多边形为面围成的多面体，它体现了数学的对称美．如图，将正方体沿交于一顶点的三条棱的中点截去一个三棱锥，共截去八个三棱锥，得到的半正多面体的表面积为12+43，则关于该半正多面体的下列说法中正确的是( )．A.AB =2B.该半正多面体的外接球的表面积为6πC.AB 与平面BCD 所成的角为π4 D.与AB 所成的角是π3的棱共有16条18半正多面体(semiregularsolid )亦称“阿基米德多面体”，是由边数不全相同的正多边形围成的多面体，体现了数学的对称美，二十四等边体就是一种半正多面体，是由正方体切截而成的，它由八个正三角形和六个正方形构成(如图所示)，若它的所有棱长都为2，则()A.BF ⊥平面EABB.AB 与PF 所成角为45°C.该二十四等边体的体积为203D.该二十四等边体多面体有12个顶点，14个面19“阿基米德多面体”也称为半正多面体，它是由边数不全相同的正多边形为面围成的多面体，体现了数学的对称美．如图，将正方体沿交于同一顶点的三条棱的中点截去一个三棱锥，共截去八个三棱锥，得到的半正多面体的表面积为12+43，则关于该半正多面体的下列说法中正确的是()A.AB 与平面BCD 所成的角为π4B.AB =22C.与AB 所成的角是π3的棱共有16条 D.该半正多面体的外接球的表面积为6π20半正多面体亦称“阿基米德多面体”，是由边数不全相同的正多边形围成的多面体，体现了数学的对称美．二十四等边体就是一种半正多面体，是由正方体切截而成的，它由八个正三角形和六个正方形围成(如图所示)，若它所有棱的长都为2，则()A.BC ⊥平面ABEB.该二十四等边体的体积为4023C.ME 与NP的夹角为60°D.该二十四等边体的外接球的表面积为16π21有很多立体图形都体现了数学的对称美，其中半正多面体是由两种或两种以上的正多边形围成的多面体，半正多面体因其最早由阿基米德研究发现，故也被称作阿基米德体.如图，这是一个棱数为24，棱长为2的半正多面体，它的所有顶点都在同一个正方体的表面上，可以看成是由一个正方体截去八个一样的四面体所得.若点E 为线段BC 上的动点(包含端点)，则下列说法正确的是()A.该半正多面体的体积为163B.当点E 运动到点B 时，DE ⎳FGC.当点E 在线段BC 上运动时(包含端点)，AH 始终与DE 垂直D.直线DE 与平面AFHG 所成角的正弦值的取值范围为0,2222很多立体图形都体现了数学的对称美，其中半正多面体是由两种或两种以上的正多边形围成的多面体，半正多面体因其最早由阿基米德研究发现，故也被称作阿基米德体．如图，这是一个棱数24，棱长为22的半正多面体，它所有顶点都在同一个正方体的表面上，可以看成是由一个正方体截去八个一样的四面体所得的．下列结论正确的有()A.该半正多面体的表面积为48+323B.AG⊥平面BCDGC.点B到平面ACD的距离为433D.若E为线段BC的中点，则异面直线DE与AF所成角的余弦值为351023很多立体图形都体现了数学的对称美，其中半正多面体是由两种或两种以上的正多边形围成的多面体，半正多面体因其最早由阿基米德研究发现，故也被称作阿基米德体．如图，这是一个棱数为24，棱长为2的半正多面体，它的所有顶点都在同一个正方体的表面上，可以看成是由一个正方体截去八个一样的四面体所得，则下列各选项正确的是()A.该半正多面体的体积为203B.A，C，D，F四点共面C.该半正多面体外接球的表面积为12πD.若点E为线段BC上的动点，则直线DE与直线AF所成角的余弦值的取值范围为12,2 224半正多面体亦称“阿基米德体”，是由边数不全相同的正多边形为面的多面体．如图，将正四面体每条棱三等分，截去顶角所在的小正四面体，得到一个有八个面的半正多面体．点A、B、C是该多面体的三个顶点，且棱长AB=2，则下列结论正确的是()A.该多面体的表面积为243B.该多面体的体积为4623C.该多面体的外接球的表面积为22πD.若点M是该多面体表面上的动点，满足CM⊥AB时，点M的轨迹长度为4+43三、填空题25很多立体图形都体现了数学的对称美，其中半正多面体是由两种或两种以上的正多边形围成的多面体，半正多面体因其最早由阿基米德研究发现，故也被称作阿基米德体.如图，这是一个棱数为24，棱长为2的半正多面体，它的所有顶点都在同一个正方体的表面上，可以看成是由一个正方体截去八个一样的四面体所得.若E 为线段BC 的中点，则直线DE 与直线AF 所成角的余弦值为.26“阿基米德多面体”也称半正多面体，是由边数不全相同的正多边形围成的多面体，它体现了数学的对称美.二十四等边体就是一种半多正多面体．如图，棱长为1的正方体截去八个一样的四面体，就得到二十四等边体，则该几何体的体积为．27半正多面体亦称“阿基米德体”“阿基米德多面体”，是以边数不全相同的正多边形为面的多面体.某半正多面体由4个正三角形和4个正六边形构成，其可由正四面体切割而成，如图所示.已知MN =1，若在该半正多面体内放一个球，则该球表面积的最大值为.28半正多面体亦称“阿基米德体”“阿基米德多面体”，是由边数不全相同的正多边形为面的多面体.某半正多面体由4个三角形和4个正六边形构成，其可由正四面体切割而成，如图所示.若点G 在直线BC 上，且BG =5BC,BC =1，则直线EF 与直线AG 所成角的余弦值为．29半正多面体(semiregularsolid )亦称“阿基米德多面体”，是由边数不全相同的正多边形围成的多面体，体现了数学的对称美.二十四等边体就是一种半正多面体，是由正方体切截而成的，它由八个正三角形和六个正方形构成(如图所示)，若它的所有棱长都为2，则正确的序号是.①BF ⊥平面EAB ； ②AB 与PF 所成角为45°；③该二十四等边体的体积为203； ④该二十四等边体外接球的表面积为8π.30将棱长为12的正四面体沿棱长的三等分点处截去四个小正四面体后，所得的多面体称为阿基米德体，如图所示.若点N 在阿基米德体的表面上运动，且直线MN 与直线AB 始终满足MN ⊥AB ，则动点N 的轨迹所围成平面图形的面积是.四、双空题31半正多面体(又称作“阿基米德体”)，是由两种或两种以上的正多边形围成的多面体，其构成体现了数学的对称美．如图，这是一个棱数为24，棱长为2的半正14面体，它的所有顶点都在同一个正方体的表面上，可以看成是由一个正方体沿共顶点的三条棱的中点截去八个相同的三棱锥所得，则这个半正多面体的体积为﹔若点E 为线段BC 上的动点，则直线DE 与平面AFG 所成角的正弦值的取值范围为32阿基米德多面体也称为半正多面体，是以边数不全相同的正多边形为面围成的多面体．如图，已知阿基米德多面体的所有顶点均是一个棱长为2的正方体各条棱的中点，则该阿基米德多面体的体积为；若M，N是该阿基米德多面体表面上任意两点，则M，N两点间距离的最大值为．33“阿基米德多面体”也称为半正多面体，是由边数不全相同的正多边形为面围成的多面体，它体现了数学的对称美.如图，将一个棱长为2正方体沿交于一顶点的三条棱的中点截去一个三棱锥，共可截去八个三棱锥，得到八个面为正三角形，六个面为正方形的“阿基米德多面体”，则该多面体的表面积为；其外接球的表面积为.34有很多立体图形都体现了数学的对称美，其中半正多面体是由两种成两种以上的正多边形围成的多面体，半正多面体因其最早由阿基米德研究发现，故也被称作阿基米德体.如图，这是一个棱数为24，棱长为2的半正多面体，它的所有顶点都在同一个正方体的表面上，可以看成是由一个正方体截去八个一样的四面体所得，这个正多面体的表面积为.若点E为线段BC上的动点，则直线DE与直线AF 所成角的余弦值的取值范围为.35如图，将正四面体每条棱三等分，截去顶角所在的小正四面体，余下的多面体就成为一个半正多面体，亦称“阿基米德体”．点A，B，M是该多面体的三个顶点，点N是该多面体外接球表面上的动点，且总满足MN⊥AB，若AB=4，则该多面体的表面积为；点N轨迹的长度为．阿基米德多面体一、单选题1半正多面体亦称“阿基米德多面体”是由边数不全相同的正多边形围成的多面体，体现了数学的对称美．二十四等边体就是一种半正多面体，是由八个正三角形和六个正方形构成的(如图所示)，则异面直线AB 与CF 所成的角为()A.π6B.π4C.π3D.π2【答案】C【分析】依题意将图形放到正方体中，如图所示，由正方体的性质可得∠PQM 为异面直线AB 与CF 所成的角，即可得解；【详解】解：二十四等边体可认为是由正方体切去八个全等的三棱锥得到的，如图所示，可知AB ⎳PQ ，CF ⎳MQ ，所以∠PQM 为异面直线AB 与CF 所成的角，因为△PQM 是等边三角形，所以∠PQM =π3，故异面直线AB 与CF 所成的角为π3；故选：C2“阿基米德多面体”也称为半正多面体，是由边数不全相同的正多边形围成的多面体，它体现了数学的对称美．如图是以一正方体的各条棱的中点为顶点的多面体，这是一个有八个面为正三角形，六个面为正方形的“阿基米德多面体”.若该多面体的棱长为1，则经过该多面体的各个顶点的球的表面积为()A.8πB.4πC.3πD.2π【答案】B【分析】将该多面体补形为正方体，得到经过该多面体的各个顶点的球为正方体ABCD-EFGH的棱切球，求出该正方体的边长，求出棱切球的半径，得到表面积.【详解】将该多面体补形为正方体，则由OR=1，AO=AR,AO⊥AR，所以由勾股定理得：AO=AR=22，所以正方体的边长为22×2=2，所以经过该多面体的各个顶点的球为正方体ABCD-EFGH的棱切球，所以棱切球的直径为该正方体的面对角线，长度为2×2=2，故过该多面体的各个顶点的球的半径为1，球的表面积为4π×12=4π.故选：B3半正多面体亦称“阿基米德多面体”，是由边数不全相同的正多边形围成的多面体，体现了数学的对称美．二十四等边体就是一种半正多面体，它是由正方体的各条棱的中点连接形成的几何体、它由八个正三角形和六个正方形围成(如图所示)，若它所有棱的长都为2，则下列说法错误的是()A.该二十四等边体的表面积为24+83B.QH⊥平面ABEC.直线AH与PN的夹角为60°D.该半正多面体的顶点数V、面数F、棱数E，满足关系式V+F-E=2【答案】B【分析】由三角形和正方形面积公式即可求出二十四等边体的表面积，线面垂直判定定理，利用平移求异面直线夹角，推理分析即可判断结果.【详解】对于A，S□ABCD=22=4，S△ABE=12×32×2×2=3，S表=6S□ABCD+8S△ABE=6×4+8×3=24+83，故A正确；对于B，由图可知QH⎳BF,BF⊥EB,但BF与AB和AE都不垂直，所以QH不可能与平面ABE垂直，故B错误；对于C，由图可知AH⎳AD，而直线AH与AD的夹角为60°，所以直线AH与PN的夹角为60°，故C正确；对于D，该半正多面体的顶点数为12、面数为14、棱数为24，满足12+14-24=2，故D正确；故选：B.4“阿基米德多面体”也称为半正多面体，半正多面体是由两种或多种正多边形面组成，而又不属于正多面体的凸多面体．如图，某广场的一张石凳就是一个阿基米德多面体，它是由正方体截去八个一样的四面体得到的．若被截正方体的棱长为40cm，则该阿基米德多面体的表面积为()A.4800+16003cm2 B.4800+48003cm2C.3600+36003cm2 D.3600+12003cm2【答案】A【分析】通过图形可知阿基米德多面体是由六个全等的正方形和八个全等的等边三角形构成，分别求解正方形和等边三角形面积，加和即可.【详解】由题意知：阿基米德多面体是由六个全等的正方形和八个全等的等边三角形构成，其中正方形边长和等边三角形的边长均为202+202=202；∴阿基米德多面体的表面积S=6×2022+8×12×202×202×32=4800+16003cm2.故选：A.5“阿基米德多面体”也称为半正多面体，是由边数不全相同的正多边形为面围成的多面体，它体现了数学的对称美.如图，将一个正方体沿交于一顶点的三条棱的中点截去一个三棱锥，共可截去八个三棱锥，得到八个面为正三角形，六个面为正方形的“阿基米德多面体”，则该多面体中具有公共顶点的两个正三角形所在平面的夹角正切值为()A.22B.1C.2D.22【答案】D【分析】将该多面体放在正方体中，利用空间向量的坐标运算，求出平面EFG 和平面GHK 的法向量，即可求平面EFG 和平面GHK 夹角的余弦值，进而可求解.【详解】将该“阿基米德多面体”放入正方体中，如图，平面EFG 和平面GHK 为有公共顶点的两个正三角形所在平面，建立如图所示空间直角坐标系，设正方体的棱长为2，则E (1,0,2),F (2,1,2),G (2,0,1),H (2,1,0),K (1,0,0),设平面EFG 的法向量为m=(x ,y ,z ),EF =(1,1,0),EG =(1,0,-1),所以EF ⋅m=x +y =0EG ⋅m=x -z =0，令x =1,y =-1,z =1，所以m =(1,-1,1),设平面GHK 的法向量为n=(a ,b ,c ),GH =(0,1,-1),GK =(-1,0,-1),所以GH ⋅n=b -c =0GK ⋅n=-a -c =0，令a =1,b =-1,c =-1，所以n =(1,-1,-1),设平面平面EFG 和平面GHK 的夹角为θ，则cos <m ,n >=m ⋅n m ⋅n=13×3=13，因为平面EFG 和平面GHK 的夹角为锐角，所以cos θ=cos <m ,n > =13，所以sin θ=1-cos 2θ=223,tan θ=sin θcos θ=22，故选：D6如图，将正方体沿交于同一顶点的三条棱的中点截去一个三棱锥，如此共可截去八个三棱锥，截取后的剩余部分称为“阿基米德多面体”，它是一个24等边半正多面体．从它的棱中任取两条，则这两条棱所在的直线为异面直线的概率为()A.1023B.1223C.2969D.5069【答案】B【分析】分一条直线位置于上(或下)底面，另一条不在底面；两条直线都位于上下底面时；两条直线都不在上下底面时计数，再根据古典概型公式求解即可.【详解】解：当一条直线位置于上(或下)底面，另一条不在底面时，共有10×8=80对异面直线，当两条直线都位于上下底面时，有4×2=8对异面直线，当两条直线都不在上下底面时，有7×8=56对异面直线，所以，两条棱所在的直线为异面直线的概率为P=80+56+8C224=1223故选：B7半正多面体(semiregular solid)亦称“阿基米德多面体”，是由边数不全相同的正多边形围成的多面体，体现了数学的对称美．下图是棱长为2的正方体截去八个一样的四面体，得到的一个半正多面体，则下列说法错误的是()A.该半正多面体是十四面体B.该几何体外接球的体积为4π3C.该几何体的体积与原正方体的体积比为5∶6D.原正方体的表面积比该几何体的表面积小【答案】D【分析】由题意求该几何体的体积与表面积，由外接球的半径求体积，对选项逐一判断即得.【详解】由图可知该半正多面体的表面是由6个正方形和8个等边三角形构成，所以为十四面体，该半正多面体是十四面体，故A正确；该几何体外接球的球心为原正方体的中心，故外接球半径为1，外接球的体积为4π3，故B正确；对于C，该几何体的体积V=V正方体-8V四面体=(2)3-8×13×12×12×22=523，正方体体积为22，故该几何体的体积与原正方体的体积比为5∶6，故C正确；对于D，该几何体有6个面为正方形，8个面为等边三角形，S表=6×12+8×34×1=6+23<12，即原正方体的表面积比该几何体的表面积大，故D 错误．故选：D ．8“阿基米德多面体”这称为半正多面体(semi -regularsolid )，是由边数不全相同的正多边形为面围成的多面体，它体现了数学的对称美.如图所示，将正方体沿交于一顶点的三条棱的中点截去一个三棱锥，共可截去八个三棱锥，得到八个面为正三角形、六个面为正方形的一种半正多面体.已知AB =322，则该半正多面体外接球的表面积为()A.18πB.16πC.14πD.12π【答案】A【分析】根据正方体的对称性可知：该半正多面体外接球的球心为正方体的中心O ，进而可求球的半径和表面积.【详解】如图，在正方体EFGH -E 1F 1G 1H 1中，取正方体、正方形E 1F 1G 1H 1的中心O 、O 1，连接E 1G 1,OO 1,OA ,O 1A ，∵A ,B 分别为E 1H 1,H 1G 1的中点，则E 1G 1=2AB =32，∴正方体的边长为EF =3，故OO 1=O 1A =32，可得OA =OO 21+O 1A 2=322，根据对称性可知：点O 到该半正多面体的顶点的距离相等，则该半正多面体外接球的球心为O ，半径R =OA =322，故该半正多面体外接球的表面积为S =4πR 2=4π×3222=18π.故选：A .9中国有悠久的金石文化，印信是金石文化代表之一，印信的形状多为长方体､正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”.半正多面体是由两种或两种以上的正多边形围成的多面体，古希腊著名数学家阿基米德研究过此类多面体的性质，故半正多面体又被称为“阿基米德多面体”.半正多面体体现了数学的对称美，如图，是一个棱数为24的半正多面体，它的所有顶点都在同一个。

微专题 阿基米德三角形基础回顾：圆锥曲线的弦与过弦的端点的两条切线所围成的三角形叫做阿基米德三角形。

特殊地，过抛物线22=y px 的焦点F 任作一条弦AB ，抛物线在点,A B 处的两条切线相交于点M ，∆MAB 为阿基米德三角形.B A ,在其准线L 的上投影分别为B A '',,则有如下结论：1. 交点M 在22=y px 准线上2. 切线交点与弦中点连线平行于对称轴3. 过抛物线准线上任一点作抛物线的切线，则过两切点的弦必过焦点4. ⊥MA MB ，⊥MF AB5. MN 与抛物线的交点平分线段MN6. MB 平分BA B '∠, 7.MA 平分角AB A '∠8. 2MF FB FA =⋅ 9. MAB S ∆2min p = 二、典例解析题型一 两切线交点的轨迹1. 过抛物线22=y px 的焦点F 任作一条弦AB ，抛物线在点,A B 处的两条切线相交于点M ，则M 在22=y px 的准线上 ，且⊥MA MB ，⊥MF AB ，证明：设直线AB 的方程为2=+px my .由22,,2⎧=⎪⎨=+⎪⎩y px p x my 可得2220y pmy p --=.显然0∆> 设1122(,),(,)A x y B x y ，则122y y pm +=，212y y p =-.抛物线在,A B 两点的切线方程分别为()11y y p x x =+，()22y y p x x =+.解之得1212,2,2⎧=⎪⎪⎨+⎪=⎪⎩y y x p y y y 由此求得两切线的交点坐标12(,)22+-y y P M所以M 在22=y px 的准线上.22212121⋅=⋅==--AM BMp p p p k k y y y y p,∴⊥MA MB(,)=-MF p pm ，2121(,)=--AB x x y y()()()21212121022p p MF AB p x x pm y y p my my pm y y ⎛⎫⋅=---=+----= ⎪⎝⎭∴⊥MF AB .题型二 阿基米德三角形面积的最小值2.抛物线的弦与过弦的端点的两条切线所围成的三角形称为阿基米德三角形．阿基米德三角形有一些有趣的性质，如若抛物线的弦过焦点，则过弦的端点的两条切线的交点在其准线上．设抛物线y 2＝4px （p ＞0），弦AB 过焦点，△ABQ 为其阿基米德三角形，则△ABQ 的面积的最小值为_______．解：由于若抛物线的弦过焦点，则过弦的端点的两条切线的交点在其准线上，且△P AB 为直角三角型，且角P 为直角，S ＝P A •PB ≤，由于AB 是通径时，即AB ＝2p 最小，故S ≤p 2，故答案为：p 2．题型三 阿基米德三角形的形状的判断2. 抛物线的弦与过弦的端点的两条切线所围成的三角形常被称为阿基米德三角形，阿基米德三角形有一些有趣的性质，如：若抛物线的弦过焦点，则过弦的端点的两条切线的交点在其准线上． 设抛物线y 2＝2px （p ＞0），弦AB 过焦点，△ABQ 为阿基米德三角形，则△ABQ 为（ ） A ．锐角三角形 B ．直角三角形 C ．钝角三角形D ．随Q 位置变化前三种情况都有可能 解：如图所示．设Q，A （x 1，y 1），B （x 2，y 2）．则，．设直线AB ：my ＝x ﹣，联立，化为y 2﹣2pmy ﹣p 2＝0，得到y 1+y 2＝2pm ，．设过点A 的切线为，联立，化为，∵直线是抛物线的切线，∴＝0，化为pk 1＝y 1．设过点B 的切线为，同理可得pk 2＝y 2． ∴p 2k 1k 2＝y 1y 2．∴，解得k 1k 2＝﹣1．∴．即△ABQ 是直角三角形．故选：B ．题型四 阿基米德三角形的判断.4若M 在22=y px 的准线上，且⊥MA MB ，则,MA MB 是抛物线的两条切线,∆MAB 为阿基米德三角形.证明：过22=y px 的焦点F 任作一条弦AB ，过B A ,分别作抛物线的两条切线,设它们交于点M ',则M '在22=y px 的准线上，且B M A M '⊥'，由抛物线的焦点弦的性质知，2=-px 是以AB 为直径的圆的切线，又M 在2=-px 上，且⊥MA MB ，则可得'M 与M 重合.所以,MA MB 是抛物线的两条切线.∆MAB 为阿基米德三角形.方法总结：1.圆锥曲线的弦与过弦的端点的两条切线所围成的三角形叫做阿基米德三角形。

阿基米德定律试题及答案一、单项选择题1. 阿基米德定律描述的是液体对物体的哪种力？A. 重力B. 浮力C. 摩擦力D. 张力答案：B2. 阿基米德定律中，物体所受的浮力与其排开液体的什么成正比？A. 质量B. 体积C. 密度D. 压力答案：B3. 在阿基米德定律中，液体的密度如何影响物体所受的浮力？A. 无关B. 成正比C. 成反比D. 无法确定答案：B二、填空题4. 阿基米德定律的数学表达式为：\( F_b = \rho \cdot V \cdot g\)，其中 \( F_b \) 表示________，\( \rho \) 表示________，\( V \) 表示________，\( g \) 表示________。

答案：浮力；液体的密度；排开液体的体积；重力加速度5. 当一个物体完全浸没在液体中时，它所受的浮力等于________。

答案：排开液体的重量三、简答题6. 解释为什么物体在液体中会浮起来。

答案：物体在液体中浮起来是因为液体对物体施加的浮力与物体的重力相等但方向相反。

如果物体的密度小于液体的密度，那么它所受的浮力将大于其重力，导致物体上浮。

7. 描述阿基米德定律在船舶设计中的应用。

答案：在船舶设计中，阿基米德定律用于计算船体在水中所受的浮力，确保船舶有足够的排水量来支撑其重量。

设计师利用这一原理来确定船体的形状和尺寸，以确保船舶在不同载荷下的稳定性和浮力。

四、计算题8. 一个体积为0.02立方米的木箱完全浸没在水中，水的密度为1000千克/立方米，重力加速度为9.8牛顿/千克，求木箱所受的浮力。

答案：首先计算木箱排开水的重量，即 \( \rho \cdot V = 1000 \, \text{kg/m}^3 \times 0.02 \, \text{m}^3 = 20 \, \text{kg} \)。

然后计算浮力 \( F_b = m \cdot g = 20 \, \text{kg} \times 9.8 \, \text{N/kg} = 196 \, \text{N} \)。

高考与阿基米德三角形试题答案1．（2008年江西卷理科第21题）21．（本小题满分12分）1．证明：（1）设1122(,),(,)A x y B x y ，由已知得到120y y ≠，且22111x y -=，22221x y -=，设切线PA 的方程为：11()y y k x x -=-由1122()1y y k x x x y -=-⎧⎨-=⎩ 得2221111(1)2()()10k x k y kx x y kx ------=从而2222211114()4(1)()4(1)0k y kx k y kx k ∆=-+--+-=,解得11x k y =因此PA 的方程为：111y y x x =- 同理PB 的方程为：221y y x x =-又0(,)P m y 在PA PB 、上，所以1011y y mx =-，2021y y mx =- 即点1122(,),(,)A x y B x y 都在直线01y y mx =-上 又1(,0)M m也在直线01y y mx =-上,所以三点A M B 、、共线 （2）垂线AN 的方程为：11y y x x -=-+， 由110y y x x x y -=-+⎧⎨-=⎩得垂足1111(,)22x y x y N ++，设重心(,)G x y所以11111111()321(0)32x y x x m x y y y +⎧=++⎪⎪⎨+⎪=++⎪⎩ 解得1139341934x y m x y x m y ⎧--⎪=⎪⎪⎨⎪-+⎪=⎪⎩由22111x y -= 可得11(33)(33)2x y x y m m --+-=即2212()39x y m --=为重心G所在曲线方程 2．（2008年山东卷理科第22题）解：（Ⅰ）证明：由题意设221212120(2)22x x A x B x x x M x p p p ⎛⎫⎛⎫<- ⎪ ⎪⎝⎭⎝⎭，，，，，，．由22x py =得22x y p =，得xy p'=，所以1MA x k p =，2MB x k p=． 因此直线MA 的方程为102()x y p x x p +=-，直线MB 的方程为202()xy p x x p+=-． 所以211102()2x x p x x p p +=-，① 222202()2x x p x x p p+=-．② 由①、②得121202x x x x x +=+-， 因此1202x xx +=，即0122x x x =+． 所以A M B ，，三点的横坐标成等差数列．（Ⅱ）解：由（Ⅰ）知，当02x =时，将其代入①、②并整理得：2211440x x p --=， 2222440x x p --=，所以12x x ，是方程22440x x p --=的两根，因此124x x +=，2124x x p =-，又222101221222ABx x x x x p p k x x p p-+===-，所以2AB k p =．由弦长公式得AB ==又AB =1p =或2p =， 因此所求抛物线方程为22x y =或24x y =．（Ⅲ）解：设33()D x y ，，由题意得1212()C x x y y ++，， 则CD 的中点坐标为12312322x x x y y y Q ++++⎛⎫⎪⎝⎭，，设直线AB 的方程为011()x y y x x p-=-， 由点Q 在直线AB 上，并注意到点121222x x y y ++⎛⎫⎪⎝⎭，也在直线AB 上， 代入得033x y x p=．若33()D x y ，在抛物线上，则2330322x py x x ==， 因此30x =或302x x =．即(00)D ，或2022x D x p ⎛⎫ ⎪⎝⎭，．（1）当00x =时，则12020x x x +==，此时，点(02)M p -，适合题意．（2）当00x ≠，对于(00)D ，，此时2212022x x C x p ⎛⎫+ ⎪⎝⎭，，2212022CDx x pk x +=221204x x px +=，又0AB x k p =，AB CD ⊥， 所以22220121220144AB CDx x x x x k k p px p++===-，即222124x x p +=-，矛盾． 对于20022x D x p ⎛⎫ ⎪⎝⎭，，因为2212022x x C x p ⎛⎫+ ⎪⎝⎭，，此时直线CD 平行于y 轴，又00AB x k p=≠，所以直线AB 与直线CD 不垂直，与题设矛盾， 所以00x ≠时，不存在符合题意的M 点．综上所述，仅存在一点(02)M p -，适合题意． 3．（2007年江苏卷理科19题）解：（1）设过C 点的直线为y kx c =+，所以()20x kx c c =+>，即20x kx c --=，设A ()()1122,,,x yB x y ，OA =()11,x y ，()22,OB x y =，因为2OA OB ⋅=，所以12122x x y y +=，即()()12122x x kx c kx c +++=，()221212122x x k x x kc x x c +-++=所以222c k c kc k c --++=，即220,c c --=所以()21c c ==-舍去（2）设过Q的切线为()111y y k x x -=-，/2y x =，所以112k x =，即2211111222y x x x y x x x =-+=-，它与y c =-的交点为M 11,22x cc x ⎛⎫-- ⎪⎝⎭，又21212,,2222x x y y k k P c ⎛⎫++⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭，所以Q ,2k c ⎛⎫- ⎪⎝⎭，因为12x x c =-,所以21c x x -=，所以M 12,,222x x k c c ⎛⎫⎛⎫+-=- ⎪⎪⎝⎭⎝⎭,所以点M 和点Q 重合，也就是QA 为此抛物线的切线。

第80讲阿基米德三角形知识梳理如图所示，AB 为抛物线22(0)x py p =>的弦，11(,)A x y ，22(,)B x y ，分别过,A B 作的抛物线的切线交于点P ，称PAB △为阿基米德三角形，弦AB为阿基米德三角形的底边．1、阿基米德三角形底边上的中线平行于抛物线的轴．2、若阿基米德三角形的底边即弦AB 过抛物线内定点()00 C x y ，，则另一顶点P 的轨迹为一条直线．3、若直线l 与抛物线没有公共点，以l 上的点为顶点的阿基米德三角形的底边过定点．4、底边长为a 的阿基米德三角形的面积的最大值为38a p．5、若阿基米德三角形的底边过焦点，则顶点Q 的轨迹为准线，且阿基米德三角形的面积的最小值为2p ．6、点P 的坐标为1212,22x x x x p ⎛⎫+ ⎪⎝⎭；7、底边AB 所在的直线方程为()121220; x x x py x x +--=8、PAB △的面积为3128PAB x x S p-=．9、若点P 的坐标为()00,x y ，则底边AB 的直线方程为()000x x p y y -+=．10、如图1，若E 为抛物线弧AB 上的动点，点E 处的切线与PA ，PB 分别交于点C ，D ，则||||||||||||AC CE PD CP ED DB ==.11、若E 为抛物线弧AB 上的动点，抛物线在点E 处的切线与阿基米德三角形PAB △的边PA ，PB 分别交于点C ，D ，则2EABPCDS S = ．12、抛物线和它的一条弦所围成的面积，等于以此弦为底边的阿基米德三角形面积的23．图1必考题型全归纳题型一：定点问题例1．（2024·山西太原·高二山西大附中校考期末）已知点()0,1A -，()0,1B ，动点P 满足PB AB PA BA =⋅．记点P 的轨迹为曲线C ．（1）求C 的方程；（2）设D 为直线=2y -上的动点，过D 作C 的两条切线，切点分别是E ，F ．证明：直线EF 过定点．例2．（2024·陕西西安·西安市大明宫中学校考模拟预测）已知动圆M 恒过定点10,8F ⎛⎫⎪⎝⎭，圆心M 到直线14y =-的距离为1,8d d MF =+．(1)求M 点的轨迹C 的方程；(2)过直线1y x =-上的动点Q 作C 的两条切线12,l l ，切点分别为,A B ，证明：直线AB 恒过定点．例3．（2024·全国·高二专题练习）已知平面曲线C 满足：它上面任意一定到10,2⎛⎫⎪⎝⎭的距离比到直线32y =-的距离小1.(1)求曲线C 的方程；(2)D 为直线12y =-上的动点，过点D 作曲线C 的两条切线，切点分别为A B ､，证明：直线AB 过定点；(3)在（2）的条件下，以50,2E ⎛⎫⎪⎝⎭为圆心的圆与直线AB 相切，且切点为线段AB 的中点，求四边形ADBE 的面积.变式1．（2024·陕西·校联考三模）已知直线l 与抛物线2:2(0)C x py p =>交于A ，B 两点，且OA OB ⊥，OD AB ⊥，D 为垂足，点D 的坐标为(1,1)．(1)求C 的方程；(2)若点E 是直线4y x =-上的动点，过点E 作抛物线C 的两条切线EP ，EQ ，其中P ，Q 为切点，试证明直线PQ 恒过一定点，并求出该定点的坐标．变式2．（2024·安徽·高二合肥市第八中学校联考开学考试）抛物线的弦与在弦两端点处的切线所围成的三角形被称为“阿基米德三角形”．对于抛物线C ：2y ax =给出如下三个条件：①焦点为10,2F ⎛⎫⎪⎝⎭；②准线为12y =-；③与直线210y -=相交所得弦长为2．(1)从以上三个条件中选择一个，求抛物线C 的方程；(2)已知ABQ 是（1）中抛物线的“阿基米德三角形”，点Q 是抛物线C 在弦AB 两端点处的两条切线的交点，若点Q 恰在此抛物线的准线上，试判断直线AB 是否过定点？如果是，求出定点坐标；如果不是，请说明理由．变式3．（2024·湖北武汉·高二武汉市第四十九中学校考阶段练习）已知抛物线2:C y ax =（a 是常数）过点(2,2)P -，动点1,2D t ⎛⎫- ⎪⎝⎭，过D 作C 的两条切线，切点分别为A ，B ．(1)求抛物线C 的焦点坐标和准线方程；(2)当1t =时，求直线AB 的方程；(3)证明：直线AB 过定点．变式4．（2024·全国·高三专题练习）已知动点P 在x 轴及其上方，且点P 到点(0,1)F 的距离比到x 轴的距离大1.（1）求点P 的轨迹C 的方程；（2）若点Q 是直线4y x =-上任意一点，过点Q 作点P 的轨迹C 的两切线QA ､QB ，其中A ､B 为切点，试证明直线AB 恒过一定点，并求出该点的坐标.题型二：交点的轨迹问题例4．（2024·全国·高三专题练习）已知抛物线C 的顶点为原点，其焦点()0,F c (0)c >到直线:20l x y --=．(1)求抛物线C 的方程；(2)设点0(P x ，0)y 为直线l 上一动点，过点P 作抛物线C 的两条切线PA ，PB ，其中A ，B 为切点，求直线AB 的方程，并证明直线AB 过定点Q ；(3)过（2）中的点Q 的直线m 交抛物线C 于A ，B 两点，过点A ，B 分别作抛物线C 的切线1l ，2l ，求1l ，2l 交点M 满足的轨迹方程．例5．（2024·全国·高三专题练习）已知抛物线2:4C x y =的焦点为F ，过点F 作直线l 交抛物线C 于A 、B 两点；椭圆E 的中心在原点，焦点在x 轴上，点F 是它的一个顶点，且其离心率2e =．(1)求椭圆E 的方程；(2)经过A 、B 两点分别作抛物线C 的切线1l 、2l ，切线1l 与2l 相交于点M ．证明：点M 定在直线1y =-上；(3)椭圆E 上是否存在一点M '，经过点M '作抛物线C 的两条切线M A ''、(M B A '''、B '为切点），使得直线A B ''过点F ？若存在，求出切线M A ''、M B ''的方程；若不存在，试说明理由．例6．（2024·全国·高三专题练习）已知动点Q 在x 轴上方，且到定点()0,1F 距离比到x 轴的距离大1.（1）求动点Q 的轨迹C 的方程；（2）过点()1,1P 的直线l 与曲线C 交于A ，B 两点，点A ，B 分别异于原点O ，在曲线C 的A ，B 两点处的切线分别为1l ，2l ，且1l 与2l 交于点M ，求证：M 在定直线上.变式5．（2024·全国·高三专题练习）已知动点P 与定点(1,0)F 的距离和它到定直线:4l x =的距离之比为12，记P 的轨迹为曲线C ．(1)求曲线C 的方程；(2)过点(4,0)M 的直线与曲线C 交于,A B 两点，,R Q 分别为曲线C 与x 轴的两个交点，直线,AR BQ 交于点N ，求证:点N 在定直线上．变式6．（2024·全国·高三专题练习）已知点F 为抛物线2:2(0)C x py p =>的焦点，点M 、N 在抛物线上，且M 、N 、F 三点共线.若圆22:(2)(3)16P x y -+-=的直径为MN .（1）求抛物线C 的标准方程；（2）过点F 的直线l 与抛物线交于点A ，B ，分别过A 、B 两点作抛物线C 的切线1l ，2l ，证明直线1l ，2l 的交点在定直线上，并求出该直线.变式7．（2024·全国·高三专题练习）下面是某同学在学段总结中对圆锥曲线切线问题的总结和探索，现邀请你一起合作学习，请你思考后，将答案补充完整．(1)圆222:O x y r +=上点()00,M x y 处的切线方程为．理由如下：．(2)椭圆22221(0)x y a b a b+=>>上一点()00,x y 处的切线方程为；(3)(,)P m n 是椭圆22:13x L y +=外一点，过点P 作椭圆的两条切线，切点分别为A ，B ，如图，则直线AB 的方程是．这是因为在()11,A x y ，()22,B x y 两点处，椭圆L 的切线方程为1113x x y y +=和2213x x y y +=．两切线都过P 点，所以得到了1113x m y n +=和2213x my n +=，由这两个“同构方程”得到了直线AB 的方程；(4)问题（3）中两切线PA ，PB 斜率都存在时，设它们方程的统一表达式为()y n k x m -=-，由22()33y n k x m x y -=-⎧⎨+=⎩，得222(13)6()3()30k x k n km x n km ++-+--=，化简得Δ0=，得222(3)210m x mnk n -++-=．若PA PB ⊥，则由这个方程可知P 点一定在一个圆上，这个圆的方程为．（5）抛物线22(0)y px p =>上一点()00,x y 处的切线方程为00()y y p x x =+；（6）抛物线2:4C x y =，过焦点F 的直线l 与抛物线相交于A ，B 两点，分别过点A ，B 作抛物线的两条切线1l 和2l ，设()11,A x y ，()22,B x y ，则直线1l 的方程为112()x x y y =+．直线2l 的方程为222()x x y y =+，设1l 和2l 相交于点M ．则①点M 在以线段AB 为直径的圆上；②点M 在抛物线C 的准线上．题型三：切线垂直问题例7．（2024·全国·高三专题练习）已知抛物线C 的方程为24x y =，过点P 作抛物线C 的两条切线，切点分别为,A B .（1）若点P 坐标为()0,1-，求切线,PA PB 的方程；（2）若点P 是抛物线C 的准线上的任意一点，求证：切线PA 和PB 互相垂直.例8．（2024·全国·高三专题练习）已知抛物线C 的方程为24x y =，点P 是抛物线C 的准线上的任意一点，过点P 作抛物线C 的两条切线，切点分别为,A B ，点M 是AB 的中点.（1）求证：切线PA 和PB 互相垂直；（2）求证：直线PM 与y 轴平行；（3）求PAB 面积的最小值.例9．（2024·全国·高三专题练习）已知中心在原点的椭圆1Γ和抛物线2Γ有相同的焦点(1,0)，椭圆1Γ的离心率为12，抛物线2Γ的顶点为原点.(1)求椭圆1Γ和抛物线2Γ的方程；(2)设点P 为抛物线2Γ准线上的任意一点，过点P 作抛物线2Γ的两条切线PA ，PB ，其中,A B 为切点.设直线PA ，PB 的斜率分别为1k ，2k ，求证：12k k 为定值.变式8．（2024·全国·高三专题练习）已知中心在原点的椭圆1C 和抛物线2C 有相同的焦点()1,0，椭圆1C 过点31,2G ⎛⎫⎪⎝⎭，抛物线2C 的顶点为原点．()1求椭圆1C 和抛物线2C 的方程；()2设点P 为抛物线2C 准线上的任意一点，过点P 作抛物线2C 的两条切线PA ，PB ，其中A ，B 为切点．①设直线PA ，PB 的斜率分别为1k ，2k ，求证：12k k 为定值；②若直线AB 交椭圆1C 于C ，D 两点，PAB S ，PCD S 分别是PAB ，PCD 的面积，试问：PABPCDS S 是否有最小值？若有，求出最小值；若没有，请说明理由．变式9．（2024·全国·高三专题练习）抛物级22(0)x py p =>的焦点F 到直线2py =-的距离为2.（1）求抛物线的方程；（2）设直线1y kx =+交抛物线于()11,A x y ，()22,B x y 两点，分别过A ，B 两点作抛物线的两条切线，两切线的交点为P ，求证：PF AB ⊥.变式10．（2024·河南驻马店·校考模拟预测）已知抛物线E ：()220x py p =>的焦点为F ，点P 在E 上，直线l ：20x y --=与E 相离．若P 到直线l 的距离为d ，且PF d +的最小值为2．过E 上两点,A B 分别作E 的两条切线，若这两条切线的交点M 恰好在直线l 上．（1）求E 的方程；（2）设线段AB 中点的纵坐标为n ，求证：当n 取得最小值时，MA MB ⊥．题型四：面积问题例10．（2024·全国·高三专题练习）已知抛物线C 的方程为()220x py p =>，点3,2A x ⎛⎫ ⎪⎝⎭是抛物线上的一点，且到抛物线焦点的距离为2．（1）求抛物线的方程；（2）点Q 为直线12y =-上的动点，过点Q 作抛物线C 的两条切线，切点分别为D ，E ，求QDE △面积的最小值．例11．（2024·全国·高三专题练习）已知抛物线22x py =上一点()0,1M x 到其焦点F 的距离为2．（1）求抛物线的方程；（2）如图，过直线:2l y =-上一点A 作抛物线的两条切线AP ，AQ ，切点分别为P ，Q ，且直线PQ 与y 轴交于点N ．设直线AP ，AQ 与x 轴的交点分别为B ，C ，求四边形ABNC 面积的最小值．例12．（2024·全国·高三专题练习）已知抛物线2:2(0)C x py p =>的焦点到原点的距离等于直线:440l x y --=的斜率.（1）求抛物线C 的方程及准线方程；（2）点P 是直线l 上的动点，过点P 作抛物线C 的两条切线，切点分别为A ，B ，求PAB 面积的最小值.变式11．（2024·全国·高三专题练习）如图，已知抛物线2:2(0)C y px p =>上的点R 的横坐标为1，焦点为F ，且||2RF =，过点(4,0)P -作抛物线C 的两条切线，切点分别为A 、B ，D 为线段PA 上的动点，过D 作抛物线的切线，切点为E （异于点A ，B ），且直线DE 交线段PB 于点H .(1)求抛物线C 的方程；(2)（i ）求证：||||AD BH +为定值；（ii ）设EAD ，EBH △的面积分别为12S S ，，求12133S S S =+的最小值.变式12．（2024·全国·高三专题练习）已知点A （﹣4，4）、B （4，4），直线AM 与BM 相交于点M ，且直线AM 的斜率与直线BM 的斜率之差为﹣2，点M 的轨迹为曲线C ．（1）求曲线C 的轨迹方程；（2）Q 为直线y=﹣1上的动点，过Q 作曲线C 的切线，切点分别为D 、E ，求△QDE 的面积S 的最小值．变式13．（2024·河南开封·河南省兰考县第一高级中学校考模拟预测）已知点()F ，平面上的动点S 到F 的距离是S 40+=的距离的2倍，记点S 的轨迹为曲线C ．(1)求曲线C 的方程；(2)过直线:2l y =上的动点()(),22P s s >向曲线C 作两条切线1l ，2l ，1l 交x 轴于M ，交y 轴于N ，2l 交x 轴于T ，交y 轴于Q ，记PNQ V 的面积为1S ，PMT △的面积为2S ，求12S S ⋅的最小值．题型五：外接圆问题例13．（2024·全国·高三专题练习）已知P 是抛物线C ：2134y x =-的顶点，A ，B 是C 上的两个动点，且4PA PB ⋅=- ．（1）试判断直线AB 是否经过某一个定点？若是，求这个定点的坐标；若不是，说明理由；（2）设点M 是PAB 的外接圆圆心，求点M 的轨迹方程．例14．（2024·高二单元测试）已知点P 是抛物线21:34C y x =-的顶点，A ，B 是C 上的两个动点，且4PA PB ⋅=- .（1）判断点()0,1D 是否在直线AB 上？说明理由；（2）设点M 是△PAB 的外接圆的圆心，点M 到x 轴的距离为d ，点()1,0N ，求MN d -的最大值.例15．（2024·全国·高三专题练习）已知点P 是抛物线21:34C y x =-的顶点，A ，B 是C 上的两个动点，且4PA PB ⋅=- .（1）判断点()0,1D -是否在直线AB 上？说明理由；（2）设点M 是△PAB 的外接圆的圆心，求点M 的轨迹方程.题型六：最值问题例16．（2024·全国·高三专题练习）如图已知()2,P t -是直线2x =-上的动点，过点P 作抛物线24y x =的两条切线，切点分别为,A B ，与y 轴分别交于,C D.（1）求证：直线AB 过定点，并求出该定点；（2）设直线AB 与x 轴相交于点Q ，记,A B 两点到直线PQ 的距离分别为12,d d ；求当12AB d d +取最大值时PCD 的面积.例17．（2024·湖南·高三校联考阶段练习）在直角坐标系xoy 中，已知抛物线()2:20C x py p =>，P 为直线1y x =-上的动点，过点P 作抛物线C 的两条切线，切点分别为,A B ，当P 在y 轴上时，OA OB ⊥.(1)求抛物线C 的方程；(2)求点O 到直线AB 距离的最大值.例18．（2024·辽宁沈阳·校联考二模）从抛物线的焦点发出的光经过抛物线反射后，光线都平行于抛物线的轴，根据光路的可逆性，平行于抛物线的轴射向抛物线后的反射光线都会汇聚到抛物线的焦点处，这一性质被广泛应用在生产生活中．如图，已知抛物线()2:21C x py p =>，从点()4,9发出的平行于y 轴的光线照射到抛物线上的D 点，经过抛物线两次反射后，反射光线由G 点射出，经过点()1,5-．(1)求抛物线C 的方程；(2)已知圆()22:34M x y +-=，在抛物线C 上任取一点E ，过点E 向圆M 作两条切线EA 和EB ，切点分别为A 、B ，求EA EB ⋅ 的取值范围．变式14．（2024·贵州·高三校联考阶段练习）已知抛物线()2:20C x py p =>上的点()02,y 到其焦点F 的距离为2.(1)求抛物线C 的方程；(2)已知点D 在直线l ：=3y -上，过点D 作抛物线C 的两条切线，切点分别为,A B ，直线AB 与直线l 交于点M ，过抛物线C 的焦点F 作直线AB 的垂线交直线l 于点N ，当MN 最小时，求ABMN 的值.变式15．（2024·黑龙江大庆·高二大庆实验中学校考阶段练习）已知抛物线2:4C y x =，点P 为直线2x =-上的任意一点，过点P 作抛物线C 的两条切线，切点分别为A ，B ，则点()0,1M 到直线AB 的距离的最大值为（）A ．1B ．4C ．5D题型七：角度相等问题例19．设抛物线2:C y x =的焦点为F ，动点P 在直线:20l x y --=上运动，过P 作抛物线C 的两条切线PA 、PB ，且与抛物线C 分别相切于A 、B 两点.（1）求△APB 的重心G 的轨迹方程.（2）证明∠PFA=∠PFB ．例20．（2024·全国·高三专题练习）已知F ，F '分别是椭圆221:171617C x y +=的上、下焦点，直线1l 过点F '且垂直于椭圆长轴，动直线2l 垂直1l 于点G ，线段GF 的垂直平分线交2l 于点H ，点H 的轨迹为2C .(1)求轨迹2C 的方程；(2)若动点P 在直线:20l x y --=上运动，且过点P 作轨迹2C 的两条切线PA 、PB ，切点为A 、B ，试猜想PFA ∠与PFB ∠的大小关系，并证明你的结论的正确性.例21．（2024·江苏南通·高三统考阶段练习）在平面直角坐标系xOy中，已知圆22=>交于点M，N（异于原点O），MN恰为该圆的+-=与抛物线2:2(0)C x py pG x y:(1)1直径，过点E（0，2）作直线交抛物线于A，B两点，过A，B两点分别作抛物线C的切线交于点P．(1)求证：点P的纵坐标为定值；∠=∠．(2)若F是抛物线C的焦点，证明：PFA PFBy x=的焦点为F，动点P 变式16．（2024·全国·高三专题练习）如图所示，设抛物线C：2x y--=上运动，过P作抛物线C的两条切线PA，PB，切点分别为A，B，在直线l：20求证：AFB BFP∠=∠.变式17．（2024·全国·高三专题练习）在平面直角坐标系xOy中，已知点E(0，2)，以OE为直径的圆与抛物线C∶x2=2py(p>0)交于点M，N(异于原点O)，MN恰为该圆的直径，过点E作直线交抛物线与A，B两点，过A，B两点分别作拋物线C的切线交于点P.（1）求证∶点P的纵坐标为定值；（2）若F是抛物线C的焦点，证明∶∠PFA=∠PFB。

抛物线中的阿基米德三角形典例：已知曲线C ：y =22x ，D 为直线y =12-上的动点，过D 作C 的两条切线，切点分别为A ，B .（1）证明：直线AB 过定点：（2）若以E (0，52)为圆心的圆与直线AB 相切，且切点为线段AB 的中点，求四边形ADBE 的面积.结论1.若),(00y x P 为准线上任一一点，则直线AB 过抛物线的焦点F . 结论2.过F 的直线与抛物线交于B A ,两点，以B A ,分别为切点做两条切线，则这两条切线的交点),(00y x P 的轨迹即为抛物线的准线.若),(00y x P 为准线上任一一点，则有：结论3.直线AB 的方程为)(22000y y p y y p x x +=+=. 结论4.AB PF ⊥.结论5.PB AP ⊥.结论6.直线AB 的中点为M ，则PF 平行于抛物线的对称轴.结论7.ABP ∆面积最小值为2p .1．已知抛物线C ：()220x py p =>，过点10,2P ⎛⎫- ⎪⎝⎭作抛物线C 的两条切线PA ，PB ，A ，B 为切点，若直线AB 经过抛物线C 的焦点，则抛物线C 的方程为（ ） A ．28x y = B ．24x y = C ．22x y = D ．2x y =2．已知曲线24x y =，动点P 在直线3y =-上，过点P 作曲线的两条切线12,l l ，切点分别为,A B ，则直线AB 截圆22650x y y +-+=所得弦长为（ ）A B ．2 C ．4 D ．3．已知点1F 是抛物线2:2C x py =的焦点，点2F 为抛物线C 的对称轴与其准线的交点，过2F 作抛物线C 的切线，设其中一个切点为A ，若点A 恰好在以12,F F 为焦点的双曲线上，则双曲线的离心率为（ ）A 1-B ．1C 1D ．24.已知点)1,23(-M ，直线l 过抛物线y x C 4:2=的焦点且交抛物线于B A ,两点，且AM 恰好与抛物线C 相切，那么线段AB 的中点坐标为_______.5.已知点)1,1(-M ，直线l 过抛物线x y C 4:2=的焦点且斜率为k 并交抛物线于B A ,两点，若90=∠AMB ，则=k _______.。

阿基米德三角形在高考中的应用在咱们高中数学的世界里，有一个神秘又有趣的家伙，叫做阿基米德三角形。

这玩意儿可不像它名字听起来那么高大上、遥不可及，实际上，在高考中，它可是能帮咱大显身手的“秘密武器”！先来说说啥是阿基米德三角形。

简单来讲，抛物线的弦与过弦的端点的两条切线所围成的三角形就叫阿基米德三角形。

这名字听起来是不是有点拗口？别担心，咱们举个例子就明白啦。

我记得之前给学生们讲这部分内容的时候，有个叫小明的同学，一开始那是一头雾水，满脸写着“这都是啥呀”。

我就给他画了个抛物线，标上几个点，然后一点点引导他理解弦和切线的概念。

小明瞪着大眼睛，紧紧盯着黑板，那认真的劲儿，让我都忍不住笑了。

阿基米德三角形在高考中的应用那可多了去了。

比如说，它可以用来解决抛物线中的最值问题。

想象一下，你正在考场上，面对一道求最值的题目，心里正发慌呢，这时候突然想起阿基米德三角形的相关性质，一下子就找到了解题的突破口，那感觉，简直爽歪歪！再比如，利用阿基米德三角形还能巧妙地处理抛物线中的面积问题。

有这么一道题：已知抛物线的方程和其中一条弦的两个端点坐标，让求由这条弦和抛物线所围成的图形的面积。

这时候，如果能熟练运用阿基米德三角形的知识，把问题转化一下，答案就会呼之欲出。

我之前在研究高考真题的时候，发现好多省份的试卷里都有阿基米德三角形的影子。

就拿去年的某套试卷来说，有一道选择题，看似很复杂，其实就是在考查阿基米德三角形中切线斜率的关系。

当时我就在想，如果考生们提前掌握了这个知识点，这道题简直就是送分题啊！咱们学习阿基米德三角形，可不能死记硬背那些公式和性质，得真正理解它的本质。

就像搭积木一样，只有明白了每一块积木的作用，才能搭出漂亮的城堡。

还记得有一次课堂小测验，我故意出了一道有关阿基米德三角形的难题，想看看同学们掌握得怎么样。

结果大部分同学都做得不太好，一个个愁眉苦脸的。

课后我就找了几个同学交流，发现他们只是记住了公式，却没有真正理解其中的逻辑。

高中数学阿基米德三角形1.在平面直角坐标系xOy中，过y轴正方向上一点C(0,c)作一条直线，与抛物线y=x^2相交于AB两点。

一条垂直于x轴的直线，分别与线段AB和直线l:y=-c交于P,Q。

1）若OA×OB=2，求c的值；2）若P为线段AB的中点，证明QA为此抛物线的切线；3）是否存在一个点P，使得QA为此抛物线的切线？请说明理由。

2.抛物线(p>0)，点M(x,y)在抛物线C2上，过M作C1的切线，切点为A,B（当M为原点O时，A,B重合于O）x=1/2，切线MA的斜率为-1/2.I）求p的值；II）当M在C2上运动时，求线段AB中点N的轨迹方程（当A,B重合于O时，中点为O）。

3.设抛物线方程为x^2=2py(p>0)，M为直线y=-2p上任意一点，过M引抛物线的切线，切点分别为A，B。

Ⅰ）证明：A，M，B三点的横坐标成等差数列；Ⅱ）已知当M点的坐标为(2，-2p)时，AB=4√10.求此时抛物线的方程；Ⅲ）是否存在点M，使得点C关于直线AB的对称点D 在抛物线x^2=2py(p>0)上，其中，点C满足OC=OA+OB（O 为坐标原点）？若存在，求出所有适合题意的点M的坐标；若不存在，请说明理由。

4.对每个正整数n，An(xn,yn)是抛物线x^2=4y上的点，过焦点F的直线FAn角抛物线于另一点Bn(sn,tn)。

Ⅰ）证明：xn*sn=-4 (n≥1)；Ⅱ）取xn=2，并记Cn为抛物线上分别以An与Bn为切点的两条切线的交点。

试证：FC1+FC2+。

+FCn=2n-2-n+1+1.5.设抛物线C:y=x^2的焦点为F，动点P在直线l:x-y-2=0上运动，过P作抛物线C的两条切线PA、PB，且与抛物线C 分别相切于A、B两点。

1）求△APB的重心G的轨迹方程；2）证明∠PFA=∠PFB。

6.已知抛物线x^2=4y的焦点为F，A、B是热线上的两动点，且AF=λFB(λ>0)。

专题5 阿基米德三角形综合训练一、单选题1．抛物线上任意两点A ，B 处的切线交于点P ，称PAB △为“阿基米德三角形”，当线段AB 经过抛物线的焦点F 时，PAB △具有以下特征： ①P 点必在抛物线的准线上；②PF AB ⊥．若经过抛物线24y x =的焦点的一条弦为AB ，“阿基米德三角形”为PAB △，且点P 的纵坐标为4，则直线AB 的方程为（ ） A ．210x y −−= B ．220x y +−= C ．210x y +−=D ．220x y −−=（2022·江西九江·高二期末）2．阿基米德（Archimedes ，公元前287年-公元前212年），出生于古希腊西西里岛叙拉古（今意大利西西里岛上），伟大的古希腊数学家、物理学家，与高斯、牛顿并称为世界三大数学家．有一类三角形叫做阿基米德三角形．．．．．．．（过抛物线的弦与过弦端点的两切线所围成的三角形），他利用“通近法”得到抛物线的弦与抛物线所围成的封闭图形的面积等于阿基米德三角形面积的23（即右图中阴影部分面积等于PAB △面积的23）．若抛物线方程为22(0)y px p =>，且直线2px =与抛物线围成封闭图形的面积为6，则p =（ ）A ．1B ．2C ．32D ．33．阿基米德（公元前287年～公元前212年）是古希腊伟大的物理学家、数学家和天文学家.他研究抛物线的求积法得出著名的阿基米德定理，并享有“数学之神”的称号.抛物线的弦与过弦的端点的两条切线所围成的三角形被称为阿基米德三角形.如图，PAB △为阿基米德三角形.抛物线22(0)x py p =>上有两个不同的点()()1122,,,A x y B x y ，以A ，B 为切点的抛物线的切线,PA PB 相交于P .给出如下结论，其中正确的为（ ）（1）若弦AB 过焦点，则ABP △为直角三角形且90APB ︒∠=； （2）点P 的坐标是1212,22x x x x +⎛⎫⎪⎝⎭；（3）PAB △的边AB 所在的直线方程为()121202x x py x x x −−=+； （4）PAB △的边AB 上的中线与y 轴平行（或重合）.A ．（2）（3）（4）B ．（1）（2）C ．（1）（2）（3）D ．（1）（3）（4）（2020·云南师大附中高三月考）4．过抛物线()220y px p =>的焦点F 作抛物线的弦与抛物线交于A 、B 两点，M 为AB 的中点，分别过A 、B 两点作抛物线的切线1l 、2l 相交于点P .PAB △又常被称作阿基米德三角形.下面关于PAB △的描述： ①P 点必在抛物线的准线上； ②AP PB ⊥；③设()11,A x y 、()22,B x y ，则PAB △的面积S 的最小值为22p ； ④PF AB ⊥； ⑤PM 平行于x 轴. 其中正确的个数是（ ） A ．2B ．3C ．4D ．5（2022·河南·林州一中高二开学考试）5．我们把圆锥曲线的弦AB 与过弦的端点A ，B 处的两条切线所围成的三角形PAB △（P 为两切线的交点）叫做“阿基米德三角形”．抛物线有一类特殊的“阿基米德三角形”，当线段AB 经过抛物线的焦点F 时，PAB △具有以下性质：①P 点必在抛物线的准线上； ②PA PB ⊥； ③PF AB ⊥．已知直线():1l y k x =−与抛物线24y x =交于A ，B 点，若8AB =，则抛物线的“阿基米德三角形” PAB △的面积为（ ） A ．82B ．42C ．22D 26．过抛物线()220y px p =>的焦点F 作抛物线的弦，与抛物线交于A ，B 两点，分别过A ，B 两点作抛物线的切线1l ，2l 相交于点P ，PAB △又常被称作阿基米德三角形．PAB △的面积S 的最小值为（ ）A ．23pB ．22pC ．2pD 227．抛物线的弦与过弦的端点的两条切线所围成的三角形常被称为阿基米德三角形，阿基米德三角形有一些有趣的性质，如：若抛物线的弦过焦点，则过弦的端点的两条切线的交点在其准线上.设抛物线22(0)y px p =>，弦AB 过焦点，ABQ △为阿基米德三角形，则ABQ △为（ ）. A ．锐角三角形 B ．直角三角形C ．钝角三角形D ．随Q 位置变化前三种情况都有可能关系（2022·重庆·西南大学附中高二月考）8．我们把圆锥曲线的弦AB 与过弦的端点A ，B 处的两条切线所围成的三角形PAB △（P 为两切线的交点）叫做“阿基米德三角形”，抛物线有一类特殊的“阿基米德三角形”，当线段AB 经过抛物线的焦点F 时，PAB △具有以下性质：①P 点必在抛物线的准线上；②PA PB ⊥；③PF AB ⊥.已知直线l ：(1)y k x =−与抛物线C ：24y x =交于A ，B 点，若8AB =，记此时抛物线 C 的“阿基米德三角形”为PAB △，则P 点为（ ） A ．()1,2−± B ．()1,2− C ．()1,2−−D ．()1,1−±（2022·陕西西安·二模）9．阿基米德（公元前287年-公元前212年）是古希腊伟大的物理学家、数学家、天文学家，不仅在物理学方面贡献巨大，还享有“数学之神”的称号．抛物线上任意两点A ，B 处的切线交于点P ，称三角形P AB 为“阿基米德三角形”.已知抛物线C ：28x y =的焦点为F ，过A ，B360y −+=，关于“阿基米德三角形”△P AB ，下列结论不正确的是（ ） A ．323AB =B ．PA PB ⊥C ．PF AB ⊥D ．点P 的坐标为)2−10．圆锥曲线的弦与过弦的端点的两条切线所围成的三角形叫做阿基米德三角形.过抛物线焦点F 作抛物线的弦，与抛物线交于A 、B 两点，分别过A 、B 两点做抛物线的切线l 1，l 2相交于P 点，那么阿基米德三角形P AB 满足以下特性：①P 点必在抛物线的准线上；②△P AB 为直角三角形，且APB ∠为直角；③PF ⊥AB .已知P 为抛物线24x y =的准线上一点，则阿基米德三角形P AB 的面积的最小值为（ ） A ．2 B ．3 C ．4 D ．5二、多选题11．过抛物线()220y px p =>的焦点F 作抛物线的弦，与抛物线交于A ，B 两点，M 为AB的中点，分别过A ，B 两点作抛物线的切线1l ，2l 相交于点P ，PAB △又常被称作阿基米德三角形．下面关于PAB △的描述其中正确的是（ ） A ．P 点必在抛物线的准线上；B ．设()11,A x y ，()22,B x y ，则PAB △的面积S 的最小值为22p ；C ．PF AB ⊥D ．PM 平行于x 轴． （2022·重庆·模拟）12．阿基米德（公元前287年——公元前212年）是古希腊伟大的物理学家、数学家、天文学家，不仅在物理学方面贡献巨大，还享有“数学之神”的称号．抛物线上任意两点A 、B 处的切线交于点P ，称PAB △为“阿基米德三角形”．已知抛物线C ：28x y =的焦点为F ，过A 、B 360y −+=，关于“阿基米德三角形”PAB △，下列结论正确的是（ ）A ．323AB =B ．PA PB ⊥C ．点P 的坐标为)3,2−D ．PF AB ⊥（2022·江苏徐州·模拟）13．阿基米德是古希腊伟大的物理学家、数学家、天文学家，享有“数学之神”的称号．若抛物线上任意两点A ，B 处的切线交于点P ，则称PAB △为“阿基米德三角形”．已知抛物线28x y =的焦点为F ，过抛物线上两点A ，B 的直线的方程为20x y −+=，弦AB 的中点为C ，则关于“阿基米德三角形”PAB △，下列结论正确的是（ ） A ．点(3,2)P −B ．PC x ⊥轴C ．PA PB ⊥D ．PF AB ⊥（2022江苏省前黄高级中学高三月考）14．阿基米德是伟大的物理学家，更是伟大的数学家，他曾经对高中教材中的抛物线做过系统而深入的研究，定义了抛物线阿基米德三角形：抛物线的弦与弦的端点处的两条切线围成的三角形称为抛物线阿基米德三角形.设抛物线C ：2yx 上两个不同点,A B 横坐标分别为1x ，2x ，以,A B 为切点的切线交于P 点.则关于阿基米德三角形PAB 的说法正确的有（ ）A ．若AB 过抛物线的焦点，则P 点一定在抛物线的准线上 B ．若阿基米德三角形PAB 33C ．若阿基米德三角形PAB 为直角三角形，则其面积有最小值14D ．一般情况下，阿基米德三角形PAB 的面积212||4x x S −=（2022湖北·武汉市第十一中学高二月考）15．抛物线的弦与过弦的端点的两条切线所围成的三角形常被称为阿基米德三角形，阿基米德三角形有一些有趣的性质，如：若抛物线的弦过焦点，则过弦的端点的两条切线的交点在其准线上．设抛物线22(0)y px p =>，弦AB 过焦点F ，ABQ △为其阿基米德三角形，则下列结论一定成立的是（ ） A ．存在点Q ，使得0QA QB ⋅> B ．||||AQ AB AF AB ⋅=⋅C ．对于任意的点Q ，必有向量QA QB +与向量(1,0)a =−共线D ．ABQ △面积的最小值为2p（2022·江苏·徐州市第七中学高三月考）16．阿基米德的“平衡法”体现了近代积分法的基本思想，他用平衡法求得抛物线弓形（抛物线与其弦AB 所在直线围成的图形）面积等于此弓形的内接三角形（内接三角形ABC 的顶点C 在抛物线上，且在过弦AB 的中点与抛物线对称轴平行或重合的直线上）面积的43.现已知直线32y x p =−+与抛物线2:2(0)E y px p =>交于A ，B 两点，且A 为第一象限的点，E 在A 处的切线为l ，线段AB 的中点为D ，直线//DC x 轴所在的直线交E 于点C ，下列说法正确的是（ ）A ．若抛物线弓形面积为8，则其内接三角形的面积为6B ．切线l 的方程为220x y p −+=C ．若()1*4n n ABC A S n N −∆⋅=∈，则弦AB 对应的抛物线弓形面积大于()121423n n A A A A n −++++≥ D ．若分别取AC BC ，的中点1V ，2V ，过1V ，2V 且垂直y 轴的直线分别交E 于1C ，2C ，则1214ACC BCC ABC S S S ∆∆∆+=三、填空题（2022·浙江台州·高三期末）17．古希腊著名数学家阿基米德是这样求抛物弓形面积的：以抛物弓形的弦为底，以抛物线上平行于弦的切线的切点作弓形的内接三角形；在以该内接三角形两腰为弦的两个抛物线弓形内用同样的方法作出内接三角形，等等．从第二次开始，每次作出的内接三角形面积之和是前一次所作出的内接三角形面积和的14．若第一次所作的内接三角形面积为1，则第三次所作的内接三角形面积和为________． （2020·江苏无锡·高三月考）18．被誉为“数学之神”之称的阿基米德（前287—前212），是古希腊伟大的物理学家、数学家、天文学家，他最早利用逼近的思想证明了如下结论：抛物线的弦与抛物线所围成的封闭图形的面积，等于抛物线的弦与经过弦的端点的两条切线所围成的三角形面积的三分之二．这个结论就是著名的阿基米德定理，其中的三角形被称为阿基米德三角形．在平面直角坐标系心中，已知直线l ：y ＝4与抛物线C ：214y x =交于A ，B 两点，则弦与拋物线C 所围成的封闭图形的面积为_______．19．抛物线的弦与过弦的端点的两条切线所围成的三角形常称为阿基米德三角形，因为阿基米德最早利用逼近的思想证明了：抛物线的弦与抛物线所围成的封闭图形的面积等于阿基米德三角形面积的23．已知(2,1),(2,1)A B −为抛物线2:4C x y =上两点，则在A 点处抛物线C 的切线的斜率为_______；弦AB 与抛物线所围成的封闭图形的面积为_________． 四、解答题（2022·江苏苏州·模拟）20．已知椭圆22122:1(0)x y C a b a b+=>>且经过1(2,0)P −，231,2P ⎛⎫ ⎪⎝⎭，331,2P ⎛⎫− ⎪⎝⎭，4(1,1)P −中的三点，抛物线22:2(0)C y px p =>，椭圆1C 的右焦点是抛物线2C 的焦点．(1)求曲线1C ，2C 的方程；(2)点P 是椭圆1C 的点，且过点P 可以作抛物线2C 的两条切线，切点为A ，B ，求三角形PAB 面积的最大值． （2022·广东·高二月考）21．已知线段AB 是抛物线24y x =的弦，且过抛物线焦点F .(1)过点B 作直线与抛物线对称轴平行，交抛物线的准线于点E ，求证：A O E 、、三点共线(O 为坐标原点)；(2)设M 是抛物线准线上一点，过M 作抛物线的切线，切点为11A B 、. 求证：（i ）两切线互相垂直；（ii ）直线11A B 过定点，请求出该定点坐标. （2022·浙江·赫威斯育才高中模拟）22．如图，过点(,)P m n 作抛物线2:2(0)C x py p =>的两条切线PA ，PB ，切点分别是A ，B ，动点Q 为抛物线C 上在A ，B 之间部分上的任意一点，抛物线C 在点Q 处的切线分别交PA ，PB 于点M ，N .(1)若AP PB ⊥，证明：直线AB 经过点0,2p ⎛⎫⎪⎝⎭；(2)若分别记PMN ，ABQ △的面积为1S ，2S ，求12S S 的值. 23．过抛物线的一条弦的中点作平行于抛物线对称轴的平行线（或与对称轴重合），交抛物线于一点，称以该点及弦的端点为顶点的三角形为这条弦的阿基米德三角形（简称阿氏三角形）.现有抛物线M :2y ax =，直线l ：y bx c =+（其中a ，b ，c 是常数，且0a >），直线l 交抛物线M 于A ，B 两点，设弦AB 的阿氏三角形是ABC .（1）指出抛物线M 的焦点坐标和准线方程； （2）求ABC 的面积（用a ，b ，c 表示）；（3）称AB 的阿氏ABC 为一阶的；AC 、BC 的阿氏ACD △、BCE 为二阶的；AD 、DC 、CE 、EB 的阿氏三角形为三阶的；……，由此进行下去，记所有的()*k k ∈N阶阿氏三角形的面积之和为k S ，探索k S 与1k S +之间的关系，并求()12lim n n S S S →∞+++专题3 阿基米德三角形 微点2 阿基米德三角形综合训练专题3 阿基米德三角形 微点2 阿基米德三角形综合训练 一、单选题1．抛物线上任意两点A ，B 处的切线交于点P ，称PAB △为“阿基米德三角形”，当线段AB 经过抛物线的焦点F 时，PAB △具有以下特征： ①P 点必在抛物线的准线上；②PF AB ⊥．若经过抛物线24y x =的焦点的一条弦为AB ，“阿基米德三角形”为PAB △，且点P 的纵坐标为4，则直线AB 的方程为（ ） A ．210x y −−= B ．220x y +−= C ．210x y +−=D ．220x y −−=（2022·江西九江·高二期末）2．阿基米德（Archimedes ，公元前287年-公元前212年），出生于古希腊西西里岛叙拉古（今意大利西西里岛上），伟大的古希腊数学家、物理学家，与高斯、牛顿并称为世界三大数学家．有一类三角形叫做阿基米德三角形．．．．．．．（过抛物线的弦与过弦端点的两切线所围成的三角形），他利用“通近法”得到抛物线的弦与抛物线所围成的封闭图形的面积等于阿基米德三角形面积的23（即右图中阴影部分面积等于PAB △面积的23）．若抛物线方程为22(0)y px p =>，且直线2px =与抛物线围成封闭图形的面积为6，则p =（ ）A ．1B ．2C ．32D ．33．阿基米德（公元前287年～公元前212年）是古希腊伟大的物理学家、数学家和天文学家.他研究抛物线的求积法得出著名的阿基米德定理，并享有“数学之神”的称号.抛物线的弦与过弦的端点的两条切线所围成的三角形被称为阿基米德三角形.如图，PAB △为阿基米德三角形.抛物线22(0)x py p =>上有两个不同的点()()1122,,,A x y B x y ，以A ，B 为切点的抛物线的切线,PA PB 相交于P .给出如下结论，其中正确的为（ ） （1）若弦AB 过焦点，则ABP △为直角三角形且90APB ︒∠=；（2）点P 的坐标是1212,22x x x x +⎛⎫⎪⎝⎭；（3）PAB △的边AB 所在的直线方程为()121202x x py x x x −−=+； （4）PAB △的边AB 上的中线与y 轴平行（或重合）.A ．（2）（3）（4）B ．（1）（2）C ．（1）（2）（3）D ．（1）（3）（4）（2020·云南师大附中高三月考）4．过抛物线()220y px p =>的焦点F 作抛物线的弦与抛物线交于A 、B 两点，M 为AB 的中点，分别过A 、B 两点作抛物线的切线1l 、2l 相交于点P .PAB △又常被称作阿基米德三角形.下面关于PAB △的描述： ①P 点必在抛物线的准线上； ②AP PB ⊥；③设()11,A x y 、()22,B x y ，则PAB △的面积S 的最小值为22p ； ④PF AB ⊥； ⑤PM 平行于x 轴. 其中正确的个数是（ ） A ．2B ．3C ．4D ．5（2022·河南·林州一中高二开学考试）5．我们把圆锥曲线的弦AB 与过弦的端点A ，B 处的两条切线所围成的三角形PAB △（P 为两切线的交点）叫做“阿基米德三角形”．抛物线有一类特殊的“阿基米德三角形”，当线段AB 经过抛物线的焦点F 时，PAB △具有以下性质： ①P 点必在抛物线的准线上； ②PA PB ⊥； ③PF AB ⊥．已知直线():1l y k x =−与抛物线24y x =交于A ，B 点，若8AB =，则抛物线的“阿基米德三角形” PAB △的面积为（ ） A ．82B ．42C ．22D 26．过抛物线()220y px p =>的焦点F 作抛物线的弦，与抛物线交于A ，B 两点，分别过A ，B 两点作抛物线的切线1l ，2l 相交于点P ，PAB △又常被称作阿基米德三角形．PAB △的面积S 的最小值为（ ）A ．23pB ．22pC ．2pD 227．抛物线的弦与过弦的端点的两条切线所围成的三角形常被称为阿基米德三角形，阿基米德三角形有一些有趣的性质，如：若抛物线的弦过焦点，则过弦的端点的两条切线的交点在其准线上.设抛物线22(0)y px p =>，弦AB 过焦点，ABQ △为阿基米德三角形，则ABQ △为（ ）. A ．锐角三角形 B ．直角三角形C ．钝角三角形D ．随Q 位置变化前三种情况都有可能关系（2022·重庆·西南大学附中高二月考）8．我们把圆锥曲线的弦AB 与过弦的端点A ，B 处的两条切线所围成的三角形PAB △（P 为两切线的交点）叫做“阿基米德三角形”，抛物线有一类特殊的“阿基米德三角形”，当线段AB 经过抛物线的焦点F 时，PAB △具有以下性质：①P 点必在抛物线的准线上；②PA PB ⊥；③PF AB ⊥.已知直线l ：(1)y k x =−与抛物线C ：24y x =交于A ，B 点，若8AB =，记此时抛物线 C 的“阿基米德三角形”为PAB △，则P 点为（ ） A ．()1,2−± B ．()1,2− C ．()1,2−−D ．()1,1−±（2022·陕西西安·二模）9．阿基米德（公元前287年-公元前212年）是古希腊伟大的物理学家、数学家、天文学家，不仅在物理学方面贡献巨大，还享有“数学之神”的称号．抛物线上任意两点A ，B 处的切线交于点P ，称三角形P AB 为“阿基米德三角形”.已知抛物线C ：28x y =的焦点为F ，过A ，B 3360x y −+=，关于“阿基米德三角形”△P AB ，下列结论不正确的是（ ） A ．323AB =B ．PA PB ⊥C ．PF AB ⊥D ．点P 的坐标为)3,2−10．圆锥曲线的弦与过弦的端点的两条切线所围成的三角形叫做阿基米德三角形.过抛物线焦点F 作抛物线的弦，与抛物线交于A 、B 两点，分别过A 、B 两点做抛物线的切线l 1，l 2相交于P 点，那么阿基米德三角形P AB 满足以下特性：①P 点必在抛物线的准线上；②△P AB 为直角三角形，且APB ∠为直角；③PF ⊥AB .已知P 为抛物线24x y =的准线上一点，则阿基米德三角形P AB 的面积的最小值为（ ） A ．2 B ．3 C ．4 D ．5二、多选题11．过抛物线()220y px p =>的焦点F 作抛物线的弦，与抛物线交于A ，B 两点，M 为AB的中点，分别过A ，B 两点作抛物线的切线1l ，2l 相交于点P ，PAB △又常被称作阿基米德三角形．下面关于PAB △的描述其中正确的是（ ） A ．P 点必在抛物线的准线上；B ．设()11,A x y ，()22,B x y ，则PAB △的面积S 的最小值为22p ； C ．PF AB ⊥ D ．PM 平行于x 轴． （2022·重庆·模拟）12．阿基米德（公元前287年——公元前212年）是古希腊伟大的物理学家、数学家、天文学家，不仅在物理学方面贡献巨大，还享有“数学之神”的称号．抛物线上任意两点A 、B 处的切线交于点P ，称PAB △为“阿基米德三角形”．已知抛物线C ：28x y =的焦点为F ，过A 、B 360y −+=，关于“阿基米德三角形”PAB △，下列结论正确的是（ ） A ．323AB =B ．PA PB ⊥C ．点P 的坐标为)2−D ．PF AB ⊥（2022·江苏徐州·模拟）13．阿基米德是古希腊伟大的物理学家、数学家、天文学家，享有“数学之神”的称号．若抛物线上任意两点A ，B 处的切线交于点P ，则称PAB △为“阿基米德三角形”．已知抛物线28x y =的焦点为F ，过抛物线上两点A ，B 的直线的方程为20x y −+=，弦AB 的中点为C ，则关于“阿基米德三角形”PAB △，下列结论正确的是（ ）A ．点2)P −B ．PC x ⊥轴C ．PA PB ⊥D ．PF AB ⊥（2022江苏省前黄高级中学高三月考）14．阿基米德是伟大的物理学家，更是伟大的数学家，他曾经对高中教材中的抛物线做过系统而深入的研究，定义了抛物线阿基米德三角形：抛物线的弦与弦的端点处的两条切线围成的三角形称为抛物线阿基米德三角形.设抛物线C ：2yx 上两个不同点,A B 横坐标分别为1x ，2x ，以,A B 为切点的切线交于P 点.则关于阿基米德三角形PAB 的说法正确的有（ ）A ．若AB 过抛物线的焦点，则P 点一定在抛物线的准线上 B ．若阿基米德三角形PAB 33C ．若阿基米德三角形PAB 为直角三角形，则其面积有最小值14D ．一般情况下，阿基米德三角形PAB 的面积212||4x x S −=（2022湖北·武汉市第十一中学高二月考）15．抛物线的弦与过弦的端点的两条切线所围成的三角形常被称为阿基米德三角形，阿基米德三角形有一些有趣的性质，如：若抛物线的弦过焦点，则过弦的端点的两条切线的交点在其准线上．设抛物线22(0)y px p =>，弦AB 过焦点F ，ABQ △为其阿基米德三角形，则下列结论一定成立的是（ ） A ．存在点Q ，使得0QA QB ⋅> B ．||||AQ AB AF AB ⋅=⋅C ．对于任意的点Q ，必有向量QA QB +与向量(1,0)a =−共线D ．ABQ △面积的最小值为2p（2022·江苏·徐州市第七中学高三月考）16．阿基米德的“平衡法”体现了近代积分法的基本思想，他用平衡法求得抛物线弓形（抛物线与其弦AB 所在直线围成的图形）面积等于此弓形的内接三角形（内接三角形ABC 的顶点C 在抛物线上，且在过弦AB 的中点与抛物线对称轴平行或重合的直线上）面积的43.现已知直线32y x p =−+与抛物线2:2(0)E y px p =>交于A ，B 两点，且A 为第一象限的点，E 在A 处的切线为l ，线段AB 的中点为D ，直线//DC x 轴所在的直线交E 于点C ，下列说法正确的是（ ）A ．若抛物线弓形面积为8，则其内接三角形的面积为6B ．切线l 的方程为220x y p −+=C ．若()1*4n n ABC A S n N −∆⋅=∈，则弦AB 对应的抛物线弓形面积大于()121423n n A A A A n −++++≥ D ．若分别取AC BC ，的中点1V ，2V ，过1V ，2V 且垂直y 轴的直线分别交E 于1C ，2C ，则1214ACC BCC ABC S S S ∆∆∆+=三、填空题（2022·浙江台州·高三期末）17．古希腊著名数学家阿基米德是这样求抛物弓形面积的：以抛物弓形的弦为底，以抛物线上平行于弦的切线的切点作弓形的内接三角形；在以该内接三角形两腰为弦的两个抛物线弓形内用同样的方法作出内接三角形，等等．从第二次开始，每次作出的内接三角形面积之和是前一次所作出的内接三角形面积和的14．若第一次所作的内接三角形面积为1，则第三次所作的内接三角形面积和为________． （2020·江苏无锡·高三月考）18．被誉为“数学之神”之称的阿基米德（前287—前212），是古希腊伟大的物理学家、数学家、天文学家，他最早利用逼近的思想证明了如下结论：抛物线的弦与抛物线所围成的封闭图形的面积，等于抛物线的弦与经过弦的端点的两条切线所围成的三角形面积的三分之二．这个结论就是著名的阿基米德定理，其中的三角形被称为阿基米德三角形．在平面直角坐标系心中，已知直线l ：y ＝4与抛物线C ：214y x =交于A ，B 两点，则弦与拋物线C 所围成的封闭图形的面积为_______．19．抛物线的弦与过弦的端点的两条切线所围成的三角形常称为阿基米德三角形，因为阿基米德最早利用逼近的思想证明了：抛物线的弦与抛物线所围成的封闭图形的面积等于阿基米德三角形面积的23．已知(2,1),(2,1)A B −为抛物线2:4C x y =上两点，则在A 点处抛物线C 的切线的斜率为_______；弦AB 与抛物线所围成的封闭图形的面积为_________． 四、解答题（2022·江苏苏州·模拟）20．已知椭圆22122:1(0)x y C a b a b+=>>且经过1(2,0)P −，231,2P ⎛⎫ ⎪⎝⎭，331,2P ⎛⎫− ⎪⎝⎭，4(1,1)P −中的三点，抛物线22:2(0)C y px p =>，椭圆1C 的右焦点是抛物线2C 的焦点．(1)求曲线1C ，2C 的方程；(2)点P 是椭圆1C 的点，且过点P 可以作抛物线2C 的两条切线，切点为A ，B ，求三角形PAB 面积的最大值． （2022·广东·高二月考）21．已知线段AB 是抛物线24y x =的弦，且过抛物线焦点F .(1)过点B 作直线与抛物线对称轴平行，交抛物线的准线于点E ，求证：A O E 、、三点共线(O 为坐标原点)；(2)设M 是抛物线准线上一点，过M 作抛物线的切线，切点为11A B 、. 求证：（i ）两切线互相垂直；（ii ）直线11A B 过定点，请求出该定点坐标.（2022·浙江·赫威斯育才高中模拟）22．如图，过点(,)P m n 作抛物线2:2(0)C x py p =>的两条切线PA ，PB ，切点分别是A ，B ，动点Q 为抛物线C 上在A ，B 之间部分上的任意一点，抛物线C 在点Q 处的切线分别交PA ，PB 于点M ，N .(1)若AP PB ⊥，证明：直线AB 经过点0,2p ⎛⎫ ⎪⎝⎭；(2)若分别记PMN ，ABQ △的面积为1S ，2S ，求12S S 的值. 23．过抛物线的一条弦的中点作平行于抛物线对称轴的平行线（或与对称轴重合），交抛物线于一点，称以该点及弦的端点为顶点的三角形为这条弦的阿基米德三角形（简称阿氏三角形）.现有抛物线M :2y ax =，直线l ：y bx c =+（其中a ，b ，c 是常数，且0a >），直线l 交抛物线M 于A ，B 两点，设弦AB 的阿氏三角形是ABC .（1）指出抛物线M 的焦点坐标和准线方程； （2）求ABC 的面积（用a ，b ，c 表示）；（3）称AB 的阿氏ABC 为一阶的；AC 、BC 的阿氏ACD △、BCE 为二阶的；AD 、DC 、CE 、EB 的阿氏三角形为三阶的；……，由此进行下去，记所有的()*k k ∈N 阶阿氏三角形的面积之和为k S ，探索k S 与1k S +之间的关系，并求()12lim n n S S S →∞+++.参考答案：1．A【分析】由PAB △为“阿基米德三角形”，且线段AB 经过抛物线24y x =的焦点，得到点(1,4)P −，进而得到直线PF 的斜率，再由PF AB ⊥，得到直线AB 的斜率即可.【详解】设抛物线的焦点为F ，由题意可知，抛物线24y x =的焦点坐标为(1,0)F ，准线方程为1x =−， 因为PAB △为“阿基米德三角形”，且线段AB 经过抛物线24y x =的焦点， 所以点P 必在抛物线的准线上， 所以点(1,4)P −，∴直线PF 的斜率为40211−=−−−． 又因为PF AB ⊥，所以直线AB 的斜率为12，所以直线AB 的方程为10(1)2y x −=−，即210x y −−=，故选：A ． 2．D【分析】根据题目所给条件可得阿基米德三角形的面积，再利用三角形面积公式即可求解. 【详解】由题意可知，当过焦点的弦垂直于x 轴时，即2p x =时，22212263323⎛⎫=⋅⋅== ⎪⎝⎭PABS p p p ，即3p =， 故选：D ． 3．D【分析】设211,2x A x p ⎛⎫ ⎪⎝⎭，222,2x B x p ⎛⎫ ⎪⎝⎭，12x x <，由导数的几何意义得切线斜率， 利用焦点弦性质得221PA PBp k k p−⋅==−，正确； 写出切线方程，联立求出P 点坐标，得（2）错误；用,A B 两点坐标表示出AB k ，写出直线AB 方程，并化简可得（3）正确； 设N 为抛物线弦AB 的中点，立即得（4）正确；【详解】由题意设211,2x A x p ⎛⎫ ⎪⎝⎭，222,2x B x p ⎛⎫ ⎪⎝⎭，12x x <，由22x py =，得22x y p =，则x y p '=，所以1PAx k p =，2PB x k p =，若弦AB 过焦点，∴212x x p =−，∴221PA PB p k k p−⋅==−，∴PA PB ⊥，故（1）正确；以点A 为切点的切线方程为2111()2x x y x x p p−=−，以点B 为切点的切线方程为2222()2x x y x x p p −=−，联立消去y 得122x x x +=，将122x x x +=代入2111()2x x y x x p p−=−，得122x x y p =，所以1212,22x x x x P p ⎛⎫+ ⎪⎝⎭，故（2）错误； 设N 为抛物线弦AB 的中点，N 的横坐标为122N x x x +=，因此则直线PN 平行于y 轴，即平行于抛物线的对称轴，故（4）正确；设直线AB 的斜率为222121122121222x x y y x x p p k x x x x p−−+===−−，故直线AB 的方程为21121()22x x x y x x p p+−=−，化简得1212()20x x x py x x +−−=，故（3）正确， 故选：D.．【点睛】本题考查直线与抛物线相交，考查导数的几何意义，焦点弦性质，考查学生的推理论证能力，属于中档题． 4．B【解析】作出图形，设点()11,A x y 、()22,B x y ，设直线AB 的方程为2px my =+，将直线AB 的方程与抛物线方程联立，列出韦达定理，求出直线1l 、2l 的方程，求出点P 的坐标，可判断①的正误；利用直线PA 、PB 斜率的关系可判断②的正误；计算出PAB △的面积S 的表达式，可判断③的正误；利用直线PF 、AB 的斜率关系可判断④的正误；求出直线PM 的斜率，可判断⑤的正误.综合可得出结论.【详解】先证明出抛物线()220y px p =>在其上一点()00,x y 处的切线方程为00y y px px =+.证明如下：由于点()00,x y 在抛物线22y px =上，则2002y px =，联立2002y px y y px px ⎧=⎨=+⎩，可得20022y y y px =+，即220020y y y y −+=，0∆=，。

【高中数学数学文化鉴赏与学习】专题5 阿基米德（以阿基米德为背景的高中数学考题题组训练）一、单选题1．阿基米德不仅是著名的物理学家，也是著名的数学家，他利用“逼近法”得到椭圆的面积除以圆周率等于椭圆的长半轴长与短半轴长的乘积．若椭圆C 的焦点在x 轴上，且椭圆C 的离心率为35，面积为20π，则椭圆C 的标准方程为（ ）A ．22154x y +=B ．2212516x y +=C ．22145x y +=D ．2251162x y +=【答案】B 【解析】 【分析】根据已知条件求得,a b ，由此求得正确答案. 【详解】依题意22235π20πc a ab a b c ⎧=⎪⎪=⎨⎪=+⎪⎩，解得5,4,3a b c ===.由于椭圆焦点在x 轴上，所以椭圆C 的标准方程为2212516x y +=.故选：B2．阿基米德不仅是著名的物理学家，也是著名的数学家，他利用“逼近法”得到椭圆的面积除以圆周率等于椭圆的长半轴长与短半轴长的乘积．若椭圆C 的焦点在x 轴上，且椭圆C 的离心率为23，面积为．则椭圆C 的标准方程为（ ） A ．2212036x y +=B ．22195x y +=C ．2213620x y +=D ．22159x y +=【答案】C 【解析】 【分析】设出椭圆方程，由题意可得ab =，结合离心率以及,,a b c 的关系，可得出答案. 【详解】设椭圆C 的标准方程为()222210x y a b a b+=>>，焦距为2c ，则22223c a ab a b c⎧=⎪⎪⎨=⎪⎪=+⎩，解得6a b =⎧⎪⎨=⎪⎩，∴椭圆C 的标准方程为2213620x y +=，故选：C ．3．阿波罗尼斯是古希腊著名数学家，与阿基米德､欧几里得并称为亚历山大时期数学三巨匠，他研究发现：如果一个动点P 到两个定点的距离之比为常数λ（0λ>，且1λ≠），那么点P 的轨迹为圆，这就是著名的阿波罗尼斯圆.若点C 到()()1,0,1,0A B -C 到直线280x y -+=的距离的最小值为（ ） A．BC．D【答案】A 【解析】 【分析】设(,)C x y，依题意||||CA CB =C 的轨迹方程，再求出圆心到直线的距离，即可求出点C 到直线距离的最小值； 【详解】解：设(,)C x y，则||||CA CB ==22(2)3x y -+=，所以点C 的轨迹为以()2,0D为圆心，r =D 到直线280x y -+=的距离d ==所以点C 到直线280x y-+=的距离的最小值为 故选：A4．阿基米德是伟大的古希腊数学家，他和高斯、牛顿并列为世界三大数学家，他一生最为满意的一个数学发现就是“圆柱容球”定理，即圆柱容器里放了一个球，该球顶天立地，四周碰边（即球与圆柱形容器的底面和侧面都相切），球的体积是圆柱体积的三分之二，球的表面积也是圆柱表面积的三分之二．今有一“圆柱容球”模型，其圆柱表面积为24π，则该模型中圆柱的体积为（ ）A ．323π B ．4π C ．16π D ．3【答案】C 【解析】 【分析】由题意可知，圆柱的底面直径等于圆柱的高，然后由圆柱表面积为24π，可求出圆柱的底面半径，从而可求出圆柱的体积 【详解】由题意可知，圆柱的底面直径等于圆柱的高，设圆柱的底面半径为r ，则圆柱的高为2r ，因为圆柱表面积为24π，所以222224r r r πππ⋅+=，解得2r =， 所以圆柱的高为4，所以圆柱的体积为22416ππ⨯⨯=， 故选：C5．阿基米德（Archimedes ，公元前287年-公元前212年）是古希腊伟大的数学家，物理学家和天文学家，他推导出的结论“圆柱内球体的体积是圆柱体积的三分之二，并且球的表面积也是圆柱表面积的三分之二”是其毕生最满意的数学发现，后人按照他生前的要求，在他的墓碑上刻着一个圆柱容器里放了一个球，该球与圆柱的两个底面及侧面均相切，圆柱的底面直径与高都等于球的直径．如图所示，若球的体积为12π，则圆柱的体积为（ ）A ．8πB ．12πC ．18πD ．24π【答案】C【解析】 【分析】根据给定条件，求出球半径，再利用圆柱的体积公式计算作答. 【详解】设球半径为R ，依题意，34123R ππ=，解得39R =，显然，圆柱的底面圆半径为R ，高2h R =，所以圆柱的体积为23218R h R πππ==. 故选：C6．阿基米德（公元前287年-公元前212年）不仅是著名的物理学家，也是著名的数学家，他利用“逼近法”得到椭圆的面积除以圆周率等于椭圆的长半轴与短半轴的乘积．若椭圆C 的对称轴为坐标轴，焦点在y 轴上，且椭圆C，面积为12π，则椭圆C 的方程为（ ）A ．221916x y +=B ．221169x y +=C ．22134x y +=D ．22143x y +=【答案】A 【解析】 【分析】利用待定系数法求椭圆的标准方程. 【详解】可设椭圆C 的方程为22221(0)x y a b b a+=>>，由题意可得：22212c e a ab b a c ππ⎧==⎪⎪⎪=⎨⎪=-⎪⎪⎩，解得：2221697a b c ⎧=⎪=⎨⎪=⎩，所以椭圆C 的方程为221916x y +=. 故选：A7．“圆柱容球”是阿基米德生前最引以为豪的发现，他死后，墓碑上刻着一个“圆柱容球”的几何图形．如图，球与圆柱的侧面及上、下底面相切，设圆柱体积与球的体积之比为m ，圆柱的表面积与球的表面积之比为n ，则mn=（ ）A ．12B ．1C ．2D ．4【答案】B 【解析】 【分析】设球的半径为R ，结合题图有圆柱的底面圆的半径为R ，高为2R ，利用圆柱、球体的体积、表面积公式求体积和面积，进而得到它们的比值，即可得答案. 【详解】设球的半径为R ，则圆柱的底面圆的半径为R ，高为2R ，则圆柱的体积为312V R π=，球的体积为3243V R π=，则1232V m V ==， 圆柱的表面积为2212226S R R R R πππ=⋅+=，球的表面积为224S R π=，则1232S n S ==， 所以1mn=. 故选：B8．古希腊数学家阿基米德利用“逼近法”得到椭圆的面积除以圆周率等于椭圆的长半轴长与短半轴长的乘积.若椭圆C 的中心为原点，焦点1F ，2F 均在y 轴上，椭圆C 的面积为，且短轴长为C 的标准方程为（ ） A ．22112x y +=B ．22143x y +=C ．22134x y +=D ．221163x y +=【答案】C 【解析】 【分析】设出椭圆的标准方程，根据已知条件，求得,,a b c ，即可求得结果. 【详解】因为椭圆C 的焦点在y 轴上，故可设其方程为22221y xab+=，根据题意可得ab =，2b =2,a b == 故所求椭圆方程为：22134x y +=.故选：C.9．阿基米德（Archimedes ，公元前287年-公元前212年），出生于古希腊西西里岛叙拉古（今意大利西西里岛上），伟大的古希腊数学家、物理学家，与高斯、牛顿并称为世界三大数学家．有一类三角形叫做阿基米德三角形．．．．．．．（过抛物线的弦与过弦端点的两切线所围成的三角形），他利用“通近法”得到抛物线的弦与抛物线所围成的封闭图形的面积等于阿基米德三角形面积的23（即右图中阴影部分面积等于PAB △面积的23）．若抛物线方程为22(0)y px p =>，且直线2px =与抛物线围成封闭图形的面积为6，则p =（ ）A ．1B ．2C ．32D ．3【答案】D 【解析】 【分析】根据题目所给条件可得阿基米德三角形的面积，再利用三角形面积公式即可求解. 【详解】由题意可知，当过焦点的弦垂直于x 轴时，即2p x =时，22212263323⎛⎫=⋅⋅== ⎪⎝⎭PABS p p p ，即3p =， 故选：D ．10．如图，在平面直角坐标系中，阿基米德曲线与坐标轴依次交于点()()()()()()()()123456781,0,0,2,3,0,0,4,5,0,0,6,7,0,0,8,A A A A A A A A ----，按这样的规律继续下去.则以下命题中，正确的特称命题是（ ）A ．对于任意正整数2,22n n n A A n +=+B ．存在正整数1,2022n n n A A +=C ．存在正整数1,n n n A A +为有理数D ．对于任意正整数1,n n n A A +为无理数 【答案】C 【解析】 【分析】由选项A,D 的命题为全称命题，排除；又1n n A A +==即可求解. 【详解】解：选项A,D 的命题为全称命题，故排除；由1n n A A +，可知1n n A A +为奇数，因为2022为偶数，故排除选项B ；当3n =，易知345A A =，故正确选项为C . 故选：C.11．阿基米德（公元前287年-公元前212年）是古希腊伟大的物理学家、数学家、天文学家，不仅在物理学方面贡献巨大，还享有“数学之神”的称号．抛物线上任意两点A ，B 处的切线交于点P ，称三角形P AB 为“阿基米德三角形”.已知抛物线C ：28x y =的焦点为F ，过A ，B 360y -+=，关于“阿基米德三角形”∴P AB ，下列结论不正确的是（ ） A ．323AB =B ．PA PB ⊥C ．PF AB ⊥D ．点P 的坐标为)2-【答案】D 【解析】 【分析】联立方程可解得()2,3A B ⎛⎫ ⎪ ⎪⎝⎭，则323AB =，根据导数可得A B k k ==PA PB ⊥，利用点斜式可求得两条切线方程320y ++=60y --=，联立求P 2⎫-⎪⎪⎝⎭，再求PF k =PF AB ⊥．【详解】联立方程23608y x y -+==⎪⎩，消去x 得：2320120y y -+=，解得123y =或26y即()2,3A B ⎛⎫ ⎪ ⎪⎝⎭，则323AB =，A 正确； ∴28x y =，即2,84x x y y '==对于()2,3A B ⎛⎫ ⎪ ⎪⎝⎭，切线斜率分别为A B k k ==∴1A B k k =-，即PA PB ⊥，B 正确； 在点A的切线方程为23y x -=⎝⎭320y ++= 同理可得在点B60y --=联立方程32060y y ++=--=⎪⎩，解得2x y ⎧=⎪⎨⎪=-⎩P 2⎫-⎪⎪⎝⎭，D 不正确； ∴()0,2F，则PF k ==AB k =∴1PF AB k k =-，即PF AB ⊥，C 正确； 故选：D ．12．阿基米德在他的著作《关于圆锥体和球体》中计算了一个椭圆的面积．当我们垂直地缩小一个圆时，我们得到一个椭圆，椭圆的面积等于圆周率π与椭圆的长半轴长与短半轴长的乘积，已知椭圆2222:1(0)x y C a b a b+=>>的面积为，两个焦点分别为12,F F ，点P 为椭圆C 的上项点．直线y kx =与椭圆C 交于A ，B 两点，若,PA PB 的斜率之积为89-，则椭圆C 的长轴长为（ ） A．3 B ．6C ．D ．【答案】B 【解析】 【分析】由题意得到方程组ab =和2289b a =∴，即可解出a 、b ，求出长轴长.【详解】椭圆的面积S ab π==，即ab = 因为点P 为椭圆C 的上项点，所以()0,P b .因为直线y kx =与椭圆C 交于A ，B 两点，不妨设(),A m n ，则(),B m n --且22221m n a b +=，所以22222a n m a b=-. 因为,PA PB 的斜率之积为89-，所以89n b n b m m---⋅=--，把22222a n m a b=-代入整理化简得：2289b a =∴∴∴联立解得：3,a b == 所以椭圆C 的长轴长为2a =6. 故选：B13．“阿基米德多面体”也称半正多面体，是由边数不全相同的正多边形围成的多面体，它体现了数学的对称美.如图是以一正方体的各条棱的中点为顶点的多面体，这是一个有八个面为正三角形，六个面为正方形的“阿基米德多面体”，若该多面体的棱长为1，则经过该多面体的各个顶点的球的体积为（ ）A ．43πB C ．4π D ．8π【答案】A 【解析】 【分析】将该多面体放入正方体中，可以间接确定该多面体外接球的球心，从而求出其外接球的体积 【详解】将该多面体放入正方体中, 如图所示.由于多面体的棱长为1,的正方体连接各棱中点所得,所以该多面体外接球的球心为正方体体对角线的中点，其外接球直径等于正方体的面对角线长，即2R =所以1R =所以该多面体外接球的体积 34433V R ππ==. 故选：A.14．我们把圆锥曲线的弦AB 与过弦的端点A ，B 处的两条切线所围成的三角形PAB △（P 为两切线的交点）叫做“阿基米德三角形”，抛物线有一类特殊的“阿基米德三角形”，当线段AB 经过抛物线的焦点F 时，PAB △具有以下性质：∴P 点必在抛物线的准线上；∴PA PB ⊥；∴PF AB ⊥.已知直线l ：(1)y k x =-与抛物线C ：24y x =交于A ，B 点，若8AB =，记此时抛物线 C 的“阿基米德三角形”为PAB △，则P 点为（ ） A ．()1,2-± B ．()1,2- C ．()1,2-- D ．()1,1-±【答案】A 【解析】 【分析】设11(,)A x y ，22(,)B x y ，求出过,A B 点的切线方程，两方程联立方程组解得P 点坐标，直线AB 的方程(1)y k x =-代入抛物线方程，应用韦达定理得1212,x x x x +，由焦点弦长公式求得k ，从而可得P 点坐标． 【详解】设11(,)A x y ，22(,)B x y ，过A 点的切线方程为11()y y m x x -=-，由112()4y y m x x y x -=-⎧⎨=⎩得2114440y y y x m m -+-=，1124164(4)0y x m m ∆=--=，2112104y y m m -+=，12m y =，切线方程为1112()-=-y y x x y ，化简得1122yy x x =+，同理过B 点的切线方程是2222yy x x =+，由11222222yy x x yy x x =+⎧⎨=+⎩，得12121242()y y x x x y y y ⎧=⎪⎪⎨-⎪=-⎪⎩，由2(1)4y k x y x=-⎧⎨=⎩，得2222(24)0k x k x k -++=， 212224k x x k ++=，121=x x ，直线AB 过焦点(1,0)F ，所以212224228k AB x x k+=++=+=，1k =±， 2212121616y y x x ==，12,y y 异号，所以124y y =-，1214y y =-， 12122()22x x y y k-==±-，所以(1,2)P -±．15．古希腊数学家阿基米德最为满意的一个数学发现是“圆柱容球”，即在球的直径与圆柱底面的直径和圆柱的高相等时，球的体积是圆柱体积的23，且球的表面积也是圆柱表面积的23.已知体积为的圆柱的轴截面为正方形.则该圆柱内切球的表面积为（）A．12πB．C．6πD．【答案】A 【解析】【分析】由题目给出的条件可知，圆柱内切球的表面积圆柱表面积的23，通过圆柱的体积求出圆柱底面圆半径和高，进而得出表面积，再计算内切球的表面积.【详解】设圆柱底面圆半径为r，则圆柱高为2r，圆柱体积22r rπ⋅=，解得r=柱内切球的直径与圆柱底面的直径和圆柱的高相等，所以内切球的表面积是圆柱表面积的2 3，圆柱表面积为2218ππ⨯⨯⨯=，所以内切球的表面积为218123ππ⨯=.故选：A.16．阿基米德既是古希腊著名的物理学家，也是著名的数学家，他利用“逼近法”得到椭圆的面积除以圆周率等于椭圆的长半轴长与短半轴长的乘积.若椭圆C的中心为原点，焦点1F、2F在x轴上，椭圆C的面积为，且离心率为12，则C的标准方程为（）A．22143x y+=B．22112xy+=C．22134x y+=D．221163x y+=【答案】A【解析】【分析】设椭圆方程为22221(0)x ya ba b+=>>，解方程组22212abcaa b c⎧=⎪⎪=⎨⎪=+⎪⎩即得解.解：设椭圆方程为22221(0)x y a b a b+=>>，由题意可知，椭圆C的面积为ab π=，且a 、b 、c 均为正数，即22212ab c a a b c ⎧=⎪⎪=⎨⎪=+⎪⎩，解得21a b c =⎧⎪=⎨⎪=⎩ 因为椭圆C 的焦点在x 轴上，所以C 的标准方程为22143x y +=. 故选：A.17．阿基米德螺线广泛存在于自然界中，具有重要作用，如图，在平面直角坐标系xOy 中，螺线与坐标轴依次交于点()()()()()()1234561,0,0,2,3,0,0,4,5,0,0,6A A A A A A ----､()()787,0,0,8A A ，并按这样的规律继续下去，给出下列两个结论：∴存在正整数12,n n n n A A A ++的面积为2022；∴对于任意正整数12,n n n n A A A ++为锐角三角形.则（ ）A ．∴错误，∴错误B ．∴正确，∴错误C ．∴错误，∴正确D ．∴正确，∴正确【答案】C 【解析】 【分析】 由题设可得122(1)n n n A A A Sn ++=+，△12n n n A A A ++中最大边为2n n A A +且2221122n n n n n n A A A A A A +++++>，即可判断结论的正误.【详解】 由题设知：1221(1)(22)(1)2n n n A A A Sn n n ++=++=+且*N n ∈，而224419362022452025=<<=，所以不存在n 使△12n n n A A A ++的面积为2022，∴错误； 又△12n n n A A A ++中最大边为2n n A A +，且2222222(1)(1)(2)4864(1)484n n n n n n n n n ++++++=++>+=++，所以2221122||||n n n n n n A A A A A A +++++>，故对于任意正整数12,n n n n A A A ++为锐角三角形，∴正确. 故选：C18．我们把圆锥曲线的弦AB 与过弦的端点A ，B 处的两条切线所围成的三角形PAB △（P 为两切线的交点）叫做“阿基米德三角形”．抛物线有一类特殊的“阿基米德三角形”，当线段AB 经过抛物线的焦点F 时，PAB △具有以下性质： ∴P 点必在抛物线的准线上； ∴PA PB ⊥； ∴PF AB ⊥．已知直线():1l y k x =-与抛物线24y x =交于A ，B 点，若8AB =，则抛物线的“阿基米德三角形” PAB △顶点P 的纵坐标为（ ） A ．±1 B ．2± C ．3±D ．12±【答案】B 【解析】 【分析】确定直线():1l y k x =-过抛物线焦点，联立抛物线方程，得到根与系数的关系式，利用弦长公式可求得21k =，结合PAB △具有的性质，可求得答案. 【详解】抛物线的焦点为()1,0F ，准线方程为1x =-， 直线():1l y k x =-经过抛物线的焦点， 由题意0k ≠，设()11,A x y ，()22,B x y ，联立()241y x y k x ⎧=⎪⎨=-⎪⎩，得()2222240k x k x k -++=，所以212224k x x k ++=，121=x x ，212224228k AB x x k+=++=+=，解得21k =， ∴1k =±，当1k =时，1PF k =-，所以直线PF 方程为：1y x =-+，因为PAB △为“阿基米德三角形”，所以点P 必在抛物线的准线1x =-上， 所以点()1,2P -，由抛物线对称性可知，当1k =-时，()1,2P --， 故选：B ．19．圆锥曲线的弦与过弦的端点的两条切线所围成的三角形叫做阿基米德三角形.过抛物线焦点F 作抛物线的弦，与抛物线交于A 、B 两点，分别过A 、B 两点做抛物线的切线l 1，l 2相交于P 点，那么阿基米德三角形P AB 满足以下特性：∴P 点必在抛物线的准线上；∴∴P AB 为直角三角形，且APB ∠为直角；∴PF ∴AB .已知P 为抛物线24x y =的准线上一点，则阿基米德三角形P AB 的面积的最小值为（ ） A ．2 B ．3 C ．4 D ．5【答案】C 【解析】 【分析】设出直线AB 方程，联立抛物线求得124x x =-，通过PF ∴AB 求得1202x x x +=，进而得到M 为AB 中点，由PABPAMPBMS SS=+表示出三角形P AB 的面积，结合基本不等式求出最小值即可. 【详解】易知，焦点(0,1)F ，准线方程1y =-，直线AB 斜率必然存在，设:1AB y kx =+，22121212(,),(,),0,044x x A x B x x x ><，0(,1)P x -，联立24x y =化简得2440x kx --=， 显然120,4x x ∆>=-；又PF ∴AB 可得0PF AB ⋅=，即()2221021,2,044x x x x x ⎛⎫-⋅--= ⎪⎝⎭，化简得1202x x x +=，过P 作//PM y 轴交AB 于M 点，可得M 为AB 中点，故22121244,22x x x xM ⎛⎫+ ⎪+ ⎪ ⎪ ⎪⎝⎭，故2212121211441222PABPAMPBMx x SSSPM xx x x ⎛⎫+⎪=+=⋅-=⋅+⋅- ⎪ ⎪⎪⎝⎭()()()221212122114216216x x x x x x ⎡⎤+-⋅-⎡⎤=+⋅+-≥+⋅=⎡⎤⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦⎣⎦，当且仅当122x x =-=时取等. 故三角形P AB 的面积的最小值为4.故选：C.20．半正多面体（semiregular solid ）亦称“阿基米德多面体”，是由边数不全相同的正多边形围成的多面体，体现了数学的对称美．二十四等边体就是一种半多正多面说法错误的是（ ）A ．该几何体外接球的表面积为4πB ．该几何体外接球的体积为4π3C ．该几何体的体积与原正方体的体积比为2：3D ．该几何体的表面积比原正方体的表面积小 【答案】C 【解析】 【分析】由题意求该几何体的体积与表面积，由外接球的半径求体积与表面积，对选项逐一判断【详解】由题意得该几何体外接球的球心为原正方体的中心，故外接球半径为1，外接球的表面积为4π，体积为4π3，故A ，B 正确对于C ，该几何体的体积33118832V V V =--⨯⨯⨯=正方体四面体正方体体积为5:6，故C 错误， 对于D ，该几何体有6个面为正方形，8个面为等边三角形26181612S =⨯+=+表，故D 正确 故选：C 二、填空题21．半正多面体亦称为“阿基米德多面体”，是由边数不全相同的正多边形为面围成的多面体，如图所示.这是一个将正方体沿交于一顶点的三条棱的中点截去一个三棱锥，共截去八个三棱，得到八个面为正三角形，六个面为正方形的“阿基米德多面体”花岗岩石凳，已知此石凳的棱长为，则此石凳的体积是___________3cm .【答案】11520000 【解析】 【分析】由题意可知，该正多面体是由棱长为240cm 的正方体沿各棱中点截去8个三棱锥所得到的，再由正方体的体积减去八个三棱锥的体积求解 【详解】如图所示，该石凳是由棱长为240cm 的正方体沿各棱中点截去8个三棱锥所得到的， 所以该石凳的体积为：3112402402408(120120)12011520000cm 32V =⨯⨯-⨯⨯⨯⨯⨯=故答案为：1152000022．阿基米德（公元前287—公元前212年）不仅是著名的物理学家，也是著名的数学家，他利用“逼近法”得到椭圆的面积除以圆周率等于椭圆的长半轴长与短半轴长的乘积．已知椭圆()2222:10x y C a b a b+=>>经过点)P，则当be a+取得最大值时，椭圆的面积为_________．【答案】 【解析】 【分析】利用基本不等式得出be a+取得最大值时的条件结合222b c a +=可知222a b =，再利用点)P 在椭圆方程上，故可求得a 、b 的值,进而求出椭圆的面积.【详解】b c b e a a a +=+=由基本不等式222b c bc +≥≤=b c =时取得最大值，由222b c a +=可知222a b =，∴椭圆C 经过点)P，∴22211a b +=，解得2a =，b =则椭圆的面积为πS ab ==.故答案为：.23．阿基米德多面体（Archimedeanpolyhedra ）是由两种或三种正多边形面组成的半正多面体.它共有13种，其特点是棱长相等.如图1，顺次连接棱长为2的正方体各棱的中点，得到一个阿基米德多面体，如图2，在此阿基米德多面体的所有棱中任取两条，则两条棱垂直的概率为___________.【答案】423【解析】 【分析】根据图形，先求出24条棱中的所有组合，再求两条棱垂直的情况，分别计算出每一类情况中的垂直情况即可求解.【详解】此阿基米德多面体共有24条棱，任取2条，共有2241223276C =⨯=种.两条棱垂直有两类情况：∴都来自同一个正方形：2446=⨯种； ∴来自对面的两个正方形：2483=⨯种. 故所求概率为48427623P ==. 故答案为：42324．半正多面体亦称阿基米德多面体，是由边数不全相同的正多边形为面的多面体．如图所示，将正方体沿交于一顶点的三条棱的中点截去一个三棱锥，如此共可截去八个三棱锥，得到一个有十四个面的半正多面体，其中八个面为正三角形，六个面为正方形，它们的边长都相等，称这样的半正多面体为二十四等边体．现有一个体积为1V 的二十四等边体，其外接球体积为2V ，则21V V =_________________.【答案】5【解析】 【分析】利用割补法可得二十四等边体的体积，再结合对称性可得外接球球心与半径，可得外接球体积，进而得解. 【详解】设该半多面体是由棱长为2的正方体沿正方体各棱的中点截去8个三棱锥所得，内侧即为二十四等边体，其体积111202228111323V =⨯⨯-⨯⨯⨯⨯⨯=；由二十四等边体的对称性可知， 如图所示，其外接球的球心即为正方体中心O，半径为中心到一个顶点的距离，则R =故3243V π==从而215V V =.. 25．高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的称号，他和阿基米德、牛顿并列为世界三大数学家．用其名字命名的“高斯函数”为：[]()y x x =∈R ，[]x 表示不超过x 的最大整数，如[ 1.6]2-=-，[1.6]1=，[2]=2，则关于x 的不等式2[][]120x x +-<的解集为__________. 【答案】[3,3)- 【解析】 【分析】解一元二次不等式，结合新定义即可得到结果. 【详解】∴2[][]120x x +-<， ∴4[]3x -<<， ∴33x -≤<， 故答案为：[3,3)-26．已知ABC 中角A ，B ，C 所对的边分别为a ，b ，c ，2a b cp ++=，则ABC 的面积S 得出．若ABC 的周长为15，()()()sin sin :sin sin :sin sin 4:6:5A B B C C A +++=，则ABC 的面积为___________________．【解析】 【分析】先用正弦定理解得a =3，b =5，c =7，代入海伦公式即可解得. 【详解】解：可令sin sin 4,A B k +=sin sin 6,B C k +=sin sin 5,C A k += 将上式相加：15sin sin sin ,2A B C k ++=由此可解的：753sin ,sin ,sin ,222A kB kC k === 由正弦定理：::3:5:7,a b c = 又因为：15,a b c ++=解得：a =3，b =5，c =7.所以1522a b c p ++==代入海伦公式解得：S27．传说古希腊数学家阿基米德的墓碑上刻着一个圆柱，圆柱内有一个内切球，这个球的直径恰好与圆柱的高相等．这个“圆柱容球”是阿基米德生前最引以为豪的发现．如图，在底面半径为2的圆柱12O O 内有球O 与圆柱12O O 的上、下底面及母线均相切，设,A B 分别为圆柱12O O 的上、下底面圆周上一点，且1O A 与2O B 所成的角为90，直线AB 与球O 的球面交于两点,M N ，则线段MN 的长度为______．【答案】【解析】 【分析】取AB 中点G ，由等腰三角形三线合一可得OG AB ⊥；由线面垂直的判定与性质可证得22O B O A ⊥，利用勾股定理可推导求得MG ，又OM ON =，可知G 为MN 中点，由此可得2MN MG =.【详解】12OAO OBO ≌，OA OB ∴=，取AB 中点G ，连接2,,,,,OG OA OM ON OB O A ，OA OB =，G 为AB 中点，OG AB ∴⊥；21O B O A ⊥，212O B O O ⊥，1121O A O O O =，112,O A O O ⊂平面12AO O ， 2O B ∴⊥平面12AO O ，又2O A ⊂平面12AO O ，22O B O A ∴⊥； 222118OA OO O A =+=，2222222224224AB O A O B =+=++=，OG ∴==MG ∴=OM ON =，G ∴也是MN 中点，2MN MG ∴==故答案为： 【点睛】关键点点睛：本题考查旋转体中的线段长度的求解问题，解题关键是能够熟练应用圆柱和球的结构中的长度相等的线段之间的关系，结合垂直关系，利用勾股定理来进行求解.28．圆锥曲线的弦与过弦的端点的两条切线所围成的三角形叫做阿基米德三角形.过抛物线焦点F 作抛物线的弦，与抛物线交于A ､B 两点，分别过A ､B 两点作抛物线的切线1l ，2l 相交于P 点，那么阿基米德三角形P AB 满足以下特性：∴P 点必在抛物线的准线上；∴PAB 为直角三角形，且APB ∠为直角；∴PF AB ⊥.已知P 为抛物线24x y =的准线上一点，则阿基米德三角形P AB 的面积的最小值为___________. 【答案】4 【解析】 【分析】设出直线AB 方程，联立抛物线求得124x x =-，通过PF ∴AB 求得1202x x x +=，进而得到M 为AB 中点，由PABPAMPBMS SS=+表示出三角形P AB 的面积，结合基本不等式求出最小值即可. 【详解】易知，焦点(0,1)F ，准线方程1y =-，直线AB 斜率必然存在，设:1AB y kx =+，22121212(,),(,),0,044x x A x B x x x ><，0(,1)P x -，联立241x y y kx ⎧=⎨=+⎩得2440x kx --=， 显然120,4x x ∆>=-；又PF ∴AB 可得0PF AB ⋅=，即()2221021,2,044x x x x x ⎛⎫-⋅--= ⎪⎝⎭，化简得1202x xx +=，过P 作//PM y 轴交AB 于M 点，如图所示：则1202M x x x x +==， 所以M 为AB 中点，故22121244,22x x x xM ⎛⎫+ ⎪+ ⎪ ⎪ ⎪⎝⎭，故2212121211441222PABPAMPBMx x SSSPMx x x x ⎛⎫+⎪=+=⋅-=⋅+⋅- ⎪ ⎪⎪⎝⎭()()()221212122114216216x x x x x x ⎡⎤+-⋅-⎡⎤=+⋅+-≥+⋅=⎡⎤⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦⎣⎦， 当且仅当122x x =-=时取等， 故三角形P AB 的面积的最小值为4， 故答案为：429．高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的称号，他和阿基米德，牛顿并列为世界三大数学家，用其名字命名的“高斯函数”为：对于实数x ，符号[]x 表示不超过x 的最大整数，则[]y x =称为高斯函数，例如[]3π=，[]1.082-=-，定义函数()[]f x x x =-，则下列命题中正确的序号是________．∴函数()f x 的最大值为1； ∴函数()f x 的最小值为0；∴函数()y f x =的图象与直线12y =有无数个交点 ∴()()1f x f x += 【答案】∴∴∴ 【解析】 【分析】根据高斯函数定义可得()f x 的解析式和图象，由图象判断各个选项即可. 【详解】由题意得：()[]2,211,10,011,122,23x x x x f x x x x x x x x x ⋅⋅⋅⎧⎪+-≤<-⎪⎪+-≤<⎪=-=≤<⎨⎪-≤<⎪-≤<⎪⎪⋅⋅⋅⎩，由解析式可得函数图形如下图所示，对于∴，函数()1f x <，∴错误；对于∴：函数()f x 的最小值为0，∴正确； 对于∴，函数()y f x =的图象与直线12y =有无数个交点，∴正确； 对于∴，函数()f x 满足()()1f x f x +=，∴正确； 故答案为：∴∴∴30．高斯是德国著名数学家，近代数学奠基者之一，享有“数学王子”称号，他和阿基米德、牛顿并列为世界三大数学家，用其名字命名的“高斯函数”为：设x ∈R ，用[]x 表示不超过x 的最大整数，则[]y x =称为高斯函数，例如[ 2.1]3,[2.1]2-=-=．已知函数()sin |||sin |f x x x =+，函数()[()]g x f x =，则下列命题正确的是__________．∴函数()g x 是周期函数； ∴函数()g x 的值域是{0,1,2}； ∴函数()g x 的图象关于2x π=对称； ∴方程()2g x x π⋅=只有一个实数根；【答案】∴∴ 【解析】 【分析】先研究函数()f x 的奇偶性，作出函数()f x 的图象，作出函数()g x 的图象判断∴∴的正确性，由特值判断∴的正确性，再分类讨论判断方程()2g x x π⋅=的根的个数得解.【详解】由题得函数()sin sin f x x x =+的定义域为R ,()sin sin()sin |||sin |()f x x x x x f x -=-+-=+=，所以函数()f x 为偶函数，当0x π≤≤时，()sin sin 2sin f x x x x =+=； 当2x ππ<<时，()sin sin 0f x x x =-=； 当23x ππ≤≤时，()sin sin 2sin f x x x x =+=；所以函数()f x 的图象如图所示，所以函数()g x 的图象如图所示，由函数()g x 的图象得到()g x 不是周期函数，故选项∴不正确； 所以函数()g x 的值域是{}0,1,2，故选项∴正确；由[()]144g f ππ⎛⎫-=-== ⎪⎝⎭，55[()][0]044g f ππ⎛⎫===⎪⎝⎭所以函数()g x 的图象不关于2x π=对称，故选项∴不正确；对于方程()2g x x π⋅=，当()0g x =时，0x =，方程有一个实数根； 当()1g x =时，2x π=，此时()212g π=≠，此时方程没有实数根； 当()2g x =时，x π=，此时()02g π=≠，此时方程没有实数根； 故方程()2g x x π⋅=只有一个实数根，故选项D 正确.故答案为：∴∴.。

第11讲 阿基米德三角形问题一、解答题1．设定点F (0，1)，动点E 满足：以EF 为直径的圆与x 轴相切. （1）求动点E 的轨迹C 的方程；（2）设A ，B 是曲线C 上的两点，若曲线C 在A ，B 处的切线互相垂直，求证：A ，F ，B 三点共线. 【答案】（1）x 2＝4y ；（2）证明见解析. 【分析】（1）设E 点坐标为(x ，y )，由E 到x 轴的距离等于2EF即可求解. （2）设A ，B 两点的坐标分别为2111(,)4x x ，2221(,)4x x ，利用导数求出曲线在A ，B 处切线的斜率，从而可得x 2＝－14x ，再求出AB 的斜率，证出 k AF ＝k AB ，即证.【详解】（1）设E 点坐标为(x ，y )，则EF 中点为圆心，设为E ，则E 点坐标为1,22x y +⎛⎫⎪⎝⎭.∴E 到x 轴的距离等于||2EF ， 即12y +x 2＝4y .∴点E 的轨迹C 的方程为x 2＝4y .（2）证明：由（1）知，曲线C 是以F 为焦点的抛物线，其方程可化为y ＝14x 2， 设A ，B 两点的坐标分别为2111(,)4x x ，2221(,)4x x ， ∵曲线方程为y ＝14x 2，∴y ′＝12x ，∴曲线在A ，B 处切线的斜率分别为k 1＝12x 1，k 2＝12x 2， ∵k 1k 2＝－1，∴12x 1·12x 2＝－1，∴x 2＝－14x ，∴A ，B 两点连线的斜率为k AB ＝()()22212112111114444x x x x x x x x -⎛⎫=+=-+ ⎪-⎝⎭＝－11x ＋14x 1， A ，F 两点连线的斜率为k AF ＝2111140x x --＝－11x ＋14x 1＝k AB ，∴A ，B ，F 三点共线. 【点睛】关键点点睛：本题考查了三点共线，可以证明直线的斜率相等，解题的关键是根据A ，B 两点的坐标求出x 2＝－14x ，考查了计算求解能力.2．如图，已知抛物线的焦点为F 过点的直线交抛物线于A，B两点，直线AF ，BF 分别与抛物线交于点M ，N ．（Ⅰ）求的值；（Ⅰ）记直线MN 的斜率为，直线AB 的斜率为证明：为定值【答案】（1），；（2）【解析】试题分析：（Ⅰ）依题意，设直线AB 的方程为x =my +2(m ≠0)，与抛物线方程联立消x 得关于y 的一元二次方程，根据韦达定理即可求得y 1y 2；（Ⅰ）设M(x M ，y M )，N(x N ，y N )，设直线AF ：y =y 1x1−1(x −1)与y 2=4x 联立，得y14y 2+(1−x 1)y −y 1=0,由韦达定理得，y 1y M =−4⇒y M =−4y 1，同理，y N =−4y 2，进而可得的比值，化简即可求出结果为定制．试题解析：证明：（Ⅰ）依题意，设直线AB 的方程为x =my +2(m ≠0)．将其代入，消去x ，整理得y 2−4my −8=0．从而y 1y 2=−8． （Ⅰ）AF ：y =y 1x1−1(x −1)与y 2=4x 联立，得y14y 2+(1−x 1)y −y 1=0 由韦达定理得，y 1y M =−4⇒y M =−4y 1，同理，y N =−4y 2k 1k 2=4y M +y N4y 1+y 2=y 1+y 2y M +y N=−y 1y 24=2（定值）．考点：1．抛物线的简单性质；2．直线与抛物线的性质．3．已知抛物线C ：x 2＝2py （p ＞0），直线l 交C 于A ，B 两点，且A ，B 两点与原点不重合，点M （1，2）为线段AB 的中点．（1）若直线l 的斜率为1，求抛物线C 的方程；（2）分别过A ，B 两点作抛物线C 的切线，若两条切线交于点S ，证明点S 在一条定直线上． 【答案】（1）x 2＝2y （2）证明见解析 【分析】（1）设直线l 的方程为y x t =+，代入抛物线方程，消去y ，设1(A x ，1)y ，2(B x ，2)y ，运用韦达定理，以及中点坐标公式，可得p ，即可得到所求抛物线方程；（2）求得22x y p=的导数，可得抛物线在A ，B 处的切线的斜率，由点斜式方程和点A ，B 满足抛物线方程，可得在A ，B 处的切线方程，联立两切线方程，相加，结合中点坐标公式，即可得到所求点S 所在的定直线方程． 【详解】解：（1）设直线l 的方程为y x t =+，代入抛物线2:2(0)C x py p =>，可得2220x px pt --=，设11(,)A x y ，22(,)B x y ，则122x x p +=，点(1,2)M 为线段AB 的中点，可得22p =，即1p =， 则抛物线的方程为22x y =；（2）证明：设11(,)A x y ，22(,)B x y ，点(1,2)M 为线段AB 的中点， 可得122x x +=，124y y +=，由22x y p=的导数为x y p '=，可得抛物线在A 处的切线斜率为1x p ，切线方程为111()x y y x x p -=-，由2112x py =，可得11()x x p y y =+，①同理可得22()x x p y y =+，②①+②可得1212()(2)x x x p y y y +=++， 即为2(24)x p y =+，即20x py p --=． 可得交点S 在一条定直线20x py p --=上． 【点睛】本题主要考查抛物线的方程和性质，考查直线和抛物线的位置关系，考查计算能力，属于中档题． 4．已知抛物线C ：x 2＝2py （p ＞0），F 为抛物线C 的焦点．以F 为圆心，p 为半径作圆，与抛物线C 在第一象限交点的横坐标为2． （1）求抛物线C 的方程；（2）直线y ＝kx +1与抛物线C 交于A ，B 两点，过A ，B 分别作抛物线C 的切线l 1，l 2，设切线l 1，l 2的交点为P ，求证：△P AB 为直角三角形．【答案】（1）24x y =；（2）证明见解析.【分析】（1）由题意可得M 点的坐标为(2,)2p，代入抛物线方程，即可求出p 的值； （2）设221212(,),(,)44x x A x B x ，利用导数的几何意义得到A ，B 两点处的切线斜率分别为1112k x =，2212k x =，联立直线与抛物线方程，利用韦达定理得到k 1k 2＝﹣1，从而得到△P AB 为直角三角形． 【详解】（1）记抛物线C 与圆F 在第一象限的交点为M ，由圆F 与抛物线C 的准线相切，且M 到抛物线C 准线的距离等于圆F 的半径p ， 所以M 点的坐标为(2,)2p，代入抛物线方程得：24(0)p p =>，所以2p =，所以抛物线的方程为24x y =.（2）设221212(,),(,)44x x A x B x ，由24x y =，可得y 214x =，则12y x '=， 所以A ，B 两点处的切线斜率分别为1112k x =，2212k x =，由214y kx x y=+⎧⎨=⎩，得2440x kx --=，所以12124,4x x k x x +==-， 所以1212114k k x x ==-， 所以PA PB ⊥，即PAB ∆为直角三角形． 【点睛】本题主要考查抛物线的标准方程的求解、及直线与抛物线的位置关系的综合应用,解答此类题目，通常联立直线方程与抛物线方程，应用一元二次方程根与系数的关系进行求解，此类问题易错点是复杂式子的变形能力不足，导致错解，能较好的考查考生的逻辑思维能力、运算求解能力、分析问题解决问题的能力等． 5．已知抛物线2:2(0)C x py p =>的焦点为F ，过点F 的直线分别交抛物线于,A B 两点． （1）若以AB 为直径的圆的方程为()()222316x y -+-=，求抛物线C 的标准方程；（2）过点,A B 分别作抛物线的切线12,l l ，证明：12,l l 的交点在定直线上． 【答案】（1）24x y =；（2）证明见解析. 【分析】（1）根据抛物线的定义可求圆心到准线的距离为4，从而可求抛物线的方程．（2）设()()1122,,,A x y B x y ，利用导数求出,A B 两点处的切线方程，从而可求12,l l 的交点的坐标，再联立直线和抛物线的方程可得212x x p =-，从而可得12,l l 的交点的纵坐标为定值，故12,l l 的交点在定直线上． 【详解】（1）设AB 中点为M ，A 到准线的距离为1d ，B 到准线的距离为2d ，M 到准线的距离为d ，则()2,3M 且322=M p p d y =++.由抛物线的定义可知，12,d AF d BF ==，所以128d d AB +==， 由梯形中位线可得1242d d d +==，所以342p+=，可得2p =， 所以抛物线C 的标准方程为24x y =.（2）证明：设()()1122,,,A x y B x y ，由22x py =，得22x y p=，则x y p '=，所以直线1l 的方程为()111x y y x x p-=-， 直线2l 的方程为()222x y y x x p-=-， 联立得()()111222x y y x x p x y y x x p ⎧-=-⎪⎪⎨⎪-=-⎪⎩，解得121222x x x x x y p +⎧=⎪⎪⎨⎪=⎪⎩，即直线12,l l 的交点坐标为1212,22x x x x p ⎛⎫+ ⎪⎝⎭.因为AB 过焦点0,2p F ⎛⎫⎪⎝⎭， 由题可知直线AB 的斜率存在，故可设直线AB 方程为2py kx -=， 代入抛物线22x py =中，得2220x pkx p --=，所以212x x p =-，故1222x x pp =-，所以12,l l 的交点在定直线2p y =-上．【点睛】关键点点睛：抛物线中过焦点的弦长问题要注意利用定义转化为到准线的距离问题，对于焦点在y 轴上的抛物线的切线问题，可以利用导数来求切线方程，从而简化运算． 6．已知动点Q 在x 轴上方，且到定点()0,1F 距离比到x 轴的距离大1. （1）求动点Q 的轨迹C 的方程；（2）过点()1,1P 的直线l 与曲线C 交于A ，B 两点，点A ，B 分别异于原点O ，在曲线C 的A ，B 两点处的切线分别为1l ，2l ，且1l 与2l 交于点M ，求证：M 在定直线上.【答案】（1）24x y =()0y ≠；（2）证明见解析【分析】（1）设(,)Q x y (0)y >，由到定点()0,1F 距离比到x 轴的距离大11y =，化简可得点Q 的轨迹C 的方程；（2）由题意可知，直线l 的斜率存在且不为1，设直线l 的方程为(1)1y k x =-+(1)k ≠与24x y =联立，设()11,A x y ，()22,B x y ，可得12x x +，12x x 的值，又24x y =，所以2x y '=，可得切线1l 的方程，同理可得切线2l 的方程，求出交点坐标，可得其在定直线上. 【详解】解：（1）设(,)Q x y (0)y >，1y =，化简得24x y =()0y ≠， 故轨迹C 的方程为24x y =()0y ≠.（2）由题意可知，直线l 的斜率存在且不为1，设直线l 的方程为(1)1y k x =-+(1)k ≠与24x y =联立得24440x kx k -+-=， 设()11,A x y ，()22,B x y ， 则124x x k +=，1244x x k =-，又24x y =，所以2x y '=，所以切线1l 的方程为()1112x y x x y =-+， 即21124x x y x =-，同理切线2l 的方程为22224x x y x =-联立得1222x x x k +==，1214x xy k ==-.两式消去k 得220x y --=， 当1k =时，2x =，0y =，所以交点M 的轨迹为直线220x y --=，去掉()2,0点. 因而交点M 在定直线上. 【点睛】本题主要考查轨迹方程的求法，直线与抛物线的位置关系等知识，考查学生的综合计算能力，属于难题.7．已知圆C ：x 2＋y 2＋2x －2y ＋1＝0和抛物线E ：y 2＝2px (p ＞0)，圆心C 到抛物线焦点F ． （1）求抛物线E 的方程；（2）不过原点的动直线l 交抛物线E 于A ，B 两点，且满足OA ⊥OB ． ①求证直线l 过定点；②设点M 为圆C 上任意一动点，求当动点M 到直线l 的距离最大时直线l 的方程． 【答案】（1）y 2＝12x ；（2）①证明见解析；②13x －y －156＝0． 【分析】(1) 根据题意圆心到抛物线焦点距离，利用两点之间距离公式计算可得结果（2）设直线方程()0x my t t =+≠，联立抛物线，结合条件求得两根之和与两根之积，解得12,x my =+得到定点，再得出点到线距离最大时的直线方程 【详解】(1)圆C ：x 2＋y 2＋2x －2y ＋1＝0，可得圆心C (－1，1)，半径r ＝1， 抛物线E ：y 2＝2px (p ＞0)的焦点(,0)2p F ，准线方程为2px =，圆心C 到抛物线焦点F =解得p ＝6，即抛物线方程为y 2＝12x .(2)①证明：设直线l 的方程为x ＝my ＋t ，A (x 1，y 1)，B (x 2，y 2)，则212+y xx my t ⎧=⎨=⎩整理得：y 2－12my －12t ＝0， 所以y 1＋y 2＝12m ，y 1y 2＝－12t ． 由于OA ⊥OB ．则x 1x 2＋y 1y 2＝0． 即(m 2＋1)y 1y 2＋mt (y 1＋y 2)＋t 2＝0． 整理得t 2－12t ＝0， 由于t ≠0，解得t ＝12． 故直线的方程为x ＝my ＋12， 直线经过定点P (12，0)．②当CP ⊥l 且动点M 经过PC 的延长线时，动点M 到动直线l 的距离取得最大值．113MP CP k k ==-， 则113m =-． 此时直线l 的方程为：11213x y =+， 即13x －y －156＝0． 【点睛】本题在解答直线与抛物线位置关系时需设出直线方程，这里给出x my t =+形式的直线方程，方便计算，根据题目意思解得直线恒过定点，再结合题意，求得当与直线垂直时的直线方程即可.8．已知抛物线24x y =的焦点为F ，A ，B 是抛物线上的两个动点，且(0)AF FB λλ=>，过A ，B 两点分别作抛物线的切线，设其交点为P .（1）若直线PA 与x ，y 轴分别交于点M ，N ，且MON △的面积为12，求||AF 的值； （2）记ABP △的面积为S ，求S 的最小值，并指出S 最小时对应的点P 的坐标. 【答案】(1)2;(2)APBS 有最小值4，此时(0,1)P -.【分析】（1）先求出以点A 为切点的抛物线的切线PA 方程，得出11,02M x ⎛⎫ ⎪⎝⎭，()12410,N x -利用面积求出A 点的纵坐标，然后求出AF ．（2）先分别写出直线PA ，PB 方程，利用都过点P 写出直线AB ，代入抛物线方程利用弦长公式求出AB ，及点()0,1P x -到直线AB 的距离，写出APB S表达式及最值．【详解】（1）设()00,P x y ，()11,A x y ，()22,B x y ，则120x x ≠，抛物线方程写成214y x =，12y x '=，则以点A 为切点的抛物线的切线PA 的方程为：()1111:2PA l y y x x x -=-，又21114y x =，即21111:24PA l y x x x =-，11,02M x ⎛⎫∴ ⎪⎝⎭，()12410,N x -，12MONS OM ON ∴=⋅ 23111111122416x x x =⨯⨯-=，故31116x 12=，∴12x =，211114y x ==，从而11122pAF y =+=+=. （2）由（1）知21111:24PA l y x x x =-，即：1112y x x y =-，同理221:2PB l y x x y =-，由直线PA ，PB都过点()00,P x y ，即001100221212y x x y y x x y⎧=-⎪⎪⎨⎪=-⎪⎩，则点()11,A x y ，()22,B x y 的坐标都满足方程0012x x y y -=，即直线AB 的方程为：0012x x y y -=，又由直线AB 过点()0,1F ，∴01y =-， 联立021124x x y x y⎧-=-⎪⎨⎪=⎩得20240x x x --=，12AB x ∴=-124x x ==，点()0,1P x -到直线AB的距离d =，12APBSAB d ∴=⋅==13244APBS∴=，当且仅当时00x =，APB S 有最小值4，此时()0,1P -.【点睛】本题考查抛物线的定义，直线与抛物线的位置关系，考查导数知识的运用，考查学生分析解决问题的能力，属于中档题． 9．已知以动点P 为圆心的P 与直线l ：12x =-相切，与定圆F ：221(1)4x y -+=相外切. （Ⅰ）求动圆圆心P 的轨迹方程C ；（Ⅰ）过曲线C 上位于x 轴两侧的点M 、N （MN 不与x 轴垂直）分别作直线l 的垂线，垂足记为1M 、1N ，直线l 交x 轴于点A ，记1AMM ∆、AMN ∆、1ANN ∆的面积分别为1S 、2S 、3S ，且22134S S S =，证明：直线MN 过定点.【答案】（Ⅰ）24y x =；（Ⅰ）详见解析. 【分析】（Ⅰ）根据题意，点P 到直线1x =-的距离与到(1,0)F 的距离相等，由抛物线的定义可得解；（Ⅰ）设111,2M y ⎛⎫- ⎪⎝⎭、21,2N y ⎛⎫- ⎪⎝⎭，用坐标表示1S 、2S 、3S ，利用韦达定理，代入即得解. 【详解】（Ⅰ）设(,)P x y ，P 半径为R ，则12R x =+，1||2PF R =+，所以点P 到直线1x =-的距离与到(1,0)F 的距离相等，故点P 的轨迹方程C 为24y x =.（Ⅰ）设()11,M x y ，()22,N x y ，则111,2M y ⎛⎫-⎪⎝⎭、21,2N y ⎛⎫- ⎪⎝⎭设直线MN ：x ty n =+（0t ≠）代入24y x =中得2440y ty n --=124y y t +=，1240y y n =-<∵1111122S x y =+⋅、3221122S x y =+⋅ ∴131********S S x x y y ⎛⎫⎛⎫=++ ⎪⎪⎝⎭⎝⎭12121122ty n ty n y y ⎛⎫⎛⎫=++++ ⎪⎪⎝⎭⎝⎭()22121211422t y y n t y y n n ⎡⎤⎛⎫⎛⎫=+++++⋅-⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦2221144422nt t n n n ⎡⎤⎛⎫⎛⎫=-++++⋅⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦221242t n n ⎡⎤⎛⎫=++⋅⎢⎥ ⎪⎝⎭⎢⎥⎣⎦又21211112222S n y y n =+⋅-=+∴()()22222211116164422S n t n n t n ⎛⎫⎛⎫=+⋅+=+⋅+ ⎪ ⎪⎝⎭⎝⎭ 222222131114842222S S S nt n t n n n ⎛⎫⎛⎫=⇔=+⇔=+⇒= ⎪ ⎪⎝⎭⎝⎭∴直线MN 恒过1,02⎛⎫⎪⎝⎭【点睛】本题考查了直线和抛物线综合，考查了学生综合分析，转化划归，数学运算的能力，属于中档题. 10．已知点P 是抛物线21:34C y x =-的顶点，A ，B 是C 上的两个动点，且4PA PB ⋅=-. （1）判断点()0,1D 是否在直线AB 上？说明理由；（2）设点M 是△PAB 的外接圆的圆心，点M 到x 轴的距离为d ，点()1,0N ，求MN d -的最大值.【答案】（1）不在，证明见详解；（2 【分析】（1）假设直线方程y kx b =+，并于抛物线方程联立，结合韦达定理，计算4PA PB ⋅=-，可得1b =-，然后验证可得结果.（2）分别计算线段,PA PB 中垂线的方程，然后联立，根据（1）的条件可得点M 的轨迹方程22y x =，然后可得焦点F ，结合抛物线定义可得18MN d NF -≤+，计算可得结果. 【详解】（1）设直线方程y kx b =+，()()1122,,,A x y B x y 根据题意可知直线斜率一定存在，()0,3P-则()224430134y kx b x kx b y x =+⎧⎪⇒--+=⎨=-⎪⎩()121243,4x x b x x k =-++=()241648k b ∆=-++()()1122,3,,3PA x y PB x y =+=+则()()121233PA PB x x y y ⋅=+++()12121239PA PB x x y y y y ⋅=++++()()()2212121212y y kx b kx b k x x kb x x b =++=+++ ()1212122y y kx b kx b k x x b +=+++=++()()()2212121369PA PB k x x k kb x x b b ⋅=+++++++由4PA PB ⋅=-所以()()()22121213694k x x k kb x x b b +++++++=-将()121243,4x x b x x k =-++=代入上式 化简可得2210b b ++=，所以1b =- 则直线方程为1y kx =-，所以直线过定点()0,1-，()2416480k b ∆=-++>所以可知点()0,1D 不在直线上. （2）设(),M M M x y线段PA 的中点为113,22x y E -⎛⎫⎪⎝⎭ 线段PB 的中点为223,22x y G -⎛⎫⎪⎝⎭则直线PA 的斜率为113PA y k x +=， 直线PB 的斜率为223PB y k x +=可知线段PA 的中垂线的方程为11113232y x x y x y -⎛⎫-=-- ⎪+⎝⎭由211134y x =-，所以上式化简为2121418x y x x =-+- 即线段PA 的中垂线的方程为2121418x y x x =-+- 同理可得：线段PB 的中垂线的方程为2222418x y x x =-+- 则()22121222222112122141832481832M M x x x x x y x x x x x x x x y x y x ⎧⎧+=-+-⎪=-⎪⎪⎪⇒⎨⎨++-⎪⎪=-+-=⎪⎪⎩⎩由（1）可知：()12124,438x x k x x b +==-+=-所以()12122221212322832M M M M x x x x x x k y k x x x x y ⎧+=-⎪=⎧⎪⇒⎨⎨=++-⎩⎪=⎪⎩即()2,2M k k，所以点M 轨迹方程为22y x=焦点为10,8F ⎛⎫⎪⎝⎭，所以1188MN d MN MF MN MF ⎛⎫-=--=-+⎪⎝⎭当,,M N F 三点共线时，MN d -有最大所以1188MN d MN MF NF -=-+≤+=【点睛】本题考查直线于抛物线的综合应用，第（1）问中难点在于计算处b ，第（2）问中关键在于得到点M 的轨迹方程，直线与圆锥曲线的综合常常要联立方程，结合韦达定理，属难题. 11．已知点P 是抛物线21:34C y x =-的顶点，A ，B 是C 上的两个动点，且4PA PB ⋅=-. （1）判断点()0,1D -是否在直线AB 上？说明理由； （2）设点M 是△PAB 的外接圆的圆心，求点M 的轨迹方程. 【答案】（1）点()0,1D -在直线AB 上，理由见解析（2）212x y =【分析】（1）由抛物线的方程可得顶点P 的坐标，设直线AB 的方程，与抛物线联立求出两根之和及两根之积，求出数量积PA PB ，再由题意4PA PB =-可得直线AB 恒过(0,1)-，即得D 在直线AB 上；（2）设A ，B 的坐标，可得直线PA ，PB 的斜率及线段PA ，PB 的中点坐标，进而求出线段PA ，PB 的中垂线的方程，两个方程联立求出外接圆的圆心M 的坐标，由（1）可得M 的横纵坐标关于参数k 的表达式，消参数可得M 的轨迹方程． 【详解】(1) 点()0,1D -在直线AB 上.理由如下， 由题意, 抛物线21:34C y x =-的顶点为(0,3)P - 因为直线与抛物线有2个交点， 所以设直线AB 的方程为()()1122,,,y kx b A x y B x y =+，联立2134y x y kx b⎧=-⎪⎨⎪=+⎩得到244(3)0x kx b --+=，其中21616(3)0k b ∆=++>，12121244(3)4(3)x x k x x b x x b +==-+=-+，所以()21212242y y k x x b k b +=++=+，()()()2212121212y y kx b kx b k x x kb x x b =++=+++2224(3)4k b k b b =-+++2212k b =-+因为()()1122,3,,3PA x y PB x y =+=+所以()()121233PA PB x x y y ⋅=+++()12111239x x y y y y =++++()()2224(3)123429b k b k b =-++-++++223b b =+-4=，所以2221(1)0b b b ++=+=， 解得1b =-， 经检验，满足>0∆，所以直线AB 的方程为1y kx =-，恒过定点()0,1D -.（2）因为点M 是PAB ∆的外接圆的圆心，所以点M 是三角形PAB 三条边的中垂线的交点， 设线段PA 的中点为F ，线段PB 的中点为为E ， 因为(0,3)P -，设1(A x ，1)y ，2(B x ，2)y所以1(2x F ，13)2y -，2(2x E ，23)2y -，113PA y k x +=，223PB y k x +=，所以线段PA 的中垂线的方程为：11113()232y x xy x y --=--+， 因为A 在抛物线上，所以211134y x +=，PA 的中垂线的方程为：211143()82x x y x x -+=--，即211418x y x x =-+-，同理可得线段PB 的中垂线的方程为：222418x y x x =-+-， 联立两个方程211222418418x y x x x y x x ⎧=-+-⎪⎪⎨⎪=-+-⎪⎩，解得1212221212()3288Mx x x x x x x x x y +⎧=-⎪⎪⎨++-⎪=⎪⎩， 由（1）可得124x x k +=，124(3)8x x b =-+=-，所以8432M k x k -⨯=-=，22221212122()288M x x x x x x y k +++===， 即点2(,2)M k k ，所以212M M x y =， 即点M 的轨迹方程为：212x y =． 【点睛】本题考查求直线恒过定点的方程及直三角形外接圆的性质，和直线与椭圆的综合应用，属于难题． 12．抛物线2:2(0)C x py p =>的焦点为F ，过F 且垂直于y 轴的直线交抛物线C 于,M N 两点，O 为原点，OMN 的面积为2. （1）求拋物线C 的方程.（2）P 为直线()00:0l y y y =<上一个动点，过点P 作拋物线的切线，切点分别为,A B ，过点P 作AB 的垂线，垂足为H ，是否存在实数0y ，使点P 在直线l 上移动时，垂足H 恒为定点？若不存在，说明理由；若存在，求出0y 的值，并求定点H 的坐标.【答案】（1）24x y =；（2）存在这样的0y ，当01y =-时，H 坐标为(0,1).【分析】（1）先根据抛物线的性质，结合题中条件，得到||2MN p =，由三角形面积列出方程求出p ，即可得出抛物线方程；（2）先设()()()112200,,,,,A x y B x y P x y ，直线AP 的方程为()11y y k x x -=-，根据直线与抛物线相切，得到112x xy y +=，进而推出AB 的方程为002x x y y +=，根据PH AB ⊥，得到PH 方程，由两直线方程，即可求出0y ，确定出结果. 【详解】（1）由题意得，点,M N 的纵坐标均为2p ，由222p x p =⋅，解得x p =±，则||2MN p =， 由2111||||222222CMN p S MN OF p p =⋅⋅=⋅⋅==△，解得2p =， 故抛物线C 的方程为24x y =.（2）假设存在实数0y ，使点P 在直线l 上移动时，垂足H 恒为定点， 设()()()112200,,,,,A x y B x y P x y ，直线AP 的方程为()11y y k x x -=-，将抛物线方程变形为24x y =，则2x y '=，所以12x k =， 所以AP 的方程为()1112x y y x x -=-. 因为2114x y =，所以直线AP 的方程为112x x y y +=. 把()00,P x y 代入AP 的方程得10012x x y y +=. 同理可得2002.2x x y y +=构造直线方程为002x xy y +=，易知,A B 两点均在该直线上，所以直线AB 的方程为002x xy y +=.故AB 恒过点()00,y -. 因为PH AB ⊥，所以可设PH 方程为()0002x x x y y -=--，化简得()0022xx y y =--- 所以PH 恒过点()00,2y +.当002y y -=+，即01y =-时，AB 与PH 均恒过(0,1)， 故存在这样的0y ，当01y =-时，H 坐标为(0,1).【点睛】 关键点点睛：求解本题第二问的关键在于用0y 分别表示出直线AB 和PH 的方程；根据题中条件，先设点的坐标，以及直线AP 的方程，由直线与抛物线相切，得出直线AP 方程，推出AB 的方程，进而确定PH 的方程，即可求解.13．已知抛物线C ：22y x =的焦点为F ，平行于x 轴的两条直线12,l l 分别交C 于A B ，两点，交C 的准线于P Q ，两点．（Ⅰ）若F 在线段AB 上，R 是PQ 的中点，证明//AR FQ ； （Ⅰ）若PQF ∆的面积是ABF ∆的面积的两倍，求AB 中点的轨迹方程. 【答案】（Ⅰ）见解析；（Ⅰ）21y x =-． 【分析】设22111,0,,,,,,,,222222a b a b A B b P a Q b R ⎛⎫⎛⎫+⎛⎫⎛⎫⎛⎫--- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⇒l 的方程为2(x a -+ )0b y ab +=．（Ⅰ）由F 在线段AB 上⇒10ab +=，又122211a b a b abk b k a a ab a a---=====-=+-⇒//AR FQ ；（Ⅰ）设l 与x 轴的交点为()1,0D x ⇒1111,2222ABF PQF a b S b a FD b a x S ∆∆-=-=--=⇒111222a b b a x ---=⇒10x =（舍去），11x =．设满足条件的AB 的中点为(),E x y ．当AB 与x 轴不垂直时⇒()211y x a b x =≠+-⇒2a by +=⇒()211y x x =-≠．当AB 与x 轴垂直时⇒E 与D 重合⇒所求轨迹方程为21y x =-． 【详解】 由题设1,02F ⎛⎫⎪⎝⎭，设12:,:l y a l y b ==，则0ab ≠，且 22111,0,,,,,,,,222222a b a b A B b P a Q b R ⎛⎫⎛⎫+⎛⎫⎛⎫⎛⎫--- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭．记过,A B 两点的直线为l ，则l 的方程为()20x a b y ab -++=（Ⅰ）由于F 在线段AB 上，故10ab +=， 记AR 的斜率为1,k FQ 的斜率为2k ，则122211a b a b abk b k a a ab a a---=====-=+-， 所以//AR FQ（Ⅰ）设l 与x 轴的交点为()1,0D x ， 则1111,2222ABF PQF a b S b a FD b a x S ∆∆-=-=--=， 由题设可得111222a b b a x ---=，所以10x =（舍去），11x =． 设满足条件的AB 的中点为(),E x y ． 当AB 与x 轴不垂直时，由AB DE k k =可得()211yx a b x =≠+-． 而2a by +=，所以()211y x x =-≠． 当AB 与x 轴垂直时，E 与D 重合，所以，所求轨迹方程为21y x =- 【点睛】本题考查了1.抛物线定义与几何性质；2.直线与抛物线位置关系；3.轨迹求法．14．如图，设抛物线y 2=2px(p >0)的焦点为F ，抛物线上的点A 到y 轴的距离等于|AF|–1.（Ⅰ）求p 的值；（Ⅰ）若直线AF 交抛物线于另一点B ，过B 与x 轴平行的直线和过F 与AB 垂直的直线交于点N ，AN 与x 轴交于点M.求M 的横坐标的取值范围. 【答案】（Ⅰ）p=2；（Ⅰ）(−∞,0)∪(2，+∞). 【解析】试题分析：本题主要考查抛物线的几何性质、直线与抛物线的位置关系等基础知识，同时考查解析几何的基本思想方法和综合解题能力.试题解析：（Ⅰ）由题意可得，抛物线上点A 到焦点F 的距离等于点A 到直线x=–1的距离，由抛物线的定义得p2=1，即p=2.（Ⅰ）由（Ⅰ）得，抛物线的方程为y 2=4x,F(1,0)，可设A(t 2,2t),t ≠0,t ≠±1.因为AF 不垂直于y 轴，可设直线AF: x=sy+1，(s ≠0)，由{y 2=4x ，x =sy +1 消去x 得y 2−4sy −4=0，故y 1y 2=−4，所以，B(1t 2,−2t ). 又直线AB 的斜率为2t t 2−1，故直线FN 的斜率为−t 2−12t .从而得直线FN:y =−t 2−12t(x −1)，直线BN:y =−2t.所以N(t 2+3t 2−1,−2t).设M(m,0)，由A ，M ，N 三点共线得2t t 2−m=2t+2t t 2−t 2+3t 2−1，于是m =2t 2t 2−1.所以m ＜0或m ＞2.经检验，m ＜0或m ＞2满足题意.综上，点M 的横坐标的取值范围是(−∞,0)∪(2,+∞). 【考点】抛物线的几何性质、直线与抛物线的位置关系.【思路点睛】（Ⅰ）当题目中出现抛物线上的点到焦点的距离时，一般会想到转化为抛物线上的点到准线的距离．解答本题时转化为抛物线上的点到准线的距离，进而可得点到y 轴的距离；（Ⅰ）通过联立方程组可得点Β的坐标，进而可得点Ν的坐标，再利用Α，Μ，Ν三点共线可得m 用含有t 的式子表示，进而可得Μ的横坐标的取值范围.15．如图，已知点P 是y 轴左侧（不含y 轴）一点，抛物线2:4C y x 上存在不同的两点A 、B ，满足PA 、PB 的中点均在抛物线C 上.（1）求抛物线C 的焦点到准线的距离；（2）设AB 中点为M ，且(,)P P P x y ，(,)M M M x y ，证明：P M y y =；（3）若P 是曲线2214y x +=（0x <）上的动点，求PAB ∆面积的最小值.【答案】（1）2；（2）证明见解析；（3） 【分析】（1）直接利用抛物线定义得到答案.（2）设00(,)P x y ，211(,)4y A y ，222(,)4y B y ，根据AP 中点在抛物线上得到2210100280y y y x y -+-=，同理得到12,y y 是二次方程22000280y y y x y -+-=的两不等实根，计算得到答案.（3）设t =，代换得到30121()||2M S x x y y =--=计算得到答案.【详解】（1）焦点坐标为（1,0），准线方程为x ＝－1，所以，焦点到准线的距离为2.（2）设00(,)P x y ，211(,)4y A y ，222(,)4y B y ，则PA 中点为20011(,)282x y y y ++，由AP 中点在抛物线上可得220101()4()228y y x y +=+，化简得2210100280y y y x y -+-=，显然21y y ≠， 且对2y 也有2220200280y y y x y -+-=，所以12,y y 是二次方程22000280y y y x y -+-=的两不等实根，所以1202y y y +=，1202M P y y y y y +===. （3）121()(||||)2M P M M S x x y y y y =--+-0121()||2M x x y y =--， 由（1）可得1202y y y +=，212008y y x y =-，2220000012(2)4(8)8(4)0()y x y y x y y ∆=--=->≠，此时00(,)P x y 在半椭圆221(0)4y x x +=<上，∴2220000008(4)8[4(1)4]32(1)y x x x x x ∆=-=--=--，∵010x -≤<，∴>0∆，∴12||||y y a -===， 2222200012121200042(8)()2||888M P y x y y y y y y y x x x x x --++--=-=-=-2006(44)38x x -=-2003(1)x x =--，所以23012001()||2M S x x y y x x =--=--=，2t =，所以34S =∈，即PAB ∆的面积的最小值是 【点睛】本题考查了面积的最值问题，证明坐标关系，综合性强，计算量大，意在考查学生的综合应用能力和计算能力.16．设抛物线2:C y x =的焦点为F ，动点P 在直线:20l x y --=上运动，过P 作抛物线C 的两条切线PA 、PB ，且与抛物线C 分别相切于A 、B 两点. （1）求△APB 的重心G 的轨迹方程. （2）证明∠PFA=∠PFB ． 【答案】(1)21(42)3y x x =-+(2)见解析 【解析】本试题主要考查了轨迹方程的求解和证明角的相等问题． 解：（1）设切点A ，B 坐标分别为()200,x x 和()211x x ，()10xx ≠，∴切线AP 的方程为：20020x x y x --=；切线BP 的方程为：21120x x y x --=；由于P 既在AP 又在BP 上，所以20021120{20P P P P x x y x x x y x --=--=解得0101{2p p x x x y x x +==，0101(,)2x x P x x + 所以APB 的重心G 的坐标为013pG p x x x x x ++==，()2222010101010143333pp p G y y y x y x x x x x x x x y ++-+-++====， 所以234P G G y y x =-+，由点P 在直线l 上运动，从而得到重心G 的轨迹方程为：()23420x y x --+-=，即()21423y x x =-+． （2）方法1：因为20014FA x x ⎛⎫=-⎪⎝⎭，，0101124x x FP x x +⎛⎫=- ⎪⎝⎭，，21114FB x x ⎛⎫=- ⎪⎝⎭，． 由于P 点在抛物线外，则0FP ≠．，同理有，AFP PFB ∴∠=∠．方法2：①当100x x =时，由于10x x ≠，不妨设00x =，则00y =，所以P 点坐标为102x ⎛⎫⎪⎝⎭，，则P 点到直线AF 的距离为：112x d =；而直线BF 的方程：2111144x y x x --=，即211111044x x x y x ⎛⎫--+= ⎪⎝⎭．所以P 点到直线BF 的距离为：1211221142124x x x d x ⎛⎫+ ⎪⎝⎭===+所以12d d =，即得AFP PFB ∠=∠．②当100x x ≠时，直线AF 的方程：()200114040x y x x --=--，即200011044x x x y x ⎛⎫--+= ⎪⎝⎭，直线BF 的方程：()211114040x y x x --=--，即211111044x x x y x ⎛⎫--+= ⎪⎝⎭，所以P 点到直线AF 的距离为：201001120124124x x x x xd x -⎛⎫+ ⎪-⎝⎭===+， 同理可得到P 点到直线BF 的距离，因此由12d d =，可得到AFP PFB ∠=∠．17．如下图，设抛物线方程为()220x py p =>，M 为直线2y p =-上任意一点，过M 引抛物线的切线，切点分别为A ，B ．（Ⅰ）设线段AB 的中点为N ； （Ⅰ）求证：MN 平行于y 轴；（Ⅰ）已知当M 点的坐标为()22p -，时，AB =，求此时抛物线的方程； （Ⅰ）是否存在点M ，使得点C 关于直线AB 的对称点D 在抛物线()220x pyp =>上，其中，点C 满足OC OA OB =+（O 为坐标原点）．若存在，求出所有适合题意的点M 的坐标；若不存在，请说明理由．【答案】（Ⅰ）（Ⅰ）证明见解析；（Ⅰ）22x y =或24x y =；（Ⅰ）仅存在一点()0,2M p -适合题意.【分析】（Ⅰ）（Ⅰ）设出,,,A B N M 的坐标，利用导数求得切线,MA MB 的方程，结合N 是线段AB 的中点进行化简，得到,M N 两点的横坐标相等，由此证得MN 平行于y 轴.（Ⅰ）利用AB =p ，进而求得抛物线方程.（Ⅰ）设出D 点坐标，由C 点坐标求得线段CD 中点的坐标，由直线AB 的方程和抛物线的方程，求得D 点的坐标，由此进行分类讨论求得M 点的坐标. 【详解】（Ⅰ）（Ⅰ）证明：由题意设211,2x A x p ⎛⎫ ⎪⎝⎭，222,2x B x p ⎛⎫ ⎪⎝⎭，12x x <，()33,N x y ，()0,2M x p -．由22x py =得22x y p=，则x y p '=，所以1MA x k p =，2MB x k p =．因此直线MA 的方程为()102x y p x x p+=-， 直线MB 的方程为()202x y p x x p+=-． 所以()2111022x x p x x p p +=-，①()2222022x x p x x p p+=-．② 由①、②得121202x x x x x +=+-，因此1202x xx +=，即012322x x x x =+=，也即03x x =.所以MN 平行于y 轴．（Ⅰ）解：由（Ⅰ）知，当02x =时，将其代入①、②并整理得：2211440x x p --=，2222440x x p --=，所以1x ，2x 是方程22440x x p --=的两根，因此124x x +=，2124x x p =-，又222101221222ABk x x x x x p p x x p p-+===-，所以2AB k p=．由弦长公式的AB ==．又AB =，所以1p =或2p =， 因此所求抛物线方程为22x y =或24x y =．（Ⅰ）解：设()44,D x y ，由题意得()1212,C x x y y ++， 则CD 的中点坐标为124124,22x x x y y y Q ++++⎛⎫⎪⎝⎭， 设直线AB 的方程为()011x y y x x p-=-， 由点Q 在直线AB 上，并注意到点1212,22x x y y ++⎛⎫⎪⎝⎭也在直线AB 上，代入得044x y x p=． 若()44,D x y 在抛物线上，则2440422x py x x ==，因此40x =或402x x =．即()0,0D 或2022,x D x p ⎛⎫ ⎪⎝⎭．（1）当00x =时，则12020x x x +==，此时，点()0,2M p -适合题意．（2）当00x ≠，对于()0,0D ，此时221202,2x x C x p ⎛⎫+ ⎪⎝⎭，2212221200224CDx x x x pk x px ++==， 又0ABx k p =，AB CD ⊥，所以22220121220144AB CD x x x x x k k p px p ++⋅=⋅==-，即222124x x p +=-，矛盾．对于20022,x D x p ⎛⎫ ⎪⎝⎭，因为221202,2x x C x p ⎛⎫+ ⎪⎝⎭，此时直线CD 平行于y 轴，又00AB x k p=≠， 所以直线AB 与直线CD 不垂直，与题设矛盾， 所以00x ≠时，不存在符合题意得M 点．综上所述，仅存在一点()0,2M p -适合题意． 【点睛】本小题主要考查直线和抛物线的位置关系，考查运算求解能力，属于难题.。

第18讲阿基米德三角形知识与方法阿基米德（约公元前287年一前212年)，是伟大的古希腊哲学家、百科式科学家、数学家、物理学家,并且享有“力学之父”的美称.他在求体积或面积时采用的“平衡法”一档杆原理,被后人命名为“阿基米德方法”.正是由于他对当时数学作出的突出贡献以及对后世数学发展的深邃影响,他又被后人誉为“数学之神”.本节主要探讨的阿基米德三角形指的是圆锥曲线（椭圆、双曲线、拋物线）的弦与过弦的端点的两条切线所围成的三角形.阿基米德三角形得名于阿基米德在研究与拋物线有关的面积问题时得出的一个结论:抛物线的弦与拋物线所围成的封闭图形的面积,等于抛物线的弦与过弦的端点的两条切线所围成的三角形面积的三分之二.（结论的证明利用了“平衡法”)该结论的变式叙述可见于《普通高中课程标准实验教科书·数学选修3-1（A版):数学史选讲》(人民教育出版社2007年1月第2版).接下来，我们就去探讨一下阿基米德三角形中蕴藏的一些重要性质:条件：已知抛物线C:x2=2py(p>0),如图所示,D为某一直线l上的动点,过D作C的两条切线,切点分别为A,B,F为直线AB与y轴的交点,则有以下结论成立:结论1.1直线AB的方程为(x1+x2)x−2py−x1x2=0.证明:设A(x1,y1),则x12=2py1.由于y′=xp ,所以切线DA的斜率为x1p,故切线DA的方程为x1x=p(y+y1)(1)设B(x2,y2),同理可得DB的方程为x2x=p(y+y2)(2) (1)÷(2)化简后,可得y=x1x22p(3)将(3)代入(1),可得x=x1+x22,所以点D的坐标为(x1+x22,x1x22p)故直线AB的方程为(x1+x2)x−2py−x1x2=0说明:特别的,当D为直线y=−p2上的动点时,直线AB的方程为(x1+x2)x−2py+p2=0且该直线过拋物线的焦点F.第二部分中的典例第（1）问考查的就是该性质的具体运用.结论1.2k DF⋅k AB=k DA⋅k DB=x1x2p2证明:由结论1.1的证明可知点F的坐标为(0,−x1x22p)又k DF=2x1x2p(x1+x2),k AB=x1+x22p,k DA=x1p,k DB=x2p,所以结论1.2得证.说明:特别的,当D为直线y=−p2上的动点时，有DF⊥AB,DA⊥DB；且此时△DAB面积的达到最小,其最小值为p2.第三部分中的第2题、第3题考查的均是该条性质及推论的运用,如若我们对上述性质比较熟悉,则审题结束时答案或许已了然于心.结论1.3在阿基米德△DAB中,有∠DFA=∠DFB.证明:如图,过点A,B分别作抛物线准线的垂线AA1,BB1,垂足为A1,B1.连接A1D,B1D,DF,AF,BF,A1F,则k A1F =−px1,k AD=x1p.易知,AD⊥A1F.又AA1=AF,所以AD垂直且平分A1F,故A1D=DF,∠DA1A=∠DFA.同理可得B1D=DF,∠DB1B=∠DFB,所以A1D=B1D=DF,∠DA1B1=∠DB1A1.进而∠DA1A=∠DB1B,即∠DFA=∠DFB.说明:第三部分中的第4题的第（2）问恰恰就考查了这一结论.结论1.4DA,AB,DB的斜率成等差数列、A,D,B三点的横坐标成等差数列.证明:结合结论1.2的证明过程以及点D坐标(x1+x22,x1x22p),稍作运算，便可证得该结论.说明:第三部分中的第5题的第（1）问中就涉及到了这一结论.结论1.5线段FA,FD,FB的长度之间的关系为FD2=x12x22p2+p2|x1x2|⋅FA⋅FB−p2.证明:经过简单计算即可得到上述结果.说明:特别的,当D为直线y=−p2上的动点时,有线段FA,FD,FB的长度成等比数列.结论1.6若以E(0,−5x1x22p)为圆心的圆与直线AB相切于点T,则四边形ADBE的面积为|x1−x2|38p −x1x2⋅|x1−x2|p证明:易知DA ⃗⃗⃗⃗⃗ =(x 1−x 22,x 1(x 1−x 2)2p ),DB ⃗⃗⃗⃗⃗⃗ =(x 2−x 12,x 2(x 2−x 1)2p). 利用面积公式S ΔDAB =12√DA ⃗⃗⃗⃗⃗ 2⋅DB ⃗⃗⃗⃗⃗⃗ 2−(DA ⃗⃗⃗⃗⃗ ⋅DB⃗⃗⃗⃗⃗⃗ )2,可得 S △DAB=12|x 1−x 22⋅x 2(x 2−x 1)2p −x 2−x 12⋅x 1(x 1−x 2)2p |=|x 1−x 2|38p又S △EAB =12|EF|⋅|x 1−x 2|=12(−5x 1x 22p +x 1x 22p )⋅|x 1−x 2|=−x 1x 2⋅|x 1−x 2|p所以S 四边形 ADBE =S Δ+S ΔA =|x 1−x 2|38p−x 1x 2⋅|x 1−x 2|p.说明：当D 为直线y =−p2上的动点,且E (0,5p2)时,则四边形ADBE 的面积为|x 1−x 2|38p+p |x 1−x 2|.结论1.7△DAB 的重心G 满足的方程为4x 2−6py −x 1x 2=0. 证明:过程从略，感兴趣的读者可自行尝试证明.说明:当D 为直线y =−p2上的动点时，△DAB 的重心G 的轨迹方程为4x 2−6py +p 2=0结论1.8 若P 为拋物线弧AB 上一点,拋物线在点P 处的切线与直线..分别交与M,N 两点,则S △DMN :S △PAB =1:2证明:设P (x 3,y 3),则有x M =x 1+x 32,x N =x 2+x32所以AMMD =MP PN=DNNB =|x 1−x 3||x 2−x 3|.设AM MD =MP PN =DNNB=a,S △PMD =b 因为S ΔPMAS ΔPMD=AM MD =a ,所以S ΔPMA =ab同理S △PND =ba ,S ΔPNB =ba 2,所以S △DMN =b (1+1a ). 又S ΔNMD S △BAD=MD⋅DN AD⋅BD=a(a+1)2,所以S ΔBAD =b ⋅(a+1)3a 2.所以S ΔPBA =S ΔDAB −S △DMN −S ΔPAM −S ΔPBN =b ⋅2(a+1)a所以SΔDMN:S△PAB=1:2.值得注意的是抛物线的性质远也不止这些，上述所列诸条,大多数是在区域模拟考试及高考中经常出现的.众所周知,以阿基米德三角形为背景的直线的定点、三角形的面积、轨迹、最值等相关问题是高考和模拟考考查的热点也是难点.纸上得来终觉浅,接下来我们不妨从多个视角去赏析一道高考题,以进一步体会阿基米德三角形的相关性质.典型例题【例1】已知曲线C:y=12x2,D为直线y=−12上的动点,过D作C的两条切线,切点分别为A,B.(1)证明：直线AB过定点;(2)若以E(0,52)为圆心的圆与直线AB相切，且切点为线段AB的中点,求四边形ADBE的面积.强化训练1.如图,抛物线C1:x2=4y,C2:x2=−2py(p>0).点M(x0,y0)在拋物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O).当x0=1−√2时,切线MA的斜率为−12.(1)求p的值;(2)当M在C2上运动时,求线段AB中点N的轨迹方程(A,B重合于O时,中点为O).2.已知抛物线x 2=4y 的焦点为F,A,B 是抛物线上的两动点,且AF⃗⃗⃗⃗⃗ =λFB ⃗⃗⃗⃗⃗ (λ>0)过A,B 两点分别作扡物线的切线,设其交点为M .(1)证明FM̅̅̅̅̅⋅AB ⃗⃗⃗⃗⃗ 为定值; (2)设△ABM 的面积为S ,写出S =f(λ)的表达式,并求S 的最小值.3.如图,等边三角形OAB 的边长为8√3,且其三个顶点均在拋物线E:x 2=2py(p >0)上. (1)求抛物线E 的方程;(2)设动直线l 与抛物线E 相切于点P ,与直线y =−1相交于点Q .证明以PQ 为直径的圆恒过y 轴上某定点.4.如图，设抛物线C:y =x 2的焦点为F ,动点P 在直线l:x −y −2=0上运动,过P 作拋物线C 的两条切线PA,PB ,且与抛物线C 分别相切于A,B 两点. (1)求△APB 的重心G 的轨迹方程; (2)证明∠PFA =∠PFB .5.如图,设抛物线方程为 x 2=2py(p >0),M 为直线y =−2p 上任意一点,过M 引抛物线的切线,切点分别为 A,B .(1)求证：A,M,B 三点的横坐标成等差数列;(2)已知当M 点的坐标为(2,−2p)时，|AB|=4√10,求此时抛物线的方程;(3)是否存在点M ,使得点C 关于直线AB 的对称点D 在拋物线x 2=2py(p >0)上，其中点C 满足 OC⃗⃗⃗⃗⃗ =OA ⃗⃗⃗⃗⃗ +OB⃗⃗⃗⃗⃗ （O 为坐标原点).若存在,求出所有适合题意的点的坐标;若不存在,请说明理由.。