相似三角形综合训练(二)

27.2相似三角形同步练习一．选择题1．如图，△ABC∽△DCA，∠B＝33°，∠D＝117°，则∠BAD的度数是（）A．150°B．147°C．135°D．120°2．两个相似三角形对应角平分线的比为4：3，那么这两个三角形的面积的比是（）A．2：3B．4：9C．16：36D．16：93．下列条件中，不能判断△ABC与△DEF相似的是（）A．∠A＝∠D，∠B＝∠F B．且∠B＝∠DC．D．且∠A＝∠D4．如图，在△ABC中，点D、E分别在边AB、AC上，下列条件中能判断△ABC∽△AED 的是（）①∠AED＝∠B；②∠ADE＝∠C；③＝；④＝．A．①②B．①②③C．①②④D．①②③④5．如图，在平行四边形ABCD中，点E在边DC上，DE：EC＝5：2，连接AE交BD于点F，则△DEF的面积与△BAF的面积之比为（）A．5：7B．10：4C．25：4D．25：496．已知点E、F分别在△ABC的AB、AC边上，则下列判断正确的是（）A．若△AEF与△ABC相似，则EF∥BCB．若AE×BE＝AF×FC，则△AEF与△ABC相似C．若，则△AEF与△ABC相似D．若AF•BE＝AE•FC，则△AEF与△ABC相似7．如图，在△ABC，D是BC上一点，BD：CD＝1：2，E是AD上一点，DE：AE＝1：2，连接CE，CE的延长线交AB于F，则AF：AB为（）A．1：2B．2：3C．4：3D．4：78．如图，在▱ABCD中，AC与BD相交于点O，E为OD的中点，连接AE并延长交DC于点F，则△DEF与四边形EFCO的面积比为（）A．1：4B．1：5C．1：6D．1：79．如图，AD∥BC，∠D＝90°，AD＝3，BC＝4，DC＝6，若在边DC上有点P，使△P AD 与△PBC相似，则这样的点P有（）A．1 个B．2 个C．3 个D．4 个10．如图，在矩形ABCD中，E是AD边的中点，BE⊥AC于F，连接DF，若BF＝，BC ＝3，则DF＝（）A．4B．3C．2D．二．填空题11．已知△ABC∽△A′B′C′，且AB＝3cm，A′B′＝5cm，则相似比为．12．如图，△ABC中，CA＝CB，点E在BC边上，点D在AC边上，连接AE、DE，若AB ＝AE，2∠AEB+∠ADE＝180°，BE＝8，CD＝，则CE＝．13．如图，在△ABC中，若DE∥BC，EF∥CD，AE＝2EC，则AF：FD：DB＝．14．如图，D、E分别是△ABC的边AB、BC上的点，且DE∥AC，AE、CD相交于点O，若S△DOE：S△COA＝1：25，则的值是．15．如图，在矩形ABCD中，AD＝2，AB＝4，E、F分别是AB、CD边上的动点，EF⊥AC，则AF+CE的最小值为．三．解答题16．如图，点P是菱形ABCD的对角线AC上一点，连接DP并延长，交AB于点F，交CB 的延长线于点E．求证：（1）△APB≌△APD；（2）PD2＝PE•PF．17．如图，在△ABC中，点D、E分别在AB、AC上，DE、BC的延长线相交于点F，且EF•DF＝CF•BF．求证：△CAB∽△DAE．18．如图，AF，AG分别是△ABC和△ADE的高，∠BAF＝∠DAG．（1）求证：△ABC∽△ADE；（2）若DE＝3，，求BC的长．参考答案一．选择题1．解：∵△ABC∽△DCA，∴∠BAC＝∠D＝117°，∠DAC＝∠B＝33°，∴∠BAD＝∠BAC+∠DAC＝150°，故选：A．2．解：∵两个相似三角形对应角平分线的比为4：3，∴它们的相似比为4：3，∴它们的面积比为16：9．故选：D．3．解：A、∠A＝∠D，∠B＝∠F，可以得出△ABC∽△DFE，故此选项不合题意；B、＝且∠B＝∠D，不是两边成比例且夹角相等，故此选项符合题意；C、＝＝，可以得出△ABC∽△DEF，故此选项不合题意；D、＝且∠A＝∠D，可以得出△ABC∽△DEF，故此选项不合题意；故选：B．4．解：∵∠A＝∠A，∴∠AED＝∠B或∠ADE＝∠C时，△ABC∽△AED．∵＝，∴＝∵∠A＝∠A，∴△ABC∽△AED，故①②③可以判断三角形相似，故选：B．5．解：设DE＝5k，EC＝2k，则CD＝7k，∵四边形ABCD是平行四边形，∴AB＝CD＝7k，DE∥AB，∴△DEF∽△BAF，∴＝＝＝，故选：D．6．解：选项A错误，∵△AEF与△ABC相似，可能是∠AEF＝∠C，推不出EF∥BC．选项B错误，由AE×BE＝AF×FC，推不出△AEF与△ABC相似．选项C错误，由，推不出△AEF与△ABC相似．选项D正确．理由：∵AF•BE＝AE•FC，∴＝，∴EF∥BC，∴△AEF∽△ABC．故选：D．7．解：过D作DH∥AB交CF于H，如图，∵DH∥BF，∴＝，∵BD：CD＝1：2，∴CD：BC＝2：3，∴BF＝DH，∵DH∥AF，∴＝＝2，∴AF＝2DH，∴AF：BF＝2DH：DH＝4：3，∴AF：AB＝4：7．故选：D．8．解：∵四边形ABCD是平行四边形，∴BO＝DO，AB∥CD，∵E为OD的中点，∴DE＝EO＝DO，∴BO＝2EO，BE＝3DE，∵DF∥AB，∴△DFE∽△BAE，∴＝（）2＝，设S△DEF＝x，则S△BEA＝9x，∵BO＝2OE，∴S△AOB＝6x＝S△DOC，∴四边形EFCO的面积＝5x，∴△DEF与四边形EFCO的面积比＝1：5，故选：B．9．解：∵AB⊥BC，∴∠B＝90°．∵AD∥BC∴∠A＝180°﹣∠B＝90°，∴∠P AD＝∠PBC＝90°．设DP的长为x，则CP长为6﹣x．若AB边上存在P点，使△P AD与△PBC相似，那么分两种情况：①若△APD∽△BPC，则DP：CP＝AD：BC，即x：（6﹣x）＝3：4，解得：x＝②若△APD∽△BPC，则DP：PC＝AD：BC，即x：4＝3：（6﹣x），整理得：x2﹣6x+12＝0，∵△＜0，这种情形不存在，∴满足条件的点P的个数是1个，故选：A．10．解：如图，连接BD，∵∠AEF＝∠BEA，∠AFE＝∠BAE＝90°，∴△AEF∽△BEA，∴＝，∵AE＝ED，∴＝，又∵∠FED＝∠DEB，∴△FED∽△DEB，∴∠EFD＝∠EDB，∵∠EFD+∠DFC＝90°，∠EDB+∠ODC＝90°，∴∠DFC＝∠ODC，∵在矩形ABCD中，OC＝AC，OD＝BD，AC＝BD，∴OD＝OC，∴∠OCD＝∠ODC，∴∠DFC＝∠OCD，∴DF＝DC，在Rt△BCF中，FC＝＝＝2，∵AD∥BC，∴△AEF∽△CBF，∴＝＝，∴AF＝FC＝，∴AB＝＝＝3，∴DF＝3，故选：B．二．填空题11．解：由题意得，＝，∵△ABC∽△A′B′C′，∴△ABC与△A′B′C′的相似比为＝，故答案为：．12．解：如图，过点A作AM⊥BE于E，过点D作DN⊥EC于N，∵CA＝CB，AB＝AE，∴∠B＝∠CAB，∠B＝∠AEB，∴∠B＝∠CAB＝∠AEB，∵∠B+∠BAC+∠C＝180°，∠B+∠AEB+∠BAE＝180°，∴∠C＝∠BAE，∴2∠AEB+∠C＝180°，又∵2∠AEB+∠ADE＝180°，∴∠C＝∠ADE，又∵∠ADE＝∠C+∠DEC，∴∠C＝∠DEC，∴DE＝DC＝，∵AB＝AE，AM⊥BE，DE＝CC，DN⊥EC，∴BM＝ME＝BE＝4，EN＝NC＝EC，AM∥DN，∴△CDN∽△CAM，∴，∴，∴EC＝12，EC＝﹣5（不合题意舍去），故答案为：12．13．解：∵EF∥CD，AE＝2EC，∴＝＝2，∵DE∥BC，∴＝＝2，设DF＝m，则AF＝2m，AD＝3m，DB＝m，∴AF：DF：DB＝2m：m：m＝4：2：3．故答案为：4：2：3．14．解：∵DE∥AC，∴△DOE∽△COA，∴＝（）2＝，∴＝，∵DE∥AC，∴△BDE∽△BAC，∴＝，∴＝，故答案为：．15．解：如图所示：设DF＝x，则FC＝4﹣x；过点C作CG∥EF，且CG＝EF，连接FG，当点A、F、G三点共线时，AF+FG的最值小；∵CG∥EF，且CG＝EF，∴四边形CEFG是平行四边形；∴EC∥FG，EC＝FG，又∵点A、F、G三点共线，∴AF∥EC，又∵四边形ABCD是矩形，∴AE∥DC，∠D＝90°，∴四边形AECF是平行四边形，∴OA＝OC，OE＝OF，又∵EF⊥AC，AF＝CF＝4﹣x，在Rt△ADF中，由勾股定理得：AD2+DF2＝AF2，又∵AD＝2，DF＝x，则FC＝4﹣x，∴22+x2＝（4﹣x）2，解得：x＝，∴AF＝，在Rt△ADC中，由勾股定理得：AD2+DC2＝AC2，∴AC＝，∴AO＝，又∵OF∥CG，∴△AOF∽△ACG，∴＝，∴AG＝5，又∵AG＝AF+FG，FG＝EC，∴AF+EC＝5，故答案为5．三．解答题16．证明：（1）∵四边形ABCD是菱形，∴AB＝AD，∠BAC＝∠DAC，在△ABP和△ADP中，，∴△ABP≌△ADP（SAS）；（2）∵△ABP≌△ADP，∴PB＝PD，∠ADP＝∠ABP，∵AD∥BC，∴∠ADP＝∠E，∴∠E＝∠ABP，又∵∠FPB＝∠EPB，∴△EPB∽△BPF，∴，∴PB2＝PE•PF，∴PD2＝PE•PF．17．证明：∵EF•DF＝CF•BF．∴，∵∠EFC＝∠BFD，∴△EFC∽△BFD，∴∠CEF＝∠B，∴∠B＝∠AED，∵∠CAB＝∠DAE，∴△CAB∽△DAE．18．（1）证明：∵AF，AG分别是△ABC和△ADE的高，∴AF⊥BC，AG⊥DE，∴∠AFB＝90°，∠AGD＝90°，∴∠BAF+∠B＝90°，∠DAG+∠ADG＝90°，∵∠BAF＝∠DAG，∴∠B＝∠ADG，又∵∠EAD＝∠BAC，∴△ABC∽△ADE；（2）解：∵△ADE∽△ABC，∴，∵，BC＝3，∴，∴BC＝．。

专题02相似三角形选择填空题之压轴题训练(2)一、选择题（本大题共12题）1.（徐汇2020一模6）下列命题中，假命题是（）A.凡有内角为︒30的直角三角形都相似；B.凡有内角为︒45的等腰三角形都相似；C.凡有内角为︒60的直角三角形都相似；D.凡有内角为︒90的等腰三角形都相似．2.（进才北2019十月6）如图，在ABC 中，D 、E 分别在边AB 、AC 上，//DE BC ，//EF CD 交AB 于F ，那么下列比例式中正确的是()A.AF DEDF BC=; B.DF AFDB DF=; C.EF DECD BC=; D.AF ADBD AB=.3.（金山2019期中6）如图，在△ABC 中，D 、E 分别为AB 、AC 边上的点，DE//BC ，点F 为BC 边上的一点，连接AF 交DE 于点G ，那么下列结论中一定正确的是（）A.AD AEAB EC=;B .AG EGGF CF=; C.EG GDCF FB=; D.AG DEFG BC=.4.（黄浦2020一模6）如图，点D 、E 分别在△ABC 的两边BA 、CA 的延长线上，下列条件能判定ED ∥BC 的是（）A ．AD DEAB BC=;B ．AD AEAC AB=;C ．AD •AB ＝DE •BC ;D ．AD •AC ＝AB •AE.5.（闵行2019期中6）如图，在△ABC 中，∠A=60︒，CD 、BE 分别是边AB 、AC 上的高线，联结DE ，那么△ADE 和△ACB 的周长之比为（）A.12;B .32; C.14; D.34.6.（松江2021一模6）如图，已知在Rt ABC 中，90C ∠=︒，点G 是ABC 的重心，GE AC ⊥，垂足为E ，如果8CB =，则线段GE 的长为（）A.53； B.73； C.83； D.103.7.（普陀2019期中6）如图，四边形ABCD 的对角线AC 与BD 相交于点O ，2OA =，3OB =，6OC =，4OD =，那么下列结论中，错误的是（）A.OAD OBC ∠=∠;B.12AB CD =; C.12AOB DOC C C ∆∆=;D.19AOD BOC S S ∆∆=.8.（杨浦2021一模6）在梯形ABCD 中，AD ∥BC ，对角线AC 与BD 相交于点O ，下列说法中，错误的是（）A ．S △AOB ＝S △DOC ；B ．AOB BOC S OD S OB∆∆=； C.AOD BOC S OA S OC ∆∆=;D ．ABD ABC S ADS BC ∆∆=.9.（普陀2021一模6）如图，四边形ABCD 的对角线AC 与BD 相交于点O ，OA OD OBOC=，由此推得的正确结论是()A.OA ABOD CD=； B.OA ADOC BC=； C.OB ABOD CD=； D.AB ADCD BC=．10.（浦东南片联合2019期中6）如图，在RT △ABC 中，∠C=90°，BC=3，AC=4，四边形DEGF 为内接正方形，那么AD ：DE ：EB 为（）A.3︰4︰5;B.16︰12︰9;C.9︰12︰16D.16︰9︰25.11.（杨浦黄兴2019九月6）如图，把△ABC 沿AB 边平移到△DEF 的位置，它们重叠部分的面积是△ABC 面积的一半，若AB ，则此三角形移动的距离是（）A.﹣1；B.；C.1；D.22.12.（闵行2021一模6）古希腊艺术家发现当人的头顶至肚脐的长度（上半身的长度）与肚脐至足底的长度（下半身的长度）的比值为“黄金分割数”时，人体的身材是最优美的．一位女士身高为154cm ，她上半身的长度为62cm ，为了使自己的身材显得更为优美，计划选择一双合适的高跟鞋，使自己的下半身长度增加．你认为选择鞋跟高为多少厘米的高跟鞋最佳？（）A ．4cm ；B ．6cm ；C ．8cm ；D ．10cm.二、填空题（本大题共12题）13.（奉贤2019期中18）如图，在△ABC 中，∠ABC ＝90°，AB ＝6，BC ＝8．点M 、N 分别在边AB 、BC 上，沿直线MN 将△ABC 折叠，点B 落在点P 处，如果AP ∥BC 且AP=4，那么BN=________．14.（嘉定2019期中18）如图，在Rt △ABC 中，∠C ＝90°，AB ＝13，BC ＝5，点D 、E 分别在边BC 、AC 上，且BD ＝CE ，将△CDE 沿DE 翻折，点C 落在点F 处，且DF ∥AB ，则BD 的长为．15.（崇明2021一模18）在ABC 中，AB =，45B ∠=︒，60C ∠=°．点D 为线段AB 的中点，点E 在边AC 上，连结DE ，沿直线DE 将ADE 折叠得到'A DE ．连接'AA ，当'A E AC ⊥时，则线段'AA 的长为________．16.（松江2021一模18）如图，已知矩形纸片ABCD ，点E 在边AB 上，且1BE =，将CBE △沿直线CE 翻折，使点B 落在对角线AC 上的点F 处，联结DF ，如果点D,F,E 在同一直线上，则线段AE 的长为．17.（长宁金山2020一模18）18.如图，在Rt ABC 中，90ABC ∠=︒，2AB =，4BC =，点P 在边BC 上，联结AP ，将ABP △绕着点A 旋转，使得点P 与边AC 的中点M 重合，点B 的对应点是点B '，则BB '的长等于_____．18.（浦东四署2019期中18）如图，在Rt ABC ∆中，090C ∠=，点D 在边AB 上，线段DC 绕点D 逆时针旋转，端点C 恰巧落在边AC 上的点E 处.如果ADm DB =，AE n EC=.那么用含n 的代数式表示m 是：m =__________________.20.（静安2021一模18）在Rt△ABC中，∠C=90°，AB=13，2tan3B （如图），将△ABC绕点C旋转后，点A落在斜边AB上的点A’，点B落在点B’，A’B’与边BC相交于点D，那么CDA'D的值为．21.（杨浦黄兴2019九月18）如图，在平面直角坐标系中有两点A（4，0），B（0，2），如果点C在x轴上（C与A不重合）当点C的坐标为_____时，使得△BOC∽△AOB．22.（黄浦2021一模18）已知一个矩形的两邻边长之比为1：2.5，一条平行于边的直线将该矩形分为两个小矩形，如果所得两小矩形相似，那么这两个小矩形的相似比为________．23.（浦东2021一模18）如图，△ABC中，AB＝10，BC＝12，AC＝8，点D是边BC 上一点，且BD：CD＝2：1，联结AD，过AD中点M的直线将△ABC分成周长相等的两部分，这条直线分别与边BC、AC相交于点E、F，那么线段BE的长为．24.（新竹园2019九月18）如图，等边△ABC的边长为10，点M是边AB上一动点，将等边△ABC沿过点M的直线折叠，该直线与直线AC交于点N，使点A落在直线BC上的点D处，且BD：DC=1：4，折痕为MN，则AN的长为_____．专题02相似三角形选择填空题之压轴题训练(2)一、选择题（本大题共12题）1.（徐汇2020一模6）下列命题中，假命题是（）A.凡有内角为︒30的直角三角形都相似；B.凡有内角为︒45的等腰三角形都相似；C.凡有内角为︒60的直角三角形都相似；D.凡有内角为︒90的等腰三角形都相似．【答案】B ；【解析】解：凡有内角为30︒的直角三角形都相似,故A 为真命题；凡有内角为45︒的等腰三角形不一定相似，45︒是顶角还是底角不确定，故B 是假命题；凡有内角为60︒的直角三角形都相似，故C 为真命题；凡有内角为90︒的等腰三角形都相似，故D 为真命题；因此假命题为B ，答案选B.2.（进才北2019十月6）如图，在ABC 中，D 、E 分别在边AB 、AC 上，//DE BC ，//EF CD 交AB 于F ，那么下列比例式中正确的是()A.AF DEDF BC=; B.DF AFDB DF=; C.EF DECD BC=; D.AF ADBD AB=.【答案】C;【解析】解:A 、∵EF ∥CD ，DE ∥BC ，∴AF AE DF EC =，AE DEAC BC=，∵CE≠AC ，∴AFDE DF BC ≠，故本选项错误；B 、∵EF ∥CD ，DE ∥BC ，∴AF AE DF EC =，AE ADEC BD =，∴AF AD DF BD =，∵AD≠DF ，∴DF AF DB DF ≠，故本选项错误；C 、∵EF ∥CD ，DE ∥BC ，∴DE AE BC AC =，EF AE CD AC =，∴EF DE CD BC =，故本选项正确；D 、∵EF ∥CD ，DE ∥BC ，∴AD AE ABAC =，AF AE AD AC =，∴AF AD AD AB =，∵AD≠DF ，∴AF AD BD AB≠，故本选项错误.故答案选C.3.（金山2019期中6）如图，在△ABC 中，D 、E 分别为AB 、AC 边上的点，DE//BC ，点F 为BC 边上的一点，连接AF 交DE 于点G ，那么下列结论中一定正确的是（）A.AD AEAB EC=;B .AG EGGF CF=; C.EG GDCF FB=; D.AG DEFG BC=.【答案】C ；【解析】解：∵DE//BC ，∴AD AEAB AC =，故A 错误；∵DE//BC ，∴AG EG AF CF=，故B 错误；∵DE//BC ，∴AG EG DG AF CF BF ==，故C 正确；∵DE//BC ，∴AG AE DE AF AC BC==，故D 错误；因此答案选C.4.（黄浦2020一模6）如图，点D 、E 分别在△ABC 的两边BA 、CA 的延长线上，下列条件能判定ED ∥BC 的是（）A ．AD DEAB BC=;B ．AD AEAC AB=;C ．AD •AB ＝DE •BC ;D ．AD •AC ＝AB •AE.【答案】D ；【解析】解：∵∠EAD ＝∠CAB ，∴当AE ADAC AB=，即AD •AC ＝AB •AE ，∴ED ∥BC ，故答案选D ．5.（闵行2019期中6）如图，在△ABC 中，∠A=60︒，CD 、BE 分别是边AB 、AC 上的高线，联结DE ，那么△ADE 和△ACB 的周长之比为（）A.12;B .32; C.14; D.34.【答案】A ；【解析】解：∵在△ABC 中，∠A=60︒，CD ⊥AB,BE ⊥AC ，易知△ADC ∽△AEB ，∴AD ACAE AB=，又∠A=∠A ，∴△ADE ∽△ACB ，故△ADE 和△ACB 的周长之比为AD:AC ，在Rt △ABC 中，∠A=60︒，∴AD ：AC=1：2，故答案选A.6.（松江2021一模6）如图，已知在Rt ABC 中，90C ∠=︒，点G 是ABC 的重心，GE AC ⊥，垂足为E ，如果8CB =，则线段GE 的长为（）A.53； B.73； C.83； D.103.【答案】C ；【解析】解：如图，连接AG 并延长交BC 于点D ． 点G 是△ABC 的重心，∴点D 为BC 的中点，21AG GD =，∵CB=8，∴142CD BD BC ===，∵GE AC ⊥，∴90AEG ∠=︒，∵90C ∠=︒，∴90AEG C ∠=∠=︒，∵EAG CAD ∠=∠（公共角），∴△AEG ∽△ACD ，∴EG AG CD AD =，∵21AG GD =，∴23AG AD =，∴243EG AG AD ==，∴83EG =．故选：C ．7.（普陀2019期中6）如图，四边形ABCD 的对角线AC 与BD 相交于点O ，2OA =，3OB =，6OC =，4OD =，那么下列结论中，错误的是（）A.OAD OBC ∠=∠;B.12AB CD =; C.12AOB DOC C C ∆∆=; D.19AOD BOC S S ∆∆=.【答案】D;【解析】解:∵OA =2，OB =3，OC=6，OD=4，∴23OA OD OB OC ==,∵∠AOD=∠BOC,∴△OAD ∽△OBC,∴OAD OBC ∠=∠，49AOD BOC S S ∆∆=,故A 正确，D 错误；∵OA=2，OB=3，OC=6，OD=4，∴12OA OB OD OC ==,∵∠AOB=∠DOC,∴△OAB ∽△ODC,∴12AB CD =,12AOB DOC C C ∆∆=,故B 正确，C 正确；故选D.8.（杨浦2021一模6）在梯形ABCD 中，AD ∥BC ，对角线AC 与BD 相交于点O ，下列说法中，错误的是（）A ．S △AOB ＝S △DOC ；B ．AOB BOC S OD S OB ∆∆=； C.AOD BOC S OA S OC ∆∆=;D ．ABD ABC S ADS BC∆∆=.【答案】C ；【解答】解：如图，∵AD ∥BC ，∴S △ABC ＝S △DCB ，即S △AOB +S △OBC ＝S △OBC +S △DOC ，S △AOB ＝S △DOC ，所以A 选项的结论正确；∵AD ∥BC ，∴OA OD OC OB =，∵AOB BOC S OA S OC ∆∆=，∴AOB BOC S OD S OB ∆∆=；所以B 选项的结论正确；∵AD ∥BC ，∴△AOD ∽△COB ，∴2AOD BOC S OA S OC ∆∆⎛⎫= ⎪⎝⎭，所以C 选项的结论错误；∵AD ∥BC ，∴点B 到AD 的距离等于点A 到BC 的距离，∴ABD ABC S AD S BC∆∆=，所以D 选项的结论正确；故答案选C．9.（普陀2021一模6）如图，四边形ABCD 的对角线AC 与BD 相交于点O ，OA OD OBOC=，由此推得的正确结论是()A.OA ABOD CD=； B.OA ADOC BC=； C.OB ABOD CD=； D.AB ADCD BC=．【答案】A ；【解析】解：∵OA OD OB OC =,∴OA OBOD OC=，又∠AOB=∠DOC ，∴△AOB ∽△DOC ，∴OA ABOD CD=，故A 正确；因此答案选A.10.（浦东南片联合2019期中6）如图，在RT △ABC 中，∠C=90°，BC=3，AC=4，四边形DEGF 为内接正方形，那么AD ：DE ：EB 为（）A.3︰4︰5;B.16︰12︰9;C.9︰12︰16D.16︰9︰25.【答案】B ；【解析】解：设正方形边长为a ，即：DF=FG=EG=DE=a ；∵FD AB ⊥，四边形DEGF 为内接正方形，∴90ADF C ∠=∠= ，又∵A A ∠=∠，∴ADF ACB ∽，∴ADDF AC BC =,即：43AD a=，解得43AD a =；同理可得：BEG BCA ∆∆∽,∴BEEG BCCA =，即：34BE a=，解得34BE a =；∴43::::16:12:934AD DE EB a a a ==．故选B ．11.（杨浦黄兴2019九月6）如图，把△ABC 沿AB 边平移到△DEF 的位置，它们重叠部分的面积是△ABC 面积的一半，若AB，则此三角形移动的距离是（）A.﹣1；B.；C.1；D.22.【答案】A ；【解析】解：∵△ABC 沿AB 边平移到△DEF 的位置，∴AC ∥DF ，∴△ABC ∽△DBG ，∴DBG ABC S S ＝（DB AB ）2＝12，∴AB ：DB：1，∵AB，∴DB ＝1，∴AD﹣1．故选：A ．12.（闵行2021一模6）古希腊艺术家发现当人的头顶至肚脐的长度（上半身的长度）与肚脐至足底的长度（下半身的长度）的比值为“黄金分割数”时，人体的身材是最优美的．一位女士身高为154cm ，她上半身的长度为62cm ，为了使自己的身材显得更为优美，计划选择一双合适的高跟鞋，使自己的下半身长度增加．你认为选择鞋跟高为多少厘米的高跟鞋最佳？（）A ．4cm ；B ．6cm ；C ．8cm ；D ．10cm.【答案】C;【解答】解：∵一位女士身高为154cm ，她上半身的长度为62cm ，∴她下半身的长度为92cm ，设鞋跟高为x 厘米时，她身材显得更为优美，根据题意得6292x+≈0.618，解得x ≈8.3（cm ）．经检验x ＝8.3为原方程的解，所以选择鞋跟高为8厘米的高跟鞋最佳．故答案选C ．二、填空题（本大题共12题）13.（奉贤2019期中18）如图，在△ABC 中，∠ABC ＝90°，AB ＝6，BC ＝8．点M 、N 分别在边AB 、BC 上，沿直线MN 将△ABC 折叠，点B 落在点P 处，如果AP ∥BC 且AP=4，那么BN=________．【答案】132;【解析】解：如图，连接BP ，交MN 于点O ；则BO=PO ，BO ⊥MN ；∵∠ABC=90°，∴∠MBO+∠NBO=∠NBO+∠BNO ，∴∠MBO=∠BNO ；∵AP ∥BC ，且∠ABC=90°，∴∠BAP=90°；由勾股定理得：BP 2=AB 2+AP 2，∵AB=6，AP=4，∴，ABP=∠BNO ，∴△ABP ∽△OBN ，∴AP PB BO BN =BN =解得：BN=132．14.（嘉定2019期中18）如图，在Rt △ABC 中，∠C ＝90°，AB ＝13，BC ＝5，点D 、E 分别在边BC 、AC 上，且BD ＝CE ，将△CDE 沿DE 翻折，点C 落在点F 处，且DF ∥AB ，则BD 的长为．【答案】4529；【解答】解：如图，延长DF 交AC 于点G ，设BD ＝CE ＝x ，∵∠C ＝90°，AB ＝13，BC ＝5，∴AC 12，∵将△CDE 沿DE 翻折，点C 落在点F 处，∴EF ＝CE ＝x ，∵DF ∥AB ，∴∠A ＝∠EGF ，∴△ABC ∽△GEF ，∴AB BC GE EF=，即133GE x =，解得GE ＝133x ，∴CG ＝GE +CE ＝133x x +=163x ，∵DF ∥AB ，∴CG CD AC BC =，即1653125x x -=，解得x ＝4529．即BD ＝4529．15.（崇明2021一模18）在ABC 中，AB =，45B ∠=︒，60C ∠=°．点D 为线段AB 的中点，点E 在边AC 上，连结DE ，沿直线DE 将ADE 折叠得到'A DE ．连接'AA ，当'A E AC ⊥时，则线段'AA 的长为________．【答案】;【解析】解：过点A作AM⊥BC,在Rt△ABM中，AM=AB⨯sin45°=2=42,AC=AM÷∵'A E AC⊥，∠AEA´=90°,∵△ADE≌△A´DE,∴∠AED=∠A´ED=45°,∴∠AED=∠B,∵∠DAE=∠CAB,∴△ADE∽△ACB,AE AD AB AC=，=,AE==.16.（松江2021一模18）如图，已知矩形纸片ABCD，点E在边AB上，且1BE=，将CBE△沿直线CE翻折，使点B落在对角线AC上的点F处，联结DF，如果点D,F,E 在同一直线上，则线段AE的长为．【答案】152;【解析】解：设AE=x，则AB=x+1，∵折叠，∴BE=EF=1，BEC FEC∠=∠，∵四边形ABCD是矩形，∴AB//CD，∴BEC DCE∠=∠，∴FEC DCE∠=∠，∴1DE DC AB x===+，∵AC DE⊥，∴90AFE DAE∠=∠=︒，∵AEF DEA∠=∠，∴AEF DEA∽，∴AE EFDE EA=，即2AE DE EF=⋅，∴()211x x=+⋅，解x=或，∴12AE=．17.（长宁金山2020一模18）18.如图，在Rt ABC中，90ABC∠=︒，2AB=，4BC=，点P在边BC上，联结AP，将ABP△绕着点A旋转，使得点P与边AC的中点M重合，点B的对应点是点B'，则BB'的长等于_____．;【解析】解:如图，延长AB'交BC 于E ，过点B'作B'D ⊥AB 于点D ，∵∠ABC ＝90︒，AB ＝2，BC ＝4，∴AC=∵点M 是AC 中点，∴AM∵将△ABP绕着点A 旋转，使得点P 与边AC 的中点M 重合，∴AP ＝AM∠PAB ＝∠CAE ，AB ＝AB'＝2，∵AP 2＝AB 2＋PB 2，∴PB ＝1，∴2BA PB =,又2BC AB=,∴BA BC PB AB =且∠ABP ＝∠ABC ＝90°，∴△ABP ∽△CBA ，∴∠PAB ＝∠C ，∴∠C ＝∠CAE ，∴CE ＝AE ，∵AE 2＝AB 2＋BE 2，∴CE 2＝4＋（4−CE ）2，∴CE ＝AE ＝52，∴BE ＝32，∵B'D ∥BC ，∴△AB'D ∽△AEB ，∴''AB AD B D AE AB BE ==∴2'53222AD B D ==，∴AD ＝85，B'D ＝65，∴BD ＝AB-AD=2-85=25，∴BB'==．18.（浦东四署2019期中18）如图，在Rt ABC ∆中，090C ∠=，点D 在边AB 上，线段DC 绕点D 逆时针旋转，端点C 恰巧落在边AC 上的点E 处.如果AD m DB =，AE n EC=.那么用含n 的代数式表示m 是：m =__________________.【答案】21n +;【解析】解：作DH ⊥AC 于H ，如图，∵线段DC 绕点D 逆时针旋转，端点C 恰巧落在边AC 上的点E 处，∴DE=DC ，∴EH=CH ，∵AE n EC=，即AE=nEC ，∴AE=2nEH=2nCH ，∵∠C=90°，∴DH ∥BC ，∴AD AH DB HC =，即AE EH 2nCH CH m 2n 1HC CH++===+.故答案为：2n+1．【答案】245；【解析】解：如图，90,10,cos AB == ∵旋转，∴CB '=CB=8=10，设A 'B '与AC ∴∠B 'FC=∠B 'CA CA ',∴''''B C CF A B A =∴8832'10B F ⨯==cosA=35,可知tanA=328'55B E =-=20.（静安2021一模18）在Rt △ABC 中，∠C =90°，AB =13，2tan 3B =（如图），将△ABC 绕点C 旋转后，点A 落在斜边AB 上的点A’，点B 落在点B’，A’B’与边BC 相交于点D ，那么CD A'D 的值为．【答案】3135；【解析】解:过C 作CE ⊥AB 交AB 于E 点，∵2tan 3B =，∴23AC BC =，设AC=2x ，BC=3x ，在Rt △ABC 中，22)13AB x x ===13，∴x=，∴AC=，BC=，1122ABC S BC AC AB CE ∆== ，∴CE=BC AC AB=6，∵2tan 3CE B EB ==，∴EB=9，∵Rt △A 'B 'C 由Rt △ABC 旋转而得，∴∠B=∠B '，AC=A 'C ，∵CE ⊥AA '，∴AE=EA '，AE=AB-EB=13-9=4，∴AE=EA '=4，A 'B=EB-EA '=9-4=5，又∵∠A 'DB=∠CDB '，∴△A 'DB ∽△CDB '，∴''''5CD CB CB A D A B A B ===即'5CD A D =.21.（杨浦黄兴2019九月18）如图，在平面直角坐标系中有两点A （4，0），B （0，2），如果点C 在x 轴上（C 与A 不重合）当点C 的坐标为_____时，使得△BOC ∽△AOB ．【答案】（1，0）或（﹣1，0）；【解析】解：∵△BOC∽△AOB，∴BOAO=OCOB，∴24＝OC2，∴OC＝1，∵点C在x轴上，∴点C的坐标为（1，0）或（﹣1，0）．故答案为（1，0）或（﹣1，0）．22.（黄浦2021一模18）已知一个矩形的两邻边长之比为1：2.5，一条平行于边的直线将该矩形分为两个小矩形，如果所得两小矩形相似，那么这两个小矩形的相似比为________．【答案】1或0.5或2;【解析】解：如图所示，矩形ABCD中，AB：AD=1：2.5，∴AD=BC,若直线l∥AD，交AB、CD于E、F,根据题意和图形可知：矩形AEFD∽矩形BEFC，此时这两个小矩形的相似比为AD：BC=1；根据相似图形的性质，两个相似图形中长边必定对应长边，故此时不存在其它情况；若直线l∥AB，交AD、BC于E、F，此时存在两种情况：①若矩形ABFE∽矩形DCFE，如下图所示，此时这两个小矩形的相似比为AB：DC=1；②若矩形BAEF∽矩形EDCF，如下图所示，∴AB AEDE CD=，设AB=CD=a，AE=x，则AD=2.5a，DE=2.5a x-，∴2.5a xa x a=-，解得：x=0.5a或x=2a，当x=0.5a时，这两个小矩形的相似比为AE：CD=0.5a：a=0.5；当x=2a时，这两个小矩形的相似比为AE：CD=2a：a=2；综上：这两个小矩形的相似比为1或0.5或2．23.（浦东2021一模18）如图，△ABC中，AB＝10，BC＝12，AC＝8，点D是边BC 上一点，且BD：CD＝2：1，联结AD，过AD中点M的直线将△ABC分成周长相等的两部分，这条直线分别与边BC、AC相交于点E、F，那么线段BE的长为．【答案】2；【解答】解：如图，∵点D 是BC 的中点，BC ＝12，∴BD ：CD ＝2：1，∴BD ＝8，CD＝4，过点M 作MH ∥AC 交CD 于H ，∴△DHM ∽△DAC ，∴MH DH DM AC CD AD==，∴点M 是AD 的中点，∴AD ＝2DM ，∵AC ＝8，∴1842MH DH ==，∴MH ＝4，DH ＝2，过点M 作MG ∥AB 交BD 于G ，同理得，BG ＝DE ＝4，∵AB ＝10，BC ＝12，AC ＝8，∴△ABC 的周长为10+12+8＝30，∵过AD 中点M 的直线将△ABC 分成周长相等的两部分，∴CE +CF ＝15，设BE ＝x ，则CE ＝12﹣x ，∴CF ＝15﹣（12﹣x ）＝3+x ，EH ＝CE ﹣CH ＝CE ﹣（CD ﹣DH ）＝12﹣x ﹣2＝10﹣x ，∵MH ∥AC ，∴△EHM ∽△ECF ，∴MH EH CF CE =，∴410312x x x-=+-，∴x ＝2或x ＝9，当x ＝9时，CF ＝12＞AC ，点F 不在边AC 上，此种情况不符合题意，即BD ＝x ＝2，故答案为：2．24.（新竹园2019九月18）如图，等边△ABC 的边长为10，点M 是边AB 上一动点，将等边△ABC 沿过点M 的直线折叠，该直线与直线AC 交于点N ，使点A 落在直线BC 上的点D 处，且BD ：DC=1：4，折痕为MN ，则AN 的长为_____．【答案】7或653；【解析】解：①当点A 落在如图1所示的位置时，∵△ACB 是等边三角形，∴∠A=∠B=∠C=∠MDN=60°，∵∠MDC=∠B+∠BMD ，∠B=∠MDN ，∴∠BMD=∠NDC ，∴△BMD ∽△CDN ．∴得BD DM BM CN DN CD==，∵BD ：DC=1：4，BC=10，∴DB=2，CD=8，设AN=x=DN ，则CN=10﹣x ，∴2108DM BM x x ==-，∴DM=210x x -，BM=1610x -，∵BM+DM=10，∴210x x -+1610x-=10，解得x=7，∴AN=7；②当A 在CB 的延长线上时，如图2，与①同理可得△BMD ∽△CDN ．∴得BD DM BM CN DN CD ==，∵BD ：DC=1：4，BC=10，∴DB=103，CD=403，设AN=x ，则CN=x ﹣10，∴10340103DM BM x x ==-，∴DM=()10310x x -，BM=()400910x -，∵BM+DM=10，∴()10310x x -+()400910x -=10，解得：x=653，故AN=7或653．。

2021-2022学年浙教版九年级数学上册《第4章相似三角形》期末综合复习训练2（附答案）1．已知，那么下列等式中，不成立的是（）A．B．C．（y≠﹣4a）D．4x＝3y2．下列线段中，能成比例的是（）A．3cm，6cm，8cm，9cm B．3cm，5cm，6cm，9cmC．3cm，6cm，7cm，9cm D．3cm，6cm，9cm，18cm3．如图，已知点D、F在△ABC的边AB上，点E在边AC上，且DE∥BC，要使得EF∥CD，还需添加一个条件，这个条件可以是（）A．B．C．D．4．如图，AB与CD相交于点E，AD∥BC，，CD＝16，则DE的长为（）A．3B．6C．D．105．若将一个正方形的各边长扩大为原来的4倍，则这个正方形的面积扩大为原来的（）A．16倍B．8倍C．4 倍D．2 倍6．如图，在△ABC中，AB＝9，BC＝18，AC＝12，点D在边AC上，且CD＝4，过点D 作一条直线交边AB于点E，使△ADE与△ABC相似，则DE的长是（）A．12B．16C．12或16D．以上都不对7．附加题：若x＝，则x＝．8．已知线段a＝4，b＝1，如果线段c是线段a、b的比例中项，那么c＝．9．如图，△ABC中，D在AC上，且AD：DC＝1：n，E为BD的中点，AE的延长线交BC 于F，那么的值为（用n表示）．10．利用复印机的缩放功能放大一个三角形，将原图中边长为3，5，6的三角形的最长边放大到8，那么放大后的那个三角形的周长为．11．如图，一个矩形广场的长为90m，宽为60m，广场内有两横，两纵四条小路，且小路内外边缘所围成的两个矩形相似，如果两条横向小路的宽均为1.2m，那么每条纵向小路的宽为m．12．两个相似三角形周长的差是4cm，面积的比是16：25，那么这两个三角形的周长分别是cm和cm13．如图，在▱ABCD中，AC，BD相交于点O，点E是OA的中点，连接BE并延长交AD 于点F，已知S△AEF＝4，则下列结论：①＝；②S△BCE＝36；③S△ABE＝12；④△AEF ∽△ACD，其中一定正确的是．（填序号）14．如图，在直线m上摆放着三个等边三角形：△ABC、△HFG、△DCE，已知BC＝CE，F、G分别是BC、CE的中点，FM∥AC，GN∥DC．设图中三个平行四边形的面积依次是S1，S2，S3，若S1+S3＝12，则S2＝．15．如图，数学兴趣小组测量校园内旗杆的高度，小华拿一支刻有厘米分划的小尺，站在距旗杆30米的地方，手臂向前伸直，小尺竖直，看到尺上约12个分划恰好遮住旗杆，已知臂长60cm，则旗杆高为米．16．如图，在平面直角坐标系中，矩形AOCB的两边OA，OC分别在x轴和y轴上，且OA ＝2．OC＝1，则矩形AOCB的对称中心的坐标是；在第二象限内，将矩形AOCB以原点O为位似中心放大为原来的倍，得到矩形A1OC1B1，再将矩形A1OC1B1以原点O为位似中心放大倍，得到矩形A2OC2B2，…，按此规律，则矩形A4OC4B4的对称中心的坐标是．17．如图，四边形ABCD与四边形ABFE都是矩形，AB＝3，AD＝6.5，BF＝2．（1）求下列各线段的比：，，；（2）指出AB，BC，CF，CD，EF，FB这六条线段中的成比例线段（写一组即可）18．如图，D在AB上，且DE∥BC交AC于E，F在AD上，且AD2＝AF•AB．求证：EF∥CD．19．如图，BC，AD相交于点C，△ABC∽△DEC，AC＝4.8，CD＝1.6，BC＝9.3．（1）求CE的长；（2）求证：BC⊥AD．20．如图，已知△ABC是边长为6cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC匀速运动，其中点P运动的速度是1cm/s，点Q运动的速度是2cm/s，当点Q到达点C时，P、Q两点都停止运动，设运动时间为t（s），解答下列问题：（1）当t＝2时，判断△BPQ的形状，并说明理由；（2）设△BPQ的面积为S（cm2），求S与t的函数关系式；（3）作QR∥BA交AC于点R，连接PR，当t为何值时，△APR∽△PRQ．21．如图示，正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上，EF与BC相交于点G，连接CF．①求证：△DAE≌△DCF；②求证：△ABG∽△CFG．22．已知：线段OA⊥OB，点C为OB中点，D为线段OA上一点．连接AC，BD交于点P．（1）如图1，当OA＝OB，且D为OA中点时，求的值；（2）如图2，当OA＝OB，且时，求tan∠BPC的值．（3）如图3，当AD：AO：OB＝1：n：时，直接写出tan∠BPC的值．参考答案1．解：A、∵，∴＝，此选项正确，不合题意；B、∵，∴＝﹣，此选项错误，符合题意；C、∵，∴＝，此选项正确，不合题意；D、∵，∴4x＝3y，此选项正确，不合题意；故选：B．2．解：A、∵3×9≠6×8，故此选项错误；B、∵3×9≠5×6，故此选项错误；C、∵3×9≠6×7，故此选项错误；D、∵3×18＝6×9，故此选项正确；故选：D．3．解：∵DE∥BC，∴，∴当时，，∴EF∥CD，故C选项符合题意；而A，B，D选项不能得出EF∥CD，故选：C．4．解：∵AD∥BC，∴△CBE∽△AED，∴BE：AE＝CE：ED＝3：5，∵CD＝16．CE+ED＝CD，∴DE＝，故选：D．5．解：根据正方形面积的计算方法和积的变化规律，如果一个正方形的边长扩大为原来的4倍，那么正方形的面积是原来正方形面积的4×4＝16倍．故选：A．6．解：∵∠A＝∠A，分为两种情况：①DE∥BC（即∠ADE＝∠C），∴△ADE∽△ACB，∴＝，∴，∴DE＝12，②∠ADE′＝∠B，∵∠A＝∠A，∴△ADE∽△ABC，∴＝，∴＝，∴AE＝＞AB，不合题意，故选：A．7．解：①a+b+c＝0时，b+c＝﹣a，c+a＝﹣b，a+b＝﹣c，∴x＝＝＝﹣1；②a+b+c≠0时，x＝＝＝．综上所述，x＝或﹣1．故答案为：或﹣1．8．解：根据比例中项的概念结合比例的基本性质，得：比例中项的平方等于两条线段的乘积．则c2＝4×1，c＝±2，（线段是正数，负值舍去），故c＝2；故答案为2．9．证明：∵AD：DC＝1：n，∴AD：AC＝1：（n+1）．作DG平行于AF交BC于G，则＝，根据比例的性质知，＝＝，又E是BD的中点，∴EF是△BGD的中位线，∴BF＝FG．∴＝．故答案为：．10．解：因为原图中边长为3，5，6的三角形的最长边放大到8，所以放大前后的两个三角形的周长比为6：8＝14：，故答案为：11．解：设每条纵向小路的宽为xm．∵小路内外边缘所围成的两个矩形相似，∴，解得，x＝1.8，或，解得x＝25.8（不符合实际意义）故答案为：1.8．12．解：由题意，相似比＝4：5，两个相似三角形周长的比是4：5，可得：5x﹣4x＝4，解得：x＝4，所以这两个三角形的周长分别是16cm，20cm；故答案为：16；2013．解：∵在▱ABCD中，AO＝AC，∵点E是OA的中点，∴AE＝CE，∵AD∥BC，∴△AFE∽△CBE，∴＝＝，∵AD＝BC，∴AF＝AD，∴＝；故①正确；∵S△AEF＝4，＝（）2＝，∴S△BCE＝36；故②正确；∵＝＝，∴＝，∴S△ABE＝12，故③正确；∵BF不平行于CD，∴△AEF与△ADC只有一个角相等，∴△AEF与△ACD不一定相似，故④错误，故答案为：①②③．14．解：设AC与FH交于P，CD与HG交于Q，∵F、G分别是BC、CE的中点，AB∥HF∥DC∥GN，∴MF＝AC＝BC，PF＝AB＝BC，又∵BC＝CE＝CG＝GE，∴CP＝MF，CQ＝BC，QG＝GC＝CQ＝AB，∴S1＝S，S3＝2S，∵S1+S3＝12，∴S+2S＝12，∴S＝4.8，故答案为：4.8．15．解：由题意可知△ABC是等腰三角形，AG为高，∴BG＝BC，DF＝DE＝×12cm＝0.06m，AF为臂长，即60cm＝0.6m．AG＝30m，由题意可知△AFD∽△AGB，即＝，即＝，解得BG＝3m，∴BC＝2BG＝2×3＝6m．16．解：∵OA＝2．OC＝1，∴B（﹣2，1），∴矩形AOCB的对称中心的坐标为（﹣1，），∵将矩形AOCB以原点O为位似中心放大为原来的倍，得到矩形A1OC1B1，∴B1（﹣3，），同理可得B2（﹣，），B3（﹣，），B4（﹣，），∴矩形A4OC4B4的对称中心的坐标是（﹣，）．故答案为（﹣1，），（﹣，）．17．解：（1）∵四边形ABCD与四边形ABFE都是矩形，AB＝3，AD＝6.5，BF＝2，∴CD＝EF＝AB＝3，BC＝AD＝6.5，CF＝BC﹣BF＝4.5，∴＝＝，＝＝，＝；（2）成比例线段有＝．18．证明：∵DE∥BC，∴，∵AD2＝AF•AB，∴，∴，∴EF∥DC．19．解：（1）∵△ABC∽△DEC，∴又∵AC＝4.8，CD＝1.6，BC＝9.3∴EC＝3.1；（2）∵△ABC∽△DEC，∴∠ACB＝∠DCE，∵∠ACB+∠DCE＝180°，∴∠ACB＝∠DCE＝90°，∴BC⊥AD．20．解：（1）△BPQ是等边三角形当t＝2时AP＝2×1＝2，BQ＝2×2＝4∴BP＝AB﹣AP＝6﹣2＝4∴BQ＝BP又∵∠B＝60°∴△BPQ是等边三角形；（2）过Q作QE⊥AB，垂足为E在Rt△BEQ中，∠BQE＝90°﹣∠B＝30°，QB＝2t，∴BE＝t，QE＝t由AP＝t，得PB＝6﹣t∴S△BPQ＝×BP×QE＝（6﹣t）×t＝﹣t ∴S＝﹣t；（3）∵QR∥BA∴∠QRC＝∠A＝60°，∠RQC＝∠B＝60°∴△QRC是等边三角形∴QR＝RC＝QC＝6﹣2t∵BE＝BQ•cos60°＝×2t＝t∴EP＝AB﹣AP﹣BE＝6﹣t﹣t＝6﹣2t∴EP∥QR，EP＝QR∴四边形EPRQ是平行四边形∴PR＝EQ＝t又∵∠PEQ＝90°，∴∠APR＝∠PRQ＝90°∵△APR∽△PRQ，∴，∴解得t＝∴当t＝时，△APR∽△PRQ．21．证明：①∵正方形ABCD，等腰直角三角形EDF，∴∠ADC＝∠EDF＝90°，AD＝CD，DE＝DF，∴∠ADE+∠ADF＝∠ADF+∠CDF，∴∠ADE＝∠CDF，在△ADE和△CDF中，，∴△ADE≌△CDF；②延长BA到M，交ED于点M，∵△ADE≌△CDF，∴∠EAD＝∠FCD，即∠EAM+∠MAD＝∠BCD+∠BCF，∵∠MAD＝∠BCD＝90°，∴∠EAM＝∠BCF，∵∠EAM＝∠BAG，∴∠BAG＝∠BCF，∵∠AGB＝∠CGF，∴△ABG∽△CFG．22．解：（1）过D作DE∥CO交AC于E，∵D为OA中点，∴AE＝CE＝，，∵点C为OB中点，∴BC＝CO，，∴，∴PC＝＝，∴＝2；（2）过点D作DE∥BO交AC于E，∵，∴＝＝，∵点C为OB中点，∴，∴，∴PC＝＝，过D作DF⊥AC，垂足为F，设AD＝a，则AO＝4a，∵OA＝OB，点C为OB中点，∴CO＝2a，在Rt△ACO中，AC＝＝＝2a，又∵Rt△ADF∽Rt△ACO，∴，∴AF＝，DF＝，PF＝AC﹣AF﹣PC＝2a﹣﹣＝，tan∠BPC＝tan∠FPD＝＝．（3）与（2）的方法相同，设AD＝a，求出DF＝a，PF＝a，所以tan∠BPC＝．。

2020初中数学中考一轮复习基础达标训练：相似三角形2（附答案）1．如图，P 为平行四边形ABCD 边AB 上一点，E 、F 分别为PD 、PC 的三等分点（靠近P ），则阴影部分的面积与四边形CDEF 的面积比为（ ）A ．12B ．103C ．98D ．542．如图，已知////AB CD EF ，那么下列结论正确的是（ ）A ．AD BCDF CE=B ．BC DFCE AD= C ．CD BCEF BE= D ．CD ADEF AF= 3．有一个正六边形，将其按比例缩小，使得缩小后的正六边形的面积为原正六边形面积的，已知原正六边形一边为3，则后来正六边形的边长为( ) A ．9B ．3C ．D ．4．如图，BD 、CE 是ABC △的两条高，BD 、CE 相交于O ，则下列结论不正确的是（ ）．A ．ADE V ∽ABC △B ．DOE △∽COB △C ．BOE △∽COD △D ．BOE △∽BDE V5．如图，已知12∠∠=，若再增加一个条件不一定能使结论ADE ABC V V ∽成立，则这个条件是（ ）A ．DB ∠∠= B ．AEDC ∠∠=C ．AD AEAB AC=D ．AD DEAB BC=6．如图DE // BC ，AD :DB=2:1，那么△ADE 与△ABC 的相似比为（ ）A ．16B ．23C ．14D ．27．如图，的高AD ，BE 交于点0，连接DE ，则图中相似三角形共有（ ）A ．4对B ．6对C ．7对D ．8对8．如图，在△ABC 中，AC ＝15，BC ＝18，cos C ＝35，DE ∥BC ，DF ⊥BC ，若S △BFD ＝2S △BDE ，则CD 长为（ ）A ．7.5B ．9C ．10D ．59．已知线段a ，b ，c ，d 是比例线段，其中b 2cm =，c 3cm =，d 6cm =，则a 等于( )A ．1cmB ．4cmC ．9cmD ．36cm10．在比例尺为1：100000的地图上，相距3m 的两地，它们的实际距离为_____km ． 11．如图，直线112y x =+与x 轴，y 轴分别相交于A ，B 两点，与双曲线4y x=（0x >）相交于点P ，过P 作PC x ⊥轴于点C ，2OC =，在点P 右侧的双曲线上取一点M ，作MH x ⊥轴于H ，当以点M ，C ，H 为顶点的三角形与AOB ∆相似，则点M 的坐标是__________．12．如图，已知D 是BC 边延长线上的一点，DF 交AC 边于E 点，且AF ＝1，BC ＝3CD ，AE ＝2EC ，则FB 长为_____．13．如果两个相似三角形的面积比是1：9，那么这两个三角形的相似比是______． 14．如图，在ABC V 中，AB AC ，M 为AC 边上一点．要使ABC BCM V V ∽，还需要添加一个条件，这个条件可以是________．（只需填写一个你认为适当的条件即可）15．如图，在矩形中，E 是边的延长线上一点，连接交边于点F 若AB =4，BC =6，DE =2，则AF 的长为___.16．若两个三角形的相似比为3：4，则这两个三角形的面积比为________． 17．如图，直线y ＝12x+1与x 轴交于点A ，与y 轴交于点B ，△BOC 与△B′O′C′是以点A 为位似中心的位似图形，且相似比为1：3，则点B 的对应点B′的坐标为_____．18．如图，A ，B 两点分别位于一个池塘的两端，为了测量A 、B 之间的距离，小天想了一个办法：在地上取一点C ，使它可以直接到达A 、B 两点，连接AC ，BC ，在AC上取一点M，使AM=3MC，作MN//AB交BC于点N，测得MN=36m，则A、B两点间的距离为_____.19．如图，将边长为8的正方形纸片ABCD沿着EF折叠，使点C落在AB边的中点M 处．点D落在点D'处，MD'与AD交于点G，则△AMG的内切圆半径的长为______.20．如图，AD⊥BC，垂足为D，BE⊥AC，垂足为E，AD与BE相交于点F，连接ED．求证：CD CB CE CA⋅=⋅21．一天晚上，小颖由路灯A下的B处向正东走到C处时，测得影子CD的长为1米，当她继续向正东走到D处时，测得此时影子DE的一端E到路灯A的仰角为45°，已知小颖的身高为1.5米，那么路灯AB的高度是多少米？22．如图，AD DE AEAB BC AC==，求证：ABD ACE∠=∠.23．如图，AD 为ABC △的角平分线，BE AD ⊥的延长线于E ，CF AD ⊥于F ，BF 、EC 的延长线交于点P ，求证：CF//AP24．在ABC V 中，ACB 90∠=o ，AC BC 2==，点C 在直线m 上，m//AB ，DBE 45∠=o ，其中点D 、E 分别在直线AC 、m 上，将DBE ∠绕点B 旋转(点D 、E都不与点C 重合)．()1当点D 在边AC 上时(如图1)，设CE x =，CD y =，求y 关于x 的函数解析式，并写出定义域；()2当BCE V 为等腰三角形时，求CD 的长．25．如图，四边形ABCD 中，AB ＝AD ，边BC 、CD 的垂直平分线交于四边形内部一点O ，连接BO 、DO ，已知BO ∥AD ．（1）判断四边形ABOD 的形状？并证明你的结论；（2）连接AO 并延长，交BC 于点E ，若CE ＝25，BE ＝65，∠ODC ＝45°． ①求AB 的长．②若∠BAD ＝135°，求AO•AE 的值．26．如图，ABC △是等边三角形，点D ，E 分别在BC ，AC 上，且BD CE ，AD 与BE 相交于点F.AEF V 与ABE △相似吗？说说你的理由.27．《九章算术》有一道这样的题，原文如下：“今有邑，东西七里，南北九里，各中开门，出东门一十五里有木，问：出南门几何步而见木？”大意为：今有一座长方形小城（如图），东西向城墙长7里，南北向城墙长9里，各城墙正中均开一城门，走出东门15里处有棵大树，问走出南门多少步恰好有望见这棵树.请解答上述问题（注：1里=300步）.参考答案1．D 【解析】 【分析】根据平行四边形的性质和相似三角形的判定和性质定理即可得到结论． 【详解】解：∵四边形ABCD 是平行四边形， ∴S △CPD ＝12S 四边形ABCD ， ∵E 、F 分别为PD 、PC 的三等分点， ∴13PE PF PD PC ==， ∵∠EPF ＝∠DPC ， ∴△PEF ∽△PDC ，∴19PEF PDC S S =n n ， ∴CDEF 89PDC S S n 四边形=，∴CDEF ABCD49S S =四边形四边形， ∴阴影部分的面积与四边形CDEF 的面积比为54， 故选：D ． 【点睛】本题考查相似三角形的判定与性质、平行四边形的性质，解题的关键是明确题意，找出所求问题需要的条件，画出合适的辅助线，利用数形结合的思想解答问题． 2．A 【解析】 【分析】已知AB ∥CD ∥EF ，根据平行线分线段成比例定理，对各项进行分析即可． 【详解】 ∵AB ∥CD ∥EF ，DF CE故选A．【点睛】本题考查平行线分线段成比例定理，找准对应关系，避免错选其他答案．3．C【解析】【分析】先由位似图形的性质可得这两个正六边形相似；再由缩小后的正六边形的面积为原正六边形面积的可得相似比为1:，进而求解即可.【详解】∵这两个正六边形是位似图形，∴这两个正六边形相似.∵缩小后的正六边形的面积为原正六边形面积的，∴相似比为1:.∵原正六边形的边长为3，∴后来正六边形的边长为=.故选C.【点睛】本题考查本题考查位似图形的应用，需掌握位似图形的性质.4．D【解析】【分析】根据相似三角形的判定定理，找出图中的全等三角形，即可得到答案.【详解】∵BD、CE是△ABC的高，∴∠ADB=∠AEC=90°，又∵∠A=∠A∴△ADB∽△AECAE AC又∵∠A=∠A∴△ADE∽△ABC，故A正确；∵BD、CE是△ABC的高，∴∠OEB=∠ODC=90°，又∵∠EOB=∠DOC∴△BOE∽△COD，故C正确；∵△BOE∽△COD∴OE OB= OD OC又∵∠DOE=∠COB∴△DOE∽△COB，故B正确；无法判定△BOE∽△BDE，故D错误；故选D.【点睛】本题考查相似三角形的判定与性质，熟练掌握相似三角形的判定定理是解决本题的关键. 5．D【解析】【分析】根据12∠=∠可得∠DAE=∠BAC，因此只要再找一组角相等或一组对应边成比例即可. 【详解】解：∵12∠=∠，∴∠DAE=∠BAC.选项A、B中，根据两角分别相等的两个三角形相似可得△ADE∽△ABC；选项C中根据两边成比例且夹角相等的两个三角形相似可得△ADE∽△ABC；选项D中，由于∠DAE与∠BAC，不是成比例两边的夹角，所以不一定能使△ADE∽△ABC. 故选D.【点睛】本题考查了相似三角形的判定，熟练掌握相似三角形的判定方法是解题的关键.6．B【解析】【分析】 先求出ADAB的值，再由相似三角形的对应边成比例即可得出结论． 【详解】解：∵AD ：DB=2：1，23∴=AD AB ∵DE ∥BC ， ∴△ADE ∽△ABC ，∴△ADE 与△ABC 的相似比= 23AD AB = 故选：B ． 【点睛】本题考查的是相似三角形的性质，熟知相似三角形对应边的比等于相似比是解答此题的关键． 7．D 【解析】 【分析】根据相似三角形的判定定理解答即可. 【详解】 解：∵的高AD ，BE 交于点O ，∴.又∵，，，∴.∵，∴，∴，又∵，∴，∴，则，∴.又∵，∴.故选D. 【点睛】本题考查了相似三角形的性质及其判定，解题的关键是熟练掌握这些性质. 8．C 【解析】【分析】设CD=5x ，CF=3x ，先证△AED ∽△ABC ，得到ED BC =AD AC，又由S △BFD =2S △BDE ，即12ED•DF=12×12BF•DF ，解得x=2，即可求CD=5×2=10． 【详解】设CD=5x ，CF=3x ，则AD=15-5x ，BF=18-3x ，∵DE ∥BC ，∴△AED ∽△ABC ， 即ED BC =AD AC ， 即18ED =15515x -， ED=18(155)15x -（1） ∵S △BFD =2S △BDE ， 即12ED•DF=12×12BF•DF ， 即ED=12（18-3x ）（2） 由（1）（2）得x=2，故CD=5×2=10． 故选：C ．【点睛】本题较复杂，涉及到三角形相似及平行线的性质，需同学们熟练掌握．9．A【解析】【分析】根据a 、b 、c 、d 是成比例线段，得a ：b c =：d ，再根据比例的基本性质，求出a 的值即可．【详解】a Q 、b 、c 、d 是成比例线段，a ∴：bc =：d ，b 2cm =Q ，c 3cm =，d 6cm =，a1cm∴=；故选A．【点睛】本题考查了比例线段，写比例式的时候一定要注意顺序，再根据比例的基本性质进行求解．10．300．【解析】【分析】首先根据地图的比例尺，求出在地图上相距3m的两地的实际距离，然后将实际距离的单位换算为km即可.【详解】3÷1100000＝300000（m），300000m＝300km；答：它们的实际距离为300km；故答案为：300．【点睛】本题考查比例尺的应用，学会换算单位也是本题的难点.11．(4,1)或(12)+【解析】【分析】先求出点A、点B的坐标，设点M的坐标为（m，n），分两种情况：当△MCH∽△BAO和△MCH∽△ABO时，由相似得比例求出m的值，即可得出点M的坐标．【详解】解：直线y=12x+1与x轴，y轴分别相交于A，B两点，令x=0得y=1，令y=0得x=-2，∴A（-2，0），B（0，1）．设点M的坐标为（m，n），∵点M在双曲线4yx=上，∴n=4m．当△MCH∽△BAO时，可得CH MH AO BO=，即221 m n -=，∴m-2=2n，即m-2=8m，∴m2-2m-8=0，解得：m1=4，m2=-2（舍去），∴n=4m=1，∴M（4，1）；当△MCH∽△ABO时，可得CH MH BO AO=，即212 m n -=整理得：2m-4=4m，∴m2-2m-2=0，解得：m1m2，∴n=，∴M（，）．综上，M（4，1）或M（）．故答案为：（4，1）或（，）．【点睛】此题属于反比例函数综合题，涉及的知识有：相似三角形的判定和性质，一次函数图象与性质，反比例函数图象上点的坐标特征，设出点M的坐标然后分两种情况进行讨论是解本题的关键．12．2．【解析】【分析】过C作CG∥AB交DF于G，于是得到△CDG∽△BDF，△CEG∽△AFE，根据相似三角形的性质得CGBF＝CDBD，CGAF＝CEAE，求得BF＝4CG，AF＝2CG，即可得到结论．【详解】过C作CG∥AB交DF于G，∴△CDG∽△BDF，△CEG∽△AFE，∴CGBF＝CDBD，CGAF＝CEAE∵BC＝3CD，∴CDBD＝14，∴CGBF＝14，∴BF＝4CG，∵AE＝2EC，∴CGAF＝12，∴AF＝2CG，∵AF＝1，∴BF＝2；故答案为：2．【点睛】此题主要考查相似三角形的判定与性质，解题的关键是根据相似三角形的性质列出比例式求解.13．1：3【解析】【分析】由两个相似三角形的面积比是1：9，根据相似三角形的面积比等于相似比的平方，即可求得答案．【详解】解：∵两个相似三角形的面积比是1：9，∴这两个三角形的相似比是：1：3．故答案为：1：3．【点睛】本题考查了相似三角形的性质．此题比较简单，注意掌握定理的应用是解此题的关键． 14．BM BC =或ABC BMC ∠∠=或A MBC ∠∠=（答案不唯一）【解析】【分析】要使△ABC ∽△BCM ，可以再添加BM ＝BC 或∠ABC ＝∠BMC 或∠A ＝∠MBC 从而根据有两组角对应相等的两个三角形相似来判定．【详解】因为AB ＝AC ，所以∠ABC ＝∠C ，若BM ＝BC 或∠ABC ＝∠BMC 或∠A ＝∠MBC （答案不唯一），则△ABC ∽△BCM ．故答案为BM =BC 或∠ABC =∠BMC 或∠A =∠MBC （答案不唯一）．【点睛】这是一道考查相似三角形的判定的开放性的题，答案不唯一．15．4【解析】【分析】由四边形ABCD是矩形，推出，，设，则由，可得，由此构建方程即可解决问题．【详解】解：四边形ABCD是矩形，，，设，则，，∽，，，，．故答案为4.【点睛】本题考查相似三角形的判定和性质，矩形的性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．16．9：16【解析】【分析】根据相似三角形面积的比等于相似比的平方解答即可．【详解】解：∵两个三角形的相似比为3：4，∴这两个三角形的面积比为9：16，故答案为：9：16．【点睛】本题考查的是相似三角形的性质，掌握相似三角形面积的比等于相似比的平方是解题的关键．17．（﹣8，﹣3）或（4，3）．【解析】【分析】先解得点A 和点B 的坐标，再利用位似变换可得结果．【详解】解：∵直线y ＝12x+1与x 轴交于点A ，与y 轴交于点B 令x=0可得y=1；令y=0可得x=-2，∴点A 和点B 的坐标分别为（-2，0）；（0，1），∵△BOC 与△B′O′C′是以点A 为位似中心的位似图形，且相似比为1：3，13OB OA O B AO ∴==′′′ ∴O′B′=3，AO′=6，∴B′的坐标为（-8，-3）或（4，3）．故答案为：（-8，-3）或（4，3）．【点睛】本题主要考查了位似变换和一次函数图象上点的坐标特征，得出点A 和点B 的坐标是解答此题的关键．18．144m【解析】【分析】根据MN ∥AB ，可得△CMN ∽△CAB ，然后再根据相似三角形的性质可得MN CM AB AC =，再代入数进行计算即可．【详解】解：∵MN ∥AB ，∴△CMN ∽△CAB ， ∴MN CM AB AC=， ∵AM=3MC ，MN=36m ，∴3614 AB，AB=144m，故答案为144m．【点睛】此题主要考查了相似三角形的判定和性质，关键是掌握相似三角形对应边成比例．19．4 3【解析】【分析】由勾股定理可求ME=5，BE=3，通过证明△AMG∽△BEM，可得AG=163，GM=203，即可求解．【详解】∵将边长为8的正方形纸片ABCD沿着EF折叠，使点C落在AB边的中点M处．∴ME=CE，MB=12AB=4=AM，∠D'ME=∠C=90°，在Rt△MBE中，ME2=MB2+BE2，∴ME2=16+（8-ME）2，∴ME=5，∴BE=3，∵∠D'ME=∠DAB=90°=∠B∴∠EMB+∠BEM=90°，∠EMB+∠AMD'=90°∴∠AMD'=∠BEM，且∠GAM=∠B=90°∴△AMG∽△BEM∴AM AG GM BE MB ME ＝＝∴4345AG GM＝＝，∴AG=163，GM=203∴△AMG的内切圆半径的长=423 AG AM GM+-=故答案为：4 3 .【点睛】此题考查三角形内切圆和内心，勾股定理，相似三角形的判定和性质，熟练运用相似三角形的性质求AG，GM的长度是本题的关键．20．证明见详解【解析】【分析】根据垂直得出∠BEC=∠ADC=90°，求出∠CBE=∠DAC，根据相似三角形的判定定理得出即可.【详解】证明：∵AD⊥BC，BE⊥AC，∴∠BEC=∠ADC=90°，∵∠BCE=∠ACD（公共角），∴∠CBE=∠CAD，∴△CBE∽△CAD，∴CE CB CD CA=即：CD CB CE CA⋅=⋅【点睛】本题考查了相似三角形的判定和性质的应用，能熟练地运用定理进行推理是解此题的关键．21．AB=4.5m【解析】【分析】如图，根据已知可得AB＝BE，再证明△DCM∽△DBA，然后利用相似三角形的性质得出DC BDMC AB=，设AB＝x，代入数据后解方程即可求出AB的高度．【详解】解：如图，∵∠ABE ＝90°，∠E ＝45°，∴∠E ＝∠EAB ＝∠EFD ＝45°， ∴AB ＝BE ，DE =DF =1.5，∵MC ∥AB ，∴△DCM ∽△DBA ，∴DC BD MC AB=， 设AB ＝x ，则BD ＝x ﹣1.5， ∴1 1.51.5x x -=， 解得：x ＝4.5．∴路灯A 的高度AB 为4.5m ．【点睛】此题主要考查了相似三角形的应用和投影问题，根据已知得出AB ＝BE 、熟练掌握相似三角形的判定和性质是解题关键．22．见解析【解析】【分析】由AD DE AE AB BC AC==，得到△ADE ∽△ABC ，根据相似三角形的性质得到∠DAE=∠BAC ，根据角的和差得到∠DAB=∠EAC ，推出△ADB ∽△AEC ，即可得到结论．【详解】证明:∵AD DE AE AB BC AC==， ∴ADE ABC ∆∆∽.∴DAE BAC ∠=∠.∴DAB EAC ∠=∠. ∵AD AE AB AC=， ∴ADBC AEC ∆∆∽.∴ABD ACE ∠=∠.【点睛】考查了相似三角形的判定和性质，熟练掌握相似三角形的判定和性质是解题的关键． 23．见解析【解析】【分析】由条件可得CF ∥BE ，结合条件可证明△BAE ∽△ACF ，可得到CP AF PE AE =，则有CF ∥AP ． 【详解】证明：∵CF ⊥AE ，BE ⊥AE ，∴CF ∥BE ， ∴CP CF PE BE=，∠AFC ＝∠AEB ＝90°， ∵AD 是∠BAC 的平分线，∴∠BAE ＝∠EAC ，∴△BAE ∽△CAF ， ∴AF CF AE BE=， ∴CP AF PE AE =， ∴CF ∥AP ．【点睛】本题主要考查平行线分线段成比例的逆定理及相似三角形的判定和性质，掌握相似三角形的对应边成比例是解题的关键，注意由线段对应成比例也可以证明平行．24．（1）y 2x =<<；（2）当BCE V 为等腰三角形时，CD 的长为2或2或2．【解析】【分析】(1)证明△ADB ∽△CEB ，通过比例式找到y 与x 的关系；(2)分情况讨论，①当BE=CE 时，C 、D 重合，不符合题意，舍去；②当BC=BE 时，如图1；③当BC=CE 时，有两种图形(如图2、3).画出对应图形后，根据等腰三角形的性质，求出底角度数，再转化为边之间的关系即可求解．【详解】解：()1m //AB Q ，ECB CBA 45∠∠∴==o ．A ECB 45∠∠∴==o ．DBA 45CBD ∠∠=-o Q ，EBC 45CBD ∠∠=-o ，DBA EBC ∠∠∴=．ADB V ∴∽CEB V．AD AB CE BC ∴=，即2y x -=．y 2x ∴=-<<；()2①当BE CE =时，C 、D 重合，不符合题意，舍去；②当BC BE =时，如图1，ECB 45∠=o Q ，CEB 45∠∴=o ，CBE 90∠∴=o ．则CBD 90DBE 45∠∠=-=o o ．ABD 454590∠∴=+=o o o ．A 45∠=o Q ，ABD ∴V 是等腰直角三角形．AD 4∴=，CD 422∴=-=；③当BC CE =时，Ⅰ.如图2，ECB 45∠=o Q ，CBE 67.5∠∴=o ．ABD CBE 67.5∠∠∴==o ．ADB 1804567.567.5o o o o ∠∴=--=．ABD ADB ∠∠∴=，AD AB 22∴==．CD 222∴=-；Ⅱ.如图3，则BCE 135∠=o ，CBE 22.5∠∴=o ．ABD 22.5o ∠∴=，CAB 45∠=o Q ，ADB 4522.522.5∠∴=-=o o o ．AD AB 22∴==．CD 222∴=+．所以当BCE V 为等腰三角形时，CD 的长为2或222或222．【点睛】本题主要考查相似三角形的判定和性质、等腰三角形的判定和性质，还考查了分类讨论思想，解题的关键是画出对应图形进行求解．25．（1）证明见解析（2）10（3）100【解析】【分析】（1）连接AO 、CO ，根据中垂线知OB ＝OC ＝OD ，证△ABO ≌△ADO 得∠BAO ＝∠DAO ，由BO ∥AD 知∠BOA ＝∠DAO ，从而得∠BAO ＝∠BOA ，据此知AB ＝BO ，继而得证；（2）连接CO 、DE ，设DE 交OC 于点P ，先证△BOE ≌△DOE 得BE ＝DE 、∠OBE ＝∠ODE ，结合∠OBC ＝∠OCB 知∠OCE ＝∠ODE ，由∠EPC ＝∠OPD 知∠CEP ＝∠DOP ＝90°，根据CE 2+DE 2＝DC 2知CE 2+BE 2＝2AB 2，代入计算可得；（3）由△BOE ≌△DOE ，∠DEB ＝90°知∠OEB ＝∠OED ＝45°，结合四边形ABOD 是菱形，∠BAD ＝135°知∠ABO ＝45°，从而得∠ABO ＝∠AEB ，证△ABO ∽△AEB 得AO•AE ＝AB 2，代入计算可得．【详解】解：（1）四边形ABOD 是菱形，理由如下：如图1，连接AO、CO，∵边BC、CD的垂直平分线交于点O，∴OB＝OC＝OD，又AB＝AD，AO＝AO，∴△ABO≌△ADO（SSS），∴∠BAO＝∠DAO，∵BO∥AD，∴∠BOA＝∠DAO，∴∠BAO＝∠BOA，∴AB＝BO，∴AB＝BO＝OD＝AD，∴四边形ABOD是菱形；（2）如图2，连接CO、DE，设DE交OC于点P，∵∠ODC＝45°，OC＝OD，∴∠COD＝90°，△OCD是等腰直角三角形，∴CD22AB，∵四边形ABOD是菱形，∴∠DOA＝∠BOA，∴∠BOE＝∠DOE，在△BOE和△DOE中，∵B0D0BOE DOE0E0E=⎧⎪∠=∠⎨⎪=⎩，∴△BOE≌△DOE（SAS），∴BE＝DE、∠OBE＝∠ODE，∵∠OBC＝∠OCB，∴∠OCE＝∠ODE，又∵∠EPC＝∠OPD，∴∠CEP＝∠DOP＝90°，在Rt△DCE中，CE2+DE2＝DC2，即CE2+BE2＝2AB2，∵CE＝BE＝∴2AB2＝（2+（2＝200，∴AB＝10；（3）由（2）知△BOE≌△DOE，∠DEB＝90°，∴∠OEB＝∠OED＝45°，∵四边形ABOD是菱形，∠BAD＝135°，∴∠ABO＝45°，∴∠ABO＝∠AEB，又∵∠BAO＝∠EAB，∴△ABO∽△AEB，∴AB AD AE AB=，∴AO•AE＝AB2，∵AB＝10，∴AO•AE＝100．【点睛】本题是相似三角形的综合问题，解题的关键是掌握菱形的判定与性质、全等三角形和相似三角形的判定与性质及等腰直角三角形的性质等知识点．26．答案见解析【解析】【分析】证ABD BCE ∽△△，得BAD CBE ∠=∠，再证ABE FAE ∠=∠，可进一步证AEF BEA ∽△△.【详解】解：相似.理由如下：∵BD CE =，60ABC C ∠=∠=︒，AB BC =，∴ABD BCE ∽△△，∴BAD CBE ∠=∠，∵60ABC BAC ∠=∠=︒，∴ABE FAE ∠=∠.又∵AEF BEA ∠=∠，∴AEF BEA ∽△△.【点睛】考核知识点：相似三角形的判定和性质.熟记相似三角形的判定和性质的内容是关键. 27．315步【解析】【分析】根据题意写出AB 、AC 、CD 的长，根据相似三角形的性质得到比例式，计算即可．【详解】解：由题意，得15AB =里， 4.5AC =里， 3.5CD =里，∵DE CD ⊥，AC CD ⊥∴//AC DE ，易得ACB ∆∽DEC ∆， ∴DE DC AC AB=， 即 3.54.515DE =， 解得 1.05DE =（里）315=（步）∴走出南门315步恰好能望见这棵树.【点睛】本题考查了相似三角形的应用，根据题意得出相似三角形是解决此题的关键．。

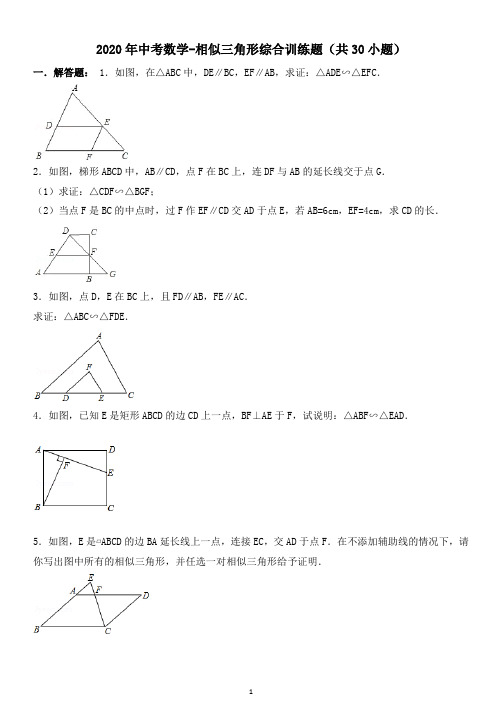
2020年中考数学-相似三角形综合训练题（共30小题）一．解答题：1．如图，在△ABC中，DE∥BC，EF∥AB，求证：△ADE∽△EFC．2．如图，梯形ABCD中，AB∥CD，点F在BC上，连DF与AB的延长线交于点G．（1）求证：△CDF∽△BGF；（2）当点F是BC的中点时，过F作EF∥CD交AD于点E，若AB=6cm，EF=4cm，求CD的长．3．如图，点D，E在BC上，且FD∥AB，FE∥AC．求证：△ABC∽△FDE．4．如图，已知E是矩形ABCD的边CD上一点，BF⊥AE于F，试说明：△ABF∽△EAD．5．如图，E是▱ABCD的边BA延长线上一点，连接EC，交AD于点F．在不添加辅助线的情况下，请你写出图中所有的相似三角形，并任选一对相似三角形给予证明．6．已知：如图①所示，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，且点B，A，D在一条直线上，连接BE，CD，M，N分别为BE，CD的中点．（1）求证：①BE=CD；②△AMN是等腰三角形；（2）在图①的基础上，将△ADE绕点A按顺时针方向旋转180°，其他条件不变，得到图②所示的图形．请直接写出（1）中的两个结论是否仍然成立；（3）在（2）的条件下，请你在图②中延长ED交线段BC于点P．求证：△PBD∽△AMN．7．如图，在4×3的正方形方格中，△ABC和△DEF的顶点都在边长为1的小正方形的顶点上．（1）填空：∠ABC= _________ °，BC= _________ ；（2）判断△ABC与△DEC是否相似，并证明你的结论．8．如图，已知矩形ABCD的边长AB=3cm，BC=6cm．某一时刻，动点M从A点出发沿AB方向以1cm/s 的速度向B点匀速运动；同时，动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动，问：（1）经过多少时间，△AMN的面积等于矩形ABCD面积的？（2）是否存在时刻t，使以A，M，N为顶点的三角形与△ACD相似？若存在，求t的值；若不存在，请说明理由．9．如图，在四边形ABCD中，若AB∥DC，AD=BC，对角线BD、AC把梯形分成了四个小三角形．（1）列出从这四个小三角形中任选两个三角形的所有可能情况，并求出选取到的两个三角形是相似三角形的概率是多少；（注意：全等看成相似的特例）（2）请你任选一组相似三角形，并给出证明．10．如图△ABC中，D为AC上一点，CD=2DA，∠BAC=45°，∠BDC=60°，CE⊥BD于E，连接AE．（1）写出图中所有相等的线段，并加以证明；（2）图中有无相似三角形？若有，请写出一对；若没有，请说明理由；（3）求△BEC与△BEA的面积之比．11．如图，在△ABC中，AB=AC=a，M为底边BC上的任意一点，过点M分别作AB、AC的平行线交AC 于P，交AB于Q．（1）求四边形AQMP的周长；（2）写出图中的两对相似三角形（不需证明）；（3）M位于BC的什么位置时，四边形AQMP为菱形并证明你的结论．12．已知：P是正方形ABCD的边BC上的点，且BP=3PC，M是CD的中点，试说明：△ADM∽△MCP．13．如图，已知梯形ABCD中，AD∥BC，AD=2，AB=BC=8，CD=10．（1）求梯形ABCD的面积S；（2）动点P从点B出发，以1cm/s的速度，沿B⇒A⇒D⇒C方向，向点C运动；动点Q从点C出发，以1cm/s的速度，沿C⇒D⇒A方向，向点A运动，过点Q作QE⊥BC于点E．若P、Q两点同时出发，当其中一点到达目的地时整个运动随之结束，设运动时间为t秒．问：①当点P在B⇒A上运动时，是否存在这样的t，使得直线PQ将梯形ABCD的周长平分？若存在，请求出t的值；若不存在，请说明理由；②在运动过程中，是否存在这样的t，使得以P、A、D为顶点的三角形与△CQE相似？若存在，请求出所有符合条件的t的值；若不存在，请说明理由；③在运动过程中，是否存在这样的t，使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．14．已知矩形ABCD，长BC=12cm，宽AB=8cm，P、Q分别是AB、BC上运动的两点．若P自点A出发，以1cm/s的速度沿AB方向运动，同时，Q自点B出发以2cm/s的速度沿BC方向运动，问经过几秒，以P、B、Q为顶点的三角形与△BDC相似？15．如图，在△ABC中，AB=10cm，BC=20cm，点P从点A开始沿AB边向B点以2cm/s的速度移动，点Q从点B开始沿BC边向点C以4cm/s的速度移动，如果P、Q分别从A、B同时出发，问经过几秒钟，△PBQ与△ABC相似．16．如图，∠ACB=∠ADC=90°，AC=，AD=2．问当AB的长为多少时，这两个直角三角形相似．17、已知，如图，在边长为a的正方形ABCD中，M是AD的中点，能否在边AB上找一点N（不含A、B），使得△CDM与△MAN相似？若能，请给出证明，若不能，请说明理由．18．如图在△ABC中，∠C=90°，BC=8cm，AC=6cm，点Q从B出发，沿BC方向以2cm/s的速度移动，点P从C出发，沿CA方向以1cm/s的速度移动．若Q、P分别同时从B、C出发，试探究经过多少秒后，以点C、P、Q为顶点的三角形与△CBA相似？19．如图所示，梯形ABCD中，AD∥BC，∠A=90°，AB=7，AD=2，BC=3，试在腰AB上确定点P的位置，使得以P，A，D为顶点的三角形与以P，B，C为顶点的三角形相似．20．△ABC和△DEF是两个等腰直角三角形，∠A=∠D=90°，△DEF的顶点E位于边BC的中点上．（1）如图1，设DE与AB交于点M，EF与AC交于点N，求证：△BEM∽△CNE；（2）如图2，将△DEF绕点E旋转，使得DE与BA的延长线交于点M，EF与AC交于点N，于是，除（1）中的一对相似三角形外，能否再找出一对相似三角形并证明你的结论．21．如图，在矩形ABCD中，AB=15cm，BC=10cm，点P沿AB边从点A开始向B以2cm/s的速度移动；点Q沿DA边从点D开始向点A以1cm/s的速度移动．如果P、Q同时出发，用t（秒）表示移动的时间，那么当t为何值时，以点Q、A、P为顶点的三角形与△ABC相似．22．如图，路灯（P点）距地面8米，身高1.6米的小明从距路灯的底部（O点）20米的A点，沿OA所在的直线行走14米到B点时，身影的长度是变长了还是变短了？变长或变短了多少米？23．阳光明媚的一天，数学兴趣小组的同学们去测量一棵树的高度（这棵树底部可以到达，顶部不易到达），他们带了以下测量工具：皮尺，标杆，一副三角尺，小平面镜．请你在他们提供的测量工具中选出所需工具，设计一种测量方案．（1）所需的测量工具是：_________ ；（2）请在下图中画出测量示意图；（3）设树高AB的长度为x，请用所测数据（用小写字母表示）求出x．24．如图，李华晚上在路灯下散步．已知李华的身高AB=h，灯柱的高OP=O′P′=l，两灯柱之间的距离OO′=m。

相似三角形经典练习题一．选择题（共9小题）1．在直角三角形中，两直角边分别为3和4，则这个三角形的斜边与斜边上的高的比为（ ）A．B．C．D．2．如图，在Rt△ABC中，AD为斜边BC上的高，若S△CAD=3S△ABD，则AB：AC等于（ ）A．1：3B．1：4C．1：D．1：23．如图，在△ABC中，D，E分别是边AB，AC的中点，△ADE和四边形BCED的面积分别记为S1，S2，那么的值为（ ）A．B．C．D．4．如图，▱ABCD中，Q是CD上的点，AQ交BD于点P，交BC的延长线于点R，若DQ：CQ=4：3，则AP：PR=（ ）A．4：3 B．4：7 C．3：4 D．3：75．如图，△ADE∽△ACB，其中∠AED=∠B，那么能成立的比例式是（ ）A．B．C．D．6．如图，在△ABC中，AB=AC=5，BC=6，点M为BC的中点，MN⊥AC于点N，则MN等于（ ）A．B．C．D．7．如图，△ABC，AB=12，AC=15，D为AB上一点，且AD=AB，在AC上取一点E，使以A、D、E为顶点的三角形与ABC相似，则AE等于（ ）A．B．10C．或10D．以上答案都不对8．如图，小正方形的边长均为1，则下列图中的三角形（阴影部分）与△ABC 相似的是（ ）A．B．C．D．9．如图，△ABC中，∠B=90°，AB=6，BC=8，将△ABC沿DE折叠，使点C落在AB边上的C′处，并且C′D∥BC，则CD的长是（ ）A．B．C．D．二．填空题（共11小题）10．a=4，b=9，则a、b的比例中项是 ．11．在△ABC中，∠ACB=90°，CD⊥AB于点D，则下列说法正确的有 （填序号）．①AC•BC=AB•CD；②AC2=AD•DB；③BC2=BD•BA；④CD2=AD•DB．12．如图，Rt△ABC中，AC⊥BC，CD⊥AB于D，AC=8，BC=6，则AD= ．13．如图，DE∥AC，BE：EC=2：1，AC=12，则DE= ．14．如图，平行四边形ABCD中，E是BD上一点，AE的延长线与BC的延长线交于F，与CD交于G，若AE=4，EG=3，则EF= ．15．如图，在平行四边形ABCD中，M、N为AB的三等分点，DM、DN分别交AC于P、Q两点，则AP：PQ：QC= ．16．如图，若∠B=∠DAC，则△ABC∽ ，对应边的比例式是 ．17．如图，将①∠BAD=∠C；②∠ADB=∠CAB；③AB2=BD•BC；④；⑤；⑥中的一个作为条件，另一个作为结论，组成一个真命题，则条件是 ，结论是 ．（注：填序号）18．已知：AM：MD=4：1，BD：DC=2：3，则AE：EC= ．19．如图，将三个全等的正方形拼成一个矩形ADHE，则：∠ABE+∠ACE+∠ADE等于 度．20．一张等腰三角形纸片，底边长为15cm，底边上的高长22.5cm．现沿底边依次从下往上裁剪宽度均为3cm的矩形纸条，如图所示．已知剪得的纸条中有一张是正方形，则这张正方形纸条是第 张．三．解答题（共10小题）21．如图，D，E分别是AC，AB上的点，．已知△ABC的面积为60cm2，求四边形BCDE的面积．22．如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上，已知纸板的两条直角边DE=40cm，EF=20cm，测得边DF离地面的高度AC=1.5m，CD=8m，求树高AB．23．已知：平行四边形ABCD，E是BA延长线上一点，CE与AD、BD交于G、F．求证：CF2=GF•EF．24．平行四边形ABCD中，AB=28，E、F是对角线AC上的两点，且AE=EF=FC，DE交AB于点M，MF交CD于点N．求AM、CN的长．25．如图，A，B，D，E四点在⊙O上，AE，BD的延长线相交于点C，直径AE为8，OC=12，∠EDC=∠BAO．（1）求证：；（2）计算CD•CB的值，并指出CB的取值范围．26．已知△ABC，延长BC到D，使CD=BC．取AB的中点F，连接FD交AC 于点E．（1）求的值；（2）若AB=a，FB=EC，求AC的长．27．如图△ABC中，边BC=60，高AD=40，EFGH是内接矩形，HG交AD于P，设HE=x，（1）求矩形EFGH的周长y与x的函数关系式；（2）求矩形EFGH的面积S与x的函数关系式．28．如图，在平面直角坐标系中，已知OA=12厘米，OB=6厘米．点P从点O 开始沿OA边向点A以1厘米/秒的速度移动；点Q从点B开始沿BO边向点O以1厘米/秒的速度移动．如果P、Q同时出发，用t（秒）表示移动的时间（0≤t≤6），那么（1）设△POQ的面积为y，求y关于t的函数解析式；（2）当△POQ的面积最大时，将△POQ沿直线PQ翻折后得到△PCQ，试判断点C是否落在直线AB上，并说明理由；（3）当t为何值时，△POQ与△AOB相似．29．如图在△ABC中，∠C=90°，BC=8cm，AC=6cm，点Q从B出发，沿BC 方向以2cm/s的速度移动，点P从C出发，沿CA方向以1cm/s的速度移动．若Q、P分别同时从B、C出发，试探究经过多少秒后，以点C、P、Q为顶点的三角形与△CBA相似？30．如图，已知A、B两点的坐标分别为（40，0），（0，30），动点P从点A 开始在线段AO上以每秒2个长度单位的速度向原点O运动，动直线EF从x 轴开始以每秒1个单位长度的速度向上平行移动（即EF∥x轴），并且分别与y轴、线段AB交于点E、F，连接EP、FP，设动点P与动直线EF同时出发，运动时间为t秒．（1）求t=15时，△PEF的面积；（2）当t为何值时，△EOP与△BOA相似．相似三角形经典练习题20161115参考答案与试题解析一．选择题（共9小题）1．在直角三角形中，两直角边分别为3和4，则这个三角形的斜边与斜边上的高的比为（ ）A．B．C．D．【考点】勾股定理．【分析】本题主要利用勾股定理和面积法求高即可．【解答】解：∵在直角三角形中，两直角边分别为3和4，∴斜边为5，∴斜边上的高为=．（由直角三角形的面积可求得）∴这个三角形的斜边与斜边上的高的比为5：=．故选A．【点评】此题考查了勾股定理和利用面积法求高，此题考查了学生对直角三角形的掌握程度．2．如图，在Rt△ABC中，AD为斜边BC上的高，若S△CAD=3S△ABD，则AB：AC等于（ ）A．1：3B．1：4C．1：D．1：2【考点】相似三角形的判定与性质．【分析】根据已知及相似三角形的面积比等于相似比的平方，即可求解．【解答】解：∵∠ADC=∠ADB=90°，∠C=∠BAD∴△ACD∽△BAD∵S △CAD =3S △ABD ，且这两三角形高相等∴AB ：AC=1：故选C ．【点评】本题考查了三角形的面积公式，及相似三角形的判定及性质．　3．如图，在△ABC 中，D ，E 分别是边AB ，AC 的中点，△ADE 和四边形BCED 的面积分别记为S 1，S 2，那么的值为（ ）A ．B ．C ．D ．【考点】三角形中位线定理；相似三角形的判定与性质．【分析】根据已知可得到△ADE ∽△ABC ，从而可求得其面积比，则不难求得的值．【解答】解：根据三角形的中位线定理，△ADE ∽△ABC ，DE ：BC=1：2，所以它们的面积比是1：4，所以=，故选C ．【点评】本题考查了三角形的中位线定理和相似三角形的性质：（1）相似三角形周长的比等于相似比；（2）相似三角形面积的比等于相似比的平方；（3）相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比．　4．（2012秋•桐城市校级月考）如图，▱ABCD 中，Q 是CD 上的点，AQ 交BD 于点P ，交BC 的延长线于点R ，若DQ ：CQ=4：3，则AP ：PR=（ ）A ．4：3B ．4：7C ．3：4D ．3：7【考点】相似三角形的判定与性质；平行四边形的性质．【分析】利用“平行线法”证得△ADQ∽△RCD，则对应边成比例：=；同理，证得△ADP∽△RBP，则=，即=．【解答】解：如图，∵在▱ABCD中，AD∥BC，且AD=BC，∴△ADQ∽△RCD，∴=，即=，∴RC=AD．同理，△ADP∽△RBP，则=，即=，∴==，即AP：PR=4：7．故选：B．【点评】本题考查了相似三角形的判定与性质，平行四边形的性质．平行四边形的性质：①边：平行四边形的对边相等．②角：平行四边形的对角相等．③对角线：平行四边形的对角线互相平分．5．如图，△ADE∽△ACB，其中∠AED=∠B，那么能成立的比例式是（ ）A．B．C．D．【考点】相似三角形的性质．【分析】本题可根据相似三角形的性质求解，已知了∠AED和∠B对应相等，因此AD、AC是对应边，AE、AB是对应边，DE、BC是对应边，根据相似三角形的对应边的比例相等，即可判断哪个选项正确．【解答】解：∵△ADE∽△ACB，且∠AED=∠B∴AD、AE、DE的对应边分别是AC、AB、BC因而有故本题选A．【点评】本题主要考查了相似三角形的性质，找准相似三角形的对应边是解题的关键．6．（2008•安徽）如图，在△ABC中，AB=AC=5，BC=6，点M为BC的中点，MN⊥AC于点N，则MN等于（ ）A．B．C．D．【考点】勾股定理；等腰三角形的性质．【分析】连接AM，根据等腰三角形三线合一的性质得到AM⊥BC，根据勾股定理求得AM的长，再根据在直角三角形的面积公式即可求得MN的长．【解答】解：连接AM，∵AB=AC，点M为BC中点，∴AM⊥CM（三线合一），BM=CM，∵AB=AC=5，BC=6，∴BM=CM=3，在Rt△ABM中，AB=5，BM=3，∴根据勾股定理得：AM===4，又S△AMC=MN•AC=AM•MC，∴MN==．故选：C．【点评】综合运用等腰三角形的三线合一，勾股定理．特别注意结论：直角三角形斜边上的高等于两条直角边的乘积除以斜边．7．（2012秋•杞县校级期末）如图，△ABC，AB=12，AC=15，D为AB上一点，且AD=AB，在AC上取一点E，使以A、D、E为顶点的三角形与ABC 相似，则AE等于（ ）A．B．10C．或10D．以上答案都不对【考点】相似三角形的性质．【分析】△ADE与△ABC相似，则存在两种情况，即△AED∽△ACB，也可能是△AED∽△ABC，应分类讨论，求解．【解答】解：如图（1）当∠AED=∠C时，即DE∥BC则AE=AC=10（2）当∠AED=∠B时，△AED∽△ABC∴，即AE=综合（1），（2），故选C．【点评】会利用相似三角形求解一些简单的计算问题．8．（2009•新疆）如图，小正方形的边长均为1，则下列图中的三角形（阴影部分）与△ABC相似的是（ ）A．B．C．D．【考点】相似三角形的判定．【分析】根据网格中的数据求出AB，AC，BC的长，求出三边之比，利用三边对应成比例的两三角形相似判断即可．【解答】解：根据题意得：AB==，AC=，BC=2，∴AC：BC：AB=：2：=1：：，A、三边之比为1：：2，图中的三角形（阴影部分）与△ABC不相似；B、三边之比为：：3，图中的三角形（阴影部分）与△ABC不相似；C、三边之比为1：：，图中的三角形（阴影部分）与△ABC相似；D、三边之比为2：：，图中的三角形（阴影部分）与△ABC不相似．故选C．【点评】此题考查了相似三角形的判定，熟练掌握相似三角形的判定方法是解本题的关键．9．（2006•大兴安岭）如图，△ABC中，∠B=90°，AB=6，BC=8，将△ABC沿DE折叠，使点C落在AB边上的C′处，并且C′D∥BC，则CD的长是（ ）A．B．C．D．【考点】翻折变换（折叠问题）．【分析】先判定四边形C′DCE是菱形，再根据菱形的性质计算．【解答】解：设CD=x，根据C′D∥BC，且有C′D=EC，可得四边形C′DCE是菱形；即Rt△ABC中，AC==10，，EB=x；故可得BC=x+x=8；解得x=．故选A．【点评】本题通过折叠变换考查学生的逻辑思维能力，解决此类问题，应结合题意，最好实际操作图形的折叠，易于找到图形间的关系．二．填空题（共11小题）10．a=4，b=9，则a、b的比例中项是　±6　．【考点】比例线段．【分析】根据比例中项的概念，设a、b的比例中项是c，则c2=ab，再利用比例的基本性质计算得到c的值．【解答】解；设a、b的比例中项是c，则c2=ab∵a=4，b=9，∴c2=ab=36，解得：c=±6；故填： 6或6．【点评】此题考查了比例中项，关键是理解比例中项的概念，当比例式中的两个内项相同时，即叫比例中项．11．在△ABC中，∠ACB=90°，CD⊥AB于点D，则下列说法正确的有　①③④　（填序号）．①AC•BC=AB•CD；②AC2=AD•DB；③BC2=BD•BA；④CD2=AD•DB．【考点】相似三角形的判定与性质．【分析】由在△ABC中，∠ACB=90°，CD⊥AB，易证得∠BDC=∠BCA=∠CDA=90°，又由∠A=∠A，∠B=∠B，根据有两角对应相等的三角形相似，即可证得△ACD∽△ABC，△BDC∽△BCA，则可得△ACD∽△CBD，根据相似三角形的对应边成比例，即可求得答案．【解答】解：∵在△ABC中，∠ACB=90°，CD⊥AB，∴AC•BC=AB•CD，即∴AC•BC=AB•CD，故①正确；∵△ABC中，∠ACB=90°，CD⊥AB于点D，∴BC2=BD•BA，故③正确；∴△ACD∽△CBD，∴，∴AC2=AD•AB，CD2=AD•DB，故②错误，④正确．故答案为：①③④．【点评】此题考查了相似三角形的判定与性质．此题难度适中，解题的关键是注意数形结合思想的应用，注意对应线段的对应关系与比例变形．12．（2011春•武侯区校级期末）如图，Rt△ABC中，AC⊥BC，CD⊥AB于D，AC=8，BC=6，则AD=　6.4　．【考点】相似三角形的判定与性质；勾股定理．【分析】由于AC⊥BC，CD⊥AB，可得一组对应角相等，再加上一对公共角，可证△ACD∽△ABC，利用比例线段可求AD．（可先利用勾股定理求出AB）【解答】解：∵AC⊥BC，CD⊥AB，∴∠ACB=90°，∠ADC=90°，∠A=∠A，∴△ADC∽△ACB，∴=，又∵在Rt△ABC中，AB===10，∴=，AD=6.4．【点评】解答此题不仅用到相似三角形的性质，还要结合勾股定理求出相应的边长，方可进行计算．13．如图，DE∥AC，BE：EC=2：1，AC=12，则DE=　8　．【考点】相似三角形的判定与性质；平行线的性质．【分析】根据DE∥AC，证得△BED∽△BCA，再由相似三角形对应线段成比例可得出答案．【解答】解：由DE∥AC可得△BED∽△BCA，∴==，又AC=12，可得DE=8．故填8．【点评】本题考查平行线的知识，注意相似三角形对应线段成比例的性质．14．如图，平行四边形ABCD中，E是BD上一点，AE的延长线与BC的延长线交于F，与CD交于G，若AE=4，EG=3，则EF= ．【考点】相似三角形的判定与性质；平行四边形的性质．【分析】由平行四边形的定义得出AB∥CD，再根据平行线的性质得到∠ABE=∠FDE，∠EAB=∠EFD，然后根据两角对应相等的两三角形相似即可证明△ABE∽△FDE；根据相似三角形对应边成比例得出①，再证明△BEG ∽△DEA，得出②，等量代换得到，于是得到结论．【解答】证明：∵四边形ABCD是平行四边形，∴AB∥CD，∴∠ABE=∠FDE，∠EAB=∠EFD，∴△ABE∽△FDE，∴①，∵四边形ABCD是平行四边形，∴AD∥BC，∴∠GBE=∠ADE，∠G=∠DEA，∴△BEG∽△DEA，∴②，由①②可得，，∵AE=4，EG=3，∴EF=．故答案为：．【点评】此题考查了相似三角形的判定和性质以及平行四边形的性质．此题难度适中，注意掌握数形结合思想的应用．15．（2012•通州区校级模拟）如图，在平行四边形ABCD中，M、N为AB的三等分点，DM、DN分别交AC于P、Q两点，则AP：PQ：QC=　5：3：12　．【考点】相似三角形的判定与性质；平行四边形的性质．【分析】根据题意，可得出△AMP∽△CDP和△ANQ∽△CDQ，可分别得到AP、PQ、QC的关系式，进而求出AP、PQ、QC的比值．【解答】解：由已知得：△AMP∽△CDP，∴AM：CD=AP：PC=AP：（PQ+QC）=，即：3AP=PQ+QC，①△ANQ∽△CDQ，∴AN：CD=AQ：QC=（AP+PQ）：QC=，即2QC=3（AP+PQ），②解①、②得：AQ=AC，PQ=AQ AP=AC，QC=AC AQ=AC，∴AP：PQ：QC=5：3：12．【点评】主要考查了三角形相似的性质和平行四边形的性质，要熟练掌握灵活运用．16．（2014秋•肥西县期末）如图，若∠B=∠DAC，则△ABC∽　△DAC　，对应边的比例式是　==　．【考点】相似三角形的性质．【分析】根据两角对应相等的两个三角形相似可解，再根据相似三角形的性质写出对应边的比例式．【解答】解：在△ABC和△DAC中，∵∠C=∠C，∠B=∠DAC；∴△ABC∽△DAC；∴==【点评】考查相似三角形的判定定理：（1）两角对应相等的两个三角形相似．（2）两边对应成比例且夹角相等的两个三角形相似．（3）三边对应成比例的两个三角形相似．17．（2012•牡丹江模拟）如图，将①∠BAD=∠C；②∠ADB=∠CAB；③AB2=BD•BC；④；⑤；⑥中的一个作为条件，另一个作为结论，组成一个真命题，则条件是　①　，结论是　③或④　．（注：填序号）【考点】命题与定理．【分析】根据相似三角形的判定和性质进行分析．【解答】解：因为若∠BAD=∠C，则△ABC∽△DBA，故=，=，条件是①，结论是③或④．【点评】解答此题的关键是要熟知真命题与假命题的概念．真命题：判断正确的命题叫真命题；假命题：判断错误的命题叫假命题．18．（2014春•江都市期末）已知：AM：MD=4：1，BD：DC=2：3，则AE：EC=　8：5　．【考点】平行线分线段成比例．【分析】过点D作DF∥BE，再根据平行线分线段成比例，而为公共线段，作为中间联系，整理即可得出结论．【解答】解：过点D作DF∥BE交AC于F，∵DF∥BE，∴△AME∽△ADF，∴AM：MD=AE：EF=4：1=8：2∵DF∥BE，∴△CDF∽△CBE，∴BD：DC=EF：FC=2：3∴AE：EC=AE：（EF+FC）=8：（2+3）∴AE：EC=8：5．【点评】本题主要考查平行线分线段成比例定理的应用，作出辅助线，利用中间量EF即可得出结论．19．（2012秋•桐城市校级月考）如图，将三个全等的正方形拼成一个矩形ADHE，则：∠ABE+∠ACE+∠ADE等于　90　度．【考点】相似三角形的判定与性质；正方形的性质．【分析】设正方形的边长为1，根据正方形的性质得到∠ABE=45°，BE=，再利用勾股定理计算出CE=，则BE：BD=BC：BE=：2，加上公共角，于是可判断△CBE∽△EBD，则∠BDE=∠BEC，再利用三角形外角性质得∠ABE=∠BEC+∠BCE=45°，然后计算∠ABE+∠ACE+∠ADE．【解答】解：设正方形的边长为1，∵四边形AEFB为正方形，∴∠ABE=45°，BE=，在Rt△AEC中，AC=2∴CE==，∴BE：BD=：2，BC：BE=1：=：2，∴BE：BD=BC：BE，而∠CBE=∠EBD，∴△CBE∽△EBD，∴∠BDE=∠BEC，∵∠ABE=∠BEC+∠BCE=45°，∴∠ABE+∠ACE+∠ADE=45°+45°=90°．故答案为90．【点评】本题考查了相似三角形得判定与性质：如果两个三角形的两条对应边的比相等，且它们所夹的角也相等，那么这两个三角形相似；相似三角形对应角相等，对应边的比相等．也考查了勾股定理以及正方形的性质．20．（2011•连云港一模）一张等腰三角形纸片，底边长为15cm，底边上的高长22.5cm．现沿底边依次从下往上裁剪宽度均为3cm的矩形纸条，如图所示．已知剪得的纸条中有一张是正方形，则这张正方形纸条是第　6　张．【考点】相似三角形的判定与性质；等腰三角形的性质；正方形的性质．【分析】设第x张为正方形，如图，△ADE∽△ABC，则=，从而计算出x的值即可．【解答】解：如图，设第x张为正方形，则DE=3，AM=22.5 3x，∵△ADE∽△ABC，∴=，即=，解得x=6．故答案为：6．【点评】本题考查了相似三角形的判定和性质，等腰三角形的性质以及正方形的性质，注：相似三角形的对应边之比等于对应边上的高之比．三．解答题（共10小题）21．如图，D，E分别是AC，AB上的点，．已知△ABC的面积为60cm2，求四边形BCDE的面积．【考点】相似三角形的判定与性质．【分析】根据相似三角形的判定证△ADE∽△ABC，根据相似三角形的性质求出△ADE的面积，相减即可求出答案．【解答】解：∵，∠A=∠A，∴△ADE∽△ABC，∴=，∵△ABC的面积为60cm2，∴△ADE的面积是×60cm2=cm2，∴四边形BCDE的面积是60cm2 cm2=cm2，答：四边形BCDE的面积是cm2．【点评】本题主要考查对相似三角形的性质和判定的理解和掌握，能熟练地运用性质进行推理是解此题的关键．22．（2015春•苏州校级期末）如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上，已知纸板的两条直角边DE=40cm，EF=20cm，测得边DF 离地面的高度AC=1.5m，CD=8m，求树高AB．【考点】相似三角形的应用．【分析】先判定△DEF和△DBC相似，然后根据相似三角形对应边成比例列式求出BC 的长，再加上AC 即可得解．【解答】解：在△DEF 和△DBC 中，，∴△DEF ∽△DBC ，∴=，即=，解得BC=4，∵AC=1.5m ，∴AB=AC+BC=1.5+4=5.5m ，即树高5.5m ．【点评】本题考查了相似三角形的应用，主要利用了相似三角形对应边成比例的性质，比较简单，判定出△DEF 和△DBC 相似是解题的关键．23．（2015秋•北京校级期中）已知：平行四边形ABCD ，E 是BA 延长线上一点，CE 与AD 、BD 交于G 、F ．求证：CF 2=GF•EF ．【考点】平行线分线段成比例；平行四边形的性质．【分析】根据平行四边形的性质得AD ∥BC ，AB ∥CD ，再根据平行线分线段成比例定理得=，=，利用等量代换得到=，然后根据比例的性质即可得到结论．【解答】证明：∵四边形ABCD 是平行四边形，∴AD ∥BC ，AB ∥CD ，∴=，=，∴=，即CF 2=GF•EF ．【点评】本题考查了平行线分线段成比例定理：平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段成比例．也考查了平行四边形的性质．24．平行四边形ABCD中，AB=28，E、F是对角线AC上的两点，且AE=EF=FC，DE交AB于点M，MF交CD于点N．求AM、CN的长．【考点】相似三角形的判定与性质；平行四边形的性质．【分析】根据已知条件，先证明△AEM∽△CED，然后利用相似三角形的对应边成比例这一性质求得AM=AB；再来证明△AFM∽△CFN，依据相似三角形的性质求的CN的长度．【解答】解：在△AEM和△CED中，∠CAB=∠DCA（内错角相等），∠AEM=∠CED，∴△AEM∽△CED，∴，∵AE=EF=FC，∴=，∴AM=CD；∵AB=CD，∴AM=AB=14，①；在△AFM和△CFN中，∠FAM=∠FCN（内错角相等），∠AFM=∠CFN（对顶角相等），∴△AFM∽△CFN，∴=2，∴CN=AM②；∵AB=28 ③由①②③解得，CN=7．【点评】本题主要考查了相似三角形的判定定理：两个三角形中，两个对应角相等，则这两个三角形相似，以及相似三角形的性质：对应边成比例．25．（2006•长沙）如图，A，B，D，E四点在⊙O上，AE，BD的延长线相交于点C，直径AE为8，OC=12，∠EDC=∠BAO．（1）求证：；（2）计算CD•CB的值，并指出CB的取值范围．【考点】切割线定理；相似三角形的判定与性质．【分析】（1）证△CDE∽△CAB，再根据相似三角形的性质得到所求的比例式；（2）根据割线定理即可求得CD•CB的值．根据三角形的三边关系求得BC的取值范围．【解答】（1）证明：∵四边形ABDE内接于⊙O，∴∠EDC=∠BAO，∠C=∠C，∴△CDE∽△CAB，∴；（2）解：∵直径AE=8，OC=12，∴AC=12+4=16，CE=12 4=8．又∵=，∴CD•CB=AC•CE=16×8=128．连接OB，在△OBC中，OB=AE=4，OC=12，∴故BC的范围是：8≤BC＜16．【点评】本题主要考查圆、相似三角形等初中几何的重点知识，考查学生的几何论证能力，属于中等难度题．26．（2009•潍坊）已知△ABC，延长BC到D，使CD=BC．取AB的中点F，连接FD交AC于点E．（1）求的值；（2）若AB=a，FB=EC，求AC的长．【考点】三角形中位线定理；平行线分线段成比例；相似三角形的判定与性质．【分析】（1）过点F作FM∥AC，交BC于点M．根据平行线分线段成比例定理分别找到AE，CE与FM之间的关系，得到它们的比值；（2）结合（1）中的线段之间的关系，进行求解．【解答】解：（1）过点F作FM∥AC，交BC于点M，∵F为AB的中点，∴M为BC的中点，FM=AC．∵FM∥AC，∴∠CED=∠MFD，∠ECD=∠FMD．∴△FMD∽△ECD．∴．∴EC=FM=×AC=AC．∴．（2）∵AB=a，∴FB=AB=a．∵FB=EC，∴EC=a．∵EC=AC，∴AC=3EC=a．【点评】此类题要注意作平行线，能够根据平行线分线段成比例定理和相似三角形对应边成比例即可求得线段的比．27．如图△ABC中，边BC=60，高AD=40，EFGH是内接矩形，HG交AD于P，设HE=x，（1）求矩形EFGH的周长y与x的函数关系式；（2）求矩形EFGH的面积S与x的函数关系式．【考点】相似三角形的判定与性质；矩形的性质．【分析】（1）根据矩形的性质得到HG∥BC，PD=x，AP=AD x=40 x，再三角形三角形相似的判定得到△AHG∽△ABC，利用相似比可表示出HG=（40 x），然后根据矩形的周长确定y与x的关系；（2）根据矩形的面积公式求解．【解答】解：（1）∵AD⊥BC，四边形EFGH是矩形，∴HG∥BC，PD=x，AP=AD x=40 x，∴△AHG∽△ABC，∴=，即=∴HG=（40 x），∴y=2HE+2HG=2x+2×（40 x）=2x+120 3x=120 x（0＜x＜40）；（2）S=HE•HG=x•（40 x）= x2+60x（0＜x＜40）．【点评】本题考查了相似三角形的判定与性质：平行于三角形一边的直线与其他两边所截得的三角形与原三角形相似；相似三角形对应角相等，对应边的比相等．也考查了矩形得性质．28．（2004•丽水）如图，在平面直角坐标系中，已知OA=12厘米，OB=6厘米．点P从点O开始沿OA边向点A以1厘米/秒的速度移动；点Q从点B开始沿BO边向点O以1厘米/秒的速度移动．如果P、Q同时出发，用t（秒）表示移动的时间（0≤t≤6），那么（1）设△POQ的面积为y，求y关于t的函数解析式；（2）当△POQ的面积最大时，将△POQ沿直线PQ翻折后得到△PCQ，试判断点C是否落在直线AB上，并说明理由；（3）当t为何值时，△POQ与△AOB相似．【考点】二次函数综合题．【分析】（1）根据P、Q的速度，用时间t表示出OQ和OP的长，即可通过三角形的面积公式得出y，t的函数关系式；（2）先根据（1）的函数式求出y最大时，x的值，即可得出OQ和OP的长，然后求出C点的坐标和直线AB的解析式，将C点坐标代入直线AB的解析式中即可判断出C是否在AB上；（3）本题要分△OPQ∽△OAB和△OPQ∽△OBA两种情况进行求解，可根据各自得出的对应成比例相等求出t的值．【解答】解：（1）∵OA=12，OB=6，由题意，得BQ=1×t=t，OP=1×t=t．∴OQ=6 t．∴y=×OP×OQ=×t（6 t）= t2+3t（0≤t≤6）；（2）∵y= t2+3t，∴当y有最大值时，t=3∴OQ=3，OP=3，即△POQ是等腰直角三角形．把△POQ沿直线PQ翻折后，可得四边形OPCQ是正方形．∴点C的坐标为（3，3）．∵A（12，0），B（0，6），∴直线AB的解析式为y= x+6当x=3时，y=≠3，∴点C不落在直线AB上；（3）①若△POQ∽△AOB时，，即，12 2t=t，∴t=4．②若△POQ∽△BOA时，，即，6 t=2t，∴t=2．∵0≤t≤6，∴t=4和t=2均符合题意，∴当t=4或t=2时，△POQ与△AOB相似．【点评】本题主要考查了直角三角形的性质、图形的翻折变换、相似三角形的判定和性质等知识点．要注意（3）题要根据不同的相似三角形分类进行讨论．　29．（2007秋•安岳县期末）如图在△ABC中，∠C=90°，BC=8cm，AC=6cm，点Q从B出发，沿BC方向以2cm/s的速度移动，点P从C出发，沿CA方向以1cm/s的速度移动．若Q、P分别同时从B、C出发，试探究经过多少秒后，以点C、P、Q为顶点的三角形与△CBA相似？【考点】相似三角形的判定．【分析】此题要根据相似三角形的性质设出未知数，即经过x秒后，两三角形相似，然后根据速度公式求出他们移动的长度，再根据相似三角形的性质列出分式方程求解．【解答】解：设经过x秒后，两三角形相似，则CQ=（8 2x）cm，CP=xcm，（1分）∵∠C=∠C=90°，∴当或时，两三角形相似．（3分）（1）当时，，∴x=；（4分）（2）当时，，∴x=．（5分）所以，经过秒或秒后，两三角形相似．（6分）【点评】本题综合考查了路程问题，相似三角形的性质及一元一次方程的解法．30．如图，已知A、B两点的坐标分别为（40，0），（0，30），动点P从点A 开始在线段AO上以每秒2个长度单位的速度向原点O运动，动直线EF从x 轴开始以每秒1个单位长度的速度向上平行移动（即EF∥x轴），并且分别与y 轴、线段AB交于点E、F，连接EP、FP，设动点P与动直线EF同时出发，运动时间为t秒．（1）求t=15时，△PEF的面积；（2）当t为何值时，△EOP与△BOA相似．【考点】相似形综合题．【分析】（1）先根据A、B两点的坐标分别为（40，0），（0，30）得出OA及OB的长，再由EF∥x轴得出EF是△BOA的中位线，再根据三角形的面积公式即可得出结论；（2）用t表示出OE及OP的长，再分△EOP∽△BOA与△EOP∽△AOB两种情况进行讨论．【解答】解：（1）∵A、B两点的坐标分别为（40，0），（0，30），∴OA=40，OB=30．∵动直线EF从x轴开始以每秒1个单位长度的速度向上平行移动（即EF∥x 轴），∴t=15时，BE=30 15=15，∵EF∥x轴，∴EF是△BOA的中位线，∴EF=OA=20，∴S△PEF=EF•OE=×20×15=150；（2）∵动点P从点A开始在线段AO上以每秒2个长度单位的速度向原点O运动，动直线EF从x轴开始以每秒1个单位长度的速度向上平行移动（即EF∥x轴），∴OE=t，OP=40 2t，∴当△EOP∽△BOA时，=，即=，解得t=12（秒）；当△EOP∽△AOB时，=，即=．解得t=（秒）．综上所述，当t=12秒或t=秒时，△EOP与△BOA相似．【点评】本题考查的是相似形综合题，涉及到三角形中位线定理、三角形的面积公式及相似三角形的判定与性质等知识，在解答（2）时要注意进行分类讨论．。

相似三角形(压轴必刷30题专项训练)一．填空题(共9小题)1(2020秋•虹口区校级月考)一张等腰三角形纸片，底边长为15cm ，底边上的高长22.5cm ．现沿底边依次从下往上裁剪宽度均为3cm 的矩形纸条，如图所示．已知剪得的纸条中有一张是正方形，则这张正方形纸条是第6张．【分析】设第x 张为正方形，如图，△ADE ∽△ABC ，则DE BC =AM AN，从而计算出x 的值即可．【解答】解：如图，设第x 张为正方形，则DE =3(cm )，AM =(22.5-3x )(cm )，∵△ADE ∽△ABC ，∴DE BC =AM AN ，即315=22.5-3x 22.5，解得x =6．故答案为：6．【点评】本题考查了相似三角形的判定和性质，等腰三角形的性质以及正方形的性质，注：相似三角形的对应边之比等于对应边上的高之比．2(2019秋•浦东新区校级月考)如图，在平行四边形ABCD 中，E 是边BC 上的点，AE 交BD 于点F ，如果BE BC=23，那么BF FD =23．【分析】由平行四边形的性质可证△BEF ∽△DAF ，再根据相似三角形的性质得BE ：DA =BF ：DF 即可解．【解答】解：ABCD 是平行四边形，∴BC ∥AD ，BC =AD∴△BEF ∽△DAF∴BE ：DA =BF ：DF∵BC =AD∴BF ：DF =BE ：BC =2：3．【点评】本题考查了平行四边形的性质及相似三角形的判定定理和性质．3(2017秋•虹口区校级月考)如图，直角三角形ABC 中，∠ACB =90°，AB =10，BC =6，在线段AB上取一点D ，作DF ⊥AB 交AC 于点F ，现将△ADF 沿DF 折叠，使点A 落在线段DB 上，对应点记为A 1；AD 的中点E 的对应点记为E 1，若△E 1FA 1∽△E 1BF ，则AD =165．【分析】利用勾股定理列式求出AC ，设AD =2x ，得到AE =DE =DE 1=A 1E 1=x ，然后求出BE 1，再利用相似三角形对应边成比例列式求出DF ，然后利用勾股定理列式求出E 1F ，然后根据相似三角形对应边成比例列式求解得到x 的值，从而可得AD 的值．【解答】解：∵∠ACB =90°，AB =10，BC =6，∴AC =AB 2-BC 2=102-62=8，设AD =2x ，∵点E 为AD 的中点，将△ADF 沿DF 折叠，点A 对应点记为A 1，点E 的对应点为E 1，∴AE =DE =DE 1=A 1E 1=x ，∵DF ⊥AB ，∠ACB =90°，∠A =∠A ，∴△ABC ∽△AFD ，∴AD AC =DF BC ，即2x 8=DF 6，解得DF =32x ，在Rt △DE 1F 中，E 1F =DF 2+DE 12=3x 22+x 2=13x 2，又∵BE 1=AB -AE 1=10-3x ，△E 1FA 1∽△E 1BF ，∴E 1F A 1E 1=BE 1E 1F ，∴E 1F 2=A 1E 1•BE 1，即(13x 2)2=x (10-3x )，解得x =85，∴AD 的长为2×85=165．故答案为：165．【点评】本题考查了相似三角形的性质，主要利用了翻折变换的性质，勾股定理，相似三角形对应边成比例，综合题，熟记性质并准确识图是解题的关键．4(2021秋•普陀区校级月考)如图，在△ABC 中，4AB =5AC ，AD 为△ABC 的角平分线，点E 在BC 的延长线上，EF ⊥AD 于点F ，点G 在AF 上，FG =FD ，连接EG 交AC 于点H ．若点H 是AC 的中点，则AG FD的值为43．【分析】解题关键是作出辅助线，如解答图所示：第1步：利用角平分线的性质，得到BD =54CD ；第2步：延长AC ，构造一对全等三角形△ABD ≌△AMD ；第3步：过点M 作MN ∥AD ，构造平行四边形DMNG ．由MD =BD =KD =54CD ，得到等腰△DMK ；然后利用角之间关系证明DM ∥GN ，从而推出四边形DMNG 为平行四边形；第4步：由MN ∥AD ，列出比例式，求出AG FD的值．【解答】解：已知AD 为角平分线，则点D 到AB 、AC 的距离相等，设为h ．∵BD CD =S △ABD S △ACD =12AB ⋅h 12AC ⋅h =AB AC =54，∴BD =54CD ．如图，延长AC ，在AC 的延长线上截取AM =AB ，则有AC =4CM ．连接DM ．在△ABD 与△AMD 中，AB =AM ∠BAD =∠MAD AD =AD ∴△ABD ≌△AMD (SAS )，∴MD =BD =54CD ．过点M 作MN ∥AD ，交EG 于点N ，交DE 于点K ．∵MN ∥AD ，∴CK CD =CM AC =14，∴CK =14CD ，∴KD =54CD ．∴MD =KD ，即△DMK 为等腰三角形，∴∠DMK =∠DKM ．由题意，易知△EDG 为等腰三角形，且∠1=∠2；∵MN ∥AD ，∴∠3=∠4=∠1=∠2，又∵∠DKM =∠3(对顶角)∴∠DMK =∠1，∴DM ∥GN ，∴四边形DMNG 为平行四边形，∴MN =DG =2FD ．∵点H 为AC 中点，AC =4CM ，∴AH MH=23．∵MN ∥AD ，∴AG MN =AH MH ，即AG 2FD =23，∴AG FD =43．故答案为：43．方法二：如图，有已知易证△DFE ≌△GFE ，故∠5=∠B +∠1=∠4=∠2+∠3，又∠1=∠2，所以∠3=∠B ，则可证△AGH ∽△ADB设AB =5a ，则AC =4a ，AH =2a ，所以AG /AD =AH /AB =2/5，而AD =AG +GD ，故GD /AD =3/5，所以AG ：GD =2：3，F 是GD 的中点，所以AG ：FD =4：3．【点评】本题是几何综合题，难度较大，正确作出辅助线是解题关键．在解题过程中，需要综合利用各种几何知识，例如相似、全等、平行四边形、等腰三角形、角平分线性质等，对考生能力要求较高．5(2022秋•普陀区校级月考)如图，点A 1，A 2，A 3，A 4在射线OA 上，点B 1，B 2，B 3在射线OB 上，且A 1B 1∥A 2B 2∥A 3B 3，A 2B 1∥A 3B 2∥A 4B 3．若△A 2B 1B 2，△A 3B 2B 3的面积分别为1，4，则图中三个阴影三角形面积之和为10.5．【分析】已知△A 2B 1B 2，△A 3B 2B 3的面积分别为1，4，且两三角形相似，因此可得出A 2B 2：A 3B 3=1：2，由于△A 2B 2A 3与△B 2A 3B 3是等高不等底的三角形，所以面积之比即为底边之比，因此这两个三角形的面积比为1：2，根据△A 3B 2B 3的面积为4，可求出△A 2B 2A 3的面积，同理可求出△A 3B 3A 4和△A 1B 1A 2的面积．即可求出阴影部分的面积．【解答】解：△A 2B 1B 2，△A 3B 2B 3的面积分别为1，4，又∵A 2B 2∥A 3B 3，A 2B 1∥A 3B 2，∴∠OB 2A 2=∠OB 3A 3，∠A 2B 1B 2=∠A 3B 2B 3，∴△B 1B 2A 2∽△B 2B 3A 3，∴B 1B 2B 2B 3=12=A 2B 2A 3B 3，∴A 2A 3A 3A 4=12．∵S △A 2B 2A 3S △B 2A 3B3=12，△A 3B 2B 3的面积是4，∴△A 2B 2A 3的面积为=12×S △A 2B 2B 3=12×4=2(等高的三角形的面积的比等于底边的比)．同理可得：△A 3B 3A 4的面积=2×S △A 3B 2B 3=2×4=8；△A 1B 1A 2的面积=12S △A 2B 1B 2=12×1=0.5．∴三个阴影面积之和=0.5+2+8=10.5．故答案为：10.5．【点评】本题的关键是利用平行线证明三角形相似，再根据已给的面积，求出相似比，从而求阴影部分的面积．6(2017秋•徐汇区校级月考)设△ABC 的面积为1，如图①，将边BC 、AC 分别2等分，BE 1、AD 1相交于点O ，△AOB 的面积记为S 1；如图②将边BC 、AC 分别3等分，BE 1、AD 1相交于点O ，△AOB 的面积记为S 2；⋯，依此类推，则S n 可表示为　12n +1　．(用含n 的代数式表示，其中n 为正整数)【分析】连接D 1E 1，设AD 1、BE 1交于点M ，先求出S △ABE 1=1n +1，再根据AB D 1E 1=BM ME 1=n +1n 得出S △ABM ：S △ABE 1=(n +1)：(2n +1)，最后根据S △ABM ：1n +1=(n +1)：(2n +1)，即可求出S n ．【解答】解：如图，连接D 1E 1，设AD 1、BE 1交于点M ，∵AE1：AC =1：(n +1)，∴S △ABE 1：S △ABC =1：(n +1)，∴S △ABE 1=1n +1，∵AB D 1E 1=BM ME 1=n +1n ，∴BM BE 1=n +12n +1，∴S △ABM ：S △ABE 1=(n +1)：(2n +1)，∴S △ABM ：1n +1=(n +1)：(2n +1)，∴S n =12n +1．故答案为：12n +1．【点评】此题考查了相似三角形的判定与性质，用到的知识点是相似三角形的判定与性质、平行线分线段成比例定理、三角形的面积，关键是根据题意作出辅助线，得出相似三角形．7(2018秋•南岗区校级月考)已知菱形ABCD 的边长是6，点E 在直线AD 上，DE =3，连接BE 与对角线AC 相交于点M ，则MC AM的值是　2或23　．【分析】由菱形的性质易证两三角形相似，但是由于点E 的位置未定，需分类讨论．【解答】解：分两种情况：(1)点E 在线段AD 上时，△AEM ∽△CBM ，∴MC AM =BC AE=2；(2)点E在线段AD的延长线上时，△AME∽△CMB，∴MCAM =BCAE=23．【点评】本题考查了相似三角形的性质以及分类讨论的数学思想；其中由相似三角形的性质得出比例式是解题关键．注意：求相似比不仅要认准对应边，还需注意两个三角形的先后次序．8(2020秋•虹口区校级月考)如图，在△ABC中，∠ACB的内、外角平分线分别交BA及其延长线于点D、E，BC=2.5AC，则ABAD+ABAE=5．【分析】根据CD平分∠ACB，可得ABDA=BCAC，根据CE平分∠ACB的外角，可得DEAE=BCAC，进而可得结果．【解答】解：∵CD平分∠ACB，∴AB DA =BC AC，∴BD+DADA =BC+ACAC，∴AB DA =BC+ACAC，①∵CE平分∠ACB的外角，∴DE AE =BC AC，∴BE-AEAE =BC-ACAC，∴AB AE =BC-ACAC，②①+②得，AB AD +ABAE=BC+ACAC+BC-ACAC=2BCAC=2×2.5=5．故答案为：5．【点评】主要考查了相似三角形的判定及其性质的应用问题；解题的关键是灵活运用相似三角形的性质来分析、判断、推理或解答．9(2022秋•黄浦区校级月考)如图，在等腰△ABC中，AB=AC，点P在BA的延长线上，PA=1 4AB，点D在BC边上，PD=PC，则CDBC的值是　34　．【分析】过点P 作PE ∥AC 交DC 延长线于点E ，根据等腰三角形判定与性质，平行线的性质可证PB =PE ，再证△PCE ≌△PDB ，可得BD =CE ，再利用平行线分线段成比例的PA AB=CE BC ，结合线段的等量关系以及比例的性质即可得出结论．【解答】解：如图，过点P 作PE ∥AC 交DC 延长线于点E ，∵AB =AC ，∴∠B =∠ACB ，∵AC ∥PE ，∴∠ACB =∠E ，∴∠B =∠E ，∴PB =PE ，∵PC =PD ，∴∠PDC =∠PCD ，∴∠BPD =∠EPC ，∴在△PCE 和△PDB 中，PC =PD ∠BPD =∠EPC PB =PE，∴△PCE ≌△PDB (SAS )，∴BD =CE ，∵AC ∥PE ，∴PA AB =CE BC ，∵PA =14AB ，∴CE BC =14，∴BD BC =14，∴CD BC =34．故答案为：34．【点评】本题考查了等腰三角形的判定与性质，平行线分线段成比例，以及全等三角形的判定，解决问题的关键是正确作出辅助线，列出比例式．二．解答题(共21小题)10(2017秋•虹口区校级月考)在△ABC 中，∠CAB =90°，AD ⊥BC 于点D ，点E 为AB 的中点，EC 与AD交于点G ，点F 在BC 上．(1)如图1，AC ：AB =1：2，EF ⊥CB ，求证：EF =CD ．(2)如图2，AC ：AB =1：，EF ⊥CE ，求EF ：EG 的值．【分析】(1)根据同角的余角相等得出∠CAD =∠B ，根据AC ：AB =1：2及点E 为AB 的中点，得出AC =BE ，再利用AAS 证明△ACD ≌△BEF ，即可得出EF =CD ；(2)作EH ⊥AD 于H ，EQ ⊥BC 于Q ，先证明四边形EQDH 是矩形，得出∠QEH =90°，则∠FEQ =∠GEH ，再由两角对应相等的两三角形相似证明△EFQ ∽△EGH ，得出EF ：EG =EQ ：EH ，然后在△BEQ 中，根据正弦函数的定义得出EQ =12BE ，在△AEH 中，根据余弦函数的定义得出EH =32AE ，又BE =AE ，进而求出EF ：EG 的值．【解答】(1)证明：如图1，在△ABC 中，∵∠CAB =90°，AD ⊥BC 于点D ，∴∠CAD =∠B =90°-∠ACB ．∵AC ：AB =1：2，∴AB =2AC ，∵点E 为AB 的中点，∴AB =2BE ，∴AC =BE ．在△ACD 与△BEF 中，∠CAD =∠B ∠ADC =∠BFE =90°AC =BE，∴△ACD ≌△BEF ，∴CD =EF ，即EF =CD ；(2)解：如图2，作EH ⊥AD 于H ，EQ ⊥BC 于Q ，∵EH ⊥AD ，EQ ⊥BC ，AD ⊥BC ，∴四边形EQDH 是矩形，∴∠QEH =90°，∴∠FEQ =∠GEH =90°-∠QEG ，又∵∠EQF =∠EHG =90°，∴△EFQ ∽△EGH ，∴EF ：EG =EQ ：EH ．∵AC ：AB =1：3，∠CAB =90°，∴∠B =30°．在△BEQ 中，∵∠BQE =90°，∴sin B =EQ BE =12，∴EQ =12BE ．在△AEH中，∵∠AHE=90°，∠AEH=∠B=30°，∴cos∠AEH=EHAE =32，∴EH=32AE．∵点E为AB的中点，∴BE=AE，∴EF：EG=EQ：EH=12BE：32AE=1：3=3：3=33．【点评】本题考查了相似三角形的判定和性质、全等三角形的判定和性质、矩形的判定和性质，解直角三角形，综合性较强，有一定难度．解题的关键是作辅助线，构造相似三角形，并且证明四边形EQDH是矩形．11(2021秋•杨浦区校级月考)如图，已知在菱形ABCD，点E是AB的中点，AF⊥BC于点F，连接EF、ED、DF，DE交AF于点G，且DE⊥EF．(1)求证：AE2=EG•ED；(2)求证：BC2=2DF•BF．【分析】(1)根据直角三角形的性质得到AE=FE，根据菱形的性质得到AD∥BC，求得∠DAG=∠AFB =90°，然后证明△AEG∽△DEA，即可得到结论；(2)由AE=EF，AE2=EG•ED，得到FE2=EG•ED，推出△FEG∽△DEF，根据相似三角形的性质得到∠EFG=∠EDF，根据相似三角形的判定和性质即可得到结论．【解答】证明：(1)∵AF⊥BC于点F，∴∠AFB=90°，∵点E是AB的中点，∴AE=FE，∴∠EAF=∠AFE，∵四边形ABCD是菱形，∴AD∥BC，∴∠DAG=∠AFB=90°，∵DE⊥EF，∴∠FEG=90°，∴∠DAG=∠FEG，∵∠AGD=∠FGE，∴∠EFG=∠ADG，∴∠EAG=∠ADG，∵∠AEG=∠DEA，∴△AEG∽△DEA，∴AE DE =EG AE，∴AE2=EG•ED；(2)∵AE=EF，AE2=EG•ED，∴FE2=EG•ED，∴EF DE =EGEF，∵∠FEG=∠DEF，∴△FEG∽△DEF，∴∠EFG=∠EDF，∴∠BAF=∠EDF，∵∠DEF=∠AFB=90°，∴△ABF∽△DFE，∴AB DF =BF EF，∵四边形ACBD是菱形，∴AB=BC，∵∠AFB=90°，∵点E是AB的中点，∴FE=12AB=12BC，∴BC DF =BF12BC，∴BC2=2DF•BF．【点评】本题考查了相似三角形的判定和性质，菱形的性质，直角三角形的性质，正确的识别图形是解题的关键．12(2021秋•杨浦区校级月考)如图，已知在平行四边形ABCD中，AE：ED=1：2，点F为DC的中点，连接BE、AF，BE与AF交于点H．(1)求EH：BH的值；(2)若△AEH的面积为1，求平行四边形ABCD的面积．【分析】(1)延长AF，BC交于点G，证明△ADF≌△GCF(AAS)，可得AD=CG=BC，所以BG=2BC，根据AE：ED=1：2，可得AE：AD=1：3，AE：BG=1：6，，证明△AEH∽△GBH，即可解决问题；(2)在△AEH中，设AE=x，AE边上的高为h，△BGH中，BG边上的高为h′，可得平行四边形ABCD的高为h+h′，BC=3x，根据△AEH的面积为1，可得x•h=2，所以h′=6h，进而可以求平行四边形ABCD 的面积．【解答】解：(1)如图，延长AF，BC交于点G，∵四边形ABCD是平行四边形，∴AD ∥BC ，AD =BC ，∴∠D =∠DCG ，∠DAF =∠G ，∵点F 为DC 的中点，∴DF =CF ，在△ADF 和△GCF 中，∠D =∠FCG ∠DAF =∠G DF =CF，∴△ADF ≌△GCF (AAS )，∴AD =CG ，∴AD =CG =BC ，∴BG =2BC ，∵AE ：ED =1：2，∴AE ：AD =1：3，∴AE ：BG =1：6，∵AD ∥BC ，∴△AEH ∽△GBH ，∴EH ：BH =AE ：BG =1：6；(2)在△AEH 中，设AE =x ，AE 边上的高为h ，△BGH 中，BG 边上的高为h ′，∴平行四边形ABCD 的高为h +h ′，BC =3x ，∵△AEH 的面积为1，∴12x •h =1，∴x •h =2∵△AEH ∽△GBH ，∴h ：h ′=1：6，∴h ′=6h ，∴h +h ′=7h ，∴平行四边形ABCD 的面积=BC •(h +h ′)=3x •7h =21xh =42．【点评】本题考查了相似三角形的判定和性质，平行四边形的性质，平行线分线段成比例等知识，添加恰当辅助线构造相似三角形是解题的关键．13(2021春•徐汇区校级月考)如图，在菱形ABCD 中，点E 在对角线AC 上，点F 在BC 的延长线上，EF =EB ，EF 与CD 相交于点G ；(1)求证：EG •GF=CG •GD ；(2)联结DF ，如果EF ⊥CD ，那么∠FDC 与∠ADC 之间有怎样的数量关系？证明你的结论．【分析】(1)先证明△BCE ≌△DCE ，得∠EDC =∠EBC ；利用此条件再证明∠DGE ∽△FGC ，即可得到EG •GF =CG •GD．(2)利用第(1)题的结论，可证明△DGE ∽△FGC ，再利用三角形内角外角关系，即可得到∠ADC 与∠FDC 的关系．【解答】解：(1)证明：∵点E 在菱形ABCD 的对角线AC 上，∴∠ECB =∠ECD ，∵BC =CD ，CE =CE ，∴△BCE ≌△DCE ，∴∠EDC =∠EBC ，∵EB =EF ，∴∠EBC =∠EFC ；∴∠EDC =∠EFC ；∵∠DGE =∠FGC ，∴△DGE ∽△FGC ；∴EGCG =GD FG∴EG •GF =CG •GD ；(2)∠ADC =2∠FDC ．证明：∵EG CG =GD FG ，∴EG DG =CG FG，又∵∠DGF =∠EGC ，∴△CGE ∽△FGD ，∵EF ⊥CD ，DA =DC ，∴∠DAC =∠DCA =∠DFG =90°-∠FDC ，∴∠ADC =180°-2∠DAC =180°-2(90°-∠FDC )=2∠FDC ．【点评】本题主要考查了全等三角形的判定及性质、相似三角形的判定及性质、菱形的性质等知识点的综合应用，解题时注意：相似三角形的对应角相等，对应边成比例．在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用．14(2021秋•宝山区校级月考)如图，四边形DEFG 是△ABC 的内接正方形，AB =BC =6cm ，∠B =45°，则正方形DEFG 的面积为多少？【分析】过A 作AH ⊥BC 于H ，交GF 于M ，于是得到△ABH 是等腰直角三角形，求得AH =BH =2222AB =32cm ，由△AGF ∽△ABC ，得到GF BC =AM AH，求得GF =(62-6)cm ，即可得到结论．【解答】解：过A 作AH ⊥BC 于H ，交GF 于M ，∵∠B =45°，∴AH =BH =22AB =32cm ，∵GF ∥BC ，∴△AGF ∽△ABC ，∴GF BC =AM AH，即GF 6=32-GF 32，∴GF =(62-6)cm ，∴正方形DEFG 的面积=GF 2=(62-6)2=(108-722)cm ．【点评】本题考查了相似三角形的判定与性质，正方形的四条边都相等的性质，利用相似的性质：对应边的比值相等求出正方形的边长是解答本题的关键．15(2021秋•松江区月考)如图，在平行四边形ABCD 中，点E 为边BC 上一点，联结AE 并延长AE 交DC 的延长线于点M ，交BD 于点G ，过点G 作GF ∥BC 交DC 于点F ．求证：DF FC =DM CD．【分析】由GF ∥BC ，根据平行线分线段成比例定理，可得DF FC，又由四边形ABCD 是平行四边形，可得AB =CD ，AB ∥CD ，继而可证得DM AB =DG BG ，则可证得结论．【解答】证明：∵GF ∥BC ，∴DF FC =DG BG，∵四边形ABCD 是平行四边形，∴AB =CD ，AB ∥CD ，∴DM AB =DG BG ，∴DF FC =DM CD．【点评】此题考查了平行分线段成比例定理以及平行四边形的性质，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．16(2021秋•松江区月考)如图，在Rt △ABC 中，∠ACB =90°，CD ⊥AB 于D ，E 是AC 的中点，DE 的延长线与BC 的延长线交于点F ．(1)求证：FD FC =BD DC ；(2)若BC FC =54，求BD DC的值．【分析】(1)根据直角三角形斜边上中线性质求出DE =EC ，推出∠EDC =∠ECD ，求出∠FDC =∠B ，根据∠F =∠F 证△FBD ∽△FDC ，即可；(2)根据已知和三角形面积公式得出S △BDC S △FDC =54，S △BDF S △FDC =94，根据相似三角形面积比等于相似比的平方得出S △BDFS △FDC =BD DC 2=94，即可求出BD DC．【解答】(1)证明：∵CD ⊥AB ，∴∠ADC =90°，∵E 是AC 的中点，∴DE =EC ，∴∠EDC =∠ECD ，∵∠ACB =90°，∠BDC =90°∴∠ECD +∠DCB =90°，∠DCB +∠B =90°，∴∠ECD =∠B ，∴∠FDC =∠B ，∵∠F =∠F ，∴△FBD ∽△FDC ，∴FD FC =BD DC(2)解：∵BC FC =54，∴S △BDCS △FDC =54，∴S △BDFS △FDC =94，∵△FBD ∽△FDC ，∴S △BDF S △FDC =BD DC2=94，∴BD DC=32．【点评】本题考查了相似三角形的性质和判定，三角形的面积，注意：相似数据线的面积比等于相似比的平方，题目比较好，有一定的难度．17(2021春•黄浦区校级月考)如图，四边形ABCD 是矩形，E 是对角线AC 上的一点，EB =ED 且∠ABE =∠ADE ．(1)求证：四边形ABCD 是正方形；(2)延长DE 交BC 于点F ，交AB 的延长线于点G ，求证：EF •AG =BC •BE ．【分析】(1)根据邻边相等的矩形是正方形即可证明；(2)由AD ∥BC ，推出EF DE =EC EA ，同理DC AG =EC EA，由DE =BE ，四边形ABCD 是正方形，推出BC =DC，可得EFBE =BCAG解决问题；【解答】(1)证明：连接BD．∵EB=ED，∴∠EBD=∠EDB，∵∠ABE=∠ADE，∴∠ABD=∠ADB，∴AB=AD，∵四边形ABCD是矩形，∴四边形ABCD是正方形．(2)证明：∵四边形ABCD是矩形∴AD∥BC，∴EF DE =EC EA，同理DCAG=ECEA，∵DE=BE，四边形ABCD是正方形，∴BC=DC，∴EF BE =BC AG，∴EF•AG=BC•BE．【点评】本题考查相似三角形的判定和性质、矩形的性质、正方形的性质和判定等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．18(2021秋•浦东新区校级月考)如图，在△ABC中，DE∥BC，EF∥CD，求证：AD2=AF•AB．【分析】由DE∥BC，EF∥CD，可得△ADE∽△ABC，△AFE∽△ADC，然后由相似三角形的对应边成比例，证得结论．【解答】证明：∵DE∥BC，EF∥CD，∴△ADE∽△ABC，△AFE∽△ADC，∴AD：AB=AE：AC，AF：AD=AE：AC，∴AD：AB=AF：AD，∴AD2=AF•AB．【点评】此题考查了相似三角形的判定与性质．注意掌握相似三角形的对应边成比例．19(2020秋•浦东新区月考)在△ABC中，D是BC的中点，且AD=AC，DE⊥BC，与AB相交于点E，EC与AD相交于点F．(1)求证：△ABC∽△FCD；(2)若DE=3，BC=8，求△FCD的面积．【分析】(1)由DE⊥BC，D是BC的中点，根据线段垂直平分线的性质，可得BE=CE，又由AD=AC，易得∠B=∠DCF，∠FDC=∠ACB，即可证得△ABC∽△FCD；(2)首先过A作AG⊥CD，垂足为G，易得△BDE∽△BGA，可求得AG的长，继而求得△ABC的面积，然后由相似三角形面积比等于相似比的平方，求得△FCD的面积．【解答】(1)证明：∵D是BC的中点，DE⊥BC，∴BE=CE，∴∠B=∠DCF，∵AD=AC，∴∠FDC=∠ACB，∴△ABC∽△FCD；(2)解：过A作AG⊥CD，垂足为G．∵AD=AC，∴DG=CG，∴BD：BG=2：3，∵ED⊥BC，∴ED∥AG，∴△BDE∽△BGA，∴ED：AG=BD：BG=2：3，∵DE=3，∴AG=92，∵△ABC∽△FCD，BC=2CD，∴S△FCDS△ABC=(CDBC)2=14．∵S△ABC=12×BC×AG=12×8×92=18，∴S△FCD=14S△ABC=92．【点评】此题考查了相似三角形的判定与性质以及等腰三角形的性质．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用．20(2021春•静安区校级月考)已知：如图，在菱形ABCD中，点E在边BC上，点F在BA的延长线上，BE=AF，CF∥AE，CF与边AD相交于点G．求证：(1)FD=CG；(2)CG2=FG•FC．【分析】(1)根据菱形的性质得到∠FAD =∠B ，根据全等三角形的性质得到FD =EA ，于是得到结论；(2)根据菱形的性质得到∠DCF =∠BFC ，根据平行线的性质得到∠BAE =∠BFC ，根据全等三角形的性质得到∠BAE =∠FDA ，等量代换得到∠DCF =∠FDA ，根据相似三角形的判定和性质即可得到结论．【解答】证明：(1)∵在菱形ABCD 中，AD ∥BC ，∴∠FAD =∠B ，在△ADF 与△BAE 中，AF =BE ∠FAD =∠B AD =BA，∴△ADF ≌△BAE ，∴FD =EA ，∵CF ∥AE ，AG ∥CE ，∴EA =CG ，∴FD =CG ；(2)∵在菱形ABCD 中，CD ∥AB ，∴∠DCF =∠BFC ，∵CF ∥AE ，∴∠BAE =∠BFC ，∴∠DCF =∠BAE ，∵△ADF ≌△BAE ，∴∠BAE =∠FDA ，∴∠DCF =∠FDA ，又∵∠DFG =∠CFD ，∴△FDG ∽△FCD ，∴FD FC=FG FD ，FD 2=FG •FC ，∵FD =CG ，∴CG 2=FG •FC ．【点评】本题考查了相似三角形的判定和性质，全等三角形的判定和性质，菱形的性质，熟练掌握相似三角形的性质是解题的关键．21(2021秋•浦东新区校级月考)如图，梯形ABCD 中，AD ∥BC ，BC =2AD ，点E 为边DC 的中点，BE 交AC 于点F ．求：(1)AF ：FC 的值；(2)EF ：BF 的值．【分析】(1)延长BE 交直线AD 于H ，如图，先由AD ∥BC 得到△DEH ∽△CEB ，则有DH BC =DE CE，易得DH =BC ，加上BC =2AD ，所以AH =3AD ，然后证明△AHF ∽△CFB ，再利用相似比可计算出AF ：FC 的值；(2)由△DEH ∽△CEB 得到EH ：BE =DE ：CE =1：1，则BE =EH =12BH ，由△AHF ∽△CFB 得到FH ：BF =AF ：FC =3：2；于是可设BF =2a ，则FH =3a ，BH =BF +FH =5a ，EH =52a ，接着可计算出EF =FH -EH =12a ，然后计算EF ：BF 的值．【解答】解：(1)延长BE 交直线AD 于H ，如图，∵AD ∥BC ，∴△DEH ∽△CEB ，∴DH BC =DE CE，∵点E 为边DC 的中点，∴DE =CE ，∴DH =BC ，而BC =2AD ，∴AH =3AD ，∵AH ∥BC ，∴△AHF ∽△CFB ，∴AF ：FC =AH ：BC =3：2；(2)∵△DEH ∽△CEB ，∴EH ：BE =DE ：CE =1：1，∴BE =EH =12BH ，∵△AHF ∽△CFB ，∴FH ：BF =AF ：FC =3：2；设BF =2a ，则FH =3a ，BH =BF +FH =5a ，∴EH =52a ，∴EF =FH -EH =3a -52a =12a ，∴EF ：BF =12a ：2a =1：4．【点评】本题考查了相似三角形的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形；在运用相似三角形的性质时，主要通过相似比得到线段之间的关系．22(2021秋•浦东新区校级月考)已知：如图，在△ABC 中，BD 是∠ABC 的平分线，过点D 作DE ∥CB ，交AB 于点E ，AD DC =13，DE =6．(1)求AB 的长；(2)求S △ADE S △BCD．【分析】(1)由∠ABD =∠CBD ，DE ∥BC 可推得∠EDB =∠CBD ，进而推出∠ABD =∠EDB ，由此可得BE =DE =6，由DE ∥BC 可得AE EB =AD DC=13，进而证得AE =2，于是可得结论；(2)△ADE 看成以DE 为底，高为h 1，△BCD 看成以BC 为底，高为h 2，由平行线分线段成比例定理和相似三角形的性质可得h 1h 2=AD DE =13，DE BC =14，进而证得结论．【解答】解：(1)BD 平∠ABC ，∴∠ABD =∠CBD ，∵DE ∥BC ，∴∠EDB =∠CBD ，∴∠ABD =∠EDB ，∴BE =DE =6，∵DE ∥BC ，∴AE EB =AD DC =13，∴AE 6=13，∴AE =2，∴AB =AE +BE =8；(2)△ADE 看成以DE 为底，高为h 1，△BCD 看成以BC 为底，高为h 2，∵DE ∥CB ，∴△AED ∽△ABC ，∴h 1h 2=AD DE =13，DE BC =14，∴S △ADE S △BCD =12DE ⋅h 112BC ⋅h 2=112．【点评】本题主要考查了等腰三角形的性质，平行线分线段成比例定理和相似三角形的性质，三角形的面积等知识，熟练应用平行线分线段成比例定理和相似三角形的性质是解决问题的关键．23(2022春•长宁区校级月考)已知：如图，在平行四边形ABCD 中，AC 、DB 交于点E ，点F 在BC 的延长线上，联结EF 、DF ，且∠DEF =∠ADC ．(1)求证：EFBF =AB DB；(2)如果BD 2=2AD •DF ，求证：平行四边形ABCD 是矩形．【分析】(1)由已知条件和平行四边形的性质易证△ADB ∽△EBF ，再由相似三角形的性质：对应边的比值相等即可证明：EF BF =AB DB；(2)由(1)可得BD 2=2AD •BF ，又因为BD 2=2AD •DF ，所以可证明BF =DF ，再由等腰三角形的性质可得∠DEF =90°，所以∠ADC =∠DEF =90°，进而可证明平行四边形ABCD 是矩形．【解答】解：(1)证明：∵平行四边形ABCD ，∴AD ∥BC ，AB ∥DC∴∠BAD +∠ADC =180°，又∵∠BEF +∠DEF =180°，∴∠BAD +∠ADC =∠BEF +∠DEF ，∵∠DEF =∠ADC ，∴∠BAD =∠BEF ，∵AD ∥BC ，∴∠EBF =∠ADB ，∴△ADB ∽△EBF ，∴EF BF =AB DB；(2)∵△ADB ∽△EBF ，∴AD BD =BE BF，在平行四边形ABCD 中，BE =ED =12BD ，∴AD •BF =BD •BE =12BD 2，∴BD 2=2AD •BF ，又∵BD 2=2AD •DF ，∴BF =DF ，∴△DBF 是等腰三角形，∵BE =DE ，∴FE ⊥BD ，即∠DEF =90°，∴∠ADC =∠DEF =90°，∴平行四边形ABCD 是矩形．【点评】本题考查了平行四边形的性质、相似三角形的判断和性质以及矩形的判断，其中(2)小题证明△DBF 是等腰三角形是解题的关键．24(2021秋•宝山区校级月考)已知，如图，在梯形ABCD中，AD∥BC，BC=6，点P是射线AD上的点，BP交AC于点E，∠CBP的角平分线交AC于点F，且CF=13AC时．求AP+BP的值．【分析】延长BF交射线AP于M，根据AD∥BC，根据两直线平行，内错角相等可得∠M=∠CBM，再根据角平分线的定义可得∠PBM=∠CBM，从而得到∠M=∠PBM，根据等角对等边可得BP=PM，求出AP+BP=AM，再根据AC=13CF求出AE=2CF，然后根据△MAF和△BCF相似，利用相似三角形对应边成比例列式求解即可．【解答】解：如图，延长BF交射线AP于M，∵AD∥BC，∴∠M=∠CBM，∵BF是∠CBP的平分线，∴∠PBM=∠CBM，∴∠M=∠PBM，∴BP=PM，∴AP+BP=AP+PM=AM，∵CF=13AC，则AF=2CF，由AD∥BC得，△MAF∽△BCF，∴AMBC =AFCF=2，∴AM=2BC=2×6=12，即AP+BP=12．【点评】本题考查了相似三角形的判定与性质，角平分线的定义，平行线的性质，延长BF构造出相似三角形，求出AP+BP=AM并得到相似三角形是解题的关键，也是本题的难点．25(2020秋•虹口区校级月考)已知：如图，已知△ABC与△ADE均为等腰三角形，BA=BC，DA= DE．如果点D在BC边上，且∠EDC=∠BAD．点O为AC与DE的交点．(1)求证：△ABC∽△ADE；(2)求证：DA•OC=OD•CE．【分析】(1)根据三角形的外角的性质和角的和差得到∠B=∠ADE，由于BABC=DADE=1，根据得到结论；(2)根据相似三角形的性质得到∠BAC=∠DAE，于是得到∠BAD=∠CAE=∠CDE，证得△COD∽△EOA，根据相似三角形的性质得到OCOE =ODOA，由∠AOD=∠COE，推出△AOD∽△COE，根据相似三角形的性质即可得到结论．【解答】证明：(1)∵∠ADC =∠ABC +∠BAD =∠ADE +∠EDC ，∴∠B =∠ADE ，∵BA BC=DA DE =1，∴△ABC ∽△ADE ；(2)∵△ABC ∽△ADE ，∴∠BAC =∠DAE ，∴∠BAD =∠CAE =∠CDE ，∵∠COD =∠EOA ，∴△COD ∽△EOA ，∴OC OE =OD OA，∵∠AOD =∠COE ，∴△AOD ∽△EOC ，∴DA ：CE =OD ：OC ，即DA •OC =OD •CE ．【点评】本题考查了相似三角形的判定和性质，三角形的外角的性质，熟练掌握相似三角形的判定定理是解题的关键．26(2021秋•金山区校级月考)已知：如图，在梯形ABCD 中，AD ∥BC ，点E 在边AD 上，CE 与BD 相交于点F ，AD =4，AB =5，BC =BD =6，DE =3．(1)求证：△DFE ∽△DAB ；(2)求线段CF 的长．【分析】(1)AD ∥BC ，DE =3，BC =6，DF FB =DE BC=36=12，DF DA =DE DB ．又∠EDF =∠BDA ，即可证明△DFE ∽△DAB ．(2)由△DFE ∽△DAB ，利用对应边成比例，将已知数值代入即可求得答案．【解答】证明：(1)∵AD ∥BC ，DE =3，BC =6，∴DF FB =DE BC =36=12，∴DF BD =12，∵BD =6，∴DF =2．∵DA =4，∴DF DA =24=12，DE DB =36=12．∴DF DA=DE DB ．又∵∠EDF =∠BDA ，∴△DFE ∽△DAB ．(2)∵△DFE ∽△DAB ，∴EF AB =DE DB ．∵AB =5，∴EF 5=36，∴EF =52=2.5．∵DE ∥BC ，∴CFEF =BC DE ．∴CF 2.5=63，∴CF =5．(或利用△CFB ≌△BAD )．【点评】此题考查学生对梯形和相似三角形的判定与性质的理解和掌握，第(2)问也可利用△CFB ≌△BAD 求得线段CF 的长，不管学生用了哪种方法，只要是正确的，就要积极地给予表扬，以此激发学生的学习兴趣．27(2020秋•宝山区月考)如图，正方形DEFG 的边EF 在△ABC 的边BC 上，顶点D 、G 分别在边AB 、AC 上，已知△ABC 的边BC =15，高AH =10，求正方形DEFG 的边长和面积．【分析】高AH 交DG 于M ，如图，设正方形DEFG 的边长为x ，则DE =MH =x ，所以AM =10-x ，再证明△ADG ∽△ABC ，则利用相似比得到x 15=10-x 10，然后根据比例的性质求出x ，再计算x 2的值即可．【解答】解：高AH 交DG 于M ，如图，设正方形DEFG 的边长为x ，则DE =MH =x ，∴AM =AH -MH =10-x ，∵DG ∥BC ，∴△ADG ∽△ABC ，∴DG BC =AM AH，即x 15=10-x 10，∴x =6，∴x 2=36．答：正方形DEFG 的边长和面积分别为6，36．【点评】本题考查了相似三角形的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形；也考查了正方形的性质．28(2021秋•闵行区校级月考)如图，在Rt △ABC 中，∠ACB =90°，CD ⊥AB ，M 是CD 上的点，DH ⊥BM 于H ，DH 的延长线交AC 的延长线于E ．求证：(1)△AED ∽△CBM ；(2)AE •CM =AC •CD ．【分析】(1)由于△ABC 是直角三角形，易得∠A +∠ABC =90°，而CD ⊥AB ，易得∠MCB +∠ABC =90°，利用同角的余角相等可得∠A =∠MCB ，同理可证∠1=∠2，而∠ADE =90°+∠1，∠CMB =90°+∠2，易证∠ADE =∠CMB ，从而易证△AED ∽△CBM ；(2)由(1)知△AED ∽△CBM ，那么AE ：AD =CB ：CM ，于是AE •CM =AD •CB ，再根据△ABC 是直角三角形，CD 是AB 上的高，易知△ACD ∽△CBD ，易得AC •CD =AD •CB ，等量代换可证AE •CM =AC •CD ．【解答】证明：(1)∵△ABC 是直角三角形，∴∠A +∠ABC =90°，∵CD ⊥AB ，∴∠CDB =90°，即∠MCB +∠ABC =90°，∴∠A =∠MCB ，∵CD ⊥AB ，∴∠2+∠DMB =90°，∵DH ⊥BM ，∴∠1+∠DMB =90°，∴∠1=∠2，又∵∠ADE =90°+∠1，∠CMB =90°+∠2，∴∠ADE =∠CMB ，∴△AED ∽△CBM ；(2)∵△AED ∽△CBM ，∴AE BC =AD CM，∴AE •CM =AD •CB ，∵△ABC 是直角三角形，CD 是AB 上的高，∴△ACD ∽△CBD ，∴AC ：AD =CB ：CD ，∴AC •CD =AD •CB ，∴AE •CM =AC •CD ．【点评】本题考查了相似三角形的判定和性质、直角三角形斜边上的高所分成的两个三角形与这个直角三角形相似．解题的关键是证明∠A =∠MCB 以及∠ADE =∠CMB ．29(2022秋•徐汇区校级月考)如图，在直角坐标平面内有点A (6，0)，B (0，8)，C (-4，0)，点M 、N 分别为线段AC 和射线AB 上的动点，点M 以2个单位长度/秒的速度自C 向A 方向做匀速运动，点N 以5个单位长度/秒的速度自A 向B 方向做匀速运动，MN 交OB 于点P ．(1)求证：MN ：NP 为定值；(2)若△BNP 与△MNA 相似，求CM 的长；(3)若△BNP 是等腰三角形，求CM 的长．【分析】(1)过点N 作NH ⊥x 轴于点H ，然后分两种情况进行讨论，综合两种情况，求得MN ：NP 为定值53．(2)当△BNP 与△MNA 相似时，当点M 在CO 上时，只可能是∠MNB =∠MNA =90°，所以△BNP ∽△MNA ∽△BOA ，所以AM AN =AB AO ，所以10-2k 5k =106，k =3031，即CM =6031；当点M 在OA 上时，只可能是∠NBP =∠NMA ，所以∠PBA =∠PMO ，根据题意可以判定不成立，所以CM =6031．(3)由于等腰三角形的特殊性质，应分三种情况进行讨论，即BP =BN ，PB =PN ，NB =NP 三种情况进行讨论．【解答】证明：(1)过点N 作NH ⊥x 轴于点H ，设AN =5k ，得：AH =3k ，CM =2k ，①当点M 在CO 上时，点N 在线段AB 上时：∴OH =6-3k ，OM =4-2k ，∴MH =10-5k ，∵PO ∥NH ，∴MN NP =MH OH=10-5k 6-3k =53，②当点M 在OA 上时，点N 在线段AB 的延长线上时：∴OH =3k -6，OM =2k -4，∴MH =5k -10，∵PO ∥NH ，∴MN NP =MH OH=5k -103k -6=53；解：(2)当△BNP 与△MNA 相似时：①当点M 在CO 上时，只可能是∠MNB =∠MNA =90°，∴△BNP ∽△MNA ∽△BOA ，∴AMAN =AB AO，。

相似三角形专题练习（培优）附答案一、基础知识（不局限于此）(一).比例1.第四比例项、比例中项、比例线段；2.比例性质：（1）基本性质：bc ad d c b a =⇔= ac b c bb a =⇔=2 （2）合比定理：d dc b b ad c b a ±=±⇒= （3）等比定理：)0.(≠+++=++++++⇒==n d b ban d b m c a n m d c b a3.黄金分割：如图，若AB PB PA ⋅=2，则点P 为线段AB 的黄金分割点．4．平行线分线段成比例定理(二)相似1.定义:我们把具有相同形状的图形称为相似形.2.相似多边形的特性:相似多边的对应边成比例,对应角相等.3.相似三角形的判定● （1）平行于三角形一边的直线与其它两边相交，所构成的三角形与原三角形相似。

● （2）如果两个三角形的三组对应边的比相等，那么这两个三角形相似。

● （3）如果两个三角形的两组对应边的比相等，并且相应的夹角相等，那么这两个三角形相似。

● （4）如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似。

4.相似三角形的性质● （1）对应边的比相等，对应角相等. ● （2）相似三角形的周长比等于相似比.● （3）相似三角形的面积比等于相似比的平方.● （4）相似三角形的对应边上的高、中线、角平分线的比等于相似比. 5.三角形中位线定义:连接三角形两边中点的线段 叫做三角形的中位线. 三角形中位线性质: 三角形的中位线平行于第三边，并且等于它的一半。

6.梯形的中位线定义：梯形两腰中点连线叫做梯形的中位线.梯形的中位线性质: 梯形的中位线平行于两底并且等于两底和的一半. 7.相似三角形的应用:１、利用三角形相似，可证明角相等；线段成比例（或等积式）； ２、利用三角形相似，求线段的长等3、利用三角形相似，可以解决一些不能直接测量的物体的长度。

如求河的宽度、求建筑物的高度等。

2020中考数学相似三角形专题训练（含答案）一、选择题：1. 如图，把△ABC沿着BC的方向平移到△DEF的位置，它们重叠部分的面积是△ABC面积的一半，若BC=，则△ABC移动的距离是（ ）A．B．C．D．﹣答案：D．2.如图，在△ABC中，D、E分别为AB、AC边上的点，DE∥BC，点F为BC边上一点，连接AF交DE于点G，则下列结论中一定正确的是（ ）A．=B．=C．=D．=答案：C3. 如图，在▱ABCD中，AC，BD相交于点O，点E是OA的中点，连接BE并延长交AD于点F，已知S△AEF=4，则下列结论：①=；②S△BCE=36；③S△ABE=12；④△AEF～△ACD，其中一定正确的是（ ）A．①②③④ B．①④ C．②③④D．①②③答案D．4.如图，矩形ABCD中，AE⊥BD于点E，CF平分∠BCD，交EA的延长线于点F，且BC=4，CD=2，给出下列结论：①∠BAE=∠CAD；②∠DBC=30°；③AE=；④AF=2，其中正确结论的个数有（ ）A．1个B．2个C．3个D．4个答案C．二、填空题：5.已知AB∥CD，AD与BC相交于点O．若=，AD=10，则AO= ．答案：4．6. 在△ABC在，AB=6，AC=5，点D在边AB上，且AD=2，点E在边AC上，当AE= 时，以A、D、E为顶点的三角形与△ABC相似．答案：或．7.经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形，如果其中一个是等腰三角形，另外一个三角形和原三角形相似，那么把这条线段定义为原三角形的“和谐分割线”．如图，线段CD是△ABC的“和谐分割线”，△ACD为等腰三角形，△CBD和△ABC相似，∠A=46°，则∠ACB的度数为．故答案为113°或92°．8.如图，四边形ABCD中，AD∥BC，CM是∠BCD的平分线，且CM⊥AB，M为垂足，AM= AB．若四边形ABCD的面积为，则四边形AMCD的面积是．答案：1．9. （2017内江）如图，正方形ABCD中，BC=2，点M是边AB的中点，连接DM，DM与AC交于点P，点E在DC上，点F在DP上，且∠DFE=45°．若PF=，则CE= ．答案：．10.如图，在▱ABCD中，∠B=30°，AB=AC，O是两条对角线的交点，过点O作AC的垂线分别交边AD，BC于点E，F，点M是边AB的一个三等分点，则△AOE与△BMF的面积比为．故答案为3：4．三、解答题：11.如图，在△ABC中，AB=AC，点E在边BC上移动（点E不与点B，C重合），满足∠DEF=∠B，且点D、F分别在边AB、AC上．（1）求证：△BDE∽△CEF；（2）当点E移动到BC的中点时，求证：FE平分∠DFC．【解答】解：（1）∵AB=AC，∴∠B=∠C，∵∠BDE=180°﹣∠B﹣∠DEB，∠CEF=180°﹣∠DEF﹣∠DEB，∵∠DEF=∠B，∴∠BDE=∠CEF，∴△BDE∽△CEF；（2）∵△BDE∽△CEF，∴，∵点E是BC的中点，∴BE=CE，∴，∵∠DEF=∠B=∠C，∴△DEF∽△CEF，∴∠DFE=∠CFE，∴FE平分∠DFC．12.如图示，正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上，EF与BC相交于点G，连接CF．①求证：△DAE≌△DCF；②求证：△ABG∽△CFG．【解答】证明：①∵正方形ABCD，等腰直角三角形EDF，∴∠ADC=∠EDF=90°，AD=CD，DE=DF，∴∠ADE+∠ADF=∠ADF+∠CDF，∴∠ADE=∠CDF，在△ADE和△CDF中，，∴△ADE≌△CDF；②延长BA到M，交ED于点M，∵△ADE≌△CDF，∴∠EAD=∠FCD，即∠EAM+∠MAD=∠BCD+∠BCF，∵∠MAD=∠BCD=90°，∴∠EAM=∠BCF，∵∠EAM=∠BAG，∴∠BAG=∠BCF，∵∠AGB=∠CGF，∴△ABG∽△CFG．13. 如图，在▱ABCD中过点A作AE⊥DC，垂足为E，连接BE，F为BE上一点，且∠AFE=∠D．（1）求证：△ABF∽△BEC；（2）若AD=5，AB=8，sinD=，求AF的长．【解答】（1）证明：∵四边形ABCD是平行四边形，∴AB∥CD，AD∥BC，AD=BC，∴∠D+∠C=180°，∠ABF=∠BEC，∵∠AFB+∠AFE=180°，∴∠C=∠AFB，∴△ABF∽△BEC；（2）解：∵AE⊥DC，AB∥DC，∴∠AED=∠BAE=90°，在Rt△ABE中，根据勾股定理得：BE===4，在Rt△ADE中，AE=AD•sinD=5×=4，∵BC=AD=5，由（1）得：△ABF∽△BEC，∴，即，解得：AF=2．∵△ADF∽△DEC，14. 在Rt△ABC中，∠ACB=90°，点D与点B在AC同侧，∠DAC＞∠BAC，且DA=DC，过点B作BE∥DA交DC于点E，M为AB的中点，连接MD，ME．（1）如图1，当∠ADC=90°时，线段MD与ME的数量关系是　MD=ME　；（2）如图2，当∠ADC=60°时，试探究线段MD与ME的数量关系，并证明你的结论；（3）如图3，当∠ADC=α时，求的值．【解答】解：（1）如图1，延长EM交AD于F，∵BE∥DA，∴∠FAM=∠EBM，∵AM=BM，∠AMF=∠BME，∴△AMF≌△BME，∴AF=BE，MF=ME，∵DA=DC，∠ADC=90°，∴∠BED=∠ADC=90°，∠ACD=45°，∵∠ACB=90°，∴∠ECB=45°，∴∠EBC=∠BED﹣∠ECB=45°=∠ECB，∴CE=BE，∴AF=CE，∵DA=DC，∴DF=DE，∴DM⊥EF，DM平分∠ADC，∴∠MDE=45°，∴MD=ME，故答案为MD=ME；（2）MD=ME，理由：如图2，延长EM交AD于F，∵BE∥DA，∴∠FAM=∠EBM，∵AM=BM，∠AMF=∠BME，∴△AMF≌△BME，∴AF=BE，MF=ME，∵DA=DC，∠ADC=60°，∴∠BED=∠ADC=60°，∠ACD=60°，∵∠ACB=90°，∴∠ECB=30°，∴∠EBC=∠BED﹣∠ECB=30°=∠ECB，∴CE=BE，∴AF=CE，∵DA=DC，∴DF=DE，∴DM⊥EF，DM平分∠ADC，∴∠MDE=30°，在Rt△MDE中，tan∠MDE=，∴MD=ME．（3）如图3，延长EM交AD于F，∵BE∥DA，∴∠FAM=∠EBM，∵AM=BM，∠AMF=∠BME，∴△AMF≌△BME，∴AF=BE，MF=ME，延长BE交AC于点N，∴∠BNC=∠DAC，∵DA=DC，∴∠DCA=∠DAC，∴∠BNC=∠DCA，∵∠ACB=90°，∴∠ECB=∠EBC，∴CE=BE，∴AF=CE，∴DF=DE，∴DM⊥EF，DM平分∠ADC，∵∠ADC=α，∴∠MDE=，在Rt△MDE中，=tan∠MDE=tan．15. （1）阅读理解：如图①，在四边形ABCD中，AB∥DC，E是BC的中点，若AE 是∠BAD的平分线，试判断AB，AD，DC之间的等量关系．解决此问题可以用如下方法：延长AE交DC的延长线于点F，易证△AEB≌△FEC，得到AB=FC，从而把AB，AD，DC转化在一个三角形中即可判断．AB、AD、DC之间的等量关系为　AD=AB+DC　；（2）问题探究：如图②，在四边形ABCD中，AB∥DC，AF与DC的延长线交于点F，E 是BC的中点，若AE是∠BAF的平分线，试探究AB，AF，CF之间的等量关系，并证明你的结论．（3）问题解决：如图③，AB∥CF，AE与BC交于点E，BE：EC=2：3，点D在线段AE 上，且∠EDF=∠BAE，试判断AB、DF、CF之间的数量关系，并证明你的结论．【解答】解：（1）如图①，延长AE交DC的延长线于点F，∵AB∥DC，∴∠BAF=∠F，∵E是BC的中点，∴CE=BE，在△AEB和△FEC中，，∴△AEB≌△FEC，∴AB=FC，∵AE是∠BAD的平分线，∴∠DAF=∠BAF，∴∠DAF=∠F，∴DF=AD，∴AD=DC+CF=DC+AB，故答案为：AD=AB+DC；（2）AB=AF+CF，证明：如图②，延长AE交DF的延长线于点G，∵E是BC的中点，∴CE=BE，∵AB∥DC，∴∠BAE=∠G，在△AEB和△GEC中，，∴△AEB≌△GEC，∴AB=GC，∵AE是∠BAF的平分线，∴∠BAG=∠FAG，∵AB∥CD，∴∠BAG=∠G，∴∠FAG=∠G，∴FA=FG，∴AB=CG=AF+CF；（3）AB=（CF+DF），证明：如图③，延长AE交CF的延长线于点G，∵AB∥CF，∴△AEB∽△GEC，∴==，即AB=CG，∵AB∥CF，∴∠A=∠G，∵∠EDF=∠BAE，∴∠FDG=∠G，∴FD=FG，∴AB=CG=（CF+DF）．。

27.2相似三角形综合训练练习人教版2024—2025学年九年级下册一、填空1.已知==，且a +b ﹣2c=6，则a 的值为2.如图，E 为▱ABCD 的边AB 延长线上的一点，且BE ：AB=2：3，连接DE 交BC于点F ，则CF ：AD= ．3.如图，已知AB ∥CD ，AD 与BC 相交于点O ．若=，AD=10，则AO= ．4.如图，△ABC 中，点D 、E 分别在边AB 、BC 上，DE ∥AC ．若BD=4，DA=2，BE=3，则EC= ．5.如图，DE ∥AB ，AC=3AD ，S △ABC =5，则△CED 的面积是 ．6.如图，∠B=∠ACD=90°，BC ∥AD ，若AC=6，AD=10，则AB= ．7.两个相似三角形的最短边分别是5cm 和3cm ，它们的周长之差是12cm ，那么小三角形的周长为 ．8.如图，在△ABC 中，点D 是边AB 上的一点，∠ADC=∠ACB ，AD=2，BD=6，则边AC 的长为9.如图，在平行四边形ABCD 中，点E 在边DC 上，DE ：EC=3：1，连接AE 交BD 于点F ，则△DEF 的面积与△BAF 的面积之比为10.如图，AB ∥GH ∥CD ，点H 在BC 上，AC 与BD 交于点G ，AB=2，CD=3，则GH 的长为 ．11.如图，梯形ABCD 中，AB ∥CD ，∠B=∠C=90°，点F 在BC 边上，AB=8，CD=2，BC=10，若△ABF 与△FCD 相似，则CF 的长为 ．第2题第5题 第6题第8题第10题 第9题 第11题12.如图，△ABC 是等边三角形，被一平行于BC 的矩形所截，AB 被截成三等分，则图中阴影部分的面积是△ABC 的面积的 ．13.如图所示，正方形ABCD 边长是2，BE=CE ，MN=1，线段MN 的端点M 、N 分别在CD 、AD 上滑动，当DM= 时，△ABE 与以D 、M 、N 为顶点的三角形相似．14.如图，在边长为10cm 的正方形ABCD 中，P 为AB 边上任意一点（P 不与A 、B 两点重合），连结DP ，过点P 作PE ⊥DP ，垂足为P ，交BC 于点E ，则BE 的最大长度为 cm ．15.一块直角三角板ABC 按如图放置，顶点A 的坐标为（0，1），直角顶点C 的坐标为（﹣3，0），∠B=30°，则点B 的坐标为 ．二、解答题1.如图，平行四边形ABCD ，AE ⊥BC 交点E ，连接DE ，F 为DE 上一点，且∠AFE=∠B=60°．（1）求证：△ADF ∽△DEC ；（2）若AE=3，AD=4，求EF 的长．第14题第13题 第12题2.如图，四边形ABCD是菱形，对角线AC，BD相交于点O，过点D作DH⊥AB于H，交AO于G，连接OH．（1）求证：AG•GO=HG•GD；（2）若AC=8，BD=6，求DG的长．3.如图，在平面直角坐标系中，二次函数y=（x﹣a）（x﹣3）（0＜a＜3）的图象与x轴交于点A、B（点A在点B的左侧），与y轴交于点D，过其顶点C作直线CP⊥x轴，垂足为点P，连接AD、BC．（1）求点A、B、D的坐标；（2）若△AOD与△BPC相似，求a的值；（3）点D、O、C、B能否在同一个圆上？若能，求出a的值；若不能，请说明理由．4.在平面直角坐标系中，二次函数y=ax2+x+c的图象经过点C（0，2）和点D（4，﹣2）．点E是直线y=﹣x+2与二次函数图象在第一象限内的交点．（1）求二次函数的解析式及点E的坐标．（2）如图①，若点M是二次函数图象上的点，且在直线CE的上方，连接MC，OE，ME．求四边形COEM面积的最大值及此时点M的坐标．（3）如图②，经过A、B、C三点的圆交y轴于点F，求点F的坐标．5．如图，平面直角坐标系中，矩形OABC的顶点A、C分别在x轴和y轴的正半轴上，反比例函数y=在第一象限的图象分别交矩形OABC的边AB、BC边点于E、F，已知BE=2AE，四边形的OEBF的面积等于12．（1）求k的值；（2）若射线OE对应的函数关系式是y=，求线段EF的长；（3）在（2）的条件下，连结AC，试证明：EF∥AC．6.如图，正方形ABCD的边长为10，点E、F分别在边BC、CD上，且∠EAF=45°，AH⊥EF于点H，AH=10，连接BD，分别交AE、AH、AF于点P、G、Q．（1）求△CEF的周长；（2）若E是BC的中点，求证：CF=2DF；（3）连接QE，求证：AQ=EQ．。

专题02 三角形相似综合训练1．如图，在矩形ABCD 中，将ADC △绕点D 逆时针旋转90︒得到FDE B F E ，、、三点恰好在同一直线上，AC 与BE 相交于点G ，连接DG ．以下结论正确的是( )①AC BE ⊥；BCG GAD ~②；③点F 是线段CD 的黄金分割点；④CG EG = A ．①②③ B ．①③C ．①②③D ．①③④【答案】D 【详解】证明：FDE ADC ≌，∴AD DF DC DE ==，又∴四边形ABCD 是矩形，∴90ADC ∠=︒， ∴90DAC DCA ∠+∠=即DAG DEF ∠+∠=即BGC 是直角三角形，而AGD 不是直角三角形，∴②错误；Rt FCB 和Rt 中， BFC EFC ∠=∠Rt FCB Rt FDE ∽， FC BCDF DE=， BC AD DF DE DC ===，FC DFDF DC=， F 是线段CD 的黄金分割点，和DEG '中，∴SAS DCG DEG '≌（DG DG CDG ='∠=，90CDG GDA ∠+∠=︒90EDG GDA ∠'+∠=90GDG ∠'=︒，∴GDG '是等腰直角三角形，2GG DG '=EG CG '=EG EG ='故选：D ．【我思故我在】2．如图，在ABC 中，D 、E 分别在AB 边和AC 边上，//DE BC ，M 为BC 边上一点(不与B 、C 重合)，连结AM 交DE 于点N ，则( )A ．ADANANAEB ．BD MNMN CEC ．DN NEBM MCD ．DN NEMC BM,AN ANNE DN NEAM AMMCBMMC，故选相似三角形的判定和性质，解题的关键是熟练掌握3．如图，在ABC ∆中，2AC =，4BC =，D 为BC 边上的一点，且CAD B ∠=∠．若ADC ∆的面积为a ，则ABD ∆的面积为( )A ．2aB ．52aC ．3aD ．72aACD BCA ∆，再由相似三角形的性质得到答案ACD BCA ∆，2AC BC ⎛⎫= ⎪⎝⎭，即BCA ∆的面积为的面积为：．4．如图，在矩形ABCD 中，E，F分别为边BC 、CD 中点，线段AE ，AF 与对角线BD 分别交于点G ，H ．设矩形ABCD 的面积为S ，则以下4个结论中：①AG ：GE =2：1 ②BG ：GH ：HD =1：1：1；③12325S S S S ++=；④ 246124S S S =：：：：正确的结论有( )A ．1个B ．2个C ．3个D ．4个【答案】C∴,BGE DGA ∽ 2,AG AD BGGE BE DG===②∴AG AD BGGE BE DG==13BG BD =，1所以本题的3个结论符合题意； 故选：C ．【我思故我在】本题考查了矩形的性质，三角形相似的性质和判定，三角形面积等知识，解题的关键是理解题意，等底同高三角形面积相等，相似三角形面积的比等于相似比的平方． 5．如图，在正方形ABCD 中，BPC △是等边三角形，BP 、CP 的延长线分别交AD 于E 、F ，连接BD 、DP ，BD 与CF 相交于点H ．给出以下结论：①3BE AE =；②DFP BPH ；③2DP PH PC =⋅；④若2AB =，则1BPD S △．其中正确结论的是( )A ．①②③④B ．②③④C ．①②④D ．①③④从而证明DFP BPH ，正确；利用DPH CPD ~，得DP PC ，将ΔBPD S 转化为S 四边形解：BPC ∆是等边三角形，BC ，60PBC PCB BPC ∠=∠=∠=ABCD 中，AB BC CD =，A ∠30ABE DCF ∴∠==︒2BE AE ∴=故①错误PC CD =PDC ∴∠=FDP ∴∠=DBA =∠DFP ∠=DFP BPH ∴~，故②正确；30PDH PCD ∠=∠=︒DPH CPD ∴~，∴DP PHPC DP=， 2DP PH PC ∴=⋅，故③正确；如图，过点P 作PM正方形的边长6．如图， 在平行四边形ABCD 中， 点,M N 分别是AD BC 、上的点， 且22AM DM BN CN ==，， 点O 是CM ， DN 的交点， 直线AB 分别与CM DN ，的延长线交于点,P Q ． 若平行四边形ABCD 的面积为144 ， 则POQ △的面积为( )A ．72B ．216C ．268D ．300∴AMP DMC ∽， AP AMDC DM=， 2AM DM = 2AP AMDC DM==， 2AP CD =， ∴COD POQ ∽， 1215h CD h PQ ==， ∴∴POQ 的高为56h ，144ABCDS CD h =⋅=151POQS=故选：D 【我思故我在】的性质及平行四边形的性质是解题的关键．7．如图，在正方形ABCD 中，点G 是BC 上一点，且12GC BG =，连接DG 交对角线AC 于F 点，过D 点作DE DG ⊥交CA 的延长线于点E ，若5AE =，则DF 的长为( )A ．BC ．92D ，证明DEH DGC ∽，推出，求出5EH HA ==延长线于H ，DE DG ⊥EDG ∠∴21∴∠+∠1∠∠∴=DEH DGC ∴∽，∴EH DHGC DC =， 12GC BG =， ∴设GC x =，则BG =∴3EH DHGC x=， AC 是正方形DAC ∴∠EAH ∠=HEA ∴∠=EH HA ∴=2EH HA ∴+EH HA ∴=在正方形8．已知，如图，平行四边形ABCD 中，:1:3=CE BE ，且1EFC S =△，那么ABCS=_____．ACD ABC SS =，证明1:4AD =，则CE AD =． 9．P 是ABC 边上的任一点(P 不与A 、B 、C 重合)，过点P 的一条直线截ABC ，如果截得的三角形与ABC 相似，我们称这条直线为过点P 的∴ABC 的“相似线”．Rt ABC △中，90C ∠=︒，30B ∠=︒，当点P 是边BC 上一个三等分点时(PB PC >)，过点P 的ABC 的“相似线”最多有___________条．【答案】4【分析】根据相似线的定义，可知截得的三角形与ABC 有一个公共角，分①公共角为A ∠时；②公共角为B ∠时；③公共角为C ∠时；三种情况进行讨论，即可得出答案．【详解】解：①当公共角为A ∠时，不存在；②公共角为B ∠时，过点P 作PD BC ⊥，交AB 于点D ，如图所示：∴90DPB C ∠=∠=︒，B B ∠=∠，∴BPD BCA ∽；过点P 作PD AB ⊥于点D ，如图所示：∴90PDB C ∠=∠=︒，B B ∠=∠，∴BPD BAC ∽△△；③公共角为C ∠时，连接AP ，如图所示：∴30B ∠=︒，∴2AB AC =，设AC a =，则2AB a =，∴ACP BCA∽；过点P作PD AB∥，交∴CDP CAB∽；综上分析可知，过点的ABC的“相似线故答案为：4.【我思故我在】本题主要考查了相似三角形的判定，平行线的性质，勾股定理，解题的关键是熟练掌握三角形相似的判定方法．10．如图，在ABC中，6BC=，AE AFEB FC=，动点P在射线EF上，BP交CE于点D，CBP∠的平分线交CE于点Q，当14CQ CE=时，EP BP+的值为______．【答案】18【分析】如图，延长EF交BQ的延长线于G．首先证明PB PG=，EP PB EG+=，由EG BC∥，11．如图，在矩形ABCD中，点E，F分别是,==∠=︒∠=︒，则BC的长度是___________．3,6,30,45BE CD FED FDE【答案】3##3+【分析】作FN DE ⊥于点N ，延长DE 交CB 的延长线于点M ，先证FND ∆是等腰直角三角形，设FN x =，利用勾股定理、含30度角的直角三角形的性质求出DN ，EF ，NE 的长度，FDE ∠=DFN ∴∠FND ∴∆是等腰直角三角形．由题意得：设FN x =FED ∠=2EF FN ∴=NE ∴=DE DN ∴=3BE =，AE BE ∴=又EAD ∠=EAD ∴∆∆≌AD BM ∴=EBM ∠=EBM ∴∆∽BM BE MN NF ∴=解得：BM 12．如图，在ABC 中，146AB AC ==，，在AC 上取一点D ，使2AD =，如果在AB 上取点E ，使ADE 和ABC 相似，则AE =___________．①ABC AED ；②ABC ADE ；可根据各四条线段的比例关系式求出AE 的长．此时ADE ACB ，::AC AE AD =，146AC AD ==，，此时ADE ABC ，::AC AD AE =，146AC AD ==，，67=， 故答案为：143或67．13．如图是某风车示意图，其相同的四个叶片均匀分布，水平地面上的点M 在旋转中心O 的正下方，某一时刻，太阳光线恰好垂直照射叶片OA 、OB ，此时各叶片影子在点M 右侧成线段CD ．测得8.5m MC =，13m CD =，垂直于地面的木棒EF 与影子FG 的比为23：．则点O 、M 之间的距离等于___________m ；【答案】10【分析】连接OM 交AC 于点H ，过点C 作CN BD ⊥，通过证明HMC EFG HAO ∽∽△△△，通过相似三角形对应边成比例即可解答．【详解】解：连接OM 交AC 于点H ，过点C 作CN BD ⊥，14．如图，在平行四边形ABCD 中，点E 在边BC 上，连结AE 并延长，交对角线BD 于点F 、DC 的延长线于点G ．如果23CE BE =，求FE EG的值．15．矩形ABCD 中，AC BD ，为对角线，6cm 8cm AB BC ==，，E 为DC 中点，动点P 从点A 出发沿AB 方向，向点B 运动，动点Q 同时以相同速度，从点B 出发沿BC 方向向点C 运动，P 、Q 的速度都是1cm/秒，其中一个动点到达终点时，另一个动点也随之停止运动，设运动时间为x 秒．()06t <<(1)PQ AC ∥时，求运动时间t ；(2)PQ BD ⊥时，求运动时间t ；(3)当t 为何值时，以点P ，B ，Q 为顶点的三角形与QCE 相似？(4)连接PE PQE ，△的面积能否达到矩形ABCD 面积的三分之一，若能求出t 的值；若不能，说明理由．7BP BQBP BQ为顶点的三角形与QCE相似216．解答题=；(1)如图1，ABC和ADE都是等边三角形，连接BD、CE，求证，BD CE[类比探究](2)如图2，ABC 和ADE 都是等腰直角三角形，90ABC ADE ∠=∠=︒，连接BD CE ，．求BD CE的值．[拓展提升](3)如图3，ABC 和ADE 都是直角三角形，90ABC ADE ∠=∠=︒，2AC AE AB AD==．连接BD CE 、，延长CE 交BD 于点F ，连接AF ．若AFC ∠恰好等于90︒，请直接写出此时AF BF CF ，，之间的数量关系．证明BAD CAE ∽，从而得出结果；B 作BH CF ⊥，垂足为点AOF BOH ∆∽，根据对应边成比例，【详解】(1)解：∴ABC 和ADE 都是等边三角形，AC ，AD AE =，∠∠DAE BAC =BAC BAE ∠-∠，即：在BAD 和CAE 中，AB AC DAB EAC AD AE =∠=∠=，(SAS BAD CAE ≌△△BD CE =．∴ABC 和ADE 都是等腰直角三角形，45BAC =∠=︒，ADE ∠ADE △∽，AE AC ，则AD AB AE AC=，BAE BAC -∠=∠-∠在BAD 和CAE 中，DAB EAC =∠，AD AE ∴BAD CAE ∽，BD AB CE AC =， 令AB x =，根据勾股定理可得：2BD AB x CE AC x===(3)∴BAD CAE ∽，ACE ABD ∠=∠，在FOB ∆和AOC ∆中，ACE ABD ∠=∠，∠60OFB OAC ∠=∠=设FH x =，OH y =，则17．在△ABC 中，90ACB ∠=，BE 是AC 边上的中线，点D 在射线BC 上．(1)如图1，点D 在BC 边上，:1:2CD BD =，AD 与BE 相交于点P ，过点A 作AF BC ，交BE 的延长线于点F ，易得AP PD的值为 ； (2)如图2，在△ABC 中，90ACB ∠=，点D 在BC 的延长线上，AD 与AC 边上的中线BE 的延长线交于点P ，:1:2DC BC =，求AP PD的值； (3)在(2)的条件下，若CD=2，AC=6，则BP= ．18．在∴ABC 中，CA CB =，ACB α∠=，点P 在平面内不与点A ，C 重合，连接AP ，将线段AP 绕点P 逆时针旋转α得到线段DP ，连接,,AD BD CP ．(1)如图①，当60α=︒，BD CP的值是 ，直线BD 与直线CP 相交所成的较小角的度数是 ． (2)如图②，当90α=︒时，请写出BD CP的值及直线BD 与直线CP 相交所成的较小角的度数，并说明理由． (3)当90α=︒时，若点E ，F 分别是,CA CB 中点，点P 在直线EF 上，请直接写出当C ，P ，D 在同一直线上时，求AD CP 的值． ，ABC 是等腰直角三角形，根据等腰直角三角形的性质证明，利用相似的性质即可得解；上，和P 在线段解：如图，延长CP 交60︒，∴ABC 是等边三角形，由题意可知∴PAD 是等边三角形，PAD ∠=∠CAP ∠+∠在CAP 和BAD 中，CA BA CAP BAD AP AD =⎧⎪∠=∠⎨⎪=⎩，CAP BAD △≌△ (SAS),PC BD ACP =∠=∠在AOC 和△1BD PC=，直线BD ∴ABC 是等腰直角三角形，CAB ∠=∠∴ AB AC =AB AD AC AP∴=CAB ∠+∠AD是ABC的中位线，2219．如图，点E是矩形ABCD的边AB的中点，F是BC边上一动点(点F与点B，点C不重合)，线段DE和:AF相交于点P，连接PC．(1)若在线段DP 上取一点Q ，使得2DP EQ =，连接AQ ，猜想PC 与AQ 的关系并证明；(2)若AF DE ⊥时，8,10AB AD ==，求BF 的长；(3)当点F 为BC 的中点时，求AP PF 的值． AEQCDP ∆，即可得出结论；，再判断出DAE ABF ，即可得出结论；，先判断出(AAS)ADE BGE ∆≅∆，再判断出2,2AD BF BG BF ==，进而判断出，即可得出结论．∴90BAF AED ．90BAF AFB ∠+∠=︒，AED AFB ∠=∠，90DAE ABF ∠=∠=︒，∴DAEABF ， AD AE AB BF =，即1083.2BF =；(3)解：如图，延长AD GC ，APD FPG ∆，23AD GF ==．【我思故我在】此题查了矩形的性质，构造出相似三角形是解本题的关键．。

6.7用相似三角形解决问题(2)-苏科版九年级数学下册培优训练一、选择题1、下列属于中心投影的有（）①台灯下笔筒的影子；②房后的荫凉；③美术课上，灯光下临摹用的静物的影子；④房间里花瓶在灯光下的影子；⑤在空中低飞的老鹰在地上的影子．A．5个B．4个C．3个D．2个2、如图，三角板在灯光照射下形成投影，三角板与其投影的相似比为2：5，且三角板的一边长为8cm．则投影三角板的对应边长为（）A．20cm B．10cm C．8cm D．3.2cm3、圆桌面（桌面中间有一个直径为0.4 m的圆洞）正上方的灯泡（看作一个点）发出的光线照射平行于地面的桌面后，在地面上形成如图的圆环形阴影．已知桌面直径为1.2 m，桌面离地面1 m，若灯泡离地面3 m，则地面圆环形阴影的面积是（）A．0.324π m2B．0.288π m2 C．1.08π m2D．0.72π m24AC走向路灯BD，当他走到点P时，发现身后他影子的顶部刚好接触到路灯AC的底部，当他向前再步行20 m到达点Q时，发现身前他影子的顶部刚好接触到路灯BD的底部，已知丁轩同学的身高是1.5 m，两个路灯的高度都是9m，则两路灯之间的距离是( )A．24 m B．25 m C．28m D．30m5、如图，杆AO，BO′在地面上的投影分别是A′O，B′O′，则下列判断正确的是（）A．B．C．D．以上三种都有可能6、如图所示，平地上一棵树高为6米，两次观察地面上的影子，第一次是当阳光与地面成60°时，第二次是阳光与地面成30°时，第二次观察到的影子比第一次长（）A. 6-3B. 4C. 6D. 3-2二、填空题7、圆桌面(桌面中间有一个直径为1 m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后，在地面上形成如图所示的圆环形阴影．已知桌面直径为2 m，桌面离地面1 m，若灯泡离地面2 m，则地面圆环形阴影的面积是_________．8、下列现象属于中心投影的是___________（只填序号）．9、如图是小孔成像原理的示意图，根据图中标注的尺寸，如果物体AB的高度为36 cm，那么它在暗盒中所成的像CD的高度应为cm.10、如图，三角尺在灯泡O的照射下在墙上形成影子．现测得OA=20 cm，OA'=50 cm，这个三角尺的周长与它在墙上形成的影子的周长之比是________．11、如图，甲、乙两盏路灯底部间的距离是30米，一天晚上，当小华走到距路灯乙底部5米处时，发现自己的身影顶部正好接触路灯乙的底部．已知小华的身高为1.5米，那么路灯甲的高为______米．12、如图，我方侦察员在距敌方200 m处发现敌人的一座建筑物，但不知其高度又不能靠近建筑物进行测量，机灵的侦察员食指竖直举在右眼前，闭上左眼，并将食指前后移动，使食指恰好将该建筑物遮住．若此时眼睛到食指的距离约为40 cm，食指的长约为8 cm，敌方建筑物的高度为_________13、如图，火焰的光线穿过小孔O，在竖直的屏幕上形成倒立的实像，像的长度BD＝2cm，OA＝60cm，OB＝15cm，则火焰AC的长度为．14、墙壁CD上D处有一盏灯（如图），小明站在A处测得他的影长与身长相等，都为1.6m，他向墙壁走1m到B处时发现影子刚好落在A点，则灯泡与地面的距离CD= ．三、解答题15、如图，花丛中有一路灯杆AB，在灯光下，大华在D点处的影长DE＝3 m，沿BD方向行走到达G点，DG＝5 m，这时大华的影长GH＝5 m．如果大华的身高为2 m，求路灯杆AB的高度．16、如图，王华同学在晚上由路灯AC走向路灯BD，当他走到点P时，发现身后他影子的顶部刚好接触到路灯AC的底部，当他向前再步行12m到达Q点时，发现身前他影子的顶部刚好接触到路灯BD的底部．已知王华同学的身高是1.6m，两个路灯的高度都是9.6m．（1）求两个路灯之间的距离；（2）当王华同学走到路灯BD处时，他在路灯AC下的影子长是多少？17、高高的路灯挂在路边的上方，高傲而明亮，小明拿着一根2米长的竹竿，想量一量路灯的高度，直接量是不可能的．于是，他走到路灯旁的一个地方，竖起竹竿（即AE），这时，他量了一下竹竿的影长（AC）正好是1米，他沿着影子的方向走，向远处走出两根竹竿的长度（即AB=4米），他又竖起竹竿，这时竹竿的影长正好是一根竹竿的长度（即BD=2米）．此时，小明抬头瞧瞧路灯，若有所思地说：“噢，我知道路灯有多高了！”同学们，请你和小明一起解答这个问题：（1）在图中作出路灯O的位置，并作OP⊥l于P．（2）求出路灯O的高度，并说明理由18、如图，在路灯下，小明的身高如图中线段AB所示，他在地面上的影子如图中线段AC所示，小亮的身高如图中线段FG所示，路灯灯泡在线段DE上．(1)请你确定灯泡所在的位置，并画出小亮在灯光下形成的影子；(2)如果小明的身高AB＝1.6 m，他的影子长AC＝1.4 m，且他到路灯的距离AD＝2.1 m，求灯泡的高．19、如图，电灯P在横杆AB的正上方，AB在灯光下的影子为CD，AB∥CD，AB＝1.5 m，CD＝4.5 m，点P到CD的距离为2.7 m，求AB与CD间的距离.6.7用相似三角形解决问题(2)-苏科版九年级数学下册培优训练（答案）一、选择题1、下列属于中心投影的有（ C ）①台灯下笔筒的影子；②房后的荫凉；③美术课上，灯光下临摹用的静物的影子；④房间里花瓶在灯光下的影子；⑤在空中低飞的老鹰在地上的影子．A．5个B．4个C．3个D．2个2、如图，三角板在灯光照射下形成投影，三角板与其投影的相似比为2：5，且三角板的一边长为8cm．则投影三角板的对应边长为（）A．20cm B．10cm C．8cm D．3.2cm【解析】设投影三角尺的对应边长为xcm，∵三角尺与投影三角尺相似，∴8：x＝2：5，解得x＝20．故选：A．3、圆桌面（桌面中间有一个直径为0.4 m的圆洞）正上方的灯泡（看作一个点）发出的光线照射平行于地面的桌面后，在地面上形成如图的圆环形阴影．已知桌面直径为1.2 m，桌面离地面1 m，若灯泡离地面3 m，则地面圆环形阴影的面积是（D）A．0.324π m2B．0.288π m2 C．1.08π m2D．0.72π m24AC走向路灯BD，当他走到点P时，发现身后他影子的顶部刚好接触到路灯AC的底部，当他向前再步行20 m到达点Q时，发现身前他影子的顶部刚好接触到路灯BD的底部，已知丁轩同学的身高是1.5 m，两个路灯的高度都是9m，则两路灯之间的距离是( D )A．24 m B．25 m C．28m D．30m5、如图，杆AO，BO′在地面上的投影分别是A′O，B′O′，则下列判断正确的是（B）A．B．C．D．以上三种都有可能6、如图所示，平地上一棵树高为6米，两次观察地面上的影子，第一次是当阳光与地面成60°时，第二次是阳光与地面成30°时，第二次观察到的影子比第一次长（B）A. 6-3B. 4C. 6D. 3-2二、填空题7、圆桌面(桌面中间有一个直径为1 m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后，在地面上形成如图所示的圆环形阴影．已知桌面直径为2 m，桌面离地面1 m，若灯泡离地面2 m，则地面圆环形阴影的面积是3π_m2 ．8、下列现象属于中心投影的是____③④_______（只填序号）．9、如图是小孔成像原理的示意图，根据图中标注的尺寸，如果物体AB的高度为36 cm，那么它在暗盒中所成的像CD的高度应为16 cm.10、如图，三角尺在灯泡O的照射下在墙上形成影子．现测得OA=20 cm，OA'=50 cm，这个三角尺的周长与它在墙上形成的影子的周长之比是____2:5____．11、如图，甲、乙两盏路灯底部间的距离是30米，一天晚上，当小华走到距路灯乙底部5米处时，发现自己的身影顶部正好接触路灯乙的底部．已知小华的身高为1.5米，那么路灯甲的高为___9 ____米．12、如图，我方侦察员在距敌方200 m处发现敌人的一座建筑物，但不知其高度又不能靠近建筑物进行测量，机灵的侦察员食指竖直举在右眼前，闭上左眼，并将食指前后移动，使食指恰好将该建筑物遮住．若此时眼睛到食指的距离约为40 cm，食指的长约为8 cm，敌方建筑物的高度为___40m ______13、如图，火焰的光线穿过小孔O，在竖直的屏幕上形成倒立的实像，像的长度BD＝2cm，OA＝60cm，OB＝15cm，则火焰AC的长度为．【解析】连接AC、BD，∵CA⊥AB，DB⊥AB，∴∠CAO＝∠DBO＝90°，∵∠COA＝∠DOB，∴△AOC∽△BOD，∴，∵BD＝2cm，OA＝60cm，OB＝15cm，∴，解得：AC＝8cm，答：火焰AC的长度为8cm．故答案为8cm．14、墙壁CD上D处有一盏灯（如图），小明站在A处测得他的影长与身长相等，都为1.6m，他向墙壁走1m到B处时发现影子刚好落在A点，则灯泡与地面的距离CD= ．【解答】解：如图：X根据题意得：BG=AF=AE=1.6m，AB=1m∵BG ∥AF ∥CD, ∴△EAF ∽△ECD ，△ABG ∽△ACD, ∴AE ：EC=AF ：CD ，AB ：AC=BG ：CD设BC=xm ，CD=ym ，则CE=（x+2.6）m ，AC=（x+1）m ，则, 即=， 解得：x=， 把x=代入=，解得：y=，∴CD=m ． 故答案为：m ．三、解答题15、如图，花丛中有一路灯杆AB ，在灯光下，大华在D 点处的影长DE ＝3 m ，沿BD 方向行走到达G 点，DG ＝5 m ，这时大华的影长GH ＝5 m ．如果大华的身高为2 m ，求路灯杆AB 的高度．解：∵CD ∥AB ，∴△EAB ∽△ECD.∴CD AB ＝DE BE ，即2AB ＝33＋BD①. ∵FG ∥AB ，∴△HFG ∽△HAB.∴FG AB ＝HG HB ，即2AB ＝5BD ＋5＋5②. 由①②得33＋BD ＝5BD ＋5＋5，解得BD ＝7.5.∴将BD ＝7.5代入①中，解得AB ＝7. 答：路灯杆AB 的高度为7 m.16、如图，王华同学在晚上由路灯AC 走向路灯BD ，当他走到点P 时，发现身后他影子的顶部刚好接触到路灯AC 的底部，当他向前再步行12m 到达Q 点时，发现身前他影子的顶部刚好接触到路灯BD 的底部．已知王华同学的身高是1.6m ，两个路灯的高度都是9.6m ．（1）求两个路灯之间的距离；（2）当王华同学走到路灯BD 处时，他在路灯AC 下的影子长是多少？【解答】解：（1）由对称性可知AP=BQ ，设AP=BQ=xm∵MP ∥BD ∴△APM ∽△ABD,∴,∴,∴x=3经检验x=3是原方程的根，并且符合题意．∴AB=2x+12=2×3+12=18（m ）, 答：两个路灯之间的距离为18米．[来源:Z&xx&]（2）设王华走到路灯BD 处头的顶部为E ，连接CE 并延长交AB 的延长线于点F ，则BF 即为此时他在路灯AC 的影子长，设BF=ym∵BE∥AC, ∴△EBF∽△CAF, ∴，即解得y=3.6，,经检验y=3.6是分式方程的解．答：当王华同学走到路灯BD处时，他在路灯AC下的影子长是3.6米．17、高高的路灯挂在路边的上方，高傲而明亮，小明拿着一根2米长的竹竿，想量一量路灯的高度，直接量是不可能的．于是，他走到路灯旁的一个地方，竖起竹竿（即AE），这时，他量了一下竹竿的影长（AC）正好是1米，他沿着影子的方向走，向远处走出两根竹竿的长度（即AB=4米），他又竖起竹竿，这时竹竿的影长正好是一根竹竿的长度（即BD=2米）．此时，小明抬头瞧瞧路灯，若有所思地说：“噢，我知道路灯有多高了！”同学们，请你和小明一起解答这个问题：（1）在图中作出路灯O的位置，并作OP⊥l于P．（2）求出路灯O的高度，并说明理由解：（1）（2）由于BF=DB=2（米），即∠D=45°，所以，DP=OP=灯高，△COP中AE⊥CP，OP⊥CP，∴AE∥OP ∴△CEA∽△COP，即，设AP=x，OP=h则：①，DP=OP表达为2+4+x=h②，联立①②两式得：x=4，h=10，∴路灯有10米高．18、如图，在路灯下，小明的身高如图中线段AB所示，他在地面上的影子如图中线段AC所示，小亮的身高如图中线段FG所示，路灯灯泡在线段DE上．(1)请你确定灯泡所在的位置，并画出小亮在灯光下形成的影子；(2)如果小明的身高AB＝1.6 m，他的影子长AC＝1.4 m，且他到路灯的距离AD＝2.1 m，求灯泡的高．解：(1)如图，点O为灯泡所在的位置，线段FH为小亮在灯光下形成的影子.(2)由已知可得，ABOD＝CACD，∴1.6OD＝1.41.4＋2.1，∴OD＝4 m，∴灯泡的高为4 m.19、如图，电灯P在横杆AB的正上方，AB在灯光下的影子为CD，AB∥CD，AB＝1.5 m，CD＝4.5 m，点P到CD的距离为2.7 m，求AB与CD间的距离.解：∵AB∥CD，∴△PAB∽△PCD.设CD与AB间的距离为x m，则ABCD＝2.7－x2.7，即1.54.5＝2.7－x2.7，解得x＝1.8，∴AB与CD间的距离是1.8 m.11 / 11。

一、相似三角形中的动点问题1.如图，在Rt△ABC 中，∠ACB=90°，AC=3，BC=4，过点B 作射线BB1∥AC．动点D 从点A 出发沿射线AC 方向以每秒5个单位的速度运动，同时动点E 从点C 沿射线AC 方向以每秒3个单位的速度运动．过点D 作DH⊥AB 于H ，过点E 作EF⊥AC 交射线BB1于F ，G 是EF 中点，连接DG ．设点D 运动的时间为t 秒． （1）当t 为何值时，AD=AB ，并求出此时DE 的长度；（2）当△DEG 与△ACB 相似时，求t 的值．2.如图，在△ABC 中，ABC ＝90°，AB=6m ，BC=8m ，动点P 以2m/s 的速度从A 点出发，沿AC 向点C 移动．同时，动点Q 以1m/s 的速度从C 点出发，沿CB 向点B 移动．当其中有一点到达终点时，它们都停止移动．设移动的时间为t 秒．（1）①当t=2.5s 时，求△CPQ 的面积；②求△CPQ 的面积S （平方米）关于时间t （秒）的函数解析式；（2）在P ，Q 移动的过程中，当△CPQ 为等腰三角形时，求出t 的值．3.如图1，在Rt△ABC 中，ACB ＝90°，AC ＝6，BC ＝8，点D 在边AB 上运动，DE 平分CDB 交边BC 于点E ，EM⊥BD，垂足为M ，E N⊥CD，垂足为N ．（1）当AD ＝CD 时，求证：DE∥AC；（2）探究：AD 为何值时，△BME 与△CNE 相似？4.如图所示，在△ABC 中，BA ＝BC ＝20cm ，AC ＝30cm ，点P 从A 点出发，沿着AB 以每秒4cm 的速度向B 点运动；同时点Q 从C 点出发，沿CA 以每秒3cm 的速度向A 点运动，当P 点到达B 点时，Q 点随之停止运动．设运动的时间为x ．（1）当x 为何值时，PQ∥BC？（2）△APQ 与△CQB 能否相似？若能，求出AP 的长；若不能说明理由．5.如图，在矩形ABCD 中，AB=12cm ，BC=6cm ，点P 沿AB 边从A 开始向点B 以2cm/s 的速度移动；点Q 沿DA 边从点D 开始向点A 以1cm/s 的速度移动．如果P 、Q 同时出发，用t （s ）表示移动的时间（0＜t ＜6）。

挑战2023年中考数学选择、填空压轴真题汇编专题08 相似三角形综合压轴真题训练一．平行线分线段成比例（共1小题）1．（2022•襄阳）如图，在△ABC中，D是AC的中点，△ABC的角平分线AE 交BD于点F，若BF：FD＝3：1，AB+BE＝3，则△ABC的周长为．二．相似三角形的性质和判定2．（2022•鞍山）如图，在正方形ABCD中，点E为AB的中点，CE，BD交于点H，DF⊥CE于点F，FM平分∠DFE，分别交AD，BD于点M，G，延长MF交BC于点N，连接BF．下列结论：①tan∠CDF＝；②S△EBH：S△DHF ＝3：4；③MG：GF：FN＝5：3：2；④△BEF∽△HCD．其中正确的是.（填序号即可）．3．（2022•眉山）如图，四边形ABCD为正方形，将△EDC绕点C逆时针旋转90°至△HBC，点D，B，H在同一直线上，HE与AB交于点G，延长HE与CD的延长线交于点F，HB＝2，HG＝3．以下结论：①∠EDC＝135°；②EC2＝CD•CF；③HG＝EF；④sin∠CED＝．其中正确结论的个数为（）A ．1个B ．2个C ．3个D ．4个4．（2022•东营）如图，已知菱形ABCD 的边长为2，对角线AC 、BD 相交于点O ，点M ，N 分别是边BC 、CD 上的动点，∠BAC ＝∠MAN ＝60°，连接MN 、OM ．以下四个结论正确的是（ ）①△AMN 是等边三角形；②MN 的最小值是；③当MN 最小时S △CMN ＝S 菱形ABCD ；④当OM ⊥BC 时，OA 2＝DN •AB ．A ．①②③B ．①②④C ．①③④D ．①②③④5．（2022•绍兴）将一张以AB 为边的矩形纸片，先沿一条直线剪掉一个直角三角形，在剩下的纸片中，再沿一条直线剪掉一个直角三角形（剪掉的两个直角三角形相似），剩下的是如图所示的四边形纸片ABCD ，其中∠A ＝90°，AB ＝9，BC ＝7，CD ＝6，AD ＝2，则剪掉的两个直角三角形的斜边长不可能是（ ）A．B．C．10D．6．（2022•连云港）如图，将矩形ABCD沿着GE、EC、GF翻折，使得点A、B、D恰好都落在点O处，且点G、O、C在同一条直线上，同时点E、O、F在另一条直线上．小炜同学得出以下结论：①GF∥EC；②AB＝AD；③GE ＝DF；④OC＝2OF；⑤△COF∽△CEG．其中正确的是（）A．①②③B．①③④C．①④⑤D．②③④7．（2022•遂宁）如图，正方形ABCD与正方形BEFG有公共顶点B，连接EC、GA，交于点O，GA与BC交于点P，连接OD、OB，则下列结论一定正确的是（）①EC⊥AG；②△OBP∽△CAP；③OB平分∠CBG；④∠AOD＝45°；A．①③B．①②③C．②③D．①②④8．（2022•金华）如图是一张矩形纸片ABCD，点E为AD中点，点F在BC上，把该纸片沿EF折叠，点A，B的对应点分别为A′，B′，A′E与BC相交于点G，B′A′的延长线过点C．若＝，则的值为（）A．2B．C．D．9．（2022•乐山）如图，等腰△ABC的面积为2，AB＝AC，BC＝2．作AE ∥BC且AE＝BC．点P是线段AB上一动点，连结PE，过点E作PE的垂线交BC的延长线于点F，M是线段EF的中点．那么，当点P从A点运动到B点时，点M的运动路径长为（）A．B．3C．2D．4 10．（2022•海南）如图，菱形ABCD中，点E是边CD的中点，EF垂直AB交AB的延长线于点F，若BF：CE＝1：2，EF＝，则菱形ABCD的边长是（）A．3B．4C．5D．11．（2022•黑龙江）如图，正方形ABCD的对角线AC，BD相交于点O，点F 是CD上一点，OE⊥OF交BC于点E，连接AE，BF交于点P，连接OP．则下列结论：①AE⊥BF；②∠OP A＝45°；③AP﹣BP＝OP；④若BE：CE ＝2：3，则tan∠CAE＝；⑤四边形OECF的面积是正方形ABCD面积的．其中正确的结论是（）A．①②④⑤B．①②③⑤C．①②③④D．①③④⑤12．（2022•辽宁）如图，在正方形ABCD中，对角线AC，BD相交于点O，点E是OD的中点，连接CE并延长交AD于点G，将线段CE绕点C逆时针旋转90°得到CF，连接EF，点H为EF的中点．连接OH，则的值为．13．（2022•辽宁）如图，在Rt△ABC中，∠ACB＝90°，∠B＝60°，BC＝2，点P为斜边AB上的一个动点（点P不与点A、B重合），过点P作PD⊥AC，PE⊥BC，垂足分别为点D和点E，连接DE，PC交于点Q，连接AQ，当△APQ为直角三角形时，AP的长是．14．（2022•绍兴）如图，AB＝10，点C是射线BQ上的动点，连结AC，作CD ⊥AC，CD＝AC，动点E在AB延长线上，tan∠QBE＝3，连结CE，DE，当CE＝DE，CE⊥DE时，BE的长是．15．（2022•甘肃）如图，在矩形ABCD中，AB＝6cm，BC＝9cm，点E，F分别在边AB，BC上，AE＝2cm，BD，EF交于点G，若G是EF的中点，则BG的长为cm．16．（2022•新疆）如图，四边形ABCD是正方形，点E在边BC的延长线上，点F在边AB上，以点D为中心，将△DCE绕点D顺时针旋转90°与△DAF 恰好完全重合，连接EF交DC于点P，连接AC交EF于点Q，连接BQ，若AQ•DP＝3，则BQ＝．17．（2022•苏州）如图，在矩形ABCD中，＝．动点M从点A出发，沿边AD向点D匀速运动，动点N从点B出发，沿边BC向点C匀速运动，连接MN．动点M，N同时出发，点M运动的速度为v1，点N运动的速度为v2，且v1＜v2．当点N到达点C时，M，N两点同时停止运动．在运动过程中，将四边形MABN沿MN翻折，得到四边形MA′B′N．若在某一时刻，点B 的对应点B′恰好与CD的中点重合，则的值为．18．（2022•湖北）如图1，在△ABC中，∠B＝36°，动点P从点A出发，沿折线A→B→C匀速运动至点C停止．若点P的运动速度为1cm/s，设点P的运动时间为t（s），AP的长度为y（cm），y与t的函数图象如图2所示．当AP恰好平分∠BAC时t的值为．19．（2022•随州）如图1，在矩形ABCD中，AB＝8，AD＝6，E，F分别为AB，AD的中点，连接EF．如图2，将△AEF绕点A逆时针旋转角θ（0°＜θ＜90°），使EF⊥AD，连接BE并延长交DF于点H．则∠BHD的度数为，DH的长为．20．（2022•娄底）如图，已知等腰△ABC的顶角∠BAC的大小为θ，点D为边BC上的动点（与B、C不重合），将AD绕点A沿顺时针方向旋转θ角度时点D落在D′处，连接BD′．给出下列结论：①△ACD≌△ABD′；②△ACB∽△ADD′；③当BD＝CD时，△ADD′的面积取得最小值．其中正确的结论有（填结论对应的应号）．21．（2022•牡丹江）如图，在等腰直角三角形ABC和等腰直角三角形ADE中，∠BAC＝∠DAE＝90°，点D在BC边上，DE与AC相交于点F，AH⊥DE，垂足是G，交BC于点H．下列结论中：①AC＝CD；②AD2＝BC•AF；③若AD＝3，DH＝5，则BD＝3；④AH2＝DH•AC，正确的是．22．（2022•丹东）如图，四边形ABCD是边长为6的菱形，∠ABC＝60°，对角线AC与BD交于点O，点E，F分别是线段AB，AC上的动点（不与端点重合），且BE＝AF，BF与CE交于点P，延长BF交边AD（或边CD）于点G，连接OP，OG，则下列结论：①△ABF≌△BCE；②当BE＝2时，△BOG 的面积与四边形OCDG面积之比为1：3；③当BE＝4时，BE：CG＝2：1；④线段OP的最小值为2﹣2．其中正确的是．（请填写序号）三．相似三角形的应用23．（2022•衢州）希腊数学家海伦给出了挖掘直线隧道的方法：如图，A，B是两侧山脚的入口，从B出发任作线段BC，过C作CD⊥BC，然后依次作垂线段DE，EF，FG，GH，直到接近A点，作AJ⊥GH于点J．每条线段可测量，长度如图所示．分别在BC，AJ上任选点M，N，作MQ⊥BC，NP⊥AJ，使得＝＝k，此时点P，A，B，Q共线．挖隧道时始终能看见P，Q处的标志即可．（1）CD﹣EF﹣GJ＝km．（2）k＝．24．（2022•温州）如图是某风车示意图，其相同的四个叶片均匀分布，水平地面上的点M在旋转中心O的正下方．某一时刻，太阳光线恰好垂直照射叶片OA，OB，此时各叶片影子在点M右侧成线段CD，测得MC＝8.5m，CD＝13m，垂直于地面的木棒EF与影子FG的比为2：3，则点O，M之间的距离等于米．转动时，叶片外端离地面的最大高度等于米．。

重难点02 相似三角形模型及其综合题综合训练中考数学中《相似三角形模型及其综合题综合训练》部分主要考向分为五类：一、K型相似二、8字图相似三、A字图相似四、母子型相似五、手拉手相似相似三角形的综合题中各种相似模型的掌握是解决对应压轴题的便捷方法，所以本专题是专门针对相似三角形模型压轴题的，对提高类型的学生可以自主训练。

考向一：K型相似1．（2023•锡山区校级四模）如图，矩形ABCD中，AB＝10，BC＝8．点P在AD上运动（点P不与点A、D重合）将△ABP沿直线翻折，使得点A落在矩形内的点M处（包括矩形边界），则AP的取值范围是，连接DM并延长交矩形ABCD的AB边于点G，当∠ABM＝2∠ADG时，AP的长是．2．（2023•福田区模拟）综合与探究在矩形ABCD的CD边上取一点E，将△BCE沿BE翻折，使点C恰好落在AD边上的点F处．（1）如图①，若BC＝2BA，求∠CBE的度数；（2）如图②，当AB＝5，且AF•FD＝10时，求EF的长；（3）如图③，延长EF，与∠ABF的角平分线交于点M，BM交AD于点N，当NF＝AN+FD时，请直接写出的值．3．（2023•桐柏县一模）【初步探究】（1）把矩形纸片ABCD如图①折叠，当点B的对应点B'在MN的中点时，填空：△EB'M△B'AN （“≌”或“∽”）．【类比探究】（2）如图②，当点B的对应点B'为MN上的任意一点时，请判断（1）中结论是否成立？如果成立，请写出证明过程；如果不成立，请说明理由．【问题解决】（3）在矩形ABCD中，AB＝4，BC＝6，点E为BC中点，点P为线段AB上一个动点，连接EP，将△BPE沿PE折叠得到△B'PE，连接DE，DB'，当△EB'D为直角三角形时，BP的长为．考向二：8字图相似1．（2023•海州区校级二模）“关联”是解决数学问题的重要思维方式．角平分线的有关联想就有很多……【问题提出】（1）如图①，PC是△P AB的角平分线，求证：．小明思路：关联“平行线、等腰三角形”，过点B作BD∥P A，交PC的延长线于点D，利用“三角形相似”．小红思路：关联“角平分线上的点到角的两边的距离相等”，过点C分别作CD⊥P A交P A于点D，作CE⊥PB交PB于点E，利用“等面积法”．请根据小明或小红的思路，选择一种并完成证明．【理解应用】（2）如图②，在Rt△ABC中，∠BAC＝90°，D是边BC上一点．连接AD，将△ACD沿AD所在直线折叠，使点C恰好落在边AB上的E点处，落AC＝1，AB＝2，则DE的长为．【深度思考】（3）如图③，△ABC中，AB＝6，AC＝4，AD为∠BAC的角平分线．AD的垂直平分线EF交BC延长线于点F，连接AF，当BD＝3时，AF的长为．【拓展升华】（4）如图④，PC是△P AB的角平分线，若AC＝3，BC＝1，则△P AB的面积最大值是．2．（2023•衢州二模）如图1，在正方形ABCD中，点E在线段BC上，连接AE，将△ABE沿着AE折叠得到△AFE，延长EF交CD于点G．（1）求证：DG＝FG；（2）如图2，当点E是BC中点时，求tan∠CGE的值；（3）如图3，当时，连接CF并延长交AB于点H，求的值．考向三：A字图相似1．（2023•宿城区一模）如图，在矩形ABCD中，AB＝5，AD＝3，先将△ABC沿AC翻折到△AB′C处，再将△AB'C沿翻折到△AB'C'处，延长CD交AC′于点M，则DM的长为．2．（2023•沙坪坝区校级模拟）如图，△ABC中，D在AB上，E在BC上，∠AED＝∠ABC，F在AE上，EF＝DE．（1）如图1，若CE＝BD，求证：BE＝CF；（2）如图2，若CE＝AD，G在DE上，∠EFG＝∠EFC，求证：CF＝2GF；（3）如图3，若CE＝AD，EF＝2，∠ABC＝30°，当△CEF周长最小时，请直接写出△BCF的面积．3．（2023•中山区模拟）如图，在平面直角坐标系中，直线y＝﹣x+4与x轴，y轴分别交于点A、B，点P为射线AO上的一个动点，过点P作PQ⊥AB于点Q，将沿PQ翻折得到R．设△PQR与△AOB重合部分的面积为S，点P的坐标为（m，0）．（1）求AR的长．（用含m的代数式表示）（2）求S关于m的函数解析式，并直接写出自变量m的取值范围．考向四：母子型相似1．（2023•樊城区模拟）【基础巩固】（1）如图1，在△ABC中，D为AB上一点，∠ACD＝∠B．求证：AC2＝AD•AB．【尝试应用】（2）如图2，在▱ABCD中，E为BC上一点，F为CD延长线上一点，∠BFE＝∠A．若BF ＝6，AD＝9，求CE的长．【拓展提高】（3）如图3，在菱形ABCD中，E是AB上一点，F是△ABC内一点，EF∥AC，AC＝2EF，连接DE、DF分别交AC于M，N，∠EDF＝∠BAD，DF＝AE，若MN＝18，求EF的值．2．（2023•润州区二模）如图1，在△ABC中，点D在边AB上，点P在边AC上，若满足∠BPD＝∠BAC，则称点P是点D的“和谐点”．（1）如图2，∠BDP+∠BPC＝180°．①求证：点P是点D的“和谐点”；②在边AC上还存在某一点Q（不与点P重合），使得点Q也是点D的“和谐点”，请在图2中仅用圆规作图，找出点Q的位置，并写出证明过程．（保留作图痕迹）（2）如图3，以点A为原点，AB为x轴正方向建立平面直角坐标系，已知点B（6，0），C（2，4），点P在线段AC上，且点P是点D的“和谐点”．①若AD＝1，求出点P的坐标；②若满足条件的点P恰有2个，直接写出AD长的取值范围是．考向五：手拉手相似1．（2023•宝安区校级三模）【问题背景】已知D、E分别是△ABC的AB边和AC边上的点，且DE∥BC，则△ABC∽△ADE，把△ADE绕着A逆时针方向旋转，连接BD和CE．①如图2，找出图中的另外一组相似三角形；②若AB＝4，AC＝3，BD＝2，则CE＝；【迁移应用】在Rt△ACB中，∠BAC＝90°，∠C＝60°，D、E，M分别是AB、AC、BC中点，连接DE和CM．①如图3，写出CE和BD的数量关系；②如图4，把Rt△ADE绕着点A逆时针方向旋转，当D落在AM上时，连接CD和CE，取CD中点N，连接MN，若，求MN的长．【创新应用】如图5：，BC＝4，△ADE是直角三角形，∠DAE＝90°，tan∠ADE＝2，将△ADE绕着点A旋转，连接BE，F是BE上一点，，连接CF，请直接写出CF的取值范围．2．（2023•东港市二模）（1）问题发现：如图1，已知正方形ABCD，点E为对角线AC上一动点，将BE绕点B顺时针旋转90°到BF处，得到△BEF，连接CF．填空：①＝；②∠ACF的度数为；（2）类比探究：如图2，在矩形ABCD和Rt△BEF中，∠EBF＝90°，∠ACB＝∠EFB＝60°，连接CF，请分别求出的值及∠ACF的度数；（3）拓展延伸：如图3，在（2）的条件下，将点E改为直线AC上一动点，其余条件不变，取线段EF 的中点M，连接BM，CM，若，则当△CBM是直角三角形时，请直接写出线段CF的长．3．（2023•晋中模拟）综合与实践问题情境：（1）如图1，在△ABC和△ADE中，AB＝AC，AD＝AE．如图2，将△ABC绕顶点A按逆时针方向旋转15°得到△AB'C'，连接B′D，C′E，求证：B′D＝C′E．深入研究：（2）①如图3，在正方形ABCD和正方形CEFG中，已知点B，C，E在同一直线上，连接DE，AF，交于点P，求AF：DE的值；②如图4，若将正方形CEFG绕点C按顺时针方向旋转一定角度，AF：DE的值变化吗？请说明理由．拓展应用：（3）如图5，若把正方形ABCD和正方形CEFG分别换成矩形ABCD和矩形CEFG，且AD：AB＝CG：CE＝k，请直接写出此时AF：DE的值．（建议用时：150分钟）1．（2023•菏泽）（1）如图1，在矩形ABCD中，点E，F分别在边DC，BC上，AE⊥DF，垂足为点G．求证：△ADE∽△DCF．【问题解决】（2）如图2，在正方形ABCD中，点E，F分别在边DC，BC上，AE＝DF，延长BC到点H，使CH＝DE，连接DH．求证：∠ADF＝∠H．【类比迁移】（3）如图3，在菱形ABCD中，点E，F分别在边DC，BC上，AE＝DF＝11，DE＝8，∠AED＝60°，求CF的长．2．（2023•济南）在矩形ABCD中，AB＝2，AD＝2，点E在边BC上，将射线AE绕点A逆时针旋转90°，交CD延长线于点G，以线段AE，AG为邻边作矩形AEFG．（1）如图1，连接BD，求∠BDC的度数和的值；（2）如图2，当点F在射线BD上时，求线段BE的长；（3）如图3，当EA＝EC时，在平面内有一动点P，满足PE＝EF，连接P A，PC，求P A+PC的最小值．3．（2023•武汉）问题提出如图（1），E是菱形ABCD边BC上一点，△AEF是等腰三角形，AE＝EF，∠AEF＝∠ABC＝α（α≥90°），AF交CD于点G，探究∠GCF与α的数量关系．问题探究（1）先将问题特殊化，如图（2），当α＝90°时，直接写出∠GCF的大小；（2）再探究一般情形，如图（1），求∠GCF与α的数量关系．问题拓展将图（1）特殊化，如图（3），当α＝120°时，若，求的值．4．（2023•内蒙古）已知正方形ABCD，E是对角线AC上一点．（1）如图1，连接BE，DE．求证：△ABE≌△ADE；（2）如图2，F是DE延长线上一点，DF交AB于点G，BF⊥BE．判断△FBG的形状并说明理由；（3）在第（2）题的条件下，BE＝BF＝2．求的值．5．（2023•湖州）【特例感知】（1）如图1，在正方形ABCD中，点P在边AB的延长线上，连结PD，过点D作DM⊥PD，交BC的延长线于点M．求证：△DAP≌△DCM．【变式求异】（2）如图2，在Rt△ABC中，∠ABC＝90°，点D在边AB上，过点D作DQ⊥AB，交AC于点Q，点P在边AB的延长线上，连结PQ，过点Q作QM⊥PQ，交射线BC于点M．已知BC＝8，AC＝10，AD ＝2DB，求的值．【拓展应用】（3）如图3，在Rt△ABC中，∠BAC＝90°，点P在边AB的延长线上，点Q在边AC上（不与点A，C重合），连结PQ，以Q为顶点作∠PQM＝∠PBC，∠PQM的边QM交射线BC于点M．若AC＝mAB，CQ＝nAC（m，n是常数），求的值（用含m，n的代数式表示）．6．（2023•鞍山）如图，在△ABC中，AB＝AC，∠BAC＝α，点D是射线BC上的动点（不与点B，C重合），连接AD，过点D在AD左侧作DE⊥AD，使AD＝kDE，连接AE，点F，G分别是AE，BD的中点，连接DF，FG，BE．（1）如图1，点D在线段BC上，且点D不是BC的中点，当α＝90°，k＝1时，AB与BE的位置关系是，＝．（2）如图2，点D在线段BC上，当α＝60°，k＝时，求证：BC+CD＝2FG．（3）当α＝60°，k＝时，直线CE与直线AB交于点N，若BC＝6，CD＝5，请直接写出线段CN的长．7．（2023•益阳）如图，在Rt△ABC中，∠ACB＝90°，AC＞BC，点D在边AC上，将线段DA绕点D按顺时针方向旋转90°得到DA′，线段DA′交AB于点E，作A′F⊥AB于点F，与线段AC交于点G，连接FC，GB．（1）求证：△ADE≌△A′DG；（2）求证：AF•GB＝AG•FC；（3）若AC＝8，tan A＝，当A′G平分四边形DCBE的面积时，求AD的长．8．（2023•福建）如图1，在△ABC中，∠BAC＝90°，AB＝AC，D是AB边上不与A，B重合的一个定点．AO ⊥BC于点O，交CD于点E．DF是由线段DC绕点D顺时针旋转90°得到的，FD，CA的延长线相交于点M．（1）求证：△ADE∽△FMC；（2）求∠ABF的度数；（3）若N是AF的中点，如图2，求证：ND＝NO．9．（2022•湖北）问题背景：一次数学综合实践活动课上，小慧发现并证明了关于三角形角平分线的一个结论．如图1，已知AD是△ABC的角平分线，可证＝．小慧的证明思路是：如图2，过点C作CE∥AB，交AD的延长线于点E，构造相似三角形来证明＝．尝试证明：（1）请参照小慧提供的思路，利用图2证明：＝；应用拓展：（2）如图3，在Rt△ABC中，∠BAC＝90°，D是边BC上一点．连接AD，将△ACD沿AD所在直线折叠，点C恰好落在边AB上的E点处．①若AC＝1，AB＝2，求DE的长；②若BC＝m，∠AED＝α，求DE的长（用含m，α的式子表示）．10．（2022•宁波）【基础巩固】（1）如图1，在△ABC中，D，E，F分别为AB，AC，BC上的点，DE∥BC，BF＝CF，AF交DE于点G，求证：DG＝EG．【尝试应用】（2）如图2，在（1）的条件下，连结CD，CG．若CG⊥DE，CD＝6，AE＝3，求的值．【拓展提高】（3）如图3，在▱ABCD中，∠ADC＝45°，AC与BD交于点O，E为AO上一点，EG∥BD交AD于点G，EF⊥EG交BC于点F．若∠EGF＝40°，FG平分∠EFC，FG＝10，求BF的长．11．（2023•广州）如图，AC是菱形ABCD的对角线．（1）尺规作图：将△ABC绕点A逆时针旋转得到△ADE，点B旋转后的对应点为D（保留作图痕迹，不写作法）；（2）在（1）所作的图中，连接BD，CE．①求证：△ABD～△ACE；②若tan∠BAC＝，求cos∠DCE的值．。

相似三角形综合测试卷一、选择题(10题共30分)1．用放大镜将图形放大，应该属于（ ） A 、相似变换 B 、平移变换 C 、对称变换D 、旋转变换2 一个铝质三角形框架三条边长分别为24cm ，30cm ，36cm ，要做一个与它相似的铝质三角形框架，现有长为27cm ，45cm 的两根铝材，要求以其中的一根为一边，从另一根上截下两段（允许有余料）作为另外两边，截法有（ ） A 、0种 B 、1种 C 、2种 D 、3种3、如图1，P 是Ｒt △ABC 斜边BC 上异于B 、C 的一点，过P 点作直线截△ABC ，使截得的三角形与△ABC 相似，满足这样条件的直线共有（ ） A ．1条 B ．2条 C ．3条 D ．4条4、已知△ABC 与△DEF 的相似比为1︰2 ，△ABC 的周长为30cm ，△ DEF 的三边之比为 4︰5︰6，则△DEF 的最长边为（ ） A 44cm B 40cm C 36cm D 24cm5、在平面直角坐标系中，已知点E （-4，2），F （-2，-2），以原点O 为位似中心，相似比为21，把△EFO 缩小，则点E 的对应点E′的坐标是（ ） A ．（-2，1）B ．（-8，4）C ．（-8，4）或（8，-4） D ．（-2，1）或（2，-1） 6、如图，AB 是⊙O 的直径，C 、D 是⊙O 上的点，∠CDB=30°，过点C 作⊙O 的切线交AB 的延长线于E ，则sin ∠E 的值为（ ） A ．21 B ．23 C ．22 D ．33 7、如图，Rt △ABC 中，∠A=90°，AD ⊥BC 于点D ，若BD ：CD=3：2，则tanB=（ ） A 、23B ．32 C ．26 D ．36 8、如图，边长为6的大正方形中有两个小正方形，若两个小正方形的面积分别为S 1，S 2，则S 1+S 2的值为（ ） A ．16 B ．17 C ．18 D ．19 9、某数学课外实习小组想利用树影测量树高，他们在同一时刻测得一身高为1.5米的同学的影子长为1.35米，因大树靠近一栋建筑物，大树的影子不全在地面上，他们测得地面部分的影子长BC ＝3.6米，墙上影子高CD ＝1.8米，则树高AB （ ）A.2 .8B.3 .8C.4 .8D.5.810．如图，△ABC 中，CD ⊥AB 于D ，一定能确定△ABC 为直角三角形的条件的个数是（ ）①∠1=∠A ；②；③∠B+∠2=90°；④BC ：AC ：AB=3：4：5；⑤AC•BD=AD•CD ．A.2B.3C.4D.5二、填空题（6题共18分） 11、如图，在4×4的正方形方格中，△ABC 和△DEF 的顶点都在边长为1的小正方形的顶点上． （1）填空：∠ABC =_____°，BC =_____；（2）△ABC 与△DEF 是否相似？__________（填相似或不相似）12、如图，把矩形ABCD 对折，折痕为MN ，矩形DMNC 与矩形ABCD 相似，已知AB =4． （1）AD 的长为_______；（2）矩形DMNC 与矩形ABCD 的相似比为_________。