下载文档原格式
统计学基础平均指标和变异指标平均指标和变异指标是统计学中常用的两种指标，用于描述数据分布的中心趋势和离散程度。
在统计分析中，这两个指标的应用非常广泛。
1.平均指标：平均指标是用来表示数据分布的中心位置的指标，常见的平均指标有平均数、中位数和众数。
-平均数：平均数是指一组数据之和除以数据个数，表示了数据的平均水平。
平均数的计算方法是将所有数据相加，然后除以数据个数。
例如，对于一组数据：2，3，5，7，10，平均数的计算方式为(2+3+5+7+10)/5=5.4-中位数：中位数是将数据按照大小顺序排列后位于中间位置的数值，它划分了数据的中间位置。
如果数据个数为奇数，则中位数为排序后的中间值；如果数据个数为偶数，则中位数为排序后中间两个值的平均值。
中位数对于数据的极端值不敏感，适用于数据有异常值的情况，能够更好地表示数据的中心位置。
例如，对于一组奇数个数据：1，3，5，7，9，中位数为5；对于一组偶数个数据：2，4，6，8，中位数为(4+6)/2=5-众数：众数是一组数据中出现次数最多的数值，表示了数据中的高频值。
一个数据集可以有一个或多个众数。
如果一个数据集没有重复值，那么它没有众数。
例如，对于一组数据：1，2，3，4，4，4，5，众数为42.变异指标：变异指标是用来度量数据分布的离散程度，可以用来描述数据的稳定性和可变性。
常见的变异指标有极差、方差和标准差。
-极差：极差是一组数据的最大值和最小值之间的差异，表示了数据的全距。
极差越大，数据的离散程度越大；极差越小，数据的离散程度越小。
例如，对于一组数据：2，3，5，7，10，极差为(10-2)=8-方差：方差是一组数据与其平均数之间偏离程度的平均值的统计量，表示了数据分布的离散程度。
方差的计算公式是每个数值与平均数之差的平方之和除以数据个数。
例如，对于一组数据：2，3，5，7，10，平均数为5.4，方差的计算方式为[(2-5.4)^2+(3-5.4)^2+(5-5.4)^2+(7-5.4)^2+(10-5.4)^2]/5≈7.04-标准差：标准差是方差的平方根，是一个衡量数据分布离散程度的指标。
第五章综合指标学习要点：了解各种指标的概念及作用，掌握相对指标、平均指标的特点及计算方法，变异指标的计算方法。
§1、总量指标§2、相对指标§3、平均指标§4、变异指标学习知识点：前言：1、总量指标是反映社会经济现象发展的总规模、总水平的综合指标。
将总体单位数相加或总体单位标志值相加，就可以得到说明在一定时间、空间条件下某种现象总体的总规模、总水平的指标，即总量指标。
如：2010年年年末为1339724852亿，反映是我国人口的总规模。
总量指标的作用：第一、总量指标可以用来反映一个国家的基本国情国力，反映一个地区、一个部门或一个单位的人力、物力和财力，是人们对客观事物认识的起点。
第二、总量指标可以用来作为制定政策、制定计划和实行科学管理的基本依据，也是检查政策、计划执行情况，反映社会经济活动绝对效果的重要指标。
第三、总量指标可以用来研究客观现象的数量表现及其发展的变化趋势。
第四、总量指标是计算相对指标和平均指标的基础。
一、总量指标的种类：1、按其反映现象总体内容的不同：• 总体单位总量（简称单位总量）：指总体内所有单位的总数，表示总体本身规模的大小。
对于一个确定的统计总体，其总体单位总量是唯一确定的。
• 总体标志总量（简称标志总量）：指总体中各单位标志值总和。
对于确定的统计总体，标志总量不是唯一的，而是随着标志的不同可计算不同的标志。
• 例：我们研究某市三级医院的基本情况，则全市三级医院的总数量是总体单位总量，而全部三级医院职工总人数、全部三级医院职工工资总额等就是总体指标总量。
2、按反映时间状况的不同，可分为时期指标和时点指标。
• 时期指标指反映某社会经济现象在一段时间活动结果的总量指标，它反映的是一段时间连续发生变化过程。
如产品总量、货物运输量、商品销售量、国内生产总量等。
• 时点指标是反映社会经济现象在某一时间（瞬间）状况上的总量指标。
如人口数、职工数、设备台数等。
第五章平均指标与变异指标教学目的与要求：本章主要介绍了经济统计中广泛应用的一种综合指标，即平均指标。
并在此基础上，详细论述了反映总体特征的另一指标，即标志变异指标。
通过本章的学习和应用能力的训练，重点要求是：1、深刻理解平均指标和变异指标的基本理论和分析方法2、掌握计算平均指标的各种方法及运用原则3、对平均指标进行分析，阐述影响平均指标大小的原因4、明确平均指标与变异指标的区别与联系5、掌握变异指标的计算方法，并能运用标志变异指标说明平均数的代表性基本理论和分析方法。
重点掌握：1、平均制表的分析方法。
2、变异指标的计算意义。
教学方式：用多媒体课件讲练结合。
课时安排：理论4学时，实训2学时第一节平均指标的概念和作用一、平均指标的概念1、定义平均指标又称平均数，它是统计分析中最常用的统计指标之一。
它反映了社会经济现象中某一总体各单位某一数量在一定时间、地点条件下所达到的一般水平，或者反映某一总体、某一指标在不同时间上发展的一般水平。
2、特点第一，同质性，即总体内各单位的性质是相同的。
第二，抽象性，即总体内各同质单位虽然存在数量差异，但在计算平均数时并不考虑这种差异，即把这种差异平均掉了。
第三，代表性，即尽管各总体单位的标志值大小不一，但我们可以用平均数这一指标值来代表所有标志值。
二、平均指标的作用1、可以用来比较同类现象在不同地区、部门、单位（即不同总体）发展的一般水平，用以说明经济发展的高低和工作质量的好坏。
2、可以用来对统一总体某一现象在不同时期上进行比较，以反映该现象的发展趋势或规律。
如对同一地区人均年收入逐年进行比较来反映该地区居民生活水平的发展趋势或规律。
1、可以作为论断事物的一种数量标准。
2、可以用来分析现象之间的依存关系。
3、可以估算和推算其他有关数字三、平均指标的种类平均指标按其性质可分为静态平均数和动态平均数。
静态平均数反映的是同质总体内各单位某一数量标志在一定时间地点条件的一般水平，动态平均数反映的是某一总体某一指标值在不同时间上的一般水平。
第五章平均指标和标志变异指标一、单项选择题1．平均指标反映( )。
A. 总体分布的集中趋势B. 总体分布的离散趋势Ｃ. 总体分布的大概趋势 D. 总体分布的一般趋势2．平均指标是说明( )。
A. 各类总体某一数量标志在一定历史条件下的一般水平B. 社会经济现象在一定历史条件下的一般水平Ｃ. 同质总体内某一数量标志在一定历史条件下的一般水平D. 大量社会经济现象在一定历史条件下的一般水平3．计算平均指标最常用的方法和最基本的形式：（）A．中位数 B. 众数C. 调和平均数D. 算术平均数4．算术平均数的基本计算公式( )。
A.总体部分总量与总体单位数之比B.总体标志总量与另一总体总量之比Ｃ. 总体标志总量与总体单位数之比D. 总体标志总量与权数系数总量之比5．加权算术平均数中的权数为（）。
A. 标志值B. 权数之和Ｃ. 单位数比重 D. 标志值总量6．权数对算术平均数的影响作用决定于（）。
A. 权数的标志值 B. 权数的绝对值Ｃ. 权数的相对值 D. 权数的平均值7．加权算术平均数的大小（）。
A. 主要受各组标志值大小的影响，而与各组次数的多少无关B. 主要受各组次数大小的影响，而与各组标志值的多少无关Ｃ. 既受各组标志值大小的影响，又受各组次数多少的影响D. 既与各组标志值的大小无关，也与各组次数的多少无关8．在变量数列中，若标志值较小的组权数较大时，计算出来的平均数（）。
A. 接近于标志值小的一方B. 接近于标志值大的一方Ｃ. 接近于平均水平的标志值 D. 不受权数的影响9．假如各个标志值都增加5个单位,那么算术平均数会:( )。
A. 增加到5倍B. 增加5个单位C. 不变D. 不能预期平均数的变化10．各标志值与平均数离差之和（）。
A.等于各变量平均数离差之和B. 等于各变量离差之和的平均数Ｃ. 等于零 D. 为最大值11．当计算一个时期到另一个时期的销售额的年平均增长速度时,应采用哪种平均数?( )A. 众数B. 中位数C. 算术平均数D. 几何平均数12．众数是（）。
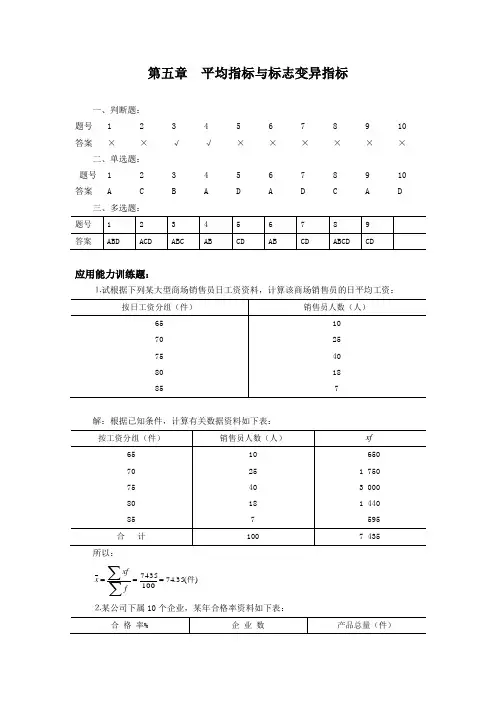
第五章 平均指标与标志变异指标一、判断题： 题号 1 2 3 4 5 6 7 8 9 10 答案××√√××××××二、单选题： 题号 1 2 3 4 5 6 7 8 9 10 答案ACBADADCAD三、多选题：应用能力训练题：⒈试根据下列某大型商场销售员日工资资料，计算该商场销售员的日平均工资：解：根据已知条件，计算有关数据资料如下表：所以：)(35.741007435件===∑∑f xf x⒉某公司下属10个企业，某年合格率资料如下表：要求：计算该产品的平均合格率解：根据题意，将有关数据计算入下表：%14.85140000119200===∑∑f xf x ⒊某市场上有三种鸡蛋，每公斤分别为16元、18元、20元，试计算： ⑴各买10公斤，平均每公斤多少钱？ ⑵各买10元，平均每公斤多少钱？ 解：⑴元）(1830102010181016............3213332211=⨯+⨯+⨯=++++++++=n n f f f f f x f x f x f x x⑵元）(85.17201018101610101010111=++++===∑∑∑∑m x m mm x x h ⒋某企业生产一种产品需顺次经过四个程序，这四个程序的废品率分别为1.2%、1.5%、1.3%和1.8%，该企业生产的平均废品率是多少？解：首先，计算该企业生产的平均合格率：%18.95%)8.11(%)3.11(%)5.11(%)2.11(......421=-⨯-⨯-⨯-=∏==n n n g x x x x x 该企业生产的平均废品率=1-95.18%=4.82%⒌某企业的销售额2011年比2010年增长7.5%，2012年比2011年增长9.8%，2013年比2012年增长6.3%，2014年比2013年增长11.4%。
计算2010年至2014年该企业销售额的平均增长速度。
第五章 平均指标 （一）填空题1．平均数可以反映总体各单位标志值分布的（集中趋势 ）。
2．社会经济统计中，常用的平均指标有（算术平均指标）、（调和平均指标）、（几何平均指标）、（中位数）和（众数）。
3．算术平均数不仅受（标志值）大小的影响，而且也受（权数 ）多少的影响。
4．各变量值与其算术平均数离差之和等于（零），各变量值与其算术平均数离差平方和为（最小）。
5．调和平均数是平均数的一种，它是（标志值倒数）的算术平均数的（倒数），又称（倒数 ）平均数。
6．几何平均数是计算平均比率和平均速度最适用的一种方法，凡是变量值的连乘积等于（总比率）或（总速度）的现象，都可以使用几何平均数计算平均比率或平均速度。
7．众数决定于（分配次数）最多的变量值，因此不受（极端值 ）的影响，中位数只受极端值的（位置）影响，不受其（大小）的影响。
（二）单项选择题1．平均数反映了（ A ）。
A 、总体分布的集中趋势B 、总体中总体单位的集中趋势C 、总体分布的离中趋势D 、总体变动的趋势 2．加权算术平均数的大小（ D ）。
A 、受各组标志值的影响最大B 、受各组次数的影响最大C 、受各组权数系数的影响最大D 、受各组标志值和各组次数的共同影响3．在变量数列中，如果变量值较小的一组权数较大，则计算出来的算术平均数（ B ）。
A 、接近于变量值大的一方 B 、接近于变量值小的一方 C 、不受权数的影响 D 、无法判断4．权数对于算术平均数的影响，决定于（ D ）。
A 、权数的经济意义 B 、权数本身数值的大小C 、标志值的大小D 、权数对应的各组单位数占总体单位数的比重 5．各总体单位的标志值都不相同时（ A ）。
A 、众数不存在 B 、众数就是最小的变量值C 、众数是最大的变量值D 、众数是处于中间位置的变量值6．凡是变量值的连乘积等于总比率或总速度的现象，要计算其平均比率或平均速度都可以采用（ C ）。
A 、算术平均法B 、调和平均法C 、几何平均法D 、中位数法7．如果次数分布中，各个标志值扩大为原来的2倍，各组次数都减小为原来的1/2，则算术平均数（ D ）。
A 、增加到原来的21 B 、稳定不变 C 、减少到原来的21D 、扩大为原来的2倍8．某公司所属三个企业计划规定的产值分别为500万元、600万元、700万元。
执行结果，计划完成程度分别为100％、115％、110％。
则该公司三个企业的平均计划完成程度为（ B ）。
A 、108.3％B 、108.9%C 、106.2D 、108.6% 9．某机械局所属的3个企业2000年完成的实际产值分别为400万元，600万元，500万元。
执行结果，计划完成程度分别为108％，106％，108％，则该局三个企业平均计划完成程度为（ C ）。
A 、％＝％％％33.1071081061083⨯⨯B 、％＝％％＋％＋33.1073108108106C 、％＝％＋％＋％＋＋19.107108500106600108400500600400D 、％＝＋＋＋％＋％2.107500600400500108600106400108⨯⨯⨯10．已知变量x 的算术平均数为x ,A 为任意数，则（ D ）。
A 、22)()∑∑--A x x x（ B 、()∑∑--22)(A x x x C 、()()∑∑-=-22A x x x D 、()()∑∑-≤-22A x x x11．当变量分布左偏时，存在（ B ）。
A 、x M M e 0 B 、x M M e 0 C 、x M M e 0 D 、x M M e ≤≤0（三）多项选择题1．算术平均数基本计算公式中（ ACD ）。
A 、分子分母属于同一个总体B 、分子分母的计量单位相同C 、分子属于分母D 、分母是分子的直接承担者E 、分子是分母的直接承担者2．计算算术平均数时，由于所掌握的资料不同，可用的公式有（ BCDE ）。
A 、总体标志总量总体单位总量 B 、n x ∑ C 、∑∑fxf D 、∑∑f f xE 、∑∑wkw3．加权算术平均数的大小（ ABCE ）。
A 、受各组次数的影响B 、受各组中值大小的影响C 、受各组标志值大小的影响D 、不受各组次数的影响E 、受各组次数和各组标志值的共同影响4．在何种条件下，加权算术平均数等于简单算术平均数（ ADE ）。
A 、各组次数相等的条件下 B 、各组次数不相等的条件下 C 、各组次数较少的条件下 D 、各组次数都为1的条件下 E 、各组权数系数都相等的条件下5．权数对平均数的影响作用表现在（ ACE ）。
A 、当标志值比较大而次数较多时，平均数接近于标志值大的一方B 、当标志值比较小而次数较少时，平均数接近标志值较小的一方C 、当标志值比较小而次数较多时，平均数接近标志值较小的一方D 、当标志值比较大而次数较少时，平均数靠近标志值较大的一方E 、当各组次数相同时，对平均数没有影响6．下列哪些情况应采用调和平均法计算（ ABCDE ）。
A 、已知各企业计划完成百分比及实际产值求平均计划完成百分比B 、已知商品单价和商品销售额求平均价格C 、已知分组的粮食亩产量及各组粮食总产量求总的平均亩产D 、已知同类数种产品单位成本及总生产费用求平均单位产品成本E 、已知投入的劳动时间相同，求单位产品耗时 7．几何平均数主要适用于（ BCDE ）。
A 、变量值的代数和等于标志总量的情况 B 、具有等比关系的变量数列C 、变量值的连乘积等于总比率的情况D 、变量值的连乘积等于总速度的情况E 、求平均比率时8．在分配偏斜适度的情况下，e M M x 、、0的关系表现为（ BC ）。
A 、()03M x M x e -=- B 、()e M x M x -=-30C 、x M M e 230-＝D 、x M M e 230-=E 、023M M x e -=9．在各种平均指标中，不受极端值影响的平均指标是（ DE ）。
A 、算术平均数 B 、调和平均数 C 、几何平均数 D 、中位数 E 、众数 （四）计算题1．某乡播种小麦22,800亩，其中35%的耕地使用良种，平均亩产750公斤，其余耕地平均亩产480公斤。
问：（1）小麦的平均亩产是多少？（2）小麦的全部产量是多少？1. （1）∑∑=⨯+⨯==5.574%65480%35750f f x X （公斤）（2）13098600228005.574=⨯=⋅∑f X 公斤2．某县2000年粮食产量资料如下：∑∑=⨯+⨯+⨯+⨯=⋅=5.3122.04754.032535.022505.0175f fx X3．某地甲乙两个农贸市场三种主要蔬菜价格及销售额资料如下：试比较该地区哪个农贸市场蔬菜平均价格高？并说明原因。
甲市场的平均价格为：32.0500160==∑∑x m m H ＝甲（元/公斤）乙市场的平均价格为：325.05005.162==∑∑xm H ＝乙(元/公斤)经计算得知，乙市场蔬菜平均价格高，其原因是乙市场价格较高的蔬菜销售量比重大于甲市场。
也可以说，乙市场蔬菜平均价格高的蔬菜销售额比重大于甲市场。
4．生产同类产品的五个企业计划完成情况如下：试求产量计划平均完成百分比. %10321702235212747038849552535747040045050036047000.140097.045010.150005.135002.1==++++=++++⨯+⨯+⨯+⨯+⨯==∑∑fxf X5．为了扩大国内居民需求，银行为此多次降低存款利润，近5年年利润率分别为7％、5％、4％、3％、2％，试计算在单利和复利情况下5年的平均年利率。
按单利计算的平均年利率：%2.45%2%3%4%5%7=++++=x按复利计算的平均年利率：%19.410419.11%)21%)(31%)(41%)(51%)(71(5=-=-+++++=x 6. 某人在银行存了一笔款，前六年的年利润率为5％，后四年的年利润率为6％，求该笔存款的年平均利润率（按复利计算）。
%4.10506.105.11046=⨯=X年平均利率＝年平均本利率－100%＝105.4%-100%=5.4%根据上述资料，计算职工家庭每户收入的众数和中位数。
试确定成绩的中位数和众数。
（1）众数：众数在50～60这一组。
5310)3001200()8001200(8001200502110=⨯-+--+=⋅∆+∆∆+=i L M （百元）中位数：中位数所在的组3150/2＝1575，故中位数在50～60这一组。
591012005002315021=⨯-=-+--∑i f S fL M mm e （百元）第五章（2） 变异指标练习题（一）填空题1.平均指标说明分布数列中变量值的（集中趋势），而标志变异指标则说明变量值的（ 离中趋势）。
2.标志变动度与平均数的代表性成（反比）。
3.全距是总体中单位标志值的（最大值）与（最小值）之差。
4.如果资料为组距数列，全距可以用（最高组的上限）和（最低组的下限）之差来近似地表示全距，他比实际的全距（ 大 ）。
5.全距受（极端变量值）的影响最大。
6.是非标志的平均数为（p ），标准差为（pq ）。
7.标准差系数是（标准差 ）与（平均数）之比，其计算公式为（xσ ）。
（二）单项选择题1.标志变异指标中易受极端变量值影响的指标有（ A ）。
A 、全距 B 、标准差 C 、平均差 D 、平均差系数 3.标志变异指标中的平均差是（ D ）。
A 、各标志值对其算术平均数的平均离差 B 、各变量值离差的平均数C 、各变量值对其算术平均数离差的绝对值的绝对值D 、各标志值对其算术平均数离差绝对值的平均数 4.平均差的主要缺点是（ C ）。
A 、与标准差相比计算复杂B 、易受极端变量值的影响C 、不符合代数方法的演算D 、计算结果比标准差数值大 5.用是非标志计算平均数，其计算结果为（ D ）。
A 、q p + B 、q p - C 、p -1 D 、p6.计算平均差时对每个离差取绝对值是因为（ C ）。
A 、离差有正有负 B 、计算方便 C 、各变量值与其算术平均数离差之和为零 D 、便于数学推导7．标准差是其各变量值对其算数平均数的（ B ）。
A 、离差平均数的平方根 B 、离差平方平均数的平方根 C 、离差平方的平均数 D 、离差平均数平方的平方根 8．计算离散系数是为了比较（ B ）。
A 、不同分布数列的相对集中程度B 、不同水平的数列的标志变动度的大小C 、相同水平的数列的标志变动度的大小D 、两个数列平均数的绝对离差 9．变量的方差等于（ A ）。
A 、变量平方的平均数减变量平均数的平方B 、变量平均数的平方减变量平方的平均数C 、变量平方平均数减变量平均数平方的开平方D 、变量平均数的平方减变量平方平均数的开平方10．两组工人加工同样的零件，甲组工人每人加工的零件分别为：25、26、28、29、32；乙组工人每人加工的零件分别为：22、25、27、30、36。
