北京十一学校小升初数学真题及答案解析

北京市十一学校小升初考试数学真题这篇北京市十一学校小升初考试数学真题是查字典数学网特地为大家整理的，希望对大家有所帮助!一、填空题(20分)1.二亿六千零四万八千写作( )，改写成用“万”作单位的数是()万。

2、，0.76和68%这三个数中最大的数是( )，最小的数是()。

3.能同时被2、3、5整除的最大的三位数是( )。

4.某班男生和女生人数的比是4:5，则男生占全班人数的( )，女生占全班人数的( )。

5.爸爸说：“我的年龄比小明的4倍多3。

” 小明说：“我今年a岁。

”用含有字母的式子表示爸爸的年龄，写作( );如果小明今年8岁，那么爸爸今年( )岁。

6.一个数除以6或8都余2，这个数最小是( );一个数去除160余4，去除240余6，这个数最大是()。

7. ÷( )=( )÷60=2:5=( )%=( )成。

8.在3.014，3 ，314%，3.1 和3. 中，最大的数是()，最小的数是( )。

9.一个圆的周长是12.56厘米，它的面积是( )平方厘米。

10.如果a= (c≠0)，那么( )一定时，()和( )成反比例;( )一定时，( )和( )成正比例。

二、选择题(将正确答案的序号填入括号内)(5分)1.一个周长是l的半圆，它的半径是( )A.l÷2B. l÷C.l÷( +2)D.l÷( +1)2. 的值是一个( )。

A.有限小数B.循环小数C.无限不循环小数3.一台电冰箱的原价是2400元，现在按七折出售，求现价多少元?列式是( )。

A.2400÷70% B.2400×70%C.2400×(1-70%)4.在下列年份中，( )是闰年。

A.1990年 B.1994年 C.2019年5.下列各式中，a和b成反比例的是( )。

A.a× =1B.a×8=C.9a=6aD.三.判断题(对的在括号内打“√”，错的打“×”)(5分)1. 6千克:7千克的比值是千克。

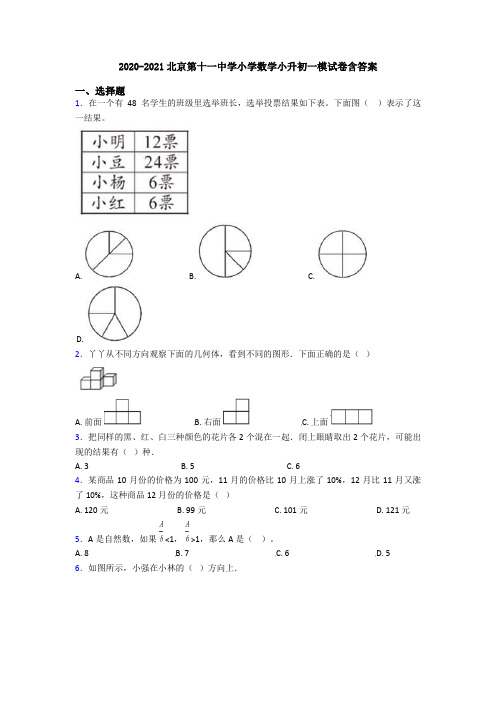
2020-2021北京第十一中学小学数学小升初一模试卷含答案一、选择题1．在一个有48名学生的班级里选举班长，选举投票结果如下表。

下面图（）表示了这一结果。

A. B. C.D.2．丫丫从不同方向观察下面的几何体，看到不同的图形．下面正确的是（）A. 前面B. 右面C. 上面3．把同样的黑、红、白三种颜色的花片各2个混在一起．闭上眼睛取出2个花片，可能出现的结果有（）种．A. 3B. 5C. 64．某商品10月份的价格为100元，11月的价格比10月上涨了10%，12月比11月又涨了10%，这种商品12月份的价格是（）A. 120元B. 99元C. 101元D. 121元5．A是自然数，如果 <1， >1，那么A是（）。

A. 8B. 7C. 6D. 56．如图所示，小强在小林的（）方向上．A. 西偏南40°B. 东偏北50C. 北偏东50°D. 南偏西40°7．一桶油，第一次用了，第二次用了剩下的，那么（）A. 第一次用得多B. 第二次用得多C. 两次用得同样多D. 无法比较8．小丽从家里出发，先向东偏南45°方向走500m，再向正西方走100m，现在她的位置在家的（）方向．A. 东北B. 西北C. 东南D. 西南9．甲车间的出勤率比乙车间高，以下说法正确的是（）A. 甲车间的总人数一定比乙车间多B. 甲车间的出勤人数一定比乙车间多C. 甲车间的未出勤人数一定比乙车间少D. 以上说法都不对10．一种商品的价格先提价30%后，再打7折出售，现在售价是原价的（）A. 70%B. 100%C. 109%D. 91% 11．笑笑在班级里进行了一项调查，并把调查结果制成如右图所示的统计图。

笑笑可能进行的调查内容是（）。

A. 你最喜欢什么宠物B. 你有几只宠物C. 你的宠物几岁了12．如图，以长方形的边a作底面周长，边b作高，分别可以围成一个长方体、正方体和圆形纸筒，再分别给它们别故一个底面。

北京十一学校新初一分班考试数学 1.4.12018-26÷5.2.30%的盐水里加6克盐和1千克水，这时盐水中盐和水的比是3.在一次运动会中，甲班参加田赛的有15人，参加径赛的有12人，参加田赛又参加径赛的有7人，没有参加比赛的有21人．那么甲班共有______人．4.一项工程甲独做6小时完成，乙独做8小时完成，两人合做2小时，余下的由甲独做还要 小时完成．5.甲乙两数是自然数，如果甲的5/18恰好是乙数的1/12，那么甲乙两数之和最小是多少 （甲乙为正整数）6.4个人踢足球赛，每两队比一场，赢5分，输0分，平1分（1）有可能的几种分数（2）某足球队至少得多少分保证第一（并列第一）（3）四支球队7：3：2：2可能吗？7.某人运一批货物，现在运了5次，共运了总数的53多一些，43少一些，最多一共要运 次。

8.小明给同学打电话，其中一位电话号码忘了，他一次性拨打对的可能是9.把1-7填入圆中，每三个圆中的和最小是10.A 、B 、C 、D 、E 、F 六人下棋，每两人下一局，已知现在A 下了5局，B 下了4局，C 下了3局，E 下了2局，F 下了1局。

问D 现在下了 局。

11.两人在400米的跑道上赛跑，甲每秒跑8米，乙每秒跑5米，问 秒后，两人又在起点相遇。

12.0.ABAB 是个纯循环小数，已知小数点后20位的和位80，这个分数最小是 （用分数表示）13.第2018个图有 个实心圆。

14.750名学生，40名老师，学生票30元/张，成人票60元/张，团体45 元/张（团60人及以上） 方案①750名学生买学生票，老师买成人票方案②700名学生买学生票，剩下90人买团体票（1）算出哪种方案更划算（2）自行设计最优方案15.1、4、9完全平方数，18、27完全立方数，2、3、5、7、10、11、12...非平方也非立方数列，数列中第99个 是16.8个猴子有一个比其他7个轻，问最少称次能找出最轻的猴子。

十一中学小升初分班考试数学真题练习初中马上就要开学了，小升初考生马上就要进入新一阶段的学习生活了，开学后初中都会举行小升初分班考试，为了帮助大家轻松应对小升初分班考试，下面为大家带来十一中学小升初分班考试数学真题练习，希望大家认真认真阅读。

一、填空题：1.在1991，1992，1993，1994，1995，1996，1997这七个数中，不能写成两个自然数的平方差的数是____2.如图，阴影部分S1的面积比阴影部分S2的面积大12平方厘米，且BD=4厘米，DC=1厘米，则线段AB=______厘米.3.一个人在河中游泳，逆流而上，在A处将帽子丢失，他向前游了15分后，才发现帽子丢了，立即返回去找，在离A处15千米的地方追到了帽子，则他返回来追帽子用了______分.4.乒乓球单打决赛在甲、乙、丙、丁四位选手中进行，赛前，有些人预测比赛结果，A说：甲第4;B说：乙不是第2，也不是第4;C说：丙的名次在乙的前面;D说：丁将得第1.比赛结果表明，四个人中只有一人预测错了.那么，甲、乙、丙、丁四位选手的名次分别为：_______.5.如图，正立方体边长为2，沿每边的中点将每个角都切下去，则所得到的几何体有______条棱.6.一本书，如果每天读50页，那么5天读不完，6天又有余;如果每天读70页，那么3天读不完，4天又有余;如果每天读n页，恰可用n天读完(n是自然数).这本书的页数是______.使每一横行，每一竖行，两对角线斜行中三个数的和都相等.8.有本数学书共有600页，则数码0在页码中出现的次数是______.9.张明骑自行车，速度为每小时14千米，王华骑摩托车，速度为每小时35千米，他们分别从A、B两点出发，并在A、B两地不断往返行驶，且两人第四次相遇(两人同时到达同一地点叫做相遇)与第五次相遇的地点恰好相距120千米，那么，A、B两地之间的距离是______千米.10.某次数学竞赛原定一等奖8人，二等奖16人，现在将一等奖中最后4人调整为二等奖，这样得二等奖的学生的平均分提高了1.2分，得一等奖的学生的平均分提高了4分，那么原来一等奖平均分比二等奖平均分多______分.二、解答题：11.学校要建一段围墙，由甲、乙、丙三个班完成，已知甲班单独干需要20小时完成，乙班单独干需要24小时完成，丙班单独干需要28小时完成，如果先由甲班工作1小时，然后由乙班接替甲班干1小时，再由丙班接替乙班干1小时，再由甲班接替丙班干1小时，三个班如此交替着干，那么完成此任务共用了多少时间?12.如图甲、乙、丙三个皮带轮的半径比分别为：5∶3∶7，求它们的转数比.当甲轮转动7圈时，乙、丙两轮各转多少圈?13.甲、乙、丙三个小孩分别带了若干块糖，甲带的最多，乙带的较少，丙带的最少.后来进行了重新分配，第一次分配，甲分给乙、丙，各给乙、丙所有数少4块，结果乙有糖块最多;第二次分配，乙给甲、丙，各给甲、丙所有数少4块，结果丙有糖块最多;第三次分配，丙给甲、乙，各给甲、乙所有数少4 块，经三次重新分配后，甲、乙、丙三个小孩各有糖块44块，问：最初甲、乙、丙三个小孩各带糖多少块?14.甲容器中有纯桔汁16升，乙容器中有水24升，问怎样能使甲容器中纯桔汁含量为60%，乙容器中纯桔汁含量为20%，甲、乙容器各有多少升?15.有12头羊14天可以吃完12亩草，13头羊44天可以吃完22亩草，问多少头羊60天可以吃完50亩草?16.如图，一个棱长为5的正方体，在它的上下、左右、前后各面中心挖去一个底面是1的正方形，高为2的长方体洞，求挖后此形体的表面积是多少?17.其余88人是群众，则此工厂共有多少人.18.某钟表，在6月29日零点比标准时间慢5分，它一直走到7月6日上午6时，比标准时间快5分，那么这只表所指时间是正确的时刻应该是在哪月哪日哪时?(零点和7时都指的是标准时间)19.某出版社出版某种书，今年每册书的成本比去年增加10%，但售价不变，因此每本利润下降了40%，那么今年这种书的成本在售价中所占的百分数是多少?20.两个整数A、B的最大公约数是C，最小公倍数是D，并且已知C不等于1，也不等于A或B，C+D=187，那么A+B等于多少? 21.老师在黑板上写了从11开始的若干个连续自然数(如11，12，13)，后来擦掉了其中一个数，剩下的数的平均数是23。

北京市重点中学小升初考题 6试卷说明：全卷共21题，满分100分，考试时间：60分钟 一、选择题（共10题，每题4分，共40分）11.甲乙两人植树，若甲单独完成甲比乙所需的时间多丄，若两人合干，则完成任务时乙比甲多植 50棵,3这批树共有（）A 300 棵B 350 棵C 400 棵D 450 棵 2•有两人分别从甲、乙两地同时相向而行，在A 处相遇。

如果两人各自提速 20%，仍从甲、乙两地同时相向而行，在B 处相遇，则（）（A ）A 在甲与B 之间 （B ）B 在甲与A 之间 （C ）A 与B 重合 （D ）A ，B 的位置关系不 3•有一台天平，只有 5克和30克砝码各一个，现在要把 300克的盐分成三等分，那么，最少要用天平称（）次.A •3 B •4 C •5 D • 64•甲乙丙三位长跑运动员同时同地出发跑步，甲平均每秒钟跑 跑了18.3千米•他们三人按平均速度由大到小的顺序排列是 A 丙甲乙 B 乙甲丙 C 甲乙丙 D 5•甲乙丙丁四个杯子中都盛有糖水，甲杯中含糖 1.2 %，乙杯中的糖和水分别为 3克和297克，丙杯中含水98. 7%，丁杯中原含糖3克水240克，后来又加入了 70克水.则四杯水中含糖百分比最低的是（）A 甲 B乙 C丙 D 丁6•计算机中常用的十六进制是逢16进I 的记数制，采用数字 0-9和字母A. F 共16个记数符号；这些符号与十进制的数的对应关系如下表:例如，用十六进制表示： E+D=1B 则A X B=（）A 6EB 72C 5FD B07.（如图）有孔正方体的表面积（含孔内各面）是 A. 258 B . 234 C . 222 D . 2IO &右上图为某三岔路间内，在上述路段中，同一路段上驶入与驶出的车辆数相等 ），则（）5米，乙平均每分钟跑 288米，丙一小时（） 甲丙乙 十六进制 0 1 2 3 4 5 6 7 8 十进制0 1 23 45678EI 交通环岛的简化模型，在某高峰时段，单位时间进出路口如图所示，图中X 1，X 2，X 3分别表示该时段单位时间通过路段AB, BC, CA 的机动车辆数（假设：单位时A ，B, C 的机动车辆数(A) X 1 > X 2 > X3 (B) X1> X 3 > X 2 (C) X2> X 3 > X1 (D)X 3 > X2 > X 19.对于任意的两个实数对 (a,b)和(c , d)，规定(a,b)=(c , d)当且仅当a=c,b=d ;运算“：”为：(a, b) :(c ，d)=(ac-bd ，bc+ad)，运算“二”为：(a,b):门(c ，d)=(a+c,b+d).设 p, q € R ,若(1 , 2) : (p , q)=(5 , O)则(1 , 2)二(p,q)=()A. (4 , O) B . (2 , O) C . (O , 2)D . (O ，一 4) 10.编辑一个运算程序：I &仁2, m & n=k , m & (n+1)=k+2，贝U 1 & 2005的输出结果为()A. 4008 B . 4006 C . 4012 D . 4010二、填空题（共11题，共60分）11 .右图是某企业 2000年至2003年四年来关于生产销售的一张统计图表（注：利润=销售额-生产成本）•对这四年有以下几种说法：（1） 该企业的利润逐年提高；（2） 2000年〜2001年该企业销售额增长率最快： （3） 2001年〜2002年该企业生产成本增长率最快； （4）2002年〜2003年该企业利润增长幅度比2000年〜2001年利润增长幅度大.其中说法正确的是 ____________________ （6分）（注：把你认为正确的说法序号都填上 ）.12. 一件商品按成本价提高 50%后标价，再打 8折（标价的80% ）销售，销售价为240元.则这件商品的成本价是 _______ 元.（4分）13、某校三年级原来男、女生人数之比是 5： 7,第二学期又转来 5名男生，则男、女生人数之比就为 3：4,问原来有男生 ______ 人，女生 ____ 人.（6分）1114、把金放在水里称，其重量减轻—，把银放在水里称，其重量减轻—。

1 2 3答案解析标注【拓展思维】 计算模块 > 分数 > 分数运算 > 分小四则混合运算原式．答案解析标注【拓展思维】 计算模块 > 分数 > 分数巧算 > 提取公因数/式（4分）=4原式．答案解析标注【课内】 数与运算 > 加法 > 分数加法（真分数） > 异分母分数加法（4分）计算：．5原式．答案解析标注【拓展思维】 计算模块 > 分数 > 分数巧算 > 乘法分配律 > 分数拆数法构造分配律（4分）6原式．答案解析标注【课内】 数与运算 > 运算律【拓展思维】 计算模块 > 整数 > 整数分配律 > 整数乘法巧算之分配律（4分） ．7原式．答案解析标注【拓展思维】 计算模块 > 整数 > 整数提取公因数 > 整数乘法巧算之提取公因数（普通型）（4分）8提取公因数答案解析标注【拓展思维】 计算模块 > 小数 > 循环小数 > 循环小数加减运算（4分） ．9．答案解析标注【拓展思维】 计算模块 > 分数 > 分数巧算 > 凑整（4分）计算： ．10原式===．故答案为：．答案解析（4分）11标注【拓展思维】 计算模块 > 分数 > 繁分数 > 繁分数计算．答案解析标注【课内】 式与方程 > 简易方程（一元一次） > 解简易方程 > 分数简易方程（4分）A. B. C. D.已知，是（ ）12C 同时取倒数①②③．（4分）求未知数．13答案解析标注【拓展思维】 计算模块 > 方程基础 > 一元一次方程 > 分数、小数系数方程（2分）．（1）（2分）．（2）（1）（2）（1）．（2）．答案解析标注【拓展思维】 计算模块 > 方程基础 > 一元一次方程 > 分数、小数系数方程（4分）解方程：14解含有分数的方程核心在于要把分母全部消除，就是乘以分母的最小公倍数，那么方程可以写成，解得答案（4分）解下列方程组：（1），则 ， ；（2），则 ， ．151．2．3．解析标注【拓展思维】 计算模块 > 方程基础 > 多元一次方程组 > 整数系数方程组（）解：①得：③③②得 ．．将代入①得：．．所以这个方程组的解为．（）解：①得：③②③得：．．将代入①得：．．所以这个方程组的解为．①②①②答案（4分）A.， B.， C.， D.，如图，在图中，只有一个三角形，图由图变化而来，相当于在图中增加了一条线段，多产生了个三角形，新产生的三角形一定与添加的这条线段有关，所以图中共有个三角形，按照这个思路推算下去，则图中共有（ ） 个三角形，图中共有（ ） 个三角形．16解析标注【拓展思维】 计数模块 > 几何计数 > 分类枚举法数图形 > 常规图形枚举计数 > 三角形图三三角形个数：（个），图四三角形个数：(个)．答案解析标注【拓展思维】 计数模块 > 几何计数 > 分类枚举法数图形 > 常规图形枚举计数 > 梯形（4分）图中共有 个等腰梯形．17如下图每种有个，共有（个）．答案（4分）黑板上有一个五位数字串，擦掉其中连续的两个数字，并将它们的差写在那个位置，这时黑板上的数字串为，开始黑板上写的数字串有多少种可能？18、、、解析标注【拓展思维】 计数模块 > 枚举法综合 > 字典排序法 > 组数 > 卡片组数差为的种，差为的种，差为的种，差为的种，算了遍，算了遍，所以为种答案解析标注【拓展思维】 应用题模块 > 页码问题 > 数码综合问题（4分）一本数学书共有页，则数码在页码中出现的次数是 ．19分类数，数码在个位出现的次数，数码在十位出现的次数，，．答案解析标注【拓展思维】 数论模块 > 位值原理与进制 > 数与数字 > 数、数位、数字的认识（4分）A. B. C. D.在至这个整数中，有多少个数含数字？（ ）20B 不妨将1至9999的自然数均看作四位数，凡位数不到四位的自然数在前面补0．使之成为四位数．先求不含数字的这样的四位数共有几个，即有这九个数字所组成的四位数的个数．则个位、十位、百位、千位每一位都可有九种写法，所以，根据乘法原理，由这九个数字组成的四位数个数为，即不含的数的个数有个于是，到含有数字的自然数共有个，另外中还有一个，所以一共有．（4分）这个自然数的所有数字之和为 ．21答案解析标注【拓展思维】 计算模块 > 整数 > 整数加减 > 整数加减巧算之分组法用配对方法，与，与，与，……，与，共对．每对数字之和都是所以所有数字之和为．答案解析标注【拓展思维】 计数模块 > 加乘原理 > 加乘原理综合（4分）由、、、四个数字（即可全用也可不全用）组成的非零自然数，按照从小到大，排在第 个．22一位数:个两位数:个三位数: 个四位数:先考虑千位是的，有个；千位是的，有、、、、、、共个，所以比小的共有个，所以 排在第个 ．（4分）如下图，把B C D 这五部分用四种不同的颜色着色，且相邻的部分不能使用同一种颜色，不相邻的部分可以使用同一种颜色，那么这幅图一共有 种不同的着色方法．23、、、、答案解析标注【拓展思维】 计数模块 > 加乘原理 > 染色计数问题从接触面最多的入手，再按照相邻原则依次考虑．从开始考虑，有种着色方法．着色后，有种着色方法着色后，有种着色方法着色后，有种着色方法．着色后，有种着色方法．共有种着色方法．答案解析标注【拓展思维】 计数模块 > 加乘原理 > 组数问题 > 有特殊要求的组数问题（4分）用两个，一个，一个，可以组成多少个不重复的位数？24这道题由于3有2个，是其中最特殊的，所以从它入手．先从四位数的4个数位中选择个来放，有种选法；然后剩下的两个数位放和，有种放法；根据乘法原理，共有种不同的方法，所以可以组成个不重复的四位数．（4分）A.， B.， C.， D.，大家知道，在平面内画一个角，可以把平面分成两部分（即角的内部和角的外部），请你想一想，在平面内如果画出两个角，这两个角最多可以把平面分成（ ）个部分；如果画出三个角，这三个角最多可以把平面分成（ ）个部分．25。

2010年十一小升初真题（一）一、填空题1.15=（） 16=0.625=（）：8 （）2. 4 吨50 千克=（）吨3.45 小时=（）时（）分3. 计算：3-5+7-9+11-13+ +1995-1997+1999=4. 某笔奖金原计划8 人均分，现退出一人，其余每人多得2 元，则这笔奖金共元5. 甲乙两地相距20 千米，在一幅地图上，量得两地的距离是4 厘米，这幅地图的比例是6. 甲、乙两辆汽车，甲在西地，乙在东地，同时向东开行，甲每小时行60 千米，乙每小时行48 千米，行了5 小时后，甲在乙后面24 千米处，那么东西两地相隔千米。

7. 两支蜡烛一样长，第一支能点4 小时，第二支能点3 小时，同时点燃这两支蜡烛，小时后第一支的长度是第二支的两倍。

8. 七名学生在一次数学竞赛中共得110 分，各人得分互不相同，其中得分最高的是19 分，那么最低得分至少是分9. 将0，1，2，3，4，5，6，7，8，9 这十个数字中，选出六个填在下面方框中，使算式成立，一个方框一个数字，各个方框数字不相同：□+□□=□□□，则算式中的三位数最大是10. 游泳池里，一些学生在学游泳，男同学律戴蓝色游泳帽，女同学一律戴红色游泳帽，有趣的是，在每个男同学看来，蓝色游泳帽与红色游泳帽一样多；而在每个女同学看来，蓝色游泳帽多一倍，那么游泳池里有个学生在学游泳，（每位同学都看不到自己戴的游泳帽的颜色）11. 一桶农药，第一次倒出 2/7 然后倒回桶内 120 克，第二次倒出桶中剩下农药的 3/8，第三次倒出 320 克，桶中还剩下 80 克，原来桶中有农药克12. 已知两数的差与这两数的商都等于 7，那么这两个数的和是13. 两个同样大小的正方体的积木，每个正方体上相对的两个面上写的数之和都等于 9，现将这两个正方体并列放置在 桌面，看得见的五个面的数字如图 1 所示，则看不见的七 个面上的数的和等于3579x x xx14. 一组按规律排列的式子：，，，， （xy 0），其中第 6 个式子是yy2y 3 y 4，第 n 个式子是15. 一串有黑有白，其排列有一定规律的珠子，被盒子遮住一部分（如图2），则这串珠子被盒子遮住的部分有颗16. 如图 3，图中共有 19 个圆，如果把连在一起的两个圆称为一对，那么图中相连的圆共有 对17. 如图所示，在正方形 ABCD 中，红色、绿色正方形的面积分别是27 和 12，且红、绿两个正方形有一个顶点重合，黄色正方形的一个 顶点位于红色正方形两条对角线的交点，另一个顶点位于绿色正方形 两条对角线的交点，则黄色正方形的面积为二、选择题18. 掷一枚质地均匀的正方体骰子，骰子的六个面上分别刻有 1 到 6 的点数，掷得面朝上的点数为奇数的可能性为（ ） 1 1 1 1 ABCD2346142 3 5红红红19. 如图所示的正方体的展开图是（）A B C D20. 如图，将一正方形按如图方式分成n 个大小形状完全相同的长方形，上、下各横排两个，中间竖排若干个，则n 的值为（）A 4B 6C 8D 1021. 如图，用边长为1 的正方形覆盖3 3 的正方形网格，一次最多覆盖边长为1 的正方形网格（覆盖一部分就算覆盖）的个数是（）A 7B 6C 5D 422. 图4 是汪老师早晨出门散步时，离家的距离y 与时间x 之间的关系图，若用黑点表示汪老师家的位置，则汪老师散步行走的路线可能是（）23. 将如下图所示的圆心角为90 的扇形纸片AOB 围成圆锥形纸帽，使扇菜的两条半径OA 与OB 重合（按缝粘贴部分忽略不计），则围成的圆锥形纸帽是（）A B C D三、计算题24. 计算（1） 1.4 ⨯ 4-11÷ （1.8-1）7 5 5（2）36 ⨯（1-1+1）2 3 43 （3）485 1-1841 2-1 +0.25+33 31 3-2 -303 5（4） 2.5 ÷ 0.75 ⨯ 1⨯ 13÷1.4 ⨯3⨯2 5 4 5 3（5）1⨯ 2 ⨯ 3 + 2 ⨯ 4 ⨯ 6 + 7 ⨯14 ⨯ 21 1⨯ 3⨯ 5 + 2 ⨯ 6 ⨯10 + 7 ⨯ 21⨯ 35（6）20093 - 2 ⨯ 20092 - 2007 20093 + 20092 - 201025. 圆柱体的表面积是2512 平方厘米，底面半径是10 厘米，这个圆柱体的体积是多少立方厘米？26. 图中三角形ABC 是直角三角形，AB=20，阴影（1）的面积比阴影（2）的面积小23，求BC 的长度是多少？AB C四、解应用题27. 一列快车和一列慢车，同时从甲、乙两站出发，相向而行，经过6 小时相遇，相遇后快车继续行驶3 小时后到达乙站。