应用光学第四章棱镜习题解答
- 格式:ppt
- 大小:638.50 KB
- 文档页数:29


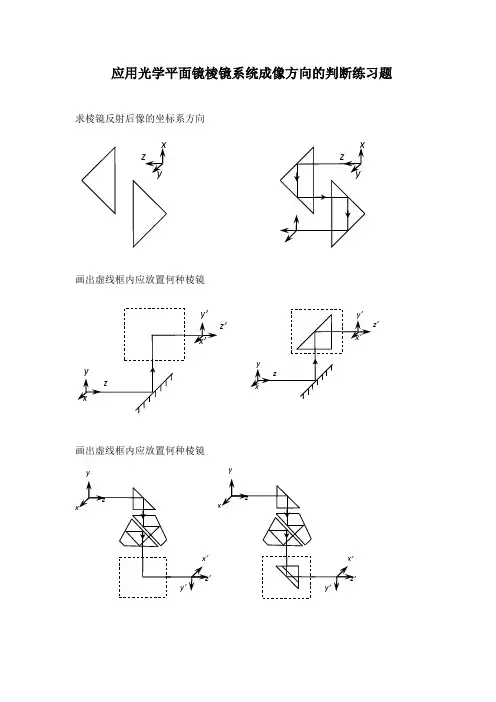
应用光学平面镜棱镜系统成像方向的判断练习题
求棱镜反射后像的坐标系方向
画出虚线框内应放置何种棱镜
画出虚线框内应放置何种棱镜
y
y
z ’
z ’
x y
z
求棱镜反射后像的坐标系方向
根据下列平面镜棱镜系统中的成像方向要求,画出虚线框内所需的反射棱镜类型。
x
y
z
屋脊棱镜
屋脊棱镜
幸福,时时刻刻围绕在你身旁。
如果你从母亲手中接过饭碗,心存温馨,那就是幸福;如果你在灯下读着朋友来信,品味友情,那
就是幸福;如果你独坐一隅,静静听歌,凝神遐思,那就是幸福。

色散和棱镜对光的分光作用光,作为自然界中不可或缺的一部分,一直吸引着人类去探索和研究。
光的本质是电磁波,其在真空中的传播速度为常数,即299,792,458米/秒。
然而,当光进入不同介质时,其速度会发生变化,导致光的传播方向发生偏折,这一现象称为折射。
而当光通过某些特定介质时,还会出现色散现象,即光的不同波长会被分散开来。
本文将重点介绍色散和棱镜对光的分光作用。
色散现象色散是光在通过某些介质时,不同波长的光被分散开来的现象。
这种现象的原因在于不同波长的光在同一介质中的折射率不同。
折射率是描述光在介质中传播速度与在真空中传播速度之比的物理量,其与光的波长有关。
当光通过介质时,波长较长的光速度较快,波长较短的光速度较慢,因此光会发生偏折,从而使不同波长的光分散开来。
色散现象在日常生活中随处可见,例如彩虹、夕阳和光谱等。
彩虹是由于阳光在雨滴中发生色散,将白光分解为七种颜色;夕阳则是由于太阳光在大气中发生色散,使得天空呈现出绚丽的橙红色;光谱则是将光通过光谱仪进行分光,得到的光谱中包含了不同波长的光,从而可以研究光的组成和物质的性质。
棱镜对光的分光作用棱镜是一种具有透明介质截面的几何光学元件,其对光的分光作用主要是基于色散现象。
当光通过棱镜时,不同波长的光在介质中的折射率不同,从而发生色散,使光分散成不同颜色的光谱。
棱镜对光的分光作用可以通过以下几个步骤来描述:1.入射光的折射:当光线垂直射入棱镜时,由于棱镜的形状和折射率,光线会发生折射,并在棱镜内部发生一次全反射。
2.色散现象:当折射后的光线在棱镜内部传播时,由于不同波长的光在介质中的折射率不同,会发生色散现象,即光的不同颜色会被分散开来。
3.出射光谱:色散后的光线从棱镜的另一侧射出,形成一条光谱,其颜色顺序通常为红、橙、黄、绿、蓝、靛、紫。
棱镜类型棱镜有多种类型,其中最常见的是** prism 和 rhomboid prism**。
•Prism:这是一种具有固定形状和折射率的棱镜。


1λ第四章 习题及答案 1。
双缝间距为1mm ,离观察屏1m ,用钠灯做光源,它发出两种波长的单色光 =589.0nm 和2λ=589.6nm ,问两种单色光的第10级这条纹之间的间距是多少? 解:由杨氏双缝干涉公式,亮条纹时:dDm λα=(m=0, ±1, ±2···) m=10时,nm x 89.511000105891061=⨯⨯⨯=-,nm x 896.511000106.5891062=⨯⨯⨯=- m x x x μ612=-=∆2。
在杨氏实验中,两小孔距离为1mm ,观察屏离小孔的距离为50cm ,当用一片折射率1.58的透明薄片帖住其中一个小孔时发现屏上的条纹系统移动了0.5cm ,试决定试件厚度。
21r r l n =+∆⋅22212⎪⎭⎫⎝⎛∆-+=x d D r 22222⎪⎭⎫⎝⎛∆++=x d D r x d x d x d r r r r ∆⋅=⎪⎭⎫⎝⎛∆--⎪⎭⎫ ⎝⎛∆+=+-222))((221212mm r r d x r r 2211210500512-=⨯≈+⋅∆=-∴ ,mm l mm l 2210724.110)158.1(--⨯=∆∴=∆-3.一个长30mm 的充以空气的气室置于杨氏装置中的一个小孔前,在观察屏上观察到稳定的干涉条纹系。
继后抽去气室中的空气,注入某种气体,发现条纹系移动了25个条纹,已知照明光波波长λ=656.28nm,空气折射率为000276.10=n 。
试求注入气室内气体的折射率。
0008229.10005469.0000276.1301028.6562525)(600=+=⨯⨯=-=-∆-n n n n n l λ4。
垂直入射的平面波通过折射率为n 的玻璃板,透射光经透镜会聚到焦点上。
玻璃板的厚度沿着C 点且垂直于图面的直线发生光波波长量级的突变d,问d 为多少时焦点光强是玻璃板无突变时光强的一半。

作业:习题1、 解:据题意,分别求出光孔AB 和透镜L 1经其前面的光学系统成像。
光孔前面无光学系统,其经前面光学系统成的像为其本身;透镜前面无光学系统,其经前面光学系统成的像亦为其本身。
1)由于物在无限远,光孔直径35mm 小于透镜直径40mm ,所以开口直径35mm 的光孔为孔径光阑,也是入瞳;出瞳为孔径光阑经后方光学系统所成的像:设孔径光阑AB 经L 1成像为A´B´。
由高斯公式和垂轴放大率公式得)(10010050100)50('''mm f l lf l -=+-⨯-=+=——在L 1左侧100mm )(703550100''mm y l l y =⨯--==——出瞳直径为70 mm 2)当物在透镜前300mm 处,光孔对物点的张角为 07.0503002/351≈-=tgu透镜(像L 1´)对物点的张角为 06667.03002/402≈=tgu 比较u 1、u 2可 知,透镜(像L 1´) 对物点的张角u 2小 于光孔(像)对物 点的张角(见下图)故透镜L 1为孔径光 阑、入瞳和出瞳。
可见,同一 光学系统,当物 距不同时,其孔 径光阑不同,随 着l 减少,原来 限制光束的光孔 失去限制光束的 作用,而由透镜 框内孔限制光束。
习题4 解:1)根据光通量和辐射通量的关系式有:lm e 76.01051523=⨯⨯=Φ=Φ-η2)据发光强度定义式 ΩΦ=I ,当激光束的发散角u 很小时,立体角2u w π=所以,发光强度:(cd)10512.15024.0760000)104.0(76.076.06232⨯≈=⨯⨯==Φ=-ππαw I 3)据光亮度定义式 dSw dSI L ⋅⋅Φ=⋅=θθcos cos 和 0=θ,2)2(d dS π=得光亮度:)/(101.927577536.11004.3)10(14.35024.010476.0dS L 21212236m cd w ⨯≈⨯=⨯⨯⨯⨯=⋅Φ=- 4)由 2cos rI E θ=和 0=θ得激光束在5m 远处屏幕上产生的光照度: )(10051.6510512.1cos 4262lx r I E ⨯≈⨯==θ例题:例1.两个薄凸透镜L 1和L 2的口径均为4cm ,L 1的焦距为8cm ,L 2的焦距为3cm ,L 2在L 1之后5cm ,对于平行于光轴入射的光线,求系统的孔径光阑、入射光瞳和出射光瞳。

应用光学习题本习题供学习、复习使用。
精练这些习题及作业和课件上的例题有助于掌握、理解应用光学课程的基本知识、理论和规律。
应用光学的基本问题包括在本习题内,但不仅限于本习题。
本习题仅供课程学习时参考。
习题中一些问题提供了解答,限于时间,其它则略去。
一、筒答题1、几何光学的基本定律及其内容是什么?答:几何光学的基本定律是自钱传播定律、独立传播定W:、反射定律和折射定律。
直线传播定律:光线在均匀透明介质中按直线传播。
独立传播定律:不同光源的光在通过介质某点时互不影响。
反射定律:反射光线位于入射面内;反射角等于入射角:折射定律:折射光线位于入射面内:入射角和折射角正弦之比,对两种定的介j员来说,是=个和入射角无关的常数n isin/,-msin/。
22、理想光学系统的基点和基面有哪些?理想光学系统的基点包指物方焦点、{象方焦点;物方主点、像方主点:物方节点、像方节点。
基面包括:物方焦平丽、像方然平面:物方主平丽、像方主平面;物方节平面、像方节平面。
3、什么是光学系统的孔役光阑和视场光阙?答:孔径光阑是限制轴上物点成像光束立体角的光阔。
晴荡艾丽王辅前有字亩7茧事宝肯车夜夜古国的光册J。
4、常见非正常跟有哪两种?如何校正常见非正常1'常见正常目艮包括近视酬远视盹近视眼将工二(远附近点)矫正到无限远,远视眼,将一丘丛(远点就近点)矫正到明视距离。
3、光'于系统极限分辨角为多大?采取什么途径可以提岗极限分辨角?答:衍射决定的极限分辨角为0=3®。
可见其与波长和孔役有关。
订蔬小波长D和增大孔径可以提高光学系统的分辨率。
I什么是共和1)也学系统、元学系统物空间、像空间?答:光学系统以一条公共制线通过系统各表面的幽率中心,该轴线称为光轴,这样的系统称为共轴光学系统。
物体所在的空间称为物空间,像所在的空间称为像空间。
、如何确定光学系统的视场Jt阙?答:将系统中除孔径光阑以外的所有光阑对其前面所有的光学零件成像到物空间;这些像中,孔径对入暗中心张角最小的一个像所对应的光阑即为光学系统的视场光阙。


考试试题纸(A卷)课程名称题号题分备注:学生不得在试题纸上答题(含填空题、选择题等客观题应用光学四五六七专业班级八九十总分一二三一、选择题(每题1分,共5分)1.发生全反射现象的必要前提是:A)光线由光疏介质到光密介质传播B)光线由光密介质到光疏介质传播C)光线在均匀介质中传播D)以上情况都可能产生2.周视照相机可以拍摄大视场景物,其利用的:A)节点的性质B)主点的性质C)焦点的性质D)以上答案都正确3.在望远镜的视度调节中,为适应近视人群,应采取的是:A)使物镜远离目镜B)使目镜远离物镜C)使目镜靠近物镜D)应同时调节物镜和目镜4.棱镜系统中加入屋脊面,其作用是:A改变光轴的方向B)改变主截面内像的方向C)改变垂轴于主截面方向上像的方向D)以上都正确5.光学系统中场镜的作用是:A)改变成像光束的位置B)减小目镜的尺寸C)不改变像的成像性质D)以上都正确二、填空题(每题2分,共10分)1.显微镜中的光学筒长指的是(2.光学系统中像方顶截距是(3.用波像差评价系统成像质量的瑞利准则是(4.望远系统中物镜的相对孔径是(5.棱镜的转动定理是(三、简答题(共20分)1.什么叫孔径光阑?它和入瞳和出瞳的关系是什么?(4分)2.什么叫视场光阑?它和入窗和出窗的关系是什么?(4分)3.几何像差主要包括哪几种?(4分)4.什么叫远心光路?其光路特点是什么?(4分)5.照相机中F数是什么意思?光圈指的是什么?(4分))))))四、分析作图题(共25分)1.已知正光组的F和F’,求轴上点A的像,要求用五种方法。
(8分)2.已知透镜的焦距公式为f'=nr1n−1n−1,l'H=−f'd,lH=−f'd,nrnr⎡⎤rd12(n−1)⎢n(1−1)+(n−1)⎥r2r2⎦⎣分析双凹透镜的基点位置,并画出FFL、BFL和EFL的位置。
(9分)3.判断下列系统的成像方向,并画出光路走向(8分)(a)五、计算题(共35分)(b)1.由已知f1′=50mm,f2′=−150mm的两个薄透镜组成的光学系统,对一实物成一放大4倍的实像,并且第一透镜的放大率β1=−2,试求:1.两透镜的间隔;2.物像之间的距离;3.保持物面位置不变,移动第一透镜至何处时,仍能在原像面位置得到物体的清晰像?与此相应的垂铀放大率为多大?(15分)2.已知一光学系统由三个零件组成,透镜1:f1′=−f1=100,口径D1=40;透镜2:f2′=−f2=120,口径D2=30,它和透镜1之间的距离为d1=20;光阑3口径为20mm,它和透镜2之间的距离d2=30。
第二章P47 1(题目见书)解:(1)运用大L 公式解该问题:对于第一条光线,11300,2L U =-=-时:11111130083.220sin sin sin(2)0.1607,9.247583.220L r I U I r ---==-== 111111sin sin 0.16070.0992, 5.69361.6199n I I I n ''==⨯==' 1111129.2475 5.6936 1.5539,sin 0.0271U U I I U '''=+-=-+-== 11111sin 0.099283.22083.220387.8481sin 0.0271r I L r mm U ''=+=+⨯=' 运用转面公式:21121387.84812385.8481, 1.5539L L d U U ''=-=-===222222385.848126.271sin sin sin1.55390.3709,21.772626.271L r I U I r --==== 22222 1.6199sin sin 0.37090.3927,23.12061.5302n I I I n ''==⨯==' 222221.553921.772623.12060.2059,sin 0.0036U U I I U '''=+-=+-== 22222sin 0.392726.27126.2712892sin 0.0036r I L r mm U ''=+=+⨯=' 32232289262886,0.2059L L d U U ''=-=-=== 3333332886(87.123)sin sin 0.00360.1229,7.056787.123L r I U I r ---==⨯=-=-- 33333 1.5302sin sin (0.1229)0.1881,10.83971n I I I n ''==⨯-=-=-' 333330.2059(7.0567)(10.8397) 3.9889,sin 0.0696U U I I U '''=+-=+---== 33333sin 0.188187.123(87.123)148.3344sin 0.0696r I L r mm U '-'=+=-+-⨯='对于第二条光线,光线与光轴平行入射,所以有:111110sin 0.1202, 6.901583.22h I I r ==== 111111sin sin 0.12020.0742, 4.25541.6199n I I I n ''==⨯==' 111110 6.9015 4.2554 2.6461,sin 0.0462U U I I U '''=+-=+-== 11111sin 0.074283.22083.220216.9726sin 0.0462r I L r mm U ''=+=+⨯=' 21121216.97262214.9726, 2.6461L L d U U ''=-=-=== 222222214.972626.271sin sin sin 2.64610.3316,19.366626.271L r I U I r --==⨯== 22222 1.6199sin sin 0.33160.3510,20.55081.5302n I I I n ''==⨯==' 222222.646119.366620.5508 1.4619,sin 0.0255U U I I U '''=+-=+-== 22222sin 0.351026.27126.271387.9866sin 0.0255r I L r mm U ''=+=+⨯=' 32232387.98666381.9866, 1.4619L L d U U ''=-=-=== 333333381.9866(87.123)sin sin 0.02550.1373,7.891887.123L r I U I r ---==⨯=-=-- 33333 1.5302sin sin (0.1373)0.2101,12.12831n I I I n ''==⨯-=-=-' 333331.4596(7.8918)(12.1283) 5.6961,sin 0.0993U U I I U '''=+-=+---== 33333sin 0.210187.123(87.123)97.2128sin 0.0993r I L r mm U '-'=+=-+-⨯=' (2)现在利用近轴光路的计算公式,再将上面的两条光线计算一下,这样可以进行比较。
第二章 P47 1(题目见书)解:(1)运用大L 公式解该问题:对于第一条光线,11300,2L U =-=-o 时:11111130083.220sin sin sin(2)0.1607,9.247583.220L r I U I r ---==-==o o 111111sin sin 0.16070.0992, 5.69361.6199n I I I n ''==⨯=='o 1111129.2475 5.6936 1.5539,sin 0.0271U U I I U '''=+-=-+-==o o o o11111sin 0.099283.22083.220387.8481sin 0.0271r I L r mm U ''=+=+⨯=' 运用转面公式:21121387.84812385.8481, 1.5539L L d U U ''=-=-===o222222385.848126.271sin sin sin1.55390.3709,21.772626.271L r I U I r --====o o 22222 1.6199sin sin 0.37090.3927,23.12061.5302n I I I n ''==⨯=='o 222221.553921.772623.12060.2059,sin 0.0036U U I I U '''=+-=+-==o o o o 22222sin 0.392726.27126.2712892sin 0.0036r I L r mm U ''=+=+⨯=' 32232289262886,0.2059L L d U U ''=-=-===o 3333332886(87.123)sin sin 0.00360.1229,7.056787.123L r I U I r ---==⨯=-=--o 33333 1.5302sin sin (0.1229)0.1881,10.83971n I I I n ''==⨯-=-=-'o 333330.2059(7.0567)(10.8397) 3.9889,sin 0.0696U U I I U '''=+-=+---==o o o o 33333sin 0.188187.123(87.123)148.3344sin 0.0696r I L r mm U '-'=+=-+-⨯='对于第二条光线,光线与光轴平行入射,所以有:111110sin 0.1202, 6.901583.22h I I r ====o 111111sin sin 0.12020.0742, 4.25541.6199n I I I n ''==⨯=='o 111110 6.9015 4.2554 2.6461,sin 0.0462U U I I U '''=+-=+-==o o o11111sin 0.074283.22083.220216.9726sin 0.0462r I L r mm U ''=+=+⨯=' 21121216.97262214.9726, 2.6461L L d U U ''=-=-===o222222214.972626.271sin sin sin 2.64610.3316,19.366626.271L r I U I r --==⨯==o o 22222 1.6199sin sin 0.33160.3510,20.55081.5302n I I I n ''==⨯=='o 222222.646119.366620.5508 1.4619,sin 0.0255U U I I U '''=+-=+-==o o o o 22222sin 0.351026.27126.271387.9866sin 0.0255r I L r mm U ''=+=+⨯=' 32232387.98666381.9866, 1.4619L L d U U ''=-=-===o 333333381.9866(87.123)sin sin 0.02550.1373,7.891887.123L r I U I r ---==⨯=-=--o 33333 1.5302sin sin (0.1373)0.2101,12.12831n I I I n ''==⨯-=-=-'o 333331.4596(7.8918)(12.1283) 5.6961,sin 0.0993U U I I U '''=+-=+---==o o o o 33333sin 0.210187.123(87.123)97.2128sin 0.0993r I L r mm U '-'=+=-+-⨯=' (2)现在利用近轴光路的计算公式,再将上面的两条光线计算一下,这样可以进行比较。
应用光学(吉林联盟)知到章节测试答案智慧树2023年最新长春理工大学第一章测试1.若光所处的介质为各向同性均匀介质,电磁波面向各方向的传播速度()参考答案:相同2.在对可见光为透明的介质中,折射率常随波长的减小而()参考答案:增大3.同一介质对不同波长的光具有不同的折射率,在对可见光为透明的介质中,以下哪一种光的折射率最小?()参考答案:红光4.同一介质对不同波长的光具有不同的折射率,在对可见光为透明的介质中,以下哪一种光的折射率最大?()参考答案:紫光5.直线传播定律忽略了电磁波的()。
参考答案:衍射6.当光线以一定的角度入射到光密-光疏介质分界面上时,有:()参考答案:折射角大于入射角7.有时看到窗户玻璃上映射的太阳光特别耀眼,这是由于在窗户玻璃表面发生了()现象。
参考答案:反射8.一个由6个折射面构成的光学系统,请问该系统将产生()个光学空间?参考答案:79.若轴上物点位于无限远位置处,则物方孔径角值为:()参考答案:0度10.单个折射面的轴向放大率与垂轴放大率存在如下关系:()参考答案:11.单个折射面的垂轴放大率、轴向放大率和角放大率都与物像距有关,三种放大率之间存在如下关系:()参考答案:12.单个折射面的角放大率与垂轴放大率存在如下关系:()参考答案:13.汽车观后镜其实就是一个孔径不太大的()镜。
参考答案:凸面14.光学系统的放大率为各个面放大率之()。
参考答案:积15.当光波在其它透明介质(如水、玻璃)中传播时,()参考答案:其波长和速度都将发生改变,但频率不变,颜色感觉也不发生改变16.设光在光密介质中传播的速度为,光在光疏介质中的传播速度为,则:()参考答案:17.一个半径为的球面镜,若一轴上物点位于无穷远位置处,其像点位于:()参考答案:位置处18.某物通过一透镜成像在该透镜内部,若透镜材料为玻璃,透镜两侧均为空气,则系统的像方介质空间是()。
参考答案:空气19.不同波长的电磁波有不同的频率,频率、波长与速度三者之间的关系为:()参考答案:20.光程是指:()参考答案:光在介质中传播的几何路程与所在的介质折射率的积21.汽车观后镜就是球面反射镜比较典型的一个应用实例,当观察者离反射镜保持同样距离时,从凸面镜内观察到的景物视场与平面镜相比(),从而能够更好的保证行车安全。