江苏省2014届高三百校联合调研测试(一)数学试题

苏州市2014届高三调研测试数学Ⅰ试题 2014．1一、填空题：本大题共14小题，每小题5分，共计70分．不需要写出解答过程，请把答案直接填在答题．．卡相应位置上．．．．．．． 1． 已知集合A = { x | x < 2 }，B = { -1，0，2，3 }，则A ∩B = ▲ ． 2． 已知i 为虚数单位，计算2(12i)(1i)+-= ▲ ． 3． 若函数()sin()f x x θ=+（π02θ<<）的图象关于直线π6x =对称，则θ = ▲ ．4． 设S n 为等差数列{a n }的前n 项和，已知S 5 = 5，S 9 = 27，则S 7 = ▲ ．5． 若圆锥底面半径为1，高为2，则圆锥的侧面积为 ▲ ．6． 运行右图所示程序框图，若输入值x ∈[-2，2]，则输出值y 的取值范围是 ▲ ．7． 已知π3sin()45x +=，π4sin()45x -=，则tan x = ▲ ．8． 函数e ln y x x =-的值域为 ▲ ．9． 已知两个单位向量a ，b 的夹角为60°，c = t a +（1 - t ）b ．若b ·c = 0，则实数t 的值为 ▲ ．10． 已知m ∈{-1，0，1}，n ∈{-1，1}，若随机选取m ，n ，则直线10mx ny ++=恰好不经过第二象限的概率是 ▲ ．11． 已知22(0),()(0)x x x f x x x x ⎧+⎪=⎨-+<⎪⎩≥，则不等式2(1)12f x x -+<的解集是 ▲ ．12． 在直角坐标系xOy 中，已知A （-1，0），B （0，1），则满足224PA PB -=且在圆224x y +=上的点P（第6题）注 意 事 项考生在答题前请认真阅读本注意事项及各题答题要求1. 本试卷共4页，包含填空题（第1题 - 第14题）、解答题（第15题 - 第20题）．本卷满分160分，考试时间为120分钟．考试结束后，请将答题卡交回．2. 答题前，请您务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．3. 请在答题卡上按照顺序在对应的答题区域内作答，在其他位置作答一律无效．作答必须用0.5毫米黑色墨水的签字笔．请注意字体工整，笔迹清楚．4. 如需作图，须用2B 铅笔绘、写清楚，线条、符号等须加黑、加粗．5. 请保持答题卡卡面清洁，不要折叠、破损．一律不准使用胶带纸、修正液、可擦洗的圆珠笔．的个数为 ▲ ．13． 已知正实数x ，y 满足24xy x y ++=，则x + y 的最小值为 ▲ ．14． 若2101m x mx -<+（m ≠ 0）对一切x ≥4恒成立，则实数m 的取值范围是 ▲ ．二、解答题：本大题共六小题，共计90分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤． 15． （本小题满分14分）在△ABC 中，设角A ，B ，C 的对边分别为a ，b ，c ，且1cos 2a C cb +=．（1）求角A 的大小；（2）若a 4b =，求边c 的大小．16． （本小题满分14分）如图，在四棱锥P - ABCD 中，四边形ABCD 是矩形，平面PCD ⊥平面ABCD ，M 为PC 中点．求证： （1）P A ∥平面MDB ； （2）PD ⊥BC ．（第16题）P M D C B A甲、乙两地相距1000km ，货车从甲地匀速行驶到乙地，速度不得超过80km/h ，已知货车每小时的运输成本（单位：元）由可变成本和固定成本组成，可变成本是速度平方的14倍，固定成本为a 元．（1）将全程运输成本y （元）表示为速度v （km/h ）的函数，并指出这个函数的定义域； （2）为了使全程运输成本最小，货车应以多大的速度行驶？18． （本小题满分16分） 如图，已知椭圆22221(0)x y a b a b+=>>的右顶点为A （2，0），点P （2e ，12）在椭圆上（e 为椭圆的离心率）． （1）求椭圆的方程；（2）若点B ，C （C 在第一象限）都在椭圆上，满足OC BA λ=，且0OC OB ⋅=，求实数λ的值．设数列{a n }满足a n +1 = 2a n + n 2 - 4n + 1．（1）若a 1 = 3，求证：存在2()f n an bn c =++（a ，b ，c 为常数），使数列{ a n + f (n ) }是等比数列，并求出数列{a n }的通项公式； （2）若a n 是一个等差数列{b n }的前n 项和，求首项a 1的值与数列{b n }的通项公式．20． （本小题满分16分）已知a ，b 为常数，a ≠ 0，函数()()e x bf x a x=+．（1）若a = 2，b = 1，求()f x 在（0，+∞）内的极值；（2）① 若a > 0，b > 0，求证：()f x 在区间[1，2]上是增函数；② 若(2)0f <，2(2)e f --<，且()f x 在区间[1，2]上是增函数，求由所有点(,)a b 形成的平面区域的面积．苏州市2014届高三调研测试数学Ⅱ（附加题） 2014．121．【选做题】本题包括A 、B 、C 、D 四小题，请选定其中两题．．．．．．，并在相应的．．．．．答题区域．．．．内作答．．．，若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．A ．选修4 - 1：几何证明选讲（本小题满分10分）如图，MN 为两圆的公共弦，一条直线与两圆及公共弦依次交于A ，B ，C ，D ，E ， 求证：AB ·CD = BC ·DE ．B ．选修4 - 2：矩阵与变换（本小题满分10分）已知a ，b ∈R ，若M =13a b -⎡⎤⎢⎥⎣⎦所对应的变换T M 把直线2x - y = 3变换成自身，试求 实数a ，b ．注 意 事 项考生在答题前请认真阅读本注意事项及各题答题要求1. 本试卷只有解答题，供理工方向考生使用．本试卷第21题有A 、B 、C 、D 4个小题供选做，每位考生在4个选做题中选答2题．若考生选做了3题或4题，则按选做题中的前2题计分．第22、23题为必答题．每小题10分，共40分．考试时间30分钟．考试结束后，请将答题卡交回. 2. 答题前，请您务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．3. 请在答题卡上按照顺序在对应的答题区域内作答，在其他位置作答一律无效．作答必须用0.5毫米黑色墨水的签字笔．请注意字体工整，笔迹清楚．4. 如需作图，须用2B 铅笔绘、写清楚，线条、符号等须加黑、加粗．5. 请保持答题卡卡面清洁，不要折叠、破损．一律不准使用胶带纸、修正液、可擦洗的圆珠笔．NME DC BA （第21-A 题）C ．选修4 - 4：坐标系与参数方程（本小题满分10分）在极坐标系中，求点M π(2,)6关于直线π4θ=的对称点N 的极坐标，并求MN 的长．D ．选修4 - 5：不等式选讲（本小题满分10分）已知x ，y ，z 均为正数．求证：111x y z yz zx xy x y z++++≥．【必做题】第22题、第23题，每题10分，共计20分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤． 22．（本小题满分10分）如图，在空间直角坐标系O - xyz 中，正四棱锥P - ABCD的侧棱长与底边长都为M ，N 分别 在P A ，BD 上，且13PM BN PA BD ==． （1）求证：MN ⊥AD ；（2）求MN 与平面P AD 所成角的正弦值．23．（本小题满分10分）设ξ为随机变量，从棱长为1的正方体ABCD - A 1B 1C 1D 1的八个顶点中任取四个点，当四点共面时，ξ= 0，当四点不共面时，ξ的值为四点组成的四面体的体积．（1）求概率P （ξ= 0）；（2）求ξ的分布列，并求其数学期望E (ξ)．（第22题）江苏省苏州市2014届高三1月第一次调研数学考试试题11 / 11。

江苏省2014届百校大联考模拟试卷地理注意事项:1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(综合题)两部分。

满分120分,考试用时100分钟。

2. 答题前,考生务必将自己的学校、班级、姓名写在密封线内。

第Ⅰ卷(选择题共60分)一、选择题:共60分。

(一)单项选择题:本大题共18小题,每小题2分,共36分。

在每小题给出的四个选项中,只有一项是符合题目要求的。

天山大峡谷陡峭狭长,山体主要由粗砂砾石组成,崖壁下部有大大小小洞穴分布,如图1所示。

图2为“岩石圈物质循环示意图”。

读图,回答12题。

1. 组成大峡谷的岩石所属类型主要为图2中的( )A. 甲B. 乙C. 丙D. 丁2. 形成崖壁下部洞穴的地质作用最有可能是图2中的( )A. ①B. ②C. ③D. ⑥2013年夏季我国东部大部分地区受高温灾害影响。

图3为“2013年7月某日14时副热带高压位置示意图”。

读图,回答34题。

3. 此时,下列地区最可能出现高温晴热天气的是( )A. 西南地区、西北地区B. 日本北部、朝鲜半岛C. 长江中下游、黄河下游D. 中南半岛、马来群岛4. 图中数码所在地区最可能有台风活动的是( )A. ①B. ②C. ③D. ④晨昏圈上有4个等分点,若其中位于南半球的一点(20°W),地方时正好为0时,据此回答56题。

5. 此时北京时间是( )A. 18:00B. 9:20C. 9:04D. 18:046. 关于此时地理现象的叙述,正确的是( )A. 天安门广场旗杆杆影朝向东北B. 江苏各地昼长与夜长差值最大C. 江苏各地日出地方时早于六点D. 地球公转速度较快水贫困测度,简单而言即对水贫困程度的测算。

图4为“我国农村水贫困测度空间格局示意图”。

读图,回答78题。

7. 我国农村水贫困程度( )A. 总体看,西北重于东南B. 由南向北逐渐加重C. 由东向西逐渐减轻D. 与经济水平成负相关8. 造成贵州省成为高水贫困地区的最主要因素是( )A. 气候B. 植被C. 地貌D. 土壤2013年9月国家领导人访问了土库曼斯坦、哈萨克斯坦、乌兹别克斯坦、吉尔吉斯斯坦,并出席二十国集团领导人第八次峰会、上海合作组织成员国元首理事会第十三次会议,行程如图5所示。

2014届江苏省高三年级百校联合调研考试英语卷一第一节：单项填空（共15题；每小题1分，满分15分）请认真阅读下面各题，从题中所给的Ａ、Ｂ、Ｃ、Ｄ四个选项中，选出最佳选项，并在答题卡上将该项涂黑。

21. Corruption is _______ problem in countries across the world, with developing countries often believed to be more serious, although there is no evidence to suggest this is _______ case.A. a; theB. the; aC. 不填; theD. a; a22. To protect the environment, the local government has put up a lot of ______ to warn thecitizens not to litter the ground.A. sighsB. sightsC. signalsD. signs23. Death toll from Typhoon Haiyan in the Philippines _______ 3,637, after the strongest stormthis year destroyed the central part of the country on Nov. 8, 2013.A. rose toB. arose fromC. rose fromD. raised to24. Don’t stand by when you come across________ have difficulty in supporting their familybecause of serious illness.A. WhoB. WhoeverC. WhicheverD. Whomever25. The keeper of the spring cleared away the leaves and branches, and wiped away the silt(淤泥) that would _______ have choked and polluted the fresh flow of water.A. thusB. otherwiseC. thereforeD. later26. Rather than sticking to the principles stubbornly, China is now adopting a new concept ineconomic policies in a/an _______way that shows its own characteristics.A. sustainableB. flexibleC. invisibleD. available27. —What if he failed in the next monthly examination again?—I don’t know. ______ heart and be reduced _____ the class?A. Will he lose; not to attendingB. Did he lose; to not attendingC. Had he lost; not to attendingD. Would he lose; to not attending28. ______ your teacher the problem with learning, theoretically, and they will help you.A. TellingB. To tellC. TellD. Having told29. — Oh, fantastic! What is your comment on the song Jingubang？— Terribly sorry! I _____.A. didn’t listenB. wasn’t listeningC. haven’t listenedD. hadn’t listened30. The famous director Li’an failed many times but he eventually _____ to achieve success.A. broke upB. broke offC. broke throughD. broke away31. The memory is still fresh in my mind _____ I was considered the apple of my formerboyfriend’s eyes during our stay in Aegean Sea.A. whenB. whereC. thatD. what32. He was admitted to our school two years ago, a top school in our hometown, _____ he hasbeen crazy about reading electronic novels, killing time.A. after thatB. since thatC. after whenD. since when33. The first time I saw him, what impressed me most were his waistline _____ nearly 3 Chinesechi and his obesity ______ 210 jin.A. measured ; weighedB. measuring; weighingC. measured; weighingD. measuring; weighed34. —Why didn’t you watch the program “Where are we going, Dad?”?—It was because something was wrong with the web TV _______ too many users were receiving it.A. whichB. thatC. through thatD. through which35.— What a bad luck! I have missed a golden chance !— Let it be. _______.A. A flower blooms more than once.B. A fault confessed is half corrected.C. A loveless life is living death.D. A problem shared is a problem halved.第二节：完形填空（共20小题；每小题1分，满分20分）请认真阅读下面短文，从短文后各题所给的A、B、C、D四个选项中，选出最佳选项，并在答题卡上将该项涂黑。

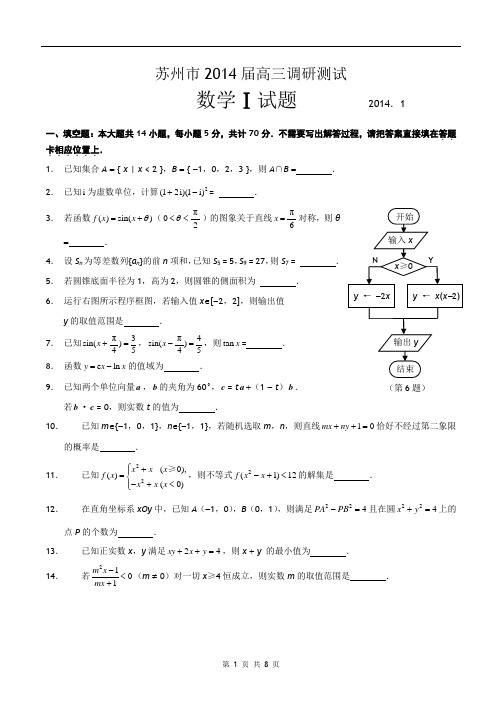
苏州市2014届高三调研测试数学Ⅰ试题 2014．1一、填空题：本大题共14小题，每小题5分，共计70分．不需要写出解答过程，请把答案直接填在答题．．卡相应位置上．．．．．．． 1． 已知集合A = { x | x < 2 }，B = { -1，0，2，3 }，则A ∩B = ． 2． 已知i 为虚数单位，计算2(12i)(1i)+-= ． 3． 若函数()sin()f x x θ=+（π02θ<<）的图象关于直线π6x =对称，则θ = ．4． 设S n 为等差数列{a n }的前n 项和，已知S 5 = 5，S 9 = 27，则S 7 = ． 5． 若圆锥底面半径为1，高为2，则圆锥的侧面积为 ． 6． 运行右图所示程序框图，若输入值x ∈[-2，2]，则输出值y 的取值范围是 ．7． 已知π3sin()45x +=，π4sin()45x -=，则tan x = ． 8． 函数e ln y x x =-的值域为 ．9． 已知两个单位向量a ，b 的夹角为60°，c = t a +（1 - t ）b ．若b ·c = 0，则实数t 的值为 ．10． 已知m ∈{-1，0，1}，n ∈{-1，1}，若随机选取m ，n ，则直线10mx ny ++=恰好不经过第二象限的概率是 ．11． 已知22(0),()(0)x x x f x x x x ⎧+⎪=⎨-+<⎪⎩≥，则不等式2(1)12f x x -+<的解集是 ．12． 在直角坐标系xOy 中，已知A （-1，0），B （0，1），则满足224PA PB -=且在圆224x y +=上的点P 的个数为 ．13． 已知正实数x ，y 满足24xy x y ++=，则x + y 的最小值为 ． 14． 若2101m x mx -<+（m ≠ 0）对一切x ≥4恒成立，则实数m 的取值范围是 ．结束 开始 x ≥0输出y （第6题）y ← x (x -2)输入xy ← -2x YN二、解答题：本大题共六小题，共计90分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．15．（本小题满分14分）在△ABC中，设角A，B，C的对边分别为a，b，c，且1cos2a C c b+=．（1）求角A的大小；（2）若15a=，4b=，求边c的大小．16．（本小题满分14分）如图，在四棱锥P-ABCD中，四边形ABCD是矩形，平面PCD⊥平面ABCD，M为PC中点．求证：（1）PA∥平面MDB；（2）PD⊥BC．PMD CBA甲、乙两地相距1000km，货车从甲地匀速行驶到乙地，速度不得超过80km/h，已知货车每小时的运输成本（单位：元）由可变成本和固定成本组成，可变成本是速度平方的14倍，固定成本为a元．（1）将全程运输成本y（元）表示为速度v（km/h）的函数，并指出这个函数的定义域；（2）为了使全程运输成本最小，货车应以多大的速度行驶？如图，已知椭圆22221(0)x y a b a b+=>>的右顶点为A （2，0），点P （2e ，12）在椭圆上（e 为椭圆的离心率）．（1）求椭圆的方程；（2）若点B ，C （C 在第一象限）都在椭圆上，满足OC BA λ= ，且0OC OB ⋅=，求实数λ的值．CBA yxO（第18题）设数列{a n }满足a n +1 = 2a n + n 2 - 4n + 1．（1）若a 1 = 3，求证：存在2()f n an bn c =++（a ，b ，c 为常数），使数列{ a n + f (n ) }是等比数列，并求出数列{a n }的通项公式；（2）若a n 是一个等差数列{b n }的前n 项和，求首项a 1的值与数列{b n }的通项公式．已知a ，b 为常数，a ≠ 0，函数()()e x bf x a x=+．（1）若a = 2，b = 1，求()f x 在（0，+∞）内的极值；（2）① 若a > 0，b > 0，求证：()f x 在区间[1，2]上是增函数；② 若(2)0f <，2(2)e f --<，且()f x 在区间[1，2]上是增函数，求由所有点(,)a b 形成的平面区域的面积．苏州市2014届高三调研测试数学Ⅱ（附加题）2014．1 21．【选做题】本题包括A、B、C、D四小题，请选定其中两题．．．．．．，并在相应的．．．．．答题区域．．．．内作答．．．，若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．A．选修4 - 1：几何证明选讲（本小题满分10分）如图，MN为两圆的公共弦，一条直线与两圆及公共弦依次交于A，B，C，D，E，求证：AB·CD = BC·DE．B．选修4 - 2：矩阵与变换（本小题满分10分）已知a，b∈R，若M=13ab-⎡⎤⎢⎥⎣⎦所对应的变换T M 把直线2x-y = 3变换成自身，试求实数a，b．C．选修4 - 4：坐标系与参数方程（本小题满分10分）在极坐标系中，求点Mπ(2,)6关于直线π4θ=的对称点N的极坐标，并求MN的长．D．选修4 - 5：不等式选讲（本小题满分10分）已知x，y，z 均为正数．求证：111x y zyz zx xy x y z++++≥．NMEDCBA【必做题】第22题、第23题，每题10分，共计20分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤． 22．（本小题满分10分）如图，在空间直角坐标系O - xyz 中，正四棱锥P - ABCD 的侧棱长与底边长都为32，点M ，N 分别在PA ，BD 上，且13PM BN PA BD ==． （1）求证：MN ⊥AD ； （2）求MN 与平面PAD 所成角的正弦值．PO N MDCB Axyz23．（本小题满分10分）设ξ为随机变量，从棱长为1的正方体ABCD - A 1B 1C 1D 1的八个顶点中任取四个点，当四点共面时，ξ= 0，当四点不共面时，ξ的值为四点组成的四面体的体积． （1）求概率P （ξ= 0）；（2）求ξ的分布列，并求其数学期望E (ξ)．（第22题）第11 页共8 页第12 页共8 页。

（本部分满分160分,时间120分钟）
一、填空题（本大题共14小题，每小题5分,共70分）
1.设复数122i ,i z z m =-=+(m ∈R ，i 为虚数单位)，若12
z z ⋅为实数,则m 的值为 ．
2。

已知集合{2,}A a a =+,{1,1,3}B =-，且A B ⊆，则实数a 的值是 ．
3。

某林场有树苗3000棵，其中松树苗400棵．为调查树苗的生长
情况，采用分层抽样的方法抽取一个容量为150的样本，则样本中松树苗的棵数为 ．
4.在ABC ∆的边AB 上随机取一点P ， 记CAP ∆和CBP ∆的面积分别为1S 和2
S ，
则122S S >的概率是 ．
【答案】13
【解析】
5。

已知双曲线22
221x y a b -=的一条渐近线方程为20x y -=，则该双曲线的离
心率为 ．
6．右图是一个算法流程图,则输出S 的值是 ．
考点：流程图和循环结构。

7.函数()lg(23)
x x
f x=-的定义域为．
8.若正三棱锥的底面边长为2,侧棱长为1，则此三棱锥的体积为．
【答案】1
6
【解析】
试题分析:记正三棱锥为P ABC
-,点P在底面ABC内的射影为点H，则。

2014年江苏省某校高考数学一模试卷一、填空题：本大题共14小题，每小题5分，共70分.把答案填在题中横线上． 1. 已知集合A ={x|2x >1}，B ={x|x <1}，则A ∩B =________． 2. 复数a−2i 1+2i（i 是虚数单位）是纯虚数，则实数a 的值为________．3. 一个社会调查机构就某地居民的月收入调查了10000人，并根据所得数据画了样本的频率分布直方图（如图）．为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10000人中再用分层抽样方法抽出100人作进一步调查，则在[2500, 3000)（元）月收入段应抽出________人．4. 某算法的伪代码如图所示，若输出y 的值为1，则输入x 的值为________．5. 已知双曲线x 24−y 2b=1的右焦点为(3, 0)，则该双曲线的渐近线方程为________．6. 已知2sinθ+3cosθ=0，则tan2θ=________．7. 已知正三棱柱底面边长是2，外接球的表面积是16π，则该三棱柱的侧棱长________． 8. 在R 上定义运算⊙:a ⊙b =ab +2a +b ，则不等式x ⊙(x −2)<0的解集是________． 9. 投掷一枚正方体骰子（六个面上分别标有1，2，3，4，5，6），向上的面上的数字记为a ，又n(A)表示集合的元素个数，A ={x||x 2+ax +3|=1, x ∈R}，则n(A)=4的概率为________．10. 函数f(x)=2sin(πx)−11−x，x ∈[−2, 4]的所有零点之和为________．11. 如图，PQ 是半径为1的圆A 的直径，△ABC 是边长为1的正三角形，则BP →⋅CQ →的最大值为________．12. 已知数列{a n }的首项a 1=a ，其前n 和为S n ，且满足S n +S n−1=3n 2(n ≥2)．若对任意的n ∈N ∗，a n <a n+1恒成立，则a 的取值范围是________．13. 已知圆C ：(x −2)2+y 2=1，点P 在直线l:x +y +1=0上，若过点P 存在直线m 与圆C 交于A 、B 两点，且点A 为PB 的中点，则点P 横坐标x 0的取值范围是________． 14. 记实数x 1，x 2，…，x n 中的最大数为max{x 1, x 2, ..., x n }，最小数为min{x 1, x 2, ..., x n }．已知实数1≤x ≤y 且三数能构成三角形的三边长，若t =max{1x , xy, y}⋅min{1x , xy, y}，则t 的取值范围是________．二、解答题：本大题共6小题，共90分.解答应写出文字说明、证明过程或演算步骤. 15. 已知a →=（3, −cos(ωx)），b →=(sin(ωx)，√3)，其中ω>0，函数f(x)=a →⋅b →的最小正周期为π．（1）求f(x)的单调递增区间；（2）在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ．且f(A2)=√3，a =√3b 求角A 、B 、C 的大小．16. 如图，在三棱锥P −ABC 中，PA ⊥PC ，AB =PB ，E ，F 分别是PA ，AC 的中点．求证： （1）EF // 平面PBC ；（2）平面BEF ⊥平面PAB ．17. 某音乐喷泉喷射的水珠呈抛物线形，它在每分钟内随时间t （秒）的变化规律大致可用y =−(1+4sin 2tπ60)x 2+20(sin tπ60)x(t 为时间参数，x 的单位：m)来描述，其中地面可作为x 轴所在平面，泉眼为坐标原点，垂直于地面的直线为y 轴． （1）试求此喷泉喷射的圆形范围的半径最大值；（2）若在一建筑物前计划修建一个矩形花坛并在花坛内装置两个这样的喷泉，则如何设计花坛的尺寸和两个喷水器的位置，才能使花坛的面积最大且能全部喷到水？ 18. 如图，在平面直角坐标系xOy 中，已知椭圆C:x 2a2+y 2b 2=1(a >b >0)的离心率为√32，以椭圆C 左顶点T 为圆心作圆T ：(x +2)2+y 2＝r 2(r >0)，设圆T 与椭圆C 交于点M 与点N ．（1）求椭圆C 的方程；（2）求TM →⋅TN →的最小值，并求此时圆T 的方程；（3）设点P 是椭圆C 上异于M ，N 的任意一点，且直线MP ，NP 分别与x 轴交于点R ，S ，O为坐标原点，求证：OR ⋅OS 为定值． 19. 已知数列{a n }满足下列条件： ①首项a 1=a ，(a >3, a ∈N ∗)； ②当a n =3k ，(k ∈N ∗)时，a n+1=a n 3；③当a n ≠3k ，(k ∈N ∗)时，a n+1=a n +1． （1）当a 4=1，求首项a 之值； （2）当a =2014时，求a 2014；（3）试证：正整数3必为数列{a n }中的某一项．20. 已知函数f(x)=a −blnx(a, b ∈R)，其图象在x =e 处的切线方程为x −ey +e =0．函数g(x)=kx (k >0)，ℎ(x)=f(x)x−1．（1）求实数a 、b 的值；（2）以函数g(x)图象上一点为圆心，2为半径作圆C ，若圆C 上存在两个不同的点到原点O 的距离为1，求k 的取值范围；（3）求最大的正整数k ，对于任意的p ∈(1, +∞)，存在实数m 、n 满足0<m <n <p ，使得ℎ(p)=ℎ(m)=g(n)．【选做题】在四小题中只能选做2题，每小题10分，共计20分．解答应写出文字说明、证明过程或演算步骤.选修4-1几何证明选讲21. 选修4−1：几何证明选讲如图，已知⊙O 的半径为1，MN 是⊙O 的直径，过M 点作⊙O 的切线AM ，C 是AM 的中点，AN 交⊙O 于B 点，若四边形BCON 是平行四边形； （1）求AM 的长； （2）求sin∠ANC ．选修4-2矩阵与变换22. 已知二阶矩阵M 有特征值λ=3及对应的一个特征向量e 1→=[11]，并且矩阵M 对应的变换将点(−1, 2)变换成(3, 0)，求矩阵M ．选修4-4参数方程与极坐标23. 已知曲线C 的极坐标方程是ρ=2sinθ，设直线l 的参数方程是{x =−35t +2，y =45t ，（t 为参数）．(1)将曲线C 的极坐标方程转化为直角坐标方程；(2)设直线l 与x 轴的交点是M ，N 为曲线C 上一动点，求|MN|的最大值．选修4-5不等式证明选讲24. 已知x 2+y 2=2，且|x|≠|y|，求1(x+y)2+1(x−y)2的最小值．25. 如图，PCBM 是直角梯形，∠PCB =90∘，PM // BC ，PM =1，BC =2，又AC =1，∠ACB =120∘，AB ⊥PC ，直线AM 与直线PC 所成的角为60∘． （1）求二面角M −AC −B 的余弦值； （2）求点C 到面MAB 的距离． 26. 已知二项式(√x 5+12x)m的展开式中第2项为常数项t ，其中m ∈N ∗，且展开式按x 的降幂排列．(1)求m 及t 的值．(2)数列{a n }中，a 1=t ，a n =t a n−1，n ∈N ∗，求证：a n −3能被4整除．2014年江苏省某校高考数学一模试卷答案1. {x|0<x <1}2. 43. 254. −1或20145. y =±√52x 6. 125 7.4√63 8. (−2, 1) 9. 13 10. 8 11. 12 12. (94, 154) 13. [−1, 2] 14. [1,1+√52)15. 解：（1）f(x)=3sinωx−√3cosωx=2√3(√32sinωx−12cosωx)=2√3sin(ωx−π6)，∵ T=2πω=π，∴ ω=2，即f(x)=2√3sin(2x−π6)，由2kπ−π2≤2x−π6≤2kπ+π2，k∈Z，得：kπ−π6≤x≤kπ+π3，k∈Z，则f(x)的单调递增区间为[kπ−π6, kπ+π3](k∈Z)；（2）∵ f(A2)=2√3sin(A−π6)=√3，∴ sin(A−π6)=12，∵ 0<A<π，∴ −π6<A−π6<5π6，即A=π3，∵ asinA =bsinB，a=√3b，∴ sinB=bsinAa =√33×√32=12，∵ a>b，∴ A>B，则B=π6，A=π3，C=π2．16. 证明：（1）在△APC中，因为E，F分别是PA，AC的中点，所以EF // PC，…又PC⊂平面PAC，EF⊄平面PAC，所以EF // 平面PBC；…（2）因为AB=PB，且点E是PA的中点，所以PA⊥BE；…又PA⊥PC，EF // PC，所以PA⊥EF，…因为BE⊂平面BEF，EF⊂平面BEF，BE∩EF=E，PA⊂平面PAB，所以平面PAB⊥平面BEF．…17. 花坛的长为10√2m，宽为5√2m，两喷水器位于矩形分成的两个正方形的中心，符合要求．…18. 依题意，得a＝2，e=ca =√32，∴ c=√3，b=√4−3=1，故椭圆C的方程为x 24+y2=1．方法一：点M与点N关于x轴对称，设M(x 1, y 1)，N(x 1, −y 1)，不妨设y 1>0． 由于点M 在椭圆C 上，所以y 12=1−x 124． (∗)由已知T(−2, 0)，则TM →=(x 1+2,y 1)，TN →=(x 1+2,−y 1)， ∴ TM →⋅TN →=(x 1+2,y 1)⋅(x 1+2,−y 1) ＝(x 1+2)2−y 12=(x 1+2)2−(1−x 124)=54x 12+4x 1+3=54(x 1+85)2−15．由于−2<x 1<2，故当x 1=−85时，TM →⋅TN →取得最小值为−15．由(∗)式，y 1=35，故M(−85,35)，又点M 在圆T 上，代入圆的方程得到r 2=1325． 故圆T 的方程为：(x +2)2+y 2=1325．方法二：点M 与点N 关于x 轴对称，故设M(2cosθ, sinθ)，N(2cosθ, −sinθ)， 不妨设sinθ>0，由已知T(−2, 0)，则TM →⋅TN →=(2cosθ+2,sinθ)⋅(2cosθ+2,−sinθ) ＝(2cosθ+2)2−sin 2θ ＝5cos 2θ+8cosθ+3 =5(cosθ+45)2−15．故当cosθ=−45时，TM →⋅TN →取得最小值为−15，此时M(−85,35)，又点M 在圆T 上，代入圆的方程得到r 2=1325．故圆T 的方程为：(x +2)2+y 2=1325．方法一：设P(x 0, y 0)，则直线MP 的方程为：y −y 0=y 0−y1x 0−x 1(x −x 0)，令y ＝0，得x R =x 1y 0−x 0y 1y 0−y 1，同理：x S =x 1y 0+x 0y 1y 0+y 1，故x R⋅x S=x12y02−x02y12y02−y12 (∗∗)又点M与点P在椭圆上，故x02=4(1−y02)，x12=4(1−y12)，代入(∗∗)式，得：x R⋅x S=4(1−y12)y02−4(1−y02)y12y02−y12=4(y02−y12)y02−y12=4．所以|OR|⋅|OS|＝|x R|⋅|x S|＝|x R⋅x S|＝4为定值．方法二：设M(2cosθ, sinθ)，N(2cosθ, −sinθ)，不妨设sinθ>0，P(2cosα, sinα)，其中sinα≠±sinθ．则直线MP的方程为：y−sinα=sinα−sinθ2cosα−2cosθ(x−2cosα)，令y＝0，得x R=2(sinαcosθ−cosαsinθ)sinα−sinθ，同理：x S=2(sinαcosθ+cosαsinθ)sinα+sinθ，故x R⋅x S=4(sin2αcos2θ−cos2αsin2θ)sin2α−sin2θ=4(sin2α−sin2θ)sin2α−sin2θ=4．所以|OR|⋅|OS|＝|x R|⋅|x S|＝|x R⋅x S|＝4为定值．19. （1）解：当a4=1时，因为a n+1=a n3，所以a3=3，此时，若a2=2，则a=6；若a2=9，则a=27或8，综上所述，a之值为6或8或27．…（2）解：当a=2014时，a2=2015，a3=2016，a4=672，a5=224，a6=225，a7=75，a8=25，a9=26，a10=27，a11=9，a12=3，a13=1，a14=2，a15=3，以下出现周期为3的数列，从而a2014=a13=1；…（3）证明：由条件知：若a n=3k，(k∈N∗)，则a n+1=a n3，a n+3≤a n3+2；若a n=3k+1，(k∈N∗)，则a n+1=a n+1=3k+2，a n+2=3k+3，a n+3=k+1<13a n+2；若a n=3k+2，(k∈N∗)，则a n+1=a n+1=3k+3，a n+2=13(a n+1)，a n+3≤13(a n+1)+1<13a n+2；…综上所述，a n+3≤13a n+2，从而a n−a n+3≥23(a n−3)，故当a n>3时，必有a n−a n+3>0，因a n∈N∗，故a n−a n+3≥1，所以数列{a n}中必存在某一项a m≤3（否则会与上述结论矛盾！）若a m=3，则a m+1=1，a m+2=2；若a m=2，则a m+1=3，a m+2=1，若a m =1，则a m+1=2，a m+2=3，综上所述，正整数3必为数列{a n }中的某一项． … 20. 解：（1） 当x =e 时，y =2，f′(x)=−bx ， 故{a −b =2−b e =1e，解得{a =1b =−1．（2）问题即为圆C 与以O 为圆心1为半径的圆有两个交点，即两圆相交． 设C(x 0，kx 0)，则1<√x 02+k 2x 02<3，即{k 2>x 02−x 04k 2<9x 02−x 04， ∵ x 02−x 04=−(x 02−12)2+14，∴ x 02−x 04≤14，∴ k 2>x 02−x 04必定有解； ∵ 9x 02−x 04=−(x 02−92)2+814，∴ 9x 02−x 04≤814，故k 2<9x 02−x 04有解，须k 2<814，又k >0，从而0<k <92．（3）显然g(x)=kx (k >0)在区间(1, +∞)上为减函数，于是g(n)>g(p)，若ℎ(p)=g(n)，则对任意p >1，有ℎ(p)>g(p)． 当x >1时，ℎ(x)>g(x)⇔k <x(1+lnx)x−1，令φ(x)=x(1+lnx)x−1(x >1)，则φ/(x)=x−2−lnx (x−1)2．令ϕ(x)=x −2−lnx(x >1)，则ϕ/(x)=x−1x>0，故ϕ(x)在(1, +∞)上为增函数，又ϕ(3)=1−ln3<0，ϕ(4)=2−ln4>0， 因此存在唯一正实数x 0∈(3, 4)，使ϕ(x 0)=x 0−2−lnx 0=0．故当x ∈(1, x 0)时，φ′(x)<0，φ(x)为减函数；当x ∈(x 0, +∞)时，φ′(x)>0，φ(x)为增函数，因此φ(x)在(1, +∞)上有最小值φ(x 0)=x 0(1+lnx 0)x 0−1，又x 0−2−lnx 0=0，化简得φ(x 0)=x 0∈(3, 4)，∴ k ≤3．下面证明：当k =3时，对0<x <1，有ℎ(x)<g(x)．当0<x <1时，ℎ(x)<g(x)⇔3−2x +xlnx >0．令ψ(x)=3−2x +xlnx(0<x <1)， 则ψ′(x)=lnx −1<0，故ψ(x)在(0, 1)上为减函数， 于是ψ(x)>ψ(1)=1>0．同时，当x ∈(0, +∞)时，g(x)=3x ∈(0,+∞)．当x ∈(0, 1)时，ℎ(x)∈R ；当x ∈(1, +∞)时，ℎ(x)∈(0, +∞)．结合函数的图象可知，对任意的正数p ，存在实数m 、n 满足0<m <n <p ，使得ℎ(p)=ℎ(m)=g(n)．综上所述，正整数k 的最大值为3．21. 解：（1）连接BM ，则 ∵ MN 是⊙O 的直径，∴ ∠MBN =90∘，∵ 四边形BCON 是平行四边形，∴ BC // MN ，又∵ AM 是⊙O 的切线，可得MN ⊥AM ，∴ BC ⊥AM ， ∵ C 是AM 的中点，∴ BC 是△ABM 的中线， 由此可得△ABM 是等腰三角形，即BM =BA ， ∵ ∠MBN =90∘，∴ ∠BMA =∠A =45∘，因此得到Rt △NAM 是等腰直角三角形，故AM =MN =2．… （2）作CE ⊥AN 于E 点，则 由（1），得△CEA 是等腰直角三角形，且AC =1 ∴ CE =√22AC =√22， ∵ Rt △MNC 中，MN =2，MC =1，∴ CN =√22+12=√5， 故Rt △ENC 中，sin∠ANC =CE NC=√1010．… 22. 解：设矩阵M =[abc d]，这里a ，b ，c ，d ∈R ， 则[a b c d ] [11]=3 [11]=[33]，故{a +b =3，c +d =3，①[a b cd ][−12]=[30]，故{−a +2b =3，−c +2d =0，②由①②联立解得{a =1，b =2，c =2，d =1，∴ M =[1 22 1]．23. 解：(1)曲C 的极坐标方程可化为：ρ2=2ρsinθ， 又x 2+y 2=ρ2，x =ρcosθ，y =ρsinθ．所以，曲C 的直角坐标方程为：x 2+y 2−2y =0．(2)将直线L 的参数方程化为直角坐标方程得：y =−43(x −2)．令y =0得x =2即M 点的坐标为(2, 0) 又曲线C 为圆，圆C 的圆心坐标为(0, 1)半径r =1，则|MC|=√5，∴ |MN|≤|MC|+r =√5+1． 所以|MN|max =√5+1.24. 解：∵ x 2+y 2=2，∴ (x +y)2+(x −y)2=4．∵ ((x +y)2+(x −y)2)(1(x+y)2+1(x−y)2)≥4，∴ 1(x+y)2+1(x−y)2≥1，当且仅当x =±√2，y =0，或x =0,y =±√2时，1(x+y)2+1(x−y)2取得最小值是1．25. 解：（1）∵ PC ⊥AB ，PC ⊥BC ，AB ∩BC =B ，∴ PC ⊥平面ABC ．在平面ABC 内，过C 作CD ⊥CB ，建立空间直角坐标系C −xyz （如图） 由题意有A(√32，−12，0)，设P(0, 0, z 0)(z 0>0)，则M(0,1,z 0)，AM →=(√32,−12,z 0)，CP →=(0,0,z 0)由直线AM 与直线PC 所成的角为600， 得AM →⋅CP →=|AM →|⋅|CP →|⋅cos600，即z 02=π2√z 02+3⋅z 0，解得z 0=1∴ CM →=(0,0,1)，CA →=(√32,−12,0)， 设平面MAC 的一个法向量为n 1→=(x 1,y 1,z 1)， 则{y 1+z 1=0√32y 1−12z 1=0，取x 1=1，得n 1→=(1,√3,−√3)，平面ABC 的法向量取为n 2→=(0,0,1)设n 1→与n 2→所成的角为θ，则cosθ=|n 1→|⋅|n 2→|˙=−√3√7．二面角M −AC −B 的平面角为锐角， 故二面角M −AC −B 的余弦值为√217．… （2）M(0, 1, 1)，A(√32，−12，0)，B(0, 2, 0)， ∴ AM →=(−√32,32,1)，MB→=(0,1,−1)．CB →=(0, 2, 0)，设平面MAB 的一个法向量m →=(x 2,y 2,z 2)， 则{−√32x 2+32y 2+z 2=0y 2−z 2=0，取z 2=1，得m →=(5√3,1,1)，则点C 到平面MAB 的距离d =|m →|˙=2√9331．… 26. 解：(1) T 2=C m 1(x 15)m−1(12x )1=C m 1⋅12⋅x m−65， 故m−65=0，m =6，t =C 61⋅12=3． (2)证明：①当n =1时，a 1=3，a 1−3=0，能被4整除． ②假设当n =k 时，a k −3能被4整除，即a k −3=4p ，其中p 是非负整数． 那么当n =k +1时，a k+1=34p+3=(1+2)4p+3=C 4p+30+C 4p+31⋅2+C 4p+32⋅22+⋯+C 4p+34p+324p+3=1+8p +6+4(C 4p+32+⋯+C 4p+34p+324p+1) =3+8p +4+4(C 4p+32+⋯+C 4p+34p+324p+1) =3+4(2p +1+C 4p+32+⋯+C 4p+34p+324p+1) 显然2p +1+C 4p+32+⋯+C 4p+34p+324p+1是非负整数， a k+1−3能被4整除．由①、②可知，命题对一切n ∈N ∗都成立．。

南通市2014届高三第一次调研测试数学Ⅰ参考答案与评分标准一、填空题：本大题共14小题，每小题5分，共70分．请把答案直接填写在答题卡相应位置上．．．．．．．．． 1． 已知集合U ={1，2，3，4，5}，A ={1，2，4}，则UA = ▲ ．【答案】{3，5}．2． 已知复数1z 13i =+，2z 3i =+(i 为虚数单位)．在复平面内，12z z -对应的点在第 ▲ 象限．【答案】二．3． 命题：“x ∃∈R ，0x ≤”的否定是 ▲ ．【答案】x ∀∈R ，||0x >．4． 在平面直角坐标系xOy 中，抛物线28y x =上横坐标为1的点到其焦点的距离为 ▲ ．【答案】3．5． 设实数x ，y 满足0 0 3 24 x y x y x y ⎧⎪⎪⎨+⎪⎪+⎩≤≤≥，≥，，，则32z x y =+的最大值是 ▲ ． 【答案】7．6． 如图是一个算法的流程图．若输入x 的值为2，则输出y 的值是 ▲ ．【答案】32-．7． 抽样统计甲，乙两个城市连续5天的空气质量指数(AQI)，数据如下：则空气质量指数(AQI)较为稳定(方差较小)的城市为 ▲ （填甲或乙）．【答案】乙．8． 已知正三棱锥的侧棱长为1．现从该正三棱锥的六条棱中随机选取两条棱，则这两条棱互相垂直的概率是 ▲ ． 【答案】25．9． 将函数()()sin 2f x x ϕ=+()0ϕ<<π的图象上所有点向右平移π6个单位后得到的图象关于原点对称，则ϕ等于 ▲ ．（第6题）【答案】π3．10．等比数列{a n }的首项为2，公比为3，前n 项和为S n ．若log 3［12a n (S 4m +1)］=9，则1n +4m的最小值是 ▲ ． 【答案】52．11．若向量()cos sin αα=，a ，()cos sin ββ=，b ，且2+⋅≤a b a b ，则cos()αβ-的值是 ▲ ． 【答案】1．12．在平面直角坐标系xOy 中，直线y x b =+是曲线ln y a x =的切线，则当a ＞0时，实数b 的最小值是 ▲ ． 【答案】1-．13．已知集合M ={(,)|3x y x -≤y ≤1}x -，N ={|P PA,(1,0),(1,0)}A B -，则表示M ∩N 的图形面积等于 ▲ ．【答案】43π+14．若函数2()2014(0)f x ax x a =++>对任意实数t ，在闭区间[1 1]t t -+，上总存在两实数1x 、2x ，使得12|()()|f x f x -≥8成立，则实数a 的最小值为 ▲ ．【答案】8．二、解答题：本大题共6小题，共90分．请在答题卡指定区域．．．．．．．内作答. 解答时应写出文字说明、证明过程或演算步骤． 15．(本小题满分14分)如图，在四棱柱1111ABCD A B C D -中，//AB CD ，1AB BC ⊥，且1AA AB =． （1）求证：AB ∥平面11D DCC ；（2）求证：1AB ⊥平面1A BC ．（1）证明：在四棱柱1111ABCD A B C D -中，//AB CD ，AB ⊄平面11D DCC ， CD ⊂平面11D DCC ，所以//AB 平面11D DCC ． ……………………………………………………………………6分 （2）证明：在四棱柱1111ABCD A B C D -中，四边形11A ABB 为平行四边形，又1AA AB =，故四边形11A ABB 为菱形．A 1B 1C 1CDD 1（第15题）从而11AB A B ⊥．…………………………………………………………………………… 9分 又1AB BC ⊥，而1A BBC B =，1 A B ，BC ⊂平面1A BC ， 所以1AB ⊥平面1A BC ． ………………………………………………………………… 14分16．(本小题满分14分)在△ABC 中，a ，b ，c 分别为角A ，B ，C 所对的边长，且c =－3b cos A ，tan C =34．（1）求tan B 的值；（2）若2c =，求△ABC 的面积．（1）解：由正弦定理，得 sin 3sin cos C B A =-，………………………………………………2分即sin()3sin cos A B B A +=-． 所以sin cos cos sin 3sin cos A B A B B A +=-． 从而sin cos 4sin cos A B B A =-．因为cos cos 0A B ≠，所以tan 4tan A B =-．……………………………………………………4分又tan tan tan tan()tan tan 1A B C A B A B +=-+=-，由（1）知，23tan 344tan 1B B =+， 解得1tan 2B =．………………………………………………………………………………6分（2）解：由（1），得sin A =sin B =，3sin 5C =． ………………………………10分由正弦定理，得sin sin 35c A a C ===．……………………………………………12分所以△ABC的面积为114sin 2223ac B ==． ………………………………14分17．(本小题满分14分)已知a 为实常数，y =f (x )是定义在(－∞，0)∪(0，+∞)上的奇函数，且当x <0时，f (x )=2x －a 3x2+1．（1）求函数f (x )的单调区间；（2）若f (x )≥a －1对一切x ＞0成立，求a 的取值范围．（1）解：由奇函数的对称性可知，我们只要讨论f (x )在区间(－∞，0)的单调性即可．f ′(x )＝2＋2a3x3，令f ′(x )＝0，得x ＝－a ． …………………………………………………2分①当a ≤0时，f ′(x )＞0，故f (x )在区间(－∞，0)是单调递增． ………………………4分②当a ＞0时，x ∈(－∞，－a )，f ′(x )＞0，所以f (x )在区间(－∞，－a )是单调递增．x ∈(－a ，0)，f ′(x )＜0，所以f (x )在区间(－a ，0)是单调减．………………………6分综上所述：当a ≤0时，f (x )单调增区间为(－∞，0)，(0，+∞)；当a ＞0时，f (x )单调增区间为(－∞，－a )，(a ，+∞)，单调减区间为(－a ，0)，(0，a )．…………………… 7分（2）解：因为f (x )为奇函数，所以当x ＞0时，f (x )＝－f (－x )＝－(－2 x －a 3x 2＋1)＝2x ＋ a 3x2－1． (9)分①当a ＜0时，要使f (x )≥a －1对一切x ＞0成立，即2x ＋ a 3x2≥a 对一切x ＞0成立．而当x ＝－a2＞0时，有－a +4a ≥a ，所以a ≥0，则与a ＜0矛盾．所以a ＜0不成立．.................................................................................11分 ②当a ＝0时，f (x )＝2x －1＞－1=a －1对一切x ＞0成立，故a ＝0满足题设要求． (12)分③当a ＞0时，由(1)可知f (x )在(0，a )是减函数，在(a ，+∞)是增函数．所以f min (x )=f (a )＝3a －1＞a －1，所以a ＞0时也满足题设要求． (13)分综上所述，a 的取值范围是[0,)+∞．…………………………………………………… 14分18．(本小题满分16分)如图，一块弓形薄铁片EMF ，点M 为EF 的中点，其所在圆O 的半径为4 dm （圆心O 在弓形EMF 内），∠EOF =23π．将弓形薄铁片裁剪成尽可能大的矩形铁片ABCD (不计损耗)， AD∥EF ，且点A 、D 在EF 上，设∠AOD =2θ．（1）求矩形铁片ABCD 的面积S 关于θ的函数关系式； （2）当矩形铁片ABCD 的面积最大时，求cos θ的值．（1）解：设矩形铁片的面积为S ，AOM θ∠=．当03θπ<<时（如图①），4cos 2AB θ=+，24sin AD θ=⨯，()()()4cos 224sin 16sin 2cos 1S ABAD θθθθ=⨯=+⨯=+．…………………………… 3分当32θππ<≤时（如图②），24cos AB θ=⨯，24sin AD θ=⨯， 故64sin cos 32sin2S AB AD θθθ=⨯==．（第18题）②①综上得，矩形铁片的面积S 关于θ的函数关系式为()16sin 2cos 1 0 332sin 2 .32S θθθθθπ⎧+<<⎪=⎨ππ⎪<⎩，，，≤……………………………………………………… 7分 （2）解：当03θπ<<时，求导，得 ()()()216cos 2cos 1sin 2sin 164cos cos 2S θθθθθθ'=++-=+-⎡⎤⎣⎦．令0S '=，得cos θ=…………………………………………………………… 10分记区间(0 )3π，0θ（唯一存在）．列表：又当32θππ<≤时，32sin2S θ=在[ )32ππ，上的单调减函数， 所以当0θθ=即cos θ时，矩形的面积最大．………………………………… 16分19．(本小题满分16分)如图，在平面直角坐标系xOy中，椭圆22221(0)y x a b a b+=>>过点(1，又椭圆内接四边形ABCD (点A 、B 、C 、D 在椭圆上)的对角线AC ，BD 相交于点1(1 )4P ，，且2AP PC =，2BP PD =．（1）求椭圆的方程；（2）求直线AB 的斜率．（1）解：依题意，22222 1314. c a a b c a b ⎧=⎪⎪⎪+=⎨⎪⎪=-⎪⎩，解得224 1.a b ⎧⎪⎨⎪⎩=，=所求椭圆的方程为2214x y +=． ………………………………………………………… 6分 （2）解：设()11 A x y ，，则221114x y +=．由2AP PC =，得()1133428x y C --，．…………………………………………………… 8分 （第19题）代入椭圆方程2214x y +=，得()()21213342148x y --+=．整理，得221111319()04216x y x y +-+-=，………………………………………………… 10分即1118x y +=-． ③ …………………………………………… 12分 设()22 B x y ，，同理可得2218x y +=-． ④ …………………………………………… 14分 ③-④，得21211y y x x -=--，即直线AB 的斜率为21211y y k x x -==--． …………………… 16分 20．(本小题满分16分)已知等差数列{a n }、等比数列{b n }满足a 1+a 2＝a 3，b 1b 2＝b 3，且a 3，a 2+ b 1，a 1+ b 2成等差数列，a 1，a 2，b 2成等比数列．（1）求数列{a n }和数列{b n }的通项公式；（2）按如下方法从数列{a n }和数列{b n }中取项：第1次从数列{a n }中取a 1， 第2次从数列{b n }中取b 1，b 2， 第3次从数列{a n }中取a 2，a 3，a 4， 第4次从数列{b n }中取b 3，b 4，b 5，b 6， ……第2n －1次从数列{a n }中继续依次取2n －1个项， 第2n 次从数列{b n }中继续依次取2n 个项， ……由此构造数列{c n }：a 1，b 1，b 2，a 2，a 3，a 4，b 3，b 4，b 5，b 6，a 5，a 6，a 7，a 8，a 9，b 7，b 8，b 9，b 10，b 11，b 12，…，记数列{c n }的前n 和为S n ．求满足S n ＜22014的最大正整数n ． （1）解：设等差数列{a n }的公差为d ，等比数列{b n }的公比为q ，依题意，得1112111111112111()2 () (2)()2[() ()(). a a d a d b b q b q a d a b q a d b a d a b q ++=+⎧⎪=⎪⎨+++=++⎪⎪+=⎩，，]，解得a 1=d =1，b 1=q =2．故a n =n ，b n =2n．…………………………………………………………………………… 6分（2）解：将a 1，b 1，b 2记为第1组，a 2，a 3，a 4，b 3，b 4，b 5，b 6记为第2组，a 5，a 6，a 7，a 8，a 9，b 7，b 8，b 9，b 10，b 11，b 12记为第3组，……以此类推，则第n 组中，有2n －1项选取于数列{a n }，有2 n 项选取于数列{b n }，前n 组共有n 2项选取于数列{a n }，有n 2＋n 项选取于数列{b n }，记它们的总和为P n ，并且有()22211222nn n n n P +++=+-． ………… 11分222014207120144545(451)222202P +-=+-->，2220141981334444(441)22(21)202P +-=---<．当2245(451)2n S +=＋（2＋22＋…＋22012）时，（第21—A 题）222014201345(451)22202n S +-=--+<．………………………………………………… 13分当2245(451)2n S +=＋（2＋22＋…＋22013)时，22201445(451)2202n S +-=-+>．可得到符合20142n S <的最大的n =452＋2012=4037．…………………………………… 16分数学Ⅱ（附加题）参考答案与评分标准21．【选做题】A ． 选修4—1：几何证明选讲 （本小题满分10分）在△ABC 中，已知CM 是∠ACB 的平分线，△AMC 的外接圆交BC 于点N ，且BN =2AM ． 求证：AB 2=AC ．证明：如图，在△ABC 中，因为CM 是∠ACM 的平分线，所以 AC AM BC BM=，① …………………………… 3分又因为BA 与BC 是圆O 过同一点B 的割线， 所以BM BA BN BC ⋅=⋅，即 BA BN BC BM=，…………………………………… 6分 又BN =2AM ，所以2 BA AM BC BM=，②…………………………… 8分 由①②，得AB 2=AC ． ……………………… 10分B ． 选修4—2：矩阵与变换 （本小题满分10分）设二阶矩阵A ，B 满足11234-⎡⎤=⎢⎥⎣⎦A ，()11001-⎡⎤=⎢⎥⎣⎦BA ，求1-B ． 解：设1a b c d -⎡⎤=⎢⎥⎣⎦B ，因为()111---=BA A B ，………………………………………………… 2分 所以10120134a b c d ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦，即21 20 340 341 a c b d a c b d +=⎧⎪+=⎪⎨+=⎪⎪+=⎩，，，，…………………………………………… 6分 解得2 1 3 21 2a b c d =-⎧⎪=⎪⎪⎨=⎪⎪=-⎪⎩，，，，所以1213122--⎡⎤⎢⎥=-⎢⎥⎣⎦B ．…………………………………………………… 10分C ．选修4—4：坐标系与参数方程 （本小题满分10分）在极坐标系中，已知曲线C ：2sin =ρθ，过极点O 的直线l 与曲线C 相交于A 、B 两点，AB =，求直线l 的方程．解：设直线l 的方程为0θθ=(ρ∈R )，() 0A 0，，()10 B ρθ，， …………………………………2分则1|0|AB =-=ρ0|2sin |θ．………………………………………………………………… 5分又AB0sin =θ …………………………………………………………… 7分解得03π=θ+2k π或03π=-θ+2k π，k ∈Z ．所以直线l 的方程为3π=θ或32π=θ (ρ∈R )． (10)分D ．选修4—5：不等式选讲 （本小题满分10分）已知x ，y ，z 均为正数，求证：111yx z yz zx xy x y z++++≥．证明：因为x ，y ，z 均为正数，所以()12y yx x yz zx z x y z++≥≥．……………………………… 4分同理可得2yz xy zx x+≥，2x z yz xy y +≥． ………………………………………………… 7分当且仅当x =y =z 均时，以上三式等号都成立．将上述三个不等式两边左，右两边分别相加，并除以2，得111yx z yz zx xy x y z ++++≥．…………………………………………………………… 10分【必做题】 22．（本小题满分10分）如图，设1P ，2P ，…，6P 为单位圆上逆时针均匀分布的六个点．现任选其中三个不同点构成一 个三角形，记该三角形的面积为随机变量S ． （1）求S =的概率；（2）求S 的分布列及数学期望()E S ．解：（1）从六个点任选三个不同点构成一个三角形共有36C种不同选法，其中S =的为有一个角是 30的直角三角形（如△145P P P ），共6212⨯=种，所以(361235C P S ===． ………………… 3分（2）S．S =的为顶角是120的等腰三角形（如△123P P P ），共6种，所以(366310C P S ==． …………………………………………………… 5分S =的为等边三角形（如△135P P P ），共2种，所以(362110C P S ==．…… 7分4（第22题）(361235C P S ==，故S 的分 又由（1）知布列为所以331()10510E S =++=．……………………………………… 10分23．（本小题满分10分）已知1，2，…，n 满足下列性质T 的排列1a ，2a ，…，n a 的个数为()f n （n ≥2，且n ∈N *）． 性质T ：排列1a ，2a ，…，n a 中有且只有一个1i i a a +>（i ∈{1，2，…，1n -}）．（1）求(3)f ；（2）求()f n ． 解：（1）当3n =时，1，2，3的所有排列有(1，2，3)，(1，3，2)，(2，1，3)，(2，3，1)， (3，1，2)，(3，2，1)，其中满足仅存在一个i ∈{1，2，3}，使得1i i a a +>的排列有 (1，3，2)，(2，1，3)，(2，3，1)，(3，1，2)，所以(3)4f =．………………………………………………………………………… 3分 （2）在1，2，…，n 的所有排列1(a ，2a ，…，)n a 中，若(11)i a n i n =-≤≤，从1n -个数1，2，3，…，1n -中选1i -个数按从小到大的顺序 排列为1a ，2a ，…，1i a -，其余按从小到大的顺序排列在余下位置，于是满足题意的排列个数为11C i n --．……………………………………………………………………… 6分若n a n =，则满足题意的排列个数为(1)f n -．……………………………………… 8分 综上，()f n =(1)f n -+1111Cn i n i ---=∑1(1)21n f n -=-+-．从而()33212()(3)(3)2112n n f n n f n --=--+=---． ……………………………… 10分。

2014届高三第一次诊断考试数学I一、填空题：本大题共14小题，每小题5分，共70分.请把答案填写在答题卡相应位置上．．．．．．．．. 1．设集合2{|log 2,}A x x x Z =<∈，则集合A 共有 ▲ 个子集． 2．已知角α的终边过点(4,3)P -，则sin 2cos αα+的值是 ▲ ．3．已知2sin()125πα+=，则7cos()12πα+的值等于 ▲ ．4．已知集合2{|lg(2)}A x y x x ==-，{|2,0}x B y y x ==>，则A B =＝ ▲ .5．已知函数()f x 是定义在(,0)(0,)-∞+∞上的偶函数，在(0,)+∞上单调递减，且1()02f >，(0f <，则函数()f x 的零点个数为 ▲ 个. 6．给出如下命题：①若“p 且q ”为假命题，则,p q 均为假命题；②命题“若a b >，则221a b >-”的否命题为“若,221a b a b ≤≤-则”； ③命题“00,20x x R ∃∈≤”的否定是“,20x x R ∀∈>”； ④ “5a ≥” 是 “2[1,2],0x x a ∀∈-≤恒成立”的充要条件.其中所有正确的命题的序号是 ▲ .7．已知1sin 3θ=-，则cos(2)πθ+的值等于 ▲ .8．已知2()23f x x x =-+，()1g x kx =-，则“2k ≤”是“()()f x g x ≥在R 上恒成立”的 ▲ 条件.（填“充分不必要、必要而不充分、充要、既不充分也不必要”之一）9．已知函数()ln a f x x x =-，(0,4]x ∈，若()y f x =图像上任意一点的切线的斜率12k ≥恒成立，则实数a 的取值范围是 ▲ . 10．设函数ln ()xf x x=在区间(,2)a a +上单调递增，则a 的取值范围为 ▲ . 11．已知函数33()sin ,[,]22f x x x x =∈-，若(31)(21)f a f a +<-，则a 的取值范围为 ▲ .12．已知函数2122,0,()log (1),0,x x x f x x x ⎧--≤⎪=⎨+>⎪⎩若,()2()x R f x ax a R ∀∈≤+∈，则a 的最大值为▲ .13．已知,,a b c R ∈，236a b c ==，(,1),a bn n n Z c+∈+∈，则n = ▲ . 14．已知0a >,函数()2x af x x a -=+[]70,410在区间上的最大值为，则a 的值为 ▲ .二、解答题：本大题共6小题，共90分.请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤.15．（本小题满分14分）已知,(0,)2αβπ∈，且7sin(2)5αβ+=sin α．（1）求证：tan()6tan αββ+=； （2）若tan 3tan αβ=，求α的值． 16．（本小题满分14分）设0a >，函数()sin cos sin cos ,[0,]2f x a x x x x x π=--∈的最大值为g (a )．（1）设sin cos ,t x x =+[0,]2x π∈，求t 的取值范围，并把()f x 表示为t 的函数()m t ；（2）求g (a )． 17．（本小题满分14分）设函数()f x 和()g x 是定义在集合D 上的函数，若,(())(())x D f g x g f x ∀∈=，则称函数()f x和()g x 在集合D 上具有性质()P D .（1）若函数()2f x x =和1()cos 2g x x =+在集合D 上具有性质()P D ，求集合D ； （2）若函数()2x f x m =+和()2g x x =-+在集合D 上具有性质()P D ，求m 的取值范围． 18．（本小题满分16分）某地发生某种自然灾害，使当地的自来水受到了污染．某部门对水质检测后，决定往水中投放一种药剂来净化水质. 已知每投放质量为m 个单位的药剂后，经过x 天该药剂在水中释放的浓度y （毫克/升）满足()y m f x =，其中()2log (4),046,42x x f x x x +<≤⎧⎪=⎨>⎪-⎩，当药剂在水中释放的浓度不低于6（毫克/升）时称为有效净化．．．．；当药剂在水中释放的浓度不低于6（毫克/升）且不高于18（毫克/升）时称为最佳净化．．．．. （1）如果投放的药剂质量为4=m ，试问自来水达到有效净化．．．．一共可持续几天? （2）如果投放的药剂质量为m ，为了使在7天（从投放药剂算起包括第7天）之内的自来水达到最佳净化．．．．，试确定应该投放的药剂质量m 的取值范围.19．（本小题满分16分）设a R ∈，函数32211()(21)()32f x x a x a a x =-+++．（1）若函数()()(0)f x g x x x'=≠为奇函数，求a 的值；（2）若函数()f x 在2x =处取得极小值，求a 的值； （3）若1a >-，试求[0,1]x ∈时，函数()f x 的最大值．20．（本小题满分16分）已知函数2()(33),[2,],2x f x x x e x a a =-+∈->-，其中e 是自然对数的底数． （1）若1a <，求函数()y f x =的单调区间；（2）求证：213()f a e>；（3）对于定义域为D 的函数()y g x =，如果存在区间[,]m n D ⊆，使得[,]x m n ∈时，()y g x =的值域是[,]m n ，则称[,]m n 是该函数()y g x =的“保值区间”． 设()()(2),(1,)x h x f x x e x =+-∈+∞，问函数()y h x =是否存在“保值区间”？若存在，请求出一个“保值区间”； 若不存在，请说明理由．2014届高三第一次诊断考试数学II （附加题）请在答题卡指定区域内．．．．．．．．作答，解答时应写出文字说明、证明过程或演算步骤． 21．（本小题满分10分）已知函数()lg(2)lg(2)f x x x =++-． （1）求函数()f x 的定义域；（2）记函数()()103f x g x x =+，求函数()g x 的值域． 22．（本小题满分10分）设α为锐角，若3cos()45απ+=，求cos(2)6πα+的值．23．（本小题满分10分）已知函数2()21f x x ax =+-，222(log )2a xg x x -=-．（1）求函数g (x )的解析式，并写出当a ＝1时，不等式g (x )＜8的解集；（2）若f (x )，g (x )同时满足下列两个条件：①[]1,4t ∃∈，使2(3)(4)f t f t --=；②(,],()8x a g x ∀∈-∞<．求实数a 的取值范围．24．（本小题满分10分）已知函数()ln f x ax x =-，()e 3ax g x x =+，其中a ∈R ． （1）求()f x 的极值；（2）若存在区间I ，使()f x 和()g x 在区间I 上具有相同的单调性，求a 的取值范围．海门市2014届高三第一次调研考试数学I 参考答案与评分标准1. 8；2. 1-；3. 25-；4. (1,2)；5. 2；6. ②③；7. 79-；8. 充分不必要；9. [4,)+∞；10. [0,2]e -；11. 1[,0)4-；12. 2；13. 4；14. 12．15. （1）证明：7sin(2)5αβ+=sin α，7sin[()]sin[()]5αββαββ∴++=+-，7sin()cos()sin [sin()cos()sin ]5cos cos αββαββαββαββ∴+++=+-+，sin()6cos()sin cos αββαββ∴+=+① ………4分,(0,),(0,)2αβαβπ∈∴+∈π，若cos()0αβ+=，则由①sin()0αβ+=与(0,)αβ+∈π矛盾，cos()0αβ∴+≠，………5分 ∴①两边同除以cos()cos αββ+得：tan()6tan αββ+=； ………7分（2）解：由（1）得tan()6tan αββ+=，tan tan 6tan 1tan tan αββαβ+=-， (10)分tan 3tan αβ=，1tan tan 3βα∴=，24tan 32tan 11tan 3ααα∴=-(0,)2απ∈，tan 1α∴=，从而4πα=． (14)分16. 解：（1）sin cos ),4t x x πα=++3[0,],[,]2444x x ππππ∈∴+∈，sin()124πα≤+≤，1t ∴≤≤，即t 的取值范围为， ………3分（另解：[0,]2x π∈，sin cos t x x ∴=+=，由2[0,]x π∈得0sin21x ≤≤，1t ∴≤≤sin cos t x x =+，21sin cos 2t x x -∴=， ………5分22111(),222t m t a t at t a t -∴=⋅-=--∈，0a>； ………7分（2）由二次函数的图象与性质得：①当1a <，即1)a >-时，1()2g a m a == ………10分②当1a ≥，即01)a <≤时，()(1)g a m ==………13分11),2()1).a a g a a ⎧>⎪∴=⎨⎪<≤⎩………14分17. 解：（1）()2f x x =，1()cos 2g x x =+， ∴由(())(())f g x g f x =得：112(cos )cos222x x +=+， ………2分变形得：24cos 4cos 30x x --=，1cos 2x ∴=-或3cos 2x =（啥去）， ………5分22,3x k k Z ππ∴=±∈，22,3D x x k k Z ππ⎧⎫∴==±∈⎨⎬⎩⎭； ………7分（2）()2x f x m =+，()2g x x =-+，∴由(())(())f g x g f x =得：22(2)2x x m m -++=-++， ………9分 变形得：42222x x m -=+，D ≠∅，且4242x x +≥，224m ∴-≥，1m ∴≤-，即m 的取值范围为(,1]-∞-． ………14分 （其它解法参照上述评分标准给分） 18. 解：（1）由题设：投放的药剂质量为4=m ，自来水达到有效净化．．．．4()6f x ⇔≥ ………2分3()2f x ⇔≥2043log (4)2x x <≤⎧⎪⇔⎨+≥⎪⎩或46322x x >⎧⎪⎨≥⎪-⎩ ………4分 04x ⇔<≤或46x <≤，即：06x <≤， 亦即：如果投放的药剂质量为4=m ，自来水达到有效净化．．．．一共可持续6天； ………8分 （2）由题设：(0,7],6()18x mf x ∀∈≤≤，0m >， ………10分()2log (4),046,42x x f x x x +<≤⎧⎪=⎨>⎪-⎩， 2(0,4],6log (4)18x m x ∴∀∈≤+≤，且6(4,7],6182mx x ∀∈≤≤-，………12分 26318m m ≥⎧∴⎨≤⎩且665318m m ⎧≥⎪⎨⎪≤⎩， ………14分3656m m ≤≤⎧∴⎨≤≤⎩， 56m ∴≤≤， 亦即：投放的药剂质量m 的取值范围为[5,6]. ………16分 19. 解：（1）22()(21)()f x x a x a a '=-+++， ………1分2()()(21),0f x a ag x x a x x x '+==+-+≠，()()(0)f x g x x x'=≠为奇函数，0,()()0x g x g x ∴∀≠-+=，即210,a +=12a ∴=-； ………4分（2）22()(21)()f x x a x a a '=-+++()[(1)]x a x a =--+ ………5分………7分由题设12a +=，1a ∴=； ………8分（另解：由(2)0f '=得：2320a a -+=，1a ∴=或2a =，再验证得1a =）（3）由（2）知：①1a ≥时，()f x 在[0,1]上是增函数，2max 1[()](1)6f x f a ∴==-；………10分②0a =时，()f x 在[0,1]上是减函数，max [()](0)0f x f ∴==； ………11分 ③01a <<时，()f x 在[0,]a 上是增函数，()f x 在[,1]a 上是减函数，32max 11[()]()32f x f a a a ∴==+； ………13分④10a -<<时，()f x 在[0,1]a +上是减函数，()f x 在[1,1]a +上是增函数，21(1)(0)(6f f a a a -=-=， ()1i a ∴-<<时，(1)(0)f f >，2max 1[()](1)6f x f a ∴==-； ()0ii a ≤<时，(1)(0)f f ≤，max [()](0)0f x f ∴==； ………15分 综上：2max 321,116[()]0,011,0 1.32a a a f x a a a a ⎧--<<≥⎪⎪⎪⎪∴≤≤⎨⎪⎪+<<⎪⎪⎩，， ………16分 20. 解：（1）2()()(1),[2,],2x x f x x x e x x e x a a '=-=-∈->-，………2分由表知道：①20a -<≤时，(2,)x a ∈-时，()0f x '>，∴函数()y f x =的单调增区间为(2,)a -； ………3分②01a <<时，(2,0)x ∈-时，()0f x '>，(0,)x a ∈时，()0f x '<，∴函数()y f x =的单调增区间为(2,0)-，单调减区间为(0,)a ；………4分（2）证明：2()(33),2a f a a a e a =-+>-2()()(1),2a a f a a a e a a e a '=-=->-，极小值………6分 332225()1313132(1)(2)0e f f e e e e----=-=>> (1)(2)f f ∴>- ………7分 由表知：[0,)a ∈+∞时，()(1)(2)f a f f ≥>-， (2,0)a ∈-时，()(2)f a f >-，2a ∴>-时，()(2)f a f >-，即213()f a e>； ………8分（3）2()()(2)(21),(1,)x xh x f x x e x x e x =+-=-+∈+∞，2()(1),(1,)x h x x e x '=-∈+∞， (1,)x ∴∈+∞时，()0h x '>，()y h x ∴=在(1,)+∞上是增函数， ………9分 函数()y h x =存在“保值区间”1[,]()()n m m n h m m h n n >>⎧⎪⇔=⎨⎪=⎩⇔关于x 的方程()h x x =在(1,)+∞有两个不相等的实数根，………11分 令2()()(21),(1,)x H x h x x x x e x x =-=-+-∈+∞， 则2()(1)1,(1,)x H x x e x '=--∈+∞， 2[()](21),(1,)x H x x x e x ''=+-∈+∞(1,)x ∈+∞时，2[()](21)0x H x x x e ''=+->， ()H x '∴在(1,)+∞上是增函数，2(1)10,(2)310H H e ''=-<=->，且()y H x '=在[1,2]图象不间断， 0(1,2),x ∴∃∈使得0()0H x '=， ………13分 0(1,)x x ∴∈时，()0H x '<，0(,)x x ∈+∞时，()0H x '>，∴函数()y H x =在0(1,)x 上是减函数，在0(,)x +∞上是增函数，(1)10H =-<，0(1,],()0x x H x ∴∈<，∴函数()y H x =在(1,)+∞至多有一个零点，即关于x 的方程()h x x =在(1,)+∞至多有一个实数根， ………15分 ∴函数()y h x =是不存在“保值区间”． ………16分 （其它解法参照上述评分标准给分）海门市2014届高三第一次调研考试数学II 参考答案与评分标准21. 解：（1）由2020x x +>⎧⎨->⎩得22x -<<，∴函数()f x 的定义域为(2,2)-； ………5分（2）()2()103(2)(2)334,(2,2)f x g x x x x x x x x =+=+-+=-++∈-，325(2)6,()24g g -=-=，∴函数()g x 的值域为25(6,]4-． ………10分22. 解：(0,)2πα∈，(,)444αππ3π∴+∈，3cos()45απ+=，4sin()45απ∴+=， ………2分24sin 2()425απ∴+=，7cos2()425απ+=- ………6分 cos(2)cos[2()]64πππαα∴+=+-1cos2()2()244ππαα=++． ………10分 （其它解法参照上述评分标准给分） 23. 解：（1）令2log t x =，则2t x =，222(log )2a xg x x -=-，22()22t t a g t +-∴=-22()22x x ag x +-∴=-， ………2分 当a ＝1时，不等式21()8228(22)(24)0x x x x g x +<⇔-<⇔+-<， 24x ∴<，2x ∴<，即不等式g (x )＜8的解集为(,2)-∞； ………4分（2）2()21f x x ax =+-，∴由①[1,4]t ∃∈，2(3)(4)f t f t --=得：[1,4]t ∃∈，2(3)42at t --+=-即[1,4]t ∃∈，22(2)2a t =--，[2,6]a ∴∈-； ………6分由②(,],()8x a g x ∀∈-∞<得：48(,],222xa xx a ∀∈-∞>-令2,(,]x x a μ=∈-∞，则882,(0,2]2x a x y μμμ=-=-∈，易知函数8y μμ=-在(0,2]a 上是增函数，max 822a a y ∴=-，24812,21log 3222a a a a a ∴>-∴<<+， ………9分综上，实数a 的取值范围为21[2,1log 3)2-+． ………10分24. 解：（1）11()ax f x a x x-'=-=，0,x a R >∈ ① 当0a ≤时，()0f x '<，故()f x 在(0,)+∞上单调递减，从而()f x 没有极大值，也没有极小值． ………2分② 当0a >时，令()0f x '=，得1x =，()f x ∴的极小值为()1ln f a a=+；没有极大值； ………4分（2）()e 3,(,),axg x a x a R '=+∈-∞+∞∈0(1)当0a >时，显然 ()0g x '>，从而()g x 在(,)-∞+∞上单调递增，由（1）得，此时()f x 在1(,)a+∞上单调递增，符合题意；………5分0(2)当0a =时，()g x 在(,)-∞+∞上单调递增，()ln f x x =-在(0,)+∞上单调递减，不合题意． ………6分0(3)当0a <时，令()0g x '=，则13ln()x =-， ()g x ' 0a <时， ∴由题设得：13ln()0a a->，3a ∴<- ………9分综上a 的取值范围是(,3)(0,)-∞-+∞． ………10分。

启东市2014届第一次测试数学试题注 意 事 项1．本试卷包含填空题（第1题～第14题，共14题）、解答题（第15题～第20题，共6题），总分160分，考试时间为120分钟．2．答题前，请您务必将自己的姓名、考试证号用书写黑色字迹的0.5毫米签字笔填写在答题纸上．3．请认真核对监考员所粘贴的条形码上的姓名、考试证号是否与您本人的相符． 4．请用书写黑色字迹的0.5毫米签字笔在答题卡纸的指定位置答题，在其它位置作答一律无效．一、填空题：本大题共14小题，每小题5分，共70分。

不需写出解答过程，请把答案直接填写在答题卡相应位置上。

1．已知集合(]2 1A =-，，[)1 2B =-，，则A B = ▲ ．2．命题“若a b >，则22ac bc >（∈b a ,R ）”否命题的真假性为 ▲ （从真、假中选一个）3．已知扇形的周长是8cm ，圆心角为2 rad ，则扇形的弧长为 ▲ cm ．4．已知α为钝角，且21sin =α，则与角α终边相同的角β的集合为 ▲ ．5．集合},3,2,0,1,2{--=A ,集合},1|||{R x x x B ∈>=,集合B A 的真子集有 ▲ 个． 6．化简)23cos()2sin()sin()cos(αππααππα-⋅-⋅--的结果是 ▲ ．7．已知命题p ：“正数a 的平方不等于0”，命题q ：“若a 不是正数，则它的平方等于0”， 则p 是q 的 ▲ ．（从“逆命题、否命题、逆否命题、否定”中选一个填空） 8．已知01a <<，则满足xx acos sin ＞1的角x 所在的象限为 ▲ ．9．定义在R 上的函数()f x ，对任意x ∈R 都有)()3(x f x f =+，当)0,3(-∈x 时，x x f 3)(=，则=)2014(f ▲ ．10．若函数k x x x f -+=2log )((k ∈Z *)在区间(2,3)上有零点，则k = ▲ ．11．设f (x )是定义在R 上的奇函数，且y = f (x )的图像关于直线x =12对称，则f (1)+ f (2)+f(3)+f (4) +f (5)=__ ▲___．12．曲线2(1)1()e (0)e 2x f f x f x x '=-+在点(1，f (1))处的切线方程为 ▲ ． 13．正实数21,x x 及)(x f 满足1414)(+-=x x x f ，且1)()(21=+x f x f ，则)(21x x f +的最小值等于 ▲ ．14．已知平面上的线段l 及点P ，任取l 上的一点Q ，线段PQ 长度的最小值称为点P 到线段l 的距离，记为d (P ,l )．设A (-3,1)，B (0,1)，C (-3,-1)，D (2,-1)，AB l =1,CD l =2，若),(y x P 满足),(),(21l P d l P d =，则y 关于x 的函数解析式为 ▲ ．二、解答题：本大题共6小题，共90分。