电磁学4电势梯度电势能
- 格式:ppt
- 大小:1.43 MB
- 文档页数:26
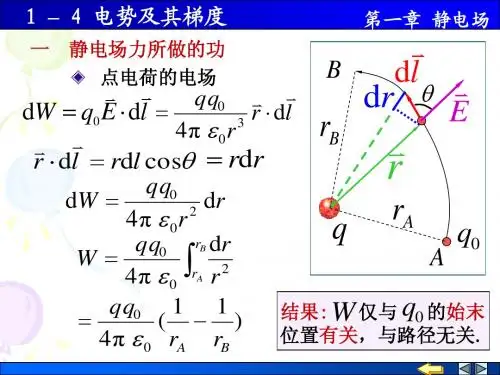


《电势能和电势》电势梯度理解《电势能和电势——电势梯度理解》在物理学中,电势能和电势是非常重要的概念,而电势梯度则是对电势变化的一种描述。
理解这些概念对于深入掌握电学知识至关重要。
首先,让我们来谈谈电势能。
想象一下,有一个带电荷的粒子在电场中。
就好像这个粒子在一个有力量的“场”里,这个场能够对它做功。
当这个粒子在电场中移动时,电场对它做的功就转化为了粒子的电势能。
电势能就像是粒子在电场中储存的一种能量。
比如说,一个正电荷在正的电势区域,它就具有较高的电势能;而在负的电势区域,它的电势能就较低。
接下来是电势。
电势可以理解为电场中某一点的“电位”。
它类似于地理中的海拔高度,只不过这里的“高度”是表示电场中电势能的大小。
电势是一个相对的概念,我们通常会选择一个参考点,规定它的电势为零,然后来确定其他点的电势。
那么,什么是电势梯度呢?简单来说,电势梯度就是电势在空间中变化的快慢程度。
想象一下,你在爬山,山坡陡峭的地方就是梯度大的地方,你需要花费更多的力气才能往上爬;而平缓的地方梯度小,爬起来相对轻松。
在电场中也是一样,电势梯度大的地方,电场强度就大,电荷受到的力也就越大;电势梯度小的地方,电场强度就小,电荷受到的力也小。
为了更直观地理解电势梯度,我们可以通过一个简单的例子来说明。
假设有两块平行的金属板,分别带有正电荷和负电荷,从而在它们之间形成了一个均匀的电场。
我们沿着电场线的方向来观察电势的变化。
如果从带正电荷的金属板向带负电荷的金属板移动,电势会逐渐降低。
而且,在这个均匀电场中,电势的变化是均匀的,也就是说电势梯度是恒定的。
但在实际情况中,电场往往不是均匀的,电势梯度也会随之变化。
比如,在一个点电荷产生的电场中,离电荷越近的地方,电势梯度越大;离电荷越远的地方,电势梯度越小。
电势梯度在许多实际应用中都有着重要的作用。
例如,在电子设备中,了解电势梯度可以帮助我们设计更有效的电路和器件。
在电力传输中,对电势梯度的掌握有助于优化输电线路,减少能量损耗。

高中物理电磁学知识点一)电场1、库仑力:F=kq1q2/r^2(适用条件:真空中点电荷)其中k=9×10^9 N·m^2/C^2为静电力恒量。
电场力:F = Eq(F与电场强度的方向可以相同,也可以相反)2、电场强度:电场强度是表示电场强弱的物理量。
定义式:E=F/q,单位为N/C。
对于点电荷,电场场强E=kq/r^2;对于匀强电场,电场场强E=U/d。
3、电势,电势能:电势:Φ=E·d(顺着电场线方向,电势越来越低)电势能:E电=qΦ4、电势差U,又称电压:U=WAB/q,其中WAB为电场力做功。
5、电场力做功和电势差的关系:WAB=qUAB6、粒子通过加速电场:粒子受到电场力加速,速度增加。
7、粒子通过偏转电场的偏转量:粒子通过偏转电场的偏转角与电场强度、粒子电荷、粒子速度和偏转电场长度有关。
8、电的电容:c=Q/U,其中Q为电的带电量,U为电的电压。
对于平行板电,电容为c=εS/4πkd,其中ε为介电常数,S为平行板面积,d为平行板间距。
二)直流电路1、电流强度的定义:I=ΔQ/Δt,单位为A(安培)。
微观式:I=nev,其中n为单位体积电子个数,e为电子电荷量,v为电子漂移速度。
2、电阻定律:U=IR,其中U为电压,I为电流强度,R为电阻。
电阻率ρ只与导体材料性质和温度有关,与导体横截面积和长度无关,单位为Ω·m。
3、串联电路总电阻:R=R1+R2+R3,电压分配为U1=R1/(R1+R2)·U,U2=R2/(R1+R2)·U,功率分配为P1=R1/(R1+R2)·P,P2=R2/(R1+R2)·P。
4、并联电路总电阻:1/R=1/R1+1/R2+1/R3,两个电阻并联R=R1R2/(R1+R2),电流分配为I1=R2/(R1+R2)·I2,功率分配为P1=R2/(R1+R2)·P,P2=R1/(R1+R2)·P。


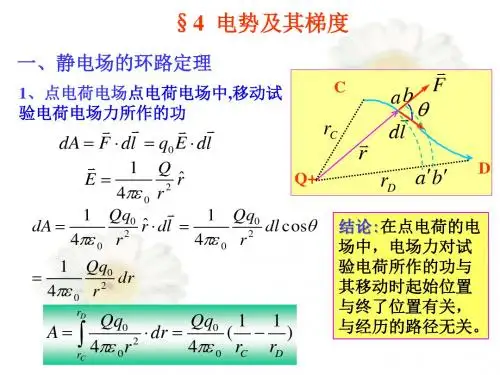

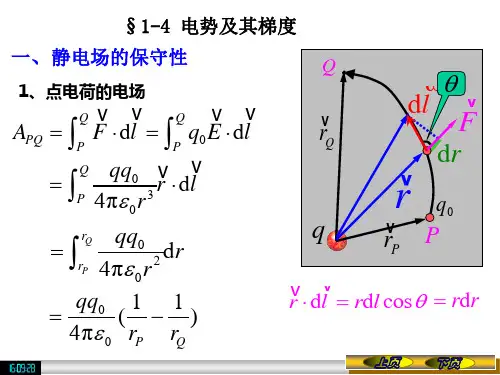


电势能和电势的知识点总结公式电势能和电势是电学中重要的概念,它们描述了电场中电荷的能量和电场的特性。
本文将从电势能和电势的定义、计算公式以及它们的应用等方面进行详细介绍。
一、电势能的定义与计算公式电势能是指电场中带电体由于位置的变化而具有的能量。
当一个电荷在电场中从A点移动到B点时,电势能的变化等于电荷移动过程中受到的力所做的功。
电势能的计算公式为:电势能(U)= 电荷(q)× 电势差(ΔV)其中,电势差(ΔV)表示A点到B点的电势差异,单位是伏特(V)。
二、电势的定义与计算公式电势是指电场中单位正电荷所具有的能量。
电势可以理解为电场对电荷施加的力的强弱。
电势的计算公式为:电势(V)= 电势能(U)/ 电荷(q)电势的单位也是伏特(V)。
三、电势能和电势的关系电势能和电势是密切相关的,它们之间存在着如下关系:电势差(ΔV)= 电势(V2)- 电势(V1)即电势差等于两个点的电势之差。
根据电势差的定义,可以得出电势能的计算公式:电势能(U)= 电荷(q)× 电势差(ΔV)这个公式也是电势能的定义公式之一。
四、电势能和电势的应用电势能和电势在电学中有着广泛的应用。
以下是其中几个应用领域:1. 电荷在电场中的运动:电势能和电势可以描述电荷在电场中的运动情况。
当电荷在电场中受到力的作用时,根据电势能的定义,可以计算出电势能的变化。
这对于研究电荷的运动轨迹和速度等信息非常重要。
2. 电势差和电场强度:电势差和电场强度是电学中两个重要的概念。
电势差可以用来计算电场强度,而电场强度又可以用来计算电势差。
它们之间的关系是电场强度等于电势差的负梯度。
3. 电势能的转化和利用:电势能可以被转化和利用。
例如,将电势能转化为动能或热能,可以用于做功、发电等。
这在能量转化和利用方面具有重要的意义。
4. 电势能的储存:电势能也可以被储存。
例如,将电势能储存在电容器中,可以实现电能的储存和释放。
这在电路中具有重要的应用,如电容器的充放电过程。