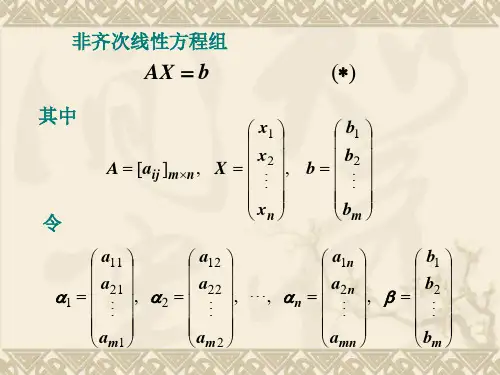
第2.5节非齐次线性方程组
- 格式:ppt
- 大小:396.50 KB
- 文档页数:22

线性方程组解的构造(解法)一、齐次线性方程组的解法【定义】r ()=r<n, 若AX=0(A为m n矩阵)的一组解为ξ1,ξ2,L ,ξn r, 且知足:A(1)ξ1,ξ2,L, ξn r线性没关 ;(2)AX=0的) 任一解都可由这组解线性表示 .则称ξ,ξ,L ,ξ为 AX=0的基础解系 .12n r称 X k1ξ1k2ξ2L k n rξn r为 AX = 0的通解。
此中 k1, k2, , k n-r为随意常数).齐次线性方程组的重点问题就是求通解,而求通解的重点问题是求基础解系.【定理】若齐次线性方程组AX=0有解,则(1)若齐次线性方程组AX=0( A 为m n 矩阵)知足 r ( A)n ,则只有零解;(2)齐次线性方程组有非零解的充要条件是 r ( A) n .(注:当 m n 时,齐次线性方程组有非零解的充要条件是它的系数队列式 A 0.)注: 1、基础解系不独一,可是它们所含解向量的个数同样,且基础解系所含解向量的个数等于n r ( A) .2、非齐次线性方程组AX B 的同解方程组的导出方程组(简称“导出组”)为齐次线性方程组AX O 所对应的同解方程组。
由上述定理可知,若 m 是系数矩阵的行数(也即方程的个数), n 是未知量的个数,则有:( 1)当 m n 时, r ( A) m n ,此时齐次线性方程组必定有非零解,即齐次方程组中未知量的个数大于方程的个数就必定有非零解;( 2)当m n 时,齐次线性方程组有非零解的充要条件是它的系数队列式 A0 ;( 3)当m n 且 r ( A) n 时,若系数矩阵的队列式 A 0 ,则齐次线性方程组只有零解;( 4)当m n 时,若 r ( A)n ,则存在齐次线性方程组的同解方程组;若 r ( A)n ,则齐次线性方程组无解。
1、求AX = 0 ( A 为m n矩阵)通解的三步骤(1)A行 C (行最简形);写出同解方程组CX =0.(2)求出 CX =0的基础解系ξ1,ξ2,L,ξn r;(3)写出通解X k1ξ1k2ξ2 L k n rξn r此中 k1, k2, , k n-r为随意常数.2x 1 3x 2 x 3 5x 4 0, 3x 1 x 2 2x 3 x 4 0,【例题 1】 解线性方程组x 2 3x 3 6x 4 0,4x 1 x 12x 24x 37x 40.解法一: 将系数矩阵 A 化为阶梯形矩阵明显有 r ( A)4 n ,则方程组仅有零解,即x 1 x 2 x 3 x 4 0 .解法二: 因为方程组的个数等于未知量的个数(即 mn )(注意: 方程组的个数不等于未知量的个数 (即m n ),不能够用队列式的方法来判断) ,进而可计算系数矩阵 A 的队列式:2 3 1 5 3 1 2 1 A1 3 327 0 ,知方程组仅有零解,即 x 1 x2 x3 x4 0 .4 6 1247注: 此法仅对 n 较小时方便x 1 x 2 x 3 x 4 x 5 0, 3x 12x 2 x 3 x 4 3x 5 0,【例题 2】 解线性方程组x 2 2 x 3 2x 4 6x 5 0,5x 1 4x 23x 33x 4x 50.解: 将系数矩阵 A 化为简化阶梯形矩阵可得 r ( A) 2n ,则方程组有无量多解,其同解方程组 为x 1 x 3x 4 5x 5 ,(此中 x 3 , x 4 , x 5 为自由未知量)x 22x 3 2 x 46x 5.令 x 3 1 , x 4 0 , x 5 0 ,得 x 1 1, x 2 2 ; 令 x 3 0 , x 4 1, x 5 0 ,得 x 1 1, x 2 2 ; 令 x 30 , x 4 0 , x 51,得 x 1 5, x 26 ,于是获得原方程组的一个 基础解系 为1 1 5 22611,20,30.0 1 01所以,原方程组的 通解 为Xk 1 1 k 2 2 k 3 3 ( k 1 , k 2 , k 3 R ) .二、非齐次线性方程组的解法求 AX = b 的解( A m n, r ( A)r )用初等行变换求解,不如设前r 列线性没关c 11 c12L c1 rL c1n d1 c22 L c2r L c2 n d2 O M M M行c rr L crn d r此中 c ii0(i 1,2,L , r ), 所以知( AMb)dr 1 0 M 0(1) d r 10 时,原方程组无解.(2)d r 1 0, r n 时,原方程组有独一解.(3) d r 10, r < n 时,原方程组有无量多解.其通解为 X0k1ξ1 k2ξ2 L kn rξn r, k1 , k2,L , k n r为随意常数。



非齐次线性方程矩阵求解非齐次线性方程矩阵求解是线性代数中的一种重要内容。
它用于求解非齐次线性方程组,是求解线性方程组的基础,也是机器学习中非常常用的一种技术。
本文运用矩阵理论来研究非齐次线性方程组的求解方法。
一、阵理论的基础矩阵理论是实数空间和复数空间的一种数学工具,它用来研究向量空间,描述和分析一般线性变换,以及用线性方程组的形式来求解线性变换。
矩阵的定义:矩阵是一种模板,用于描述矩阵变换的表示形式,包括实数空间中的矩阵和复数空间中的矩阵,记作A,n×n。
其中A=(ai,j )i,j=1,2,…,n,其中ai,j实数或复数。
二、阵方程通过上面矩阵的定义,我们可以知道,每个矩阵都有一系列方程,这些方程中包括了矩阵变换的形式:矩阵方程:AX=B其中A是n×n的矩阵,X是n×1的列向量,B是n×1的列向量。
三、阵的求解当我们已经知道矩阵的形式,接下来就是要求解这个方程了。
求解矩阵的方法是,先把矩阵A分解成几个具有更简单形式的矩阵,然后求解每个矩阵,在把答案合成一个新矩阵。
1.斯消元法:高斯消元法是最常用的一种求解矩阵的方法,它的思想是先把矩阵分解成三角形矩阵,然后把矩阵中的每一行进行消元,最后求解出答案。
2.矩阵法:逆矩阵法是一种更容易的求解矩阵的方法,它的思想是先求出矩阵A的逆矩阵,然后把原矩阵A和答案B矩阵相乘,就得到了X,即解。
四、齐次线性方程组非齐次线性方程组是一组非齐次线性方程,它的形式可以表示为:AX=B。
其中,A是n×n的矩阵,X是n×1的列向量,B是n×1的列向量,并且B不为零。
非齐次线性方程的解可以用上述求解矩阵的两种方法来求解。
五、例分析下面给出一个关于非齐次线性方程组的实例:A=[3, -2, 4][5, 8, -1][2, 1, 6]B=[11][25][12]解:用高斯消元法求解,首先将矩阵A分解为三角形矩阵:[3, -2, 4][0, 5, -6][0, 0, 0]接下来,对每一行进行消元,将矩阵A转换为:[1, -2/3, 1][0, 1, -6/5][0, 0, 0]由于矩阵A第三行为0,这时可以知道,原方程组的解是不存在的。




线代知识点总结一、线性代数的基本概念1.1 向量向量是具有大小和方向的量,通常用有向线段表示。
在数学中,向量可以用坐标表示,如二维向量可以表示成(x, y),三维向量可以表示成(x, y, z)。
向量还可以表示为列向量或行向量。
1.2 矩阵矩阵是由一组按照长方阵列的数按照一定规律排列的数集合,其中横的一排叫做行,纵的一排叫做列。
矩阵通常用大写字母表示,如A,B等。
1.3 线性组合给定一组向量{v1, v2, …, vn}和一组标量{c1, c2, …, cn},称c1v1 + c2v2 + … + cnvn为这组向量的线性组合。
其中c1, c2, …, cn为标量,v1, v2, …, vn为向量。
1.4 线性相关与线性无关如果存在一组不全为零的标量{c1, c2, …, cn},使得c1v1 + c2v2 + … + cnvn = 0,则称向量{v1, v2, …, vn}线性相关;否则称线性无关。
1.5 矩阵运算矩阵加法:矩阵A和矩阵B相加,得到的结果矩阵的对应元素为A和B对应元素之和。
矩阵乘法:矩阵A与矩阵B相乘,得到的结果矩阵C的第i行第j列元素为A的第i行与B的第j列对应元素乘积的和。
1.6 矩阵的转置矩阵的转置是将矩阵的行和列互换得到的新矩阵。
如果矩阵A的维度为m×n,则它的转置矩阵记作A^T,维度为n×m。
1.7 矩阵的逆如果矩阵A存在逆矩阵B,即AB=BA=I,其中I为单位矩阵,则称矩阵A可逆。
非奇异矩阵(行列式不为0)的逆矩阵存在且唯一。
1.8 行列式行列式是一个与方阵相关的标量值,用来描述一个方阵的某些性质。
一个n阶方阵的行列式记作|A|,可以表示成一个数值。
1.9 矩阵的秩矩阵A的秩是指矩阵中线性无关的行或列的最大数目。
秩的计算可以通过行、列简化矩阵后观察矩阵中非零行或列的数量得出。
二、线性方程组与矩阵2.1 线性方程组线性方程组是由一系列的线性方程组成,形式通常为a1x1 + a2x2 + … + anxn = b。

高等教育自学考试衔接考试(课程代码02198)《线性代数》考试大纲课程目标:线性代数课程是高等教育自学考试工科类专业的一门重要的基础理论课,它是为培养满足工科类专业人才的需要而设置的。
通过本课程的自学,使考生系统地学习并获得有关行列式、矩阵、n维向量、线性方程组、矩阵的特征值与特征向量、实二次型的基本知识、必要的基本理论和常用的基本方法。
在此过程中,注重培养考生的抽象思维能力好逻辑推理能力,不断提高自学能力,并为后继课程的学习提供必要的数学基础。
第一章行列式第一节行列式的定义识记:行列式的定义掌握:熟练计算二阶与三阶行列式及简单的n阶行列式。
第二节行列式的性质识记:行列式的性质与计算掌握:掌握并会熟练运用行列式的性质。
第三节行列式按一行(或一列)展开识记:行列式的按一行(或一列)展开定义。
领会:了解行列式的按其第一列展开的递归定义。
掌握:掌握行列式的基本方法。
第四节行列式按k行(或k列)展开识记:清楚行列式中元素的余子式和代数余子式的定义。
领会:余子式和代数余子式计算。
第五节克拉默法则识记:知道克拉默法则掌握:会用克拉默法则求解简单的线性方程组。
克拉默法则。
要求达到“简单应用”层次。
第二章矩阵第一节矩阵的定义识记:矩阵的定义。
要求达到“识记”层次。
了解:知道三角矩阵、对角矩阵、单位矩阵和零矩阵的定义。
第二节矩阵运算识记:矩阵运算及其运算规律。
要求达到“综合应用”层次掌握:掌握矩阵相等与加、减法的定义及其可运算的条件和运算律,掌握矩阵乘法的定义和可乘条件;掌握矩阵乘法的运算法则;注意矩阵乘法不满足交换定律和消去律,知道矩阵乘法与数的乘法的区别。
第三节矩阵分块识记:知道分块矩阵的定义。
掌握:分块矩阵的加法、数科和乘法运算。
第四节可逆矩阵识记:理解可逆矩阵的概念与性质。
方阵的逆矩阵,要求达到“领会”层次。
理解方阵的伴随矩阵的定义。
掌握:熟练掌握方阵可逆条件和求逆运算律,会用伴随矩阵求二阶和三阶矩阵的逆矩阵。
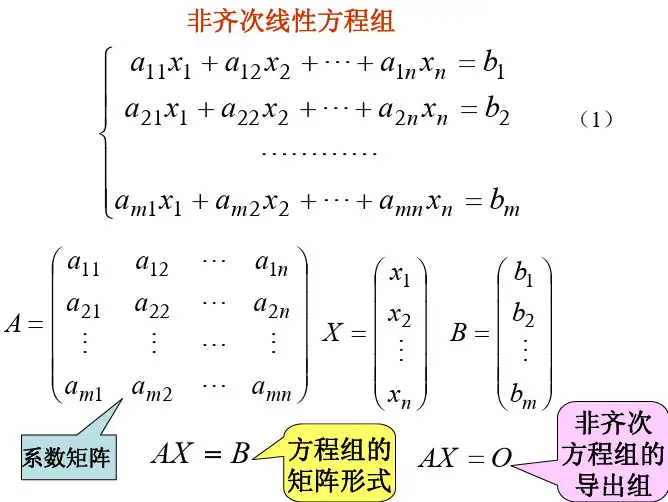
非齐次线性方程组解法
非齐次线性方程组的通解=齐次线性方程组的通解+非齐次线性
方程组的一个特解(η=ζ+η*)。
非齐次线性方程组是常数项不全为零的线性方程组。
1、非齐次线性方程组解法
非齐次线性方程组Ax=b的求解步骤:
(1)对增广矩阵B施行初等行变换化为行阶梯形。
若R(A)<R(B),则方程组无解。
(2)若R(A)=R(B),则进一步将B化为行最简形。
(3)设R(A)=R(B)=r;把行最简形中r个非零行的非0首元所对应的未知数用其余n-r个未知数(自由未知数)表示,并令自由未知数分别等于C1,C2……,Cn-r,即可写出含n-r个参数的通解。
2、非齐次线性方程组解的判别
如果系数矩阵的秩小于增广矩阵的秩,方程组无解;如果系数矩阵的秩等于增广矩阵的秩,方程组有解。
在有解的情况下,如果系数矩阵的秩等于未知数的个数,非齐次线性方程组有唯一解。
如果系数矩阵的秩小于未知数的个数,非齐次线性方程组有无穷多解,如果有无穷多解,先求所对应齐次线性方程组的基础解系,再求出非齐次线性方程组的一个特解。
由此可知:如果非齐次线性方程组有无穷多解,则其对应的齐次线性方程组一定有非零解,且非齐次线性方程组的全部解(通解)可表示为:对应齐次线性方程组的通解+非齐次线性方程组的特解。
齐次线性方程和非齐次线性方程组的区别
齐次线性和非齐次的区别:
1、常数项不同:
齐次线性方程组的常数项全部为零,非齐次方程组的常数项不全为零。
2、表达式不同:
齐次线性方程组表达式:Ax=0;非齐次方程组程度常数项不全为零:Ax=b。
在一个线性代数方程中,如果其常数项(即不含有未知数的项)为零,就称为齐次线性方程。
线性方程也称一次方程式。
指未知数都是一次的方程。
其一般的形式是ax+by+...+cz+d=0。
线性方程的本质是等式两边乘以任何相同的非零数,方程的本质都不受影响。
因为在笛卡尔坐标系上每一个一次方程的表示都是一条直线。
组成一次方程的每个项须是常数或者是一个常数和一个变量的乘积。
且方程中须包含一个变量,因为如果没有变量只有常数的式子是代数式而非方程式。
线性方程组解的结构(解法)一、齐次线性方程组的解法【定义】 r (A )= r <n ,若AX = 0(A 为m n ⨯矩阵)的一组解为,,,n r -12L ξξξ ,且满足: (1) ,,,n r -12L ξξξ线性无关;(2) AX = 0 的)任一解都可由这组解线性表示. 则称,,,n r -12L ξξξ为AX = 0的基础解系.称n r n r k k k --=+++1122L X ξξξ为AX = 0的通解 。
其中k 1,k 2,…, k n-r 为任意常数). 齐次线性方程组的关键问题就是求通解, 而求通解的关键问题是求基础解系. 【定理】 若齐次线性方程组AX = 0有解,则(1) 若齐次线性方程组AX = 0(A 为m n ⨯矩阵)满足()r A n =,则只有零解; (2) 齐次线性方程组有非零解的充要条件是()r A n <.(注:当m n =时,齐次线性方程组有非零解的充要条件是它的系数行列式0A =.)注:1、基础解系不唯一,但是它们所含解向量的个数相同,且基础解系所含解向量的个数等于()n r A -. 2、非齐次线性方程组AX B =的同解方程组的导出方程组(简称“导出组”)为齐次线性方程组AX O =所对应的同解方程组。
由上述定理可知,若m 是系数矩阵的行数(也即方程的个数),n 是未知量的个数,则有:(1) 当m n <时,()r A m n ≤<,此时齐次线性方程组一定有非零解,即齐次方程组中未知量的个数大于方程的个数就一定有非零解;(2)当m n =时,齐次线性方程组有非零解的充要条件是它的系数行列式0A =; (3)当m n =且()r A n =时,若系数矩阵的行列式0A ≠,则齐次线性方程组只有零解; (4)当m n >时,若()r A n ≤,则存在齐次线性方程组的同解方程组;若()r A n >,则齐次线性方程组无解。