七年级数学勾股定理的应用举例
- 格式:pdf
- 大小:1.40 MB
- 文档页数:8

初中数学如何证明勾股定理在解决实际问题中的应用。
勾股定理是初中数学中的重要定理之一,它描述了直角三角形中直角边的平方和等于斜边的平方。
虽然在学习数学的过程中,我们经常通过几何证明来理解勾股定理,但是它在解决实际问题中的应用也是非常广泛的。
在本文中,我们将探讨勾股定理在实际问题中的应用,并通过具体的例子来加深理解。
1. 建筑工程中的应用勾股定理在建筑工程中有着广泛的应用。
例如,在设计房屋的时候,我们需要确定墙壁的角度和长度。
通过使用勾股定理,我们可以计算出两面墙壁之间的距离,从而确保房屋的结构和稳定性。
此外,在设计楼梯和斜坡的过程中,勾股定理也可以用来计算出坡度和高度,以确保安全性。
2. 导航系统中的应用勾股定理在导航系统中也有着重要的应用。
例如,在GPS系统中,我们经常需要确定两个位置之间的距离和方向。
通过使用勾股定理,我们可以计算出两个坐标之间的直线距离,从而确定最短路径和导航方向。
此外,勾股定理还可以用来计算出飞机、船只和汽车等交通工具的速度和位移。
3. 物理学中的应用勾股定理在物理学中也有着广泛的应用。
例如,在力学中,我们经常需要计算物体在斜面上的运动情况。
通过使用勾股定理,我们可以计算出物体在斜面上的加速度、速度和位移等参数。
此外,在光学中,勾股定理可以用来计算出光线的入射角和折射角,从而帮助我们理解光的传播和折射规律。
4. 金融领域中的应用勾股定理在金融领域中也有着一定的应用。
例如,在投资领域,我们经常需要计算投资组合的风险和回报。
通过使用勾股定理,我们可以构建一个有效的投资组合,以最大化回报并降低风险。
此外,在贷款和利率计算中,勾股定理可以用来计算出贷款的利率和还款期限等关键参数。
综上所述,勾股定理在解决实际问题中有着广泛的应用。
无论是在建筑工程、导航系统、物理学还是金融领域,勾股定理都发挥着重要的作用。
通过了解和应用勾股定理,我们可以更好地理解和解决实际问题,提高数学应用能力,并将数学知识与实际生活相结合。

勾股定理的应用举例2篇勾股定理的应用举例勾股定理是数学中的一个基本定理。
它描述了直角三角形中的关系,即直角边的平方和等于斜边的平方。
勾股定理的应用非常广泛,涉及到很多领域,例如建筑、导航和物理等。
本文将为大家介绍勾股定理的两个具体应用举例。
应用举例一:建筑工程在建筑工程中,勾股定理可以用来计算建筑物的高度、角度和距离等关键参数。
例如,在施工一个高楼大厦时,我们需要测量建筑物的高度。
我们可以选择一根足够长的棍子,然后将其竖直地插入地面,并用一个测量仪器测量其与地面的距离。
接下来,我们选择一个合适的位置,利用勾股定理计算出建筑物的高度。
具体步骤如下:首先,我们选择一个较平坦的地面作为测量点,然后找到一个较高的地点,例如楼顶、山峰或者其他高出地面的位置。
在测量点上,我们放置一个测量仪器,并将其竖直朝上。
然后,我们利用一根棍子或者其他辅助工具,使其与测量仪器的光线相交。
此时,我们可以通过测量棍子与地面的距离,再通过勾股定理计算出建筑物的高度。
应用举例二:导航系统勾股定理在导航系统中也有广泛应用。
通过勾股定理,我们可以确定两个位置之间的距离和方向。
例如,在使用GPS导航时,勾股定理被用来计算两个坐标点之间的直线距离。
具体步骤如下:首先,我们获取起点的坐标和终点的坐标。
然后,利用勾股定理计算出两个坐标点之间的距离。
接下来,我们可以利用导航系统提供的方向指引,沿着距离最短的路径前往目的地。
勾股定理在导航系统中的应用不仅仅限于计算直线距离。
通过结合导航系统提供的地图数据,我们可以利用勾股定理计算出实际路径的长度。
在实际的导航过程中,我们需要考虑道路的弯曲程度和交通状况等因素,以确定最优的路径。
总结:勾股定理作为一项基本的数学原理,被广泛应用于各个领域。
本文介绍了勾股定理在建筑工程和导航系统中的应用举例。
在建筑工程中,我们可以通过勾股定理计算建筑物的高度;在导航系统中,我们可以利用勾股定理计算两个坐标点之间的距离和实际路径的长度。

浅谈勾股定理在初中数学中的应用勾股定理是古代中国数学家在解决实际问题时发现的一条重要性质,其中最著名的例子便是勾股三元组。
在初中数学中,勾股定理是一个必修的知识点,也是必须掌握的基础。
在本文中,我们将浅谈勾股定理在初中数学中的应用。
1. 直角三角形的判定一个直角三角形的特点是:其中两条边的平方和等于斜边平方。
这正是勾股定理的内容。
因此,当我们已知三角形的三边长时,可以利用勾股定理来判定这个三角形是否为直角三角形。
如果两条短边的平方和等于长边的平方,则这个三角形是直角三角形。
2. 在平面直角坐标系中的应用平面直角坐标系是初中数学中比较重要的一个知识点。
在平面直角坐标系中,我们可以利用勾股定理求两点之间的距离。
假设平面直角坐标系中有两个点A(x1,y1)和B(x2,y2),那么点A和点B之间的距离为:AB = √((x2 - x1)^2 + (y2 - y1)^2)这就是勾股定理的应用。
我们可以将点A和点B看成直角三角形的两个顶点,求出它们之间的距离。
3. 图形的面积公式在学习初中数学时,我们经常需要求解各种图形的面积。
其中有一类图形是直角三角形和直角梯形等。
我们可以利用勾股定理来求解这些图形的面积公式。
例如,对于一个直角三角形,其面积可表示为:S = 1/2 * b * h其中,b和h分别代表直角三角形的短边和长边。
利用勾股定理,我们可以将长边表示为√(b^2 + h^2),代入上式得:S = 1/2 * b * √(b^2 + h^2)这就是直角三角形的面积公式。
4. 解决实际问题勾股定理的最初应用就是为了解决实际问题。
在初中数学中,我们依旧能够利用勾股定理解决一些实际问题。
例如,当我们需要测量山上的高度时,我们可以选择一条距离山脚以及山顶较远的直路段做为勾股定理中的斜边,然后用测角仪测量斜边和水平线之间的夹角,以及两边之间的距离。
这样,就可以利用勾股定理计算出山顶的高度。
总之,勾股定理是一个非常重要的数学定理,在初中数学中有着广泛的应用。

勾股定理的应用勾股定理是数学中的一条重要定理,它描述了直角三角形中三条边之间的关系。
作为一位初中数学特级教师,我深知勾股定理在数学学习中的重要性。
它不仅是数学知识的基础,还具有广泛的应用价值。
在本文中,我将以对应标题题型进行举例、分析和说明,以帮助中学生和他们的父母更好地理解和应用勾股定理。
一、直角三角形的边长关系勾股定理表明,直角三角形的两条直角边的平方和等于斜边的平方。
以一个具体的例子来说明,假设直角三角形的直角边分别为3和4,斜边为x,则根据勾股定理可以得到3²+4²=x²。
通过计算,我们可以得到x=5。
这个例子告诉我们,当我们知道直角三角形的两条直角边时,可以利用勾股定理求解斜边的长度。
二、勾股定理在测量中的应用勾股定理在测量中有广泛的应用。
例如,在房屋装修中,我们经常需要测量墙角的直角度数。
如果我们知道两面墙的长度分别为3米和4米,那么根据勾股定理,我们可以求得对角线的长度为5米。
这样,我们就可以精确地确定墙角的直角度数,以便进行装修。
三、勾股定理在导航中的应用勾股定理在导航中也有重要的应用。
例如,在航海中,船只需要确定自己的位置和目标位置之间的距离和方向。
如果我们知道船只当前的位置和目标位置之间的直角距离和水平距离,那么根据勾股定理,我们可以求得船只需要行驶的斜距离和方向。
这样,船只就可以根据勾股定理的计算结果来进行导航,确保安全到达目的地。
四、勾股定理在建筑中的应用勾股定理在建筑中也有广泛的应用。
例如,在设计房屋时,我们需要确保墙壁之间的角度为90度。
如果我们知道两面墙的长度分别为6米和8米,那么根据勾股定理,我们可以计算出对角线的长度为10米。
通过测量对角线的长度,我们可以确保墙壁之间的角度为直角,从而保证房屋的结构稳定性。
总结起来,勾股定理是一条重要的数学定理,不仅在数学学习中起到基础性的作用,还在实际生活中具有广泛的应用。
通过学习和理解勾股定理,我们可以更好地解决测量、导航、建筑等实际问题。

勾股定理的应用举例与解题方法勾股定理是一条著名的数学定理,它在几何学和代数学中具有广泛的应用。
本文将通过举例和解题方法来探讨勾股定理的应用。
一、求解直角三角形的边长勾股定理最常见的应用就是求解直角三角形的边长。
直角三角形是指一个角度为90度的三角形。
在这种三角形中,直角边即为斜边相对的两条边。
根据勾股定理,斜边的平方等于两条直角边的平方和。
举例1:已知一个直角三角形的一条直角边长度为5,另一条直角边长度为12,求斜边的长度。
解题方法:根据勾股定理可以得到:斜边的平方 = 直角边1的平方 + 直角边2的平方代入已知条件可得:斜边的平方 = 5² + 12² = 25 + 144 = 169开方得到斜边的长度为13。
因此,该直角三角形的斜边长度为13。
二、验证三条边是否构成直角三角形通过勾股定理,我们还可以验证三条边是否构成直角三角形。
举例2:已知三条边的长度分别为3、4、5,判断它们是否构成直角三角形。
解题方法:按照勾股定理,如果三条边的平方和等于斜边的平方,那么它们所构成的就是直角三角形。
代入已知条件可得:3² + 4² = 9 + 16 = 25而斜边的平方为5² = 25由此可见,两者相等,所以这三条边构成了直角三角形。
三、解决几何问题勾股定理不仅可以用于解决三角形问题,还可以应用于其他几何问题。
举例3:已知一个矩形的两条边长分别为5和12,求对角线的长度。
解题方法:由于矩形的对角线可以看作是直角三角形的斜边,我们可以利用勾股定理来求解。
根据勾股定理可以得到:对角线的平方 = 矩形的一条边长的平方 +矩形的另一条边长的平方代入已知条件可得:对角线的平方 = 5² + 12² = 25 + 144 = 169开方得到对角线的长度为13。
因此,该矩形的对角线长度为13。
四、应用于物理问题勾股定理还可以应用于物理问题的求解中。
举例4:一个投射角度为45度的物体以10 m/s的速度抛出,求物体在水平方向上的飞行距离。

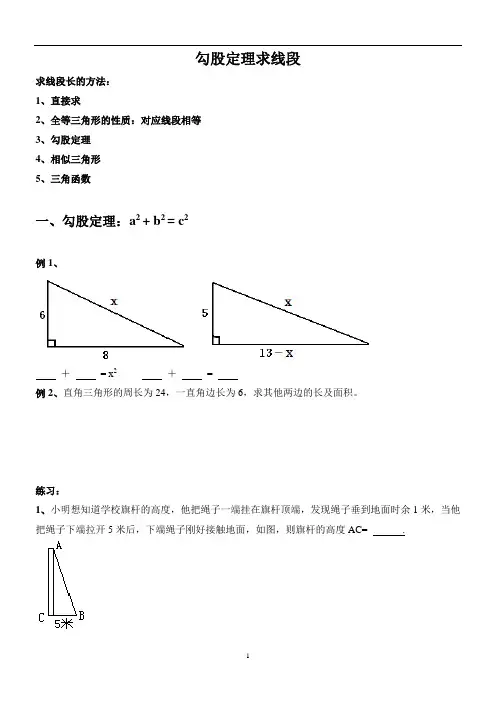
勾股定理求线段求线段长的方法:1、直接求2、全等三角形的性质:对应线段相等3、勾股定理4、相似三角形5、三角函数一、勾股定理:a2 + b2 = c2例1、+= x2+=例2、直角三角形的周长为24,一直角边长为6,求其他两边的长及面积。
练习:1、小明想知道学校旗杆的高度,他把绳子一端挂在旗杆顶端,发现绳子垂到地面时余1米,当他把绳子下端拉开5米后,下端绳子刚好接触地面,如图,则旗杆的高度AC= .2、如图所示,一架长2.5米的梯子,斜靠在一面竖直的墙上,这时梯子底端离墙0.7米,为了安装壁灯,梯子顶端需要离地面2米,请你计算一下,此时梯子底端应再向远离墙面的方向拉多远?3、铁路上A、B两站(视为直线上两点)相距25km,C,D为两村庄(视为两个点),CA⊥AB于点A,DB⊥AB于点B,已知CA=15千米,DB=10千米。
现要在A、B之间建一个土特产收购站E,使得C、D两村到E站的距离相等,此时AE= .二、勾股定理只能用于直角三角形例3、在△ABC中,∠ACB=90o,AC=9,BC=12,则AB上的高CD的长度为例4、如图所示,在△ABC中,AB=AC=5,BC=6,点M为BC的中点,MN⊥AC于点N,则MN等于?1、等腰三角形底边上的高为8,周长为32,则三角形的面积为2、如果Rt△两直角边的比为5∶12,则:斜边上的高与斜边的比为3、已知,如图,在Rt△ABC中,∠C=90°,∠1=∠2,CD=4,BD=5,则AC的长为三、折叠问题观察下列两幅图,试说明折叠与轴对称之间有怎样的关系?例5、如图所示,有一块直角三角形纸片,两直角边AC=6 cm,BC=8 cm.现将直角边AC沿AD折叠,使C点落在斜边AB上E处,求CD的长.1、如图所示,有一张直角三角形纸片,两直角边AC=6cm,BC=8cm,将Rt△ABC折叠,使点B 与点A重合,折痕为DE。
求:CD的长2、如图,在长方形纸片ABCD中,AD=9cm,AB=3cm,将其折叠使点D与点B重合,折叠后BE的长是()。

勾股定理在实际问题中的应用举例一、利用勾股定理解决立体图形问题勾股定理是揭示直角三角形的三条边之间的数量关系,可以解决许多与直角三角形有关的计算与证明问题,在现实生活中有着极其广泛的应用,下面就如何运用勾股定理解决立体图形问题举例说明,供参考。
一、长方体问题例1、如图1,图中有一长、宽、高分别为5cm 、4cm 、3cm 的木箱,在它里面放入一根细木条(木条的粗细、变形忽略不计),要求木条不能露出木箱,请你算一算,能放入的细木条的最大长度是( )A 、41cmB 、34cmC 、50cmD 、75cm分析:图中BD 为长方体中能放入的最长的木条的长度,可先连接BC ,根据已知条件,可以判断BD 是Rt △BCD 的斜边,BD 是Rt △BCD 的斜边,根据已知条件可以求出BC 的长,从而可求出BD 的长。
解:在Rt △ABC 中,AB=5,AC=4,根据勾股定理,得BC=22AC AB +=41,在Rt △BCD 中,CD=3,BC=41,BD=22CD BC +=50。
所以选C 。
说明:本题的关键是构造出直角三角形,利用勾股定理解决问题。
二、圆柱问题例2、如图2,是一个圆柱形容器,高18cm ,底面周长为60cm ,在外侧距下底1cm 的点S 处有一蜘蛛,与蜘蛛相对的容器的上口外侧距开口处1cm 的点F 出有一苍蝇,急于捕获苍蝇充饥的蜘蛛,所走的最短路线的长度是多少?分析:勾股定理是平面几何中的一个重要定理,在遇到立体图形时,需根据具体情况,把立体图形转化为平面图形,从而使空间问题转化为平面问题。
由题意可知,S 、F 两点是曲面上的两点,表示两点间的距离显然不能直接画出,但我们知道圆柱体的侧面展开图是一个长方形,,于是我们就可以画出如图3的图,这样就转化为平面中的两点间的距离问题,从而使问题得解。
解:画出圆柱体的侧面展开图,如图3,由题意,得SB=60÷2=30(cm ),FB=18―1―1=16(cm ),在Rt △SBF 中,∠SBF=90°,由勾股定理得,SF=22FB SB +=221630+=34(cm ),所以蜘蛛所走的最短路线的长度是34cm 。


勾股定理在实际问题中的应用勾股定理是数学中的重要定理.它揭示了直角三角形三边之间的数量关系,把数与形统一起来.勾股定理不仅在数学的发展中起着重要的作用,而且在现实世界中有着广泛的应用.下面举例说明勾股定理在实际生活中的应用.一、少走几步路例1.如图1,学校有一块长方形花铺,有极少数人从A 走到B ,为了避开拐角C 走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了 步路(假设2步为1米),却踩伤了花草. 分析:由图可见,走出来的“路”是直角边分别为3m和4m的直角三角形的斜边,由勾股定理,得该“路”的长为5m,因此,行人仅仅少走了2米(即10步)路.点评:爱护花草人人有责,仅仅因为少走10步而不惜踩伤花草,破坏环境的确是大不应该的。
由此可见,只有懂得“三角形两边之和大于第三边”的人才知道走“捷径”的比经过拐角处的路程近些,但掌握的数学知识如果不能用正当的行为上,那将是数学的悲哀。
二、票价为多少元呢?例2.如图2,A 、B 、C 、D 是四个小镇,它们之间(除B 、C 外)都有笔直的公路相连接,公共汽车行驶于城镇之间,其票价与路程成正比.已知各城镇间的公共汽车票价如下:A ↔B :10元;A ↔C :12.5元;A ↔D :8元;B ↔D :6元;C ↔D :4.5元.为了B 、C 之间的交通方便,要在B 、C 之间建成笔直公路,请按上述标准计算出B 、C 之间的公路的票价为多少元.分析:因为票价与路程成正比,故可将票价视为路程来处理,即AB=10,AD=8,BD=6,AC=12.5,CD=4.5,利用勾股定理求解.解:因为票价与路程成正比,故可把票价视为路程来处理.已知:AB=10,AD=8,BD=6,AC=12.5,CD=4.5.因为AD 2+BD 2=82+62=64+36=100=102=AB 2,所以△ABD 为直角三角形,且∠ADB=90°. 连接BC ,在Rt △BDC 中,CD=4.5,BD=6,所以224.567.5BC =+=.故B 、C 之间公共汽车票价为7.5元.点评:本题是利用勾股定理来解决生活中的实际问题.本题的技巧是将票价视为路程来处理,这一点与代数中的换元法极为相似.三、最短路程是多少例3如图3,一圆柱的底面周长为24cm ,高AB 为4cm ,BC 是直径,一只蚂蚁从点A 出发沿着圆柱体的表面爬行到点C 的最短路程大约是( )A .6cmB .12cmC .13cmD .16cm分析:把圆柱沿直径BC 剪开成两半,展开成平面后可得如图4,则蚂蚁从点A 爬行到“路”4m 3m 图1 AB C 图2 A B图3AC 图4 B点C 的最短路程是矩形的对角线AC 的长,由已知,AB=4,BC=12,故AC=22412+≈12.6≈13(cm ),故选C .点评:解立体图形问题的基本思想是把立体图形平面化,因此,圆柱问题通常要把它沿一条母线剪开,然后铺展为矩形,这里要注意到蚂蚁从点A 出发到点C ,当圆柱沿母线AB 展开成矩形时,点C 对应的是矩形一边的中点。
初中数学:勾股定理的妙用勾股定理是几何学中的一个基本定理,也被称为毕达哥拉斯定理。
它是平面直角三角形中最为重要的关系之一,揭示了直角三角形的三条边之间的关系。
在初中阶段,学生们通常会接触这一概念。
在这篇文章中,我们将深入探讨勾股定理的定义、公式、简单推导方法以及实际应用。
让我们一起揭开勾股定理的神秘面纱,发现其在生活和学习中的多种妙用。
勾股定理的定义与公式勾股定理具体可以表述为:在一个直角三角形中,直角所对的边(即斜边)的平方等于另外两条边(即直角边)的平方和。
用数学公式表示为:[ c^2 = a^2 + b^2 ]其中,( c ) 是斜边的长度,( a ) 和 ( b ) 是直角边的长度。
勾股定理的推导虽然在初中阶段通常不要求学生进行深刻的数学推导,但理解其推导过程有助于加深对定理本质的理解。
以下为一种简单的推导方式:构造一个正方形设直角三角形的两条直角边为 ( a ) 和 ( b ),斜边为 ( c )。
考虑一个以 ( c ) 为边长的大正方形,其面积为 ( c^2 )。
填充小正方形在大正方形内,可以构造出四个与原三角形相同的直角三角形,构成一个小正方形。
小正方形每条边的长度均为 ( a ) 和 ( b ),其面积为 ( (a+b)^2 )。
面积关系大正方形的面积等于四个小三角形面积之和加上小正方形的面积,因此有: [ c^2 = 4(ab) + (a-b)^2 ] 简化后可得 ( c^2 = a^2 +b^2 ),从而完成对勾股定理的推导。
勾股定理在日常生活中的应用勾股定理不仅理论上有重要意义,在现实生活中也有广泛应用。
以下是一些实例:建筑与施工在建筑施工过程中,为确保墙体、门窗、楼梯等设施的垂直或水平方向,工人常使用勾股定理来测量。
例如,要确保一堵墙是直角,可以测量基座的一边和另一边,并应用勾股定理来判断。
地理测量在地图测绘时,如果我们知道两个地点之间的直线距离和其中一个地点到水平方向(东或西或南或北)的远近,可以利用勾股定理计算出另一个地点的位置。
勾股定理的典型应用举例勾股定理,在数学中有着非常重要的应用。
下面就举例说明。
1、拼图中用勾股定理例1、(温州市)在直线l 上依次摆放着七个正方形(如图所示)。
已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S 1、S 2、S 3、S 4,则S 1+S 2+S 3+S 4=_______。
解析:设面积为S 1的正方形的边长AB=x ,面积为S 2的正方形的边长DE=y ,面积为S 3的正方形的边长PQ=m ,面积为S 4的正方形的边长ST=n ,我们易证△BAC ≌△CDE ,△GFH ≌△HMO ,△QPR ≌△RTS ,所以,根据勾股定理,得:x 2+y 2=BC 2=1,y 2+z 2=GH 2=2,z 2+m 2=QR 2=3,x 2+y 2+y 2+z 2+z 2+m 2=1+2+3,x 2+y 2 +z 2+m 2+(z 2+y 2)=1+2+3,x 2+y 2 +z 2+m 2+(z 2+y 2)=1+2+3,x 2+y 2 +z 2+m 2=4,即S 1+S 2+S 3+S 4=4。
2、正方形网格上用勾股定理例2、在5×5的正方形网格上,如图2,在三角形ABC 中,三角形的三边的长分别为a ,b ,c ,则a 、b 、c 的大小的关系是 :A a <b <cB c <a <bC c <b <aD b <a <c (04广州)分析 :假设每个正方形的边长为1,分别在三个阴影三角形中,根据勾股定理,得:AC=b=,=+2215AB=c==,2232+13BC=a==231+10所以,b <a <c ,因此,D 是正确的。
解:选D 。
例3、在5×5的正方形网格上,如图3,在三角形ABC 中,三角形的三边的长分别为a ,b ,c ,则点B 到AC 的距离是 。
分析:直接求这个距离,比较不容易,如果通过求三角形ABC 的面积,后利用面积公式求就容易多了。
初中数学几何培优第十一讲:勾股定理的应用知识解读无论是解决实际问题,还是解决一些数学问题,勾股定理都有着广泛的应用。
典列示范一、在数轴上作出表示的点例1如图3-11-1,矩形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是________【提示】这个点到原点的距离等于线段OB的长,OB是Rt△AOB 的斜边,根据勾股定理可得OB的长,就是这个点表示的实数。
【技巧点评】实数与数轴上的点是一一对应的,有理数在数轴上较易找到它对应的点,若要在数轴上直接标出无理数对应的点较难.由此我们借助勾股定理,将在数轴上表示无理数的问题转化为化长为无理数的线段长问题。
第一步:利用勾股定理拆分出哪两条线段长的平方和等于所画线段(斜边)长的平方,注意一般其中一条线段的长是整数;第二步:以数轴原点为直角三角形斜边的顶点,构造直角三角形;第三步:以数轴原点圆心,以斜边长为半径画弧,即可在数轴上找到表示该无理数的点。
二、在网格中作长度为无理数的线段例2如图3-11-3,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫格点,以格点为顶点分别按下列要求画三角形。
(1)使三角形的三边长分别为3,(在图①中画一个即可)(2)使三角形为钝角三角形且面积为4.(在图②中画一个即可)【提示】(1)长度为3的线段很好作,主要考虑如何作出长度为,的线段和把三条线段组合成一个三角形。
由于=8=22+22,因此可以构造一个两直角边分别为2和2的直角三角形,这个直角三角形的斜边长就是.同理要构造一个长度为的线段,可构造一个直角边分别为2和1的直角三角形。
(2)确定三角形的底和高分别为1和8或2和4,然后设法使三角形称为钝角三角形。
【解答】【技巧点评】在网格中作出长的线段的步骤,第一步设法将n表示成两个整数的平方和;第二步构造直角三角形,使得两条直角边等于第一步得出的两个整数的值.三、梯子下滑问题例3如图3-11-5,一架2.5米长的梯子AB,斜靠在一竖直的墙AC上,这时,梯足B到墙底端C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么梯足也将向外移0.4米吗?【提示】本题中出现两个直角三角形,考虑应用勾股定理,在Rt△ABC中,由AB和BC可求出AC,则A1C=AC-AA1,而A1B1与AB均为梯子之长,在Rt△A1B1C中,再次运用勾股定理求出B1C,由此便可求出梯子向外移动的距离BB1.【解答】【技巧点评】梯子下滑问题,实际上是两个直角三角形问题,比如在本题中,两个直角三角形之间的联系是,AC=A1C+0.4,分别在两个直角三角形中应用勾股定理求出AC,A1C,即可解决问题.四、长方体的对角线例4有一根长170cm的木棒,放在长、宽、高分别是40cm,30cm,120cm的木箱中,露在木箱外边的长度至少为cm.【提示】如图3-11-7,和△是直角三角形,先在中应用勾股定理求出A′C′的长,然后在△AA′C′中应用勾股定理求出AC′的长.【技巧点评】长宽高分别为a,b,c的长方体的对角线长.五、立体图形表明的最短路径例5如图3-11-8,正四棱柱的底面边长为1.5cm,侧棱长为4cm,求一只蚂蚁从正四棱柱底面上的点A沿着棱柱表面爬到C1处的最短路程的长.【提示】要求最短路程,需要将正四棱柱展开成平面图形,再利用勾股定理求解,由于从A点到点C1的面上有两种情况,故需分类讨论。
生活中的勾股定理数学源于实际,数学的发展主要依赖于生产实践,从数学应用的角度来处理数学,阐释数学,呈现数学,使学生了解到数学是有用的,数学就在我们身边.利用勾股定理可以解决实际生活中的许多问题.下面举例分析如下:一.地基挖的合格吗?例1 如图2,是一农民建房时挖地基的平面图,按标准应为长方形,他在挖完后测量了一下,发现AB=DC=8m ,AD=BC=6m ,AC=9m ,请你帮他看一下挖的是否合格?分析:本题是数学问题在生活中的实际应用,所以我们要把实际问题转化成数学问题来解决,运用直角三角形的判别条件,来验证它是否为直角三角形. ∵,819,10086222222===+=+AC DC AD∴222AC DC AD ≠+,所以△ADC 不是直角三角形,∴,900≠∠ADC 而标准为长方形,所以四个角应为直角.所以该农民挖的不合格.评注:勾股定理的逆定理,在解决实际问题中、有着广泛的应用,可以用它来判定直角,家里建房时,常需要在现场画出直角,在没有测量角的一起的情况下,工人是如常利用勾股定理的逆定理得到直角.二. 木棒能放进木箱吗?例1 有一根70cm 长的木棒,要放在长、宽、高分别是50cm ,30cm ,40cm 的木箱中,能放进去吗?分析:由于木棒长为70cm ,远大于各面的边长,而且比每个面的对角线还要长,故按各面的大小都放不进去,但要注意木箱的形状是立体图形,可以利用空间的最大长度.解:能放进去.如图4,连接111,AC C A ,在Rt △111C B A 中,3400305022211211211=+=+=C B B A C A .在Rt △11C AA 中,500034004022112121=+=+=C A AA AC ,∵5000>270,∴170AC > (cm)∴70cm 长的木棒,能放进这只木箱中.评注:解决此题的关键在于明确1AC 即为木箱所能容纳的最大长度,这里充分利用了木箱各邻边的垂直关系,创造了连续运用勾股定理的条件,同时还能培养学生的空间想象力.。
勾股定理的几种简单应用勾般定理是数学中一个重要的定理之一,是解决有关直角三角形问题的有效途径,也是沟通几何与代数的一个重要桥梁,它的应用十分广泛.现举几例,供同学们赏析.一、勾股定理在网格中的应用例1已知正方形的边长为1,(1)如图a .①分别求出图(b),(c),(d)中对角线的长 .②九个小正方形排成一排,对角线的长度(用含n 的式子表示)为 .分析 借助于网格,构造直角三角形,直接利用勾股定理.解二、勾般定理在最短距离中的应用例2 如图,已知C 是SB 的中点,圆锥的母线长为10cm ,侧面展开图是一个半圆,A 处有一只蜗牛想吃到C 处的食物,它只能沿圆锥曲面爬行.请你求出蜗牛爬行的最短路程. 分析 在求解几何图形两点间最短距离的问题时,将几何体表面展开,求展开图中两点之间的距离,展开过程中必须要弄清楚所要求的是哪两点之间的距离,以及它们在展开图中的相应位置.解 该圆锥表面展开图如图所示.根据两点之间线段最短,线段AC 的长即为蜗牛爬行的最短路程.10AS cm =,52AS CS cm ==,90ASC ∠=︒. 在Rt ASC 中,90ASC ∠=︒,22210025125AC AS CS =+=+=,AS ∴=答:蜗牛爬行的最短路程为.点评 在求立体几何图形的问题时,一般是通过平面展开图,将其转化成平面图形间题,然后求解.三、勾股定理在生活中的应用例3 如图,学校有一块长方形花园,有较少数同学为了避开拐角走“捷径”,在校园内走出了一条“路”.请同学们算一算,其实这些同学仅仅少走多少步路,却踩伤了花草.(假设1步为0.5m )分析 把走“捷径”路长求出,就可以算出少走几步路.解 原来走的路长437AB BC m =+=+=.在Rt ABC 中,90ABC ∠=︒,222224325AC AB BC =+=+=.5AC ∴=.即走“捷径”路长为5m ,少走了752m -=.点评 走“捷径”问题为出发点是常遇到情况,在考查勾股定理的同时,融入了环保教育:少走几步路,就可以留下一片期待的绿色.四、勾股定理在实际生活中的应用例4 小华想知道自家门前小河的宽度,于是按以下办法测出了如下数据:小华在河岸边选取点A ,在点A 的对岸选取一个参照点C ,测得30CAD ∠=︒,小华沿河岸向前走30m 选取点B ,并测得60CBD ∠=︒.请根据以上数据,用你所学的数学知识,帮小华计算小河的宽度.分析 先根据题意画出示意图,过点C 作CE AD ⊥于点E ,设BE x =,则在Rt ACE 中,可得出CE ,利用等腰三角形的性质可得出BC ,继而在Rt BCE 中,利用勾股定理可求出x 的值,也可得出CE 的长度.解 过点C 作CE AD ⊥于点.由题意可得:30AB =,30CAD ∠=︒,60CBD ∠=︒.30ACB CAB ∴∠=∠=︒,30BA AB ∴==.设BE x =,在Rt BCE 中,可得CE =. 又222BC BE CE =+,即229003x x =+,15x ∴=,CE ∴=答:小华自家门前的小河的宽度为.点评 此题考查直角三角形的应用,解答本题的关键在于画出示意图,将问题转化为解直角三角形的问题.。