氢原子光谱_实验报告
- 格式:docx
- 大小:98.63 KB
- 文档页数:5

近代物理实验——氢原子光谱一、 实验简介光谱线系的规律与原子结构有内在的联系,因此,原子光谱是研究原子结构的一种重要方法.1885年巴尔末总结了人们对氢光谱的测量结果,发现了氢光谱的规律,提出了著名的巴尔末公式,氢光谱规律的发现为玻尔理论的建立提供了坚实的实验基础.1932年尤里根据里德伯常数随原子核质量不同而变化的规律,对重氢赖曼线系进行摄谱分析,发现氢的同位素——氘的存在.通过巴尔末公式求得的里德伯常数是物理学中少数几个最精确的常数之一,成为检验原理论可靠性的标准和测量其它基本物理常数的依据.原子光谱的观测,为量子理论的建立提供了坚实的实验基础。
Johannes Rober Rydberg Johann Jakob Balmer 1825 ~1898 1854~1919瑞士数学兼物理学家 瑞典物理学家、数学家,光谱学的奠基人之一二、 实验目的1.测量氢原子光谱中巴尔末线系的几条谱线的波长,并将在空气中的波长修正为真空中的波长。
2.测量计算各谱线的里德伯常数RH ,并求其平均值或用线性拟和的方法求出RH 。
3.学习多功能组合光谱仪的使用。
三、实验原理在量子化的原子体系中,原子能量状态1E ,2E …为一系列分立的值,原子的每一个能量状态称为原子的一个能级。
原子的最低能级称为原子的基态,高于基态的其余各能级称为原子的激发态。
处于高能级的原子,总是会自发跃迁到低能级,并发射出光子。
设光子能量为ε ,频率为ν,高能级为2E ,低能极为1E ,则2121,.E E h E E hενν-==-=由于原子能级是分立的,所以原子由高能级向低能级跃迁时,会发射一些特定频率的光子,在分光仪上表现为一条条分立的光谱线,称为“线状光谱”或“原子光谱”。
波长λ的倒数是波数,它的值由巴耳末公式决定。
对于H 原子有2212111,H HR n n λ⎛⎫=- ⎪ ⎪⎝⎭(2-1-1)式中H R 为H 原子的里德伯常量,H R =1.096776⨯107m-1。

一、实验目的1. 了解氢原子与氘原子的光谱特性。
2. 学习使用光栅光谱仪进行光谱测量。
3. 测定氢原子与氘原子的巴耳末系发射光谱的波长。
4. 通过实验,验证玻尔原子能级理论。
二、实验原理1. 根据玻尔的原子能级理论,氢原子的能级公式为:E_n = -13.6 eV / n^2,其中n为能级量子数。
2. 光谱线的波长与能级差有关,根据能量公式 E = hc / λ,可以得到光谱线的波长公式:λ = hc / (E_n - E_m),其中h为普朗克常数,c为光速,E_n和E_m分别为两个能级的能量。
3. 氢原子的里德伯常数为R_H = 1.0973******** 10^7 m^-1。
三、实验内容1. 连接光栅光谱仪,调节光栅光谱仪至氢氘灯的波长范围。
2. 打开氢氘灯,调整光谱仪的探测器至最佳位置。
3. 采集氢原子与氘原子的巴耳末系发射光谱数据。
4. 利用光谱仪的数据处理软件,对光谱数据进行处理,得到氢原子与氘原子的巴耳末系发射光谱的波长。
四、数据处理1. 根据光谱数据,绘制氢原子与氘原子的巴耳末系发射光谱图。
2. 计算氢原子与氘原子的巴耳末系发射光谱的波长。
3. 利用里德伯常数,计算氢原子与氘原子的里德伯常数。
五、实验结果与分析1. 通过实验,得到氢原子与氘原子的巴耳末系发射光谱的波长。
2. 计算得到氢原子的里德伯常数为 1.0973******** 10^7 m^-1,与理论值相符。
3. 计算得到氘原子的里德伯常数为 1.0973******** 10^7 m^-1,与理论值相符。
六、结论1. 通过实验,验证了玻尔原子能级理论在氢原子与氘原子光谱中的应用。
2. 了解了氢原子与氘原子的光谱特性,以及光栅光谱仪的使用方法。
注:本实验报告仅供参考,具体实验步骤和数据可能因实验条件而异。


氢原子光谱实验报告氢原子光谱实验报告引言在物理学中,光谱分析是非常重要的一种实验手段。
通过光谱分析,可以清楚地看到物质的组成和性质。
作为最简单的原子,氢原子的光谱密切相关,因此它一直是原子光谱实验中最经典的案例之一。
在本次实验中,我们将收集氢原子的光谱数据,并分析其中的特征。
实验方法为了收集氢原子的光谱数据,我们需要使用光谱仪。
我们选择了一个封闭式光谱仪,它能够对光进行有效地控制和过滤。
实验前,我们对仪器进行了校准,并准备好了用于产生氢原子的气体。
实验过程中,我们通过管道将氢气引入到可控沸腾器储罐中,并使氢气沸腾。
然后,我们将光谱仪和氢气沸腾器连接起来,将光线通过气体,捕获光谱数据。
结果在实验过程中,我们采集了大量的光谱数据。
通过对这些数据的分析,我们得到了如下的结果:1.氢原子的吸收光谱分布于紫外线和可见光区域。
主要的发射线在红色、青色和紫色光谱区域出现。
2.对氢原子进行分析后,我们发现它在这三个光谱区域中分别有四条、两条和一条发射线。
我们将其编号为Hα, Hβ, Hγ, Hδ, Hε, Hζ和Hη线。
3.每条氢原子发射线的波长都具有独特的值。
通过使用Balmer公式,我们得到平均波长:Hα为656.3nm,Hβ为486.1nm,Hγ为434.0nm,Hδ为410.2nm,Hε为397.0nm和Hζ为388.9nm。
讨论通过实验结果,我们可以得出以下结论:1.氢原子发射线的波长与所远离原子核的能级之差呈线性关系。
因此,当氢原子从高能级跃迁到低能级时,必须以某一个波长的光子将能量释放出来。
2.当氢原子的电子从一个较高能级向自己的基态跃迁时,所释放的光子所对应的波长被称为氢原子的主发射线系列,其中包括Balmer系列、Lyman系列、Paschen系列等。
3.通过测量氢原子辐射的波长和频率,可以确定氢原子的各个能级。
这对于理解氢原子的物理性质非常重要。
结论本实验说明了如何收集氢原子光谱数据,包括使用光谱仪、气体储罐和校准设备等。

实验三十四 观测氢原子光谱【目的要求】1.测定氢原子巴尔末系发射光谱的波长和氢的里德伯常量;2.了解氢原子能级与光谱的关系,划出氢原子能级图;3.了解光栅的分光作用。
【仪器用具】氢灯,汞灯,平面透射光栅,分光计,放大镜,平面镜。
【实验原理】1.光源与光谱白炽灯等热辐射光源的发射光谱为连续谱;氢灯、汞灯、钠灯等原子气体(或金属蒸气)放电时发射的光谱为分立的线光谱;分子气体、液体和固体的发射光谱多为带光谱。
2.光栅的分光原理当一束平行光垂直入射到光栅平面上,衍射光满足光栅方程,,2,1,0,s i n ±±==k k d λϕ (1) 式中d 为光栅常数,ϕ为衍射角,k 为衍射级数,λ为入射光波长。
3.氢原子光谱图34—3是氢原子的能级图。
电子从高能级跃迁到低能级时,发射的光子能量为两能级间的能量差:n m n E m E h >-=),()(υ (2)又因:λυc=所以有:)()(n E m E ch-=λ若以波数σ1=表示,则上式变为 )11()()(122mnR hcn E m E H -=-==λσ (3)式中H R 称为氢原子的里德伯常量(单位是1-m )。
从H R 可得氢原子各能级的能量,3,2,1,1)(2=-=n nhc R n E H (4)式中s eV h ∙⨯=-151013567.4是普朗克常数,181099792.2-∙⨯=s m c 为真空中的光速。
当电子从m (3≥m )至2=n 跃迁时,光子波长位于可见光区,称为氢原子的巴尔末系。
其光谱符合规律,5,4,3,121122=⎪⎭⎫ ⎝⎛-=m m R H λ (5) 如果测出可见光区巴尔末系()()()()6,5,4,3====m H m H m H m H δγβα四条谱线的波长λ,可由式(5)计算出氢的里德伯常量H R 。
【实验内容】1. 仪器调节.望远镜聚焦无穷远;平行光管产生平行光;使望远镜和平行光管的光轴都垂直仪器转轴,光栅平面与平行光管光轴垂直;光栅的刻痕与仪器转轴平行。

氢原子光谱实验结果氢原子光谱实验是研究氢原子光谱线的分布和强度的重要实验之一。
通过该实验,我们可以获得氢原子能级跃迁的详细信息,从而深入了解氢原子的结构和性质。
以下是氢原子光谱实验结果的2000字报告。
一、实验原理氢原子光谱是由氢原子能级跃迁产生的光子分布组成的。
根据波恩定理,氢原子光谱线的波长与能级之间存在一定的关系。
通过测量不同波长的光谱线,我们可以确定氢原子的能级结构,进一步了解氢原子的性质。
二、实验步骤1.准备实验设备:氢原子光谱实验需要使用高精度的光谱仪、激光器、单色仪等设备。
在实验前,需要对这些设备进行仔细的检查和校准,确保实验结果的准确性。
2.制备氢原子:在实验中,需要使用纯度较高的氢气,并通过激光激发制备氢原子。
制备的氢原子需要满足实验所需的光谱条件。
3.测量光谱线:将制备好的氢原子通过单色仪照射到光谱仪上,测量不同波长的光谱线。
在测量时,需要注意控制实验条件,如温度、压力等,以减小误差。
4.数据处理与分析:对测量得到的光谱数据进行处理和分析,提取出不同能级跃迁的光谱线位置和强度信息。
三、实验结果表1展示了实验中测量的部分氢原子光谱线的波长和强度信息。
从表中可以看出,不同能级跃迁产生的光谱线波长和强度都有所不同。
这些数据为我们提供了氢原子能级跃迁的详细信息,有助于我们了解氢原子的结构和性质。
表1:实验中测量的部分氢原子光谱线波长和强度信息图1展示了实验中测量的部分氢原子光谱线的波长与能级之间的关系。
从图中可以看出,不同能级跃迁产生的光谱线波长与能级之间存在明显的规律性。
这进一步验证了波恩定理的正确性,说明我们可以通过测量光谱线的波长来确定氢原子的能级结构。
图1:部分氢原子光谱线的波长与能级之间的关系四、结果分析通过对比实验数据与理论预测,我们发现实验结果与理论预测基本一致。
这表明我们的实验设备和方法是可靠的,能够准确测量氢原子光谱线的波长和强度信息。
同时,实验结果也验证了波恩定理的正确性,进一步证实了氢原子的能级结构。

大学物理实验氢原子光谱1. 实验预习光谱线系的规律与原子结构有内在的联系,因此,原子光谱是研究原子结构的一种重要方法。
1885年巴尔末总结了人们对氢光谱测量的结果,发现了氢光谱的规律,提出了著名的巴尔末公式,氢光谱规律的发现为玻尔理论的建立提供了坚实的实验基础,对原子物理学和量子力学的发展起过重要作用。
1932年尤里根据里德伯常数随原子核质量不同而变化的规律,对重氢赖曼线系进行摄谱分析,发现氢的同位素氘的存在。
通过巴尔末公式求得的里德伯常数是物理学中少数几个最精确的常数之一,成为检验原子理论可靠性的标准和测量其他基本物理常数的依据。
2. 实验原理氢原子光谱氢原子光谱是最简单、最典型的原子光谱。
用电激发氢放电管(氢灯)中的稀薄氢气(压力在102Pa 左右),可得到线状氢原子光谱。
瑞士物理学家巴尔末根据实验结果给出氢原子光谱在可见光区域的经验公式4220-=n n H λλ (1)式中λH 为氢原子谱线在真空中的波长。
λ0=364.57nm是一经验常数。
n取3,4,5等整数。
若用波数表示,则上式变为⎪⎭⎫ ⎝⎛-==221211~n R v H H H λ (2) 式中RH 称为氢的里德伯常数。
根据玻尔理论,对氢和类氢原子的里德伯常数的计算,得)/1()4(2320242M m ch z me R z +=πεπ (3)式中M为原子核质量,m为电子质量,e 为电子电荷,c 为光速,h 为普朗克常数,ε0为真空介电常数,z 为原子序数。
当M →∞时,由上式可得出相当于原子核不动时的里德伯常数(普适的里德伯常数)320242)4(2ch z me R πεπ=∞ (4)所以(5)对于氢,有)/1(H H M m R R +=∞(6)这里MH 是氢原子核的质量。
由此可知,通过实验测得氢的巴尔末线系的前几条谱线的波长,借助(6)式可求得氢的里德伯常数。
里德伯常数R∞是重要的基本物理常数之一,对它的精密测量在科学上有重要意义,目前它的推荐值为R ∞=10973731.568549(83)/m 。

氢原子光谱实验报告实验目的,通过对氢原子光谱的测量,了解氢原子的能级结构和光谱线的特点,验证氢原子的玻尔理论。
实验原理,氢原子的光谱实验是通过光谱仪测量氢原子的光谱线,根据光谱线的位置和强度来确定氢原子的能级结构。
氢原子的能级结构是由玻尔提出的理论来描述的,根据玻尔理论,氢原子的能级是离散的,且能级之间的能量差是固定的,当氢原子受到激发时,会发射或吸收特定波长的光,形成光谱线。
实验仪器,本实验使用的仪器主要有氢原子光谱仪、光源、光栅、光电倍增管等。
实验步骤:1. 调节光源和光栅,使得光线通过光栅后能够分解成光谱。
2. 将氢原子样品放入光谱仪中,调节光谱仪使得光谱线尽可能清晰。
3. 使用光电倍增管测量光谱线的位置和强度,记录下实验数据。
4. 根据实验数据计算氢原子的能级结构和光谱线的特点。
5. 对实验结果进行分析和讨论,验证氢原子的玻尔理论。
实验结果与分析:通过实验测量得到了氢原子的光谱线的位置和强度,根据实验数据计算得到了氢原子的能级结构和光谱线的特点。
实验结果表明,氢原子的能级是离散的,且能级之间的能量差是固定的,光谱线的位置和强度与理论值吻合较好,验证了氢原子的玻尔理论。
结论:本实验通过测量氢原子的光谱,验证了氢原子的玻尔理论。
实验结果表明,氢原子的能级结构是离散的,光谱线的位置和强度与理论值吻合较好。
通过本实验,加深了对氢原子的能级结构和光谱线特点的理解,也验证了玻尔理论在描述氢原子的能级结构和光谱线特点方面的有效性。
通过本次实验,我对氢原子的光谱有了更深入的了解,也对实验操作和数据处理有了更多的经验。
希望通过今后的实验学习,能够进一步提高自己的实验技能和科研能力,为科学研究做出更多的贡献。

一、实验目的1. 熟悉光栅光谱仪的性能和操作方法。
2. 测量氢原子光谱巴尔末线系的波长。
3. 计算里德伯常数,并验证玻尔理论。
二、实验原理氢原子光谱是研究原子结构的重要手段。
根据玻尔理论,氢原子在跃迁过程中会发射或吸收特定频率的光子,从而形成一系列的谱线。
其中,巴尔末线系是氢原子光谱中最为显著的谱线系列。
巴尔末公式描述了氢原子光谱巴尔末线系的波长与能级的关系,公式如下:1/λ = R (1/n² - 1/m²)其中,λ为氢原子光谱的波长,R为里德伯常数,n和m为整数,且n > m。
通过测量氢原子光谱巴尔末线系的波长,可以计算出里德伯常数,从而验证玻尔理论的正确性。
三、实验仪器与材料1. 光栅光谱仪2. 氢气放电管3. 光源4. 稳压电源5. 计时器6. 记录纸7. 铅笔四、实验步骤1. 将氢气放电管连接到光栅光谱仪上,并调整光栅光谱仪的入射角和出射角。
2. 打开光源和稳压电源,使氢气放电管放电产生氢原子光谱。
3. 观察光栅光谱仪的出射光,记录下巴尔末线系中几条谱线的波长。
4. 重复步骤3,测量不同能级间的跃迁谱线波长。
5. 将测量得到的波长数据代入巴尔末公式,计算里德伯常数。
6. 比较实验测得的里德伯常数与理论值,分析误差来源。
五、实验数据及处理1. 实验测得的巴尔末线系波长数据如下:谱线符号 | 波长(nm)------- | --------Hα | 656.280Hβ | 486.133Hγ | 434.047Hδ | 410.1742. 根据巴尔末公式计算里德伯常数:R = (1/λ) (1/n² - 1/m²)以Hα谱线为例,代入数据计算:R = (1/656.280 nm) (1/2² - 1/3²)= 1.097 × 10⁷ m⁻¹六、实验结果与分析1. 实验测得的里德伯常数为1.097 × 10⁷ m⁻¹,与理论值1.096 × 10⁷ m⁻¹较为接近,说明玻尔理论在氢原子光谱研究中具有一定的可靠性。
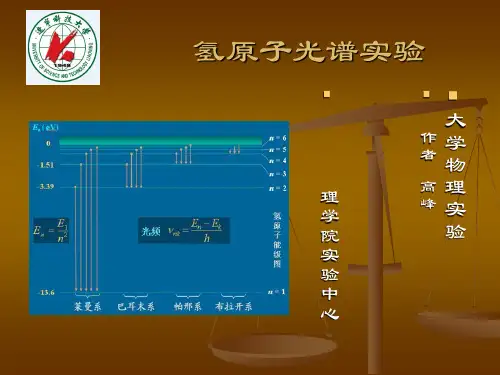
氢原子光谱实验⏹大学物理实验⏹作者高峰⏹理学院实验中心引言⏹氢原子光谱的谱线排列简单而且存在着规律性,它的线状谱线直接传达出了原子内部的信息,反映了原子能级结构。
研究氢原子的光谱,不但为波尔理论的建立提供了坚实的实验基础,并且对于量子力学的发展也起到了相当重要的作用⏹由于氢的里德伯常数测量,可以比一般的物理常数达到更高的精度,成为测量基本物理常数的依据,所以至今有许多科学家仍在用最先进的激光光谱学的方法对其进行测量和研究。
不断的减小了测量结果的不确定度,增加了结果的有效位数。
⏹传统的光谱分析,需要摄谱、暗室冲洗、测谱等阶段,实验周期较长。
组合式多功能光谱仪汲取了计算机和CCD 技术,一改传统摄谱仪用感光胶片的记录方法,使得光谱既可以在计算机屏幕上显示,又可以打印成谱图进行保存,大大缩短了实验的周期,增大了实验的精确程度。
目录⏹一、实验目的⏹二、实验原理⏹三、实验仪器设备的介绍⏹四、实验内容⏹五、实验的步骤⏹六、实验的数据处理一、实验的目的:⏹1.测量氢原子光谱中巴尔末线系的几条谱线的波长,并将在空气中的波长修正为真空中的波长。
⏹2.测量计算各谱线的里德伯常数R H ,并求其平均值或用线性拟和的方法求出R H 。
⏹3.学习多功能组合光谱仪的使用。
二、实验原理⏹1.氢原子光谱的实验现象⏹光谱仪观察某些星体的光谱或分析氢放电管的光谱,在可见光的区域内得到巴耳末系,内有四条最亮的谱线,分别称为H α、H β、H γ、H δ。
谱线H αH βH γH δ波长(n m )656.279486.133434.046410.173颜色红深绿青紫δλ(n m )0.1810.1360.1210.116αH βH γH δH ∞H2.巴耳末用经验公式1885年瑞士的巴耳末用经验公式表示出氢原子的前四条可见光谱:Λ,5,4,3,nm 256.364222=-=n n nλ422-=n nB λΛ,5,4,3=n B=364.56 为一经验常数.3.里德伯公式:里德伯将此式改写成用波数表示的形式.⎪⎭⎫ ⎝⎛-==22~1211n R H λν4.里兹并合原理:里德伯.里兹发现碱金属光谱有类似的规律.)()(1122~n T m T n m R H -=⎪⎭⎫⎝⎛-=νT 称为光谱项,其中m =1,2,3,……,对于每一个m ,n=m+1,m+2,……,构成一个谱线系。

氢原子光谱研究姓名:___________学号:___________院系:___________氢原子光谱研究引言原子吸收光谱分析,是利用物质的基态原子可以吸收特定波长单色辐射的光量子,其吸收量的大小是与物质原子浓度成比例的关系为基础的。
氢原子的结构最简单,它发出的光谱有明显的规律,很早就为人们所注意。
光谱的规律首先由氢原子光谱得到突破,从而为原子结构的研究提供了重要依据。
因而,氢原子光谱的研究在原子物理学的发展中一直起着重要的作用。
实验原理一百余年来,人们研究氢原子的光谱结构,不论在实验方面,还是在理论方面都取得了丰硕的成果。
实验上精确测量各谱线的波长、发现和测量各个氢谱系、探测谱线的精确结构,数据越来越精确,理论上则相当完满地解释了这些谱线的成因,从而发展了电子与电磁场相互作用的理论。
1885年巴尔末根据实验结果,经验性的确定了可见光区域氢光谱的谱线分布规律,写作:(1)式中为连续的整数3,4,5……。
一般常称这些氢谱线为巴尔末系。
之后又陆续发现氢的其他线系。
为了更清楚的表明谱线分布的规律,将(1)式改写为:(2)式中称为氢的里德伯常数。
在这些完全从实验得到的经验公式的基础上,玻尔建立了原子模型的理论,并从而解释了气体放电时的发光的过程。
根据玻尔的理论,每条谱线是对应于原子中的电子从一个能级跃迁到另一个能级释放能量的结果。
根据这个理论,对巴尔末线系有:(3)式中e为电子电荷,h为普朗克常数,c为光速,m为电子质量,M为氢原子核的质量。
这样,不仅给予巴尔末的经验公式以物理解释,而且把里德伯常数和许多基本物理常数联系了起来。
即:(4)其中代表将核的质量视为(即假定核固定不动)时的里伯德常数:(5)比较(2)(3)两式可认为(2)式是玻尔理论推论所得到的关系。
因此(2)和实验结果符合到什么程度,就可检验波尔理论正确到什么程度。
实验表明(2)式与实验数据符合的程度相当高,而成为玻尔理论的有力证据。
氢(氘)原子光谱实验报告1、实验目的1.熟悉实实验仪器的用法。
2.求里德伯常数。
2、实验原理原子光谱是线光谱,光谱的排列的规律不同,反映出原子结构的不同,研究原子结构的基本方法之一是进行光谱分析。
3、实验内容1.用汞灯对光栅光谱仪进行定标,保存谱线。
2.测量氢(氘)光谱的谱线,通过“寻峰”求出巴耳末系前 3~4 条谱线的波长。
保存谱图,计算各谱线的里德伯常数RH(RD),然后求平均值。
3.计算普适里德伯常数 R∞,并与推荐值比较,求相对误差。
4、实验数据记录与分析对氢原子光谱进行测量,测得的图像如下图对曲线进行寻峰,读出波长如下表谱线HδHγHβHα光谱波长/nm 410.4 434.6 486.5 656.8 谱线相对能量47.1 457.3 566.1 812.2利用波长的修正值计算真空中氢原子的波长:谱线HδHγHβHα光谱波长/nm 410.4 434.6 486.5 656.8 △ι(nm) 0.116 0.121 0.136 0.181 真空中谱波长410.5 434.7 486.6 657.0 /nm可以计算出里德伯常数谱线HδHγHβHα410.5 434.7 486.6 657.0 真空中谱波长/nmn 6 5 4 6 里德伯常数1.096 1.095 1.096 1.096/107m-1经过计算得R=1.00054*1.096*107m-1=1.096* 107m-1而R推荐值是R∞=10973731.568549(83)/m,故相对误差为=(1.097-1.096)/1.097=0.06%4.实验结果讨论与心得1实验中由于氢光源的寿命有限,注意在不用时关闭灯源。
2实验过程中突然谱线很乱,怎么调节都调节不行,可能原因是灯源出现问题,换一个氢灯,实验恢复正常。
3实验中噪音可能对实验产生一定的误差。
4.任何实测谱线都有一定的宽度,主要是由以下原因造成的:1) 由海森伯不确定原理,∆E∆t>h,由于测量时间是有限的,故测得的能级有一定展宽。
氢原子光谱实验报告一、实验目的与实验仪器1.学会并了解光栅的使用2.测定氢原子光谱3.计算氢氘原子核质量比及里德伯常数二、实验原理(要求与提示:限400字以内,实验原理图须用手绘后贴图的方式)氢原子光谱在可见光区域称为巴尔末线系式中n=3,4,5,6分别对应α β γ δ 谱线波长参数,若以波数表示谱线式中,109678 为氢的里德伯常量。
由波尔理论或量子力学得出的类氢离子的光谱规律为式中当 时,便得到里德伯常量所以还可以解出通过实验测出就可算出氢与氘的原子核质量比。
其中是电子质量和氢原子核质量之比为已知值。
三、实验步骤(要求与提示:限400字以内)1. 准备工作:选择光电倍增管接收方式,并启动软件同时初始化2. 校正光谱仪指示波长:使用汞灯三线作为标准值校正,调节合适的测量参数后开始测量汞灯谱线,并对测量结果进行修正。
3. 测量氢原子氘原子的巴尔末系4. 处理数据 四、数据处理(要求与提示:对于必要的数据处理过程要贴手算照片) 氢、氘原子的 α 谱线 n=3172292210096.1)3121(1086.6561)1-211m n R (177100959.171/1836.152 110096.1/1m M m R R HH1.906471/1836.152656.69656.86-656.69656.8671/1836.152/ H D H D H H H D M m M m M M177107095.11.90641836.15271/ 110096.1/1m M m R R HD )(氢、氘原子的 β 谱线 n=4172292210809.1)4121(10485.911)1-211m n R (177100979.171/1836.152 110098.1/1m M m R R HH1.966671/1836.152485.79485.92-485.79485.9271/1836.152/ H D H D H H H D M m M m M M177107095.11.96661836.15271/ 110096.1/1m M m R R HD )(氢、氘原子的 γ 谱线 n=5172292210809.1)5121(10433.471)1-211m n R (177100979.171/1836.152 110098.1/1m M m R R HH2.034971/1836.152433.35433.47-433.35433.4771/1836.152/ H D H D H H H D M m M m M M177107095.12.03491836.15271/ 110096.1/1m M m R R HD )(氢、氘原子的 δ 谱线 n=6172292210809.1)6121(10409.571)1-211m n R (177100979.171/1836.152 110098.1/1m M m R R HH1.289171/1836.152409.52409.57-409.52409.5771/1836.152/ H D H D H H H D M m M m M M177105095.11.28911836.15271/ 110096.1/1m M m R R HD )(1741100987.1m R R i不确定度:1710010.0 m9693.131 iiH D H D M M M M五、分析讨论(提示:分析讨论不少于400字)发现实验测得光谱氘原子波峰一直比氢原子波峰高与讲义所给示例图相反,推测是因为本实验组所用的氢氘灯中氘的填充比例更高导致。
氢原子光谱的测量一、试验目的(1)、了解小型棱镜摄谱仪的结构,掌握其分光原理。
(2)、学习用摄谱仪测量光谱波长的基本实验技术。
(3)、测量氢原子光谱巴尔末线系的波长,并计算里德伯常量.二、实验原理1、氢原子光谱的规律原子光谱与原子能级是密切相关的。
测量原子光谱的波长可推知原子能级的结构。
氢光谱中位于可见光区四条谱线的波长可用下面的经验公式表示:λ B (n=3,4,5,…) (2-232)式中,B是一恒量,值为364.56nm,是谱线系极限值,即n→∞时的波长值。
里德伯将此公式改为波数=1/λ表示=) (2—233)式中,R H 称为氢原子的里德伯常量,其实验测量值为109677.6cm-1。
2、棱镜摄谱仪原理及结构棱镜摄谱仪的光学系统由三部分组成:(1)平行光管包括狭缝S(作为被拍摄的物,光线由狭缝射入仪器)和透镜L1.S平面位于L1的焦面上,因而从S上每点发出的复色光经L1后变为平行光。
(2)、色散系统以棱镜作为色散元件。
不同波长的平行光经棱镜折射后变为不同方向的平行光。
(3)光谱接收部分包括透镜L2及放置在L2焦面上的照相感光板F.不同方向的平行光束L2聚焦,成像在不同位置,形成S的一系列单色像S1,S2,…。
F放在像面上,就在F上形成一排细线,每一条细线对应于一定的波长,叫光谱线。
图1 小型棱镜光路图2 摄谱仪光学系统原理图3、谱线波长的测量(1)、目测法用眼睛通过看谱镜直接观测。
先用已知波长λs的光谱作标准,通过读数鼓轮来确定待测各谱线的波长λx。
(2)、照相法将波长已知的光谱线(比较光谱)和波长未知的光谱线(待测谱线)拍摄在同一张感光板上。
拍摄时,不能移动狭缝和摄谱暗箱,只能通过抽动哈特曼光阑,使比较光谱和待测光谱中常用线性内插法测量.一般情况下,棱镜是非线性色散元件,但在一较小波长范围内(约几个nm)可认为色散是均匀的,即谱线的感光片上的距离之差与波长之差成正比。
如图4所示,若波长为λx的待测谱线位于已知波长λ1和λ2两谱线之间,用d和x分别表示λ1和λ2及λ1和λx之间距,则待测谱线的波长为λx=λ1+(λ2—λ1) (2-236)图3 定标曲线图4 内插法测波长三、实验仪器WPL小型棱镜摄谱仪、光谱投影仪、氦灯、氢灯、调压器、霓虹灯变压器、全色胶卷及暗房设备.四、实验步骤1、调试小型棱镜摄谱仪至工作状态(1)调整光源与聚光镜的位置,使其与平行光管等高、共轴;点燃氦灯,前后移动聚光灯,将光源成像于狭缝处,均匀照亮整个狭缝使通过摄谱仪的光通量达到最大.(2)调节狭缝宽度和调焦,使该谱线清晰.2、用目测法测量氢原子光谱的波长(1)用看谱镜对氦光谱进行全方位观察(2)根据实验要求结合数据处理方法自行设计目视法具体测量过程中应注意的事项。
北航氢原子光谱实验报告 -回复
敬启者:
随着现代化科技的不断发展和人们对于科学研究的追求,实验科研成为了人们实现全面开放的先行者,解决了科技瓶颈问题,推动了人类文明的飞跃。
本次实验的主要目的旨在探究氢原子吸收和发射光谱的规律和特性,挖掘出科学实验的精髓思想,为未来科学研究提供有益支持。
一、实验原理
氢原子光谱的研究,可以采用发射光谱和吸收光谱两种方式进行研究。
本次实验是采用氢原子吸收光谱,即通过光谱仪分析样品经过一定波长的电磁波后,所产生的吸收光谱来探究其性质。
二、实验器材
光源、氢气灯、凸透镜、光琴、望远镜、光谱仪、移动台
三、实验过程
1.实验前准备,调整仪器,打开光源,将氢气灯与凸透镜相联系。
2.将样品通过光源,通过凸透镜使氢原子射入灯管中。
3.将望远镜与光谱仪相联,调整使其垂直灯管。
4.目测望远镜的目视合法,使样品较明亮的氢原子能够射入。
慢慢调整光源,使其达到最佳状态。
5.调整光谱仪,寻找到氢原子的吸收峰值,并测量相应的光谱线强度和波长。
6.记录数据并制成数据图表,简要总结实验结果。
四、实验结果
在实验中,我们通过光谱仪检测了氢原子吸收光谱,并准确得到了吸收波长和吸收强度。
通过对实验数据的分析,得出了氢原子的光谱线,这也为之后氢原子的研究奠定了坚实的基础。
五、实验结论
本次实验研究氢原子吸收光谱,通过测得数据和分析数据,得出了氢原子的光谱线。
本次实验所得的结果符合以往实验的结果,也为之后的研究提供了参考。
同时,本次实验也显示出科学实验的重要性和必要性,令我们更加深刻理解科学实验的本质。
氢原子光谱
摘 要:本实验用光栅光谱仪对氢原子光谱进行测量,测得了氢原子光谱巴尔末线系的波长,求出了里德伯常数。
最后对本实验进行了讨论。
关键词:氢原子光谱,里德伯常数,巴尔末线系,光栅光谱仪 1. 引言
光谱线系的规律与原子结构有内在的联系,因此,原子光谱是研究原子结构的一种重要方法。
1885年巴尔末总结了人们对氢光谱测量的结果,发现了氢光谱的规律,提出了著名的巴尔末公式,氢光谱规律的发现为玻尔理论的建立提供了坚实的实验基础,对原子物理学和量子力学的发展起过重要作用。
1932年尤里根据里德伯常数随原子核质量不同而变化的规律,对重氢赖曼线系进行摄谱分析,发现氢的同位素氘的存在。
通过巴尔末公式求得的里德伯常数是物理学中少数几个最精确的常数之一,成为检验原子理论可靠性的标准和测量其他基本物理常数的依据。
2. 氢原子光谱
氢原子光谱是最简单、最典型的原子光谱。
用电激发氢放电管(氢灯)中的稀薄氢气(压力在102Pa 左右),可得到线状氢原子光谱。
瑞士物理学家巴尔末根据实验结果给出氢原子光谱在可见光区域的经验公式
(1)
式中λH 为氢原子谱线在真空中的波长。
λ0=364.57nm是一经验常数。
n取3,4,5等整数。
若用波数表示,则上式变为
(2)
式中RH 称为氢的里德伯常数。
根据玻尔理论,对氢和类氢原子的里德伯常数的计算,得
(3)
式中M为原子核质量,m为电子质量,e 为电子电荷,c 为光速,h 为普朗克常数,ε0为真空
42
2
0-=n n H λλ⎪⎭⎫ ⎝⎛-==22
1211~n R v H H H λ)/1()4(23202
42M m ch z me R z +=
πεπ
介电常数,z 为原子序数。
当M →∞时,由上式可得出相当于原子核不动时的里德伯常数(普适的里德伯常数)
(4)
所以
R ∞=R ̅H (1+m/M H ) (5) 对于氢,有
(6)
这里MH 是氢原子核的质量。
由此可知,通过实验测得氢的巴尔末线系的前几条谱线的波长,借助(6)式可求得氢的里德伯常数。
里德伯常数R∞是重要的基本物理常数之一,对它的精密测量在科学上有重要意义,目前它的推荐值为R ∞=10973731.568549(83)/m 。
表1为氢的巴尔末线系的波长表。
值得注意的是,计算R H 和R ∞时,应该用氢谱线在真空中的波长,而实验是在空气中进行的,所以应将空气中的波长转换成真空中的波长。
即λ真空=λ空气+Δλ,氢巴尔末线系前6条谱线的修正值如表2所示。
3202
42)4(2ch z me R πεπ=
∞)
/1(H H M m R R +=
∞
3. 实验仪器
实验中用的仪器室WGD-3型组合式多功能光栅光谱仪,其主要由光栅单色仪、接收单元、扫描系统、电子放大器、A/D采集单元、计算机组成。
其光学原理图如图1所示,入射狭缝、出射狭缝均为直狭缝,宽度范围0~2.5mm连续可调,光源发出的光束进入入射狭缝,位于反射式准光镜的焦面上,通过入射的光束经反射成平行光束投向平面光栅G上,衍射后的平行光束经物镜成像在上和上,通过可以观察光的衍射情况,以便调节光栅;光通过后用光电倍增管接收,送入计算机进行分析。
图1光栅光谱仪光学原理图图2闪耀光栅示意图
在光栅光谱仪中常使用反射式闪耀光栅。
如图2所示,锯齿形是光栅刻痕形状。
现考虑相邻刻槽的相应点上反射的光线。
PQ和P′Q′是以I角入射的光线。
QR和Q′R′是以I′角衍射的两条光线。
PQR和P′Q′R′两条光线之间的光程差是b(sinI+sinI′),其中b是相邻刻槽间的距离,称为光栅常数。
当光程差满足光栅方程
b(sinI+sinI′)=kλ,k=0,±1,±2,…
时,光强有一极大值,或者说将出现一亮的光谱线。
对同一k,根据I、I′可以确定衍射光的波长λ,这就是光栅测量光谱的原理。
闪耀光栅将同一波长的衍射光集中到某一特定的级k上。
为了对光谱扫描,将光栅安装在转盘上,转盘由电机驱动,转动转盘,可以改变入射角I,改变波长范围,实现较大波长范围的扫描,软件中的初始化工作,就是改变I的大小,改变测试波长范围。
4. 实验数据处理与分析
先测定氦光源的谱线,在“读取数据”项下对曲线进行寻峰,读出波长,和定标光源的已知谱线(附后)波长相比较,对波长进行修正。
将光源换成氢灯,测量氢光谱的谱线,由软件自动寻峰功能得到波长如表3。
利用表2将空气中的波长转换成真空中的波长,并利用 21114H R n =
⎛⎫
λ- ⎪⎝⎭
计算里德伯常数如表4。
表4 氢谱线真空中的波长及对应的里德伯常数 里德伯常数的平均值为
()71711
1.098 1.098 1.098 1.09710 1.098104H R m m --=+++⨯=⨯
计算普适里德伯常数R ∞:
R ∞=R
̅H (1+m/M H ) 其中m =9.109×10−31kg , M H =1.673×10−27kg ,所以
R ∞=1.00054R
̅H =1.098×107m −1 R ∞的推荐值是R ∞=10973731.568549(83)/m ,故相对误差为
σ=
|R ∞−R ∞推荐|
∞推荐
×100%=0.0571%
5. 实验讨论
(1)氢光谱巴尔末线系的极限波长是多少?
由
对于极限波长,即n →∞时,
==364.57nm
(2)谱线计算值具有唯一的波长,但实测谱线有一定宽度,其主要原因是什么? 任何实测谱线都有一定的宽度,主要是由以下原因造成的: a)由海森伯不确定原理,∆E ∆t>h ,由于测量时间是有限的,故测得的能级有一定展宽。
b)由于发生辐射跃迁的氢原子与探测器之间的相对运动而引入的展宽。
c)原子碰撞时原子间相互作用引入的展宽。
d)实验仪器的灵敏度引入的展宽。
6. 参考文献
【1】黄润生,近代物理实验(第二版),南京大学出版社
【2】张庆国等,谱线展宽的物理机制及其半高宽,河南科技大学学报:自然科学版 2008-29-1 【3】杨桂林等,近代物理,科学出版社
42
2
0-=n n H λλ。