博弈论的基本要素讲义

博弈的基本要素名词解释引言：博弈论作为一门应用数学分支，用于研究决策制定者在面对不确定的情况下，如何做出最优决策的一种理论。

在博弈理论中，有一些基本概念和要素是必须理解的。

本文将对博弈的基本要素名词进行解释，使读者能够更好地理解和应用博弈论。

正文：第一部分：博弈博弈是指在一定规则和限制下进行的相互作用，涉及多个参与者，每个参与者通过采取策略来追求自身利益。

博弈的目标是找到最佳决策，并通过合理的策略选择获得最大利益。

第二部分：参与者（博弈人）参与者是指在博弈过程中有决策权和参与权的个体或组织。

他们通过制定和执行策略来实现自身的目标。

参与者可以是个人、企业、政府等，其利益冲突和合作构成了博弈论的基础。

第三部分：策略策略是参与者在博弈中制定的一系列行动方案，旨在最大化其利益。

策略可以是单一的，也可以是复杂的组合。

参与者根据对其他参与者的预测和判断，选择相应的策略以应对不同情况。

第四部分：收益收益是指参与者在博弈过程中获得的实际利益或报酬。

收益可以是经济利益、声誉、满足感等多方面的回报。

在博弈论中，收益通常被量化，以数字或数学模型表示参与者所获得的利益。

第五部分：信息信息是博弈论中至关重要的要素之一。

它涉及参与者对博弈环境和其他参与者的了解程度。

信息的不对称性会对博弈结果产生重要影响。

全面了解信息并能够准确预测对手行为的参与者通常具有较大的优势。

第六部分：博弈论的模型博弈论的模型是描述博弈过程和参与者决策的数学框架。

常见的博弈模型包括零和博弈、合作博弈、非合作博弈等。

博弈论的模型提供了分析和求解博弈问题的工具和方法，帮助参与者做出最佳决策。

结论：博弈论作为一门重要的决策理论，涉及诸多概念和要素的解释和应用。

通过理解博弈、参与者、策略、收益、信息以及博弈模型等基本要素，我们能够更好地应用博弈论，从而在面对不确定的情况下做出最优决策。

参考文献：1. Nalebuff, B.J., & Dixit, A.K. (2020).《Thinking Strategically: The Competitive Edge in Business, Politics, and Everyday Life》. W. W. Norton & Company.2. Myerson, R.B. (2013).《Game Theory: Analysis of Conflict》. Harvard University Press.3. Osborne, M.J., & Rubinstein, A. (1994).《A Course in Game Theory》. MIT Press.。

博弈论基础本讲要点：博弈论的基本思想，博弈的构成要素，简单博弈的求解方法，纳什均衡的概念，博弈的分类，动态博弈与重复博弈，信息不对称，道德风险，逆向选择，信号传递。

重点：博弈论的基本思想，纳什均衡的概念，信息不对称。

难点：博弈的构成要素，纳什均衡的概念。

讲授时间：6学时一、博弈的基本要素1、博弈论与古典经济学的区别古典经济学的基本思路：给定约束条件，考虑行为主体的最优结果。

博弈论的基本思路：以行为主体之间的相互影响为前提，考虑行为主体的最优结果。

两者的根本区别：是否考虑对方的行为。

古典经济学中消费者行为理论：假定收入、商品价格以及效用函数给定，求最优消费组合。

消费者A不会考虑消费者B的影响。

古典经济学中的厂商理论：假定生产函数、成本函数、商品价格给定，求厂商的最优生产决策。

厂商A不会考虑厂商B的影响。

古典经济学中的宏观经济理论：假定一国的资源禀赋给定，考虑价格指数、利率等因素的变化对国民收入、就业等的影响。

国家A不会考虑国家B的影响。

博弈论：每个人要考虑别人的行为怎样影响自己的选择。

扑克牌游戏：一个人不可能只顾自己出牌，而不考虑别人怎么出牌。

下棋：无论中国象棋、国际象棋、围棋，一个人在走某一步之前，都要考虑对手是怎么走的，以及对手在我走了一步之后会怎么走，以及我又会在对手走了一步之后怎么走，以至无穷。

高手与俗手的区别也就在此。

高手往往能够考虑10步甚至20步以后的变化。

总之：你的输赢不仅取决于你的决策，而且取决于你对手的决策。

2、博弈论简史博弈论的思路在古诺（Cournot,Antoine Augustin,1801-1977）的双头垄断模型中最早提出，冯•诺伊曼（John von Neumann,1903-1957）和摩根斯坦恩（Oskar Margenstern, 1902-1977）在1944年出版了《博弈论与经济行为》（Theory of Games and EconomicBehavior）一书，最早提出了博弈论的概念。

博弈论的基本要素
博弈论是研究各种决策情形下人们的行为和结果，并从中推断出
人们的行为规律和最优策略的一种数学理论。

博弈论不仅仅应用于经
济学领域，还被广泛运用于政治学、社会学、心理学、生物学等其他
领域。

博弈论的基本要素如下：
1. 博弈的参与者
博弈中的参与者可以是个人、团体、国家等等。

博弈论研究的是每个
参与者的决策和行动，以及相互之间的决策和行动的互动。

2. 博弈的规则
博弈中的规则包括参与者的行动、决策和结果等。

在博弈中，参与者
的决策和行动会影响到结果，结果反过来也会影响到参与者的决策和
行动。

3. 博弈的策略
博弈中的策略是指参与者针对不同的情况和目的所采取的行动和决策。

策略是参与者根据自身利益和对手行动的预期结果而确定的。

4. 博弈的收益
博弈中的收益指参与者针对不同的情况和目的所获得的利益或损失。

收益是参与者在决策和行动中所关注的重要因素。

5. 博弈的平衡
博弈中的平衡表示参与者在决策和行动中达成的一种状态，其中每个
参与者都采取最优策略，任何一方单方面的改变策略都无法获得更多
的收益。

总体而言，博弈论是通过推导各方当下的最优策略来解决博弈中
的问题，以实现各方的最大化利益，并在各方之间达成一种平衡状态。

一旦博弈中的各个要素都能够被充分了解和把握，那么就可以寻求最
优策略、制定适当的策略，并在不利局面下获得尽可能好的结果。

第八章 博弈论前面章节对经济人最优决策的讨论，是在简单环境下进行的，没有考虑经济人之间决策相互影响的问题。

本章讨论这个问题，建立复杂环境下的决策理论。

开展这种研究的的理论叫做博弈论，也称为对策论(Game Theory)。

最近十几年来，博弈论在经济学中得到了广泛应用，在揭示经济行为相互制约性质方面取得了重大进展。

大局部经济行为都可视作博弈的特殊情况，比方把经济系统看成是一种博弈，把竞争均衡看成是该博弈的古诺-纳什均衡。

博弈论的思想精髓与方法，已成为经济分析根底的必要组成局部。

第一节 博弈事例博弈是一种日常现象，例如棋手下棋，双方都要根据对方的行动来决定自己的行动，双方的目的都是要战胜对方，互不相容，互相影响，互相制约。

一般来讲，博弈现象的特征表现为两个或两个以上具有利害冲突的当事人处于一种不相容的状态中，一方的行动取决于对方的行动，每个当事人的收益都取决于所有当事人的行动。

当所有当事人都拿定主意作出决策时，博弈的局势就暂时确定下来。

博弈论就是研究这种不相容现象的一种理论，并把当事人叫做局中人(player)。

博弈论推广了标准的一人决策理论。

在每个局中人的收益都依赖于其他局中人的选择的情况下，追求收益最大化的局中人应该如何采取行动？显然，为了确定出可行的策略，每个局中人都必须考虑其他局中人面临的问题。

下面来举例说明。

例1．便士匹配(Matching Pennies)(二人零和博弈)设博弈中有两个局中人甲和乙，每个局中人都有一块硬币，并且各自独立安排硬币是否正面朝上。

局中人的收益情况是这样的：如果两个局中人同时出示硬币正面或反面，那么甲赢得１元，乙输掉１元；如果一个局中人出示硬币正面，另一个局中人出示硬币反面，那么甲输掉１元，乙赢得１元。

对于这个博弈，每个局中人可选择的策略都有两种：正面朝上和反面朝上，即甲和乙的策略集合都是{正面，反面}。

当甲和乙都作出选择时，博弈的局势就确定了。

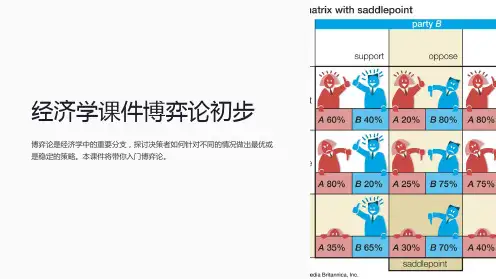
显然，该博弈的局势集合是{(正面,正面)，(正面,反面)，(反面,正面)，(反面,反面)}，即各种可能的局势的全体，也称为局势表，即表1。

博弈论（一）：基本知识1.1定义:博弈论，又称对策论，是使用严谨的数学模型研究冲突对抗条件下最优决策问题的理论，是研究竞争的逻辑和规律的数学分支。

即，博弈论是研究决策主体在给定信息结构下如何决策以最大化自己的效用，以及不同决策主体之间的均衡。

1.2基本要素：参与人、各参与人的策略集、各参与人的收益函数，是博弈最重要的基本要素。

1.3博弈的分类：博弈论根据其所采用的假设不同而分为合作博弈理论和非合作博弈理论。

两者的区别在于参与人在博弈过程中是否能够达成一个具有约束力的协议（binding agreement）。

倘若不能，则称非合作博弈（Non-cooperative game）。

合作博弈强调的是集体主义，团体理性，是效率、公平、公正；而非合作博弈则主要研究人们在利益相互影响的局势中如何选择策略使得自己的收益最大，强调个人理性、个人最优决策，其结果有时有效率，有时则不然。

目前经济学家谈到博弈论主要指的是非合作博弈，也就是各方在给定的约束条件下如何追求各自利益的最大化，最后达到力量均衡。

博弈的划分可以从参与人行动的次序和参与人对其他参与人的特征、战略空间和支付的知识、信息，是否了解两个角度进行。

把两个角度结合就得到了4种博弈：a、完全信息静态博弈，纳什均衡，Nash(1950)b、完全信息动态博弈，子博弈精炼纳什均衡，泽尔腾（1965）c、不完全信息静态博弈，贝叶斯纳什均衡，海萨尼（1967-1968）d、不完全信息动态博弈，精炼贝叶斯纳什均衡，泽尔腾（1975）Kreps, Wilson(1982) Fudenberg, Tirole(1991)1.4课程主要内容：完全信息静态博弈完全信息动态博弈不完全信息静态博弈机制设计合作博弈1.5博弈模型的两种表示形式：策略式表述(Strategic form), 扩展式表述（Extensive form）1.6占优均衡：a、占优策略：在博弈中如果不管其他参与人选择什么策略，一个参与人的某个策略给他带来的支付值始终高于其他策略，或至少不劣于其他策略，则称该策略为该参与人的严格占优策略或占优策略。

博弈论的基本概念博弈论的基本概念博弈要素:(1)决策人：在博弈中率先作出决策的一方，这一方往往依据自身的感受、经验和表面状态优先采取一种有方向性的行动。

(2) 对抗者：在博弈二人对局中行动滞后的那个人，与决策人要作出基本反面的决定，并且他的动作是滞后的、默认的、被动的，但最终占优。

他的策略可能依赖于决策人劣势的策略选择，占去空间特性，因此对抗是唯一占优的方式，实为领导人的阶段性终结行为。

(3)局中人（players）：在一场竞赛或博弈中，每一个有决策权的参与者成为一个局中人。

只有两个局中人的博弈现象称为“两人博弈”,而多于两个局中人的博弈称为“多人博弈”。

(4)策略(strategies)：一局博弈中，每个局中人都有选择实际可行的完整的行动方案，即方案不是某阶段的行动方案，而是指导整个行动的一个方案，一个局中人的一个可行的自始至终全局筹划的一个行动方案，称为这个局中人的一个策略。

如果在一个博弈中局中人都总共有有限个策略，则称为“有限博弈”，否则称为“无限博弈”。

(5)得失(payoffs)：一局博弈结局时的结果称为得失。

每个局中人在一局博弈结束时的得失，不仅与该局中人自身所选择的策略有关，而且与全局中人所取定的一组策略有关。

所以，一局博弈结束时每个局中人的“得失”是全体局中人所取定的一组策略的函数，通常称为支付（payoff）函数。

(6)次序（orders）：各博弈方的决策有先后之分，且一个博弈方要作不止一次的决策选择，就出现了次序问题；其他要素相同次序不同，博弈就不同。

(7)博弈涉及到均衡：均衡是平衡的意思，在经济学中，均衡意即相关量处于稳定值。

在供求关系中，某一商品市场如果在某一价格下，想以此价格买此商品的人均能买到，而想卖的人均能卖出，此时我们就说，该商品的供求达到了均衡。

所谓纳什均衡，它是一稳定的博弈结果。

纳什均衡(Nash Equilibrium)：在一策略组合中，所有的参与者面临这样一种情况，当其他人不改变策略时，他此时的策略是最好的。

博弈论之博弈的要素博弈论博弈论是以数学为主要分析工具，研究一个存在多个决策者或行为主体的局势中，各决策者之间彼此存在交互性决策行为的理论。

博弈论博弈论是以数学为主要分析工具，研究一个存在多个决策者或行为主体的局势中，各决策者之间彼此存在交互性决策行为的理论。

博弈的要素1.参与人(Player )参与人是指一个博弈中的决策主体，通常称为参与者或局中人。

“自然”自然人团队企业国家生物体程序……联盟博弈的要素 2.信息(Information)信息是指参与人在博弈过程中能了解和观察到的知识。

一个博弈问题所涉及的参与者的特征、行动、及相应的效用、收益等都属于“知识”。

共同知识指的是“所有参与人知道，所有参与人知道所有参与人知道，所有参与人知道所有参与人知道所有参与人知道......”的知识。

知识博弈的要素2.信息(Information)信息是指参与人在博弈过程中能了解和观察到的知识。

古董商猫主人碟子是珍贵的古董博弈的要素3.行动或策略(Action or Strategy)行动或策略是各参与人在博弈过程中的备选方案。

指参与人如何对其他参与人的行动作出反应的行动规则，它规定参与人在什么时候选择什么行动。

行动：打牌中的出牌。

行动的顺序策略：每个参与人的行动选择方案。

人若犯我，我必犯人。

人不犯我，我不犯人。

博弈的要素4.支付(Payoff)在一个特定策略组合下，各参与人得到的确定的效用或期望效用。

物质报酬社会地位自尊心利润GDP居民福利竞争力市场份额财政收入……博弈的要素博弈的要素参与人信息行动与策略支付。