博弈论基础讲义-第四章
- 格式:pdf
- 大小:293.27 KB
- 文档页数:61






博弈论前四章笔记整理第一章:博弈论基础概念。
- 博弈的定义与要素。
- 博弈是指在一定的规则下,多个参与者(至少两个)进行策略选择并得到相应结果(收益)的过程。
- 要素包括参与者(局中人)、策略(每个参与者可选择的行动方案)、收益(每个参与者在不同策略组合下的所得)。
例如在“囚徒困境”中,两个囚犯是参与者,坦白或不坦白是他们的策略,不同策略组合下的刑期长短就是收益。
- 博弈的分类。
- 按参与者数量可分为两人博弈和多人博弈。
- 按策略空间是否有限分为有限博弈和无限博弈。
如猜硬币是有限博弈(正面或反面两种策略),企业的产量竞争(产量可在一定范围内连续取值)可能是无限博弈。
- 按收益情况分为零和博弈(一方的收益就是另一方的损失,总和为零,如赌博)、常和博弈(收益总和为常数)和非零和博弈(收益总和不为零,如企业合作共同开拓市场,双方都可能获利)。
第二章:完全信息静态博弈。
- 策略式表述(标准式表述)- 通常用一个矩阵来表示,行代表一个参与者的策略,列代表另一个参与者的策略,矩阵中的元素是对应的收益组合。
以“性别战”为例,丈夫和妻子选择看电影或看球赛,就可以构建一个2×2的收益矩阵。
- 占优策略均衡。
- 占优策略是指无论其他参与者选择什么策略,该策略都是某个参与者的最优策略。
如果每个参与者都有占优策略,那么由这些占优策略组成的策略组合就是占优策略均衡。
例如在“囚徒困境”中,每个囚徒的占优策略都是坦白,所以(坦白,坦白)是占优策略均衡。
- 纳什均衡。
- 纳什均衡是指在一个策略组合中,每个参与者的策略都是对其他参与者策略的最优反应。
即给定其他参与者的策略,没有参与者有动机单方面改变自己的策略。
与占优策略均衡不同,纳什均衡并不要求每个参与者都有占优策略。
例如在“性别战”中,(看电影,看电影)和(看球赛,看球赛)都是纳什均衡。
第三章:完全信息动态博弈。
- 扩展式表述。
- 包括博弈树的构建,节点表示参与者的决策点,树枝表示可选择的策略,终端节点表示博弈的结果并标有相应的收益。


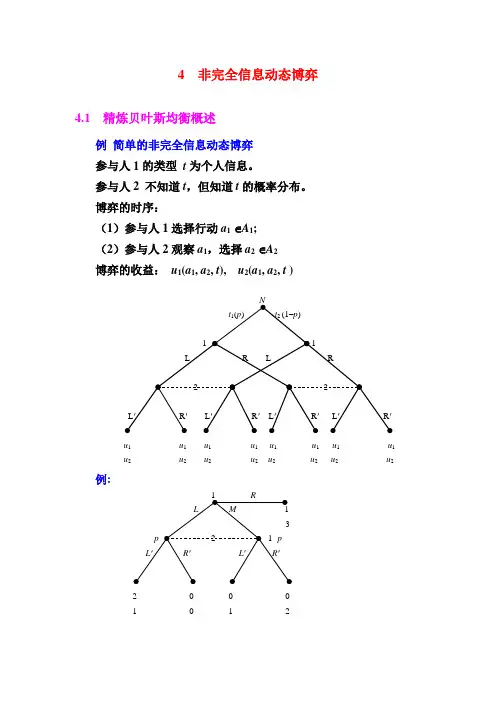
4 非完全信息动态博弈4.1 精炼贝叶斯均衡概述例简单的非完全信息动态博弈参与人1的类型t为个人信息。
参与人2 不知道t,但知道t的概率分布。
博弈的时序:(1)参与人1选择行动a1∈A1;(2)参与人2观察a1,选择a2∈A2博弈的收益:u1(a1, a2, t), u2(a1, a2, t )u1u1u1u1 u1u1u1u1u2u2u2u2 u2u2u2u2例:1 RL M 13p 2 1- pL'R'L'R'2 0 0 01 0 1 2标准式表示参与人 2L'R'L2,10,0参与人 1 M0, 20,1R1, 31, 3纯战略纳什均衡: (L,L'), (R,R')均为子博弈精炼纳什均衡(无子博弈)。
但是(R, R')不可信。
排除不可信的纳什均衡:要求1 参与人必须有一个推断(belief).要求2 参与者的战略必须满足序贯理性(sequentially rational).定义: 处于均衡路径上(on the equilibrium path)的信息集: 在均衡战略下,博弈以正的概率到达该集.要求3 在处于均衡路径上的信息集上, 推断由贝叶斯法则和参与人的均衡战略决定。
例要求3的说明参与人1的类型空间:{ t1,t2,t3,t4 }行动空间:A= { L,R}推断p i: 观察到L后,参与人1的类型是t i的概率。
推断q i: 观察到R后,参与人1的类型是t i的概率。
p1 + p2 + p3 + p4 = 1q1 + q2 + q3 + q4= 1N如果参与人1的战略: t 1选 L ,t 2选 L , t 3选R ,t 4 选R 。
参与人2对p i 与 q i 的推断:p 1 = 3.02.02.0+= 0.4, p 2 = 3.02.03.0+= 0.6, p 3 = 0, p 4 =0; q 1 = 0, q 2= 0, q 3 =3.02.02.0+= 0.4, q 4= 3.02.03.0+= 0.6,例 3个参与人的博弈。

博弈论博弈论(Game Theory),亦名“对策论”、“赛局理论”,属应用数学的一个分支,博弈论已经成为经济学的标准分析工具之一。
目前在生物学、经济学、国际关系、计算机科学、政治学、军事战略和其他很多学科都有广泛的应用。
博弈论主要研究公式化了的激励结构间的相互作用。
是研究具有斗争或竞争性质现象的数学理论和方法。
也是运筹学的一个重要学科。
博弈论考虑游戏中的个体的预测行为和实际行为,并研究它们的优化策略。
生物学家使用博弈理论来理解和预测进化论的某些结果。
参见:行为生态学(behavioral ecology)。
约翰·冯·诺依曼博弈论是二人在平等的对局中各自利用对方的策略变换自己的对抗策略,达到取胜的目的。
博弈论思想古已有之,中国古代的《孙子兵法》就不仅是一部军事著作,而且算是最早的一部博弈论著作。
博弈论最初主要研究象棋、桥牌、赌博中的胜负问题,人们对博弈局势的把握只停留在经验上,没有向理论化发展。
博弈论考虑游戏中的个体的预测行为和实际行为,并研究它们的优化策略。
近代对于博弈论的研究,开始于策墨洛(Zermelo),波雷尔(Borel)及冯·诺伊曼(von Neumann)。
1928年,冯·诺依曼证明了博弈论的基本原理,从而宣告了博弈论的正式诞生。
1944年,冯·诺依曼和摩根斯坦共著的划时代巨著《博弈论与经济行为》将二人博弈推广到n人博弈结构并将博弈论系统的应用于经济领域,从而奠定了这一学科的基础和理论体系。
1950~1951年,约翰·福布斯·纳什(John Forbes Nash Jr)利用不动点定理证明了均衡点的存在,为博弈论的一般化奠定了坚实的策墨洛(Zermelo)基础。
纳什的开创性论文《n人博弈的均衡点》(1950),《非合作博弈》(1951)等等,给出了纳什均衡的概念和均衡存在定理。
此外,塞尔顿、哈桑尼的研究也对博弈论发展起到推动作用。
R R M 4.1.a 标准式1↖2 L ’ R ’4,1 0,0 3,0 0,1 2,2 2,2纯战略纳什均衡:( L, L ’ ) ( R, R ’ )子博弈精炼纳什均衡:( L, L ’ ) ( R, R ’ )精炼贝叶斯纳什均衡:( L, L ’ )4.1.b 标准式1↖2 L ’ M ’ R ’1, 3 1, 2 4, 0 4, 0 0, 2 3, 3 2, 4 2, 4 2, 4纯战略纳什均衡:( R, M ’ )子博弈精炼纳什均衡:( R, M ’ )精炼贝叶斯均衡: 没有4.2标准式1↖2 L ’ R ’2,2 2,2 3,0 0,1 0,1 3,0六种纯战略组合,每种组合中都至少有一方存在偏离的动机,因此不存在纯战略纳什均衡,因此也就不存在纯战略精炼贝叶斯均衡。
求混合战略精炼贝叶斯均衡:设参与者1选择L 、M 、R 的概率分别为1,2,12(1)p p p p −−参与者2选择L ’和R ’的概率分别为,(1)q q −在给定参与者1的战略下,参与者2选择L ’和R ’的收益无差异,则: 1212120*1*1*0*p p p p p p +=+⇒=给定参与者2的战略,参与者1选择L 、M 、R 的收益无差异,则:12121212[3*0*(1)][0*3*(1)]2*(1)41:**,*112p q q p q q p p p p p p q +−=+−=−−====又 联立得 所以 L LML LM L RL4.3答案(见4.5)4.4表示方法第一个括号,逗号左边为type 1发送者信号,逗号右边为type 1发送者信号;第二个括号,逗号左边为接收到L 信号的反应,逗号右边为接收到R 信号的反应; P 为信号接收者对type 1发送L 的推断,q 为信号接收者对type 1发送R 的推断 (a )[(,),(,),1/2][(,),(,),1/2][(,),((1),),1/2][(,),(,),1,0]R R u u p R R d u p R R d u u p L R u d p q αα><+−===(b )[(,),(,),1/2,2/3][(,),(,),1,0][(,),(,),0,1]L L u u p q L R d u p q R L u d p q =<====中文版习题4.5答案(a )[(,),(,),1/3,1/2]R R u d p q >=(b )12121212[(,,),(,),1/3,1/2][(,,),(,),1/2,0]L L L u u p p q q L L R u d p p q q ==+<==+=。
Instructor’s Guide to Game Theory: A Nontechnical Introduction to theAnalysis of StrategyChapter 4. Nash Equilibrium1.Objectives and ConceptsThe principle objective of this chapter is to introduce the Nash equilibrium and to convey some notion of the range of possibilities and applications, including the possibilities that there may be no Nash equilibria in pure strategies and the possibility that there may be plural Nash equilibria. (Since mixed strategy equilibria are not introduced until Chapter 8, it is not possible to give a meaningful definition of pure strategies at this point, and is necessary to talk around it a bit.) Important subsidiary concepts are coordination games and Schelling points (or focal point equilibria), heuristic methods of finding the Nash equilibria, such as underlining, and refinement of Nash equilibrium.The chapter begins with an example that is based on Warren Nutter’s game-theoretic version of Bertrand competition, except that in this instance a kind of quality competition is considered. The solution to this game can be found by iterated elimination of dominated strategies (which will not be covered until Chapter 11) and reflects the intuition that it is best to be just one step ahead of the competition. Thus, while it does not have a dominant strategy equilibrium, it has some dominated strategies and a unique Nash equilibrium, and hopefully forms a natural bridge from the study of dominant strategy equilibrium.Games with plural equilibria are introduced with the game of Choosing Radio Formats. The idea that history (or other clues) can establish a Schelling point also comes in with this example. The Market Day game reinforces the idea that plural Nashequilibria can have explanatory value – explaining the persistence of what seem to be arbitrary conventions. Games without Nash equilibria (in pure strategies) are introduced with an escape-evasion game. This is an important category in itself, though the most important applications are in differential games and thus beyond the scope of the book.Accordingly, the concepts areNash EquilibriumUnique Nash EquilibriaFinding Nash EquilibriaPlural Nash EquilibriaThe difficulty of choosing among plural Nash equilibriaSchelling PointsCustom, convention and history as Schelling pointsSchelling points from the logic of the gameRefinementGames without Nash equilibria in pure strategies2. Common Study ProblemsStudents who have not yet grasped the best-response idea will find Nash equilibria even more difficult than dominant strategy equilibria. This is the crisis point for students who have not “got” best response. The best response tables (such as table 2 in the chapter) are designed to make this a little easier, so urge the student to rely on them and on underlining as intermediate steps in their analysis. I sometimes suggest to mystudents that they physically move their fingers along the column or row to pick out the biggest payoff. Making the solution as mechanical as possible will help students over that hump. Another (less troubling) problem is the relationship between Nash and dominant strategy equilibria. Taking dominant strategy equilibria first is a pedagogical convenience, since it is a little easier and will be familiar to students who have seen the Prisoner’s Dilemma in another class, but it can produce the impression that dominant strategy equilibria are not Nash equilibria. The Venn diagram (Figure 1) is meant to speak to that problem, and may need some stress in class.3. For Business StudentsThe key business concepts for this chapter are strategies of location and market niche, in the Location, Location, Location example, but also in the Radio Formats example and in the Hairstyle example in the exercises and discussion questions.4. Class AgendaFirst hour:1)Quiz on earlier material2)Introductory presentation: Nash Equilibria•Assignments3)Discussion: The Blonde Problem AgainSecond Hour:1)Discussion of quiz and assignments2)Play a coordination game in class, with random matching and without discussion.A handout description of the game is given on the next page.Another Random-Matching Two-Person GameOnce again, each person chooses between the strategies of collusion or defecting from the collusive arrangement.Put in your name and circle one of the two statements: either "my strategy is collude" or "my strategy is defect." Your instructor will tell you whether to follow directions A) or B) below.A)After you turn it in, your strategy choice will be matched with that of anotherclass member AT RANDOM, and your bonus points will be based on the payofftable above. There is to be no discussion of your strategy choices.B)You will be matched with your neighbor and may discuss your strategy choice ifyou wish.Payoffs are in GameBucks.TableArt's StrategyCollude DefectCollude (3,3)(0,2)Bob's StrategyDefect(2,0)(1,1)What will you do? Go for the big reward with a "collude" strategy or protect yourself with an "defect" strategy?Student name ____________________________My strategy is (circle one)ColludeDefect3)Discussion:a.Results of the in-class game.b.Give other examples of Schelling points in coordination games. Ideally,these should come from the students, but the following instances maystimulate the discussion if it comes slowly:i.Driving on the right or left-hand side of the road.ii.Speaking the same language.iii.Choosing a profession. Assumption: if both choose the sameprofession, it does not pay well because it is too crowded. Howmany business majors in the class? Engineering? Communications,etc?5. Answers to Exercises and Discussion Questions1.Solving the Game. Explain the advantages and disadvantages of NashEquilibrium as a solution concept for noncooperative games.Nash equilibrium is based on the idea that each player chooses the best response tothe strategy chosen by the other player. This is a clear concept of rationality wheneach person chooses in isolation from the other. Among the shortcomings are 1)Nash equilibrium may not be unique, posing the problem of determining which oftwo or more Nash equilibria may actually be chosen by rational agents, and 2) considering only the list of strategies for the game in normal form, that is, the“pure” strategies, there may not be a Nash equilibrium.2.Location, Location, Location (Again) Not all location problems have similarsolutions. Here is another one: Gacey's and Mimbel's are deciding where to puttheir stores in Metropolis, the town across the river from Gotham City. The three strategies for Metropolis are to locate downtown, in Old Town, or in the Garden District. The payoffs are shown in Table E1.Table E1 Payoffs in a New Location GameGacey'sDowntown Old Town Garden DistrictDowntown70,6060,12080,100Old Town110,7040,40120,110Mimbel'sGardenDistrict120,80110,12050,50Does this game have Nash equilibria? What strategies, if so? Which strategies would you predict that Gacey's and Mimbel's would choose? Compare and contrast this game with the location game in the chapter. What would you say about the relative importance of congestion in the location decisions of the firms in the two cases?A table modified to show the highest payouts for each player for each decision is as follows:Gacey's Downtown Old Town Garden District Downtown 70, 6060, 12080, 100Old Town110, 7040, 40120, 110M i m b e l 's Garden District 120, 80110, 12050, 50There are two Nash Equilibria. When Gacey’s locates in Old Town, Mimbels will locate in the Garden District, and vice versa. Which solution will actually be chosen is not definite.This problem is different from the one in the chapter since there are 2 NashEquilibriums instead of one, which requires a little guesswork as to which one will be the final solution. It is similar in that there is not a dominant strategy equilibrium.Congestion must be more of a problem in this scenario than in the chapterproblem. There is never a Nash equilibrium when both pick the same site. This could be explained by the congestion problem3. Drive on. Two cars meet, crossing, at the intersection of Pigtown Pike and Hiccup Lane. Each has two strategies: wait or go. The payoffs are shown in Table E2.Table E2. The Drive On Game Mercedeswait go wait0,01,5Buick go 5,1-100,-100Discuss this game, from the point of view of noncooperative solutions. Does it have a dominant strategy equilibrium? Does it have Nash equilibria? What strategies, if so? Would you predict which strategies rational drivers would choose in this game?Which? Why? Pigtown Borough has decided to put a stoplight at this intersection. How could that make a difference in the game?Here is a table modified to show the maximum payout for each driver:Mercedes Wait Go Wait0, 05, 1B u i c kGo 5, 1-100,-100Once again, there are 2 Nash Equilibria. They are for the Buick to wait and the Mercedes go, or vice versa.To determine which will happen requires guesswork. The personality of thedrivers might determine what happens. If I were in the Mercedes, I would probably not want to risk an expensive car getting damaged. Someone else, say in a CL600, mightfigure that his car is faster and that he can beat the other driver. Also, one of the drivers might just wave the other on rather than have both wait or both go.It is possible that both drivers might wait rather than run the risk of an accident, i.e. choose a risk dominant strategy.The stoplight would provide a Schelling Point to select for the equilibrium at which the driver with the green light chooses go.4. Rock, Paper, Scissors. Here is another common school-yard game called Rock, Paper, Scissors. Two children (we will call them Susan and Tess) simultaneously choose a symbol for rock, paper or scissors. The rules for winning and losing are:Paper covers rock (paper wins over rock)Rock breaks scissors (rock wins over scissors)Scissors cut paper (scissors win over paper)The payoff table is shown as Table E3.Table E3. Rock, Paper, ScissorsSusanpaper stone scissors.paper0,01,-1-1,1Tessstone-1,10,01,-1scissors1,-1-1,10,0Discuss this game, from the point of view of noncooperative solutions. Does it have a dominant strategy equilibrium? Does it have Nash equilibria? What strategies, if so? How do you think the little girls will try to play the game?Here is a table modified to show the best responses.Susanpaper stone scissors.paper0,01,-1-1,1Tessstone-1,10,01,-1scissors1,-1-1,10,0We see that there are no dominant strategies, nor are there Nash equilibriain terms of the strategies shown here. We have no basis (so far) to decide how the girls will play the game.NOTE TO INSTRUCTOR For the purist, it is not correct to say here that “thereare no Nash equilibria,” since this game has a mixed-strategy equilibrium. But, of course, we will not cover mixed strategy equilibria until a later chapter. Thecorrect statement is that there is no equilibrium in pure strategies.5. The Great Escape. Refer to Chapter 2, Question 2.Discuss this game, from the point of view of noncooperative solutions. Does it have a dominant strategy equilibrium? Does it have Nash equilibrium? What strategies, if so? How can these two opponents each rationally choose a strategy?WardenGuard walls Inspect cellsclimb No escape, success inpreventing escape Escape,failurePrisonerdig Escape,failure No escape, success inpreventing escapeThe numerical payoffs can be assigned in many different ways. Here is a simple version that interprets “no escape” as minus one for the prisoner, plus one for the warden, and “escape” as vice versa. As the underlines show, there is no Nash equilibrium. Thus far, we have no basis to say how a rational person would choose strategies in this case.WardenGuard walls Inspect cellsclimb-1,11,-1Prisonerdig1,-1-1,16. Sibling Rivalry. Refer to Chapter 2, Question 1.Discuss this game, from the point of view of noncooperative solutions. Does it have a dominant strategy equilibrium? Determine all the Nash equilibria in this game. Do some Nash Equilibria seem likelier to occur than others? Why?Irismath litmath 3.7, 3.8 4.0, 4.0Julialit 3.8, 4.0 3.7, 4.0If the siblings act independently, rationally and with self- interest (non-cooperatively), we can find two Nash equilibrium's strategies: (literature, math), (math, literature).We note that there is a Schelling point in this game: (Math, Lit) yields a certain 4.0 for both girls, which is a reason it might attract attention, and probably is more likely to be observed.7. Hairsyle.Shaggmopp, Inc. and Shear Delight are hair-cutting salons in the same strip mall, each groping for a market niche. Each can choose one of three styles: punker, contemporary sophisticate, or traditional. Those are their strategies. They already have somewhat different images, based on the personalities of the proprietors, as the names may suggest. The payoff table is shown as Table E4.Table E4. Payoffs for HaircuttersShearpunker sophisticate traditionalpunker35,2050,4060,30Shaggmoppsophisticate30,4025,2535,55traditional20,4040,4520,20Are there any dominant strategies in this game? Is there a dominant strategy equilibrium? Are there any Nash equilibria? How many? Which? How do you know?Once again, here is the modified table:ShearPunkerSophisticate Traditional Punker 35, 2050, 4060, 30Sophisticate 30, 4025, 2535, 55S h a g g m o p pTraditional20, 4040, 4520, 20Shaggmopp’s best strategy is to go punker regardless of what Shear does. This is his dominant strategy. Since Shear has no such dominant strategy, there is no dominant strategy equilibrium.The only Nash equilibrium is when Shear decides to go with the sophisticate look.Since Shear knows that Shaggmopp will probably go punk rather than sophisticate, it will choose sophisticate.6. Quiz questionPlaced on the next page for convenience in copying and printing.Student name ____________________________Quiz – Game TheoryFelix and Oscarina share their home with two cats. Felix, who has a sharp sense of smell, would like for the cat boxes to be cleaned twice a week. Oscarina, whose sense of smell is less acute, would be satisfied if they were cleaned once a week. Each would prefer not to be the one to clean the cat boxes. Their payoffs are shown on the following table.Oscarinadon't clean clean once clean twicedon't clean-5,-30,-17,-5Felixclean once-2,45,26,-4clean twice0,51,32,-3Find any and all Nash equilibria for the catbox game? Are there dominated strategies? Which? Is there a dominant strategy equilibrium? Explain.Answer:A payoff table with best responses underlined follows:Oscarinadon't clean clean once clean twicedon't clean-5,-30,-17,-5Felixclean once-2,45,26,-4clean twice0,51,32,-3The Nash equilibrium is where Felix cleans the cat box twice and Oscarina never cleans. “Clean twice” is a dominated strategy for Oscarina. Since the best response for each person depends on the strategy chosen by the other, there is no dominant strategy equilibrium.It seems that Felix, whose need is greater, will empty the catbox, if the two companions act noncooperatively. Now, it may seem odd that people who live together would act noncooperatively , but life is strange, and odd things do happen. However, a couple of years ago, Oscarina gave Felix a Christmas present – a year of catbox cleaning – and has renewed the gift, so love triumphs after all.。
第四章动态不完全信息博弈第一节. 序贯均衡的内涵一.问题的提出1.序贯理性2.一致信念二.序贯均衡的内涵1.例子2.定义a.行为战略b.序贯理性c.一致信念3.存在性三.序贯均衡的计算1.例子:一般计算2.例子:分析应用第二节. 序贯均衡的应用一.教育和信号传递1.假设2.分析二.垄断限价模型1.假设2.分析三.声誉模型1.假设2.分析四.序贯均衡之再精炼1.剔除劣弱战略2.直观标准3.垄断限价模型第四章不完全信息动态博弈第一节.序贯均衡的内涵一.问题的提出1.序贯理性——参与人在所有情况决策都是理性的,即在给定信念的条件下,以及其他参与人的选择条件下,自身选择是最优的例1:子博弈最优——纳什均衡(,)L l是否合理?——如果参与人2有机会选择,肯定选r而不是l;——(,)L l不是子博弈精炼纳什均衡。
例2:单点信息集最优——纳什均衡(,,)D a l是子博弈纳什均衡;——但如果参与人2有机会选择,但肯定选择d;——(,,)D a l不满足单点信息集理性。
例3:多点信息集最优——纳什均衡(,)A r是子博弈精炼纳什均衡;——(,)A r不满足多点信息集理性。
2.一致信念例1:与客观事实一致u=是否合理?——参与人2的信念2/3——2/3u=是不合理的,因为任何到达参与人2信息集都不可能产生此后验概率;——后验信念必须与先念信念保持一致。
例2:前后信念一致——参与人2的第2个信息集上的信念,是否合理?——不合理,给定参与人战略和第1个信息集的信念,利用贝叶斯法则计算信念与此不一致;——参与人前后信念保持一致。
例3:独立偏离——参与人3的信念0.9u =是否合理?——参与人1和参与人3的偏离是独立的,所以参与人3的合理信念为0.1u =;——不同参与人之间的偏离是独立的总结,一致信念要求:参与人偏离最小化,,参与人之间偏离是独立的;二.序贯均衡的定义1.例子——定义参与人1在信息集1.1和1.3以及参与人2在2.2上的序贯理性;——定义信息集1.3和2.2的信念?2.定义a.行为战略:参与人在某个信息集到行动集映射,——如果某个状态真正发生,参与人如何决策;——序贯理性是否满足?b.序贯理性:在任何信息集上,参与人在给定信念和所有后续行为战略,选择自身行为战略最大化预期效用。
在单结信息集上,参与人i 的行动满足:max [,] is i is s arg U x σσρ-∈ (1)在多结信息集上,参与人i 的行动满足:max ()[,] is is i is s arg x U x σπσρ-∈∑ (2)——含义,在任何信息集上行动总是最优。
c.信念一致性:在任何信息集上参与人的信念必须和行动保持一致。
如果参与人i 信念集有正概率到达,则:()()()is y sP x x P y σπσ∈=∑ (3)如果参与人i 的信息集是零概率到达,则:lim () ()lim ()k is k P x x P y σπσ=∑ (4) ——k σ是让所有信息集都到达的行为战略;——k σσ→,收敛于现有行为战略;——仅仅需求存在一个序列满足以上条件。
d.满足(1)(2)(3)和(4),则称行为战略和信念系统(,)σπ是序贯均衡。
仅满足(1)(2)和(3),则称为弱序贯均衡,但弱序贯均衡不一定是纳什均衡。
如例子中121(,,)b w z 是弱序贯均衡,但不是纳什均衡,关键在于参与人1在1.1和1.3行为没有协调一致。
标准4是非常关键的,正式把定义非均衡路径上的信念,从而定义非均衡路径上参与人的合理行为。
3.存在性a.存在性定理——任何博弈都存在代理人标准式的颤抖手均衡;——任何代理人标准式的颤抖手均衡一定是序贯均衡。
b.和纳什均衡的关系——是纳什均衡;——可利用反证法和库恩等价定理证明。
三.计算 1.例子——在信息集2.2时,参与人2的最优行为战略为'L;——给定参与人2的最优选择,参与人1在信息集1.1的最优行为战略为L。
2.例子:考虑下图扩展式博弈,求解所有的序贯均衡3,8 2,61,0 -2,7 -1,9 -1,7——首先考虑在信息集2.3时最优行动:333: 80(1)8: 77(1)7: 69(1)93e f g αααααααα⋅+⋅-=⋅+-=⋅+-=-由此可得结论:3337/8 ;2/37/8;2/3 ;e f g ααα≥⇒≤≤⇒≤⇒最优选择最优选择最优选择——分析纯战略序贯均衡3. 7/8A e α≥⇒最优选择此时参与人1最优行为战略为121.1 1.2x x →→,则这与7/8α≥矛盾。
3. 2/37/8B f α≤≤⇒最优选择为此时参与人1的最优行为战略为121.1, 1.2y y →→。
所以,根据标准4扰动行为战略满足:12121227εαεεεεε=⇒≤≤+序贯均衡:[]123,, 2/37/8y y f α≤≤3. 2/3C g α≤⇒最优选择为此时参与人1最优行为战略121.1 1.2,2/3x y α→→≤则与矛盾。
——分析混合行为战略序贯均衡33. 7/8A e f α=⇒和混合.. 7/8α=的唯一可能就是1x 和2x 的使用概率为0,或参与人1在信息集1.2上选择2x 和2y 无差异。
由此可以得到参与人2的最优行为战略:3(1)0 x 1/42(1)0 x=2/3x x x x --≤⇒≤--=⇒7/8α=时考虑参与人1的最优行为战略: 1/4x ≤,构造扰动战略11212778εαεεεε==⇒=+ 2/3x =,此时在信息集1.1最优选择为1x ,1.2的最优选择:171 y=187y α==⇒+ …序贯均衡:12337[, , (1)] x 1/48y y x e x f α=⋅+-≤ 1223371621 [, , ]87733x x y e f α=++ 33. 2/3B f g α=⇒和的混合2/3α=的唯一可能就是1x 和2x 选择概率都为0,此时要求3f 使用概率大于等于2/3。
所以,扰动的行为战略满足:11212223εαεεεε==⇒=+ …序贯均衡:12332[, , x (1)] x 2/33y y f x g α=⋅+-⋅≥3.例子:问在什么条件下(c,eg)是一个序贯均衡——构造扰动行为战略[1212,,1εεεε--]——在信息2.2最优行为是e 的条件:33(1)1/2ααα⋅≤-⇒≤,也就是:1211221/222εαεεεε=≤⇒≥+——参与人在2.3时信息集β满足:211211240.824εεβεεεε=≥=++——所以g 要成为最优选择的条件:0.20.82 x 8x ⨯≥⨯⇒≥第二节.序贯均衡的应用一.信号传递模型1.假设——存在两个参与人,信号发送者和信号接受者;——信号接受者没有私人信息,信号发送者有两种类型,t和2t;1——信号发送者首先发送信号,信号接受者在观察到发送者信号再决定自己的行动。
2.分析求解分离均衡:不同类型参与人发送不同的信号12, t H t T →→——此时参与人2的后验信念为1, q=0p =——此时参与人2的最优选择为(,)H T——显然类型为2t 的参与人肯定不是最优选择12, t T t H →→——此时参与人2的后验信念为0, q=1p =——此时参与人2的最优选择为(,)T H——此时类型为2t 的参与人肯定不是最优选择。
混同均衡:不同类型参与人发送相同的信号12, t H t H →→——此时参与人2的后验信念为0.8, 0q 1p =≤≤——此时参与人2在信息集2.2最优选择为H ;——如果参与人类型为2t 没有积极性偏离,则参与人2在2.3信息集应该选择T ,由此要求1/2q ≤——所以混同均衡为(,,) p=0.8 q 0.5H H T ≤12, t T t T →→——此时参与人2的后验信念为0.8 0p 1q =≤≤——此时参与人2在信息集2.3最优选择为H ;——如果参与人1类型为1t 的没有积极性偏离,则参与人2在2.2选择为T ,也就是要求0.5p ≤——所以混同均衡为(,,) p 0.5 q=0.8T H T ≤教育学历和信号发送的关系二.动态非对称息讨价还价1.假设——工会和企业老板就员工工资进行讨价还价;——员工的保留效用0,企业利润π服从[]0,H π上的均匀分布,企业利润是老板的私人信息;——在第一阶段,工会提出工资要求1w ,如果企业老板接受,则博弈结束,老板支付为1w π-,工会为1w ;如果拒绝,则博弈进入第二阶段;——在第二阶段,工会同样提出工资要求2w ,如果老板接受,则企业老板得到2w π-,工会得到2w ;如果拒绝,则双方各得到0; ——现在假定双方的贴现因子都为δ。
2.分析和求解——假定只有一个阶段博弈,则工会最优工资w :0H H H www πππ-⨯+⨯ 所以*/2H w π=——给定工会最优战略12(,)w w ,企业在第一阶段最优决定为:如果1ππ>,则接受工资1w ;反之则拒绝,1π满足:1211121[] 1w w w w δπδππδ-⋅-=⋅-=-即:——给定企业老板的第一阶段的最优决策,工会的后验信念为企业利润服从1[0,]π上的均匀分布,所以工会最优工资*21/2w π= ——由此可以得到:1122w πδ=-——工会第一阶段的最优决策为:11111max /2H H Hw arg w πππδπππ-∈⨯+⨯⨯ ——最优一阶条件为:11122*1222022(2)(2)2(43)H H w w w w πδδδδδπδ--+⨯=----=⨯-——所以序贯均衡为:工会第一阶段提出工资*1w ,第二阶段为*1/2;π企业在第一阶段如果*1ππ>则接受*1w ,反之则拒绝,在第二阶段如果*2w π>则接受,反之则拒绝。
三.声誉模型1.囚徒困境S2S1坦白抗拒坦白+2,+2 8,+0 抗拒+0,8 +7,+72.假设——假定囚徒有α类型为合作类型,1α-类型为自私类型——合作类型坚持冷酷战略,一开始抗拒,一旦发现对手选择坦白,则坦白到永远——自私类型的支付矩降如上图所示——以上博弈重复有限次T,并且每一阶段都能被下一阶段所观察δ=到,假定贴现因子13.分析——如以上博弈重复3次,合作是否会出现?..自私类型选择合作的最小收益:[778](1)[022]αα⨯+++-⨯++..自私类型选择不合作的最大收益:[822](1)[822]αα⨯+++-⨯++所以如果满足:4/9α≥显然在第一阶段合作是自私类型的最优选择。
——无论α多么小,只要重复次数足够大,合作肯定会出现 ..合作的最小收益:[77...8](1)[02...2]αα⨯++++-⨯+++..不合作的最大收益:[82...2](1)[82...2]αα⨯++++-⨯+++..自私类型人在第一阶段合作的条件:5(1)8(1)08/(53)T T ααα-⨯--≥⇒≥+..更加一般地,只要重复次数足够大,则所有0t T ≤,自私参与人总选择合作..机制分析…合作收益 5(1)T α-⨯…不合作收益 (1)α-…合作收益是长远收益,随着时间增加而增加,而不合作收益是眼前的利益..如果考虑贴现因子,则合作收益随着贴现因子与δ增加而增加 …合作的最小收益11[77...78](1)[02...22]T T T Tαδδδαδδδ--⨯++++-⨯+++ …不合作的最小收益11[82...22](1)[82...22]T T T T αδδδαδδδ--⨯++++-⨯+++…两者差距随着贴现因子增加而增加 1158(1)1Tδαδαδ⎡⎤--+⨯--⎢⎥-⎣⎦四.序贯均衡之再炼1.剔除劣战略标准——如果对于某一类型参与人i t ,满足以下条件,则我们称m 为i t 类型严格劣信号,[,,][,,]S i i a aMaxU m a t Min m a t < ——如果可能,i t 类参与人发送信号m 的概率为0,即信号接受者后验信()0i P t m =——以上信号传递模型存在两个信号混同均衡:(,,), 0.8, 1/2H H T p q =≤(,,), 0.5 0.8T H T P q ≤= ——利用以上标准检验: ..检验混同均衡1 对于类型1t 存在以下关系:11[,,]3[,,]0S a a MaxU H a t Min T a t =>= 11[,,]2[,,]1S a a MaxU T a t Min H a t =>=对于类型2t 存在以下关系:1111[,,]2[,,]1[,,]3[,,]0S a a S a a MaxU H a t Min T a t MaxU T a t Min H a t =>==>=T H 和都不是1t 和2t 类型的严格劣信号,因此,0.5q ≤是合理后验信念。