数学建模 之 人口模型

关于计划生育政策调整对人口数量、结构及其影响的研究【摘要】本文着重于讨论两个问题:1、从目前中国人口现状出发，对于中国未来人口数量进行预测。

2、针对深圳市讨论单独二胎政策对未来人口数量、结构及其对教育、劳动力供给与就业、养老等方面的影响。

对于问题1从中国的实际情况和人口增长的特点出发，针对中国未来人口的老龄化、出生人口性别比以及乡村人口城镇化等，提出了 Logistic 、灰色预测、等方法进行建模预测。

首先，本文建立了 Logistic 阻滞增长模型，在最简单的假设下，依照中国人口的历史数据，运用线形最小二乘法对其进行拟合， 对 2014 至 2040 年的人口数目进行了预测， 得出在 2040 年时，中国人口有 14.32 亿。

在此模型中，由于并没有考虑人口的年龄、 出生人数男女比例等因素，只是粗略的进行了预测，所以只对中短期人口做了预测，理 论上很好，实用性不强，有一定的局限性。

然后， 为了减少人口的出生和死亡这些随机事件对预测的影响， 本文建立了 GM(1,1) 灰色预测模型，对 2014 至 2040 年的人口数目进行了预测，同时还用 2002 至 2013 年的 人口数据对模型进行了误差检验，结果表明，此模型的精度较高，适合中长期的预测， 得出 2040 年时，中国人口有 14.22 亿。

与阻滞增长模型相同，本模型也没有考虑年龄 一类的因素，只是做出了人口总数的预测，没有进一步深入。

对于问题2针对深圳市人口结构中非户籍人口比重大，流动人口多这一特点，我们采用了灰色GM(1,1)模型，通过matlab 对深圳市自2001至2010年的数据进行拟合，发现其人口变化近似呈线性增长，线性相关系数高达0.99，我们就此认定其为线性相关并给出线性方程。

同理，针对其非户籍人口，我们进行matlab 拟合发现，其为非线性相关，并得出相关函数。

并做出了拟合函数0.0419775(1)17255.816531.2t X t e ⨯+=⨯-。

数学建模———关于人口增长的模型摘要：本文讨论了人口的增长问题，并预测出了2010、2020年的美国人口。

首先，我们给出了两种预测方法：第一，在假定人口增长率不变的情况下，建立指数增长模型；第二，假定人口增长率呈线性下降的情况下，建立阻滞增长模型。

对两种模型的求解，我们引入了微分方程。

其次，为了选择一种较好的预测方法，我们分别对两种模型进行了检验和讨论。

先列图表对预测值与真实值进行比较，然后定性的对模型进行讨论，最后一个阶段选择绝对误差、均方差和相关系数对两个模型的优劣进行定量的评价，选出最好的预测方法。

一、 问题的提出：人口问题是当前世界上人们最关心的问题之一，认识人口数量的变化规律，做出较为准确的预报，是有效控制人口增长前提，现根据下表给出的近两百模型一（指数增长模型）1、模型的提出背景：我们对所给的数据进行了认真仔细的分析之后，对其进行处理：将年份进行编号（i X ），人口数量计为（i Y ），以i X 为横坐标，以i Y 为纵坐标，建立直角坐标系。

然后将表格中所给的数据绘在直角坐标系中附表A ，我们发现这些点大体呈指数增长趋势固提出此模型。

附图A2、基本假设：人口的增长率是常数增长率——单位时间内人口增长率与当时人口之比。

故假设等价于：单位时间人口增长量与当时人口成正比。

设人口增长率为常数r 。

时刻t 的人口为X(t),并设X(t)可微，X(0)=X O由假设，对任意△t>0 ，有)()()(t rx tt x t t x =∆-∆+即：单位时间人口增长量=r ×当时人口数当△t 趋向于0时，上式两边取极限，即：o t →∆lim)()()(t rx tt x t t x =∆-∆+ 引入微分方程：)1( )0()(0⎪⎩⎪⎨⎧==x x t rx dtdx3、模型求解： 从（1）得rdt xdx= 两边求不定积分：c rt x +=ln∵t=0时0x x =，∴C x =0lnrt e x rt x x 00ln ln ln =+=∴rte x t x 0)(= (2) 当r>0时.表明人口按指数变化规律增长.备注； r 的确定方法：要用（4.2）式来预测人口,必须对其中的参数r 进行估计: 十年的增长率307.0ln 9.33.5==r,359.1307.0=e,则(2)式现为: t t x )359.1(9.3)(⨯=4、结论：由上函数可预测得:2010的人口为x(22):x(22)=3325.772020的人口为x(23):x(23)=4519.735、检验：根据所建立的指数模型预测1790以后近两百年的美国人口数量,在此6、模型讨论：由表可见，当人口数较少时，模型的预测结果与实际情况相差不大（不超过5%）。

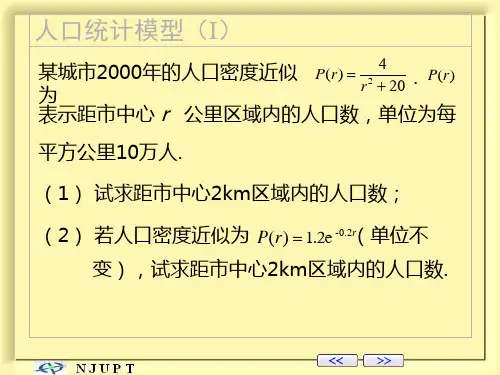
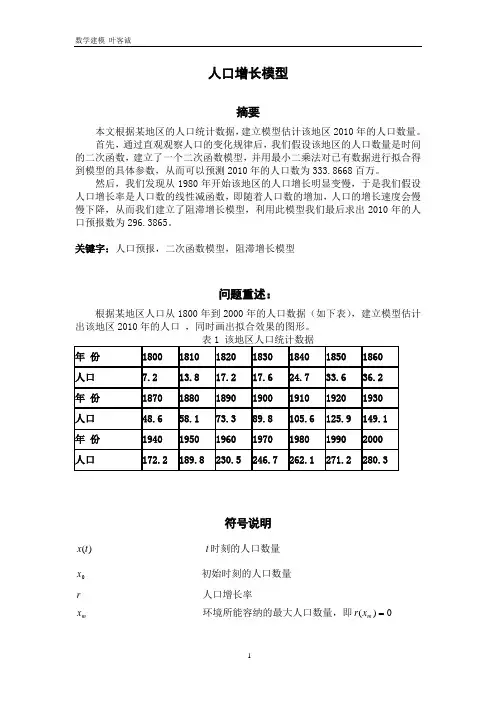
人口增长模型摘要本文根据某地区的人口统计数据，建立模型估计该地区2010年的人口数量。

首先，通过直观观察人口的变化规律后，我们假设该地区的人口数量是时间的二次函数，建立了一个二次函数模型，并用最小二乘法对已有数据进行拟合得到模型的具体参数，从而可以预测2010年的人口数为333.8668百万。

然后，我们发现从1980年开始该地区的人口增长明显变慢，于是我们假设人口增长率是人口数的线性减函数，即随着人口数的增加，人口的增长速度会慢慢下降，从而我们建立了阻滞增长模型，利用此模型我们最后求出2010年的人口预报数为296.3865。

关键字：人口预报，二次函数模型，阻滞增长模型问题重述：根据某地区人口从1800年到2000年的人口数据（如下表），建立模型估计出该地区2010年的人口 ，同时画出拟合效果的图形。

符号说明)(t x t 时刻的人口数量 0x 初始时刻的人口数量 r 人口增长率m x 环境所能容纳的最大人口数量，即0)( m x r问题分析首先，我们运用Matlab软件[1]编程（见附件1），绘制出1800年到2000年的人口数据图，如图1。

18001820184018601880190019201940196019802000图1 1800年到2000年的人口数据图从图1我们可以看出1800年到2000年的人口数是呈现增长的趋势的，而且类似二次函数增长。

所以我们可以建立了一个二次函数模型，并用最小二乘法对已有数据进行拟合得到模型的具体参数。

于是我们假设人口增长率是人口数的线性减函数，即随着人口数的增加，人口的增长速度会慢慢下降,从而我们可以建立一个阻滞增长模型。

模型建立模型一：二次函数模型我们假设该地区t时刻的人口数量的人口数量)(tx是时间t的二次函数，即：2()=++x t at bt c我们可以根据最小二乘法，利用已有数据拟合得到具体参数。

即，要求a、b和c，使得以下函数达到最小值：221(,,)()ni i i i E a b c at bt c x ==++-∑其中i x 是i t 时刻该地区的人口数，即有：2222)3.28020002000...)2.718001800(),,(-+⋅+⋅++-+⋅+⋅=c b a c b a c b a E令0,0,0E E E a b c∂∂∂===∂∂∂，可以得到三个关于a 、b 和c 的一次方程，从而可解得a 、b 和c 。

实验一 人口模型与混沌实验目的1.了解Logistic 模型的基本概念。

2.了解的1(1)n n n x rx x +=-分叉和混沌现象。

3.学习、掌握MATLAB 软件有关命令。

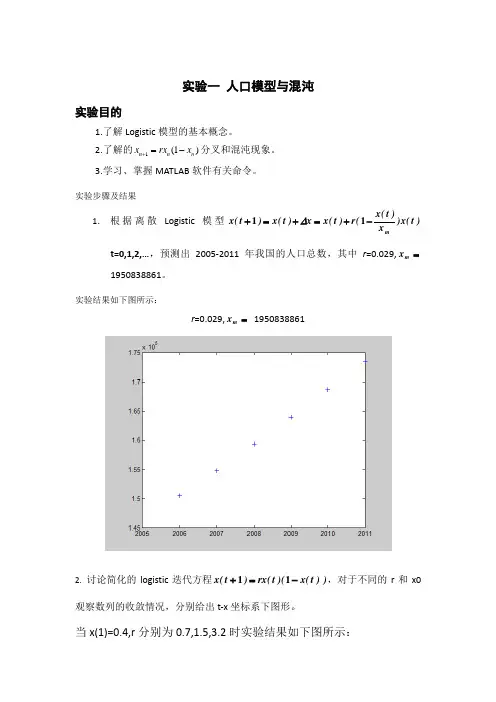
实验步骤及结果1． 根据离散Logistic 模型)t (x )x )t (x (r )t (x x )t (x )t (x m -+=+=+11∆t=0,1,2,…，预测出2005-2011年我国的人口总数，其中r =0.029,=m x1950838861。

实验结果如下图所示：r =0.029,=m x 19508388612. 讨论简化的logistic 迭代方程))t (x )(t (rx )t (x -=+11，对于不同的r 和x0观察数列的收敛情况，分别给出t-x 坐标系下图形。

当x(1)=0.4,r 分别为0.7,1.5,3.2时实验结果如下图所示：3、绘制Feigenbaum 图过程：为了观察r 对迭代格式))t (x )(t (rx )t (x -=+11的影响，将区间（0,4]以步长r ∆离散化。

对每个离散的r 值进行迭代，忽略前50个迭代值，把点5152100(,),(,),,(,)r x r x r x 显示在坐标平面上。

实验结果如下：实验代码：1.x=[2005:1:2011];y(1)=126743;r=0.029;k=1950838861;for i=1:11y(i+1)=y(i)+r*(1-y(i)/k)*y(i); endplot(x,y(6:12),'+');hold on2.x=[1:19];y(1)=0.4;r=3.2;for i=1:18y(i+1)=r*(1-y(i))*y(i);plot(x(i),y(i),'+');hold onendxlabel('t');ylabel('x');title('r=3.2,x(1)=0.4')3．for r=[0.005:0.005:4]x(1)=0.6;t=linspace(r,r,100);for j=1:99x(j+1)=r*x(j)*(1-x(j));endhold onplot(t,x,'r+','markersize',0.5); endxlabel('t');ylabel('x');title('r(0,4),x(0.6)')。

数学建模-人口增长模型人口增长模型是一种基于数理统计学方法的计算机模型，用于描绘全球各地的人口增长情况。

人口增长模型能够预测人口数量、年龄分布、死亡率、出生率、移民等方面的变化趋势，为社会规划带来指导性的建议，具有很高的实用价值。

本文将从多个方面来探究人口增长模型。

一、人口增长的三个阶段第一阶段：原始社会阶段，这个时期的人口增长缓慢。

由于食物水平低下和医疗条件落后，死亡率非常高，而出生率仍然很高。

第二阶段：传统社会阶段，人口增长迅速。

由于改进了农业技术、医疗技术以及水、电、煤等基础设施建设的改善，死亡率降低，但出生率仍然很高。

第三阶段：现代社会阶段，人口增长开始放缓。

由于生育规律的改变，人们生育晚、生育次数减少，导致出生率下降。

另一方面，医疗技术和生活水平的提高，使得人们的寿命增加，死亡率下降。

人口增长模型是一种以数学为基础、能够预测人口增长变化趋势的计算机模型。

它解决了传统的统计分析方法难以预测未来人口增长趋势的问题，方便了研究人口增长对于社会经济发展的影响。

目前，常用的人口模型有四种：1.经验模型：该模型主要是针对已有数据进行平衡分析，所以只能反映人口变动的历史趋势，难以预测未来人口变化。

2. 非参数回归模型：它又称为核回归模型，它是一种无参数模型，可以从数据本身中学习出应该如何比较好地去拟合数据，因此预测效果相较于经验模型提高了不少。

3. 参数回归模型：这种模型较为复杂，它基于特定的模型，通过拟合已有的数据，建立一个完整的模型，目的是预测新的数据变化趋势。

4. 知识驱动模型：该模型结合了经验模型和参数回归模型的基本特点，它将专家的知识与历史数据相结合，通过精细化的调整，建立能够反映人口增长趋势的模型。

该模型可广泛应用于国家人口预测、社会福利计划等领域。

人口增长有其基本的规律，这些规律可以帮助我们更好地了解和解决人口问题。

1.现代社会阶段的人口增长趋势是死亡率下降，而出生率下降，且死亡率的下降速度比出生率的下降速度快。

一、微分方程模型1.人口模型一、指数增长模型 （Malthus ）1.模型假设人口自然增长率 r 为常数，即单位时间内人口的增长量与当时的人口呈正比。

()x t :t 时刻的人口数 r :人口增长率2.模型建立 0(0)dx rx dtx x ⎧=⎪⎨⎪=⎩3.模型求解 0()r t x t x e =4.模型分析0r >⇒()x t →+∞ 人口将按指数规律无限增长！ 0r =⇒0()x t x ≡ 人口将始终保持不变！ 0r <⇒()0x t → 人口将按指数规律减少直至绝灭。

M a l t h u s 模型预测的优点是短期预报比较准确，但是不适合中长期预报，原因是预报时假设人口增长率 r 为常数。

没有考虑环境对人口增长的制约作用。

二、阻滞增长模型 (Logistic)1.模型假设假设人口增长率 r (x )是人口 x (t ) 的减函数 ：()1m x r x r x ⎛⎫=- ⎪⎝⎭其中: x m 为自然资源条件所能容纳的最大人口数量r 为固有增长率2.模型建立01(0)m d x x rx dt x x x ⎧⎛⎫=-⎪ ⎪⎨⎝⎭⎪=⎩ 3.模型求解：0()11mrt m x x t x e x -=⎛⎫+- ⎪⎝⎭4.模型分析（定性分析）0m x x >⇒()m x t x ↓→ 人口将递减并趋向于x m ，0m x x =⇒()m x t x ≡ 人口将始终保持x m 不变 ，00m x x <<⇒()mx t x ↑→ 人口将递增并趋向于x m ， 无论在哪种情况下，人口最终将趋向于最大人口容量！阻滞增长模型预测对中期预报比较准确，理论上很好，但是实用性也不强，原因在于预报时假设固有人口增长率 r 以及最大人口容量 x m 为定值。

实际上这两个参数（特别是 x m ）很难确定，而且会随着社会发展情况变化而变化。

中国人口增长预测模型班级：071221姓名：***学号：********摘要以2010年11月1日零时为标准时点，中国大陆31个省、自治区、直辖市和现役军人的人口共13.397亿。

13亿是一个忧虑的数字。

13亿人要吃饭、要穿衣、要上学、要就业、要住房……，消费的需求乘以13亿，就是一个庞大的数目，而我国的耕地、水资源、森林以及矿产资源本来就稀缺，再除以13亿，就少得可怜。

平均每人耕地面积只有1.4亩，水资源只相当于世界人均水平的1/4…….、中国是世界上人口最多的发展中国家，人口多，底子薄，人均耕地少，人均占有资源相对不足，是我国的基本国情，人口问题一直是制约中国经济发展的首要因素。

当前中国的人口存在着最为明显的三大特点：（1）人口基数大，人口数量的控制难度仍很大。

（2）人口整体素质不高，特别是县域及以下农村人口素质普遍偏低。

（3）人口结构不合理，城乡差别、地区差别和人口素质差别很大。

人口数量、质量和年龄分布直接影响一个地区的经济发展、资源配置、社会保障、社会稳定和城市活力。

在我国现代化进程中，必须实现人口与经济、社会、资源、环境协调发展和可持续发展，进一步控制人口数量，提高人口质量，改善人口结构。

对此，单纯的人口数量控制（如已实施多年的计划生育）不能体现人口规划的科学性。

政府部门需要更详细、更系统的人口分析技术，为人口发展策略的制定提供指导和依据。

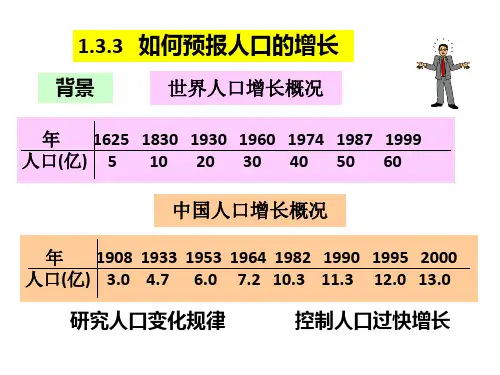
我国是世界第一人口大国，地球上每九个人中就有二个中国人，在20世纪的一段时间内我国人口的增长速度过快，如下表：有效地控制人口的增长，不仅是使我国全面进入小康社会、到21世纪中叶建成富强民主文明的社会主义国家的需要，而且对于全人类社会的美好理想来说，也是我们义不容辞的责任。

长期以来，对人口年龄结构的研究仅限于粗线条的定性分析，只能预测年龄结构分布的大致范围，无法用于分析年龄结构的具体形态。

随着对人口规划精准度要求的提高，通过数学方法来定量计算各种人口指数的方法日益受到重视，这就是人口控制和预测。

数学建模———关于人口增长的模型摘要：本文讨论了人口的增长问题，并预测出了2010、2020年的美国人口。

首先，我们给出了两种预测方法：第一，在假定人口增长率不变的情况下，建立指数增长模型；第二，假定人口增长率呈线性下降的情况下，建立阻滞增长模型。

对两种模型的求解，我们引入了微分方程。

其次，为了选择一种较好的预测方法，我们分别对两种模型进行了检验和讨论。

先列图表对预测值与真实值进行比较，然后定性的对模型进行讨论，最后一个阶段选择绝对误差、均方差和相关系数对两个模型的优劣进行定量的评价，选出最好的预测方法。

一、 问题的提出：人口问题是当前世界上人们最关心的问题之一，认识人口数量的变化规律，做出较为准确的预报，是有效控制人口增长前提，现根据下表给出的近两百模型一（指数增长模型）1、模型的提出背景：我们对所给的数据进行了认真仔细的分析之后，对其进行处理：将年份进行编号（i X ），人口数量计为（i Y ），以i X 为横坐标，以i Y 为纵坐标，建立直角坐标系。

然后将表格中所给的数据绘在直角坐标系中附表A ，我们发现这些点大体呈指数增长趋势固提出此模型。

附图A2、基本假设：人口的增长率是常数增长率——单位时间内人口增长率与当时人口之比。

故假设等价于：单位时间人口增长量与当时人口成正比。

设人口增长率为常数r 。

时刻t 的人口为X(t),并设X(t)可微，X(0)=X O由假设，对任意△t>0 ，有)()()(t rx tt x t t x =∆-∆+即：单位时间人口增长量=r ×当时人口数当△t 趋向于0时，上式两边取极限，即：o t →∆lim)()()(t rx tt x t t x =∆-∆+ 引入微分方程：)1( )0()(0⎪⎩⎪⎨⎧==x x t rx dtdx3、模型求解： 从（1）得rdt xdx= 两边求不定积分：c rt x +=ln∵t=0时0x x =，∴C x =0lnrt e x rt x x 00ln ln ln =+=∴rte x t x 0)(= (2) 当r>0时.表明人口按指数变化规律增长.备注； r 的确定方法：要用（4.2）式来预测人口,必须对其中的参数r 进行估计: 十年的增长率307.0ln 9.33.5==r,359.1307.0=e,则(2)式现为: t t x )359.1(9.3)(⨯=4、结论：由上函数可预测得:2010的人口为x(22):x(22)=3325.772020的人口为x(23):x(23)=4519.735、检验：根据所建立的指数模型预测1790以后近两百年的美国人口数量,在此6、模型讨论：由表可见，当人口数较少时，模型的预测结果与实际情况相差不大（不超过5%）。

人口模型数学建模随着人口快速增长和城市化进程的加速，人口问题越来越受到大众的关注，国家也在不断地为解决人口问题做出努力。

而在这个过程中，数学建模作为一种有效的工具正逐渐地被应用于人口模拟的研究中，而人口模型也成为了当前人口研究中最常见的方法之一。

本文将从什么是人口模型以及它的意义入手，再从人口增长模型、人口结构模型和人口流动模型三个方面介绍人口模型数学建模的相关内容，并探讨该领域的未来发展方向。

一、什么是人口模型以及它的意义人口模型是一种模拟人口数量和结构变化的方法，通过对人口数量、人口结构、人口增长和流动等关键因素进行分析和预测，来探究人口变化对社会、经济和环境等方面的影响。

而人口模型对解决实际问题具有十分重要的意义。

首先，它可以为政府制定人口政策、规划新城市、解决社会问题提供科学依据。

以我国为例，随着我国人口老龄化和人口流动的不断加剧，建立人口模型对于科学合理地规划人口方向和政策具有十分重要的意义。

其次，人口模型也可以为社会科学领域的研究提供参考，如人口迁移模型可以应用于研究人口迁移与城市结构的关系，对我国城市规划和发展的促进有重要意义。

二、人口增长模型人口增长模型是指通过对人口出生率、死亡率和人口迁移情况等因素进行计算，预测未来人口数量的变化和趋势。

在国家战略制定和人口规划中，人口增长模型是一个很重要的组成部分。

目前，应用最为广泛的人口增长模型包括基本增长模型、Malthus人口增长模型、Logistic人口增长模型和竞争性Lotka-Volterra模型等。

其中，基本增长模型是简单的指数函数，反映了人口随时间的指数增长趋势。

而Logistic人口增长模型则认为人口增长具有一定的饱和性，人均出生率一定的情况下，人口数量将趋于稳定。

三、人口结构模型人口结构模型是指通过对人口各年龄段、性别、职业、教育程度和收入等方面的分布进行计算，来了解人口的组成和各组成部分的数量变化趋势。

其中，最为经典的人口结构模型就是李约瑟模型。

数学建模人口增长模型摘要:人口的增长是当前世界上引起普遍关注的问题作为世界上人口最多的国家，我国的人口问题是十分突出的由于人口基数大尽管我国已经实行了20多年的计划生育政策人口的增长依然很快，巨大人口压力会给我国的社会政治经济医疗就业等带来了一系列的问题。

因此研究和解决人口问题在我国显得尤为重要。

我们经常在报刊上看见关于人口增长预报，说到本世纪，或下世纪中叶，全世界的人口将达到多少亿。

你可能注意到不同报刊对同一时间人口的预报在数字商场有较大的区别，这显然是由于用了不同的人口整张模型计算出来的结果。

人类社会进入20世纪以来，在科学和技术和生产力飞速发展的同时世界人口也以空前的规模增长。

人口每增加十亿的时间，有一百年缩短为十几年。

我们赖以生存的地球已经携带着他的60亿子民踏入下一个世纪。

长期以来，人类的繁殖一直在自然地进行着，只是由于人口数量的迅速膨胀和环境质量的急剧恶化，人们才猛然醒悟，开始研究人类和自然的关系、人口数量的变化规律以及如何惊醒人口控制等问题。

本论文中有两个模型：（1）：中国人口的指数增长模型，并用该模型进行预测，与实际人口数据进行比较。

（2）：中国人口的Logistic图形，标出中国人口的实际统计数据进行比较。

而且利用MATLAB图形，标出中国人口的实际统计数据，并画出两种模型的预测曲线。

关键字：人口预测；Malthus模型；Logistic模型；MATLAB软件一、问题背景及重述1.1问题的背景中国是一个人口大国，人口问题始终是制约我国发展的关键因素之一。

我国自1973年全面推行计划生育以来，生育率迅速下降，取得了举世瞩目的成就，但全面建设小康社会仍面临着人口的形势和严峻挑战。

随着我国经济的发展、国家人口政策的实施，未来我国人口高峰期到底有多少人口，专家学者们的预测结果不一。

因此，根据已有数据，运用数学建模的方法，对中国人口做出分析和预测是一个重要问题。

1.2 问题的重述下表列出了中国1982~1998年的人口统计数据，取1982年为起始年(t=0)，1982年的人口101654万人，人口自然增长率为14‰，以36亿作为我国人口的容纳量，试建立一个较好的人口数学模型并给出相应的算法和程序，并与实际人二、问题分析对于人口增长的问题，其影响因素有很多，比如：人口基数，出生率，死亡率，人口男女比例，人口年龄结构的组成，人口的迁入率和迁出率，人口的生育率和生育模式，国家的医疗发展情况，国家的政治策略等众多的因素。

论文结构合理，模型建立详细，思想明确，论述清楚程序和拟合是文章的亮点，模型建立完了没有做误差分析，如果补完整是一篇很不错的文章。

摘要•随着科学技术的发展，国内资金积累量在不断增加，但是中国人口近几年还是呈增加的趋势，这样就会影响人均收入。

由于国民收入是资金积累的一部分，国民收入变化可以反映资金积累的变化。

因此研究资金积累、国民收入与人口增长的关系可以转化成研究资金积累与人口增长的关系。

若国民平均收入与按人口平均资金积累成正比，说明仅当资金积累的相对增长率大于人口的相对增长率时，国民平均收入才是增长的。

所以认识资金积累与人口增长的关系，对国民平均收入的增长有重大意义。

本文通过微分方程建立三个模型，即人口Malthus模型、资金积累指数模型、资金积累增长率与人口增长率的二次曲线模型。

通过资金积累与人口增长的关系来分析国民平均收入。

关键词：资金积累人口增长国民平均收入资金积累增长率人口增长率一、问题的重述资金积累、国民收入、与人口增长的关系：（1）若国民平均收入x与按人口平均资金积累y成正比，说明仅当总资金积累的相对增长率k大于人口的相对增长率r时，国民平均收入才是增长的. （2）作出k(x)和r(x)的示意图，分析人口激增会引起什么后果.二、问题分析人均国民收入主要与国家资金总积累量和总人口数有关，若总人口数的增长率大于资金积累增长率，则增长的资金不能使每一位国民增加收入，只能使少量国民收入增加，因此，总体来说，国家人均收入实际上是减少的。

三、模型假设假设总资金增长和人口增长均为指数增长，资金积累增长率和人口增长率为二次曲线模型。

四、符号说明a为国民收入在总资金积累中所占比例；y(t)为总资金积累量；N（t）为总人口数；Nm为人口的峰值；x(t) 为人均国民收入；r 为人口增长率；k 为资金积累增长率。

五、模型的建立与求解（1）人口增长模型曲线如图1所示：图1通过图形，用MATLAB 编程可建立指数增长模型6110)()(⨯+=⨯tet N αα 其中0127.01=α 0058.02=α（2）总资金积累模型曲线如图2所示：图2由曲线可知资金增长是呈指数整长的并通过MATLAB编程得到指数模型：y(t)=（0.001+e x003.0） 106。

Logistic人口发展模型一、题目描述建立Logistic人口阻滞增长模型,利用表1中的数据分别根据从1954年、1963年、1980年到2005年三组总人口数据建立模型,进行预测我国未来50年的人口情况.并把预测结果与国家人口发展战略研究报告中提供的预测值进行分析比较.二、建立模型阻滞增长模型Logistic 模型阻滞增长模型的原理：阻滞增长模型是考虑到自然资源、环境条件等因素对人口增长的阻滞作用,对指数增长模型的基本假设进行修改后得到的.阻滞作用体现在对人口增长率r 的影响上,使得r 随着人口数量x 的增加而下降.若将r 表示为x 的函数)(x r .则它应是减函数.于是有：)0(,)(x x x x r dtdx==1对)(x r 的一个最简单的假定是,设)(x r 为x 的线性函数,即)0,0()(>>-=s r sxr x r2设自然资源和环境条件所能容纳的最大人口数量m x ,当m x x =时人口不再增长,即增长率0)(=m x r ,代入2式得m x rs =,于是2式为 )1()(mx x r x r -= 3将3代入方程1得：⎪⎩⎪⎨⎧=-=0)0()1(x x x x rx dtdxm 4解得：rt mme x x x t x --+=)1(1)(05三、模型求解用Matlab求解,程序如下：t=1954:1:2005;x=60.2,61.5,62.8,64.6,66,67.2,66.2,65.9,67.3,69.1,70.4,72.5,74. 5,76.3,78.5,80.7,83,85.2,87.1,89.2,90.9,92.4,93.7,95,96.259,97. 5,98.705,100.1,101.654,103.008,104.357,105.851,107.5,109.3,111. 026,112.704,114.333,115.823,117.171,118.517,119.85,121.121,122. 389,123.626,124.761,125.786,126.743,127.627,128.453,129.227,129 .988,130.756;x1=60.2,61.5,62.8,64.6,66,67.2,66.2,65.9,67.3,69.1,70.4,72.5,74 .5,76.3,78.5,80.7,83,85.2,87.1,89.2,90.9,92.4,93.7,95,96.259,97 .5,98.705,100.1,101.654,103.008,104.357,105.851,107.5,109.3,111 .026,112.704,114.333,115.823,117.171,118.517,119.85,121.121,122 .389,123.626,124.761,125.786,126.743,127.627,128.453,129.227,12 9.988;x2=61.5,62.8,64.6,66,67.2,66.2,65.9,67.3,69.1,70.4,72.5,74.5,76 .3,78.5,80.7,83,85.2,87.1,89.2,90.9,92.4,93.7,95,96.259,97.5,98 .705,100.1,101.654,103.008,104.357,105.851,107.5,109.3,111.026, 112.704,114.333,115.823,117.171,118.517,119.85,121.121,122.389, 123.626,124.761,125.786,126.743,127.627,128.453,129.227,129.988 ,130.756;dx=x2-x1./x2;a=polyfitx2,dx,1;r=a2,xm=-r/a1%求出xm和rx0=61.5;f=inline'xm./1+xm/x0-1exp-rt-1954','t','xm','r','x0';%定义函数plott,ft,xm,r,x0,'-r',t,x,'+b';title'1954-2005年实际人口与理论值的比较'x2010=f2010,xm,r,x0x2020=f2020,xm,r,x0x2033=f2033,xm,r,x0解得：xm= 180.9516千万,r= 0.0327/年,x0=61.5得到1954-2005实际人口与理论值的结果：根据国家人口发展战略研究报告我国人口在未来30年还将净增2亿人左右.过去曾有专家预测按照总和生育率2.0,我国的人口峰值在2045年将达到16亿人.根据本课题专家研究,随着我国经济社会发展和计划生育工作加强,20世纪90年代中后期,总和生育率已降到1.8左右,并稳定至今.实现全面建设小康社会人均GDP达到3000美元的目标,要求把总和生育率继续稳定在1.8左右.按此预测,总人口将于2010年、2020年分别达到13.6亿人和14.5亿人,2033年前后达到峰值15亿人左右见图1.劳动年龄人口规模庞大.我国15-64岁的劳动年龄人口2000年为8.6亿人,2016年将达到高峰10.1亿人,比发达国家劳动年龄人口的总和还要多.在相当长的时期内,中国不会缺少劳动力,但考虑到素质、技能等因素,劳动力结构性短缺还将长期存在.同时,人口与资源、环境的矛盾越来越突出.而据模型求解：2010年人口：x2010= 137.0200千万专家预测13.6亿误差为0.7% 2020年人口：x2020= 146.9839千万专家预测14.5亿误差为1.3% 2033年人口：x2033= 157.2143千万专家预测 15亿误差为4.8% 2045年人口：x2045= 164.6959千万专家预测 16亿误差为4.1%五、预测1. 1954-2005总人口数据建立模型：r=0.0327 xm=180.95162010年人口：x2010= 137.0200千万专家预测13.6亿误差为0.7% 2020年人口：x2020= 146.9839千万专家预测14.5亿误差为1.3% 2033年人口：x2033= 157.2143千万专家预测 15亿误差为4.8% 2045年人口：x2045= 164.6959千万专家预测 16亿误差为4.1% 2. 1963-2005总人口数据建立模型：r=0.0493 xm=150.52612010年人口：x2010= 134.1612千万专家预测13.6亿误差为1.4% 2020年人口：x2020= 140.0873千万专家预测14.5亿误差为3.4% 2033年人口：x2033= 144.8390千万专家预测 15亿误差为3.4% 2045年人口：x2045= 147.3240千万专家预测 16亿误差为7.6% 3.1980-2005总人口数据建立模型：r=0.0441 xm=156.32972010年人口：x2010= 135.2885千万专家预测13.6亿误差为0.5% 2020年人口：x2020= 142.1083千万专家预测14.5亿误差为2.0%2033年人口：x2033= 147.9815千万专家预测 15亿误差为1.3% 2045年人口：x2045= 151.3011千万专家预测 16亿误差为5.4%总体来看,1980-2005这一组数据拟合出的人口模型比较好,即与已有数据吻合,又与专家预测误差较小.从历史原因来分析：1954年之后的1959-1961年间,有三年自然灾害故而使得实际人口数据与估计有所偏颇.1960年之后为过渡时期.1983年之后开始实施“计划生育政策”,一直至今,所以1980-2005年间的数据与预测分析最好.。