四川省成都石室中学2020届高三数学10月月考试题 文

成都市石室中学2019~2020学年度上期高三10月月考数学试卷（文科）一、选择题：（本大题共12小题，每小题5分.）1.已知集合{|(1)(2)0},{|0}=--≤=>M x x x N x x ，则（ ） A. N M ⊆ B. M N ⊆ C. M N ⋂=∅ D. M N R =U【答案】B【详解】由题意知：()(){}{}12012M x x x x x =--≤=≤≤，则M N ⊆ 本题正确选项：B2.已知i 为虚数单位，则232019i i i i ++++L 等于（ ） A. i B. 1 C. i - D. 1- 【答案】D【详解】由于234110i i i i i i +++=--+=， 且)ni n N *∈（的周期为4，2019=4504+3⋅， 所以原式=2311i i i i i ++=--=-.故选：D3.已知命题p ：(),0x ∀∈-∞，22310x x -+>，命题q ：若0x ≥，则22310x x -+≤，则以下命题正确的为（ ）A. p 的否定为“[0,)x ∃∈+∞，22310x x -+≤”，q 的否命题为“若0x <，则22310x x -+>”B. p 的否定为“(,0)x ∃∈-∞，22310x x -+≤”，q 的否命题为“若0x <，则22310x x -+>”C. p 的否定为“[0,)x ∃∈+∞，22310x x -+≤”，q 的否命题为“若0x ≥，则22310x x -+>”D. p 的否定为“(,0)x ∃∈-∞，22310x x -+≤”，q 的否命题为“若0x ≥，则22310x x -+>” 【答案】B【详解】p 的否定为“(,0)x ∃∈-∞，22310x x -+≤”，q 的否命题为“若0x <，则22310x x -+>” 故选：B4.已知{}n a 是公差为12的等差数列，n S 为{}n a 的前n 项和.若2a ，6a ，14a 成等比数列，则5S =（ ） A.352B. 35C. 252D. 25【答案】C【详解】因为2a ，6a ，14a 成等比数列，所以226214111151133,()()()2222a a a a a a a =+=++∴=， 因此5311255542222S =⨯+⨯⨯⨯=,选C.5.中国古代数学著作《算学启蒙》中有关于“松竹并生”的问题：松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等．意思是现有松树高5尺，竹子高2尺，松树每天长自己高度的一半，竹子每天长自己高度的一倍，问在第几天会出现松树和竹子一般高？如图所示是源于其思想的一个程序框图，若输入的x ＝5，y ＝2，输出的n 为4，则程序框图中的中应填（ ）A. y ＜xB. y≤xC. x≤yD. x ＝y【答案】C【详解】解：模拟程序的运行，可得x ＝5，y ＝2，n ＝1 x 152=，y ＝4 不满足条件，执行循环体，n ＝2，x 454=，y ＝8，此时，x ＞y ， 不满足条件，执行循环体，n ＝3，x 1358=，y ＝16，此时，x ＞y ，不满足条件，执行循环体，n ＝4，x 40516=，y ＝32，此时，x ＜y ，由题意，此时，应该满足条件，退出循环，输出n 的值为4． 可得程序框图中的 中应填x ≤y ？故选：C ．6.设函数2,1(),12x x f x x x -⎧<⎪=⎨≥⎪⎩，则满足()()12f f a f a =⎡⎤⎣⎦的a 的取值范围是（ ） A. (,0]-∞ B. [0,2] C. [2,)+∞ D. (,0][2,)-∞+∞U【答案】D【详解】函数2,1(),12x x f x x x -⎧<⎪=⎨≥⎪⎩，()()12f f a f a =⎡⎤⎣⎦得到()1f a ≥ 当1a <时：()21af a -=≥解得0a ≤，即0a ≤当1a ≥时：()12af a =≥解得2a ≥，即2a ≥ 综上所述：(,0][2,)a ∈-∞+∞U故答案选D7.若直线()24y k x =-+与曲线24y x =-有两个交点，则k 的取值范围是（ ）A. [)1,+∞ B. 31,4⎡⎫--⎪⎢⎣⎭ C. 3,14⎛⎤⎥⎝⎦D. (],1-∞- 【答案】C 解析：曲线24y x =-可化为，所以图象是以原点为圆心，为半径的圆，且只包括x 轴上方的图象，而直线()24y k x =-+经过定点，当直线与该半圆相切时刚好有一个交点，可以用圆心到直线的距离等于半径，求出临界值，利用数形结合，慢慢将直线绕定点转动，当直线过圆上的一点时，正好有两个交点，此时的，再转动时仍只有一个交点，所以取值范围为3,14⎛⎤⎥⎝⎦，故选C. 8.已知2ln3a =，3ln 2b =，6c e=，则a ，b ，c 的大小关系为（ ） A. a c b >> B. b c a >> C. c a b >> D. c b a >>【答案】C【详解】由题得ln 9,ln8a b ==， ∴a b >．又633ln 32ln 32(ln 3)2e c a e e e--=-=-=⋅， 设()ln ,0f x x e x x =->，则()1e x e f x x x-'=-=， ∴当0x e <<时，()0,()f x f x '<单调递减； 当x e >时，()0,()f x f x '>单调递增。

绝密★启用前四川省成都市石室中学2020届高三年级上学期10月月考质量检测语文试题答案解析1.C【解析】试题分析：A项表述过于绝对;B项“必须完好保存”错误;D项“使之成为相关产业的配套设施”错误，原文是“这需要相应的公共设施与之配套”。

故答案为C。

2.C【解析】试题分析：“并举例说明了甄选的标准”错误,原文没有这方面的信息。

故选C。

3.B【解析】试题分析：“就说明故乡已活化了乡村记忆”错误。

故选B。

4．C（“已经全面领先世界其他导航系统”错,原文没有依据。

）5．B（“将开启北斗导航系统全球组网的时代”错,原文是“继续加快全球组网步伐”。

）6．①攻坚克难、追求卓越的精神：不断攻克难题,提高国产化率,实现多项关键技术突破。

②团结协作、顾全大局的精神：培养人才,对技术毫不保留。

③持之以恒、锲而不舍的精神：坚持20多年的研制,不断取得重大成果。

（每条2分）7．D（表妹之所以说“不要打算懒懒散散混日子”是因为她每月收入不保底,多劳多得,但并未流露出对自己得不到休息的些许不满。

）8．①从所拿工资等,看出她是捧着铁饭碗的城市劳动者；②从背着手、做派头等,看出她有优越感和虚荣心；③从扑过去抢着洗衣服等,看出她渴望通过劳动改变生活。

9．①交代小说的主要人物是表妹。

②寄托了小说的主旨：通过塑造表妹的形象赞扬了劳动之美；肯定了勤劳致富的观念；赞美了农村所蕴含的勃勃生机；讴歌了正在变革中的伟大时代。

10.B此题可用排除法解答。

“闻渊代”,这里闻渊“代”的是周用,“自”可翻译为“自己”,“闻渊代自”就变成闻渊代替自己了,于理不通,所以“闻渊代”和“自”中间要断开,“自处前辈”连在一起,据此排除A、C两项；另外,“求出避之”要连在一起,因为徐阶“求”的内容是“出避之”,翻译为“徐阶恳请将自己调出以避开他”,中间不能断开,所以排除D项,答案选B项。

11. A期满后不一定官复原职。

（注：B选项中“全国官吏”一般指文官。

）1。

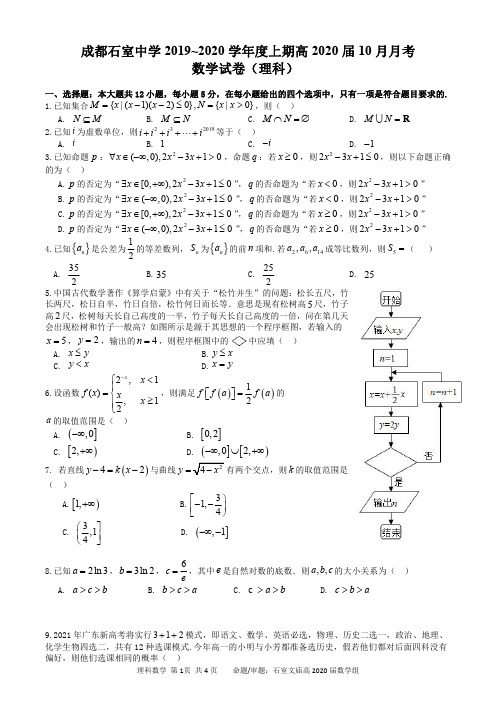
成都市石室中学2019-2020学年度上期高三10月月考数学试卷（理科）一、选择题：（本大题共12小题，每小题5分.）1.已知集合{|(1)(2)0},{|0}=--≤=>M x x x N x x ，则（ ） A. N M ⊆ B. M N ⊆ C. M N ⋂=∅ D. M N R =U【答案】B【详解】由题意知：()(){}{}12012M x x x x x =--≤=≤≤，则M N ⊆ 本题正确选项：B2.已知i 为虚数单位，则232019i i i i ++++L 等于（ ） A. i B. 1 C. i - D. 1- 【答案】D【详解】由于234110i i i i i i +++=--+=，且)ni n N *∈（的周期为4，2019=4504+3⋅，所以原式=2311i i i i i ++=--=-.故选：D3.已知命题p ：(),0x ∀∈-∞，22310x x -+>，命题q ：若0x ≥，则22310x x -+≤，则以下命题正确的为（ ）A. p 的否定为“[0,)x ∃∈+∞，22310x x -+≤”，q 的否命题为“若0x <，则22310x x -+>”B. p 的否定为“(,0)x ∃∈-∞，22310x x -+≤”，q 的否命题为“若0x <，则22310x x -+>”C. p 的否定为“[0,)x ∃∈+∞，22310x x -+≤”，q 的否命题为“若0x ≥，则22310x x -+>”D. p 的否定为“(,0)x ∃∈-∞，22310x x -+≤”，q 的否命题为“若0x ≥，则22310x x -+>” 【答案】B【详解】p 的否定为“(,0)x ∃∈-∞，22310x x -+≤”，q 的否命题为“若0x <，则22310x x -+>” 故选：B4.已知{}n a 是公差为12的等差数列，n S 为{}n a 的前n 项和.若2a ，6a ，14a 成等比数列，则5S =（ ） A.352B. 35C. 252D. 25【答案】C【详解】因为2a ，6a ，14a 成等比数列，所以226214111151133,()()()2222a a a a a a a =+=++∴=， 因此5311255542222S =⨯+⨯⨯⨯=,选C.5.中国古代数学著作《算学启蒙》中有关于“松竹并生”的问题：松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等．意思是现有松树高5尺，竹子高2尺，松树每天长自己高度的一半，竹子每天长自己高度的一倍，问在第几天会出现松树和竹子一般高？如图所示是源于其思想的一个程序框图，若输入的x ＝5，y ＝2，输出的n 为4，则程序框图中的中应填（ ）A. y ＜xB. y≤xC. x≤yD. x ＝y【答案】C【详解】解：模拟程序的运行，可得x ＝5，y ＝2，n ＝1 x 152=，y ＝4 不满足条件，执行循环体，n ＝2，x 454=，y ＝8，此时，x ＞y ， 不满足条件，执行循环体，n ＝3，x 1358=，y ＝16，此时，x ＞y ，不满足条件，执行循环体，n ＝4，x 40516=，y ＝32，此时，x ＜y ，由题意，此时，应该满足条件，退出循环，输出n 的值为4． 可得程序框图中的 中应填x ≤y ？故选：C ．6.设函数2,1(),12x x f x x x -⎧≤⎪=⎨>⎪⎩，则满足()()2f f a f a =⎡⎤⎣⎦的a 的取值范围是（ ）A. (],0-∞B. []0,2C. [)2,+∞D. (][),02,-∞+∞U【答案】D【详解】作出()y f x =的图象，可得()f x 的最小值为12， 令()t f a =，考虑()2tf t =的解， 考虑()y f t =与2ty =的图像的交点情况，如图所示故1t ≥，下面考虑()1f a ≥的解，如图所示，可得0a ≤或2a ≥．故选D.7.若直线()24y k x =-+与曲线24y x =-有两个交点，则k 的取值范围是（ ）A. [)1,+∞B. 31,4⎡⎫--⎪⎢⎣⎭C. 3,14⎛⎤ ⎥⎝⎦D. (],1-∞-【答案】C 【解析】曲线24y x =-可化为，所以图象是以原点为圆心，为半径的圆，且只包括x 轴上方的图象，而直线()24y k x =-+经过定点，当直线与该半圆相切时刚好有一个交点，可以用圆心到直线的距离等于半径，求出临界值，利用数形结合，慢慢将直线绕定点转动，当直线过圆上的一点时，正好有两个交点，此时，再转动时仍只有一个交点，所以取值范围为3,14⎛⎤⎥⎝⎦，故选C.8.已知2ln3a =，3ln 2b =，6c e=，则a ，b ，c 的大小关系为（ ） A. a c b >> B. b c a >> C. c a b >> D. c b a >>【答案】C【详解】由题得ln 9,ln8a b ==， ∴a b >． 又633ln 32ln 32(ln 3)2e c a e e e--=-=-=⋅，设()ln ,0f x x e x x =->， 则()1e x e f x x x-'=-=， ∴当0x e <<时，()0,()f x f x '<单调递减； 当x e >时，()0,()f x f x '>单调递增。

石室中学高2021届2019~2020学年度上期十月考试数学试卷参考答案二、填空题：共4题，每小题5分，合计20分.13.22116925+=y x；14．40x y+-=；15．4-；16．2．三、解答题：共6题，合计70分.17.解：（Ⅰ）22154+=x y…………5分（Ⅱ）点P的坐标(1)2±±.…………10分18．解：（Ⅰ）显然直线l斜率存在．设:l y kx=2=，解得k=l 的方程为y x=．…………6分（Ⅱ）由于CM AB⊥可知M的轨迹为以OC为直径的圆在圆C内部的部分，其方程为2230x x y-+=（533x<≤）．…………12分19. 解：（Ⅰ）设(,)P x y，(,0)A m，(0,)B n，由于3=BP PA，所以(,)3(,)-=--x y n m x y(33,3)=--m xy，即333=-⎧⎨-=-⎩x m xy n y，所以434⎧=⎪⎨⎪=⎩m xn y，…………3分又2216+=m n，从而221616169+=xy. …………4分即曲线C的方程为：2219+=xy. …………5分（Ⅱ）联立22219=+⎧⎪⎨+=⎪⎩y x txy，得2237369(1)0++-=x tx t，由22(36)4379(1)0∆=-⨯⨯->t t，可得<t，又直线2=+y x t不过(0,1)H点，且直线HM与HN的斜率存在∴1≠±t，∴<t ，且1≠±t212123699,3737-∴+=-=t t x x x x ， …………8分 1212121212114(1)()----++=+=HM HN y y x x t x x k k x x x x …………10分1212124(1)()4411--+∴=-=+x x t x x t x x t3∴=t所以t 的值为3 …………12分 20.解：（I ）曲线162+-=x x y 与y 轴的交点为(0,1)，与x 轴的交点为（).0,223(),0,223-+故可设C 的圆心为(3,)t ，则有,)22()1(32222t t +=-+解得1t =．则圆C 的半径为.3)1(322=-+t所以圆C 的方程为.9)1()3(22=-+-y x …………5分（II ）设11(,)A x y ，22(,)B x y ，其坐标满足方程组：⎪⎩⎪⎨⎧=-+-=+-.9)1()3(,022y x a y x 消去y ，得到方程.012)82(222=+-+-+a a x a x由已知可得，判别式.0416562>--=∆a a …………7分 因此，21212214,2a a x x a x x -++=-=①由于⊥OA OB ，可得,02121=+y y x x …………10分 又,,2211a x y a x y +=+=所以.0)(222121=+++a x x a x x②由①，②得1-=a ，满足,0>∆故.1-=a …………12分21. 解：（Ⅰ）由椭圆的定义知，动点M 的轨迹为椭圆22:143x y C +=.……………3分（Ⅱ）∵:l 2y kx =+，联立2223412y kx x y =+⎧⎨+=⎩，消去y ，得22(43)1640k x kx +++=. ……………4分∵ 216(123)0Δ=->k ，∴241k >. ……………5分设1122(,),(,)P x y Q x y .则1221221643443k x x k x x k ⎧+=-⎪⎪+⎨⎪=⎪+⎩. ……………7分∴22212122221616161212()44434343k k k y y k x x k k k -+++=++=-+==+++. ……8分 ∵OP OQ ON λ+=，易知0λ≠，∴122122116()(43)112()(43)N N k x x x k y y y k λλλλ⎧=+=-⎪+⎪⎨⎪=+=⎪+⎩. ……………9分又点N 在椭圆C 上， ∴22222222211611214(43)3(43)k k k λλ⨯+⨯=++. 化简，得22222644816(43)43k k k λ+==++. ……………10分∵241k >，∴2434k +>.∴2110434k <<+. ∴2160443k <<+，即204λ<<. ∴(2,0)(0,2)λ∈-. ……………12分22. 解：（Ⅰ）由题意，得123c b a==， ……………………2分222,a c b -=又3,1a b c ∴===， ……………………3分所以，椭圆C 的标准方程为22198x y +=. ……………………4分（Ⅱ）由（Ⅰ）可知，1(3,0),(3,0),(1,0)A B F --,设直线1F M 的方程为1x my =-,由题意知，0m >， …………………5分 设()11,M x y ,直线1F M 与椭圆的另一交点()22,M x y ¢, 12F MF N ，根据对称性,得()22,N x y --, ……………………6分联立228972,1,x y x my ì+=ïí=-ïî得()228916640m y my +--=,其判别式△0>,1221689my y m \+=+,1226489y y m =-+, ……………………7分 由题可知120y y >>，所以12y y -,()121240y y my y ++=, ① ……………………8分1111132y y k x my ==++,2222232y y k x my -==--+, 由12320k k +=,得1132y my ++22202y my =+,即12125640my y y y ++=,……………………9分将①式代入，得()121220640y y y y -+++=,即12780y y +=, ……………………10分 ∴()()1212150y y y y+--=,∴21615089mm?=+,解得m (11)分 ∴直线1F M 的方程为1xy -，即0y -+. ……………………12分。

成都石室中学2019~2020学年度上期高2020届10月月考 数学试卷（理科）一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的. 1.已知集合{|(1)(2)0},{|0}=--≤=>M x x x N x x ，则（ ） A. N M ⊆ B. M N ⊆ C. M N ⋂=∅ D. M N =R 2.已知i 为虚数单位，则232019i i i i ++++等于（ ） A. i B. 1 C. i - D. 1- 3.已知命题p ：2(,0),2310x x x ∀∈-∞-+>，命题q ：若0x ≥，则22310x x -+≤，则以下命题正确的为（ ）A.p 的否定为“2[0,),2310x x x ∃∈+∞-+≤”，q 的否命题为“若0x <，则22310x x -+>”B.p 的否定为“2(,0),2310x x x ∃∈-∞-+≤”，q 的否命题为“若0x <，则22310x x -+>”C.p 的否定为“2[0,),2310x x x ∃∈+∞-+≤”，q 的否命题为“若0x ≥，则22310x x -+>”D.p 的否定为“2(,0),2310x x x ∃∈-∞-+≤”，q 的否命题为“若0x ≥，则22310x x -+>” 4.已知{}n a 是公差为12的等差数列，n S 为{}n a 的前n 项和.若2614,,a a a 成等比数列，则5S =（ ） A.352B.35C. 252D. 255.中国古代数学著作《算学启蒙》中有关于“松竹并生”的问题：松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等．意思是现有松树高5尺，竹子高2尺，松树每天长自己高度的一半，竹子每天长自己高度的一倍，问在第几天会出现松树和竹子一般高？如图所示是源于其思想的一个程序框图，若输入的5x =，2y =，输出的4n =，则程序框图中的中应填（ ） A. x y ≤B.y x ≤C. y x <D.x y =6.设函数2,1(),12x x f x x x -⎧<⎪=⎨≥⎪⎩，则满足()()12f f a f a =⎡⎤⎣⎦的a 的取值范围是（ ）A. (],0-∞B. []0,2C. [)2,+∞D. (][),02,-∞⋃+∞7. 若直线()42y k x -=-与曲线y =有两个交点，则k 的取值范围是（ ）A.[)1,+∞B.31,4⎡⎫--⎪⎢⎣⎭C. 3,14⎛⎤⎥⎝⎦D. (],1-∞-8.已知2ln3a =，3ln 2b =，6c e=，其中e 是自然对数的底数．则,,a b c 的大小关系为（ ） A. a c b >> B. b c a >> C. c a b >> D. c b a >>9.2021年广东新高考将实行312++模式，即语文、数学、英语必选，物理、历史二选一，政治、地理、化学生物四选二，共有12种选课模式.今年高一的小明与小芳都准备选历史，假若他们都对后面四科没有偏好，则他们选课相同的概率（ ）A.136B.116C.18D.1610.高斯函数[]()f x x =（[]x 表示不超过实数x 的最大整数），若函数()2x xg x e e -=--的零点为0x ，则[]0()g f x =（ ）A.12e e --B.2-C. 12e e --D.2212e e-- 11.已知双曲线2222:1x y C a b -=（0,0a b >>）的焦距为4，其与抛物线2:3E y x =交于,A B 两点，O为坐标原点，若OAB ∆为正三角形，则C 的离心率为（ ）A. 2B. 2C.D. 12.已知函数31()21xx f x x x e e=-++-，其中e 是自然对数的底数．若()2(1)22f a f a -+≤，则实数a的取值范围是（ ）A. 11,2⎡⎤-⎢⎥⎣⎦B. 3,12⎡⎤-⎢⎥⎣⎦C. ⎥⎦⎤⎢⎣⎡-23,1D.1,12⎡⎤-⎢⎥⎣⎦二、填空题：本大题共4小题，每小题5分，共20分． 13.已知数列{}n a 满足11a =，11lg lg 2n n a a +=+，则5a =______． 14.现有5人要排成一排照相，其中甲与乙两人不相邻，且甲不站在两端，则不同的排法有______种．（用数字作答）15.已知球O 的内接圆锥体积为23π，其底面半径为1，则球O 的表面积为______．16.已知抛物线C ：20)2(y px p =＞的焦点为F ，且F 到准线l 的距离为2，直线1:0l x my -=与抛物线C 交于,P Q 两点（点P 在x 轴上方），与准线l 交于点R ，若3QF =，则QRF PRFS S ∆∆=______三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤． 17.（本小题满分12分）在ABC ∆中，D 是BC 上的点，AD 平分BAC ∠，sin 2sin C B =.（Ⅰ）求BDCD； （Ⅱ）若1AD AC ==，求BC 的长．18.（本小题满分12分）为建立健全国家学生体质健康监测评价机制，激励学生积极参加身体锻炼，教育部印发《国家学生体质健康标准（2014年修订）》，要求各学校每学年开展覆盖本校各年级学生的《标准》测试工作.为做好全省的迎检工作，某市在高三年级开展了一次体质健康模拟测试（健康指数满分100分），并从中随机抽取了200名学生的数据，根据他们的健康指数绘制了如图所示的频率分布直方图.（Ⅰ）估计这200名学生健康指数的平均数x 和样本方差2s （同一组数据用该组区间的中点值作代表）； （Ⅱ）由频率分布直方图知，该市学生的健康指数X 近似服从正态分布()2,N μσ，其中μ近似为样本平均数x ，2σ近似为样本方差2s . ①求(63.498.2)P X <<；②已知该市高三学生约有10000名，记体质健康指数在区间()63.4,98.2的人数为ξ，试求E ξ.1.16≈， 若随机变量X 服从正态分布()2,N μσ，则()0.683P X μσμσ-<<+≈，(22)0.955P X μσμσ-<<+≈，(33)0.997P X μσμσ-<<+≈.19.（本小题满分12分）在四棱锥P ABCD -中，//AD BC ，12AB BC CD AD ===，G 是PB 的中点，PAD ∆是等边三角形，平面PAD ⊥平面ABCD .（Ⅰ）求证：CD ⊥平面GAC ；（Ⅱ）求二面角P AG C --大小的正弦值.20.（本小题满分12分）已知椭圆()2222:10x y C a b a b +=>>过点()0,1A ，且椭圆的离心率为3．(Ⅰ)求椭圆C 的方程；(Ⅱ)斜率为1的直线l 交椭圆C 于()()1122,,,M x y N x y 两点，且12x x >．若直线3x =上存在点P ，使得PMN ∆是以M 为直角顶点的等腰直角三角形，求直线l 的方程．21.（本小题满分12分）已知函数2()12xx f x e =--．（Ⅰ）若直线y x a =+为()f x 的切线，求a 的值；（Ⅱ）若[)0,x ∀∈+∞，()f x bx ≥恒成立，求b 的取值范围22（本小题满分10分）在平面直角坐标系xOy 中,圆C ：()2244x y +-=.以原点O 为极点，x 轴的正半轴为极轴，建立极坐标系.（Ⅰ）求圆心C 的极坐标；（Ⅱ）从原点O 作圆C 的弦，求弦的中点轨迹的极坐标方程.成都石室中学2019~2020学年度上期高2020届10月月考 数学试卷（理科）答案一、选择题：B D B C A D C C D B C A 二、填空题：13. __100____．14. ___36___．15.____ 254π__．16. ___67___．三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤． 17.（本小题满分12分）解：（Ⅰ）由正弦定理可得在ABD ∆中，sin sin AD BDB BAD=∠， 在ACD ∆中，sin sin AD CDC CAD=∠，…………………………3分 又因为BAD CAD ∠=∠，sin 2sin BD CCD B==.…………………………6分 （Ⅱ）sin 2sin C B =，由正弦定理得22AB AC ==，设DC x =，则2BD x =，则222254cos cos 24AB AD BD x BAD CADAB AD +--∠==∠⋅，2222222AC AD CD x AC AD +--==⋅.…………………………9分 因为BAD CAD ∠=∠，所以2254242x x --=，解得x =32BC x ==.…………………………12分 18.（本小题满分12分）∴()14555515654075758545952075200x =⨯+⨯+⨯+⨯+⨯+⨯⨯=，…………………3分 ()()()()2222251540454575557565758575200200200200s =-⨯+-⨯+-⨯+-⨯()2209575135200+-⨯=.………………………6分（Ⅱ）①由（Ⅰ）知X 服从正态分布()75,135N ，且11.6σ≈，∴11(63.498.2)(-+2)=0.9550.6830.81922P X P X μσμσ<<=<<⨯+⨯=.………………9分②依题意，ξ服从二项分布，即()410,0.819B ξ，则8190E np ξ==.………………12分19.（本小题满分12分）解：（Ⅰ）取AD 的中点为O ，连结OP ，OC ，OB ，设OB 交AC 于H ，连结GH .//AD BC ，12AB BC CD AD ===四边形ABCO 与四边形OBCD 均为菱形 OB AC ∴⊥，//OB CD CD AC ⊥ PAD ∆为等边三角形，O 为AD 中点 PO AD ∴⊥…………………………2分平面PAD ⊥平面ABCD 且平面PAD 平面ABCD AD =. PO ⊂平面PAD 且PO AD ⊥ PO ∴⊥平面ABCD CD ⊂平面ABCD PO CD ∴⊥H ，G 分别为OB ， PB 的中点 //GH PO ∴ GH CD ∴⊥…………………………5分 又GH AC H ⋂= ,AC GH Ì平面GACCD \^平面GAC …………………………6分（Ⅱ）取BC 的中点为E ，以O 为空间坐标原点，分别以OE ，OD ，OP 的方向为x 轴、y 轴、z 轴的正方向，建立如图所示的空间直角坐标系O xyz -.…………………………7分 设4=AD，则(P ，()0,2,0A -，)C，()0,2,0D，31,2G ⎛- ⎝(0,2,AP =,3322AG ⎛= ⎝. 设平面PAG 的一法向量(),,n x y z →=.由00n AP nAG⎧⋅=⎨⋅=⎩203022y x y⎧+=⇒+=⎪⎩ y x z ⎧=⎪⇒⎨=⎪⎩. 令1z =，则()1,3,1n =-.…………………………10分.由（Ⅰ）可知，平面AGC的一个法向量()CD =.∴二面角P AG C --的平面角θ的余弦值2cos 2n CD n CDθ⋅=-=-=.二面角P AG C --…………………………12分 20.（本小题满分12分）解：（Ⅰ）由题意得2221,.b ca abc =⎧⎪⎪=⎨⎪=+⎪⎩…………………………………………3分解得23a =． 所以椭圆C 的方程为． …………………………………………4分（Ⅱ）设直线l 的方程为y x m =+，(3,)P P y ,由2213x y y x m ⎧+=⎪⎨⎪=+⎩，得2246330x mx m ++-=. …………………………6分 令223648480m m ∆=-+>，得22m -<<．1232x x m +=-，2123(1)4x x m =-． ……………………………………7分因为是以为顶角的等腰直角三角形，所以NP 平行于x 轴． ………………………………8分 过M 做NP 的垂线，则垂足Q 为线段NP 的中点．设点Q 的坐标为(),Q Q x y ，则2132Q M x x x x +===．由方程组1221221323(1)432x x m x x m x x ⎧+=-⎪⎪⎪=-⎨⎪+⎪=⎪⎩，，，解得2210m m ++=，即1m =-．而()122m =-∈-，， 所以直线的方程为． …………………………………………12分21.（本小题满分12分）解：（Ⅰ）设切点为()00,P x y ，()'xf x e x =-， ∴()000'1xf x e x =-=，……………………2分 令()xh x e x =-，则()'1xh x e =-，当0x >时，()'0h x >，()h x 在()0,∞+上为增函数； 当0x <时，()'0h x <，()h x 在(),0-∞上为减函数；2213x y +=PMN ∆PMN ∠l所以()()min 01h x h ==，所以00x =，又0200112xe x x a --=+，所以0a =．……………………4分 （Ⅱ）[)0,x ∀∈+∞，()f x bx ≥恒成立2102xx e bx ⇔---≥，[)0,x ∈+∞．令2()12xx g x e bx =---，[)0,x ∈+∞．()()'x g x e x b h x =--=，()'1x h x e =-,当0x >时，()'10xh x e =->，所以()h x 在[)0,+∞上为增函数，()min 1h x b =-，①若1b ≤，则当0x >时'()0g x >，故()g x 在[)0,+∞上为增函数，故[)0,x ∈+∞时，有()()00g x g ≥=即2102xx e bx ---≥恒成立，满足题意.…………8分②若1b >，因为()'g x 为()0,∞+上的增函数且()'010g b =-<，()()'ln 2ln ln 21ln 21ln 20g b b b b b =-->---=->⎡⎤⎣⎦，故存在()()00,ln 2x b ∈，使得()0'0g x =.当()00,x x ∈时，()'0g x <，()g x 在()00,x 为减函数，()()00g x g <=，矛盾，舍去. 综上1b ≤．………………………12分22. （本小题满分10分）解：（Ⅰ）4,2π⎛⎫⎪⎝⎭…………………………3分 （Ⅱ）4sin ρθ=………………………7分233ππθ⎛⎫<< ⎪⎝⎭……………………10分。

四川省成都市石室中学2024-2025学年高三上学期10月月考数学试卷一、单选题1．已知集合{}1,2,4A =，2{N |20}B x x x =∈+-≤，则A B =U （ ） A ．{}2,1,0,1,2,4-- B ．{}0,1,2,4 C ．{}1,2,4D ．{}12．2024年巴黎奥运会中国代表队获得金牌榜第一，奖牌榜第二的优异成绩.首金是中国组合黄雨婷和盛李豪在10米气步枪混合团体赛中获得，两人在决赛中14次射击环数如图，则（ ）A ．盛李豪的平均射击环数超过10.6B ．黄雨婷射击环数的第80百分位数为10.65C ．盛李豪射击环数的标准差小于黄雨婷射击环数的标准差D ．黄雨婷射击环数的极差小于盛李豪射击环数的极差3．已知0.10.6a =，0.6log 0.3b =，0.6log 0.4c =，则a ，b ，c 的大小关系为（ ） A ．b c a >> B ．a b c >> C ．c b a >>D ．a c b >>4．已知实数a ，b ，c 满足a b c >>，且0a b c ++=，则下列说法正确的是（ ） A ．22ab cb > B ．222a c c a+≥ C ．||||a b >D ．0ab bc +>5．“函数2()ln(22)f x x ax =-+的值域为R ”的一个充分不必要条件是（ ） A．[B．(C．()-∞+∞UD．)+∞6．核燃料是重要的能量来源之一，在使用核燃料时，为了冷却熔化的核燃料，可以不断向反应堆注入水，但会产生大量放射性核元素污染的冷却水，称为核废水.核废水中含有一种放射性同位素氚，它有可能用辐射损伤细胞和组织，影响生物的繁殖和生态平衡.已知氚的半衰期约为12年，则氚含量变成初始量的110000大约需要经过（ ）年.（lg 20.3010≈） A ．155B ．159C ．162D ．1667．若函数()y f x =的图象如图1所示，则如图2对应的函数可能是（ ）A ．(12)y f x =-B ．1(1)2y f x =-C ．(12)y f x =--D ．1(1)2y f x =--8．已知函数()11,0,2221,0.x x x f x x ⎧+>⎪=⎨⎪-≤⎩，则方程()(3)2f x f x +-=的所有根之和为（ ）A ．0B ．3C ．6D ．9二、多选题9．已知函数()f x 的定义域为R ，()()()22f x y f x f y +=+，则（ ） A ．()00f = B ．()11f =C ．()f x 是奇函数D ．()f x 在R 上单调递增10．已知复数12,z z 的共轭复数分别为21,z z ，则下列命题为真命题的是（ ）A ．1212z z z z +=+B ．1212z z z z ⋅=⋅C ．若120z z ->，则12z z >D ．若2221212z z z z +=+，则21210z z z z +⋅⋅=11．设函数()()()ln f x x a x b =++，则下面说法正确的是（ ）A ．当0,1a b ==时，函数()f x 在定义域上仅有一个零点B ．当0,0a b ==时，函数()f x 在(1,)+∞上单调递增C ．若函数()f x 存在极值点，则a b ≤D ．若()0f x ≥，则22a b +的最小值为12三、填空题12．若函数2()23f x x kx =++在[1,2]上单调，则实数k 的取值范围为． 13．若()y f x =是定义在R 上的奇函数，()(2)f x f x =-，(1)2f =，则(1)(2)(3)(2025)f f f f +++=L ．14．若过点()1,b 作曲线e x y x =的切线有且仅有两条，则b 的取值范围是．四、解答题15．已知函数()1ln 1kxf x x -=-为奇函数． (1)求实数k 的值；(2)若函数()()2xg x f x m =-+，且()g x 在区间[]2,3上没有零点，求实数m 的取值范围．16．已知三棱锥D ABC -，D 在平面ABC 上的射影为ABC V 的重心O ，15AC AB ==，24BC =.(1)证明：BC AD ⊥；(2)E 为AD 上靠近A 的三等分点，若三棱锥D ABC -的体积为432，求二面角E CO B --的余弦值．17．某小区有3000名居民，想通过验血的方法筛选乙肝病毒携带者，假设携带病毒的人占%a .为减轻工作量，随机地按n 人一组分组，然后将各组n 个人的血样混合在一起化验.若混合血样呈阴性，说明这n 个人全部阴性；若混合血样呈阳性，说明其中至少有一人的血样呈阳性，就需要对每个人再分别化验一次.(1)若0.2,20,a n ==试估算该小区化验的总次数；(2)若0.9a =，且每人单独化验一次花费10元，n 人混合化验一次花费9n +元，求当n 为何值时，每个居民化验的平均费用最少.注：假设每位居民的化验结果呈阴性还是阳性相互独立.当00.01p <<时，(1)1n p np -≈-.18．在平面直角坐标系xOy 中，已知()1,1A ，()1,1B -，动点P 满足OP mOA nOB =+u u u r u u u r u u u r，且1mn =.设动点P 形成的轨迹为曲线C . (1)求曲线C 的标准方程；(2)过点()2,2T 的直线l 与曲线C 交于M ，N 两点，试判断是否存在直线l ，使得A ，B ，M ，N 四点共圆.若存在，求出直线l 的方程；若不存在，说明理由.19．在高等数学中，我们将()y f x =在0x x =处可以用一个多项式函数近似表示，具体形式为：()()()()()()()()()200000002!!n nf x f x f x f x f x x x x x x x n ''=+'-+-+⋅⋅⋅+-+⋅⋅⋅（其中()()n fx 表示()f x 的n 次导数*3,N n n ≥∈），以上公式我们称为函数()f x 在0x x =处的泰勒展开式.当00x =时泰勒展开式也称为麦克劳林公式.比如e x 在0x =处的麦克劳林公式为：22111e 12!3!x n x x x x n =++++++L L ！，由此当0x ≥时，可以非常容易得到不等式223111e 1,e 1,e 1,226x x x x x x x x x ≥+≥++≥+++L 请利用上述公式和所学知识完成下列问题： (1)写出sin x 在0x =处的泰勒展开式.(2)若30,2x ⎛⎫∀∈ ⎪⎝⎭，sin e 1a x x >+恒成立，求a 的范围;（参考数据5ln 0.92≈）(3)估计5ln 3的近似值（精确到0.001）。

成都石室中学 2019~2020 学年度上期高 2020 届 10 月月考数学试卷（理科）一、选择题：本大题共 12 小题，每小题 5 分，在每小题给出的四个选项中，只有一项是符合题目要求的 .1. 已知集合 M{ x | (x 1)( x 2)0}, N{ x | x 0} ，则（）A. N MB. M NC. M ND. M N R2. 已知 i 为虚数单位，则 i i 2i 3 i 2019 等于（ ）iA. iB.1C.D.13. 已知命题 p ： x (,0), 2x 23x 1 0 ，命题 q ：若 x0 ，则 2x 2 3x1 0 ，则以下命题正确的为（ ）A. p 的否定为“ x [0, ), 2x 2 3x 1 0 ”， q 的否命题为“若 x 0 ，则 2x 2 3x 1 0 ”B. p 的否定为“ x ( ,0), 2x 2 3x 1 0 ”， q 的否命题为“若 x 0 ，则 2x 2 3x 1 0 ”C. p 的否定为“ x [0, ), 2x 2 3x 10 ”， q 的否命题为“若 x0 ，则 2x 2 3x 1 0 ”D. p 的否定为“x ( ,0), 2x 23x 1 0 ”， q 的否命题为“若 x 0 ，则 2x 2 3x 10 ”4. 已知a n 是公差为 1 的等差数列， S n 为 a n 的前 n 项和 . 若 a 2 , a 6 , a 14 成等比数列，则 S 5 （）35225B. 35C.D.25A.225. 中国古代数学著作《算学启蒙》中有关于“松竹并生”的问题：松长五尺，竹 长两尺，松日自半，竹日自倍，松竹何日而长等．意思是现有松树高 5 尺，竹子高 2 尺，松树每天长自己高度的一半，竹子每天长自己高度的一倍，问在第几天会出现松树和竹子一般高？如图所示是源于其思想的一个程序框图，若输入的x5， y 2 ，输出的 n 4 ，则程序框图中的中应填（ ）A. x yB. y xC.y xD. xy2 x , x116. 设函数 f ( x)x，则满足 f f axf a 的,12a 的取值范围是（2）A. ,0B. 0,2C.2,D.,0 2,7. 若直线 y 4 k x 2 与曲线 y4 x 2 有两个交点，则 k 的取值范围是（ ）A. 1,B. 1,34C.3,1 D., 148. 已知 a2ln3 ， b 3ln 2 6 ，其中 e 是自然对数的底数．则a,b, c 的大小关系为（）， ceA. a c bB. b c aC. c a bD. c b a9.2021 年广东新高考将实行 3 1 2 模式，即语文、数学、英语必选，物理、历史二选一，政治、地理、 化学生物四选二，共有 12 种选课模式 . 今年高一的小明与小芳都准备选历史，假若他们都对后面四科没有偏好，则他们选课相同的概率（）A.1B.1C.1D.13616 8 610. 高斯函数f (x)x （ x 表示不超过实数x 的最大整数），若函数 g (x)e x e x2 的零点为 x 0 ，则g f (x 0 ) =（）1 e 2B. 2C.1 21 A.e2 D. e2 ee e11. 已知双曲线 x 2 y 22 C : 2（ a 0,b0 ）的焦距为4 ，其与抛物线E : yb 21a为坐标原点，若OAB 为正三角形，则 C 的离心率为（）A.2 B.3 C. 22223x 交于 A, B 两点， O3D. 312. 已知函数 f (x)x 3 2x 1 e x1 ，其中 e 是自然对数的底数． 若 f (a 1) f 2a2 2，则实数 ae x的取值范围是（）A.1,1 B.3 ,1 C.1, 3 D.1 ,12222二、填空题：本大题共4 小题，每小题5 分，共 20 分．13. 已知数列 { a }a 11a满足 ， lg a n 1 lg a nn1，则 5______ ．214. 现有 5人要排成一排照相，其中甲与乙两人不相邻，且甲不站在两端， 则不同的排法有 ______ 种．（用数字作答）15. 已知球 O 的内接圆锥体积为2，其底面半径为1，则球 O 的表面积为 ______．316. 已知抛物线 C ： y22 px( p ＞0) 的焦点为 F ，且 F 到准线 l 的距离为 2 ，直线 l 1 : x my 5 0 与抛物线 C 交于 P, Q 两点（点 P 在 x 轴上方），与准线l 交于点 R ，若 QFSQRF______．3 ，则SPRF三、解答题：共 70 分．解答应写出文字说明、证明过程或演算步骤． 17. （本小题满分 12 分）在 ABC 中， D 是 BC 上的点， AD 平分BAC ， sin C 2sin B .（Ⅰ）求BD；CD1 ，求 BC 的长．（Ⅱ）若 AD AC成都石室中学 2019~2020 学年度上期高 2020 届 10 月月考数学试卷（理科）答案一、选择题： BDBCAD CCDBCA 二、填空题：2513.__ 100 ____． 14.___ 36___．15.____46__．16.___ 7 ___．三、解答题： 共 70 分．解答应写出文字说明、证明过程或演算步骤．17. （本小题满分 12 分） 解：（Ⅰ）由正弦定理可得在 ABD 中，ADsin BD， 在 ACD 中，ADCDsin BBAD，⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3 分sin Csin CAD又因BAD CAD ，BDsin C2 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 6 分CD sin B（Ⅱ） sin C 2sin B ，由正弦定理得 AB 2AC2 ，DCx ， BD 2x，cos BADAB 2 AD 2 BD 25 4x 2 ，2AB AD4cos CADAC 2 AD 2 CD 2 2 x 2 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 9 分2AC AD 2因 BAD CAD ，所以54 x 22 x 2，解得 x2 .422BC 3x32. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 12 分218. （本小题满分 12 分）解：（Ⅰ）由 率分布直方 可知，各区 的 数分布表如下：分 区 40,5050,6060,70 70,80 80,90 90,100数5 15 40754520∴ x45 5 55 15 6540 75 7585 45 95 20175，⋯⋯⋯⋯⋯⋯⋯ 3 分s 245 755 55 751565 7540200 452 857522220020020020095 75220. ⋯⋯⋯⋯⋯⋯⋯⋯⋯ 6 分135200（Ⅱ）①由（Ⅰ）知 X 服从正 分布 N 75,135，且11.6 ，∴ P(63.4X 98.2) P( -X+21 0.95510.819 . ⋯⋯⋯⋯⋯⋯ 9 分)=0.68322②依 意， 服从二 分布，即B 104 ,0.819 ， Enp 8190 . ⋯⋯⋯⋯⋯⋯ 12 分19. （本小题满分 12 分）解：（Ⅰ）取 AD 的中点 O ， OP ， OC ， OB ， OB 交 AC 于 H ， GH .AD / / BC ， ABBCCD1AD2四 形 ABCO 与四 形 OBCD 均 菱形 OB AC ， OB / /CD CD AC PAD 等 三角形， O AD 中点 PO AD ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 2 分平面 PAD 平面 ABCD 且平面 PAD 平面 ABCD AD . PO 平面 PAD 且 PO AD PO 平面 ABCD CD 平面 ABCD PO CD H ， G 分 OB ， PB 的中点 GH / / PO GH CD ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 5 分 又 GH AC HAC, GH ì平面 GACCD ^ 平面 GAC ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 6 分（Ⅱ）取 BC 的中点 E ，以 O 空 坐 原点， 分 以 OE ， OD ，OP 的方向 x 、 y、z的正方向，建立如 所示的空 直角坐 系O xyz . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 7 分AD4 ， P 0,0,2 3 ， A0,2,0 ， C3,1,0 ， D 0,2,0 3 1， G , , 32 2 AP0,2, 2 3 , AG3 , 3 , 3 .2 2平面 PAG 的一法向量 nx, y, z.n AP 02 y 2 3z 0 y3z由3 x 3y 3z 0.n AG 0x z2 2令 z 1， n 1,3,1 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 10 分由（Ⅰ）可知，平面AGC 的一个法向量CD3,1,0 .理科数学第 4 页共 4 页命题 / 审题：石室文庙高2020 届数学组二面角 P AG C 的平面角n CD 2 3 15 的余弦 cos2 55.n CD二面角 P AGC 大小的正弦10. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯12 分520. （本小 分 12 分）b 1,解：（Ⅰ）由 意得c6 , ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3 分a 3a 2b 2c 2 .解得 a 23．所以 C 的方程x 2y 2 1．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4 分3（Ⅱ） 直 l 的方程 yx m ， P(3, y P ) ,x 2y 2，316mx 3m 2 3 0 .6分由得 4x 2⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯y xm令36m 2 48m 2 48 0 ，得2 m 2 ．x 1 x 23m ， x x 2 (m 1) ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7 分13224因PMN 是以 PMN 角的等腰直角三角形，所以 NP 平行于 x ． ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 8分M 做 NP 的垂 ， 垂足 Q 段 NP 的中点．点 Q 的坐 x , y， x Qx Mx 1x 2 3．Q Q23m ，x 1 x 23 2由方程21)，22m 1 0 ，即 m1．x 1 x 2(m解得 m4x 1x 2 2 3 ，而 m 1 2，2 ，所以直 l 的方程．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯12 分21. （本小 分 12 分）解：（Ⅰ） 切点 P x 0 , y 0 ， f ' xe x x ，∴ f ' x 0 e x 0 x 0 1，⋯⋯⋯⋯⋯⋯⋯⋯ 2 分令 h xe x x ， h ' xe x1 ，当 x 0 ， h' x 0 ， h x 在 0,上 增函数； 当 x 0 ， h' x0 ， h x 在 ,0 上 减函数； 所以 hxminh 01 ，所以 x 0 0，又e x01x021x0 a ，所以a0 ．⋯⋯⋯⋯⋯⋯⋯⋯ 4 分2（Ⅱ）x0,， f x bx 恒成立e x x21bx0 ，x0,．22x x．令 g (x) e 1 bx ，x 0,2g ' x e x x b h x ， h ' x e x1,当 x0 ， h'x e x10，所以 h x在 0,上增函数，h xmin1 b ，①若 b1，当 x0 g '( x)0 ，故g x在 0,上增函数，故 x0,，有 g x g 00 即e x x21bx0 恒成立，足意.⋯⋯⋯⋯8分2②若 b1，因 g 'x0,上的增函数且 g ' 01b0 ，g ' ln 2b b ln b ln 2 b b 1 ln 2 1 ln 2 0 ，故存在x00,ln2b，使得 g '(x0)= 0.当 x0, x0， g 'x0 ， g x 在 0,x0减函数， g x g00 ，矛盾，舍去 .上 b 1 ．⋯⋯⋯⋯⋯⋯⋯⋯⋯12 分22.（本小分 10 分）解：（Ⅰ）4,2⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分（Ⅱ）4sin⋯⋯⋯⋯⋯⋯⋯⋯⋯ 7 分2⋯⋯⋯⋯⋯⋯⋯⋯ 10 分3318.（本小题满分 12 分）为建立健全国家学生体质健康监测评价机制，激励学生积极参加身体锻炼，教育部印发《国家学生体质健康标准（ 2014 年修订）》，要求各学校每学年开展覆盖本校各年级学生的《标准》测试工作. 为做好全省的迎检工作，某市在高三年级开展了一次体质健康模拟测试（健康指数满分100 分），并从中随机抽取了200名学生的数据，根据他们的健康指数绘制了如图所示的频率分布直方图.（Ⅰ）估计这200 名学生健康指数的平均数x 和样本方差 s2（同一组数据用该组区间的中点值作代表）；（Ⅱ）由频率分布直方图知，该市学生的健康指数X 近似服从正态分布N ,2，其中近似为样本平均数 x ，2近似为样本方差s2.①求 P(63.4X 98.2)；②已知该市高三学生约有10000 名，记体质健康指数在区间63.4,98.2的人数为，试求 E .附：参考数据 1.35 1.16 ，若随机变量 X 服从正态分布 N ,2，则P(X) 0.683 ，P(2X2) 0.955，P(3X 3 ) 0.997.19.（本小题满分 12 分）P ABCD AD / /BC AB1是在四棱锥中，，BC CDAD ，G PB2的中点，PAD 是等边三角形，平面PAD平面 ABCD .（Ⅰ）求证： CD平面 GAC ；（Ⅱ）求二面角 P AG C 大小的正弦值.20.（本小题满分 12 分）已知椭圆 C :x2y26 ．a2b2 1 a b 0 过点A 0,1，且椭圆的离心率为3( Ⅰ ) 求椭圆C的方程；( Ⅱ ) 斜率为的直线l交椭圆C于M x1, y1, N x2, y2x x x 3P两点，且．若直线上存在点，使得12PMN 是以M为直角顶点的等腰直角三角形，求直线l 的方程．21.（本小题满分 12 分）已知函数 f (x)e x x21．2（Ⅰ）若直线 y x a 为f x的切线，求 a 的值；（Ⅱ）若x0,， f x bx 恒成立，求 b 的取值范围．22.（本小题满分 10 分）xOy 中,圆C： x2y 42在平面直角坐标系 4 .以原点O为极点， x 轴的正半轴为极轴，建立极坐标系.（Ⅰ）求圆心 C 的极坐标；（Ⅱ）从原点 O 作圆 C 的弦，求弦的中点轨迹的极坐标方程.。

成都石室中学2024～2025学年度上期高2025届十月考试数学试卷一、选择题:本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确的选项填涂在答题卡相应位置.1. 已知集合{}1,2,4A =，2{N |20}B x x x =Î+-£，则A B =U （ ）A. {}2,1,0,1,2,4-- B. {}0,1,2,4C. {}1,2,4 D. {}1【答案】B 【解析】【分析】根据一元二次不等式的解法，求得{}0,1B =，结合集合并集的概念与运算，即可求解.【详解】由不等式220x x +-£，可得(2)(1)0≤x x +-，解得21x -££，所以集合{}{N |21}0,1B x x =Î-££=，又因为{}1,2,4A =，可得{}0,1,2,4A B È=.故选：B.2. 2024年巴黎奥运会中国代表队获得金牌榜第一，奖牌榜第二的优异成绩.首金是中国组合黄雨婷和盛李豪在10米气步枪混合团体赛中获得，两人在决赛中14次射击环数如图，则（ ）A. 盛李豪的平均射击环数超过10.6B. 黄雨婷射击环数的第80百分位数为10.65C. 盛李豪射击环数的标准差小于黄雨婷射击环数的标准差D. 黄雨婷射击环数的极差小于盛李豪射击环数的极差【答案】C 【解析】【分析】根据图表数据可直接判断选项A ，利用第80百分位数的解法直接判断选项B ，根据图表的分散程度即可判断选项C ，根据极差的求法直接判断选项D.【详解】由题知，盛李豪的射击环数只有两次是10.8环，5次10.6环，其余都是10.6环以下，所以盛李豪平均射击环数低于10.6，故A 错误；由于140.811.2´=，故第80百分位数是从小到大排列的第12个数10.7，故B 错误；由于黄雨婷的射击环数更分散，故标准差更大，故C 正确；黄雨婷射击环数的极差为10.89.7 1.1-=，盛李豪的射击环数极差为10.810.30.5-=，故D 错误.故选：C3. 已知0.10.6a =，0.6log 0.3b =，0.6log 0.4c =，则a ，b ，c 的大小关系为（ ）A. b c a >> B. a b c >>C. c b a >> D. a c b>>【答案】A 【解析】【分析】由对数函数的底数小于1得到函数单调递减，判断出b ，c 的大小关系，又判断出b ，c 大于1，a 小于1，从而得出结论.【详解】由于0.6log y x =(0,)+¥单调递减，故0.60.60.6log 0.3log 0.4log 0.61b c =>=>=，又∵0.100.60.61a =<=，∴b c a >>.故选：A.4. 已知实数a ，b ，c 满足a b c >>，且0a b c ++=，则下列说法正确的是（ ）A. 22ab cb > B.222a cc a+³C. ||||a b > D. 0ab bc +>【答案】C 【解析】【分析】根据已知等式可确定0,0a c ><，结合不等式性质和作差法依次判断各个选项即可.【详解】由题，0,0a c ><，取1,0,1a b c ===-，则22ab cb =，故A 错误；在2522a c c a +=-，故B 错误；0ab bc +=，故D 错误；因为22()()()0a b a b a b c a b -=+-=-->，所以22a b >，即||||a b >，故C 正确.故选：C.5. “函数2()ln(22)f x x ax =-+的值域为R ”的一个充分不必要条件是（ ）A. [B. (C. ()-¥+¥U D. )+¥【答案】D 【解析】【分析】根据对数函数的性质，先分析出对数的真数部分能取得所有的正数，然后根据二次函数与其对应二次方程的关系，求出a 的范围即可求解.【详解】因为函数2()ln(22)f x x ax =-+的值域为R ，设222y x ax =-+，则二次函数y 需要取到一切正数，对应于方程2220x ax -+=中，0D ³，即2480a -³，解得a ³或a £，从而)+¥是“函数2()ln(22)f x x ax =-+的值域为R ”的充分不必要条件.故选：D6. 核燃料是重要的能量来源之一，在使用核燃料时，为了冷却熔化的核燃料，可以不断向反应堆注入水，但会产生大量放射性核元素污染的冷却水，称为核废水.核废水中含有一种放射性同位素氚，它有可能用辐射损伤细胞和组织，影响生物的繁殖和生态平衡.已知氚的半衰期约为12年，则氚含量变成初始量的110000大约需要经过（ ）年.（lg 20.3010»）A. 155 B. 159C. 162D. 166【答案】B 【解析】【分析】根据题意列出等量关系，借助换底公式和题目给出的参考量得出结果.【详解】设氚含量变成初始量的110000大约需要经过t 年，则1211()210000t =，121log 1210000t =，即48159lg 2t =»年，故选：B.7. 若函数()y f x =的图象如图1所示，则如图2对应的函数可能是（ ）A. (12)y f x =-B. 1(1)2y f x =-C. (12)y f x =--D. 1(1)2y f x =--【答案】A 【解析】【分析】根据函数定义域求出新函数定义域判断B,D;取特殊值判断C,根据函数平移伸缩变换判断A.【详解】由()y f x =的定义域为(1,)-+¥知，1(1)2y f x =-中111,42x x ->-<，不符合图2，故排除B ，D ；对于C ，当12x =时，(0)0y f =->，不满足图2，故C 错误；将函数()y f x =图关于y 轴对称，得到()y f x =-的图，向右平移1个单位得到(1)y f x =-的图，最后纵坐标不变，横坐标变为原来的一半，得到函数(12)y f x =-的图可能为图2.故选:A.8. 已知函数()11,0,2221,0.x x x f x x ì+>ï=íï-£î，则方程()(3)2f x f x +-=的所有根之和为（ ）A. 0 B. 3C. 6D. 9【答案】C【解析】的【分析】将方程根的问题转化为函数()y f x =和2(3)y f x =--的图象交点横坐标问题，数形结合即可判断交点个数，再根据对称性求解和即可解答.【详解】方程()(3)2f x f x +-=的根为函数()y f x =和2(3)y f x =--的图象交点横坐标，由函数()11,0,2221,0.x x x f x x ì+>ï=íï-£î得，()31,3,23232,3,x x x y f x x -ì<ï=--=íï-³î如下图所示，两函数图象共有4个交点，且因为()(3)2f x f x +-=，所以函数()y f x =与函数2(3)y f x =--的图象关于点3(,1)2中心对称，故方程()(3)2f x f x +-=的所有根之和为6.故选：C.二、选择题:本大题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分， 部分选对的得部分分，有选错的得0分，.9. 已知函数()f x 的定义域为R ，()()()22f x y f x f y +=+，则（ ）A. ()00f = B. ()11f =C. ()f x 是奇函数 D. ()f x 在R 上单调递增【答案】AC 【解析】【分析】通过赋值法及特例逐项判断即可.【详解】由()()()22f x y f x f y +=+知，当0x y ==时， ()()030f f =，即()00f =，故A 正确；取()f x x =-，则()f x 满足条件()()()22f x y f x f y +=+，但()11f =-，且()f x 是在R 上单调递减，故B ，D错误；当,x t y t =-=时，()()()2f t f t f t =-+，即()()f t f t -=-，故C 正确.故选：AC.10. 已知复数12,z z 的共轭复数分别为21,z z ，则下列命题为真命题的是（ ）A. 1212z z z z +=+B. 1212z z z z ×=×C. 若120z z ->，则12z z >D. 若2221212z z z z +=+，则21210z z z z +××=【答案】ABD 【解析】分析】设出1i z a b =+，2i z c d =+，,,,R a b c d Î，结合共轭复数及模长定义与复数运算法则逐项计算可判断A 、B 、D ；举出反例可判断C.【详解】设1i z a b =+，2i z c d =+，且,,,R a b c d Î，则1i z a b =-，2i z c d =-；对A ：12i i ()i z z a b c d a c b d +=+++=+++，12()i a c z b d z +=+-+所以12()i a c z b d z -=+++，所以1212z z z z +=+，故A 正确；对B ：12i)(i)()i (()z z a b c d ac bd bc ad ++=--+=，12i)(i)()i (()z z a b c d ac bd bc ad --=--+=，故B 正确；对C ：当1212i,2i z z =+=时，满足1210z z -=>，但不能得出12z z >，故C 错误；对D ：2121212121211221212()()()()z z z z z z z z z z z z z z z z z z +=++=++=+++22121212z z z z z z =+++，故11220z z z z +=，故D 正确.故选：ABD.11. 设函数()()()ln f x x a x b =++，则下面说法正确的是（ ）A. 当0,1a b ==时，函数()f x 在定义域上仅有一个零点B. 当0,0a b ==时，函数()f x 在(1,)+¥上单调递增C. 若函数()f x 存在极值点，则a b£【D. 若()0f x ³，则22a b +的最小值为12【答案】ABD 【解析】【分析】代入0,1a b ==得到()f x 解析式，结合对数运算可得A 正确；求导分析单调性可得B 正确；当a b £时求导分析，当a b >利用换元法二次求导数分析可得C 错误；由复合函数同增异减得到()f x 的单调性，再结合二次函数取值可得D 正确；【详解】对于A ，当0,1a b ==时，()ln(1)f x x x =+，由()0f x =得，0x =，函数()f x 在定义域上仅有一个零点，故A 正确；对于B ，当0a b ==时，函数()ln f x x x =，当1x >时，()ln 10f x x ¢=+>，故函数()f x 在(1,)+¥上单调递增，故B 正确；对于C ，()ln()ln()1x a a bf x x b x b x b x b+-¢=++=+++++，当a b £时，函数()f x ¢在定义域上单调递增，且当x b ®-时，()f x ¥¢®-，当x ®+¥时，()f x ¥¢®+，此时函数()f x ¢存在零点0x ，即函数()f x 在0(,)b x -上单调递减，在0(,)x +¥上单调递增，故此时函数()f x 存在极值点，当a b >时，设()ln()1a b g x x b x b-=++++，则()2212()()a b x b a g x x b x b x b -+-=-=+++¢，令()0g x ¢=，则2x a b =-，故函数()f x ¢在(,2)b a b --上单调递减，在(2,)a b -+¥上单调递增，故()()2ln()2f x f a b a b ¢³¢-=-+，故当21e b a b <<+时，函数()f x ¢存在零点，函数()f x 存在极值点，综上，当函数()f x 存在极值点时，21eb a b <<+或a b £，故C 错误；对于D ，()()ln 0x a x b ++³恒成立，当()0f x =时，x a =-或1x b =-，当且仅当两个零点重合时， 即1a b -=-，因为y x a =+为增函数，设()()1ln ln 1y x b x a =+=++，则1y 在(1,)a a ---上单调递减，在(,)a -+¥上单调递增，所以函数()f x 在(1,)a a ---上单调递减，在(,)a -+¥上单调递增，满足()()ln 0x a x b ++³， 则22212212a b b b +=-+³，当12b =时取“=”，故D 正确，故选：ABD.三、填空题:本题共3小题，每小题5分，共15分.12. 若函数2()23f x x kx =++在[1,2]上单调，则实数k 的取值范围为_____．【答案】8k £-或4k ³-【解析】【分析】运用二次函数的单调性知识，结合对称轴可解.【详解】函数2()23f x x kx =++的对称轴为04k x =-，故当24k -³或14k-£时，函数()f x 在[1,2]上单调，即8k £-或4k ³-，故答案为:8k £-或4k ³-.13.若()y f x =是定义在R 上的奇函数，()(2)f x f x =-，(1)2f =，则(1)(2)(3)(2025)f f f f +++=L ________．【答案】2【解析】【分析】根据题意，推得(4)()f x f x +=，得到()y f x =的周期为4，再求得(1),(2),(3),(4)f f f f 的值，结合周期性，即可求解.【详解】因为函数()y f x =是定义在R 上的奇函数，故()()f x f x -=-，又因为()(2)f x f x =-，所以(2)()f x f x -=--，故(2)()f x f x +=-，所以(4)(2)()f x f x f x +=-+=，即()y f x =的周期为4，由于()y f x =为定义在R 上的奇函数，且(1)2f =，可得(0)0f =，(2)(0)0f f ==，(3)(1)(1)2f f f =-=-=-，所以(1)(2)(3)(4)0f f f f +++=，则(1)(2)(3)(2025)f f f f +++=L 506[(1)(2)(3)(4)](1)2f f f f f ´++++=.故答案为：2.14. 若过点()1,b 作曲线e x y x =的切线有且仅有两条，则b 的取值范围是______．【答案】25[0,e)e ìü-íýîþU 【解析】【分析】由题意，设切点000(,e )xx x ，利用相切性质得到关于0,b x 的关系式0200(1)e xb x x =-+，将切线条数问题转化为关于0x 的方程解的个数问题求解，再分离参数转化为函数2()(1)e x g x x x =-+的图象与直线y b =的交点个数问题，构造函数研究函数的单调性与最值，数形结合求b 的范围即可.【详解】设切点为000(,e )xx x ，()(1)e x f x x ¢=+，故切线方程为00000e (1)e ()x x y x x x x -=+-，将()1,b 代入切线方程得00000e(1)e (1)x x b x x x -=+-，0200(1)e x b x x \=-+，过点()1,b 作曲线e x y x =的切线有且仅有两条,则关于0x 的方程0200(1)e xb x x =-+有两解，可转化为直线y b =与函数2(1)e x y x x =-+的图象有两个交点.令2()(1)e x g x x x =-+，则2()(2)e (1)(2)e x x g x x x x x ¢=--=--+，当2x <-时，()0f x ¢<，()f x 在(),2¥--单调递减；当2<<1x -时，()0f x ¢>，()f x 在()2,1-单调递增；当1x >时，()0f x ¢<，()f x 在(1,+∞)单调递减；故()g x 的单调减区间(,2),(1,)-¥-+¥，增区间是(2,1)-.当x ®-¥时，()0g x ®，当x ®+¥时，()g x ®-¥，且25(1)e,(2)e g g =-=-，当y b =与()y g x =有且仅有两个交点时，25[0,e)e b ìüÎÈ-íýîþ，故答案为：25[0,e)e ìüÈ-íýîþ.四、解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.15. 已知函数()1ln 1kxf x x -=-为奇函数．（1）求实数k 值；（2）若函数()()2xg x f x m =-+，且()g x 在区间[]2,3上没有零点，求实数m 的取值范围．【答案】（1）1-（2）(,4ln 3)(8ln 2,)m Î-¥--+¥U 【解析】【分析】（1）根据奇函数定义建立方程，解得1k =±，检验即可求解；（2）利用导数研究函数的单调性可知()g x 在[2,3]上单调递减，根据零点的概念建立不等式，解之即可求解.【小问1详解】因为()1ln1kxf x x -=-是奇函数，所以()()f x f x -=-， 即11ln ln ln 1111kx kx x x kx x --+=-=----， 所以1111kx x kxx +=----，故22211k x x -=-，则1k =±，当1k =时，111xx -=--显然不成立；经验证：1k =-符合题意；所以1k =-；【小问2详解】由1()ln21x x g x m x +=-+-，22()2ln 21x g x x ¢=---， 当[2,3]x Î时，()0g x ¢<，故()g x 在[2,3]上单调递减.的的故()[ln 28,ln 34]g x m m Î-+-+.因为()g x 在区间[]2,3上没有零点，所以ln 280m -+>或ln 340m -+<，解得4ln 3m <-或8ln 2m >-，即(,4ln 3)(8ln 2,)m Î-¥--+¥U .16. 已知三棱锥D ABC -，D 在平面ABC 上的射影为ABC V 的重心O ，15AC AB ==，24BC =.（1）证明：BC AD ^；（2）E 为AD 上靠近A 的三等分点，若三棱锥D ABC -的体积为432，求二面角E CO B --的余弦值．【答案】（1）证明见解析（2）【解析】【分析】（1）由题意可得AM BC ^、OD ^平面ABC ，根据线面垂直的性质可得OD BC ^，结合线面垂直的判定定理和性质即可证明；（2）建立如图空间直角坐标系，利用三棱锥的体积公式求得12OD =，由空间向量的线性运算求得()4,0,4OE =uuu r，结合空间向量法求解面面角即可.【小问1详解】如图所示，连结AO 并延长交BC 于M ，因为O 为△ABC 的重心，所以M 是BC 的中点，又因为AC AB =，所以由等腰三角形三线合一可得AM BC ^， 因为D 在平面ABC 上的射影为O ，所以OD ^平面ABC ， 又ÌBC 平面ABC ，所以OD BC ^，又,,AM OD O AM OD =ÌI 平面AMD ，所以^BC 平面AMD ， 又AD Ì平面AMD ，所以BC AD ^，【小问2详解】由（1）知AM BC ^，OD ^面ABC ，过M 作z 轴平行于OD ，则z 轴垂直于面ABC ，如图，以,MA MB 为x 轴，y 轴，建立空间直角坐标系，在ABC V 中，15AC AB ==，24BC =由（1）知，AM BC ^，故9AM ==，得11082ABC S AM BC =×=V ， 所以三棱锥A-BCD 的体积为 1110843233ABC S OD OD ×=´´=V ，则12OD =因为O 为△ABC 的重心，故133OM AM ==，则()()()()()0,12,0,0,12,0,3,0,0,9,0,0,3,0,12C B O A D -，()()()6,0,0,6,0,12,3,12,0OA AD OC ==-=--uuu r uuu r uuu r因为E 为AD 上靠近A 的三等分点，所以()12,0,43AE AD ==-uuu r uuu r，故()14,0,43OE OA AD =+=uuu r uuu r uuu r设(),,n x y z =r 为平面ECO 的一个法向量，则4403120n OE x z n OC x y ì×=+=ïí×=--=ïîuuu r r uuu rr ，取4x =，则1,4y z =-=-，故()4,1,4n =--r，易得()0,0,1m =r是平面COB 的一个法向量， 设二面角E CO B --的平面角为q ，则q 为钝角，所以cos cos ,m n m n m n q ×=-=-==r r r rr r 所以二面角E CO B --的余弦值为 【点睛】17. 某小区有3000名居民，想通过验血的方法筛选乙肝病毒携带者，假设携带病毒的人占%a .为减轻工作量，随机地按n 人一组分组，然后将各组n 个人的血样混合在一起化验.若混合血样呈阴性，说明这n 个人全部阴性；若混合血样呈阳性，说明其中至少有一人的血样呈阳性，就需要对每个人再分别化验一次.（1）若0.2,20,a n ==试估算该小区化验的总次数；（2）若0.9a =，且每人单独化验一次花费10元，n 人混合化验一次花费9n +元，求当n为何值时，每个居民化验的平均费用最少.注：假设每位居民的化验结果呈阴性还是阳性相互独立.当00.01p <<时，(1)1n p np -»-.【答案】（1）270 （2）10【解析】【分析】（1）设每组居民需化验的次数为X ，确定其取值，分别求概率，进而可得期望，即得；（2）设每组n 人总费用为Y 元，结合条件计算，然后表示出结合基本不等式即得.【小问1详解】设每组需要检验的次数为X ，若混合血样为阴性，则1X =，若混合血样呈阳性，则21X =， 所以20(1)(10.002)P X ==-，20(21)1(10.002)P X ==--， 所以202020()1(10.002)21[1(10.002)]2120(10.002)E X =´-+´--=-´-2120(1200.002) 1.8»-´-´=一共有300020150¸=组，故估计该小区化验的总次数是1.8150270´=.【小问2详解】设每组n 人总费用为Y 元，若混合血样呈阴性，则9Y n =+；若混合血样呈阳性，则119Y n =+，故(9)(10.009)n P Y n =+=-，(119)1(10.009)n P Y n =+=--()(9)0.991(119)(10.991)11100.9919n n n E Y n n n n =+×++×-=-´+每位居民的化验费用为()11100.99199911100.9911110(10.009)n n E Y n n n n n n n-´+==-´+»-´-+=911100.091 2.8n n -++³+=元 当且仅当90.09n n=，即10n =时取等号，故10n =时，每个居民化验的平均费用最少.18. 在平面直角坐标系xOy 中，已知()1,1A ，()1,1B -，动点P 满足OP mOA nOB =+uuu r uuu r uuu r，且1mn =.设动点P 形成的轨迹为曲线C .（1）求曲线C 的标准方程；（2）过点()2,2T 的直线l 与曲线C 交于M ，N 两点，试判断是否存在直线l ，使得A ，B ，M ，N 四点共圆.若存在，求出直线l 的方程；若不存在，说明理由.【答案】（1）22144x y -=（2）不存在直线l 符合题意，理由见解析【解析】【分析】（1）设(),P x y ，则由OP mOA nOB =+uuu r uuu r uuu r，可得x m n =+，y m n =-，再结合1mn =，消去,m n ，即可得曲线C 的标准方程，（2）判断直线l 的斜率存在，设l ：()22y k x =-+，设()11,M x y ，()22,N x y ，将直线方程代入曲线C 的方程，化简后利用根与系数的关系，结合中点坐标公式表示出MN 的中点H 的坐标，利用弦长公式表示出MN ，表示出线段MN 的中垂线方程，求出其与与x 轴的交点坐标为4,01k Q k æöç÷+èø，而AB 的中垂线为x 轴，所以若A ，B ，M ，N 共圆，则圆心为4,01k Q k æöç÷+èø，从而由2222224MNQA QM QH HM QH ==+=+列方程求解即可.【小问1详解】设(),P x y ，则(),OP x y =uuu r，()1,1OA =uuu r ，()1,1OB =-uuu r ，因为OP mOA nOB =+uuu r uuu r uuu r，所以()()()(),1,11,1,x y m n m n m n =+-=+-，所以x m n =+，y m n =-，所以2x y m +=，2x yn -=，又122x y x y mn +-=×=，整理得22144x y -=，即曲线C 的标准方程为22144x y -=；【小问2详解】易知当l 的斜率不存在时，直线l 与曲线C 没有两个交点，所以直线l 的斜率存在，设l ：()22y k x =-+，将直线l 与曲线C 联立，得22(2)2144y k x x y =-+ìïí-=ïî，消去y ，整理得()22212(22)4880kxk k x k k ----+-=，因为()()22224(22)4148832(1)0k k kkk k D =----+-=->且210k -¹，所以1k <且1k ¹-，设()11,M x y ，()22,N x y ，则1241k x x k +=+，21224881k k x x k -+=-，所以MN 的中点22,11kH k k æöç÷++èø，且1x M N =-=，将1241k x x k +=+，21224881k k x x k -+=-代入上式，整理得4MN =当0k ¹时，线段MN 的中垂线方程为1l ：12214111k y x x k k k k k æö=--+=-+ç÷+++èø，令y ＝0，解得41k x k =+，即1l 与x 轴的交点坐标为4,01k Q k æöç÷+èø，当k ＝0时，线段MN 的中垂线为y 轴，与x 轴交于原点，符合Q 点坐标，因为AB 的中垂线为x 轴，所以若A ，B ，M ，N 共圆，则圆心为4,01k Q k æöç÷+èø，所以2222224MNQA QM QH HM QH ==+=+，所以()2222281442211111(1)(1)k k k k k k k k k +-æöæöæö-+=++ç÷ç÷ç÷++++-èøèøèø，整理得32622100k k k -++=，即()22(1)3450k k k +-+=，因为1k <且1k ¹-，所以上述方程无解，即不存在直线l 符合题意.19. 在高等数学中，我们将()y f x =在0x x =处可以用一个多项式函数近似表示，具体形式为：()()()()()()()()()200000002!!n nf x f x f x f x f x x x x x x x n ¢¢=+¢-+-+×××+-+×××（其中()()n f x 表示()f x 的n 次导数*3,N n n ³Î），以上公式我们称为函数()f x 在0x x =处的泰勒展开式.当00x =时泰勒展开式也称为麦克劳林公式.比如e x 在0x =处的麦克劳林公式为：22111e 12!3!x n x x x x n =++++++L L ！，由此当0x ³时，可以非常容易得到不等式223111e 1,e 1,e 1,226x x x x x x x x x ³+³++³+++L 请利用上述公式和所学知识完成下列问题：（1）写出sin x 在0x =处的泰勒展开式.（2）若30,2x æö"Îç÷èø，sin e 1a xx >+恒成立，求a 的范围;（参考数据5ln 0.92»）（3）估计5ln3的近似值（精确到0.001）【答案】（1）1352111(1)sin 3!5!(21)!n n x x x x x n --+-=-+++-L L ； （2）1a ³； （3）0.511【解析】【分析】（1）求导，根据题意写出sin x 在0x =处的泰勒展开式；（2）结合sin x 在0x =处的泰勒展开式，构造函数证明3310,,sin 26x x x x æö"Î>-ç÷èø，再令31()ln(1)6g x x x x =--+，30,2x æöÎç÷èø，求导得到函数单调性，证明出30,,()02x g x æö"Î>ç÷èø，当1a ³时，31sin sin ln(1)6a x x x x x ³>->+ ，满足要求，当1a <时，令()sin ln(1)h x a x x =-+，30,2x æöÎç÷èø，易求得(0)10h a ¢=-<，所以必存在一个区间(0,)m ，使得()h x 在(0,)m 上单调递减， 所以(0,)x m Î时，()(0)0h x h <=，不合要求，从而得到答案；（3）求出ln(1)x +和ln(1)x -的泰勒展开式，得到35122ln 2135x x xx x +=+++-L ，令14x =，估计5ln3的近似值.【小问1详解】()sin cos x x ¢=，()cos sin x x ¢=-，()sin cos x x ¢-=-，()cos sin x x ¢-=，其中cos 01,sin 00==，sin x 在0x =处的泰勒展开式为：1352111(1)sin 3!5!(21)!n n x x x x x n --+-=-+++-L L ，【小问2详解】因为1352111(1)sin 3!5!(21)!n n x x x x x n --+-=-+++-L L ，由sin x 在0x =处的泰勒展开式，先证3310,,sin 26x x x x æö"Î>-ç÷èø，令3211()sin ,()cos 1,()sin 62f x x x x f x x x f x x x =-+¢=-+¢¢=-，()1cos f x x ¢¢¢=-，易知()0f x ¢¢¢>，所以()f x ¢¢在30,2æöç÷èø上单调递增，所以()(0)0f x f ¢¢>¢¢=，所以()f x ¢在30,2æöç÷èø上单调递增，所以()(0)0f x f ¢>¢=，所以()f x 在30,2æöç÷èø上单调递增，所以()(0)0f x f >=，再令31()ln(1)6g x x x x =--+，30,2x æöÎç÷èø，易得1(1)(2)2()1x x x g x x --+¢=+，所以()g x 在(0,1)上单调递增，在31,2æöç÷èø上单调递减，而3155(0)0,ln 02162g g æö==->ç÷èø，所以30,,()02x g x æö"Î>ç÷èø恒成立，当1a ³时，31sin sin ln(1)6a x x x x x ³>->+ ，所以sin e 1a x x >+成立，当1a <时，令()sin ln(1)h x a x x =-+，30,2x æöÎç÷èø，易求得(0)10h a ¢=-<，所以必存在一个区间(0,)m ，使得()h x 在(0,)m 上单调递减， 所以(0,)x m Î时，()(0)0h x h <=，不符合题意. 综上所述，1a ³.【小问3详解】因为1154ln ln,1314+=-转化研究1ln 1x x +-的结构，23456ln(1)23456x x x x x x x +=-+-+-+L ，23456ln(1)23456x x x x x x x -=-------L ，两式相减得35122ln 2135x x x x x +=+++-L ，取1,4x =得35512121ln 2((0.5108343454=´+´+´+»L ，所以估计5ln 3的近似值为0.511（精确到0.001）.【点睛】麦克劳林展开式常常用于放缩法进行比较大小，常用的麦克劳林展开式如下：()21e 12!!n x n x x x o x n +=+++++L ，()()()352122sin 13!5!21!n n n x x x x x o x n ++=-+-+-++L ，()()()24622cos 112!4!6!2!nn n x x x xx o x n =-+-++-+L ，()()()2311ln 11231n n n x x xx x o x n +++=-+-+-++L ，()2111n n x x x o x x =+++++-L ，()()()221112!nn n x nx x o x -+=+++。

四川省成都石室中学高三10月月考（数学理）一、选择题:本大题共12题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是满足题目要求的。

请将你认为正确的选项前面的代号填入机读卡。

1、已知复数z3i ）z ＝3i ，则z ＝（ ）A ．32 B. 34 C. 32 D.34 2．已知命题.01,:;25sin ,:2>++∈∀=∈∃x x R x q x R x p 都有命题使下列结论中正确的是（ ） A ．命题“q p ∧”是真命题 B ．命题“q p ⌝∧”是真命题C ．命题“q p ∧⌝”是真命题D ．命题“q p ⌝∨⌝”是假命题3、若a>1,b<0,且a b+a -b=22,则a b-a -b 的值等于（ ）A ． 6B ．±2C ．-2D ．24、lim )x x →+∞=（ ）A ．0B ．1C ．12D ．25、下列四个命题中正确的是( ) A 、若a 、b ∈R,则|a|－|b|＜|a ＋b|B 、若a 、b ∈R,则|a －b|＜|a|＋|b|C 、若实数a 、b 满足|a －b|＝|a|＋|b|,则ab ≤0D 、若实数a 、b 满足|a|－|b|＜|a ＋b|,则ab ＜06．现有四所大学进行自主招生，同时向一所高中的已获省级竞赛一等奖的甲、乙、丙、丁四位学生发出录取通知书．若这四名学生都愿意进这四所大学的任意一所就读， 则仅有两名学生被录取到同一所大学的概率为（ ）A ．12 B ．916 C ．1116D ．7247、若2)n x 的项是第8项，则展开式中含1x的项是（ ）A ．第8项B ．第9项C ．第10项D ．第11项8、 若{}A x x p x x R =+++=∈|()2210，，且，则实数中的取值范围是（ ）A ．B ．C ．D ．9、已知偶函数()f x 满足(1)()f x f x +=-，且()f x 在区间[0，1]上是增函数，则)0(),1(),5.6(f f f --的大小关系是（ ）A ．)1()0()5.6(-<<-f f fB ．)0()5.6()1(f f f <-<-C ．)1()5.6()0(-<-<f f fD ．)5.6()0()1(-<<-f f f10、如图,在平行六面体ABCD －A 1B 1C 1D 1中,若AA 1＝AB ＝AD ＝1，∠A 1AD ＝∠A 1AB ＝60°,∠BAD ＝90°,则直线A 1D 1到平面ABCD 的距离为( ) A 、1 B 、22C 、33D 、6311、函数23)1(-+=x f y 为奇函数，)(1x f y -=是)(x f y =的反函数，若0)3(=f ，则=-)3(1f （ ）A ．1- B. 1 C. 2- D. 2 12、已知数列{}n a 满足121,2,a a ==1211()n n n n n n a a a a n N a a *+++++-=∈，则200a =（ ） A ．1992199!∙ B ．201!1- C ．1982201!∙ D ．198!1-二、填空：本大题共4题，每小题4分，共16分13．函数y=(31)221x x -+的值域是 。

四川省成都市石室中学远程教育学校2020-2021学年高三数学文月考试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 设角属于第二象限，且，则角属于（）A. 第一象限B. 第二象限C. 第三象限D. 第四象限参考答案：C略2. 若，满足约束条件，则的最小值是（）A． B． C． D．参考答案：A作出不等式组所表示的平面区域，如下图：由图可知当直线经过点C（0，3）时，故选A．考点：线性规划．3. 若集合，则下列集合运算结果为空集的是：A． B. C. D.参考答案：A4. 若随机变量，且，则（）A.0.6B.0.5C.0.4D.0.3参考答案：A∵随机变量X服从正态分布N（3，σ2），∴对称轴是x=3．∵P（X≥5）=0.2，∴P（1＜X＜5）=1﹣2P（X≥5）=1﹣0.4=0.6．故选：A．5. 过双曲线的右焦点F作实轴所在直线的垂线，交双曲线于A，B两点，设双曲线的左顶点为M，若点M在以AB为直径的圆的内部，则此双曲线的离心率e的取值范围为（）A．（，＋∞） B．（1，） C．（2，＋∞） D．（1，2）参考答案：C6. 执行如图所示的程序框图，如果输入的，则输出的取值范围为（ ）A ．[－7,1]B ．[1,3]C ．[0,3]D ．[0,1]参考答案：C 7. 已知，，，则（ ）A ．B ．C ．D ．参考答案：A8. 已知集合（ ）A ．B ．C ．D ．参考答案：B略9. 函数的零点个数为（ ）A ．B ．C ．D ．参考答案：C 略10. 已知sin+cos =，∈(0，)，则tan 的值为A ．B ．C ．或D ．或参考答案：A 略二、 填空题:本大题共7小题,每小题4分,共28分11. 在一个长方体的三条棱长分别为3、8、9，若在该长方体上面钻一个圆柱形的孔后其表面积没有变化，则圆孔的半径为 ．参考答案：3【分析】设半径为r ，由题意得减少的2个圆的面积=圆柱的侧面积，由此列出方程能求出圆孔的半径．【解答】解：设半径为r ，∵在一个长方体的三条棱长分别为3、8、9，在该长方体上面钻一个圆柱形的孔后其表面积没有变化，∴减少的2个圆的面积=圆柱的侧面积， ∴2πr 2=2πr×3， 解得r=3．∴圆孔的半径为3． 故答案为：3．12. 已知函数，的四个零点，，，，且，则的值是．参考答案：分类讨论求解方程的零点： (1)；(2)；从而=2， 据此计算有：的值是.13. 若双曲线的焦距等于6，则m = ．参考答案：3由双曲线的方程知，所以 ，故填3.14. 设的展开式的各项系数之和为，二项式系数之和为，若，则 ＝.参考答案：15. 已知数列(n)的公差为3，从中取出部分项（不改变顺序）a 1,a 4,a 10,…组成等比数列，则该等比数列的公比是参考答案：216. 第十一届全运会的篮球比赛中，已知甲、乙两名运动员每场比赛的得分统计茎叶图如图所示，则发挥较稳定的运动员是 .参考答案：甲17. 已知两个不相等的平面向量，()满足||＝2，且与－的夹角为120°，则||的最大值是 .参考答案：略三、 解答题：本大题共5小题，共72分。

成都石室中学2019-2020 学年度上期高2020 届10 月月考英语试题试卷满分 150 分考试时间 120 分钟第一部分听力(共两节，满分30 分)第一节听下面5 段对话。

每段对话后有一个小题，从题中所给的A、B、C 三个选项中选出最佳选项。

听完每段对话后，你都有10 秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1 Where did the man put the woman’s bike?A. Under a street lamp.B. In a garage.C. In a backyard.2 Which floor is the Committee Room on?A. The second floor.B. The third floor.C. The fourth floor.3 How does the man feel about the article in the end?A. Satisfied.B. Annoyed.C. Bored.4 Where does the conversation probably take place?A. In a library.B. In a bookstore.C. In a teaching building.5 Why does the man call the woman?A. To ask for a sick leave.B. To ask about English classes.C. To discuss tomorrow’sschedule. 第二节听下面5 段对话或独白。

每段对话或独白后有几个小题，从题中所给的A、B、C 三个选项中选出最佳选项。

听每段对话或独白前，你将有时间阅读各个小题，每小题5 秒钟；听完后，各小题将给出5 秒钟的作答时间。

每段对话或独白读两遍。

听第 6 段材料，回答第 6、7 题。

成都石室中学2023-2024年度上期高2024届十月月考数学试题（文 ）参考答案1．已知集合MM ={xx |xx 2−3xx +2⩽0}，{|0}N x x =>，则( ) A ．N M ⊆B ．M N ⊆C ．M N =∅D ．M N R =解：已知集合MM ={xx |(xx −1)(xx −2)⩽0}={xx |1⩽xx ⩽2}，{|0}N x x =>， 则由集合的运算和集合的关系可得：M N ⊆，B 正确；故选：B ． 2．若1z =，则复数1z z+在复平面上对应的点在( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限解：1z =，则复数 141113z z +=+==+=−．对应点4(3，在第一象限．故选：D ．3．已知命题:()()p y g x y g x ==−函数与关于y 轴对称，命题，:q x R ∀∈，使4tan 4tan x x+≥下面结论正确的是( ) A ．命题“p q ∧”是真命题 B ．命题“()p q ∧¬”是假命题C ．命题“()p q ¬∨”是真命题D ．命题“()()p q ¬∧¬”是假命题A ：命题“p q ∧”为假命题:B p q ∧¬为真命题C ：“p q ¬∨”为假命题D ：“p q ¬∧¬”假命题故选：D ． 4．已知等比数列{}n a 的前n 项和为n S ，且数列313{}1,2,k k ka −=（）成等差数列，则363(S S S −=) A ．1或43 B ．1或13 C ．2或43D ．13或43解：设等比数列{}n a 的公比为q ，由2a ，52a ，83a 成等差数列可得，52843a a a =+，即4711143a qa q a q =+，化简得633410q q −+=，解得313q = 或31q =，当31q =时，3631S S S −=，当313q = 时，633343S q S S ==−．故选：B ． 5.某三棱锥的三视图如图所示，则该三棱锥的表面积是( ) A ．2B ．2+C ．43D ．23该几何体是棱长分别为2，2，1的长方体中的三棱锥P ABM −，其中：2,ABM PMA PMB PAB S S S S ∆∆∆∆====，该几何体的表面积为：222+=+ 故选：B ．6．已知函数2()log ||f x x =，设0.1214(log 3),(7),(log 25)a f bf c f −==，则a ，b ，c 的大小关系为( ) A ．b a c <<B ．c a b <<C ．c b a <<D ．a c b <<解：()f x 的定义域为R ，函数()f x 为偶函数，所以()f x 在(0,)+∞上为增函数， 所以2(3)a f log ==，因为234<<，所以222log 2log 3log 4<<，即21log 32<<， 因为7x y =在R 上为增函数，且0.10−<，所以0.100771−<<=， 因为2516>，所以44log 25log 162>=，所以0.142log 25log 370−>>>， 所以0.142(log 25)(log 3)(7)f f f −>>，所以c a b >>，故选：A ． 7．函数||1()xln x f x e +=的图象大致为( ) A ．B ．C ．D ．解：函数||1()x ln x f x e+=是非奇非偶函数，排除A 、B ，函数||1()xln x f x e +=的零点是1x e −=，当x e =时，f （e ）21e e e=<，排除选项D ．故选：C ． 8．已知向量),(sin ,2)m n θθ=，1m n ⋅=，则cos(2)3πθ+的值是( )A ．78B ．14 C ．14−D ．78−解：1sin()64πθ+= ， 2217cos(2)12sin ()12()3348ππθθ∴+=−−=−×=．故选：A ． 9．在区间[0，1]上随机取两个数x ，y ，记1p 为事件“12x y +…”的概率，2p 为事件“1||2x y −…”的概率，3p 为事件“12xy …”的概率，则( ) A ．123p p p <<B ．231p p p <<C ．312p p p <<D ．321p p p <<解：分别作出事件对应的图象如图（阴影部分）: 11:(0,)2p D ，1(2F ，0)，(0,1)A ，(1,1)B ，(1,0)C ，则阴影部分的面积11111711122288S =×−××=−=，211113112122244S =×−×××=−=，111312211111111121|222222222S dx lnx ln ln x =×+=+=−=+∫，231S S S ∴<<，即231p p p <<，故选：B ．10．已知抛物线C ：px y 22=的准线为直线1−=x，直线1:0l x my −=与C 交于P ，Q 两点（点P 在x 轴上方），与直线1−=x 交于点R ，若||3QF =，则(QRF PRFS S ∆∆= ) A ．57B ．37C ．67D ．97解：如图所示， 抛物线24y x =．||31Q QF x ==+，解得2Q x =．联立204x my y x −== ，化为：22(450x m x −++=．25P x ∴=，解得52P x =，则1||2165||1712QRF Q PRF P S x QR S PR x ∆∆++====++．故选：C ．题号1 2 3 4 5 6 7 8 9 10 11 12 答案 BDDBBACABCCB二、填空题13.1 ; 14.283π; 16. . 三、解答题17．解：（1）由21n n S a =−，得1121n n S a −−=−， 两式相减得12n n a a −=，………………..3分当1n =时，1121a S =+，则11a =， ………………..4分所以{}n a 是以1为首项，以2为公比的等比数列，所以12n n a −=；………………..6分（2）213134n n n n n b a lna −+=+=+，………………..7分{}n b 的前n 项和n T 为123n b b b b +++…+1(14164)3(123)n n −=+++…+++++…+14(1)3142n n n −++− 41(1)332n n n −++..12分 18．解：（1）由题意得，400.02500.3600.4700.23800.04900.0160x =×+×+×+×+×+×=，(4060)0.02(5060)0.3(6060)0.4(7060)0.23(8060)0.04(9060)0.014000.021000.300.41000.234000.049000.0186s =−×+−×+−×+−×+−×+−×=×+×+×+×+×+×=所以这200名学生体重的平均数为60，方差为86；………………..6分（2）由题意知抽取的7人中，(55,65)（不及格）有4人，记为1,2,3,4；(45,55)有3人，记为A ，B ，C ．随机试验的所有可能结果有：12，13，14，1A ，1B ，1C ，23，24，2A ，2B 2C ，34，3A ，3B ，3C ，4A ，4B ，4C ，AB ，AC ，BC 共21个，其中来自不同组的结果有：1A ，1B ，1C ，2A ，2B ，2C ，3A ，3B ，3C ，4A ，4B ，4C 共12个，所以所求概率为124217P==………………..12分19．证明：（1） 22DF BE ==，3EF =，BD =BE BD ∴⊥ ………………..1分 平面BDEF ⊥平面ABCD ，面BDEF 平面ABCD BD =，BE BD ⊥，BE BDEF ⊂面 BE ABCD ∴⊥面 ………………..3分AD ABCD ∴⊆面 ∴BE ⊥ AD………………..5分解(2) 1cos 5BAD ∠=，∴222282cos 85BD AB AD AB AD BAD a =+−∠==∴a =，2223OA AB OB ∴=−=，∴OA =………………..7分设点B 到平面AEF 的距离为h 。

成都石室中学2025届2024—2025学年度上期十月考试化学试卷试卷说明：满分100分，考试时间75分钟可能用到的相对原子质量：H 1 C 12 N 14 O 16 F 19 Cl 35.5 Co 59 Ag 1081．在一定条件下，动植物油脂与醇反应可制备生物柴油，化学方程式如下:下列叙述错误的是（）A．生物柴油由可由再生资源制得B．生物柴油是不同酯组成的混合物C．动植物油脂是高分子化合物D．“地沟油”可用于制备生物柴油2．设N A为阿伏加德罗常数的值，下列叙述正确的是A．标准状况下，33.6L氟化氢中含有氟原子的数目为1.5N AB．常温常压下，7.0g乙烯与丙烯的混合物中含有氢原子的数目为N AC．50mL 18.4mol/L浓硫酸与足量铜微热反应，生成SO2分子数目为0.46N AD．某密闭容器盛有0.1mol I2和0.1mol H2，在一定条件下充分反应，转移电子的数目为0.2N A 3．用下列仪器或装置进行相应实验，操作规范且能达到实验目的的是A．配制一定物质的量浓度的NaOH溶液B．除去SO2中的SO3C．滤纸过滤，分离Fe(OH)3胶体中的NaCl D．蒸干AlCl3溶液得到无水AlCl34．下列方程式书写错误是35l2↑+3H2O A．用氯酸钾与浓盐酸制氯气：K37ClO3+6H35Cl=K37Cl+3CB．硫酸四氨合铜溶液加入乙醇：[Cu(NH3)4]2++SO42−+H2O=[Cu(NH3)4]SO4⋅H2O↓C．0.01mol/LNH4Al(SO4)2溶液与0.02mol/LBa(OH)2溶液等体积混合：NH4＋+Al3＋+ 2SO42－+ 2Ba2＋+ 4OH-= 2BaSO4↓ + Al(OH)3↓ + NH3·H2OD．由1,6-己二胺和己二酸制备尼龙66：5．组成核酸的基本单元是核苷酸，下图是核酸的某一结构片段，下列说法正确的是A．DNA和RNA结构中的碱基相同，戊糖不同B．核酸的单体是核苷酸，彻底水解的产物是核苷C．核苷酸在一定条件下，既可以与酸反应，又可以与碱反应D．核酸分子中碱基通过磷酸酯键实现互补配对6．路易斯酸碱电子理论认为，凡是可以接受电子对的物质是酸，凡是可以给出电子对的物质是碱。

四川省成都石室中学2020学年度高三数学月考试卷一、选择题：只有唯一正确答案，每小题5分，共60分。

1．设集合M = {a ，b ，c }，N = {0，1}，映射f ：M →N 满足f (a ) + f (b ) = f (c )，则映射f ： M →N 的个数为 （ ）A ．1B ．2C ．3D ．4 2．函数)1(21)(x x x f --=的最大值是 （ ）A ．49B ．94C ．47D ．743．（理科）函数x x g x f )21()()(=与的图象关于y = x 对称，则f (4x －x 2)的单调递增区间为（ ）A ．（－∞，2）B ．（0，2）C ．（2，4）D ．（2，+∞）（文科）为得到函数100lg xy =的图象，可以把函数y = lg x 的图象 （ ）A ．向上平移两个单位B ．按向量)2,0(-=平移C ．向左平移两个单位D ．按向量)0,2(=a 平移4．如果2log |3|log 2121ππ≥-x ，那么sin x 的取值范围是 （ ）A ．]21,21[-B ．]1,21[-C ．]1,21()21,21[Y -D ．]1,23()23,21[Y -5．已知yxy x y x y x 则,lg lg 2lg )2lg()lg(++=++-的值为 （ ）A ．－1B ．2C ．21 D ．－1或26．设全集U 是实数集R ，}11|{},4|{2≥-=>=x x N x x M ，则图中阴影部分所表示的集合是（ ）A ．}12|{<≤-x x xB ．}22|{≤≤-x x xC ．}21|{≤<x xD ．}2|{<x x7．若方程0122=--x ax 在区间（0，1）内恰有一解，则实数a 的取值范围是 （ ）A ．a <－1B ．a >1C ．－1< a < 1D ．0≤a ＜18．（理科）若函数)0,(2)1(log )(223-∞++++=在x x b ax x f 上有最小值－5，（a ，b 为常数），则函数),0()(+∞在x f 上（ ）A ．有最大值5B ．有最小值5C ．有最大值3D ．有最大值9（文科）若函数f (x )的图象关于直线x =1对称，且当x >1时，x x x f -=32)(，则当x <1时，f (x )的表达式为（ ）A ．2)2(2)(3-+-=x x x fB ．x x x f --=3)2(2)(C ．1)1(2)(3-+-=x x x fD ．x x x f +=32)(9．定义在R 上的函数y = f (x + 1)的图象如图所示，且在定义域上， 是减函数，给出如下命题：①f (0) =1；②f (－1) =1；③若x >0， 则f (x ) <0；④若x <0，则f (x ) >0，其中正确的是 （ ）A ．②③B ．①④C ．②④D ．①③10．（理科）已知定义在R 上的偶函数f (x )满足)3()3(x f x f -=+，且当]4,3[∈x 时，x x f )21()(=，求当]2,3[--∈x 时，则函数f (x )的表达式为（ ）A ．6)21()(+=x x fB ．6)21()(-=x x f C ．x x f )21()(=D ．62)(+=x x f（文科）设f (x )是定义在实数集R 上以2为周期的奇函数，已知x x f x )21()(,)1,0(=∈时，则)12(log 2f 的值为（ ）A ．43 B ．43-C ．34-D ．34 11．设偶函数)0,(||log )(-∞-=在b x x f a 上递增，则)2()1(++b f a f 与的大小关系是（ ） A ．)2()1(+≥+b f a f B ．)2()1(+≤+b f a fC ．)2()1(+<+b f a fD ．)2()1(+>+b f a f12．（理科）设定义域为R 的函数⎪⎩⎪⎨⎧=≠-=1,11,|1|1)(x x x x f ，若关于x 的方程0)()(2=++c x bf x f 有三个不同的实数解x 1、x 2、x 3，则232221x x x ++等于（ ）A ．5B ．2222bb + C ．13 D ．2223c c +（文科）在正实数集上定义一种运算*，规则是：当a ≥b 时，a *b =b 3，当a ＜b 时，a *b =b 2，根据这一规则，方程a *b = b 3的解为 （ ）A ．3B ．33C ．3或33D ．3或9二、填空题：每小题4分，共16分。

四川省成都石室中学2020届高三数学10月月考试题 文一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的. 1.已知集合{|(1)(2)0},{|0}=--≤=>M x x x N x x ，则（ ） A. N M ⊆ B. M N ⊆ C. M N ⋂=∅ D. M N =R U 2.已知i 为虚数单位，则232019i i i i ++++L 等于（ ） A. i B. 1 C. i - D. 1- 3.已知命题p ：2(,0),2310x x x ∀∈-∞-+>，命题q ：若0x ≥，则22310x x -+≤，则以下命题正确的为（ ）A.p 的否定为“2[0,),2310x x x ∃∈+∞-+≤”，q 的否命题为“若0x <，则22310x x -+>”B.p 的否定为“2(,0),2310x x x ∃∈-∞-+≤”，q 的否命题为“若0x <，则22310x x -+>”C.p 的否定为“2[0,),2310x x x ∃∈+∞-+≤”，q 的否命题为“若0x ≥，则22310x x -+>”D.p 的否定为“2(,0),2310x x x ∃∈-∞-+≤”，q 的否命题为“若0x ≥，则22310x x -+>” 4.已知{}n a 是公差为12的等差数列，n S 为{}n a 的前n 项和.若2614,,a a a 成等比数列，则5S =（ ） A.352B.35C. 252D. 255.中国古代数学著作《算学启蒙》中有关于“松竹并生”的问题：松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等．意思是现有松树高5尺，竹子高2尺，松树每天长自己高度的一半，竹子每天长自己高度的一倍，问在第几天会出现松树和竹子一般高？如图所示是源于其思想的一个程序框图，若输入的5x =，2y =，输出的4n =，则程序框图中的中应填（ ） A. x y ≤B.y x ≤C. y x <D.x y =6.设函数2,1(),12x x f x x x -⎧<⎪=⎨≥⎪⎩，则满足()()12f f a f a =⎡⎤⎣⎦的a 的取值范围是（ ）A. (],0-∞B. []0,2C. [)2,+∞D. (][),02,-∞⋃+∞7. 若直线()42y k x -=-与曲线24y x =-有两个交点，则k 的取值范围是（ ）A.[)1,+∞B.31,4⎡⎫--⎪⎢⎣⎭C.3,14⎛⎤⎥⎝⎦D.(],1-∞- 8.已知2ln3a =，3ln 2b =，6c e=，其中e 是自然对数的底数．则,,a b c 的大小关系为（ ）A.a c b >>B. b c a >>C. c a b >>D. c b a >>9.已知(0,),2sin 2cos 212πααα∈=+，则sin α等于（ ）B.1510.函数x x x x x f sin )1()(2+-+=的零点的个数是（ ）A.1B.2C.3D.411.已知双曲线2222:1x y C a b -=（0,0a b >>）的焦距为4，其与抛物线2:E y x =交于,A B 两点，O为坐标原点，若OAB ∆为正三角形，则C 的离心率为（ ）B. 212.已知函数()sin()f x x ωϕ=+，其中0ω>，||2πϕ…，4p -为()f x 的零点：且()4f x f π⎛⎫⎪⎝⎭…恒成立，()f x 在区间,1224ππ⎛⎫⎪⎝⎭-上有最小值无最大值，则ω的最大值是（ ） A. 11B. 13C. 15D.17二、填空题：本大题共4小题，每小题5分，共20分． 13.已知数列{}n a 满足11a =，11lg lg 2n n a a +=+，则5a =______． 14.已知112,1,,,1,2,322α⎧⎫∈---⎨⎬⎩⎭，若幂函数()f x x α=为奇函数，且在()0,+∞上递减，则α=______．15.已知球O 的内接圆锥体积为23π，其底面半径为1，则球O 的表面积为______． 16.已知抛物线C ：20)2(y px p =＞的焦点为F ，且F 到准线l 的距离为2，直线1:0l x my -=与抛物线C 交于,P Q 两点（点P 在x 轴上方），与准线l 交于点R ，若3QF =，则QRF PRFS S ∆∆=______．三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤． 17.（本小题满分12分）在ABC ∆中，D 是BC 上的点，AD 平分BAC ∠，sin 2sin C B =.（Ⅰ）求BDCD； （Ⅱ）若1AD AC ==，求BC 的长．18.（本小题满分12分）随着经济的发展，个人收入的提高.自2018年10月1日起，个人所得税起征点和税率的调整.调整如下:纳税人的工资、薪金所得，以每月全部收入额减除5000元后的余额为应纳税所得额.依照个人所得税税率表，个人所得税税率表（调整前） 个人所得税税率表（调整后） 免征额3500元免征额5000元级数 全月应纳税所得额 税率（%） 级数 全月应纳税所得额 税率（%） 1 不超过1500元的部分31 不超过3000元的部分 32 超过1500元至4500元的部分 10 2 超过3000元至12000元的部分103 超过4500元至9000元的部分 20 3 超过12000元至25000元的部分 10 ………………（Ⅰ）假如小李某月的工资、薪金所得等税前收入总和不高于8000元，记x 表示总收入，y 表示应纳的税，试写出调整前后y 关于x 的函数表达式；（Ⅱ）某税务部门在小李所在公司利用分层抽样方法抽取某月100个不同层次员工的税前收入，并制成下收入（元） [)3000,5000 [)5000,7000 [)7000,9000 [)9000,11000 [)11000,13000 []13000,15000人数 304010875先从收入在[)3000,5000及[)5000,7000的人群中按分层抽样抽取7人，再从中选2人作为新纳税法知识宣讲员，求两个宣讲员不全是同一收入人群的概率；（Ⅲ）小李该月的工资、薪金等税前收入为7500元时，请你帮小李算一下调整后小李的实际收入比调整前增加了多少？19.（本小题满分12分）如图，在四棱锥P ABCD -中，AD BC ∥，12AB BC CD AD ===，G 是PB 的中点，PAD △是等边三角形，平面PAD ⊥平面ABCD . （Ⅰ）求证：CD ⊥平面GAC ；（Ⅱ）求三棱锥D GAC -与三棱锥P ABC -的体积之比.20.（本小题满分12分）已知函数()()211e xa x x f x ---=（e 为自然对数的底数）. (Ⅰ)讨论函数()f x 的单调性；(Ⅱ)求证：当3e a ≥-时，对[)0,x ∀∈+∞，()1f x ≥-.21.（本小题满分12分）已知椭圆()2222:10x y C a b a b +=>>过点()0,1A ，且椭圆的离心率为3（Ⅰ）求椭圆C 的方程；(Ⅱ)斜率为1的直线l 交椭圆C 于()()1122,,,M x y N x y 两点，且12x x >．若直线3x =上存在点P ，使得PMN ∆是以M 为直角顶点的等腰直角三角形，求直线l 的方程．22.（本小题满分10分）在平面直角坐标系xOy 中,圆C ：()2244x y +-=.以原点O 为极点，x 轴的正半轴为极轴，建立极坐标系.（Ⅰ）求圆心C 的极坐标；（Ⅱ）从原点O 作圆C 的弦，求弦的中点轨迹的极坐标方程.成都石室中学2019~2020学年度上期高2020届10月月考数学试卷（文科）答案一、选择题：B D B C A D C C A B D C 二、填空题：13. __100____．14. ___1-___．15.____ 254π__．16. ___67___．三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤． 17.（本小题满分12分）解：（Ⅰ）由正弦定理可得在ABD ∆中，sin sin AD BDB BAD=∠， 在ACD ∆中，sin sin AD CDC CAD=∠，…………………………3分 又因为BAD CAD ∠=∠，sin 2sin BD CCD B==.…………………………6分 （Ⅱ）sin 2sin C B =，由正弦定理得22AB AC ==， 设DC x =，则2BD x =，则222254cos cos 24AB AD BD x BAD CAD AB AD +--∠==∠⋅，2222222AC AD CD x AC AD +--==⋅.…………………………9分因为BAD CAD ∠=∠，所以2254242x x --=，解得x =32BC x ==.…………………………12分18.（本小题满分12分）解：（Ⅰ）调整前y 关于x 的表达式为()()0,350035000.03,350050004550000.1,50008000x y x x x x ⎧≤⎪=-⨯<≤⎨⎪+-⨯<≤⎩，调整后y 关于x 的表达式为()0,500050000.03,50008000x y x x ≤⎧=⎨-⨯<≤⎩.…………………4分 （Ⅱ）由频数分布表可知从[)3000,5000及[)5000,7000的人群中按分层抽样抽取7人，其中[)3000,5000中占3人，分别记为,,A B C ，[)5000,7000中占4人，分别记为1，2，3，4，再从这7人中选2人的所有组合有：AB ，AC ，1A ，2A ，3A ，4A ，BC ，1B ，2B ，3B ，4B ，1C ，2C ，3C ，4C ，12，13，14，23，24，34，共21种情况，…………………7分其中不在同一收入人群的有：1A ，2A ，3A ，4A ，1B ，2B ，3B ，4B ，1C ，2C ，3C ，4C ，共12种，所以所求概率为124217P ==.…………………10分 （Ⅲ）由于小红的工资、薪金等税前收入为7500元，按调整起征点前应纳个税为15003%250010%295⨯+⨯=元；按调整起征点后应纳个税为25003%75⨯=元， 由此可知，调整起征点后应纳个税少交220元， 即个人的实际收入增加了220元，所以小红的实际收入增加了220元. …………………12分19.（本小题满分12分）解：（Ⅰ）证明：取AD 的中点为O ，连接OP ，OC ，OB ，设OB 交AC 于H ，连接GH .AD BC ∵∥，12AB BC CD AD ===， ∴四边形ABCO 与四边形OBCD 均为菱形. OB AC ∴⊥，OB CD P .CD AC ∴⊥. PAD QV 等边三角形，O 为AD 中点， PO AD ∴⊥.…………………3分Q 平面PAD ⊥平面ABCD 且平面PAD I 平面ABCD AD =，PO ⊂平面PAD 且PO AD ⊥， PO ∴⊥平面ABCD .CD ⊂Q 平面ABCD ，PO CD ∴⊥.H Q ，G 分别为OB ，PB 的中点，GH PO ∴∥. GH CD ∴⊥.…………………7分又GH AC H Q ⋂=，CD \^平面GAC .…………………8分（Ⅱ）2D GAC G ADC G ADC P ABC P ABC G ABC V V V V V V ------==1:122ADC ABC S ADS BC===△△.…………………12分 20.（本小题满分12分）解：（Ⅰ）()()21exx a x a f x -++'=()()1e x x x a --=，…………………2分 由()0f x '=得1x =或x a =.当1a =时，()0f x '≥，函数()f x 在(),-∞+∞内单调递增. …………………3分当1a <时，函数()f x 在(),a -∞，()1,+∞内单调递增，在(),1a 内单调递减.…………4分 当1a >时，函数()f x 在(),1-∞，(),a +∞内单调递增，在()1,a 内单调递减. …………5分（Ⅱ）证明：要证[)0,x ∀∈+∞，()1f x ≥-，即证[)0,x ∈+∞，()min 1f x ≥-. ①由（Ⅰ）可知，当1a >，[)0,x ∈+∞时，()()(){}min min 0,f x f f a =.(0)1f =-，()1eaa f a --=. 设()1e a a g a --=，1a >，则()0e aag a '=>， ()g a ∴在()1,+∞单调递增，故()()211e g a g >=->-，即()1f a >-.∴()min =1f x -.…………………8分②当1a =时，函数()f x 在[)0,+∞单调递增，()()min 01f x f ==-.…………………9分③当3e 1a -≤<时，由（1）可知，[)0x ∈+∞，时，()()(){}min min 0,1f x f f =. 又()01f =-Q ，()()3e 3311e ea f ---=≥=-， ()min 1f x ∴=-.综上，当3e a ≥-时，对[)0,x ∀∈+∞，()1f x ≥-.…………………12分21.（本小题满分12分）解：（Ⅰ）由题意得2221,,3.b ca abc =⎧⎪⎪=⎨⎪=+⎪⎩…………………………………………3分解得23a =． 所以椭圆C 的方程为2213x y +=． …………………………………………4分（Ⅱ）设直线l 的方程为y x m =+，(3,)P P y ,由2213x y y x m ⎧+=⎪⎨⎪=+⎩，得2246330x mx m ++-=. …………………………6分 令223648480m m ∆=-+>，得22m -<<．1232x x m +=-，2123(1)4x x m =-． ……………………………………7分因为PMN ∆是以PMN ∠为顶角的等腰直角三角形，所以NP 平行于x 轴． ………………………………8分 过M 做NP 的垂线，则垂足Q 为线段NP 的中点．设点Q 的坐标为(),Q Q x y ，则2132Q M x x x x +===． 由方程组1221221323(1)432x x m x x m x x ⎧+=-⎪⎪⎪=-⎨⎪+⎪=⎪⎩，，，解得2210m m ++=，即1m =-．而()122m =-∈-，， 所以直线l 的方程为1y x =-． …………………………………………12分22.（本小题满分10分）解：（Ⅰ）4,2π⎛⎫⎪⎝⎭…………………………3分（Ⅱ）4sin ρθ=………………………7分233ππθ⎛⎫<< ⎪⎝⎭……………………10分。