2020年中考数学一轮复习基础考点及题型专题21平行四边形(含解析)

专题21 以平行四边形为背景的证明与计算考点分析【例1】（2019·重庆中考真题)在ABCD 中，BE 平分ABC ∠交AD 于点E ．（1）如图1,若30D ︒∠=,AB 6=求ABE ∆的面积；(2)如图2，过点A 作AF DC ⊥，交DC 的延长线于点F ，分别交BE ，BC 于点G ，H ，且 AB AF =．求证：ED AG FC -=．【答案】（1）32；(2）证明见解析.【解析】(1）解：作BO AD ⊥于O ，如图1所示：∵四边形ABCD 是平行四边形，∴AD BC ∥，AB CD ∥，AB CD =,30ABC D ︒∠=∠=，∴AEB CBE ∠=∠,30BAO D ︒∠=∠=， ∴1622BQ AB ==， ∵BE 平分ABC ∠，∴ABE CBE ∠=∠，∴ABE AEB ∠=∠， ∴6AE AB ==∴ABE ∆的面积11636222AE BO =⨯=⨯=; （2）证明：作AQ BE ⊥交DF 的延长线于P ，垂足为Q ，连接PB 、PE ，如图2所示:∵AB AE =，AQ BE ⊥，∴ABE AEB ∠=∠，BQ EQ =,∴PB PE =,∴PBE PEB ∠=∠，∴ABP AEP ∠=∠，∵AB CD ∥,AF CD ⊥,∴AF AB ⊥,∴90BAF ︒∠=，∵AQ BE ⊥,∴ABG FAP ∠=∠，在ABG ∆和FAP ∆中，90ABG FAP AB AF BAG AFP ︒∠=∠⎧⎪=⎨⎪∠=∠=⎩，∴(ASA)ABG AFP ∆≅∆，∴AG FP =，∵AB CD ∥，AD BC ∥,∴180ABP BPC ︒∠+∠=，BCP D ∠=∠,∵180AEP PED ︒∠+∠=，∴BPC PED ∠=∠，在BPC ∆和PED ∆中，BCP D BPC PED PB PE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴(AAS)BPC PED ∆≅∆，∴PC ED =，∴---===．ED AG PC AG PC FP FC【点睛】本题考查了平行四边形的性质、全等三角形的判定与性质、等腰三角形的判定与性质、直角三角形的性质、线段垂直平分线的性质等知识；熟练掌握平行四边形的性质，证明三角形全等是解题的关键．【例2】（2019·山东初二期末）在正方形ABCD中,E是边CD上一点（点E不与点C、D 重合)，连结BE．（感知）如图①，过点A作AF⊥BE交BC于点F．易证△ABF≌△BCE．（不需要证明）(探究）如图②，取BE的中点M，过点M作FG⊥BE交BC于点F，交AD于点G．（1）求证：BE=FG．（2）连结CM，若CM=1,则FG的长为．（应用）如图③，取BE 的中点M ，连结CM ．过点C 作CG ⊥BE 交AD 于点G ，连结EG 、MG ．若CM=3，则四边形GMCE的面积为 ．【答案】（1）证明见解析；（2）2,9.【解析】感知：∵四边形ABCD 是正方形,∴AB=BC ，∠BCE=∠ABC=90°，∴∠ABE+∠CBE=90°，∵AF ⊥BE ，∴∠ABE+∠BAF=90°，∴∠BAF=∠CBE,在△ABF 和△BCE 中，90BAF CBE AB BCABC BCE ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩， ∴△ABF ≌△BCE （ASA ）；探究：(1）如图②，过点G 作GP ⊥BC 于P ，∵四边形ABCD 是正方形,∴AB=BC ，∠A=∠ABC=90°，∴四边形ABPG 是矩形，∴PG=AB ，∴PG=BC,同感知的方法得,∠PGF=∠CBE,在△PGF 和△CBE 中，90PQF CBE PQ BCPFG ECB ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩, ∴△PGF ≌△CBE （ASA ），∴BE=FG ；（2)由(1）知,FG=BE ，连接CM,∵∠BCE=90°，点M 是BE 的中点，∴BE=2CM=2，∴FG=2，故答案为：2．应用：同探究（2）得，BE=2ME=2CM=6，∴ME=3，同探究（1)得，CG=BE=6，∵BE ⊥CG ，∴S 四边形CEGM =12CG×ME=12×6×3=9， 故答案为:9．【点睛】本题是四边形综合题，主要考查了正方形的性质，同角的余角相等,全等三角形的判定和性质，直角三角形的性质,熟练掌握相关的性质与定理、判断出CG=BE 是解本题的关键．考点集训1．（2019·四川初三期末）在矩形ABCD 中，AB=12,P 是边AB 上一点,把△PBC 沿直线PC 折叠，顶点B 的对应点是点G ，过点B 作BE ⊥CG ，垂足为E 且在AD 上,BE 交PC 于点F ．（1)如图1，若点E 是AD 的中点，求证：△AEB ≌△DEC ；(2)如图2，①求证：BP=BF ；②当AD=25，且AE ＜DE 时，求cos ∠PCB 的值；③当BP=9时，求BE •EF 的值．【答案】（1）证明见解析；（2310；③108。

2020-2021精选中考数学易错题专题复习平行四边形附答案解析一、平行四边形1．如图，将矩形纸片ABCD沿对角线AC折叠，使点B落到到B′的位置，AB′与CD交于点E.（1）求证：△AED≌△CEB′（2）若AB = 8，DE = 3，点P为线段AC上任意一点，PG⊥AE于G，PH⊥BC于H.求PG + PH的值.【答案】（1）证明见解析；（2）.【解析】【分析】（1）由折叠的性质知，，，，则由得到；（2）由，可得，又由，即可求得的长，然后在中，利用勾股定理即可求得的长，再过点作于，由角平分线的性质，可得，易证得四边形是矩形，继而可求得答案.【详解】（1）四边形为矩形，，，又，；（2），，，，在中，，过点作于，，，，，，，、、共线，，四边形是矩形，，.【点睛】此题考查了折叠的性质、矩形的性质、角平分线的性质、等腰三角形的判定与性质以及勾股定理等知识.此题难度较大，注意掌握折叠前后图形的对应关系，注意掌握辅助线的作法，注意数形结合思想的应用.2．如图，△ABC是等边三角形，AB=6cm，D为边AB中点．动点P、Q在边AB上同时从点D出发，点P沿D→A以1cm/s的速度向终点A运动．点Q沿D→B→D以2cm/s的速度运动，回到点D停止．以PQ为边在AB上方作等边三角形PQN．将△PQN绕QN的中点旋转180°得到△MNQ．设四边形PQMN与△ABC重叠部分图形的面积为S（cm2），点P运动的时间为t（s）（0＜t＜3）．（1）当点N落在边BC上时，求t的值．（2）当点N到点A、B的距离相等时，求t的值．（3）当点Q沿D→B运动时，求S与t之间的函数表达式．（4）设四边形PQMN的边MN、MQ与边BC的交点分别是E、F，直接写出四边形PEMF 与四边形PQMN的面积比为2：3时t的值．【答案】（1）（2）2（3）S=S菱形PQMN=2S△PNQ=t2；（4）t=1或【解析】试题分析：（1）由题意知：当点N落在边BC上时，点Q与点B重合，此时DQ=3；（2）当点N到点A、B的距离相等时，点N在边AB的中线上，此时PD=DQ；（3）当0≤t≤时，四边形PQMN与△ABC重叠部分图形为四边形PQMN；当≤t≤时，四边形PQMN与△ABC重叠部分图形为五边形PQFEN．（4）MN、MQ与边BC的有交点时，此时＜t＜，列出四边形PEMF与四边形PQMN的面积表达式后，即可求出t的值．试题解析：（1）∵△PQN与△ABC都是等边三角形，∴当点N落在边BC上时，点Q与点B重合．∴DQ=3∴2t=3．∴t=；（2）∵当点N到点A、B的距离相等时，点N在边AB的中线上，∴PD=DQ，当0＜t＜时，此时，PD=t，DQ=2t∴t=2t∴t=0（不合题意，舍去），当≤t＜3时，此时，PD=t，DQ=6﹣2t∴t=6﹣2t，解得t=2；综上所述，当点N到点A、B的距离相等时，t=2；（3）由题意知：此时，PD=t，DQ=2t当点M在BC边上时，∴MN=BQ∵PQ=MN=3t，BQ=3﹣2t∴3t=3﹣2t∴解得t=如图①，当0≤t≤时，S△PNQ=PQ2=t2；∴S=S菱形PQMN=2S△PNQ=t2，如图②，当≤t≤时，设MN、MQ与边BC的交点分别是E、F，∵MN=PQ=3t，NE=BQ=3﹣2t，∴ME=MN﹣NE=PQ﹣BQ=5t﹣3，∵△EMF是等边三角形，∴S△EMF=ME2=（5t﹣3）2．；（4）MN、MQ与边BC的交点分别是E、F，此时＜t＜，t=1或．考点：几何变换综合题3．如图，矩形ABCD中，AB=6，BC=4，过对角线BD中点O的直线分别交AB，CD边于点E，F．（1）求证：四边形BEDF是平行四边形；（2）当四边形BEDF是菱形时，求EF的长．413【答案】（1）证明见解析；（2【解析】分析：（1）根据平行四边形ABCD的性质，判定△BOE≌△DOF（ASA），得出四边形BEDF的对角线互相平分，进而得出结论；（2）在Rt△ADE中，由勾股定理得出方程，解方程求出BE，由勾股定理求出BD，得出OB，再由勾股定理求出EO，即可得出EF的长.详解：（1）证明：∵四边形ABCD是矩形，O是BD的中点，∴∠A=90°，AD=BC=4，AB∥DC，OB=OD，∴∠OBE=∠ODF，在△BOE和△DOF中，OBE ODF OB ODBOE DOF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BOE ≌△DOF （ASA ），∴EO=FO ，∴四边形BEDF 是平行四边形；（2）当四边形BEDF 是菱形时，BD ⊥EF ，设BE=x ，则 DE=x ，AE=6-x ，在Rt △ADE 中，DE 2=AD 2+AE 2，∴x 2=42+（6-x ）2，解得：x= 133， ∵BD=22AD AB + =213， ∴OB=12BD=13， ∵BD ⊥EF ，∴EO=22BE OB -=213， ∴EF=2EO=413． 点睛：本题主要考查了矩形的性质，菱形的性质、勾股定理、全等三角形的判定与性质，熟练掌握矩形的性质和勾股定理，证明三角形全等是解决问的关键4．如图，四边形ABCD 中，AD ∥BC ，∠A=90°，BD=BC ，点E 为CD 的中点，射线BE 交AD 的延长线于点F ，连接CF ．（1）求证：四边形BCFD 是菱形；（2）若AD=1，BC=2，求BF 的长．【答案】（1）证明见解析（2）3【解析】（1）∵AF ∥BC ，∴∠DCB =∠CDF ，∠FBC =∠BFD ，∵点E 为CD 的中点，∴DE =EC ，在△BCE与△FDE中，FBC BFDDCB CDFDE EC∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△BCE≌△FDE，∴DF=BC，又∵DF∥BC，∴四边形BCDF为平行四边形，∵BD=BC，∴四边形BCFD是菱形；（2）∵四边形BCFD是菱形，∴BD=DF=BC=2，在Rt△BAD中，AB=223BD AD-=，∵AF=AD+DF=1+2=3，在Rt△BAF中，BF=22AB AF+=23．5．如图，在菱形ABCD中，AB=4，∠BAD=120°，△AEF为正三角形，E、F在菱形的边BC，CD上．（1）证明：BE=CF．（2）当点E，F分别在边BC，CD上移动时（△AEF保持为正三角形），请探究四边形AECF的面积是否发生变化？若不变，求出这个定值；如果变化，求出其最大值．（3）在（2）的情况下，请探究△CEF的面积是否发生变化？若不变，求出这个定值；如果变化，求出其最大值．【答案】(1)见解析；（2）33）见解析【解析】试题分析：（1）先求证AB=AC，进而求证△ABC、△ACD为等边三角形，得∠4=60°，AC=AB进而求证△ABE≌△ACF，即可求得BE=CF；（2）根据△ABE≌△ACF可得S△ABE=S△ACF，故根据S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC即可解题；（3）当正三角形AEF的边AE与BC垂直时，边AE最短．△AEF的面积会随着AE的变化而变化，且当AE最短时，正三角形AEF的面积会最小，又根据S△CEF=S四边形AECF-S△AEF，则△CEF的面积就会最大.试题解析：（1）证明：连接AC，∵∠1+∠2=60°，∠3+∠2=60°，∴∠1=∠3，∵∠BAD=120°，∴∠ABC=∠ADC=60°∵四边形ABCD是菱形，∴AB=BC=CD=AD，∴△ABC、△ACD为等边三角形∴∠4=60°，AC=AB，∴在△ABE和△ACF中，，∴△ABE≌△ACF．（ASA）∴BE=CF．（2）解：由（1）得△ABE≌△ACF，则S△ABE=S△ACF．故S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC，是定值．作AH⊥BC于H点，则BH=2，S四边形AECF=S△ABC===；（3）解：由“垂线段最短”可知，当正三角形AEF的边AE与BC垂直时，边AE最短．故△AEF的面积会随着AE的变化而变化，且当AE最短时，正三角形AEF的面积会最小，又S△CEF=S四边形AECF﹣S△AEF，则△CEF的面积就会最大．由（2）得，S△CEF=S四边形AECF﹣S△AEF=﹣=．点睛：本题考查了菱形每一条对角线平分一组对角的性质，考查了全等三角形的证明和全等三角形对应边相等的性质，考查了三角形面积的计算，本题中求证△ABE≌△ACF是解题的关键．6．如图①，四边形ABCD 是知形，1,2AB BC ==，点E 是线段BC 上一动点(不与,B C 重合)，点F 是线段BA 延长线上一动点，连接,,,DE EF DF EF 交AD 于点G .设,BE x AF y ==，已知y 与x 之间的函数关系如图②所示.（1）求图②中y 与x 的函数表达式;（2）求证:DE DF ⊥;（3）是否存在x 的值，使得DEG △是等腰三角形?如果存在，求出x 的值;如果不存在，说明理由【答案】（1）y ＝﹣2x +4（0＜x ＜2）；（2）见解析；（3）存在，x ＝5455-32． 【解析】【分析】（1）利用待定系数法可得y 与x 的函数表达式；（2）证明△CDE ∽△ADF ，得∠ADF ＝∠CDE ，可得结论；（3）分三种情况：①若DE ＝DG ，则∠DGE ＝∠DEG ，②若DE ＝EG ，如图①，作EH ∥CD ，交AD 于H ，③若DG ＝EG ，则∠GDE ＝∠GED ，分别列方程计算可得结论．【详解】（1）设y ＝kx +b ，由图象得：当x ＝1时，y ＝2，当x ＝0时，y ＝4， 代入得：24k b b +=⎧⎨=⎩，得24k b =-⎧⎨=⎩， ∴y ＝﹣2x +4（0＜x ＜2）；（2）∵BE ＝x ，BC ＝2∴CE ＝2﹣x ， ∴211,4222CE x CD AF x AD -===-， ∴CE CD AF AD=，∵四边形ABCD 是矩形，∴∠C ＝∠DAF ＝90°，∴△CDE ∽△ADF ，∴∠ADF ＝∠CDE ，∴∠ADF +∠EDG ＝∠CDE +∠EDG ＝90°，∴DE ⊥DF ；（3）假设存在x 的值，使得△DEG 是等腰三角形，①若DE ＝DG ，则∠DGE ＝∠DEG ，∵四边形ABCD 是矩形，∴AD ∥BC ，∠B ＝90°，∴∠DGE ＝∠GEB ，∴∠DEG ＝∠BEG ，在△DEF 和△BEF 中，FDE B DEF BEF EF EF ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△DEF ≌△BEF （AAS ），∴DE ＝BE ＝x ，CE ＝2﹣x ，∴在Rt △CDE 中，由勾股定理得：1+（2﹣x ）2＝x 2，x ＝54； ②若DE ＝EG ，如图①，作EH ∥CD ，交AD 于H ，∵AD ∥BC ，EH ∥CD ，∴四边形CDHE 是平行四边形，∴∠C ＝90°，∴四边形CDHE 是矩形，∴EH ＝CD ＝1，DH ＝CE ＝2﹣x ，EH ⊥DG ，∴HG ＝DH ＝2﹣x ，∴AG ＝2x ﹣2，∵EH ∥CD ，DC ∥AB ，∴EH ∥AF ，∴△EHG ∽△FAG ，∴EH HG AF AG =， ∴124222x x x -=--，∴12x x ==（舍）， ③若DG ＝EG ，则∠GDE ＝∠GED ，∵AD ∥BC ，∴∠GDE ＝∠DEC ，∴∠GED ＝∠DEC ，∵∠C ＝∠EDF ＝90°，∴△CDE ∽△DFE ， ∴CE DE CD DF=， ∵△CDE ∽△ADF ， ∴12DE CD DF AD ==， ∴12CE CD =， ∴2﹣x ＝12，x ＝32，综上，x ＝54或2或32． 【点睛】 本题是四边形的综合题，主要考查了待定系数法求一次函数的解析式，三角形相似和全等的性质和判定，矩形和平行四边形的性质和判定，勾股定理和逆定理等知识，运用相似三角形的性质是解决本题的关键．7．如图1，在△ABC 中，AB ＝AC ，AD ⊥BC 于D ，分别延长AC 至E ，BC 至F ，且CE ＝EF ，延长FE 交AD 的延长线于G ．（1）求证：AE ＝EG ；（2）如图2，分别连接BG ，BE ，若BG ＝BF ，求证：BE ＝EG ；（3）如图3，取GF 的中点M ，若AB ＝5，求EM 的长．【答案】（1）证明见解析（2）证明见解析（3）5 2【解析】【分析】（1）根据平行线的性质和等腰三角形的三线合一的性质得：∠CAD＝∠G，可得AE＝EG；（2）作辅助线，证明△BEF≌△GEC（SAS），可得结论；（3）如图3，作辅助线，构建平行线，证明四边形DMEN是平行四边形，得EM＝DN＝12AC，计算可得结论．【详解】证明：（1）如图1，过E作EH⊥CF于H，∵AD⊥BC，∴EH∥AD，∴∠CEH＝∠CAD，∠HEF＝∠G，∵CE＝EF，∴∠CEH＝∠HEF，∴∠CAD＝∠G，∴AE＝EG；（2）如图2，连接GC，∵AC ＝BC ，AD ⊥BC ，∴BD ＝CD ，∴AG 是BC 的垂直平分线，∴GC ＝GB ，∴∠GBF ＝∠BCG ，∵BG ＝BF ，∴GC ＝BE ，∵CE ＝EF ，∴∠CEF ＝180°﹣2∠F ，∵BG ＝BF ，∴∠GBF ＝180°﹣2∠F ，∴∠GBF ＝∠CEF ，∴∠CEF ＝∠BCG ，∵∠BCE ＝∠CEF+∠F ，∠BCE ＝∠BCG+∠GCE ，∴∠GCE ＝∠F ，在△BEF 和△GCE 中，CE GCE F CG BF EF =⎧⎪∠=∠⎨⎪=⎩Q ， ∴△BEF ≌△GEC （SAS ），∴BE ＝EG ；（3）如图3，连接DM ，取AC 的中点N ，连接DN ，由（1）得AE＝EG，∴∠GAE＝∠AGE，在Rt△ACD中，N为AC的中点，∴DN＝12AC＝AN，∠DAN＝∠ADN，∴∠ADN＝∠AGE，∴DN∥GF，在Rt△GDF中，M是FG的中点，∴DM＝12FG＝GM，∠GDM＝∠AGE，∴∠GDM＝∠DAN，∴DM∥AE，∴四边形DMEN是平行四边形，∴EM＝DN＝12AC，∵AC＝AB＝5，∴EM＝52．【点睛】本题是三角形的综合题，主要考查了全等三角形的判定与性质，直角三角形斜边中线的性质，等腰三角形的性质和判定，平行四边形的性质和判定等知识，解题的关键是作辅助线，并熟练掌握全等三角形的判定方法，特别是第三问，辅助线的作法是关键．8．菱形ABCD中、∠BAD＝120°，点O为射线CA上的动点，作射线OM与直线BC相交于点E，将射线OM绕点O逆时针旋转60°，得到射线ON，射线ON与直线CD相交于点F．（1）如图①，点O与点A重合时，点E，F分别在线段BC，CD上，请直接写出CE，CF，CA三条段段之间的数量关系；（2）如图②，点O在CA的延长线上，且OA＝13AC，E，F分别在线段BC的延长线和线段CD的延长线上，请写出CE，CF，CA三条线段之间的数量关系，并说明理由；（3）点O在线段AC上，若AB＝6，BO＝27，当CF＝1时，请直接写出BE的长．【答案】（1）CA=CE+CF．（2）CF-CE=43AC．（3）BE的值为3或5或1．【解析】【分析】（1）如图①中，结论：CA=CE+CF．只要证明△ADF≌△ACE（SAS）即可解决问题；（2）结论：CF-CE=43AC．如图②中，如图作OG∥AD交CF于G，则△OGC是等边三角形．只要证明△FOG≌△EOC（ASA）即可解决问题；（3）分四种情形画出图形分别求解即可解决问题.【详解】（1）如图①中，结论：CA=CE+CF．理由：∵四边形ABCD是菱形，∠BAD=120°∴AB=AD=DC=BC，∠BAC=∠DAC=60°∴△ABC，△ACD都是等边三角形，∵∠DAC=∠EAF=60°，∴∠DAF=∠CAE，∵CA=AD，∠D=∠ACE=60°，∴△ADF≌△ACE（SAS），∴DF=CE，∴CE+CF=CF+DF=CD=AC，∴CA=CE+CF．（2）结论：CF-CE=43 AC．理由：如图②中，如图作OG∥AD交CF于G，则△OGC是等边三角形．∵∠GOC=∠FOE=60°，∴∠FOG=∠EOC，∵OG=OC，∠OGF=∠ACE=120°，∴△FOG≌△EOC（ASA），∴CE=FG，∵OC=OG，CA=CD，∴OA=DG，∴CF-EC=CF-FG=CG=CD+DG=AC+13AC=43AC，（3）作BH⊥AC于H．∵AB=6，AH=CH=3，∴BH=33，如图③-1中，当点O在线段AH上，点F在线段CD上，点E在线段BC上时．∵7，∴22OB BH=1，∴OC=3+1=4，由（1）可知：CO=CE+CF，∵OC=4，CF=1，∴CE=3，∴BE=6-3=3．如图③-2中，当点O在线段AH上，点F在线段DC的延长线上，点E在线段BC上时．由（2）可知：CE-CF=OC，∴CE=4+1=5，∴BE=1．如图③-3中，当点O在线段CH上，点F在线段CD上，点E在线段BC上时．同法可证：OC=CE+CF，∵OC=CH-OH=3-1=2，CF=1，∴CE=1，∴BE=6-1=5．如图③-4中，当点O在线段CH上，点F在线段DC的延长线上，点E在线段BC上时．同法可知：CE-CF=OC，∴CE=2+1=3，∴BE=3，综上所述，满足条件的BE的值为3或5或1．【点睛】本题属于四边形综合题，考查了全等三角形的判定和性质，等边三角形的性质，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会用分类讨论的思想思考问题，属于中考压轴题．9．如图，AB 为⊙O 的直径，点E 在⊙O 上，过点E 的切线与AB 的延长线交于点D ，连接BE ，过点O 作BE 的平行线，交⊙O 于点F ，交切线于点C ，连接AC（1）求证：AC 是⊙O 的切线；（2）连接EF ，当∠D= °时，四边形FOBE 是菱形．【答案】（1）见解析；（2）30.【解析】【分析】（1）由等角的转换证明出OCA OCE ∆∆≌，根据圆的位置关系证得AC 是⊙O 的切线. （2）根据四边形FOBE 是菱形，得到OF=OB=BF=EF ，得证OBE ∆为等边三角形，而得出60BOE ∠=︒，根据三角形内角和即可求出答案.【详解】（1）证明：∵CD 与⊙O 相切于点E ，∴OE CD ⊥，∴90CEO ∠=︒，又∵OC BE P ，∴COE OEB ∠=∠，∠OBE=∠COA∵OE=OB ，∴OEB OBE ∠=∠，∴COE COA ∠=∠，又∵OC=OC ，OA=OE ，∴OCA OCE SAS ∆∆≌（）， ∴90CAO CEO ∠=∠=︒，又∵AB 为⊙O 的直径，∴AC 为⊙O 的切线；（2）解：∵四边形FOBE 是菱形，∴OF=OB=BF=EF ，∴OE=OB=BE ，∴OBE ∆为等边三角形，∴60BOE ∠=︒，而OE CD ⊥，∴30D ∠=︒．故答案为30．【点睛】本题主要考查与圆有关的位置关系和圆中的计算问题，熟练掌握圆的性质是本题的解题关键.10．如图1，矩形ABCD 中，AB=8，AD=6；点E 是对角线BD 上一动点，连接CE ，作EF ⊥CE 交AB 边于点F ，以CE 和EF 为邻边作矩形CEFG ，作其对角线相交于点H ． （1）①如图2，当点F 与点B 重合时，CE= ，CG= ；②如图3，当点E 是BD 中点时，CE= ，CG= ；（2）在图1，连接BG ，当矩形CEFG 随着点E 的运动而变化时，猜想△EBG 的形状？并加以证明； （3）在图1，CG CE的值是否会发生改变？若不变，求出它的值；若改变，说明理由； （4）在图1，设DE 的长为x ，矩形CEFG 的面积为S ，试求S 关于x 的函数关系式，并直接写出x 的取值范围．【答案】（1）245，185，5，154 ；（2）△EBG 是直角三角形，理由详见解析；（3）34 ；（4）S=34x 2﹣485x+48（0≤x≤325）． 【解析】【分析】（1）①利用面积法求出CE ，再利用勾股定理求出EF 即可；②利用直角三角形斜边中线定理求出CE ，再利用相似三角形的性质求出EF 即可；（2）根据直角三角形的判定方法：如果一个三角形一边上的中线等于这条边的一半，则这个三角形是直角三角形即可判断；（3）只要证明△DCE ∽△BCG ，即可解决问题；（4）利用相似多边形的性质构建函数关系式即可；【详解】（1）①如图2中，在Rt△BAD中，BD=22AD AB+=10，∵S△BCD=12•CD•BC=12•BD•CE，∴CE=245．CG=BE=2224186()=55-．②如图3中，过点E作MN⊥AM交AB于N，交CD于M．∵DE=BE，∴CE=12BD=5，∵△CME∽△ENF，∴CM ENCE EF=，∴CG=EF=154，（2）结论：△EBG是直角三角形．理由：如图1中，连接BH．在Rt△BCF中，∵FH=CH，∴BH=FH=CH，∵四边形EFGC是矩形，∴EH=HG=HF=HC，∴BH=EH=HG ，∴△EBG 是直角三角形．（3）F 如图1中，∵HE=HC=HG=HB=HF ，∴C 、E 、F 、B 、G 五点共圆，∵EF=CG ，∴∠CBG=∠EBF ，∵CD ∥AB ，∴∠EBF=∠CDE ，∴∠CBG=∠CDE ，∵∠DCB=∠ECG=90°，∴∠DCE=∠BCG ，∴△DCE ∽△BCG ， ∴6384CG BC CE DC ===． （4）由（3）可知： 34CG CD CE CB ==， ∴矩形CEFG ∽矩形ABCD ， ∴2264CEFG ABCD S CE CE S CD ==矩形矩形（）， ∵CE 2=（325-x ）2+245）2，S 矩形ABCD =48， ∴S 矩形CEFG =34[（325-x ）2+（245）2]. ∴矩形CEFG 的面积S=34x 2-485x+48（0≤x≤325）． 【点睛】 本题考查相似三角形综合题、矩形的性质、相似三角形的判定和性质、勾股定理、直角三角形的判定和性质、相似多边形的性质和判定等知识，解题的关键是灵活运用所学知识解决问题，学会添加常用辅助线，构造相似三角形或直角三角形解决问题，属于中考压轴题．11．如图1所示，（1）在正三角形ABC 中，M 是BC 边（不含端点B 、C ）上任意一点，P 是BC 延长线上一点，N 是∠ACP 的平分线上一点，若∠AMN=60°，求证：AM=MN ． （2）若将（1）中“正三角形ABC”改为“正方形ABCD”，N 是∠DCP 的平分线上一点，若∠AMN=90°，则AM=MN 是否成立？若成立，请证明；若不成立，说明理由． （3）若将（2）中的“正方形AB CD”改为“正n 边形A 1A 2…A n “，其它条件不变，请你猜想：当∠A n ﹣2MN=_____°时，结论A n ﹣2M=MN 仍然成立．（不要求证明）【答案】0 (2)180 nn【解析】分析：（1）要证明AM=MN，可证AM与MN所在的三角形全等，为此，可在AB上取一点E，使AE=CM，连接ME，利用ASA即可证明△AEM≌△MCN，然后根据全等三角形的对应边成比例得出AM=MN．（2）同（1），要证明AM=MN，可证AM与MN所在的三角形全等，为此，可在AB上取一点E，使AE=CM，连接ME，利用ASA即可证明△AEM≌△MCN，然后根据全等三角形的对应边成比例得出AM=MN．详（1）证明：在边AB上截取AE=MC，连接ME．在正△ABC中，∠B=∠BCA=60°，AB=BC．∴∠NMC=180°-∠AMN-∠AMB=180°-∠B-∠AMB=∠MAE，BE=AB-AE=BC-MC=BM，∴∠BEM=60°，∴∠AEM=120°．∵N是∠ACP的平分线上一点，∴∠ACN=60°，∴∠MCN=120°．在△AEM与△MCN中，∠MAE=∠NMC，AE=MC，∠AEM=∠MCN，∴△AEM≌△MCN（ASA），∴AM=MN．（2）解：结论成立；理由：在边AB上截取AE=MC，连接ME．∵正方形ABCD中，∠B=∠BCD=90°，AB=BC．∴∠NMC=180°-∠AMN-∠AMB=180°-∠B-∠AMB=∠MAB=∠MAE ，BE=AB-AE=BC-MC=BM ，∴∠BEM=45°，∴∠AEM=135°．∵N 是∠DCP 的平分线上一点，∴∠NCP=45°，∴∠MCN=135°．在△AEM 与△MCN 中，∠MAE=∠NMC ，AE=MC ，∠AEM=∠MCN ，∴△AEM ≌△MCN （ASA ），∴AM=MN ．（3）由（1）（2）可知当∠A n-2MN 等于n 边形的内角时，结论A n-2M=MN 仍然成立；即∠A n-2MN=()02180n n-时，结论A n-2M=MN 仍然成立； 故答案为[()02180n n-]． 点睛：本题综合考查了正方形、等边三角形的性质及全等三角形的判定，同时考查了学生的归纳能力及分析、解决问题的能力．难度较大．12．如图，在平面直角坐标系xOy 中，四边形OABC 的顶点A 在x 轴的正半轴上，OA=4，OC=2，点D 、E 、F 、G 分别为边OA 、AB 、BC 、CO 的中点，连结DE 、EF 、FG 、GD ．（1）若点C 在y 轴的正半轴上，当点B 的坐标为（2，4）时，判断四边形DEFG 的形状，并说明理由.（2）若点C 在第二象限运动，且四边形DEFG 为菱形时，求点四边形OABC 对角线OB 长度的取值范围.（3）若在点C 的运动过程中，四边形DEFG 始终为正方形，当点C 从X 轴负半轴经过Y 轴正半轴，运动至X 轴正半轴时，直接写出点B 的运动路径长.【答案】（1）正方形（2）256OB <<（3）2π【解析】分析:（1）连接OB ，AC ，说明OB ⊥AC ，OB=AC ，可得四边形DEFG 是正方形.（2）由四边形DEFG 是菱形，可得OB=AC ，当点C 在y 轴上时，AC=25C 在x 轴上时，AC=6, 故可得结论；（3）根据题意计算弧长即可.详解：（1）正方形，如图1，证明连接OB ，AC ，说明OB ⊥AC ，OB=AC ，可得四边形DEFG 是正方形.（2）256OB <<如图2，由四边形DEFG 是菱形，可得OB=AC ，当点C 在y 轴上时，AC=25，当点C 在x 轴上时，AC=6, ∴256OB << ；（3）2π.如图3，当四边形DEFG 是正方形时，OB ⊥AC ，且OB=AC ，构造△OBE ≌△ACO ，可得B 点在以E （0，4）为圆心，2为半径的圆上运动.所以当C 点从x 轴负半轴到正半轴运动时，B 点的运动路径为2π .图1 图2 图3点睛：本题主要考查了正方形的判定，菱形的性质以及弧长的计算.灵活运用正方形的判定定理和菱形的性质运用是解题的关键.13．如图，P 是边长为1的正方形ABCD 对角线BD 上一动点（P 与B 、D 不重合），∠APE=90°，且点E 在BC 边上，AE 交BD 于点F ．（1）求证：①△PAB ≌△PCB ；②PE=PC ；（2）在点P 的运动过程中，的值是否改变？若不变，求出它的值；若改变，请说明理由；（3）设DP=x ，当x 为何值时，AE ∥PC ，并判断此时四边形PAFC 的形状．【答案】（1）见解析；（2）； （3）x=﹣1；四边形PAFC 是菱形．【解析】试题分析：（1）根据四边形ABCD 是正方形，得出AB=BC ，∠ABP=∠CBP°，再根据PB=PB ，即可证出△PAB ≌△PCB ，②根据∠PAB+∠PEB=180°，∠PEC+∠PEB=180°，得出∠PEC=∠PCB ，从而证出PE=PC ；（2）根据PA=PC ，PE=PC ，得出PA=PE ，再根据∠APE=90°，得出∠PAE=∠PEA=45°，即可求出；（3）先求出∠CPE=∠PEA=45°，从而得出∠PCE，再求出∠BPC即可得出∠BPC=∠PCE，从而证出BP=BC=1，x=﹣1，再根据AE∥PC，得出∠AFP=∠BPC=67.5°，由△PAB≌△PCB 得出∠BPA=∠BPC=67.5°，PA=PC，从而证出AF=AP=PC，得出答案．试题解析：（1）①∵四边形ABCD是正方形，∴AB=BC，∠ABP=∠CBP=∠ABC=45°．∵PB=PB，∴△PAB≌△PCB （SAS）．②由△PAB≌△PCB可知，∠PAB=∠PCB．∵∠ABE=∠APE=90°，∴∠PAB+∠PEB=180°，又∵∠PEC+∠PEB=180°，∴∠PEC=∠PAB=∠PCB，∴PE=PC．（2）在点P的运动过程中，的值不改变．由△PAB≌△PCB可知，PA=PC．∵PE=PC，∴PA=PE，又∵∠APE=90°，∴△PAE是等腰直角三角形，∠PAE=∠PEA=45°，∴=．（3）∵AE∥PC，∴∠CPE=∠PEA=45°，∴在△PEC中，∠PCE=∠PEC=（180°﹣45°）=67.5°．在△PBC中，∠BPC=（180°﹣∠CBP﹣∠PCE）=（180°﹣45°﹣67.5°）=67.5°．∴∠BPC=∠PCE=67.5°，∴BP=BC=1，∴x=BD﹣BP=﹣1．∵AE∥PC，∴∠AFP=∠BPC=67.5°，由△PAB≌△PCB可知，∠BPA=∠BPC=67.5°，PA=PC，∴∠AFP=∠BPA，∴AF=AP=PC，∴四边形PAFC是菱形．考点：四边形综合题．14．在正方形ABCD中，动点E，F分别从D，C两点同时出发，以相同的速度在直线DC，CB上移动．（1）如图①，当点E自D向C，点F自C向B移动时，连接AE和DF交于点P，请你写出AE与DF的位置关系，并说明理由；（2）如图②，当E，F分别移动到边DC，CB的延长线上时，连接AE和DF，（1）中的结论还成立吗？（请你直接回答“是”或“否”，不须证明）（3）如图③，当E，F分别在边CD，BC的延长线上移动时，连接AE，DF，（1）中的结论还成立吗？请说明理由；（4）如图④，当E，F分别在边DC，CB上移动时，连接AE和DF交于点P，由于点E，F 的移动，使得点P也随之运动，请你画出点P运动路径的草图．若AD=2，试求出线段CP 的最小值．【答案】（1）AE=DF，AE⊥DF；（2）是；（3）成立，理由见解析；（4）CP=QC﹣QP=．【解析】试题分析：（1）AE=DF，AE⊥DF．先证得△ADE≌△DCF．由全等三角形的性质得AE=DF，∠DAE=∠CDF，再由等角的余角相等可得AE⊥DF；（2）是．四边形ABCD是正方形，所以AD=DC，∠ADE=∠DCF=90°，DE=CF，所以△ADE≌△DCF，于是AE=DF，∠DAE=∠CDF，因为∠CDF+∠ADF=90°，∠DAE+∠ADF=90°，所以AE⊥DF；（3）成立．由（1）同理可证AE=DF，∠DAE=∠CDF，延长FD交AE于点G，再由等角的余角相等可得AE⊥DF；（4）由于点P在运动中保持∠APD=90°，所以点P的路径是一段以AD为直径的弧，设AD 的中点为Q，连接QC交弧于点P，此时CP的长度最小，再由勾股定理可得QC的长，再求CP即可．试题解析：（1）AE=DF，AE⊥DF．理由：∵四边形ABCD是正方形，∴AD=DC，∠ADC=∠C=90°．在△ADE和△DCF中，，∴△ADE≌△DCF（SAS）．∴AE=DF，∠DAE=∠CDF，由于∠CDF+∠ADF=90°，∴∠DAE+∠ADF=90°．∴AE⊥DF；（2）是；（3）成立．理由：由（1）同理可证AE=DF，∠DAE=∠CDF延长FD交AE于点G，则∠CDF+∠ADG=90°，∴∠ADG+∠DAE=90°．∴AE⊥DF；（4）如图：由于点P在运动中保持∠APD=90°，∴点P的路径是一段以AD为直径的弧，设AD的中点为Q，连接QC交弧于点P，此时CP的长度最小，在Rt△QDC中，QC=，∴CP=QC﹣QP=．考点：四边形的综合知识．15．（本题满分10分）如图1，已知矩形纸片ABCD中，AB＝6cm，若将该纸片沿着过点B的直线折叠（折痕为BM），点A恰好落在CD边的中点P处．（1）求矩形ABCD的边AD的长．（2）若P为CD边上的一个动点，折叠纸片，使得A与P重合，折痕为MN，其中M在边AD上，N在边BC上，如图2所示．设DP＝x cm，DM＝y cm，试求y与x的函数关系式，并指出自变量x的取值范围．（3）①当折痕MN的端点N在AB上时，求当△PCN为等腰三角形时x的值；②当折痕MN的端点M在CD上时，设折叠后重叠部分的面积为S，试求S与x之间的函数关系式【答案】（1）AD＝3；（2）y=－其中，0＜x＜3；（3）x=；（4）S=.【解析】试题分析：（1）根据折叠图形的性质和勾股定理求出AD的长度；（2）根据折叠图形的性质以及Rt△MPD的勾股定理求出函数关系式；（3）过点N作NQ⊥CD，根据Rt△NPQ 的勾股定理进行求解；（4）根据Rt△ADM的勾股定理求出MP与x的函数关系式，然后得出函数关系式.试题解析：（1）根据折叠可得BP=AB=6cm CP=3cm 根据Rt△PBC的勾股定理可得：AD＝3．（2）由折叠可知AM＝MP，在Rt△MPD中，∴∴y=－其中，0＜x＜3.（3）当点N在AB上，x≥3，∴PC≤3，而PN≥3，NC≥3.∴△PCN为等腰三角形，只可能NC＝NP．过N点作NQ⊥CD，垂足为Q，在Rt△NPQ中，∴解得x=．（4）当点M在CD上时，N在AB上，可得四边形ANPM为菱形．设MP＝y，在Rt△ADM中，，即∴ y=．∴ S=考点：函数的性质、勾股定理.。

2020-2021备战中考数学综合题专题复习【平行四边形】专题解析及答案解析一、平行四边形1．如图，平面直角坐标系中，四边形OABC为矩形，点A，B的坐标分别为（4，0），（4，3），动点M，N分别从O，B同时出发．以每秒1个单位的速度运动．其中，点M 沿OA向终点A运动，点N沿BC向终点C运动．过点M作MP⊥OA，交AC于P，连接NP，已知动点运动了x秒．（1）P点的坐标为多少（用含x的代数式表示）；（2）试求△NPC面积S的表达式，并求出面积S的最大值及相应的x值；（3）当x为何值时，△NPC是一个等腰三角形？简要说明理由．【答案】（1）P点坐标为（x，3﹣x）．（2）S的最大值为，此时x=2．（3）x=，或x=，或x=．【解析】试题分析：（1）求P点的坐标，也就是求OM和PM的长，已知了OM的长为x，关键是求出PM的长，方法不唯一，①可通过PM∥OC得出的对应成比例线段来求；②也可延长MP交BC于Q，先在直角三角形CPQ中根据CQ的长和∠ACB的正切值求出PQ的长，然后根据PM=AB﹣PQ来求出PM的长．得出OM和PM的长，即可求出P点的坐标．（2）可按（1）②中的方法经求出PQ的长，而CN的长可根据CN=BC﹣BN来求得，因此根据三角形的面积计算公式即可得出S，x的函数关系式．（3）本题要分类讨论：①当CP=CN时，可在直角三角形CPQ中，用CQ的长即x和∠ABC的余弦值求出CP的表达式，然后联立CN的表达式即可求出x的值；②当CP=PN时，那么CQ=QN，先在直角三角形CPQ中求出CQ的长，然后根据QN=CN﹣CQ求出QN的表达式，根据题设的等量条件即可得出x的值．③当CN=PN时，先求出QP和QN的长，然后在直角三角形PNQ中，用勾股定理求出PN 的长，联立CN的表达式即可求出x的值．试题解析：（1）过点P作PQ⊥BC于点Q，有题意可得：PQ∥AB，∴△CQP∽△CBA，∴∴解得：QP=x，∴PM=3﹣x，由题意可知，C（0，3），M（x，0），N（4﹣x，3），P点坐标为（x，3﹣x）．（2）设△NPC的面积为S，在△NPC中，NC=4﹣x，NC边上的高为，其中，0≤x≤4．∴S=（4﹣x）×x=（﹣x2+4x）=﹣（x﹣2）2+．∴S的最大值为，此时x=2．（3）延长MP交CB于Q，则有PQ⊥BC．①若NP=CP，∵PQ⊥BC，∴NQ=CQ=x．∴3x=4，∴x=．②若CP=CN，则CN=4﹣x，PQ=x，CP=x，4﹣x=x，∴x=；③若CN=NP，则CN=4﹣x．∵PQ=x，NQ=4﹣2x，∵在Rt△PNQ中，PN2=NQ2+PQ2，∴（4﹣x）2=（4﹣2x）2+（x）2，∴x=．综上所述，x=，或x=，或x=．考点：二次函数综合题．2．如图，在正方形ABCD中，E是边BC上的一动点（不与点B、C重合），连接DE、点C 关于直线DE的对称点为C′，连接AC′并延长交直线DE于点P，F是AC′的中点，连接DF．（1）求∠FDP的度数；（2）连接BP，请用等式表示AP、BP、DP三条线段之间的数量关系，并证明；（3）连接AC，若正方形的边长为2，请直接写出△ACC′的面积最大值．【答案】（1）45°；（2）BP+DP2AP，证明详见解析；（32﹣1．【解析】【分析】（1）证明∠CDE＝∠C'DE和∠ADF＝∠C'DF，可得∠FDP'＝12∠ADC＝45°；（2）作辅助线，构建全等三角形，证明△BAP≌△DAP'（SAS），得BP＝DP'，从而得△PAP'是等腰直角三角形，可得结论；（3）先作高线C'G，确定△ACC′的面积中底边AC为定值2，根据高的大小确定面积的大小，当C'在BD上时，C'G最大，其△ACC′的面积最大，并求此时的面积．【详解】（1）由对称得：CD＝C'D，∠CDE＝∠C'DE，在正方形ABCD中，AD＝CD，∠ADC＝90°，∴AD＝C'D，∵F是AC'的中点，∴DF⊥AC'，∠ADF＝∠C'DF，∴∠FDP＝∠FDC'+∠EDC'＝12∠ADC＝45°；（2）结论：BP+DP＝2AP，理由是：如图，作AP'⊥AP交PD的延长线于P'，∴∠PAP'＝90°，在正方形ABCD中，DA＝BA，∠BAD＝90°，∴∠DAP'＝∠BAP，由（1）可知：∠FDP＝45°∵∠DFP＝90°∴∠APD＝45°，∴∠P'＝45°，∴AP＝AP'，在△BAP和△DAP'中，∵BA DABAP DAP AP AP'=⎧⎪∠=∠⎨='⎪⎩，∴△BAP≌△DAP'（SAS），∴BP＝DP'，∴DP+BP＝PP'＝2AP；（3）如图，过C'作C'G⊥AC于G，则S△AC'C＝12AC•C'G，Rt△ABC中，AB＝BC2，∴AC ＝22(2)(2)2+=，即AC 为定值，当C 'G 最大值，△AC 'C 的面积最大，连接BD ，交AC 于O ，当C '在BD 上时，C 'G 最大，此时G 与O 重合，∵CD ＝C 'D ＝2，OD ＝12AC ＝1， ∴C 'G ＝2﹣1，∴S △AC 'C ＝112(21)2122AC C G '•=⨯-=-． 【点睛】本题考查四边形综合题、正方形的性质、等腰直角三角形的判定和性质、全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．3．如图，矩形ABCD 中，AB =6，BC =4，过对角线BD 中点O 的直线分别交AB ，CD 边于点E ，F ．（1）求证：四边形BEDF 是平行四边形；（2）当四边形BEDF 是菱形时，求EF 的长．【答案】（1）证明见解析；（2）133． 【解析】 分析：（1）根据平行四边形ABCD 的性质，判定△BOE ≌△DOF （ASA ），得出四边形BEDF 的对角线互相平分，进而得出结论；（2）在Rt △ADE 中，由勾股定理得出方程，解方程求出BE ，由勾股定理求出BD ，得出OB ，再由勾股定理求出EO ，即可得出EF 的长.详解：（1）证明：∵四边形ABCD 是矩形，O 是BD 的中点，∴∠A=90°，AD=BC=4，AB ∥DC ，OB=OD ，∴∠OBE=∠ODF ，在△BOE 和△DOF 中，OBE ODF OB ODBOE DOF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BOE ≌△DOF （ASA ），∴EO=FO ，∴四边形BEDF 是平行四边形；（2）当四边形BEDF是菱形时，BD⊥EF，设BE=x，则 DE=x，AE=6-x，在Rt△ADE中，DE2=AD2+AE2，∴x2=42+（6-x）2，解得：x= 133，∵BD=22AD AB+ =213，∴OB=12BD=13，∵BD⊥EF，∴EO=22BE OB-=213，∴EF=2EO=4133．点睛：本题主要考查了矩形的性质，菱形的性质、勾股定理、全等三角形的判定与性质，熟练掌握矩形的性质和勾股定理，证明三角形全等是解决问的关键4．如图，四边形ABCD中，对角线AC、BD相交于点O，AO=CO，BO=DO，且∠ABC+∠ADC=180°．（1）求证：四边形ABCD是矩形．（2）若∠ADF：∠FDC=3：2，DF⊥AC，求∠BDF的度数．【答案】(1)见解析；（2）18°.【解析】【分析】（1）根据平行四边形的判定得出四边形ABCD是平行四边形，求出∠ABC=90°，根据矩形的判定得出即可；（2）求出∠FDC的度数，根据三角形内角和定理求出∠DCO，根据矩形的性质得出OD=OC，求出∠CDO，即可求出答案．【详解】（1）证明：∵AO=CO，BO=DO∴四边形ABCD是平行四边形，∴∠ABC=∠ADC，∵∠ABC+∠ADC=180°，∴∠ABC=∠ADC=90°，∴四边形ABCD是矩形；（2）解：∵∠ADC=90°，∠ADF：∠FDC=3：2，∴∠FDC=36°，∵DF⊥AC，∴∠DCO=90°﹣36°=54°，∵四边形ABCD是矩形，∴OC=OD，∴∠ODC=54°∴∠BDF=∠ODC﹣∠FDC=18°．【点睛】本题考查了平行四边形的性质和判定，矩形的性质和判定的应用，能灵活运用定理进行推理是解此题的关键，注意：矩形的对角线相等，有一个角是直角的平行四边形是矩形．5．已知：如图，在平行四边形ABCD中，O为对角线BD的中点，过点O的直线EF分别交AD，BC于E，F两点，连结BE，DF．（1）求证：△DOE≌△BOF．（2）当∠DOE等于多少度时，四边形BFDE为菱形？请说明理由．【答案】（1）证明见解析；（2）当∠DOE=90°时，四边形BFED为菱形，理由见解析.【解析】试题分析：（1）利用平行四边形的性质以及全等三角形的判定方法得出△DOE≌△BOF （ASA）；（2）首先利用一组对边平行且相等的四边形是平行四边形得出四边形EBFD是平行四边形，进而利用垂直平分线的性质得出BE=ED，即可得出答案．试题解析：（1）∵在▱ABCD中，O为对角线BD的中点，∴BO=DO，∠EDB=∠FBO，在△EOD和△FOB中，∴△DOE≌△BOF（ASA）；（2）当∠DOE=90°时，四边形BFDE为菱形，理由：∵△DOE≌△BOF，∴OE=OF，又∵OB=OD，∴四边形EBFD是平行四边形，∵∠EOD=90°，∴EF⊥BD，∴四边形BFDE为菱形．考点：平行四边形的性质；全等三角形的判定与性质；菱形的判定．6．如图，在Rt△ABC中，∠B=90°，AC=60cm，∠A=60°，点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t 秒（0＜t≤15）．过点D作DF⊥BC于点F，连接DE，EF．（1）求证：AE=DF；（2）四边形AEFD能够成为菱形吗？如果能，求出相应的t值，如果不能，说明理由；（3）当t为何值时，△DEF为直角三角形？请说明理由．【答案】（1）见解析；（2）能，t=10；（3）t=152或12.【解析】【分析】（1）利用t表示出CD以及AE的长，然后在直角△CDF中，利用直角三角形的性质求得DF的长，即可证明；（2）易证四边形AEFD是平行四边形，当AD=AE时，四边形AEFD是菱形，据此即可列方程求得t的值；（3）△DEF为直角三角形，分∠EDF=90°和∠DEF=90°两种情况讨论.【详解】解：（1）证明：∵在Rt△ABC中，∠C=90°﹣∠A=30°，∴AB=12AC=12×60=30cm，∵CD=4t，AE=2t，又∵在Rt△CDF中，∠C=30°，∴DF=12CD=2t，∴DF=AE；（2）能，∵DF∥AB，DF=AE，∴四边形AEFD是平行四边形，当AD=AE时，四边形AEFD是菱形，即60﹣4t=2t，解得：t=10，∴当t=10时，AEFD是菱形；（3）若△DEF为直角三角形，有两种情况：①如图1，∠EDF=90°，DE∥BC，则AD=2AE，即60﹣4t=2×2t，解得：t=152，②如图2，∠DEF=90°，DE⊥AC，则AE=2AD，即2t2(604t)=-，解得：t=12，综上所述，当t=152或12时，△DEF为直角三角形.7．如图（1）在正方形ABCD中，点E是CD边上一动点，连接AE，作BF⊥AE，垂足为G 交AD于F（1）求证：AF＝DE；（2）连接DG，若DG平分∠EGF，如图（2），求证：点E是CD中点；（3）在（2）的条件下，连接CG，如图（3），求证：CG＝CD．【答案】（1）见解析；（2）见解析；（3）CG＝CD，见解析．【解析】【分析】（1）证明△BAF≌△ADE（ASA）即可解决问题．（2）过点D作DM⊥GF，DN⊥GE，垂足分别为点M，N．想办法证明AF＝DF，即可解决问题．（3）延长AE，BC交于点P，由（2）知DE＝CD，利用直角三角形斜边中线的性质，只要证明BC＝CP即可．【详解】（1）证明：如图1中，在正方形ABCD中，AB＝AD，∠BAD＝∠D＝90o，∴∠2+∠3＝90°又∵BF⊥AE，∴∠AGB＝90°∴∠1+∠2＝90°，∴∠1＝∠3在△BAF与△ADE中，∠1=∠3 BA=AD ∠BAF=∠D，∴△BAF≌△ADE（ASA）∴AF＝DE．（2）证明：过点D作DM⊥GF，DN⊥GE，垂足分别为点M，N．由（1）得∠1＝∠3，∠BGA＝∠AND＝90°，AB＝AD∴△BAG≌△ADN（AAS）∴AG＝DN，又DG平分∠EGF，DM⊥GF，DN⊥GE，∴DM＝DN，∴DM＝AG，又∠AFG＝∠DFM，∠AGF＝∠DMF∴△AFG≌△DFM（AAS），∴AF＝DF＝DE＝12AD＝12CD，即点E是CD的中点．（3）延长AE，BC交于点P，由（2）知DE＝CD，∠ADE＝∠ECP＝90°，∠DEA＝∠CEP，∴△ADE≌△PCE（ASA）∴AE＝PE，又CE∥AB，∴BC＝PC，在Rt△BGP中，∵BC＝PC，∴CG＝12BP＝BC，∴CG＝CD．【点睛】本题属于四边形综合题，考查了正方形的性质，全等三角形的判定和性质，角平分线的性质定理，直角三角形斜边中线的性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考压轴题．8．如图，在正方形ABCD中，E是边AB上的一动点，点F在边BC的延长线上，且CF AE=，连接DE，DF，EF. FH平分EFB∠交BD于点H.（1）求证：DE DF⊥；（2）求证：DH DF=：（3）过点H作HM EF⊥于点M，用等式表示线段AB，HM与EF之间的数量关系，并证明.【答案】（1）详见解析；（2）详见解析；（3）22EF AB HM =-，证明详见解析.【解析】【分析】（1）根据正方形性质， CF AE =得到DE DF ⊥.（2）由AED CFD △△≌，得DE DF =.由90ABC ∠=︒，BD 平分ABC ∠， 得45DBF ∠=︒.因为FH 平分EFB ∠，所以EFH BFH ∠=∠.由于45DHF DBF BFH BFH ∠=∠+∠=︒+∠,45DFH DFE EFH EFH ∠=∠+∠=︒+∠, 所以DH DF =.（3）过点H 作HN BC ⊥于点N ，由正方形ABCD 性质，得222BD AB AD AB =+=.由FH 平分,EFB HM EF HN BC ∠⊥⊥，，得HM HN =.因为4590HBN HNB ∠=︒∠=︒，，所以22sin 45HN BH HN HM ===︒. 由22cos 45DF EF DF DH ===︒，得22EF AB HM =-. 【详解】（1）证明：∵四边形ABCD 是正方形，∴AD CD =，90EAD BCD ADC ∠=∠=∠=︒.∴90EAD FCD ∠=∠=︒.∵CF AE =。

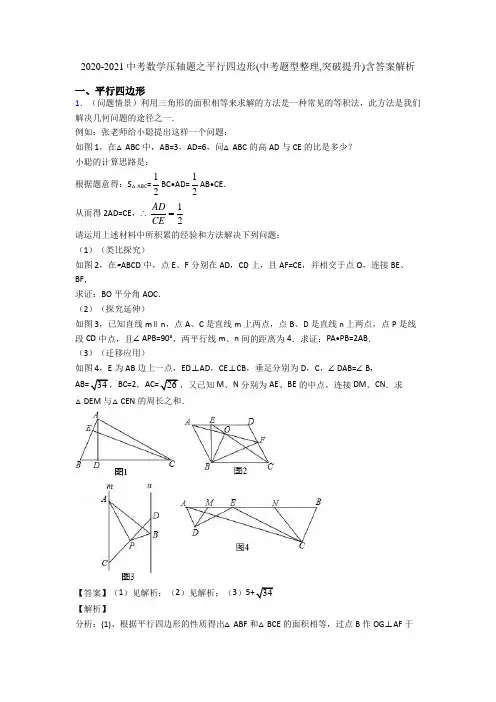
2020-2021中考数学压轴题之平行四边形(中考题型整理,突破提升)含答案解析一、平行四边形1．（问题情景）利用三角形的面积相等来求解的方法是一种常见的等积法，此方法是我们解决几何问题的途径之一．例如：张老师给小聪提出这样一个问题：如图1，在△ABC中，AB=3，AD=6，问△ABC的高AD与CE的比是多少？小聪的计算思路是：根据题意得：S△ABC=12BC•AD=12AB•CE．从而得2AD=CE，∴12 AD CE请运用上述材料中所积累的经验和方法解决下列问题：（1）（类比探究）如图2，在▱ABCD中，点E、F分别在AD，CD上，且AF=CE，并相交于点O，连接BE、BF，求证：BO平分角AOC．（2）（探究延伸）如图3，已知直线m∥n，点A、C是直线m上两点，点B、D是直线n上两点，点P是线段CD中点，且∠APB=90°，两平行线m、n间的距离为4．求证：PA•PB=2AB．（3）（迁移应用）如图4，E为AB边上一点，ED⊥AD，CE⊥CB，垂足分别为D，C，∠DAB=∠B，AB=34，BC=2，AC=26，又已知M、N分别为AE、BE的中点，连接DM、CN．求△DEM与△CEN的周长之和．【答案】（1）见解析；（2）见解析；（3）34【解析】分析：(1)、根据平行四边形的性质得出△ABF和△BCE的面积相等，过点B作OG⊥AF于G，OH⊥CE于H，从而得出AF=CE，然后证明△BOG和△BOH全等，从而得出∠BOG=∠BOH，即角平分线；(2)、过点P作PG⊥n于G，交m于F，根据平行线的性质得出△CPF和△DPG全等，延长BP交AC于E，证明△CPE和△DPB全等，根据等积法得出AB=AP×PB，从而得出答案；(3)、，延长AD，BC交于点G，过点A作AF⊥BC于F，设CF=x，根据Rt△ABF和Rt△ACF的勾股定理得出x的值，根据等积法得出AE=2DM=2EM，BE=2CN=2EN， DM+CN=AB，从而得出两个三角形的周长之和．同理：EM+EN=AB详解：证明：（1）如图2，∵四边形ABCD是平行四边形，∴S△ABF=S▱ABCD，S△BCE=S▱ABCD，∴S△ABF=S△BCE，过点B作OG⊥AF于G，OH⊥CE于H，∴S△ABF=AF×BG，S△BCE=CE×BH，∴AF×BG=CE×BH，即：AF×BG=CE×BH，∵AF=CE，∴BG=BH，在Rt△BOG和Rt△BOH中，，∴Rt△BOG≌Rt△BOH，∴∠BOG=∠BOH，∴OB平分∠AOC，（2）如图3，过点P作PG⊥n于G，交m于F，∵m∥n，∴PF⊥AC，∴∠CFP=∠BGP=90°，∵点P是CD中点，在△CPF和△DPG中，，∴△CPF≌△DPG，∴PF=PG=FG=2，延长BP交AC于E，∵m∥n，∴∠ECP=∠BDP，∴CP=DP，在△CPE和△DPB中，，∴△CPE≌△DPB，∴PE=PB，∵∠APB=90°，∴AE=AB，∴S△APE=S△APB，∵S△APE=AE×PF=AE=AB，S△APB=AP×PB，∴AB=AP×PB，即：PA•PB=2AB；（3）如图4，延长AD，BC交于点G，∵∠BAD=∠B，∴AG=BG，过点A作AF⊥BC于F，设CF=x（x＞0），∴BF=BC+CF=x+2，在Rt△ABF中，AB=，根据勾股定理得，AF2=AB2﹣BF2=34﹣（x+2）2，在Rt△ACF中，AC=，根据勾股定理得，AF2=AC2﹣CF2=26﹣x2，∴34﹣（x+2）2=26﹣x2，∴x=﹣1（舍）或x=1，∴AF==5，连接EG，∵S△ABG=BG×AF=S△AEG+S△BEG=AG×DE+BG×CE=BG（DE+CE），∴DE+CE=AF=5，在Rt△ADE中，点M是AE的中点，∴AE=2DM=2EM，同理：BE=2CN=2EN，∵AB=AE+BE，∴2DM+2CN=AB，∴DM+CN=AB，同理：EM+EN=AB ∴△DEM与△CEN的周长之和=DE+DM+EM+CE+CN+EN=（DE+CE）+[（DM+CN）+（EM+EN）]=（DE+CN）+AB=5+．点睛：本题主要考查的就是三角形全等的判定与性质以及三角形的等积法，综合性非常强，难度较大．在解决这个问题的关键就是作出辅助线，然后根据勾股定理和三角形全等得出各个线段之间的关系．2．如图，△ABC是等边三角形，AB=6cm，D为边AB中点．动点P、Q在边AB上同时从点D出发，点P沿D→A以1cm/s的速度向终点A运动．点Q沿D→B→D以2cm/s的速度运动，回到点D停止．以PQ为边在AB上方作等边三角形PQN．将△PQN绕QN的中点旋转180°得到△MNQ．设四边形PQMN与△ABC重叠部分图形的面积为S（cm2），点P运动的时间为t（s）（0＜t＜3）．（1）当点N落在边BC上时，求t的值．（2）当点N到点A、B的距离相等时，求t的值．（3）当点Q沿D→B运动时，求S与t之间的函数表达式．（4）设四边形PQMN的边MN、MQ与边BC的交点分别是E、F，直接写出四边形PEMF 与四边形PQMN的面积比为2：3时t的值．【答案】（1）（2）2（3）S=S菱形PQMN=2S△PNQ=t2；（4）t=1或【解析】试题分析：（1）由题意知：当点N落在边BC上时，点Q与点B重合，此时DQ=3；（2）当点N到点A、B的距离相等时，点N在边AB的中线上，此时PD=DQ；（3）当0≤t≤时，四边形PQMN与△ABC重叠部分图形为四边形PQMN；当≤t≤时，四边形PQMN与△ABC重叠部分图形为五边形PQFEN．（4）MN、MQ与边BC的有交点时，此时＜t＜，列出四边形PEMF与四边形PQMN的面积表达式后，即可求出t的值．试题解析：（1）∵△PQN与△ABC都是等边三角形，∴当点N落在边BC上时，点Q与点B重合．∴DQ=3∴2t=3．∴t=；（2）∵当点N到点A、B的距离相等时，点N在边AB的中线上，∴PD=DQ，当0＜t＜时，此时，PD=t，DQ=2t∴t=2t∴t=0（不合题意，舍去），当≤t＜3时，此时，PD=t，DQ=6﹣2t∴t=6﹣2t，解得t=2；综上所述，当点N到点A、B的距离相等时，t=2；（3）由题意知：此时，PD=t，DQ=2t当点M在BC边上时，∴MN=BQ∵PQ=MN=3t，BQ=3﹣2t∴3t=3﹣2t∴解得t=如图①，当0≤t≤时，S△PNQ=PQ2=t2；∴S=S菱形PQMN=2S△PNQ=t2，如图②，当≤t≤时，设MN、MQ与边BC的交点分别是E、F，∵MN=PQ=3t，NE=BQ=3﹣2t，∴ME=MN﹣NE=PQ﹣BQ=5t﹣3，∵△EMF是等边三角形，∴S△EMF=ME2=（5t﹣3）2．；（4）MN、MQ与边BC的交点分别是E、F，此时＜t＜，t=1或．考点：几何变换综合题3．如图，四边形ABCD中，对角线AC、BD相交于点O，AO=CO，BO=DO，且∠ABC+∠ADC=180°．（1）求证：四边形ABCD是矩形．（2）若∠ADF：∠FDC=3：2，DF⊥AC，求∠BDF的度数．【答案】(1)见解析；（2）18°.【解析】【分析】（1）根据平行四边形的判定得出四边形ABCD是平行四边形，求出∠ABC=90°，根据矩形的判定得出即可；（2）求出∠FDC的度数，根据三角形内角和定理求出∠DCO，根据矩形的性质得出OD=OC，求出∠CDO，即可求出答案．【详解】（1）证明：∵AO=CO，BO=DO∴四边形ABCD是平行四边形，∴∠ABC=∠ADC，∵∠ABC+∠ADC=180°，∴∠ABC=∠ADC=90°，∴四边形ABCD是矩形；（2）解：∵∠ADC=90°，∠ADF：∠FDC=3：2，∴∠FDC=36°，∵DF⊥AC，∴∠DCO=90°﹣36°=54°，∵四边形ABCD是矩形，∴OC=OD，∴∠ODC=54°∴∠BDF=∠ODC﹣∠FDC=18°．【点睛】本题考查了平行四边形的性质和判定，矩形的性质和判定的应用，能灵活运用定理进行推理是解此题的关键，注意：矩形的对角线相等，有一个角是直角的平行四边形是矩形．4．如图，△ABC中，AD是边BC上的中线，过点A作AE∥BC，过点D作DE∥AB，DE与AC、AE分别交于点O、点E，连接EC．（1）求证：AD=EC；（2）当∠BAC=Rt∠时，求证：四边形ADCE是菱形．【答案】（1）见解析；（2）见解析.【解析】【分析】（1）先证四边形ABDE是平行四边形，再证四边形ADCE是平行四边形即可；（2）由∠BAC=90°，AD是边BC上的中线，得AD=BD=CD，即可证明.【详解】(1)证明：∵AE∥BC，DE∥AB，∴四边形ABDE是平行四边形，∴AE=BD，∵AD是边BC上的中线，∴BD=DC，∴AE=DC，又∵AE∥BC，∴四边形ADCE是平行四边形.(2) 证明：∵∠BAC=90°，AD是边BC上的中线.∴AD=CD∵四边形ADCE是平行四边形，∴四边形ADCE是菱形.【点睛】本题考查了平行四边形的判定、菱形的判定、直角三角形斜边中线定理.根据图形与已知条件灵活应用平行四边形的判定方法是证明的关键.5．如图（1）在正方形ABCD中，点E是CD边上一动点，连接AE，作BF⊥AE，垂足为G 交AD于F（1）求证：AF＝DE；（2）连接DG，若DG平分∠EGF，如图（2），求证：点E是CD中点；（3）在（2）的条件下，连接CG，如图（3），求证：CG＝CD．【答案】（1）见解析；（2）见解析；（3）CG＝CD，见解析．【解析】【分析】（1）证明△BAF≌△ADE（ASA）即可解决问题．（2）过点D作DM⊥GF，DN⊥GE，垂足分别为点M，N．想办法证明AF＝DF，即可解决问题．（3）延长AE，BC交于点P，由（2）知DE＝CD，利用直角三角形斜边中线的性质，只要证明BC＝CP即可．【详解】（1）证明：如图1中，在正方形ABCD中，AB＝AD，∠BAD＝∠D＝90o，∴∠2+∠3＝90°又∵BF⊥AE，∴∠AGB＝90°∴∠1+∠2＝90°，∴∠1＝∠3在△BAF与△ADE中，∠1=∠3 BA=AD ∠BAF=∠D，∴△BAF≌△ADE（ASA）∴AF＝DE．（2）证明：过点D作DM⊥GF，DN⊥GE，垂足分别为点M，N．由（1）得∠1＝∠3，∠BGA＝∠AND＝90°，AB＝AD∴△BAG≌△ADN（AAS）∴AG＝DN，又DG平分∠EGF，DM⊥GF，DN⊥GE，∴DM＝DN，∴DM＝AG，又∠AFG＝∠DFM，∠AGF＝∠DMF∴△AFG≌△DFM（AAS），∴AF＝DF＝DE＝12AD＝12CD，即点E是CD的中点．（3）延长AE，BC交于点P，由（2）知DE＝CD，∠ADE＝∠ECP＝90°，∠DEA＝∠CEP，∴△ADE≌△PCE（ASA）∴AE＝PE，又CE∥AB，∴BC＝PC，在Rt△BGP中，∵BC＝PC，∴CG＝1BP＝BC，2∴CG＝CD．【点睛】本题属于四边形综合题，考查了正方形的性质，全等三角形的判定和性质，角平分线的性质定理，直角三角形斜边中线的性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考压轴题．6．如图，正方形ABCD的边长为8，E为BC上一定点，BE＝6，F为AB上一动点，把△BEF沿EF折叠，点B落在点B′处，当△AFB′恰好为直角三角形时，B′D的长为？465225【解析】【分析】分两种情况分析：如图1，当∠AB′F=90°时，此时A、B′、E三点共线，过点B′作B′M⊥AB，B′N⊥AD，由三角形的面积法则可求得B′M=2.4，再由勾股定理可求得B′N=3.2，在Rt△CB′N中，由勾股定理得，2222B N'+；如图2，当∠AFB′=90°+DN= 3.2 5.6时，由题意可知此时四边形EBFB′是正方形，AF=2，过点B′作B′N⊥AD，则四边形AFB′N为矩形，在Rt△CB′N中，由勾股定理得，2222B N'+；+DN=22【详解】如图1，当∠AB′F=90°时，此时A、B′、E三点共线，∵∠B=90°，∴2222++，AB BE=86∵B′E=BE=6，∴AB′=4，∵B′F=BF，AF+BF=AB=8，在Rt△AB′F中，∠AB′F=90°，由勾股定理得，AF2=FB′2+AB′2，∴AF=5，BF=3，过点B′作B′M⊥AB，B′N⊥AD，由三角形的面积法则可求得B′M=2.4，再由勾股定理可求得B′N=3.2，∴AN=B′M=2.4，∴DN=AD-AN=8-2.4=5.6，在Rt△CB′N中，由勾股定理得，B′D=2222+DN= 3.2 5.6B N'+ =4655；如图2，当∠AFB′=90°时，由题意可知此时四边形EBFB′是正方形，∴AF=2，过点B′作B′N⊥AD，则四边形AFB′N为矩形，∴AN=B′F=6，B′N=AF=2，∴DN=AD-AN=2，在Rt△CB′N中，由勾股定理得，B′D=2222+DN=22B N'+ =22；综上，可得B′D 4655或2【点睛】本题主要考查正方形的性质与判定，矩形有性质判定、勾股定理、折叠的性质等，能正确地画出图形并能分类讨论是解题的关键.7．已知AD是△ABC的中线P是线段AD上的一点（不与点A、D重合），连接PB、PC，E、F、G、H分别是AB、AC、PB、PC的中点，AD与EF交于点M；（1）如图1，当AB＝AC时，求证：四边形EGHF是矩形；（2）如图2，当点P与点M重合时，在不添加任何辅助线的条件下，写出所有与△BPE面积相等的三角形（不包括△BPE本身）．【答案】（1）见解析；（2）△APE、△APF、△CPF、△PGH．【解析】【分析】（1）由三角形中位线定理得出EG∥AP，EF∥BC，EF=12BC，GH∥BC，GH=12BC，推出EF∥GH，EF=GH，证得四边形EGHF是平行四边形，证得EF⊥AP，推出EF⊥EG，即可得出结论；（2）由△APE与△BPE的底AE=BE，又等高，得出S△APE=S△BPE，由△APE与△APF的底EP=FP，又等高，得出S△APE=S△APF，由△APF与△CPF的底AF=CF，又等高，得出S△APF=S△CPF，证得△PGH底边GH上的高等于△AEF底边EF上高的一半，推出S△PGH=12S△AEF=S△APF，即可得出结果．【详解】（1）证明：∵E、F、G、H分别是AB、AC、PB、PC的中点，∴EG∥AP，EF∥BC，EF＝12BC，GH∥BC，GH＝12BC，∴EF∥GH，EF＝GH，∴四边形EGHF是平行四边形，∵AB＝AC，∴AD⊥BC，∴EF⊥AP，∵EG∥AP，∴EF⊥EG，∴平行四边形EGHF是矩形；（2）∵PE是△APB的中线，∴△APE与△BPE的底AE＝BE，又等高，∴S△APE＝S△BPE，∵AP是△AEF的中线，∴△APE与△APF的底EP＝FP，又等高，∴S△APE＝S△APF，∴S△APF＝S△BPE，∵PF是△APC的中线，∴△APF与△CPF的底AF＝CF，又等高，∴S△APF＝S△CPF，∴S△CPF＝S△BPE，∵EF∥GH∥BC，E、F、G、H分别是AB、AC、PB、PC的中点，∴△AEF底边EF上的高等于△ABC底边BC上高的一半，△PGH底边GH上的高等于△PBC 底边BC上高的一半，∴△PGH底边GH上的高等于△AEF底边EF上高的一半，∵GH＝EF，∴S△PGH＝1S△AEF＝S△APF，2综上所述，与△BPE面积相等的三角形为：△APE、△APF、△CPF、△PGH．【点睛】本题考查了矩形的判定与性质、平行四边形的判定、三角形中位线定理、平行线的性质、三角形面积的计算等知识，熟练掌握三角形中位线定理是解决问题的关键．8．如图1，已知正方形ABCD的边CD在正方形DEFG的边DE上，连接AE，GC．(1)试猜想AE与GC有怎样的关系(直接写出结论即可)；(2)将正方形DEFG绕点D按顺时针方向旋转，使点E落在BC边上，如图2，连接AE和CG．你认为(1)中的结论是否还成立？若成立，给出证明；若不成立，请说明理由．(3)在(2)中，若E是BC的中点，且BC＝2，则C，F两点间的距离为．【答案】(1) AE＝CG，AE⊥GC；(2)成立，证明见解析；2．【解析】【分析】（1）观察图形，AE、CG的位置关系可能是垂直，下面着手证明．由于四边形ABCD、DEFG都是正方形，易证得△ADE≌△CDG，则∠1＝∠2，由于∠2、∠3互余，所以∠1、∠3互余，由此可得AE⊥GC．（2）题（1）的结论仍然成立，参照（1）题的解题方法，可证△ADE≌△CDG，得∠5＝∠4，由于∠4、∠7互余，而∠5、∠6互余，那么∠6＝∠7；由图知∠AEB＝∠CEH＝90°﹣∠6，即∠7+∠CEH＝90°，由此得证．（3）如图3中，作CM⊥DG于G，GN⊥CD于N，CH⊥FG于H，则四边形CMGH是矩形，可得CM＝GH，CH＝GM．想办法求出CH，HF，再利用勾股定理即可解决问题．【详解】(1)AE＝CG，AE⊥GC；证明：延长GC交AE于点H，在正方形ABCD与正方形DEFG中，AD＝DC，∠ADE＝∠CDG＝90°，DE＝DG，∴△ADE≌△CDG(SAS)，∴AE，CG，∠1＝∠2∵∠2+∠3＝90°，∴∠1+∠3＝90°，∴∠AHG＝180°﹣(∠1+∠3)＝180°﹣90°＝90°，∴AE⊥GC．(2)答：成立；证明：延长AE和GC相交于点H，在正方形ABCD和正方形DEFG中，AD＝DC，DE＝DG，∠ADC＝∠DCB＝∠B＝∠BAD＝∠EDG＝90°，∴∠1＝∠2＝90°﹣∠3；∴△ADE≌△CDG(SAS)，∴AE＝CG，∠5＝∠4；又∵∠5+∠6＝90°，∠4+∠7＝180°﹣∠DCE＝180°﹣90°＝90°，∴∠6＝∠7，又∵∠6+∠AEB＝90°，∠AEB＝∠CEH，∴∠CEH+∠7＝90°，∴∠EHC＝90°，∴AE⊥GC．(3)如图3中，作CM⊥DG于G，GN⊥CD于N，CH⊥FG于H，则四边形CMGH是矩形，可得CM＝GH，CH＝GM．∵BE ＝CE ＝1，AB ＝CD ＝2，∴AE ＝DE ＝CG ═DG ＝FG 5∵DE ＝DG ，∠DCE ＝∠GND ，∠EDC ＝∠DGN ，∴△DCE ≌△GND(AAS)，∴GCD ＝2，∵S △DCG ＝12•CD•NG ＝12•DG•CM ， ∴2×25， ∴CM ＝GH 45， ∴MG ＝CH 22CG CM -355， ∴FH ＝FG ﹣FG 5， ∴CF 22FH CH +22535()()55+2． 2．【点睛】 本题属于四边形综合题，考查了正方形的性质，全等三角形的判定和性质，解直角三角形等知识，解题的关键是正确寻找全等三角形解决问题，属于中考压轴题．9．正方形ABCD ，点E 在边BC 上，点F 在对角线AC 上，连AE ．(1)如图1，连EF ，若EF ⊥AC ，4AF ＝3AC ，AB ＝4，求△AEF 的周长；(2)如图2，若AF ＝AB ，过点F 作FG ⊥AC 交CD 于G ，点H 在线段FG 上(不与端点重合)，连AH ．若∠EAH ＝45°，求证：EC ＝2．+；（2）证明见解析【答案】（1）2542【解析】【分析】（1）由正方形性质得出AB＝BC＝CD＝AD＝4，∠B＝∠D＝90°，∠ACB＝∠ACD＝∠BAC＝∠ACD＝45°，得出AC＝2AB＝42，求出AF＝32，CF＝AC﹣AF＝2，求出△CEF 是等腰直角三角形，得出EF＝CF＝2，CE＝2CF＝2，在Rt△AEF中，由勾股定理求出AE，即可得出△AEF的周长；（2）延长GF交BC于M，连接AG，则△CGM和△CFG是等腰直角三角形，得出CM＝CG，CG＝2CF，证出BM＝DG，证明Rt△AFG≌Rt△ADG得出FG＝DG，BM＝FG，再证明△ABE≌△AFH，得出BE＝FH，即可得出结论．【详解】（1）∵四边形ABCD是正方形，∴AB＝BC＝CD＝AD＝4，∠B＝∠D＝90°，∠ACB＝∠ACD＝∠BAC＝∠ACD＝45°，∴AC＝2AB＝42，∵4AF＝3AC＝122，∴AF＝32，∴CF＝AC﹣AF＝2，∵EF⊥AC，∴△CEF是等腰直角三角形，∴EF＝CF＝2，CE＝2CF＝2，在Rt△AEF中，由勾股定理得：AE＝2225+=，AF EF++=+；∴△AEF的周长＝AE+EF+AF＝252322542（2）证明：延长GF交BC于M，连接AG，如图2所示：则△CGM和△CFG是等腰直角三角形，∴CM＝CG，CG2，∴BM ＝DG ，∵AF ＝AB ，∴AF ＝AD ，在Rt △AFG 和Rt △ADG 中，AG AG AF AD =⎧⎨=⎩， ∴Rt △AFG ≌Rt △ADG （HL ），∴FG ＝DG ，∴BM ＝FG ，∵∠BAC ＝∠EAH ＝45°，∴∠BAE ＝∠FAH ，∵FG ⊥AC ，∴∠AFH ＝90°，在△ABE 和△AFH 中，90B AFH AB AFBAE FAH ︒⎧∠=∠=⎪=⎨⎪∠=∠⎩， ∴△ABE ≌△AFH （ASA ），∴BE ＝FH ，∵BM ＝BE +EM ，FG ＝FH +HG ，∴EM ＝HG ，∵EC ＝EM +CM ，CM ＝CGCF ，∴EC ＝HG．【点睛】本题考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、勾股定理等知识；熟练掌握等腰直角三角形的判定与性质，证明三角形全等是解题的关键．10．如图①，在矩形ABCD 中，点P 从AB 边的中点E 出发，沿着E B C --速运动，速度为每秒2个单位长度，到达点C 后停止运动，点Q 是AD 上的点，10AQ =，设PAQ ∆的面积为y ，点p 运动的时间为t 秒，y 与t 的函数关系如图②所示.(1)图①中AB = ，BC = ，图②中m = .(2)当t =1秒时，试判断以PQ 为直径的圆是否与BC 边相切?请说明理由:(3)点p 在运动过程中，将矩形沿PQ 所在直线折叠，则t 为何值时，折叠后顶点A 的对应点A '落在矩形的一边上.【答案】(1)8,18,20;(2)不相切，证明见解析；（3）t=12、5、173. 【解析】【分析】 （1）由题意得出AB=2BE ，t=2时，BE=2×2=4，求出AB=2BE=8，AE=BE=4，t=11时，2t=22，得出BC=18，当t=0时，点P 在E 处，m=△AEQ 的面积=12AQ×AE=20即可； （2）当t=1时，PE=2，得出AP=AE+PE=6，由勾股定理求出34PQ 为直径的圆的圆心为O'，作O'N ⊥BC 于N ，延长NO'交AD 于M ，则MN=AB=8，O'M ∥AB ，MN=AB=8，由三角形中位线定理得出O'M=12AP=3，求出O'N=MN-O'M=5＜圆O'的半径，即可得出结论；（3）分三种情况：①当点P 在AB 边上，A'落在BC 边上时，作QF ⊥BC 于F ，则QF=AB=8，BF=AQ=10，由折叠的性质得：PA'=PA ，A'Q=AQ=10，∠PA'Q=∠A=90°，由勾股定理求出22AQ QF '-，得出A'B=BF-A'F=4，在Rt △A'BP 中，BP=4-2t ，PA'=AP=8-（4-2t ）=4+2t ，由勾股定理得出方程，解方程即可；②当点P 在BC 边上，A'落在BC 边上时，由折叠的性质得：A'P=AP ，证出∠APQ=∠AQP ，得出AP=AQ=A'P=10，在Rt △ABP 中，由勾股定理求出BP=6，由BP=2t-4，得出2t-4=6，解方程即可；③当点P 在BC 边上，A'落在CD 边上时，由折叠的性质得：A'P=AP ，A'Q=AQ=10，在Rt △DQA'中，DQ=AD-AQ=8，由勾股定理求出DA'=6，得出A'C=CD-DA'=2，在Rt △ABP 和Rt △A'PC 中，BP=2t-4，CP=BC-BP=22-2t ，由勾股定理得出方程，解方程即可．【详解】（1）∵点P 从AB 边的中点E 出发，速度为每秒2个单位长度，∴AB=2BE ，由图象得：t=2时，BE=2×2=4，∴AB=2BE=8，AE=BE=4，t=11时，2t=22，∴BC=22-4=18，当t=0时，点P 在E 处，m=△AEQ 的面积=12AQ×AE=12×10×4=20； 故答案为8，18，20；（2）当t=1秒时，以PQ 为直径的圆不与BC 边相切，理由如下：当t=1时，PE=2，∴AP=AE+PE=4+2=6，∵四边形ABCD是矩形，∴∠A=90°，∴PQ=2222106234AQ AP+=+=，设以PQ为直径的圆的圆心为O'，作O'N⊥BC于N，延长NO'交AD于M，如图1所示：则MN=AB=8，O'M∥AB，MN=AB=8，∵O'为PQ的中点，∴O''M是△APQ的中位线，∴O'M=12AP=3，∴O'N=MN-O'M=5＜34，∴以PQ为直径的圆不与BC边相切；（3）分三种情况：①当点P在AB边上，A'落在BC边上时，作QF⊥BC于F，如图2所示：则QF=AB=8，BF=AQ=10，∵四边形ABCD是矩形，∴∠A=∠B=∠BCD=∠D=90°，CD=AB=8，AD=BC=18，由折叠的性质得：PA'=PA，A'Q=AQ=10，∠PA'Q=∠A=90°，∴22AQ QF'-，∴A'B=BF-A'F=4，在Rt△A'BP中，BP=4-2t，PA'=AP=8-（4-2t）=4+2t，由勾股定理得：42+（4-2t）2=（4+2t）2，解得：t=12；②当点P在BC边上，A'落在BC边上时，连接AA'，如图3所示：由折叠的性质得：A'P=AP，∴∠APQ'=∠A'PQ，∵AD∥BC，∴∠AQP=∠A'PQ，∴∠APQ=∠AQP，∴AP=AQ=A'P=10，在Rt△ABP中，由勾股定理得：BP=22108-=6，又∵BP=2t-4，∴2t-4=6，解得：t=5；③当点P在BC边上，A'落在CD边上时，连接AP、A'P，如图4所示：由折叠的性质得：A'P=AP，A'Q=AQ=10，在Rt△DQA'中，DQ=AD-AQ=8，由勾股定理得：22108-，∴A'C=CD-DA'=2，在Rt△ABP和Rt△A'PC中，BP=2t-4，CP=BC-BP=18-（2t-4）=22-2t，由勾股定理得：AP2=82+（2t-4）2，A'P2=22+（22-2t）2，∴82+（2t-4）2=22+（22-2t）2，解得：t=173；综上所述，t为12或5或173时，折叠后顶点A的对应点A′落在矩形的一边上．【点睛】四边形综合题目，考查了矩形的性质、折叠变换的性质、勾股定理、函数图象、直线与圆的位置关系、三角形中位线定理、等腰三角形的判定、以及分类讨论等知识.11．如图，抛物线y=mx2+2mx+n经过A（﹣3，0），C（0，﹣32）两点，与x轴交于另一点B．（1）求经过A，B，C三点的抛物线的解析式；（2）过点C作CE∥x轴交抛物线于点E，写出点E的坐标，并求AC、BE的交点F的坐标（3）若抛物线的顶点为D，连结DC、DE，四边形CDEF是否为菱形？若是，请证明；若不是，请说明理由．【答案】（1）y=12x2+x﹣32；（2）F点坐标为（﹣1，﹣1）；（3）四边形CDEF是菱形．证明见解析【解析】【分析】将A、C点的坐标代入抛物线的解析式中，通过联立方程组求得该抛物线的解析式；根据（1）题所得的抛物线的解析式，可确定抛物线的对称轴方程以及B、C点的坐标，由CE∥x轴，可知C、E关于对称轴对称。

2020中考数学 几何复习：平行四边形（含答案）一、选择题1.如图，在四边形ABCD 中，E 是BC 边的中点，连结DE 并延长，交AB 的延长线于F 点，．添加一个条件，使四边形ABCD 是平行四边形．你认为下面四个条件中可选择的是（ ）A ．B ．C ．D ．2.如图，四边形ABCD 中，AB ＝BC ，∠ABC ＝∠CDA ＝90°，BE ⊥AD 于点E ，且四边形ABCD 的面积为8，则BE ＝（ ）A ．2B ．3C ．D ．3.如图，在□ABCD 中，已知AD ＝8㎝， AB ＝6㎝， DE 平分∠ADC 交BC 边于点E ，则BE 等于（ ） A ．2cmB ．4cmC ．6cmD ．8cm二、填空题1.如图，在□ABCD 中，∠A ＝120°，则∠D ＝_ _°.AB BF =AD BC =CD BF =A C ∠=∠F CDE ∠=∠2223ABCDAB CDEEBAFCD2．如图所示，在中，对角线相交于点，过点的直线分别交于点，若的面积为2，的面积为4，则的面积为．3.如图，在□ABCD中，BD为对角线，E、F分别是AD．BD的中点，连接EF．若EF＝3，则CD的长为．4.如图，□ABCD的对角线、相交于点，点是的中点，的周长为16cm，则的周长是 cm．5.如图，在四边形中，已知，再添加一个条件___________（写出一个即可），则四边形是平行四边形．(图形中不再添加辅助线)三、解答题1.如图，在△ABC中，∠ACB＝90°，点E为AB中点，连结CE，过点E作ED⊥BC于点D，在DE的延长线上取一点F，使AF＝CE．求证：四边形ACEF是平行四边形．ABCDY AC BD、O O AD BC、M N、CON△DOM△AOB△AC BD O E CD ABD△DOE△ABCD AB CD=ABCDD CBA5题ACDBEOO2.如图，是平行四边形对角线上两点，，求证：．3.如图，l 1、l 2、l 3、l 4是同一平面内的四条平行直线，且每相邻的两条平行直线间的距离为h ，正方形ABCD 的四个顶点分别在这四条直线上，且正方形ABCD 的面积是25.（1）连结EF ，证明△ABE、△FBE、△EDF、△CDF 的面积相等. （2）求h 的值.4.如图，E 、F 是四边形ABCD 的对角线AC 上两点，． 求证：（1）． （2）四边形是平行四边形．E F 、ABCD AC BE DF ∥AF CE=AF CE DF BE DF BE ==，，∥AFD CEB △≌△ABCD DCAB E F5.如图，在ΔABC 中，D 、E 、F 分别为边AB 、BC 、CA 的中点.证明：四边形DECF 是平行四边形.6.在所给的9×9方格中，每个小正方形的边长都是1．按要求画平行四边形，使它的四个顶点以及对角线交点都在方格的顶点上．(1)在图甲中画一个平行四边形，使它的周长是整数；(2)在图乙中画一个平行四边形，使它的周长不是整数．(注：图甲、图乙在答题纸上)7.如图：点A ．D ．B ．E 在同一直线上，AD ＝BE ，AC ＝DF ，AC ∥DF ，请从图中找出一个与∠E 相等的角，并加以证明．（不再添加其他的字母与线段）A FE D CBABDEFC8. 如图，E，F是平行四边形ABCD的对角线AC上的点，CE=AF．请你猜想：BE•与DF有怎样的位置关系和数量关系？并对你的猜想加以证明．【参考答案】 选择题1. D2. C3. B 填空题 1. 60 2. 63. 6 因为EF 是△ABD 的中位线，则AB ＝6，又AB ＝CD ，所以CD ＝6.4. 85.解答题1. 证明：∵点E 为Rt△ABC 的斜边中点，∴EC＝EA ＝EB ∴∠EAC＝∠ECA． ∵AF ＝CE ，CE ＝EA ∴AF ＝AE ， ∴∠AFE＝∠AEF． ∵∠ACB ＝∠EDB ＝90° ∴FD∥BC ∴∠AEF＝∠E AC∴∠EAC＝∠ECA＝∠AFE＝∠AEF．∴∠EAF＝180°－∠AFE－∠AEF ＝180°－∠EAC－∠ECA＝∠AEC ∴AF∥CE 又∵AF ＝CE∴四边形ACEF 是平行四边形.2. 证明：平行四边形中，，， ．180180AB CD AD BCA DB C∥°°=????或或或等ABCD AD BC ∥AD BC =ACB CAD ∴∠=∠又，， ，3. 解：连结EF∵l 1∥l 2∥l 3∥l 4，且四边形ABCD 是正方形 ∴BE∥FD，BF∥ED∴四边形EBFD 为平行四边形 ∴BE＝FD又∵l 1、l 2、l 3和l 4之间的距离为h∴S △ABE ＝BE·h，S △FBE ＝BE·h，S △EDF ＝FD·h，S △CDF ＝FD·h ∴S △ABE ＝ S △FBE ＝ S △EDF ＝ S △CDF （2）过A 点作AH⊥BE 于H 点。

中考数学一轮复习平行四边形知识归纳总结含答案一、解答题1．综合与实践．问题情境：如图①，在纸片ABCD □中，5AD =，15ABCD S =，过点A 作AE BC ⊥，垂足为点E ，沿AE 剪下ABE △，将它平移至DCE '的位置，拼成四边形AEE D '．独立思考：（1）试探究四边形AEE D '的形状．深入探究：（2）如图②，在（1）中的四边形纸片AEE D '中，在EE '．上取一点F ，使4EF =，剪下AEF ，将它平移至DE F ''的位置，拼成四边形AFF D '，试探究四边形AFF D '的形状；拓展延伸：（3）在（2）的条件下，求出四边形AFF D '的两条对角线长；（4）若四边形ABCD 为正方形，请仿照上述操作，进行一次平移，在图③中画出图形，标明字母，你能发现什么结论，直接写出你的结论．2．如图，平行四边形ABCD 的对角线AC BD 、交于点O ，分别过点C D 、作//,//CF BD DF AC ，连接BF 交AC 于点E ．(1)求证: FCE BOE ≌；(2)当ADC ∠等于多少度时，四边形OCFD 为菱形?请说明理由．3．如图正方形ABCD ，DE 与HG 相交于点O （O 不与D 、E 重合）．（1）如图（1），当90GOD ∠=︒，①求证：DE GH =； ②求证：2GD EH DE +>；（2）如图（2），当45GOD ∠=︒，边长4AB =，25HG =，求DE 的长．4．如图1，在正方形ABCD 和正方形BEFG 中，点,,A B E 在同一条直线上，P 是线段DF 的中点，连接,PG PC ．（1）求证：,PG PC PG PC ⊥=．简析：由Р是线段DF 的中点，//DC CF ，不妨延长GP 交DC 于点M ，从而构造出一对全等的三角形，即_______≅________．由全等三角形的性质，易证CMG 是_______三角形，进而得出结论；（2）如图2，将原问题中的正方形ABCD 和正方形BEFG 换成菱形ABCD 和菱形BEFG ，且60ABC BEF ∠=∠=︒，探究PG 与PC 的位置关系及PG PC的值，写出你的猜想并加以证明；（3）当6,2AB BE ==时，菱形ABCD 和菱形BEFG 的顶点都按逆时针排列，且60ABC BEF ∠=∠=︒．若点A B E 、、在一条直线上，如图2，则CP =________；若点A B G 、、在一条直线上，如图3，则CP =________．5．如图，在正方形ABCD 中，E 是边AB 上的一动点（不与点A 、B 重合），连接DE ，点A 关于直线DE 的对称点为F ，连接EF 并延长交BC 于点G ，连接DG ，过点E 作EH DE ⊥交DG 的延长线于点H ，连接BH ．（1）求证：GF GC =；（2）用等式表示线段BH 与AE 的数量关系，并证明．6．共顶点的正方形ABCD 与正方形AEFG 中，AB =13，AE =52．（1）如图1，求证：DG =BE ；（2）如图2，连结BF ，以BF 、BC 为一组邻边作平行四边形BCHF ．①连结BH ，BG ，求BH BG的值； ②当四边形BCHF 为菱形时，直接写出BH 的长．7．已知，如图，在三角形ABC ∆中，20AB AC cm ==，BD AC ⊥于D ，且16BD cm =．点M 从点A 出发，沿AC 方向匀速运动，速度为4/cm s ；同时点P 由B点出发，沿BA 方向匀速运动，速度为1/cm s ，过点P 的动直线//PQ AC ，交BC 于点Q ，连结PM ，设运动时间为()t s ()05t <<，解答下列问题：（1）线段AD =_________cm ；（2）求证：PB PQ =；（3）当t 为何值时，以P Q D M 、、、为顶点的四边形为平行四边形？8．如图1，在正方形ABCD （正方形四边相等，四个角均为直角）中，AB ＝8，P 为线段BC 上一点，连接AP ，过点B 作BQ ⊥AP ，交CD 于点Q ，将△BQC 沿BQ 所在的直线对折得到△BQC ′，延长QC ′交AD 于点N ．（1）求证：BP ＝CQ ；（2）若BP ＝13PC ，求AN 的长； （3）如图2，延长QN 交BA 的延长线于点M ，若BP ＝x （0＜x ＜8），△BMC '的面积为S ，求S 与x 之间的函数关系式．9．（解决问题）如图1，在ABC ∆中，10AB AC ==，CG AB ⊥于点G ．点P 是BC 边上任意一点，过点P 作PE AB ⊥，PF AC ⊥，垂足分别为点E ，点F ．（1）若3PE =，5PF =，则ABP ∆的面积是______，CG =______．（2）猜想线段PE ，PF ，CG 的数量关系，并说明理由．（3）（变式探究）如图2，在ABC ∆中，若10AB AC BC ===，点P 是ABC ∆内任意一点，且PE BC ⊥，PF AC ⊥，PG AB ⊥，垂足分别为点E ，点F ，点G ，求PE PF PG ++的值．（4）（拓展延伸）如图3，将长方形ABCD 沿EF 折叠，使点D 落在点B 上，点C 落在点C '处，点P 为折痕EF 上的任意一点，过点P 作PG BE ⊥，PH BC ⊥，垂足分别为点G ，点H ．若8AD =，3CF =，直接写出PG PH +的值．10．在矩形ABCD 中，BE 平分∠ABC 交CD 边于点E ．点F 在BC 边上，且FE⊥AE．（1）如图1，①∠BEC=_________°；②在图1已有的三角形中，找到一对全等的三角形，并证明你的结论；（2）如图2，FH∥CD 交AD 于点H ，交BE 于点M ．NH∥BE，NB∥HE，连接NE ．若AB=4，AH=2，求NE 的长．【参考答案】***试卷处理标记，请不要删除一、解答题1．（1）矩形；（2）菱形；（3）104）见解析【分析】（1）由平移推出AD EE '=，即可证得四边形AEE D '是平行四边形，再根据AE BC ⊥，得到90AEE '∠=︒即可得到结论；（2）由平移推出AD FF '=，证得四边形AFF D '是平行四边形，根据AE EF ⊥得到90AEE '∠=︒，再根据勾股定理求出AF=5=AD ，即可证得四边形AFF D '是菱形； （3）先利用勾股定理求出22221310DF E F E D ''+=+=，再根据菱形的面积求出F A '；（4）在BC 边上取点E ，连接AE ，平移△ABE 得到△DCF ，可得四边形AEFD 是平行四边形.【详解】(1)四边形AEE D '是矩形，在ABCD □中，//AD BC ，AD BC =，由平移可知：BE CE ''=，∴BC EE '=，∴AD EE '=，∴四边形AEE D '是平行四边形，∵AE BC ⊥，∴90AEE '∠=︒，∴四边形AEE D '是矩形；(2)四边形AFF D '是菱形，在矩形AEE D '中，//AD EE ' ，AD EE '=，由平移可知：EF E F =''，∴EE FF ''=，∴AD FF '=，∴四边形AFF D '是平行四边形，∵AE EF ⊥，∴90AEE '∠=︒，在Rt AEF ，2222345AF AE EF =+=+=， ∴AF AD =，∴四边形AFF D '是菱形；(3)连接F A ',在Rt DFE '△中，22221310DF E F E D ''=+=+=，15ABCD AFF D S S '==平行四边形菱形，∴·30F A FD '=，∴310F A '=；(4)在BC 上取一点E ，连接AE ，平移△ABE 得到△DCF ，可得四边形AEFD 是平行四边形.【点睛】此题考查了平行四边形的性质，矩形的判定定理，菱形的判定及性质，平移的性质的应用，勾股定理.2．（1）见解析；（2）当ADC 满足90ADC ∠=︒时，四边形OCFD 为菱形，证明详见解析【分析】（1）证明四边形OCFD 是平行四边形，得出OD=CF ，证出OB=CF ，再证明全等即可（2）证出四边形ABCD 是矩形，由矩形的性质得出OC=OD ，即可得出四边形OCFD 为菱形.【详解】(1)证明:∵//,//CF BD DF AC ，∴四边形OCFD 是平行四边形， OBE CFE ∠=∠，∴OD CF =，∵四边形ABCD 是平行四边形，∴OB OD =，∴OB CF =，在FCE △和BOE △中， OBE CFE BEO FEC OB CF ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴()FCE BOE AAS ≌．(2)当ADC 满足90ADC ∠=︒时，四边形OCFD 为菱形.理由如下:∵90ADC ∠=︒，四边形ABCD 是平行四边形，∴四边形ABCD 是矩形∴,,,OA OC OB OD AC BD ===∴OC OD =，∴四边形OCFD 为菱形【点睛】本题考查全等三角形判定与性质，平行四边形和菱形的判定与性质等知识，熟练掌握平行四边形的判定和性质和菱形的判定是解题的关键.3．（1）①证明见解析；②证明见解析；（2）DE =． 【分析】（1）过点D 作//DM GH 交BC 延长线于点M ，连接EH ，①由正方形的性质可得//AD BC ，AD CD =，90A ADC DCM ∠=∠=∠=︒，即可证明四边形DGHM 是平行四边形，可得DM=GH ，由90GOD ∠=︒可得∠EDM=90°，根据直角三角形两锐角互余的性质可得12∠=∠，利用ASA 可证明△ADE≌△C DM ，可得DE=DM ，即可证明DE=GH ；②由①得DM=DE ，根据勾股定理可得，利用三角形三边关系即可得结论； （2）过点D 作DN//GH 交BC 于点N ，作ADM CDN ∠=∠，DM 交BA 延长线于点M ，可证明四边形GHND 为平行四边形，可得DN HG =，GD HN =，根据勾股定理可求出CN 的长，利用AAS 可证明ADM CDN ∆∆≌，可得AM NC =，DM DN =，根据平行线的性质∠EDN=45°，根据角的和差故选可得∠MDE=∠EDN ，利用SAS 可证明MDE NDE ∆∆≌，即可证明AE CN EN +=，设AE x =，利用勾股定理可求出x 的值，进而利用勾股定理求出DE 的值即可得答案．【详解】（1）如图（1），过点D 作//DM GH 交BC 延长线于点M ，连接EH ，EM ， ①∵四边形ABCD 为正方形，∴//AD BC ，AD CD =，90A ADC DCM ∠=∠=∠=︒∴四边形DGHM 为平行四边形，∴DM=GH ，GD HM =，∵90GOD ∠=︒，∴90EDM EOH ∠=∠=︒，∴290EDC ∠+∠=︒，∵90ADC ∠=︒，∴190EDC ∠+∠=︒，∴12∠=∠，在ADE ∆和CDM ∆中12A DCM AD DC ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴ADE CDM ∆∆≌，∴DE DM =，∴DE GH =．②在DEM ∆中，∠EDM=90°，∴222DE DM EM +=，∵DE DM =，∴222DE EM =， ∴2EM DE =，在EHM ∆中，HM EH EM +>，∵GD HM =， ∴2GD EH GH +≥．（2）如图（2），过点D 作DN//GH 交BC 于点N ，则四边形GHND 为平行四边形， ∴DN HG =，GD HN =，∵90C ∠=︒，4CD AB ==，25HG DN == ∴222CN DN DC =-=，∴422BN BC CN =-=-=，作ADM CDN ∠=∠，DM 交BA 延长线于点M ，在ADM ∆和CDN ∆中90C MAD CDN ADM DC AD ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩，∴ADM CDN ∆∆≌，∴AM NC =，DM DN =，∵45GOD EOH ∠=∠=︒，∴45EDN ∠=︒，∴45ADE CDN ∠+∠=︒，∴45ADE ADN MDE ∠+∠=︒=∠，在MDE ∆和NDE ∆中MD ND MDE EDN DE DE =⎧⎪∠=∠⎨⎪=⎩，∴MDE NDE ∆∆≌，∴EM EN =，即AE AM AE CN EN +=+=，设AE x =，则BE=4-x ，在Rt BEN ∆中，2222(2)x x +=+， 解得：43x =， ∴22224410433DE AD AE ⎛⎫=+=+= ⎪⎝⎭．【点睛】本题考查正方形的性质、平行四边形的判定与性质、全等三角形的判定与性质、三角形的三边关系及勾股定理，熟练掌握相关性质及判定定理，并正确作出辅助线是解题关键．4．（1）ΔDPM,ΔFPG ；等腰直角；（2）线段PG 与PC 的位置关系是PG ⊥PC ；PG PC ＝3；（3）213【分析】（1）延长GP 交DC 于点M ，由Р是线段DF 的中点，//DC CF ，可得∠MDP=∠GFP ，DP=FP ，利用ASA 可证明△DPM ≌△FPG ；可得DM=GF ，MP=GP ，根据正方形的性质可得CM=CG ，即可证明△CMG 是等腰直角三角形，即可得答案；（2）如图，延长GP 交DC 于点H ，利用ASA 可证明△GFP ≌△HDP ，可得GP ＝HP ，GF ＝HD ，进而根据菱形的性质可证明△CHG 是等腰三角形，根据等腰三角形“三线合一”的性质可得PG ⊥PC ，∠HCP=∠GCP ，由∠ABC=60°可得∠HCG=120°，进而可得∠CGP=30°，根据含30°角的直角三角形的性质及勾股定理即可得答案；（3）利用线段的和差关系可求出图2中CG的长，由（2）可知∠CGP=30°，根据含30°角的直角三角形的性质即可求出CP的长；在图3中，延长GP到N，使GP=PN，连接DN、CN、CG，过N作NK⊥CD，交CD延长线于K，利用SAS可证明△FGP≌△DNP，可得GF=DN，∠GFP=∠NDP，根据角的和差关系可得∠CDN=120°，根据平角的定义可得∠GBC=120°，利用菱形的性质及等量代换可得DN=GB，利用SAS可证明△NDC≌△GBC，可得CN=CG，∠DCN=∠BCG，根据等腰三角形的性质可得PC⊥GN，根据角的和差关系可得∠NCG=120°，进而可得出∠CNP=30°，可得PC=12CG，根据平角的定义可得∠KDN=60°，即可得出∠KND=30°，根据含30°角的直角三角形的性质可得得出KD的长，利用勾股定理可求出KN的长，再利用勾股定理可求出CN的长，根据含30°角的直角三角形的性质即可得出PC的长．【详解】（1）如图，延长GP交DC于点M，∵Р是线段DF的中点，四边形ABCD、BEFG是正方形，点,,A B E在同一条直线上，∴//DC CF，DP=FP，CD=BC，FG=BG，在△DPM和△FPG中，MDP GFP DP FPDPM FPG ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△DPM≌△FPG，∴DM=FG，KP=GP，∴CD-DM=BC-BC，即CM=CG，∴△CMG是等腰直角三角形，∴PG⊥PC，PG=PC．故答案为：ΔDPM，ΔFPG；等腰直角（2）猜想：线段PG与PC的位置关系是PG⊥PC；PGPC3．如图，延长GP交DC于点H，∵P是线段DF的中点，∴FP＝DP，∵四边形ABCD和四边形BEFG是菱形，∴CD//AB，CF//BE，CD＝CB，GF=GB，∵点A B E、、在一条直线上，∴DC∥GF，∴∠GFP＝∠HDP，在△GFP和△HDP中，GFP HDP FP DPGPF HPD ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△GFP≌△HDP，∴GP＝HP，GF＝HD，∴CD-DH＝CB-GB，即CG＝CH，∴△CHG是等腰三角形．∴PG⊥PC，（三线合一），∠HCP=∠GCP，∵∠ABC＝∠BEF＝60°，∴∠HCG=120°，∴∠CGP=12（180°-120°）=30°，∴CG=2PC，∴PG=2222(2)3CG PC PC PC PC-=-=，∴PGPC＝3．（3）如图2，∵AB=6，BE=2，∴CG=AB-BE=4，由（2）可知∠CGP=30°，PG⊥PC，∴PC=12CG=2，如图3，延长GP到N，使GP=PN，连接DN、CN、CG，过N作NK⊥CD，交CD延长线于K，在△DNP和△FGP中，DP FPNPD GPFPN PG=⎧⎪∠=∠⎨⎪=⎩，∴△DNP≌△FGP，∴DN=GF=BG=BE=2，∠NDP=∠GFP，∵四边形ABCD和四边形BEFG是菱形，∴CD//AB，EF//BC，∵点A、B、G在一条直线上，∴DC∥EF，∴∠CDP=∠EFP，∵∠ABC=∠BEF=60°，∴∠EFG=∠CBG=120°，∴∠NDP+CDP=∠GFP+∠EFP=∠EFG=120°，即∠NDC=120°，∴∠KDN=60°，∠KND=30°，∴KD=12DN=1，NK=223DN KD-=，∴CK=CD+KD=7，∴CN=22CK NK+=213，在△CDN和△CBG中，CD BCCDN CBGND BG=⎧⎪∠=∠⎨⎪=⎩，∴CN=CG，∠DCN=∠BCG，∴PC⊥GN，∠DCN+∠NCB=∠BCG+∠NCB=∠DCB=120°，即∠NCG=120°，∴∠CNP=12（180°-∠NCG）=30°，∴PC=12CN=13．故答案为：213【点睛】本题考查正方形的性质、菱形的性质、等腰直角三角形的性质、全等三角形的判定与性质、含30°角的直角三角形的性质及勾股定理，正确作出辅助线、熟记30°角所对的直角边等于斜边的一半的性质及全等三角形的判定定理是解题关键．5．（1）详见解析；（2）2BH AE，理由详见解析【分析】1）如图1，连接DF，根据对称得：△ADE≌△FDE，再由HL证明Rt△DFG≌Rt△DCG，可得结论；（2）如图2，作辅助线，构建AM=AE ，先证明∠EDG=45°，得DE=EH ，证明△DME ≌△EBH ，则EM=BH ，根据等腰直角△AEM 得：2EM AE =，得结论；【详解】证明：（1）如图1，连接DF ，∵四边形ABCD 是正方形，∴DA DC =，90A C ∠=∠=︒，∵点A 关于直线DE 的对称点为F ，∴ADE ∆≌FDE ∆，∴DA DF DC ==，90DFE A ∠=∠=︒，∴90DFG ∠=︒，在Rt DFG ∆和Rt DCG ∆中，∵DF DC DG DG =⎧⎨=⎩∴Rt DFG ∆≌Rt DCG ∆（HL ），∴GF GC =；（2）2BH AE =，理由是：如图2，在线段AD 上截取AM ，使AM AE =，∵AD AB =，∴DM BE =，由（1）知：12∠=∠，34∠=∠，∵90ADC ∠=︒，∴123490∠+∠+∠+∠=︒，∴222390∠+∠=︒，∴2345∠+∠=︒，即45EDG ∠=︒，∵EH DE ⊥，∴90DEH ∠=︒，DEH ∆是等腰直角三角形，∴190AED BEH AED ∠+∠=∠+∠=︒，DE EH =，∴1BEH ∠=∠，在DME ∆和EBH ∆中，1DM BE BEH DE EH =⎧⎪∠=∠⎨⎪=⎩∴DME ∆≌EBH ∆∴EM BH =，Rt AEM ∆中，90A ∠=︒，AM AE =，∴EM =，∴BH ； 【点睛】本题考查了正方形的性质，全等三角形的判定定理和性质定理，对称的性质，等腰直角三角形的性质等知识，解决本题的关键是利用正方形的性质得到相等的边和相等的角，证明三角形全等，作出辅助线也是解决本题的关键．6．（1）证明见解析；（2）①BH BG =②BH 的长为或． 【分析】（1）证()DAG BAE SAS △≌△，即可得出结论；（2）①连接GH ，延长HF 交AB 于N ，设AB 与EF 的交点为M ，证()GAB GFH SAS △≌△，得GH GB =，GHF GBA ∠=∠，证GHB ∆为等腰直角三角形，即得结论；②分两种情况，证出点B 、E 、G在一条直线上，求出10AF EG ===，则5OA OG OE ===，由勾股定理求出12OB =，求出BG ，即可得出答案．【详解】（1）∵四边形ABCD 和四边形AEFG 是正方形，∴AD =AB =CB ，AG =AE ，∠DAB =∠GCE =90°，∴∠DAB ﹣∠GAF =∠GCE ﹣∠GAF ，即∠DAG =∠BAE ，在△DAG 和△BAE 中，AD AE DAG BAE AG AE =⎧⎪∠=∠⎨⎪=⎩，∴△DAG ≌△BAE (SAS)，∴DG =BE ；（2）①连接GH ，延长HF 交AB 于N ，设AB 与EF 的交点为M ，如图2所示：∵四边形BCHF 是平行四边形，∴HF //BC ，HF =BC =AB ．∵BC ⊥AB ，∴HF ⊥AB ，∴∠HFG =∠FMB ，又AG //EF ，∴∠GAB =∠FMB ，∴∠HFG =∠GAB ，在△GAB 和△GFH 中，AG FG GAB HFG AB FH =⎧⎪∠=∠⎨⎪=⎩，∴△GAB ≌△GFH (SAS)，∴GH =GB ，∠GHF =∠GBA ，∴∠HGB =∠HNB =90°，∴△GHB 为等腰直角三角形，∴BH 2=， ∴2BH BG= ②分两种情况：a 、如图3所示：连接AF、EG交于点O，连接BE．∵四边形BCHF为菱形，∴CB=FB．∵AB=CB，∴AB=FB=13，∴点B在AF的垂直平分线上．∵四边形AEFG是正方形，∴AF=EG，OA=OF=OG=OE，AF⊥EG，AE=FE=AG=FG，∴点G、点E都在AF的垂直平分线上，∴点B、E、G在一条直线上，∴BG⊥AF．∵AE=52，∴AF=EG2=AE=10，∴OA=OG=OE=5，∴OB2222AB OA=-=-=12，135∴BG=OB+OG=12+5=17，由①得：BH2=BG=172；b、如图4所示：连接AF、EG交于点O，连接BE，同上得：点B、E、G在一条直线上，OB=12，BG=OG+OB﹣OG=12﹣5=7，由①得：BH2=BG=72；综上所述：BH的长为172或72．【点睛】本题是四边形综合题目，考查了正方形的性质、菱形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、勾股定理、线段垂直平分线的判定等知识；本题综合性强，熟练掌握正方形的性质和菱形的性质，证明三角形全等是解题的关键．7．（1）12；（2）证明见详解；（3）125t s=或t=4s．【分析】（1）由勾股定理求出AD即可；（2）由等腰三角形的性质和平行线的性质得出∠PBQ=∠PQB，再由等腰三角形的判定定理即可得出结论；（3）分两种情况：①当点M在点D的上方时，根据题意得：PQ=BP=t，AM=4t，AD=12，得出MD=AD-AM=12-4t，由PQ∥MD，当PQ=MD时，四边形PQDM是平行四边形，得出方程，解方程即可；②当点M在点D的下方时，根据题意得：PQ=BP=t，AM=4t，AD=12，得出MD=AM-AD=4t-12，由PQ∥MD，当PQ=MD时，四边形PQDM是平行四边形，得出方程，解方程即可．【详解】（1）解：∵BD⊥AC，∴∠ADB=90°，∴2222201612AD AB BD=-=-=（cm），（2）如图所示：∵AB=AC，∴∠ABC=∠C，即∠PBQ=∠C，∵PQ∥AC，∴∠PQB=∠C，∴∠PBQ=∠PQB，∴PB=PQ；（3）分两种情况：①当点M在点D的上方时，如图2所示：根据题意得：PQ=BP=t，AM=4t，AD=12，∴MD=AD-AM=12-4t，∵PQ∥AC，∴PQ∥MD，∴当PQ=MD时，四边形PQDM是平行四边形，即：当t=12-4t，时，四边形PQDM是平行四边形，解得：125t=（s）；②当点M在点D的下方时，如图3所示：根据题意得：PQ=BP=t，AM=4t，AD=12，∴MD=AM-AD=4t-12，∵PQ∥AC，∴PQ∥MD，∴当PQ=MD时，四边形PQDM是平行四边形，即：当t=4t-12时，四边形PQDM是平行四边形，解得：t=4（s）；综上所述，当125t s=或t=4s时，以P、Q、D、M为顶点的四边形为平行四边形．【点睛】本题是四边形综合题目，考查了平行四边形的判定、等腰三角形的判定与性质、勾股定理以及分类讨论等知识；本题综合性强，熟练掌握平行四边形的判定方法，进行分类讨论是解决问题（3）的关键．8．（1）见解析；（2）4.8；（3）1282x x- 【分析】 （1）证明△ABP ≌△BCQ 即可得到结论；（2）证明Rt △ABN ≌△Rt △C 'BN 求出DQ ，设AN ＝NC '＝a ，则DN ＝8﹣a ，利用勾股定理即可求出a ；（3）过Q 点作QG ⊥BM 于G ，设MQ ＝BM ＝y ，则MG ＝y ﹣x ，利用勾股定理求出MQ ，再根据面积相减得到答案.【详解】解：（1）证明：∵∠ABC ＝90°∴∠BAP +∠APB ＝90°∵BQ ⊥AP∴∠APB +∠QBC ＝90°，∴∠QBC ＝∠BAP ，在△ABP 于△BCQ 中，ABP BCQ AB BCBAP QBC ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△ABP ≌△BCQ （ASA ），∴BP ＝CQ ，（2）由翻折可知，AB ＝BC '，连接BN ，在Rt △ABN 和Rt △C 'BN 中，AB ＝BC '，BN ＝BN ，∴Rt △ABN ≌△Rt △C 'BN （HL ），∴AN ＝NC '，∵BP ＝13PC ，AB ＝8， ∴BP ＝2＝CQ ，CP ＝DQ ＝6，设AN ＝NC '＝a ，则DN ＝8﹣a ，∴在Rt △NDQ 中，（8﹣a ）2+62＝（a +2）2解得：a ＝4．8，即AN ＝4．8．（3）解：过Q 点作QG ⊥BM 于G ，由（1）知BP ＝CQ ＝BG ＝x ，BM ＝MQ ．设MQ ＝BM ＝y ，则MG ＝y ﹣x ，∴在Rt △MQG 中，y 2＝82+（y ﹣x ）2， ∴322x y x =+． ∴S △BMC ′＝S △BMQ ﹣S △BC 'Q ＝1122BM QG BC QC ''⋅-⋅, ＝1321()88222x x x +⨯-⨯， ＝1282x x-． 【点睛】此题考查正方形的性质，三角形全等的判定及性质，勾股定理，正确理解题意画出图形辅助做题是解题的关键.9．（1）15，8；（2）PE PF CG +=，见解析；（3）534）4【分析】解决问题（1）只需运用面积法：ABC ABP ACP S S S ∆∆∆=+，即可解决问题；（2）解法同（1）；（3）连接PA 、PB 、PC ，作AM BC ⊥于M ，由等边三角形的性质得出152BM BC ==，由勾股定理得出2253AM AB BM =-=ABC ∆的面积12532BC AM =⨯=ABC ∆的面积BCP =∆的面积ACP +∆的面积APB +∆的面积1111()2532222BC PE AC PF AB PG AB PE PF PG =⨯+⨯+⨯=++=，即可得出答案； （4）过点E 作EQ BC ⊥，垂足为Q ，易证BE BF =，过点E 作EQ BF ⊥，垂足为Q ，由解决问题（1）可得PG PH EQ +=，易证EQ DC =，BF DF =，只需求出BF 即可．【详解】解：（1）∵PE AB ⊥，10AB =，3PE =，∴ABP ∆的面积111031522AB PE =⨯=⨯⨯=， ∵PE AB ⊥，PF AC ⊥，CG AB ⊥，且ABC ABP ACP S S S ∆∆∆=+，∴AB CG AB PE AC PF ⋅=⋅+⋅，∵AB AC =，∴358CG PE PF =+=+=.故答案为：15，8.（2）∵PE AB ⊥，PF AC ⊥，CG AB ⊥，且ABC ABP ACP S S S ∆∆∆=+，∴AB CG AB PE AC PF ⋅=⋅+⋅，∵AB AC =， ∴CG PE PF =+.（3）连接PA 、PB 、PC ，作AM BC ⊥于M ，如图2所示：∵10AB AC BC ===，∴ABC ∆是等边三角形，∵AM BC ⊥，∴152BM BC ==， ∴222210553AM AB BM =--=∴ABC ∆的面积11105325322BC AM =⨯=⨯⨯= ∵PE BC ⊥，PF AC ⊥，PG AB ⊥，∴ABC ∆的面积BCP =∆的面积ACP +∆的面积APB +∆的面积111222BC PE AC PF AB PG =⨯+⨯+⨯1()2AB PE PF PG =++ 3=∴225353PE PF PG ⨯++== （4）过点E 作EQ BC ⊥，垂足为Q ，如图3所示：∵四边形ABCD 是矩形，∴AD BC =，90C ADC ∠=∠=︒，∵8AD =，3CF =，∴5BF BC CF AD CF =-=-=，由折叠可得：5DF BF ==，BEF DEF ∠=∠，∵90C ∠=︒， ∴2222534DC DF FC =-=-=，∵EQ BC ⊥，90C ADC ∠=∠=︒，∴90EQC C ADC ∠=︒=∠=∠，∴四边形EQCD 是矩形，∴4EQ DC ==，∵//AD BC ，∴DEF EFB ∠=∠，∵BEF DEF ∠=∠，∴BEF EFB ∠=∠，∴BE BF =，由解决问题（1）可得：PG PH EQ +=，∴4PG PH +=，即PG PH +的值为4.【点睛】本题是四边形综合题目，考查了矩形的性质与判定、等腰三角形的性质与判定、平行线的性质与判定、等边三角形的性质、勾股定理等知识，考查了用面积法证明几何问题，考查了运用已有的经验解决问题的能力，体现了自主探究与合作交流的新理念，是充分体现新课程理念难得的好题．10．（1）①45；②△ADE≌△ECF，理由见解析；（2）5.【分析】（1）①根据矩形的性质得到90ABC BCD ∠=∠=︒，根据角平分线的定义得到45EBC ∠=︒，根据三角形内角和定理计算即可；②利用ASA 定理证明ADE ECF ≅；（2）连接HB ，证明四边形NBEH 是矩形，得到NE BH =，根据勾股定理求出BH 即可.【详解】（1）①∵四边形ABCD 为矩形，∴∠ABC=∠BCD=90°，∵BE 平分∠ABC，∴∠EBC=45°，∴∠BEC=45°，故答案为45；②△ADE≌△ECF，理由如下：∵四边形ABCD 是矩形，∴∠ABC=∠C=∠D=90°，AD=BC ．∵FE⊥AE，∴∠AEF=90°．∴∠AED+∠FEC=180°-∠AEF=90°．∵∠AED+∠DAE=90°，∴∠FEC=∠EAD，∵BE 平分∠ABC，∴∠BEC=45°．∴∠EBC=∠BEC．∴BC=EC．∴AD=EC．在△ADE 和△ECF 中，DAE CEF AD ECADE ECF ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△ADE≌△ECF；（2）连接HB ，如图2，∵FH∥CD，∴∠HFC=180°-∠C=90°．∴四边形HFCD 是矩形．∴DH=CF，∵△ADE≌△ECF，∴DE =CF ．∴DH=DE．∴∠DHE=∠DEH=45°．∵∠BEC=45°，∴∠HEB=180°-∠DEH -∠BEC=90°．∵NH∥BE，NB∥HE，∴四边形NBEH 是平行四边形．∴四边形NBEH是矩形．∴NE=BH．∵四边形ABCD是矩形，∴∠BAH=90°．∵在Rt△BAH中，AB=4，AH=2，【点睛】本题考查的是矩形的判定和性质、全等三角形的判定和性质以及勾股定理的应用，掌握全等三角形的判定定理和性质定理是解题的关键.。

2020年中考数学第一轮复习第五章四边形第二十一讲多边形与平行四边形【基础知识回顾】一、多边形：1、定义：在平面内，由若干条不在同一直线上的线段相连组成的图形叫做多边形，各边相等、也相等的多边形叫做正多边形2、多边形的内外角和：n(n≥3)的内角和是外角和是正n边形的每个外角的度数是，每个内角的度数是。

3、多边形的对角线：多边形的对角线是连接多边形的两个顶点的线段，从n边形的一个顶点出发有条对角线，将多边形分成个三角形，一个n边形共有条对边线【注意：1、三角形是边数最少的多边形2、所有的正多边形都是轴对称图形，正n边形共有条对称轴，边数为数的正多边形也是中心对称图形】二、平面图形的密铺：1、定义：用、完全相同的一种或几种平面图形进行拼接，彼此之间、地铺成一起，这就是平面图形的密铺，又称作平面图形的。

2、密铺的方法：⑴用同一种正多边形密铺，可以用、或⑵用两种正多边形密铺，组合方式有：和、和、和等几种【注意：能密铺的图形在一个拼接处的特点：几个图形的内角拼接在一起时，其和等于并使相等的边互相平合】三、平行四边形1、定义：两组对边分别的四边形是平行四边形，平行四边形ABCD可表示为2、平行四边形的特质：⑴平行四边形的两组对边分别⑵平行四边形的两组对角分别⑶平行四边形的对角线【注意：1、平行四边形是对称图形，对称中心是过对角线交点的任一直线被一组对边截得的线段该直线将原平行四边形分成全等的两个部分】3、平行四边形的判定：⑴用定义判定⑵两组对边分别的四边形是平行四边形⑶一组对边的四边形是平行四边形⑷两组对角分别的四边形是平行四边形⑸对角线的四边形是平行四边形【注意：特别的：一组对边平行，另一组对边相等的四边形和一组对边相等、一组对角相等的四边形都不能保证是平行四边形】4、平行四边形的面积：计算公式 ×同底（等底）同高（等高）的平行四边形面积【注意：夹在两平行线间的平行线段 两平行线之间的距离处处 】 【中考真题考点例析】考点一：多边形内角和、外角和公式例1.（2019年济南）一个n 边形的内角和是720°，则n ＝_____．对应练习1－1( 2019山东济宁12)如图，该硬币边缘镌刻的正九边形每个内角的度数是 ．对应练习1－2（2019年莱芜）若一个正n 边形的每个内角为156°，则这个正n 边形的边数是（ ） A ． 13 B ． 14 C ． 15 D ． 16 考点二：平面图形的密铺例2（漳州）用下列一种多边形不能铺满地面的是（ ） A ．正方形 B ．正十边形 C ．正六边形 D ．等边三角形 对应练习2－1（呼和浩特）只用下列图形中的一种，能够进行平面镶嵌的是（ ） A ．正十边形 B ．正八边形 C ．正六边形 D ．正五边形 考点三：平行四边形的性质例3（2019年济南）如图，在ABCD Y 中，,E F 分别是AD 和BC 上的点，DAF BCE ∠=∠．求证：BFDE =．对应练习3－1（益阳）如图，在平行四边形ABCD 中，下列结论中错误的是（ ）A ．∠1=∠2B ．∠BAD=∠BCDC ．AB=CD D ．AC ⊥BD对应练习3－2（黔西南州）已知▱ABCD 中，∠A+∠C=200°，则∠B 的度数是（ ） A ．100° B ．160° C ．80° D ．60° 考点四：平行四边形的判定例4 （2019年威海）如图，E 是□ABCD 边AD 延长线上一点，连接BE ，CE ，BD ，BE交CD 于点F 。

平行四边形(含多边形)聚焦考点1．平行四边形 (1)性质：①平行四边形两组对边分别__相等__； ②平行四边形对角相等，邻角__互补__； ③平行四边形对角线互相__平分__； ④平行四边形是__中心__对称图形． (2)判定方法：①定义：两组对边平行且相等的四边形是平行四边形； ②两组对边分别__相等__的四边形是平行四边形； ③一组对边平行且相等 的四边形是平行四边形； ④两组对角 分别相等 的四边形是平行四边形； ⑤对角线互相平分的四边形是平行四边形． 2．多边形及其性质 (1)多边形：①内角和定理：n 边形的内角和等于 (n －2)·180° ； ②外角和定理：n 边形的外角和为 360°；③对角线：过n 边形的一个顶点可引n －3条对角线，n 边形共有 n （n －3）2 条对角线．(2)正多边形：①正多边形各边相等，各内角相等，各外角相等；②正n 边形的每一个内角为（n －2）180°n (n≥3)，每一个外角为360°n；③对称性：所有的正多边形都是轴对称图形，正n 边形有_n__条对称轴；当n 是奇数时，是轴对称图形，不是中心对称图形；当n 是偶数时，既是轴对称图形又是中心对称图形.名师点睛考点1：多边形内角和计算【例题1】在一个多边形中，一个内角相邻的外角与其他各内角的和为600°.(1)如果这个多边形是五边形，请求出这个外角的度数；(2)是否存在符合题意的其他多边形？如果存在，请求出边数及这个外角的度数；如果不存在，请说明理由． 【解析】：(1)设这个外角的度数是x °.由题意，得 (5－2)×180－(180－x)＋x ＝600.解得x ＝120. 故这个外角的度数是120°.(2)存在．设这个多边形的边数为n ，这个外角的度数是x °.由题意，得 (n －2)×180－(180－x)＋x ＝600. 整理，得x ＝570－90n.∵0＜x ＜180，即0＜570－90n ＜180. 解得413<n<613.又∵n 为正整数，∴n ＝5或n ＝6. 当n ＝6时，x ＝30.故这个多边形的边数是6，这个外角的度数为30°.归纳：本题注意隐含条件的挖掘，即邻补角和为180°及凸多边形的一个内角是小于平角的角． 考点2：平行四边形的性质与判定【例题2】(2017·大庆)如图，以BC 为底边的等腰△ABC ，点D ，E ，G 分别在BC ，AB ，AC 上，且EG ∥BC ，DE ∥AC ，延长GE 至点F ，使得BE ＝BF .(1)求证：四边形BDEF 为平行四边形；(2)当∠C ＝45°，BD ＝2时，求D ，F 两点间的距离．【解析】(1)证明：∵△ABC 是等腰三角形， ∴∠ABC ＝∠C . ∵EG ∥BC ，DE ∥AC ，∴∠AEG ＝∠ABC ＝∠C ，四边形CDEG 是平行四边形， ∴∠DEG ＝∠C ＝∠AEG . ∵BE ＝BF ，∴∠F ＝∠BEF ＝∠AEG ， ∴∠F ＝∠DEG ， ∴BF ∥DE .又∵EG ∥BC ，即FE ∥BD ， ∴四边形BDEF 为平行四边形； (2)解：∵∠C ＝45°，∴∠ABC ＝∠BFE ＝∠BEF ＝45°， ∴△BDE ，△BEF 均是等腰直角三角形， ∴BF ＝BE ＝22BD ＝ 2. 过点F 作FM ⊥BD 交DB 的延长线于点M ，连接DF ，如解图所示．则△BFM 是等腰直角三角形． ∴FM ＝BM ＝22BF ＝1， ∴DM ＝3.在Rt △DFM 中，由勾股定理得DF ＝12＋32＝10. 即D ，F 两点间的距离为10.考点3： 关于平行四边形的综合探究问题【例题3】(2018四川省眉山市15分 ) 如图①，在四边形ABCD 中，AC ⊥BD 于点E ，AB=AC=BD ，点M 为BC 中点，N 为线段AM 上的点，且MB=MN.（1）求证：BN 平分∠ABE ；（2）若BD=1，连结DN ，当四边形DNBC 为平行四边形时，求线段BC 的长； （3）如图②，若点F 为AB 的中点，连结FN 、FM ，求证：△MFN ∽△BDC. 【答案】（1）证明：∵AB=AC, ∴∠ABC=∠ACB, 又∵M 为BC 中点， ∴AM ⊥BC ，在Rt△ABM中，∴∠ABC+∠MAB=90°,∵AC⊥BD，在Rt△CBE中，∴∠ACB+∠EBC=90°,∴∠MAB=∠EBC,又∵MB=MN，AM⊥BC，∴△NBM为等腰直角三角形，∴∠MBN=∠MNB=45°,∴∠EBC+∠NBE=45°,∠MAB+∠ABN=∠MNB=45°,∵∠MAB=∠EBC,∴∠NBE=∠ABN,∴BN平分∠ABE.（2）解：∵四边形DNBC为平行四边形，设BM=CM=MN=a，则DN=BC=2a，在△ABN和△DBN中，∵∴△ABN≌△DBN中（SAS），∴AN=DN=2a，在Rt△ABM中，∵BD=1，AB=AC=BD，∴AB=1，∴AM2+BM2=AB2，∴（2a+a）2+a2=1，解得：a= .∴BC=2a= .（3）解证明：∵MB=MN，M为BC中点，∴MN=MB= BC，又∵F是AB的中点，AB=AC=BD，在Rt△ABM中，∴MF=AF=BF= AB= BD，∴∠MAB=∠FMN,由（1）知∠MAB=∠EBC,∴∠FMN=∠EBC,又∵,∴△MFN∽△BDC.能力提升一、选择题：1. （2018·浙江宁波·4分）已知正多边形的一个外角等于40°，那么这个正多边形的边数为（）A．6 B．7 C．8 D．9【答案】D【解答】解：正多边形的一个外角等于40°，且外角和为360°，则这个正多边形的边数是：360°÷40°=9．故选：D．2. 在平行四边形ABCD中，∠B=60°，那么下列各式中，不能成立的是（）A．∠D=60° B．∠A=120°C．∠C+∠D=180°D．∠C+∠A=180°【答案】D【解答】解：∵四边形ABCD是平行四边形，∴∠A=∠C，∠B=∠D，而∠B=60°，∴∠A=∠C=120°，∠D=60°．所以D是错误的．故选D．3. （2018•宁波）如图，在▱ABCD中，对角线AC与BD相交于点O，E是边CD的中点，连结OE．若∠ABC=60°，∠BAC=80°，则∠1的度数为（）A．50° B．40° C．30° D．20°【答案】B【解答】解：∵∠ABC=60°，∠BAC=80°，∴∠BCA=180°﹣60°﹣80°=40°，∵对角线AC与BD相交于点O，E是边CD的中点，∴EO是△DBC的中位线，∴EO∥BC，∴∠1=∠ACB=40°．故选：B．4. （2018·浙江省台州·4分）如图，在▱ABCD中，AB=2，BC=3．以点C为圆心，适当长为半径画弧，交BC于点P，交CD于点Q，再分别以点P，Q为圆心，大于PQ的长为半径画弧，两弧相交于点N，射线CN 交BA的延长线于点E，则AE的长是（）A．B．1 C．D．【答案】B【解答】解：∵由题意可知CF是∠BCD的平分线，∴∠BCE=∠DCE．∵四边形ABCD是平行四边形，∴AB∥CD，∴∠DCE=∠E，∠BCE=∠AEC，∴BE=BC=3，∵AB=2，∴AE=BE﹣AB=1，故选：B．5. （2018•陕西•3分）点O是平行四边形ABCD的对称中心，AD＞AB，E.F分别是AB边上的点，且EF＝AB；G、H分别是BC边上的点，且GH＝BC；若S1,S2分别表示∆EOF和∆GOH的面积，则S1,S2之间的等量关系是（）. A．2S1＝3S2. B．2S1＝S2. C． S1＝3S2. D．3S1＝2S2.【答案】A【详解】过点O分别作OM⊥BC，垂足为M，作ON⊥AB，垂足为N，∵点O是平行四边形ABCD的对称中心，∴S平行四边形ABCD=AB•2ON， S平行四边形ABCD=BC•2OM，∴AB•ON=BC•OM，∵S1=EF•ON，S2=GH•OM，EF＝AB，GH＝BC，∴S1=AB•ON，S2=BC•OM，∴2S1＝3S2，故答案为：2S1＝3S2.故选A.二、填空题：6. （2018·湖南省衡阳·3分）如图，▱ABCD的对角线相交于点O，且AD≠CD，过点O作OM⊥AC，交AD于点M．如果△CDM的周长为8，那么▱ABCD的周长是．【答案】16【解答】解：∵ABCD是平行四边形，∴OA=OC，∵OM⊥AC，∴AM=MC．∴△CDM的周长=AD+CD=8，∴平行四边形ABCD的周长是2×8=16．故答案为16．7. （2018•十堰）如图，已知▱ABCD的对角线AC，BD交于点O，且AC=8，BD=10，AB=5，则△OCD的周长为．【答案】14【解答】解：∵四边形ABCD是平行四边形，∴AB=CD=5，OA=OC=4，OB=OD=5，∴△OCD的周长=5+4+5=14，故答案为14．8. （2018•株洲市•3分）如图，在平行四边形ABCD中，连接BD，且BD＝CD，过点A作AM⊥BD于点M，过点D作DN⊥AB于点N，且DN＝，在DB的延长线上取一点P，满足∠ABD＝∠MAP＋∠PAB，则AP＝_____.【答案】6【解析】分析：根据BD=CD，AB=CD，可得BD=BA，再根据AM⊥BD，DN⊥AB，即可得到DN=AM=3，依据∠ABD=∠MAP+∠PAB，∠ABD=∠P+∠BAP，即可得到△APM是等腰直角三角形，进而得到AP=AM=6．详解：∵BD=CD，AB=CD，∴BD=BA，又∵AM⊥BD，DN⊥AB，∴DN=AM=3，又∵∠ABD=∠MAP+∠PAB，∠ABD=∠P+∠BAP，∴∠P=∠PAM，∴△APM是等腰直角三角形，∴AP=AM=6，故答案为：6．9. （2018•无锡）如图，已知∠XOY=60°，点A在边OX上，OA=2．过点A作AC⊥OY于点C，以AC为一边在∠XOY内作等边三角形ABC，点P是△ABC围成的区域（包括各边）内的一点，过点P作PD∥OY交OX于点D，作PE∥OX交OY于点E．设OD=a，OE=b，则a+2b的取值范围是．【答案】2≤a+2b≤5．【解答】解：过P作PH⊥OY交于点H，∵PD∥OY，PE∥OX，∴四边形EODP是平行四边形，∠HEP=∠XOY=60°，∴EP=OD=a，Rt△HEP中，∠EPH=30°，∴EH=EP=a ，∴a+2b=2（a+b ）=2（EH+EO ）=2OH ，当P 在AC 边上时，H 与C 重合，此时OH 的最小值=OC=OA=1，即a+2b 的最小值是2；当P 在点B 时，OH 的最大值是：1+=，即（a+2b ）的最大值是5， ∴2≤a+2b ≤5．三、解答题：10. 已知n 边形的内角和θ＝(n －2)×180°.(1)甲同学说，θ能取360°；而乙同学说，θ也能取630°.甲、乙的说法对吗？若对，求出边数n ；若不对，说明理由；(2)若n 边形变为(n ＋x)边形，发现内角和增加了360°，用列方程的方法确定x. 【解析】：(1)甲对，乙不对．理由：∵θ＝360°，∴(n －2)×180＝360.解得n ＝4. ∵θ＝630°，∴(n －2)×180＝630.解得n ＝112.∵n 为整数，∴θ不能取630°. ∴甲对，乙不对． (2)依题意，得(n －2)×180＋360＝(n ＋x －2)×180. 解得x ＝2.11. (2017·河北模拟)看图回答问题：(1)内角和为2 018°，佳佳为什么说不可能？ (2)音音求的是几边形的内角和？【解析】：(1)∵n 边形的内角和是(n －2)·180°， ∴内角和一定是180°的倍数． ∵2 018÷180＝11……38， ∴内角和为2 018°不可能． (2)设漏加的内角为x °，依题意，得 (n －2)·180＝2 018＋x ， ∴x ＝180n －2 378.∵90＜x ＜180，∴90＜180n －2 378＜180. 解得133245＜n ＜141990，且n 为整数．∴多边形的边数是14.故音音求的是十四边形的内角和．12. 如图，在▱ABCD 中，E ，F 在对角线AC 上．(1)若BE ，DF 分别是△ABO ，△CDO 的中线，求证：四边形BEDF 是平行四边形；(2)若BE ，DF 分别是△ABO ，△CDO 的角平分线，四边形BEDF 还是平行四边形吗？若BE ，DF 分别是△ABO ，△CDO 的高线时，四边形BEDF 还是平行四边形吗？【点拨】(1)可从对角线互相平分上证明四边形BEDF 是平行四边形；(2)BE ，DF 分别是△ABO ，△CDO 的角平分线和高线时，可得到△BOE ≌△DOF ，仍有OE ＝OF ，则有四边形BEDF 是平行四边形． 【解答】解：(1)证明：∵四边形ABCD 是平行四边形，∴OA ＝OC ，OB ＝OD.∵BE ，DF 分别是△ABO ，△CDO 的中线， ∴OE ＝OF.∴四边形BEDF 是平行四边形． (2)∵四边形ABCD 是平行四边形， ∴OB ＝OD ，AB ∥CD. ∴∠ABO ＝∠CDO.∵BE ，DF 分别是△ABO ，△CDO 的角平分线，∴∠OBE ＝∠ODF.又∵∠BOE ＝∠DOF ，∴△BOE ≌△DOF(ASA)．∴OE ＝OF.∴四边形BEDF 是平行四边形．同理可证得BE ，DF 分别是△ABO ，△CDO 的高线时，仍有四边形BEDF 是平行四边形．13. 正方形ABCD 的边长是5，点M 是直线AD 上一点，连接BM ，将线段BM 绕点M 逆时针旋转90°得到线段ME ，在直线AB 上取点F ，使AF ＝AM ，且点F 与点E 在AD 同侧，连接EF ，DF.(1)如图1，当点M 在DA 延长线上时，求证：△ADF ≌△ABM ；(2)如图2，当点M 在线段AD 上时，求证：四边形DFEM 是平行四边形；(3)在(2)的条件下，线段AM 与线段AD 有什么数量关系时，四边形EFDM 的面积最大？并求出这个面积的最大值．图1 图2【解析】：(1)证明：∵四边形ABCD 是正方形，∴∠DAF ＝∠BAM ＝90°，AD ＝AB.在△ADF 和△ABM 中，⎩⎪⎨⎪⎧AF ＝AM ，∠DAF ＝∠BAM ，AD ＝AB ，∴△ADF ≌△ABM(SAS)．(2)证明：延长BM 交DF 于K.∵△ADF ≌△ABM ，∴DF ＝BM ，∠ABM ＝∠ADF.∵EM ＝BM ，∴EM ＝DF.∵∠ABM ＋∠AMB ＝90°，∠AMB ＝∠DMK ，∴∠ADF ＋∠DMK ＝90°.∴∠BKD ＝90°.∵∠EMB ＝90°，∴∠EMB ＝∠BKF ＝90°.∴EM ∥DF.∴四边形EFDM 是平行四边形．(3)设DM ＝x ，则AM ＝AF ＝5－x ，S ▱EFDM ＝DM ·AF ＝x(5－x)＝－(x －52)2＋254. ∵－1＜0，∴x ＝52时，▱EFDM 的面积最大，最大面积为254， 即当AM ＝12AD 时，▱EFDM 的面积最大，最大面积为254. 14. 正方形ABCD 的边长是5，点M 是直线AD 上一点，连接BM ，将线段BM 绕点M 逆时针旋转90°得到线段ME ，在直线AB 上取点F ，使AF ＝AM ，且点F 与点E 在AD 同侧，连接EF ，DF.(1)如图1，当点M 在DA 延长线上时，求证：△ADF ≌△ABM ；(2)如图2，当点M 在线段AD 上时，求证：四边形DFEM 是平行四边形；(3)在(2)的条件下，线段AM 与线段AD 有什么数量关系时，四边形EFDM 的面积最大？并求出这个面积的最大值．图1 图2解：(1)证明：∵四边形ABCD 是正方形，∴∠DAF ＝∠BAM ＝90°，AD ＝AB.在△ADF 和△ABM 中，⎩⎪⎨⎪⎧AF ＝AM ，∠DAF ＝∠BAM ，AD ＝AB ，∴△ADF ≌△ABM(SAS)．(2)证明：延长BM 交DF 于K.∵△ADF ≌△ABM ，∴DF ＝BM ，∠ABM ＝∠ADF.∵EM ＝BM ，∴EM ＝DF.∵∠ABM ＋∠AMB ＝90°，∠AMB ＝∠DMK ，∴∠ADF ＋∠DMK ＝90°.∴∠BKD ＝90°.∵∠EMB ＝90°，∴∠EMB ＝∠BKF ＝90°.∴EM ∥DF.∴四边形EFDM 是平行四边形．(3)设DM ＝x ，则AM ＝AF ＝5－x ，S ▱EFDM ＝DM ·AF ＝x(5－x)＝－(x －52)2＋254. ∵－1＜0，∴x ＝52时，▱EFDM 的面积最大，最大面积为254， 即当AM ＝12AD 时，▱EFDM 的面积最大，最大面积为254.。

中考数学一轮复习平行四边形知识点及练习题含答案一、解答题1．如图正方形ABCD ，DE 与HG 相交于点O （O 不与D 、E 重合）．（1）如图（1），当90GOD ∠=︒，①求证：DE GH =； ②求证：2GD EH DE +>；（2）如图（2），当45GOD ∠=︒，边长4AB =，25HG =，求DE 的长．2．如图1，在正方形ABCD 和正方形BEFG 中，点,,A B E 在同一条直线上，P 是线段DF 的中点，连接,PG PC ．（1）求证：,PG PC PG PC ⊥=．简析：由Р是线段DF 的中点，//DC CF ，不妨延长GP 交DC 于点M ，从而构造出一对全等的三角形，即_______≅________．由全等三角形的性质，易证CMG 是_______三角形，进而得出结论；（2）如图2，将原问题中的正方形ABCD 和正方形BEFG 换成菱形ABCD 和菱形BEFG ，且60ABC BEF ∠=∠=︒，探究PG 与PC 的位置关系及PG PC的值，写出你的猜想并加以证明；（3）当6,2AB BE ==时，菱形ABCD 和菱形BEFG 的顶点都按逆时针排列，且60ABC BEF ∠=∠=︒．若点A B E 、、在一条直线上，如图2，则CP =________；若点A B G 、、在一条直线上，如图3，则CP =________．3．已知正方形ABCD ．（1）点P 为正方形ABCD 外一点，且点P 在AB 的左侧，45APB ∠=︒．①如图（1），若点P 在DA 的延长线上时，求证：四边形APBC 为平行四边形．②如图（2），若点P 在直线AD 和BC 之间，以AP ，AD 为邻边作APQD □，连结AQ ．求∠PAQ 的度数．（2）如图（3），点F 在正方形ABCD 内且满足BC=CF ，连接BF 并延长交AD 边于点E ，过点E 作EH ⊥AD 交CF 于点H ，若EH=3，FH=1，当13AE CF =时．请直接写出HC 的长________．4．（1）如图①，在正方形ABCD 中，AEF ∆的顶点E ，F 分别在BC ，CD 边上，高AG 与正方形的边长相等，求EAF ∠的度数；（2）如图②，在Rt ABD ∆中，90,BAD AD AB ︒∠==，点M ，N 是BD 边上的任意两点，且45MAN ︒∠=，将ABM ∆绕点A 逆时针旋转90度至ADH ∆位置，连接NH ，试判断MN ，ND ，DH 之间的数量关系，并说明理由；（3）在图①中，连接BD 分别交AE ，AF 于点M ，N ，若正方形ABCD 的边长为12，GF=6，BM= 32，求EG ，MN 的长．5．如图，在边长为1的正方形ABCD 中，E 是边CD 的中点，点P 是边AD 上一点（与点A D 、不重合），射线PE 与BC 的延长线交于点Q ．（1）求证：PDE QCE ∆≅∆；（2）若PB PQ =，点F 是BP 的中点，连结EF AF 、，①求证：四边形AFEP 是平行四边形；②求PE 的长．6．已知如图1,四边形ABCD 是正方形，45EAF ︒∠= ．()1如图1,若点,E F 分别在边BC CD 、上,延长线段CB 至G ,使得BG DF =,若3,2BE BG ==，求EF 的长；()2如图2，若点,E F 分别在边CB DC 、延长线上时，求证： .EF DF BE =-()3如图3,如果四边形ABCD 不是正方形，但满足,90,45,AB AD BAD BCD EAF ︒︒=∠=∠=∠=且7, 13,5BC DC CF ===，请你直接写出BE 的长．7．（1）问题探究：如图①，在四边形ABCD 中，AB ∥CD ，E 是BC 的中点，AE 是∠BAD 的平分线，则线段AB ，AD ，DC 之间的等量关系为 ；（2）方法迁移：如图②，在四边形ABCD 中，AB ∥CD ，AF 与DC 的延长线交于点F ，E 是BC 的中点，AE 是∠BAF 的平分线，试探究线段AB ，AF ，CF 之间的等量关系，并证明你的结论；（3）联想拓展：如图③，AB ∥CF ，E 是BC 的中点，点D 在线段AE 上，∠EDF ＝∠BAE ，试探究线段AB ，DF ，CF 之间的数量关系，并证明你的结论．8．点E 在正方形ABCD 的边BC 上，点F 在AE 上，连接FB ，FD ，∠ABF=∠AFB ． （1）如图1，求证：∠AFD=∠ADF ；（2）如图2，过点F 作垂线交AB 于G ，交DC 的延长线于H ，求证：DH=2 AG ； （3）在（2）的条件下，若EF=2，CH=3，求EC 的长．9．如图，ABC ∆是边长为3的等边三角形，点D 是射线BC 上的一个动点（点D 不与点B 、C 重合），ADE ∆是以AD 为边的等边三角形，过点E 作BC 的平行线，交直线AC 于点F ，连接BE ．（1）判断四边形BCFE 的形状，并说明理由；（2）当DE AB ⊥时，求四边形BCFE 的周长；（3）四边形BCFE 能否是菱形？若可为菱形，请求出BD 的长，若不可能为菱形，请说明理由．10．如图，在长方形ABCD 中，AB ＝CD ＝6cm ，BC ＝10cm ，点P 从点B 出发，以2cm /秒的速度沿BC 向点C 运动，设点P 的运动时间为t 秒：（1）PC ＝ cm ．（用t 的代数式表示）（2）当t 为何值时，△ABP ≌△DCP ？（3）当点P 从点B 开始运动，同时，点Q 从点C 出发，以vcm /秒的速度沿CD 向点D 运动，是否存在这样v 的值，使得△ABP 与△PQC 全等？若存在，请求出v 的值；若不存在，请说明理由．【参考答案】***试卷处理标记，请不要删除一、解答题1．（1）①证明见解析；②证明见解析；（2）103DE =． 【分析】（1）过点D 作//DM GH 交BC 延长线于点M ，连接EH ，①由正方形的性质可得//AD BC ，AD CD =，90A ADC DCM ∠=∠=∠=︒，即可证明四边形DGHM 是平行四边形，可得DM=GH ，由90GOD ∠=︒可得∠EDM=90°，根据直角三角形两锐角互余的性质可得12∠=∠，利用ASA 可证明△ADE≌△CDM，可得DE=DM ，即可证明DE=GH ；②由①得DM=DE ，根据勾股定理可得2，利用三角形三边关系即可得结论； （2）过点D 作DN//GH 交BC 于点N ，作ADM CDN ∠=∠，DM 交BA 延长线于点M ，可证明四边形GHND 为平行四边形，可得DN HG =，GD HN =，根据勾股定理可求出CN 的长，利用AAS 可证明ADM CDN ∆∆≌，可得AM NC =，DM DN =，根据平行线的性质∠EDN=45°，根据角的和差故选可得∠MDE=∠EDN ，利用SAS 可证明MDE NDE ∆∆≌，即可证明AE CN EN +=，设AE x =，利用勾股定理可求出x 的值，进而利用勾股定理求出DE 的值即可得答案．【详解】（1）如图（1），过点D 作//DM GH 交BC 延长线于点M ，连接EH ，EM ， ①∵四边形ABCD 为正方形，∴//AD BC ，AD CD =，90A ADC DCM ∠=∠=∠=︒∴四边形DGHM 为平行四边形，∴DM=GH ，GD HM =，∵90GOD ∠=︒，∴90EDM EOH ∠=∠=︒，∴290EDC ∠+∠=︒，∵90ADC ∠=︒，∴190EDC ∠+∠=︒，∴12∠=∠，在ADE ∆和CDM ∆中12A DCM AD DC ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴ADE CDM ∆∆≌，∴DE DM =，∴DE GH =．②在DEM ∆中，∠EDM=90°，∴222DE DM EM +=，∵DE DM =，∴222DE EM =， ∴2EM DE =，在EHM ∆中，HM EH EM +>，∵GD HM =， ∴2GD EH GH +≥．（2）如图（2），过点D 作DN//GH 交BC 于点N ，则四边形GHND 为平行四边形， ∴DN HG =，GD HN =，∵90C ∠=︒，4CD AB ==，25HG DN ==，∴222CN DN DC =-=，∴422BN BC CN =-=-=，作ADM CDN ∠=∠，DM 交BA 延长线于点M ，在ADM ∆和CDN ∆中90C MAD CDN ADM DC AD ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩，∴ADM CDN ∆∆≌，∴AM NC =，DM DN =，∵45GOD EOH ∠=∠=︒，∴45EDN ∠=︒，∴45ADE CDN ∠+∠=︒，∴45ADE ADN MDE ∠+∠=︒=∠，在MDE ∆和NDE ∆中MD ND MDE EDN DE DE =⎧⎪∠=∠⎨⎪=⎩，∴MDE NDE ∆∆≌，∴EM EN =，即AE AM AE CN EN +=+=，设AE x =，则BE=4-x ，在Rt BEN ∆中，2222(2)x x +=+，解得：43x =， ∴22224410433DE AD AE ⎛⎫=+=+= ⎪⎝⎭．【点睛】本题考查正方形的性质、平行四边形的判定与性质、全等三角形的判定与性质、三角形的三边关系及勾股定理，熟练掌握相关性质及判定定理，并正确作出辅助线是解题关键．2．（1）ΔDPM,ΔFPG；等腰直角；（2）线段PG与PC的位置关系是PG⊥PC；PG PC＝；（3）2【分析】（1）延长GP交DC于点M，由Р是线段DF的中点，//DC CF，可得∠MDP=∠GFP，DP=FP，利用ASA可证明△DPM≌△FPG；可得DM=GF，MP=GP，根据正方形的性质可得CM=CG，即可证明△CMG是等腰直角三角形，即可得答案；（2）如图，延长GP交DC于点H，利用ASA可证明△GFP≌△HDP，可得GP＝HP，GF＝HD，进而根据菱形的性质可证明△CHG是等腰三角形，根据等腰三角形“三线合一”的性质可得PG⊥PC，∠HCP=∠GCP，由∠ABC=60°可得∠HCG=120°，进而可得∠CGP=30°，根据含30°角的直角三角形的性质及勾股定理即可得答案；（3）利用线段的和差关系可求出图2中CG的长，由（2）可知∠CGP=30°，根据含30°角的直角三角形的性质即可求出CP的长；在图3中，延长GP到N，使GP=PN，连接DN、CN、CG，过N作NK⊥CD，交CD延长线于K，利用SAS可证明△FGP≌△DNP，可得GF=DN，∠GFP=∠NDP，根据角的和差关系可得∠CDN=120°，根据平角的定义可得∠GBC=120°，利用菱形的性质及等量代换可得DN=GB，利用SAS可证明△NDC≌△GBC，可得CN=CG，∠DCN=∠BCG，根据等腰三角形的性质可得PC⊥GN，根据角的和差关系可得∠NCG=120°，进而可得出∠CNP=30°，可得PC=12CG，根据平角的定义可得∠KDN=60°，即可得出∠KND=30°，根据含30°角的直角三角形的性质可得得出KD的长，利用勾股定理可求出KN的长，再利用勾股定理可求出CN的长，根据含30°角的直角三角形的性质即可得出PC的长．【详解】（1）如图，延长GP交DC于点M，∵Р是线段DF的中点，四边形ABCD、BEFG是正方形，点,,A B E在同一条直线上，∴//DC CF，DP=FP，CD=BC，FG=BG，在△DPM和△FPG中，MDP GFPDP FPDPM FPG∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△DPM≌△FPG，∴DM=FG，KP=GP，∴CD-DM=BC-BC，即CM=CG，∴△CMG是等腰直角三角形，∴PG⊥PC，PG=PC．故答案为：ΔDPM，ΔFPG；等腰直角（2）猜想：线段PG 与PC 的位置关系是PG ⊥PC ；PG PC 3． 如图，延长GP 交DC 于点H ，∵P 是线段DF 的中点，∴FP ＝DP ，∵四边形ABCD 和四边形BEFG 是菱形，∴CD//AB ，CF//BE ，CD ＝CB ，GF=GB ，∵点A B E 、、在一条直线上，∴DC ∥GF ，∴∠GFP ＝∠HDP ， 在△GFP 和△HDP 中，GFP HDP FP DP GPF HPD ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△GFP ≌△HDP ，∴GP ＝HP ，GF ＝HD ，∴CD-DH ＝CB-GB ，即CG ＝CH ，∴△CHG 是等腰三角形．∴PG ⊥PC ，（三线合一），∠HCP=∠GCP ，∵∠ABC ＝∠BEF ＝60°，∴∠HCG=120°，∴∠CGP=12（180°-120°）=30°， ∴CG=2PC ，∴2222(2)3CG PC PC PC PC -=-=， ∴PG PC 3（3）如图2，∵AB=6，BE=2，∴CG=AB-BE=4，由（2）可知∠CGP=30°，PG⊥PC，∴PC=12CG=2，如图3，延长GP到N，使GP=PN，连接DN、CN、CG，过N作NK⊥CD，交CD延长线于K，在△DNP和△FGP中，DP FPNPD GPF PN PG=⎧⎪∠=∠⎨⎪=⎩，∴△DNP≌△FGP，∴DN=GF=BG=BE=2，∠NDP=∠GFP，∵四边形ABCD和四边形BEFG是菱形，∴CD//AB，EF//BC，∵点A、B、G在一条直线上，∴DC∥EF，∴∠CDP=∠EFP，∵∠ABC=∠BEF=60°，∴∠EFG=∠CBG=120°，∴∠NDP+CDP=∠GFP+∠EFP=∠EFG=120°，即∠NDC=120°，∴∠KDN=60°，∠KND=30°，∴KD=12DN=1，223DN KD-=，∴CK=CD+KD=7，∴22CK NK+213在△CDN和△CBG中，CD BCCDN CBG ND BG=⎧⎪∠=∠⎨⎪=⎩，∴CN=CG，∠DCN=∠BCG，∴PC⊥GN，∠DCN+∠NCB=∠BCG+∠NCB=∠DCB=120°，即∠NCG=120°，∴∠CNP=12（180°-∠NCG）=30°，∴PC=12CN=13．故答案为：2，13【点睛】本题考查正方形的性质、菱形的性质、等腰直角三角形的性质、全等三角形的判定与性质、含30°角的直角三角形的性质及勾股定理，正确作出辅助线、熟记30°角所对的直角边等于斜边的一半的性质及全等三角形的判定定理是解题关键．3．（1）①证明见详解；②45PAQ ∠=︒，见解析；（2）5．【分析】（1）①只要证明//PB AC 即可解决问题；②如图2中，连接QC ，作DT DQ ⊥交QC 的延长线于T ，利用全等三角形的性质解决问题即可；（2）如图3中，延长EH 交BC 于点G ，设AE=x ，由题意易得AB=BC=CF=EG=3x ，然后可得CG=2x ，HG=3x-3，CH=3x-1，利用勾股定理求解即可．【详解】（1）①证明：四边形ABCD 是正方形，∴//B DP C ，45DAC ∠=︒，∴135PAC ∠=︒45APB ∠=︒，∴+180APB PAC ∠∠=︒，∴//PB AC∴四边形APBC 是平行四边形；②四边形PADQ 是平行四边形，∴DQ//,//,AP AD PQ AD PQ BC ==，AD//B C ，∴,//PQ BC PQ BC =，∴四边形PQCB 是平行四边形，∴QC//BP ，∴45APQ DQC ∠=∠=︒，90ADC QDT ∠=∠=︒，∴DQ=DT ，45,T DQT ADQ CDT ∠=∠=︒∠=∠，AD=DC ，∴ADQ CDT ≌，∴45AQD T ∠=∠=︒，AP//DQ ，∴45PAQ DQA ∠=∠=︒；（3）CH=5，理由如下：如图3所示：延长EH 交BC 于点G ；四边形ABCD 是正方形，∴AB=BC ，90D ∠=︒， 又EH=3，FH=1，EH ⊥AD ，∴EH//CD ，∴90HGC ∠=︒设AE=x ，1,3AE CF BC CF ==，∴AB=BC=CF=EG=3x ， ∴CG=2x ，HG=3x-3，CH=3x-1 在Rt HGC △中，()()22222243331CG HG CH x x x +=+-=-即，解得121,2x x ==当x=1时，AB=3(不符合题意，舍去)；当x=2时，AB=6，∴CH=5．故答案为5．【点睛】本题主要考查正方形的综合问题、三角形全等及勾股定理，关键是利用已知条件及四边形的性质得到它们之间的联系，然后利用勾股定理求解线段的长即可．4．（1）见解析；（2）MN 2=ND 2+DH 2，理由见解析；（3）EG=4，MN=52【分析】（1）根据高AG 与正方形的边长相等，证明三角形全等，进而证明角相等，从而求出解． （2）用三角形全等和正方形的对角线平分每一组对角的知识可证明结论．（3）设EG=BE=x ，根据正方形的边长得出CE ，CF ，EF ，在Rt △CEF 中利用勾股定理得到方程，求出EG 的长，设MN=a ，根据MN 2=ND 2+BM 2解出a 值即可．【详解】解：（1）在Rt △ABE 和Rt △AGE 中，AB=AG ，AE=AE ，∴Rt △ABE ≌Rt △AGE （HL ）．∴∠BAE=∠GAE ．同理，∠GAF=∠DAF ．∴∠EAF ＝12∠BAD ＝45°； （2）MN 2=ND 2+DH 2．∵∠BAM=∠DAH ，∠BAM+∠DAN=45°，∴∠HAN=∠DAH+∠DAN=45°．∴∠HAN=∠MAN ，又∵AM=AH ，AN=AN ，∴△AMN ≌△AHN （SAS ）．∴MN=HN ，∵∠BAD=90°，AB=AD ，∴∠ABD=∠ADB=45°，∴∠HDN=∠HDA+∠ADB=90°，∴NH 2=ND 2+DH 2，∴MN 2=ND 2+DH 2；（3）∵正方形ABCD 的边长为12，∴AB=AG=12，由（1）知，BE=EG ，DF=FG ．设EG=BE=x ，则CE=12-x ，∵GF=6=DF ，∴CF=12-6=6，EF=EG+GF=x+6，在Rt △CEF 中，∵CE 2+CF 2=EF 2，∴（12-x ）2+62=（x+6）2，解得x=4，即EG=BE=4，在Rt △ABD 中， 22AB AD +2，在（2）中，MN 2=ND 2+DH 2，BM=DH ，∴MN 2=ND 2+BM 2．设MN=a ，则a 2＝()(2212222a+， 即a 2=()(22232a +， ∴a=52MN ＝52【点睛】本题考查正方形的性质，四边相等，对角线平分每一组对角，以及全等三角形的判定和性质，勾股定理的知识点等．5．（1）见解析；（2）①见解析；②6PE =【分析】 （1）由四边形ABCD 是正方形知∠D=∠ECQ=90°，由E 是CD 的中点知DE=CE ，结合∠DEP=∠CEQ 即可得证；（2）①由PB=PQ 知∠PBQ=∠Q ，结合AD ∥BC 得∠APB=∠PBQ=∠Q=∠EPD ，由△PDE ≌△QCE 知PE=QE ，再由EF ∥BQ 知PF=BF ，根据Rt △PAB 中AF=PF=BF 知∠APF=∠PAF ，从而得∠PAF=∠EPD ，据此即可证得PE ∥AF ，从而得证；②设AP x =，则1PD x =-，1CQ x =-，2BQ x =-，利用三角形中位线定理得到()122EF x =-，由EF AP =，构造方程即可求得23x =，在Rt PDE ∆中，利用勾股定理即可求解．【详解】 （1）∵四边形ABCD 是正方形，∴∠D=∠ECQ=90°，∵E 是CD 的中点，∴DE=CE ，又∵∠DEP=∠CEQ ，∴△PDE ≌△QCE （ASA ）；（2）①∵PB=PQ ，∴∠PBQ=∠Q ，∵AD ∥BC ，∴∠APB=∠PBQ=∠Q=∠EPD ，∵△PDE ≌△QCE ，∴PE=QE ，∵PF=BF ，∴EF 是PBQ ∆的中位线，∴EF ∥BQ ，∴在Rt △PAB 中，AF=PF=BF ，∴∠APF=∠PAF ，∴∠PAF=∠EPD ，∴PE ∥AF ，∵EF ∥BQ ∥AD ，∴四边形AFEP 是平行四边形；②设AP x =，则1PD x =-，∴1CQ x =-，∴2BQ x =-，∵EF 是PBQ ∆的中位线，∴()122EF x =-， ∵EFAP =， ∴()122x x -=， ∴23x =， 在Rt PDE ∆中，222PD DE PE +＝，即22221(1)()32PE -+＝，∴PE =． 【点睛】本题考查了正方形的性质、全等三角形的判定与性质、三角形中位线定理、平行四边形的判定和性质以及勾股定理等知识点．掌握全等三角形的判定定理和性质定理、正方形的性质是解题的关键．6．（1）5EF =；（2）见解析；（3）5BE =【分析】（1）先用SAS 证ABG ≌ADF ，可得AG=AF ，∠BAG=∠DAF ，又可证∠EAG=∠EAF ，故可用SAS 证GAE ≌FAE ，EF=GE ，即EF 长度可求；（2）在DF 上取一点G ,使得DG=BE , 连接AG ，先用SAS 证ABE ≌ADG ，可得AE=AG ，∠BAE=∠DAG ，又可证∠EAF=∠GAF ，故可用SAS 证AEF ≌AGF ，可得EF=GF ，且DG=BE ，故EF=DF-DG=DF-BE ；（3）在线段DF 上取BE=DG ，连接AG ，求证∠ABE=∠ADC ，即可用SAS 证ABE ≌ADG ，可得AE=AG ，∠BAE=∠DAG ，又可证∠EAF=∠GAF ，故可用SAS 证AEF ≌AGF ，可得EF=GF ，设BE=x ，则CE= 7+x ，EF=18-x ，根据勾股定理：222CE CF =EF +，即可求得BE 的长度．【详解】解：（1）证明：如图1所示，在正方形ABCD 中，AB=AD ，∠BAD=90°， 在ABG 和ADF 中，AB=AD ABG=ADF BG=DF ⎧⎪∠∠⎨⎪⎩∴ABG ≌ADF （SAS ），∴AG=AF ，∠BAG=∠DAF ，又∵∠DAF+∠FAB=∠FAB+∠BAG=90°，且∠EAF=45°，∴∠EAG=∠FAG-∠EAF=45°=∠EAF ， 在GAE 和FAE 中，AG=AF GAE=FAE AE=AE ⎧⎪∠∠⎨⎪⎩∴GAE ≌FAE （SAS ），∴EF=GE=GB+BE=2+3=5；（2）如下图所示，在DF 上取一点G ,使得DG=BE , 连接AG ，∵四边形ABCD 是正方形，故AB=AD ，∠ABE=∠ADG=90°， 在ABE 和ADG 中，AB=AD ABE=ADG=90BE=DG ⎧⎪∠∠︒⎨⎪⎩∴ABE ≌ADG （SAS ），∴AE=AG ，∠BAE=∠DAG ，∵∠BAG+∠DAG=90°，故∠BAG+∠BAE=90°，∵∠EAF=45°，故∠GAF=45°，∠EAF=∠GAF=45°， 在AEF 和AGF 中，AE=AG EAF=GAF=45AF=AF ⎧⎪∠∠︒⎨⎪⎩∴AEF ≌AGF （SAS ），∴EF=GF ，且DG=BE ，∴EF=DF-DG=DF-BE ；（3）BE=5，如下图所示，在线段DF 上取BE=DG ，连接AG ，∵∠BAD=∠BCD=90°，故∠ABC+∠ADC=180°，且∠ABC+∠ABE=180°，∴∠ABE=∠ADC ， 在ABE 和ADG 中，AB=AD ABE=ADG BE=DG ⎧⎪∠∠⎨⎪⎩∴ABE ≌ADG （SAS ），∴AE=AG ，∠BAE=∠DAG ，∵∠BAG+∠DAG=90°，故∠BAG+∠BAE=90°，∵∠EAF=45°，故∠GAF=45°，∠EAF=∠GAF=45°， 在AEF 和AGF 中，AE=AG EAF=GAF=45AF=AF ⎧⎪∠∠︒⎨⎪⎩∴AEF ≌AGF （SAS ），∴EF=GF ，设BE=x ，则CE=BC+BE =7+x ，EF=GF=DC+CF-DG= DC+CF-BE=18-x ，在直角三角形ECF 中，根据勾股定理：222CE CF =EF +，即：222(7+x)5=(18-x)+，解得x=5，∴BE=x=5．【点睛】本题主要考察了全等三角形的证明及性质、勾股定理，解题的关键在于添加辅助线，找出全等三角形，并用对应边/对应角相等的定理，解决该题．7．（1）AD ＝AB +DC ；（2）AB ＝AF +CF ，证明详见解析；（3）AB ＝DF +CF ，证明详见解析．【分析】（1）结论：AD ＝AB+DC ．延长AE ，DC 交于点F ，证明△ABE ≌△FEC （AAS ），即可推出AB ＝CF ，再证明DA ＝DF ，即可解决问题．（2）结论：AB ＝AF+CF ，如图②，延长AE 交DF 的延长线于点G ，证明方法类似（1）． （3）结论；AB ＝DF+CF ．如图③，延长AE 交CF 的延长线于点G ，证明方法类似（1）．【详解】解：（1）探究问题：结论：AD＝AB+DC．理由：如图①中，延长AE，DC交于点F，∵AB∥CD，∴∠BAF＝∠F，在△ABE和△FCE中，CE＝BE，∠BAF＝∠F，∠AEB＝∠FEC，∴△ABE≌△FEC（AAS），∴CF＝AB，∵AE是∠BAD的平分线，∴∠BAF＝∠FAD，∴∠FAD＝∠F，∴AD＝DF，∵DC+CF＝DF，∴DC+AB＝AD．故答案为AD＝AB+DC．（2）方法迁移：结论：AB＝AF+CF．证明：如图②，延长AE交DF的延长线于点G，∵E是BC的中点，∴CE＝BE，∵AB∥DC，∴∠BAE＝∠G．且BE＝CE，∠AEB＝∠GEC∴△AEB≌△GEC（AAS）∴AB＝GC∵AE是∠BAF的平分线∴∠BAG＝∠FAG，∵∠BAG ∠G ，∴∠FAG ＝∠G ，∴FA ＝FG ，∵CG ＝CF+FG ，∴AB ＝AF+CF ．（3）联想拓展：结论；AB ＝DF+CF ．证明：如图③，延长AE 交CF 的延长线于点G ，∵E 是BC 的中点，∴CE ＝BE ，∵AB ∥CF ，∴∠BAE ＝∠G ，在△AEB 和△GEC 中，BAE G AEB GEC BE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△AEB ≌△GEC ，∴AB ＝GC ，∵∠EDF ＝∠BAE ，∴∠FDG ＝∠G ，∴FD ＝FG ，∴AB ＝DF+CF ．【点睛】本题是四边形的综合问题，考查了全等三角形的判定与性质、等腰三角形的判定与性质、角平分线的性质、三角形三边关系等知识点，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．8．（1）见解析；（2）见解析；（3）7【分析】（1）利用等腰三角形的性质结合正方形的性质得出AF=AD ，则∠AFD=∠ADF ；（2）首先得出四边形AGHN 为平行四边形，可得FM=MD ，进而NF=NH ，ND=NH ，即可得出答案；（3）首先得出△ADN ≌△DCP （ASA ），得到PC=DN ，再利用在Rt △ABE 中，BE 2+AB 2=AE 2，即可求出答案．【详解】（1）证明：∵∠ABF=∠AFB ，∴AB=AF ，∵四边形ABCD 为正方形，∴AB=AD ，∴AF=AD ，∴∠AFD=∠ADF ；（2）证明：如图1所示：过点A 作DF 的垂线分别交DF ，DH 于M ，N 两点， ∵GF ⊥DF ，∴∠GFD=∠AMD=90°，∴AN ∥GH ，∵四边形ABCD 为正方形，∴AG ∥NH ，∴四边形AGHN 为平行四边形，∴AG=NH ，∵AF=AD ，AM ⊥FD ，∴FM=MD ，连接NF ，则NF=ND ，∴∠NFD=∠NDF ，∵∠NFD+∠NFH=∠NDF+∠H ，∴∠NFH=∠H ，∴NF=NH ，∴ND=NH ，∴DH=2NH=2AG ；（3）解：延长DF 交BC 于点P ，如图2所示：∵四边形ABCD 为正方形，∴AD ∥BC ，∴∠ADF=∠FPE ，∴∠PFE=∠AFD=∠ADF=∠FPE ，∴EF=EP=2，∵∠DAM+∠ADM=∠ADM+∠PDC ，∴∠DAM=∠PDC ，∵四边形ABCD 为正方形，∴AD=DC ，∠ADN=∠DCP ，在△ADN 和△DCP 中DAN PDC AD DCADN PCD ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△ADN ≌△DCP （ASA ），∴PC=DN ，设EC=x ，则PC=DN=x+2，DH=2x+4，∵CH=3，∴DC=AB=BC=AF=2x+1∴AE=2x+3，BE=x+1，在Rt △ABE 中，BE 2+AB 2=AE 2，∴（x+1）2+（2x+1）=（2x+3）2．整理得：x 2﹣6x+7=0，解得：x 1=7，x 2=﹣1（不合题意，舍去）∴EC=7．【点睛】本题是四边形综合题，主要考查了全等三角形的判定与性质、勾股定理、正方形的性质、平行四边形的性质等知识，解题关键是正确把握正方形的性质．9．（1）平行四边形，理由见解析；（2）9；（3）可为菱形，BD=6或0【分析】（1）先证明()EAB DAC SAS ∆≅∆，得60ABE C ∠=∠=︒，可得//AC BE ，由两组对边分别平行的四边形是平行四边形可得四边形BCFE 是平行四边形；（2）如图2，证明90AEB =︒∠，根据直角三角形30度角所对的直角边为斜边的一半可得BE 的长，根据平行四边形的周长计算方法可得结论；（3）分两种情况：①当D 在边BC 的延长线上；②当D 在边BC 上时；分别画图可得BD 的长．【详解】解：（1）如图1，四边形BCFE 是平行四边形，理由是：ABC ∆和ADE ∆是等边三角形，AB AC ∴=，AD AE =，60EAD BAC ∠=∠=︒，EAB DAC ∴∠=∠，()EAB DAC SAS ∴∆≅∆，60ABE C ∴∠=∠=︒，60BAC ∠=︒，BAC ABE ∴∠=∠，//AC BE ∴，//EF BC ，∴四边形BCFE 是平行四边形；（2）如图2，ADE ∆是等边三角形，且DE AB ⊥，30EAB DAB ∴∠=∠=︒，由（1）知：60ABE ∠=︒，90AEB ∴∠=︒， 1322BE AB ∴==， ∴四边形BCFE 的周长32()2(3)92BE BC =+=⨯+=；（3）分2种情况：①如图3，当四边形BCFE 是菱形时，BE BC =，由（1）知：3BE CD ==，336BD ∴=+=；②如图4，当四边形BCFE 是菱形时，B 和D 重合，A 和F 重合，此时0BD =；综上，BD 的长为6或0．【点睛】此题是四边形综合题，主要考查了等边三角形的性质，全等三角形的判断和性质，菱形的性质，平行四边形的判定，正确画图和分类讨论思想的运用是解本题的关键．10．（1）(10﹣2t )；（2）t ＝2.5；（3）2.4或2【分析】（1）根据P 点的运动速度可得BP 的长，再利用BC ﹣BP 即可得到CP 的长；（2）当t ＝2.5时，△ABP ≌△DCP ，根据三角形全等的条件可得当BP ＝CP 时，再加上AB ＝DC ，∠B ＝∠C 可证明△ABP ≌△DCP ；（3）此题主要分两种情况①当BA ＝CQ ，PB ＝PC 时，再由∠B ＝∠C ，可得△ABP ≌△QCP ；②当BP ＝CQ ，AB ＝PC 时，再由∠B ＝∠C ，可得△ABP ≌△PCQ ，然后分别计算出t 的值，进而得到v 的值．【详解】解：（1）点P 从点B 出发，以2cm /秒的速度沿BC 向点C 运动，点P 的运动时间为t 秒时，BP ＝2t ，则PC ＝（10﹣2t ）cm ；故答案为：（10﹣2t ）；（2）当t ＝2.5时，△ABP ≌△DCP ，∵当t ＝2.5时，BP ＝2.5×2＝5，∴PC ＝10﹣5＝5，∵在△ABP 和△DCP 中，90AB DC B C BP CP =⎧⎪∠=∠=︒⎨⎪=⎩，∴△ABP ≌△DCP （SAS ）；（3）①如图1，当BA ＝CQ ，PB ＝PC 时，再由∠B ＝∠C ，可得△ABP ≌△QCP ，∵PB＝PC，∴BP＝PC＝12BC＝5，2t＝5，解得：t＝2.5，BA＝CQ＝6，v×2.5＝6，解得：v＝2.4（秒）．②如图2，当BP＝CQ，AB＝PC时，再由∠B＝∠C，可得△ABP≌△PCQ，∵AB＝6，∴PC＝6，∴BP＝10﹣6＝4，2t＝4，解得：t＝2，CQ＝BP＝4，2v＝4，解得：v＝2；综上所述：当v＝2.4秒或2秒时△ABP与△PQC全等．【点睛】此题主要考查了全等三角形的判定，关键是掌握全等三角形全等的条件，找准对应边．。

2020-2021中考数学压轴题专题复习——平行四边形的综合含答案解析一、平行四边形1．四边形ABCD是正方形，AC与BD，相交于点O，点E、F是直线AD上两动点，且AE=DF，CF所在直线与对角线BD所在直线交于点G，连接AG，直线AG交BE于点H．（1）如图1，当点E、F在线段AD上时，①求证：∠DAG=∠DCG；②猜想AG与BE的位置关系，并加以证明；（2）如图2，在（1）条件下，连接HO，试说明HO平分∠BHG；（3）当点E、F运动到如图3所示的位置时，其它条件不变，请将图形补充完整，并直接写出∠BHO的度数．【答案】（1）①证明见解析；②AG⊥BE．理由见解析；（2）证明见解析；（3）∠BHO=45°．【解析】试题分析：（1）①根据正方形的性质得DA=DC，∠ADB=∠CDB=45°，则可根据“SAS”证明△ADG≌△CDG，所以∠DAG=∠DCG；②根据正方形的性质得AB=DC，∠BAD=∠CDA=90°，根据“SAS”证明△ABE≌△DCF，则∠ABE=∠DCF，由于∠DAG=∠DCG，所以∠DAG=∠ABE，然后利用∠DAG+∠BAG=90°得到∠ABE+∠BAG=90°，于是可判断AG⊥BE；（2）如答图1所示，过点O作OM⊥BE于点M，ON⊥AG于点N，证明△AON≌△BOM，可得四边形OMHN为正方形，因此HO平分∠BHG结论成立；（3）如答图2所示，与（1）同理，可以证明AG⊥BE；过点O作OM⊥BE于点M，ON⊥AG于点N，构造全等三角形△AON≌△BOM，从而证明OMHN为正方形，所以HO 平分∠BHG，即∠BHO=45°．试题解析：（1）①∵四边形ABCD为正方形，∴DA=DC，∠ADB=∠CDB=45°，在△ADG和△CDG中，∴△ADG≌△CDG（SAS），∴∠DAG=∠DCG；②AG⊥BE．理由如下：∵四边形ABCD为正方形，∴AB=DC，∠BAD=∠CDA=90°，在△ABE和△DCF中，∴△ABE≌△DCF（SAS），∴∠ABE=∠DCF，∵∠DAG=∠DCG，∴∠DAG=∠ABE，∵∠DAG+∠BAG=90°，∴∠ABE+∠BAG=90°，∴∠AHB=90°，∴AG⊥BE；（2）由（1）可知AG⊥BE．如答图1所示，过点O作OM⊥BE于点M，ON⊥AG于点N，则四边形OMHN为矩形．∴∠MON=90°，又∵OA⊥OB，∴∠AON=∠BOM．∵∠AON+∠OAN=90°，∠BOM+∠OBM=90°，∴∠OAN=∠OBM．在△AON与△BOM中，∴△AON≌△BOM（AAS）．∴OM=ON，∴矩形OMHN为正方形，∴HO平分∠BHG．（3）将图形补充完整，如答图2示，∠BHO=45°．与（1）同理，可以证明AG⊥BE．过点O作OM⊥BE于点M，ON⊥AG于点N，与（2）同理，可以证明△AON≌△BOM，可得OMHN为正方形，所以HO平分∠BHG，∴∠BHO=45°．考点：1、四边形综合题；2、全等三角形的判定与性质；3、正方形的性质2．已知，在矩形ABCD中，AB=a，BC=b，动点M从点A出发沿边AD向点D运动．（1）如图1，当b=2a，点M运动到边AD的中点时，请证明∠BMC=90°；（2）如图2，当b＞2a时，点M在运动的过程中，是否存在∠BMC=90°，若存在，请给与证明；若不存在，请说明理由；（3）如图3，当b＜2a时，（2）中的结论是否仍然成立？请说明理由．【答案】（1）见解析；（2）存在，理由见解析;（3）不成立．理由如下见解析.【解析】试题分析：（1）由b=2a，点M是AD的中点，可得AB=AM=MD=DC=a，又由四边形ABCD 是矩形，即可求得∠AMB=∠DMC=45°，则可求得∠BMC=90°；（2）由∠BMC=90°，易证得△ABM∽△DMC，设AM=x，根据相似三角形的对应边成比例，即可得方程：x2﹣bx+a2=0，由b＞2a，a＞0，b＞0，即可判定△＞0，即可确定方程有两个不相等的实数根，且两根均大于零，符合题意；（3）由（2），当b＜2a，a＞0，b＞0，判定方程x2﹣bx+a2=0的根的情况，即可求得答案．试题解析：（1）∵b=2a，点M是AD的中点，∴AB=AM=MD=DC=a，又∵在矩形ABCD中，∠A=∠D=90°，∴∠AMB=∠DMC=45°，∴∠BMC=90°．（2）存在，理由：若∠BMC=90°，则∠AMB+∠DMC=90°，又∵∠AMB+∠ABM=90°，∴∠ABM=∠DMC，又∵∠A=∠D=90°，∴△ABM∽△DMC，∴AM ABCD DM=，设AM=x，则x aa b x =-，整理得：x2﹣bx+a2=0，∵b＞2a，a＞0，b＞0，∴△=b2﹣4a2＞0，∴方程有两个不相等的实数根，且两根均大于零，符合题意，∴当b＞2a时，存在∠BMC=90°，（3）不成立．理由：若∠BMC=90°，由（2）可知x2﹣bx+a2=0，∵b＜2a，a＞0，b＞0，∴△=b2﹣4a2＜0，∴方程没有实数根，∴当b＜2a时，不存在∠BMC=90°，即（2）中的结论不成立．考点：1、相似三角形的判定与性质；2、根的判别式；3、矩形的性质3．在平面直角坐标系中，四边形AOBC是矩形，点O（0，0），点A（5，0），点B（0，3）．以点A为中心，顺时针旋转矩形AOBC，得到矩形ADEF，点O，B，C的对应点分别为D，E，F．（1）如图①，当点D落在BC边上时，求点D的坐标；（2）如图②，当点D落在线段BE上时，AD与BC交于点H．①求证△ADB≌△AOB；②求点H的坐标．（3）记K为矩形AOBC对角线的交点，S为△KDE的面积，求S的取值范围（直接写出结果即可）．【答案】（1）D（1，3）；（2）①详见解析；②H（175，3）；（3）30334-≤S≤30334+．【解析】【分析】（1）如图①，在Rt△ACD中求出CD即可解决问题；（2）①根据HL证明即可；②，设AH=BH=m，则HC=BC-BH=5-m，在Rt△AHC中，根据AH2=HC2+AC2，构建方程求出m即可解决问题；（3）如图③中，当点D在线段BK上时，△DEK的面积最小，当点D在BA的延长线上时，△D′E′K的面积最大，求出面积的最小值以及最大值即可解决问题；【详解】（1）如图①中，∵A（5，0），B（0，3），∴OA=5，OB=3，∵四边形AOBC是矩形，∴AC=OB=3，OA=BC=5，∠OBC=∠C=90°，∵矩形ADEF是由矩形AOBC旋转得到，∴AD=AO=5，在Rt△ADC中，CD22AD AC-，∴BD=BC-CD=1，∴D（1，3）．（2）①如图②中，由四边形ADEF是矩形，得到∠ADE=90°，∵点D在线段BE上，∴∠ADB=90°，由（1）可知，AD=AO，又AB=AB，∠AOB=90°，∴Rt△ADB≌Rt△AOB（HL）．②如图②中，由△ADB≌△AOB，得到∠BAD=∠BAO，又在矩形AOBC中，OA∥BC，∴∠CBA=∠OAB，∴∠BAD=∠CBA，∴BH=AH，设AH=BH=m，则HC=BC-BH=5-m，在Rt△AHC中，∵AH2=HC2+AC2，∴m2=32+（5-m）2，∴m=175，∴BH=175，∴H（175，3）．（3）如图③中，当点D在线段BK上时，△DEK的面积最小，最小值=12•DE•DK=12×3×（5-34）=30334，当点D在BA的延长线上时，△D′E′K的面积最大，最大面积=12×D′E′×KD′=12×3×（5+342）=303344+．综上所述，30334-≤S≤30334+．【点睛】本题考查四边形综合题、矩形的性质、勾股定理、全等三角形的判定和性质、旋转变换等知识，解题的关键是理解题意，灵活运用所学知识解决问题，学会利用参数构建方程解决问题．4．（问题情境）在△ABC中，AB＝AC，点P为BC所在直线上的任一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D、E，过点C作CF⊥AB，垂足为F．当P在BC边上时（如图1），求证：PD+PE＝CF．证明思路是：如图2，连接AP，由△ABP与△ACP面积之和等于△ABC的面积可以证得：PD+PE＝CF．（不要证明）（变式探究）（1）当点P在CB延长线上时，其余条件不变（如图3），试探索PD、PE、CF之间的数量关系并说明理由；请运用上述解答中所积累的经验和方法完成下列两题：（结论运用）（2）如图4，将长方形ABCD沿EF折叠，使点D落在点B上，点C落在点C′处，点P为折痕EF上的任一点，过点P作PG⊥BE、PH⊥BC，垂足分别为G、H，若AD ＝16，CF＝6，求PG+PH的值．（迁移拓展）（3）在直角坐标系中，直线l1：y＝-43x+8与直线l2：y＝﹣2x+8相交于点A，直线l1、l2与x轴分别交于点B、点C．点P是直线l2上一个动点，若点P到直线l1的距离为2．求点P的坐标．【答案】【变式探究】证明见解析【结论运用】8【迁移拓展】（﹣1，6），（1，10）【解析】【变式探究】连接AP，同理利用△ABP与△ACP面积之差等于△ABC的面积可以证得；【结论运用】过点E作EQ⊥BC，垂足为Q，根据勾股定理和矩形的性质解答即可；【迁移拓展】分两种情况，利用结论，求得点P到x轴的距离，再利用待定系数法可求出P的坐标．【详解】变式探究:连接AP，如图3：∵PD⊥AB，PE⊥AC，CF⊥AB，且S△ABC＝S△ACP﹣S△ABP，∴12AB•CF＝12AC•PE﹣12AB•PD．∵AB＝AC，∴CF＝PD﹣PE；结论运用:过点E作EQ⊥BC，垂足为Q，如图④，∵四边形ABCD是长方形，∴AD＝BC，∠C＝∠ADC＝90°．∵AD＝16，CF＝6，∴BF＝BC﹣CF＝AD﹣CF＝5，由折叠可得：DF＝BF，∠BEF＝∠DEF．∴DF＝5．∵∠C＝90°，∴DC2222106DF CF-=-8．∵EQ⊥BC，∠C＝∠ADC＝90°，∴∠EQC＝90°＝∠C＝∠ADC．∴四边形EQCD是长方形．∴EQ＝DC＝4．∵AD∥BC，∴∠DEF＝∠EFB．∵∠BEF＝∠DEF，∴∠BEF＝∠EFB．∴BE＝BF，由问题情境中的结论可得：PG+PH＝EQ．∴PG+PH＝8．∴PG+PH的值为8；迁移拓展:如图，由题意得：A（0，8），B（6，0），C（﹣4，0）∴AB2210，BC＝10．68∴AB＝BC，（1）由结论得：P1D1+P1E1＝OA＝8∵P1D1＝1＝2，∴P1E1＝6 即点P1的纵坐标为6又点P1在直线l2上，∴y＝2x+8＝6，∴x＝﹣1，即点P1的坐标为（﹣1，6）；（2）由结论得：P2E2﹣P2D2＝OA＝8∵P2D2＝2，∴P2E2＝10 即点P1的纵坐标为10又点P1在直线l2上，∴y＝2x+8＝10，∴x＝1，即点P1的坐标为（1，10）【点睛】本题考查了矩形的性质与判定、等腰三角形的性质与判定及勾股定理等知识点，利用面积法列出等式是解决问题的关键．5．（感知）如图①，四边形ABCD 、CEFG 均为正方形．可知BE=DG ．（拓展）如图②，四边形ABCD 、CEFG 均为菱形，且∠A=∠F ．求证：BE=DG ．（应用）如图③，四边形ABCD 、CEFG 均为菱形，点E 在边AD 上，点G 在AD 延长线上．若AE=2ED ，∠A=∠F ，△EBC 的面积为8，菱形CEFG 的面积是_______．（只填结果）【答案】见解析【解析】试题分析：探究：由四边形ABCD 、四边形CEFG 均为菱形，利用SAS 易证得△BCE ≌△DCG ，则可得BE=DG ；应用：由AD ∥BC ，BE=DG ，可得S △ABE +S △CDE =S △BEC =S △CDG =8，又由AE=3ED ，可求得△CDE 的面积，继而求得答案．试题解析：探究：∵四边形ABCD 、四边形CEFG 均为菱形，∴BC=CD ，CE=CG ，∠BCD=∠A ，∠ECG=∠F ．∵∠A=∠F ，∴∠BCD=∠ECG ．∴∠BCD-∠ECD=∠ECG-∠ECD ，即∠BCE=∠DCG ．在△BCE 和△DCG 中，BC CD BCE DCG CE CG ⎧⎪∠∠⎨⎪⎩＝＝＝ ∴△BCE ≌△DCG （SAS ），∴BE=DG ．应用：∵四边形ABCD 为菱形，∴AD ∥BC ，∵BE=DG ，∴S △ABE +S △CDE =S △BEC =S △CDG =8，∵AE=3ED ，∴S △CDE =1824⨯= , ∴S △ECG =S △CDE +S △CDG =10∴S 菱形CEFG =2S △ECG =20.6．△ABC 为等边三角形，AF AB =．BCD BDC AEC ∠=∠=∠．(1)求证：四边形ABDF 是菱形．(2)若BD 是ABC ∠的角平分线，连接AD ，找出图中所有的等腰三角形．【答案】(1)证明见解析；(2)图中等腰三角形有△ABC ，△BDC ，△ABD ，△ADF ，△ADC ，△ADE ．【解析】【分析】（1）先求证BD ∥AF ，证明四边形ABDF 是平行四边形，再利用有一组邻边相等的平行四边形是菱形即可证明；（2）先利用BD 平分∠ABC ，得到BD 垂直平分线段AC ，进而证明△DAC 是等腰三角形，根据BD ⊥AC,AF ⊥AC ，找到角度之间的关系,证明△DAE 是等腰三角形，进而得到BC ＝BD ＝BA ＝AF ＝DF ，即可解题,见详解.【详解】(1)如图1中，∵∠BCD ＝∠BDC ，∴BC ＝BD ，∵△ABC 是等边三角形，∴AB ＝BC ，∵AB ＝AF ，∴BD ＝AF ，∵∠BDC ＝∠AEC ，∴BD ∥AF ，∴四边形ABDF 是平行四边形，∵AB ＝AF ，∴四边形ABDF 是菱形．(2)解：如图2中，∵BA ＝BC ，BD 平分∠ABC ，∴BD 垂直平分线段AC ，∴DA＝DC，∴△DAC是等腰三角形，∵AF∥BD，BD⊥AC∴AF⊥AC，∴∠EAC＝90°，∵∠DAC＝∠DCA，∠DAC+∠DAE＝90°，∠DCA+∠AEC＝90°，∴∠DAE＝∠DEA，∴DA＝DE，∴△DAE是等腰三角形，∵BC＝BD＝BA＝AF＝DF，∴△BCD，△ABD，△ADF都是等腰三角形，综上所述，图中等腰三角形有△ABC，△BDC，△ABD，△ADF，△ADC，△ADE．【点睛】本题考查菱形的判定，等边三角形的性质，等腰三角形的判定等知识，属于中考常考题型，熟练掌握等腰三角形的性质是解题的关键．7．定义：我们把三角形被一边中线分成的两个三角形叫做“友好三角形”．性质：如果两个三角形是“友好三角形”，那么这两个三角形的面积相等．理解：如图①，在△ABC中，CD是AB边上的中线，那么△ACD和△BCD是“友好三角形”，并且S△ACD=S△BCD．应用：如图②，在矩形ABCD中，AB=4，BC=6，点E在AD上，点F在BC上，AE=BF，AF 与BE交于点O．（1）求证：△AOB和△AOE是“友好三角形”；（2）连接OD，若△AOE和△DOE是“友好三角形”，求四边形CDOF的面积．探究：在△ABC中，∠A=30°，AB=4，点D在线段AB上，连接CD，△ACD和△BCD是“友好三角形”，将△ACD沿CD所在直线翻折，得到△A′CD，若△A′CD与△ABC重合部分的面积等于△ABC面积的，请直接写出△ABC的面积．【答案】（1）见解析；（2）12；探究：2或2．【解析】试题分析：（1）利用一组对边平行且相等的四边形是平行四边形，得到四边形ABFE是平行四边形，然后根据平行四边形的性质证得OE=OB，即可证得△AOE和△AOB是友好三角形；（2）△AOE和△DOE是“友好三角形”，即可得到E是AD的中点，则可以求得△ABE、△ABF的面积，根据S四边形CDOF=S矩形ABCD-2S△ABF即可求解．探究：画出符合条件的两种情况：①求出四边形A′DCB是平行四边形，求出BC和A′D推出∠ACB=90°，根据三角形面积公式求出即可；②求出高CQ，求出△A′DC的面积．即可求出△ABC的面积．试题解析：（1）∵四边形ABCD是矩形，∴AD∥BC，∵AE=BF，∴四边形ABFE是平行四边形，∴OE=OB，∴△AOE和△AOB是友好三角形．（2）∵△AOE和△DOE是友好三角形，∴S△AOE=S△DOE，AE=ED=AD=3，∵△AOB与△AOE是友好三角形，∴S△AOB=S△AOE，∵△AOE≌△FOB，∴S△AOE=S△FOB，∴S△AOD=S△ABF，∴S四边形CDOF=S矩形ABCD-2S△ABF=4×6-2××4×3=12．探究：解：分为两种情况：①如图1，∵S△ACD=S△BCD．∴AD=BD=AB，∵沿CD折叠A和A′重合，∴AD=A′D=AB=×4=2，∵△A′CD与△ABC重合部分的面积等于△ABC面积的，∴S△DOC=S△ABC=S△BDC=S△ADC=S△A′DC，∴DO=OB，A′O=CO，∴四边形A′DCB是平行四边形，∴BC=A′D=2，过B作BM⊥AC于M，∵AB=4，∠BAC=30°，∴BM=AB=2=BC，即C和M重合，∴∠ACB=90°，由勾股定理得：AC=，∴△ABC的面积是×BC×AC=×2×2=2；②如图2，∵S△ACD=S△BCD．∴AD=BD=AB，∵沿CD折叠A和A′重合，∴AD=A′D=AB=×4=2，∵△A′CD与△ABC重合部分的面积等于△ABC面积的，∴S△DOC=S△ABC=S△BDC=S△ADC=S△A′DC，∴DO=OA′，BO=CO，∴四边形A′BDC是平行四边形，∴A′C=BD=2，过C作CQ⊥A′D于Q，∵A′C=2，∠DA′C=∠BAC=30°，∴CQ=A′C=1，∴S△ABC=2S△ADC=2S△A′DC=2××A′D×CQ=2××2×1=2；即△ABC的面积是2或2．考点：四边形综合题．8．如图，已知矩形ABCD中，E是AD上一点，F是AB上的一点，EF⊥EC，且EF＝EC．（1）求证：△AEF≌△DCE．（2）若DE＝4cm，矩形ABCD的周长为32cm，求AE的长．【答案】（1）证明见解析；（2）6cm.【解析】分析：（1）根据EF⊥CE，求证∠AEF=∠ECD．再利用AAS即可求证△AEF≌△DCE．（2）利用全等三角形的性质，对应边相等，再根据矩形ABCD的周长为32cm，即可求得AE的长.详解：（1）证明：∵EF⊥CE，∴∠FEC=90°，∴∠AEF+∠DEC=90°，而∠ECD+∠DEC=90°，∴∠AEF=∠ECD．在Rt△AEF和Rt△DEC中，∠FAE=∠EDC=90°，∠AEF=∠ECD，EF=EC．∴△AEF≌△DCE．（2）解：∵△AEF≌△DCE．AE=CD．AD=AE+4．∵矩形ABCD的周长为32cm，∴2（AE+AE+4）=32．解得，AE=6（cm）．答：AE的长为6cm．点睛：此题主要考查学生对全等三角形的判定与性质和矩形的性质等知识点的理解和掌握，难易程度适中，是一道很典型的题目．9．点P是矩形ABCD对角线AC所在直线上的一个动点（点P不与点A，C重合），分别过点A，C向直线BP作垂线，垂足分别为点E，F，点O为AC的中点．（1）如图1，当点P与点O重合时，请你判断OE与OF的数量关系；（2）当点P运动到如图2所示位置时，请你在图2中补全图形并通过证明判断（1）中的结论是否仍然成立；（3）若点P在射线OA上运动，恰好使得∠OEF＝30°时，猜想此时线段CF，AE，OE之间有怎样的数量关系，直接写出结论不必证明．【答案】（1）OE ＝OF ．理由见解析；（2）补全图形如图所示见解析，OE ＝OF 仍然成立；（3）CF ＝OE+AE 或CF ＝OE ﹣AE ．【解析】【分析】（1）根据矩形的性质以及垂线，即可判定()AOE COF AAS ∆≅∆，得出OE =OF ； （2）先延长EO 交CF 于点G ，通过判定()AOE COG ASA ∆≅∆，得出OG =OE ，再根据Rt EFG ∆中，12OF EG =，即可得到OE =OF ； （3）根据点P 在射线OA 上运动，需要分两种情况进行讨论：当点P 在线段OA 上时，当点P 在线段OA 延长线上时，分别根据全等三角形的性质以及线段的和差关系进行推导计算即可．【详解】（1）OE =OF ．理由如下：如图1．∵四边形ABCD 是矩形，∴ OA =OC ．∵AE BP ⊥，CF BP ⊥，∴90AEO CFO ∠=∠=︒．∵在AOE ∆和COF ∆中，AEO CFO AOE COF OA OC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴()AOE COF AAS ∆≅∆，∴ OE =OF ；（2）补全图形如图2，OE =OF 仍然成立．证明如下：延长EO 交CF 于点G ．∵AE BP ⊥，CF BP ⊥，∴ AE //CF ，∴EAO GCO ∠=∠．又∵点O 为AC 的中点，∴ AO =CO ．在AOE ∆和COG ∆中，EAO GCO AO CO AOE COG ∠=∠⎧⎪=⎨⎪∠=⎩，∴()AOE COG ASA ∆≅∆，∴ OG =OE ，∴Rt EFG ∆中，12OF EG =，∴ OE =OF ； （3）CF =OE +AE 或CF =OE -AE ． 证明如下：①如图2，当点P 在线段OA 上时．∵30OEF ∠=︒，90EFG ∠=︒，∴60OGF ∠=︒，由（2）可得：OF =OG ，∴OGF ∆是等边三角形，∴ FG =OF =OE ，由（2）可得：AOE COG ∆≅∆，∴ CG =AE ．又∵ CF =GF +CG ，∴ CF =OE +AE ；②如图3，当点P 在线段OA 延长线上时．∵30OEF ∠=︒，90EFG ∠=︒，∴60OGF ∠=︒，同理可得：OGF ∆是等边三角形，∴ FG =OF =OE ，同理可得：AOE COG ∆≅∆，∴ CG =AE ．又∵ CF =GF -CG ，∴ CF =OE -AE ．【点睛】本题属于四边形综合题，主要考查了矩形的性质、全等三角形的性质和判定以及等边三角形的性质和判定，解决问题的关键是构建全等三角形和证明三角形全等，利用矩形的对角线互相平分得全等的边相等的条件，根据线段的和差关系使问题得以解决．10．如图，抛物线交x轴的正半轴于点A，点B（，a）在抛物线上，点C是抛物线对称轴上的一点，连接AB、BC，以AB、BC为邻边作□ABCD，记点C纵坐标为n，（1）求a的值及点A的坐标；（2）当点D恰好落在抛物线上时，求n的值；（3）记CD与抛物线的交点为E，连接AE，BE，当△AEB的面积为7时，n=___________．（直接写出答案）【答案】（1）， A（3，0）；（2）【解析】试题解析：（1）把点B的坐标代入抛物线的解析式中，即可求出a的值，令y=0即可求出点A的坐标．（２）求出点D的坐标即可求解；（3）运用△AEB的面积为7，列式计算即可得解.试题解析：（1）当时，由，得（舍去），（1分）∴A（3，0）（2）过D作DG⊥轴于G，BH⊥轴于H.∵CD∥AB，CD=AB∴，∴，∴（3）11．（1）问题发现：如图①，在等边三角形ABC中，点M为BC边上异于B、C的一点，以AM为边作等边三角形AMN，连接CN，NC与AB的位置关系为；（2）深入探究：如图②，在等腰三角形ABC中，BA=BC，点M为BC边上异于B、C的一点，以AM为边作等腰三角形AMN，使∠ABC=∠AMN，AM=MN，连接CN，试探究∠ABC与∠ACN的数量关系，并说明理由；（3）拓展延伸：如图③，在正方形ADBC中，AD=AC，点M为BC边上异于B、C的一点，以AM为边作正方形AMEF，点N为正方形AMEF的中点，连接CN，若BC=10，CN=2，试求EF的长．【答案】（1）NC∥AB；理由见解析；（2）∠ABC=∠ACN；理由见解析；（3）41【解析】分析：（1）根据△ABC ，△AMN 为等边三角形，得到AB=AC ，AM=AN 且∠BAC=∠MAN=60°从而得到∠BAC-∠CAM=∠MAN-∠CAM ，即∠BAM=∠CAN ，证明△BAM ≌△CAN ，即可得到BM=CN ．（2）根据△ABC ，△AMN 为等腰三角形，得到AB ：BC=1：1且∠ABC=∠AMN ，根据相似三角形的性质得到AB AC AM AN＝，利用等腰三角形的性质得到∠BAC=∠MAN ，根据相似三角形的性质即可得到结论； （3）如图3，连接AB ，AN ，根据正方形的性质得到∠ABC=∠BAC=45°，∠MAN=45°，根据相似三角形的性质得出BM AB CN AC＝，得到BM=2，CM=8，再根据勾股定理即可得到答案． 详解：（1）NC ∥AB ，理由如下：∵△ABC 与△MN 是等边三角形，∴AB=AC ，AM=AN ，∠BAC=∠MAN =60°，∴∠BAM=∠CAN ，在△ABM 与△ACN 中， AB AC BAM CAN AM AN =⎧⎪∠=∠⎨⎪=⎩ ， ∴△ABM ≌△ACN （SAS ），∴∠B=∠ACN=60°，∵∠ANC+∠ACN+∠CAN=∠ANC+60°+∠CAN=180°，∴∠ANC+∠MAN+∠BAM=∠ANC+60°+∠CAN=∠BAN+∠ANC=180°，∴CN ∥AB ；（2）∠ABC=∠ACN ，理由如下：∵AB AM BC MN==1且∠ABC=∠AMN ， ∴△ABC ～△AMN ∴AB AC AM AN＝， ∵AB=BC ， ∴∠BAC=12（180°﹣∠ABC ）， ∵AM=MN∴∠MAN=12（180°﹣∠AMN ）， ∵∠ABC=∠AMN ，∴∠BAC=∠MAN ，∴∠BAM=∠CAN ，∴△ABM ～△ACN ，∴∠ABC=∠ACN ；（3）如图3，连接AB ，AN ，∵四边形ADBC ，AMEF 为正方形，∴∠ABC=∠BAC=45°，∠MAN=45°，∴∠BAC ﹣∠MAC=∠MAN ﹣∠MAC即∠BAM=∠CAN ， ∵2AB AM BC AN ==， ∴AB AC AM AN＝， ∴△ABM ～△ACN∴BM AB CN AC ＝， ∴CN AC BM AB ==cos45°=22， ∴22=， ∴BM=2，∴CM=BC ﹣BM=8，在Rt △AMC ，AM=2222108241AC MC +=+=，∴EF=AM=241．点睛：本题是四边形综合题目，考查了正方形的性质、等边三角形的性质、等腰三角形的性质、全等三角形的性质定理和判定定理、相似三角形的性质定理和判定定理等知识；本题综合性强，有一定难度，证明三角形全等和三角形相似是解决问题的关键．12．如图1，若分别以△ABC 的AC 、BC 两边为边向外侧作的四边形ACDE 和BCFG 为正方形，则称这两个正方形为外展双叶正方形．（1）发现：如图2，当∠C =90°时，求证：△ABC 与△DCF 的面积相等．（2）引申：如果∠C ≠90°时，（1）中结论还成立吗？若成立，请结合图1给出证明；若不成立，请说明理由；（3）运用：如图3，分别以△ABC 的三边为边向外侧作的四边形ACDE 、BCFG 和ABMN 为正方形，则称这三个正方形为外展三叶正方形．已知△ABC 中，AC =3，BC =4．当∠C =_____°时，图中阴影部分的面积和有最大值是________．【答案】（1）证明见解析；（2）成立，证明见解析；（3）18.【解析】试题分析：（1）因为AC=DC ，∠ACB=∠DCF=90°，BC=FC ，所以△ABC ≌△DFC ，从而△ABC 与△DFC 的面积相等；（2）延长BC 到点P ，过点A 作AP ⊥BP 于点P ；过点D 作DQ ⊥FC 于点Q ．得到四边形ACDE ，BCFG 均为正方形，AC=CD ，BC=CF ，∠ACP=∠DCQ ．所以△APC ≌△DQC ． 于是AP=DQ ．又因为S △ABC =12BC•AP ，S △DFC =12FC•DQ ，所以S △ABC =S △DFC ； （3）根据（2）得图中阴影部分的面积和是△ABC 的面积三倍，若图中阴影部分的面积和有最大值，则三角形ABC 的面积最大，当△ABC 是直角三角形，即∠C 是90度时，阴影部分的面积和最大．所以S 阴影部分面积和=3S △ABC =3×12×3×4=18． （1）证明：在△ABC 与△DFC 中， ∵{AC DCACB DCF BC FC∠∠＝＝＝，∴△ABC ≌△DFC ．∴△ABC 与△DFC 的面积相等；（2）解：成立．理由如下：如图，延长BC 到点P ，过点A 作AP ⊥BP 于点P ；过点D 作DQ ⊥FC 于点Q ．∴∠APC=∠DQC=90°．∵四边形ACDE ，BCFG 均为正方形，∴AC=CD ，BC=CF ，∠ACP+∠PCD=90°，∠DCQ+∠PCD=90°，∴∠ACP=∠DCQ ．∴{APC DQCACP DCQ AC CD∠∠∠∠＝＝＝，△APC ≌△DQC （AAS ），∴AP=DQ．又∵S△ABC=12BC•AP，S△DFC=12FC•D Q，∴S△ABC=S△DFC；（3）解：根据（2）得图中阴影部分的面积和是△ABC的面积三倍，若图中阴影部分的面积和有最大值，则三角形ABC的面积最大，∴当△ABC是直角三角形，即∠C是90度时，阴影部分的面积和最大．∴S阴影部分面积和=3S△ABC=3×12×3×4=18．考点：四边形综合题13．倡导研究性学习方式，着力教材研究，习题研究，是学生跳出题海，提高学习能力和创新能力的有效途径．下面是一案例，请同学们认真阅读、研究，完成“类比猜想”的问题．习题如图（1），点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则EF=BE+DF，说明理由．解答：∵正方形ABCD中，AB=AD，∠BAD=∠ADC=∠B=90°，∴把△ABE绕点A逆时针旋转90°至△ADE′，点F、D、E′在一条直线上．∴∠E′AF=90°-45°=45°=∠EAF，又∵AE′=AE，AF=AF∴△AE′F≌△AEF（SAS）∴EF=E′F=DE′+DF=BE+DF．类比猜想：（1）请同学们研究：如图（2），在菱形ABCD中，点E、F分别在BC、CD上，当∠BAD=120°，∠EAF=60°时，还有EF=BE+DF吗？请说明理由．（2）在四边形ABCD中，点E、F分别在BC、CD上，当AB=AD，∠B+∠D=180°，∠EAF=∠BAD时，EF=BE+DF吗？请说明理由．【答案】证明见解析．【解析】试题分析：（1）把△ABE绕点A逆时针旋转120°至△ADE′，如图（2），连结E′F，根据菱形和旋转的性质得到AE=AE′，∠EAF=∠E′AF，利用“SAS”证明△AEF≌△AE′F，得到EF=E′F；由于∠ADE′+∠ADC=120°，则点F、D、E′不共线，所以DE′+DF＞EF，即由BE+DF＞EF；（2）把△ABE绕点A逆时针旋转∠BAD的度数至△ADE′，如图（3），根据旋转的性质得到AE′=AE，∠EAF=∠E′AF，然后利用“SAS”证明△AEF≌△AE′F，得到EF=E′F，由于∠ADE′+∠ADC=180°，知F、D、E′共线，因此有EF=DE′+DF=BE+DF；根据前面的条件和结论可归纳出结论．试题解析：（1）当∠BAD=120°，∠EAF=60°时，EF=BE+DF不成立，EF＜BE+DF．理由如下：∵在菱形ABCD中，∠BAD=120°，∠EAF=60°，∴AB=AD，∠1+∠2=60°，∠B=∠ADC=60°，∴把△ABE绕点A逆时针旋转120°至△ADE′，如图（2），连结E′F，∴∠EAE′=120°，∠1=∠3，AE′=AE，DE′=BE，∠ADE′=∠B=60°，∴∠2+∠3=60°，∴∠EAF=∠E′AF，在△AEF和△AE′F中，∴△AEF≌△AE′F（SAS），∴EF=E′F，∵∠ADE′+∠ADC=120°，即点F、D、E′不共线，∴DE′+DF＞EF∴BE+DF＞EF；（2）当AB=AD，∠B+∠D=180°，∠EAF=∠BAD时，EF=BE+DF成立．理由如下：如图（3），∵AB=AD，∴把△ABE绕点A逆时针旋转∠BAD的度数至△ADE′，如图（3），∴∠EAE′=∠BAD，∠1=∠3，AE′=AE，DE′=BE，∠ADE′=∠B，∵∠B+∠D=180°，∴∠ADE′+∠D=180°，∴点F、D、E′共线，∵∠EAF=∠BAD，∴∠1+∠2=∠BAD，∴∠2+∠3=∠BAD，∴∠EAF=∠E′AF，在△AEF和△AE′F中，∴△AEF≌△AE′F（SAS），∴EF=E′F，∴EF=DE′+DF=BE+DF；归纳：在四边形ABCD中，点E、F分别在BC、CD上，当AB=AD，∠B+∠D=180°，∠EAF=∠BAD时，EF=BE+DF．考点：四边形综合题．14．已知：如图，四边形ABCD和四边形AECF都是矩形，AE与BC交于点M，CF与AD交于点N．（1）求证：△ABM≌△CDN；（2）矩形ABCD和矩形AECF满足何种关系时，四边形 AMCN是菱形，证明你的结论．【答案】（1）证明见解析；（2）当AB＝AF时，四边形AMCN是菱形．证明见解析；【解析】试题分析：（1）由已知条件可得四边形AMCN是平行四边形，从而可得AM=CN，再由AB=CD，∠B=∠D=90°，利用HL即可证明；（2）若四边形AMCN为菱形，则有AM=AN，从已知可得∠BAM=∠FAN，又∠B=∠F=90°，所以有△ABM≌△AFN，从而得AB=AF，因此当AB＝AF时，四边形AMCN是菱形．试题解析：（1）∵四边形ABCD是矩形，∴∠B＝∠D＝90°，AB＝CD，AD∥BC．∵四边形AECF是矩形，∴AE∥CF．∴四边形AMCN是平行四边形．∴AM＝CN．在Rt△ABM和Rt△CDN中，AB＝CD，AM＝CN，∴Rt△ABM≌Rt△CDN．（2）当AB＝AF时，四边形AMCN是菱形．∵四边形ABCD、AECF是矩形，∴∠B＝∠BAD＝∠EAF＝∠F＝90°．∴∠BAD－∠NAM＝∠EAF－∠NAM，即∠BAM＝∠FAN．又∵AB＝AF，∴△ABM≌△AFN．∴AM＝AN．由（1）知四边形AMCN是平行四边形，∴平行四边形AMCN是菱形．考点：1．矩形的性质；2．三角形全等的判定与性质；3．菱形的判定．15．如图，正方形ABCO的边OA、OC在坐标轴上，点B坐标为（3，3）．将正方形ABCO 绕点A顺时针旋转角度α（0°＜α＜90°），得到正方形ADEF，ED交线段OC于点G，ED的延长线交线段BC于点P，连AP、AG．（1）求证：△AOG≌△ADG；（2）求∠PAG的度数；并判断线段OG、PG、BP之间的数量关系，说明理由；（3）当∠1=∠2时，求直线PE的解析式；（4）在（3）的条件下，直线PE上是否存在点M，使以M、A、G为顶点的三角形是等腰三角形？若存在，请直接写出M点坐标；若不存在，请说明理由．【答案】（1）见解析（2）∠PAG =45°，PG=OG+BP．理由见解析（3）y=x﹣3．（4）、．【解析】试题分析：(1)由AO=AD，AG=AG，根据斜边和一条直角边对应相等的两个直角三角形全等，判断出△AOG≌△ADG即可．(2)首先根据三角形全等的判定方法，判断出△ADP≌△ABP，再结合△AOG≌△ADG，可得∠DAP=∠BAP，∠1=∠DAG；然后根据∠1+∠DAG+∠DAP+∠BAP=90°，求出∠PAG的度数；最后判断出线段OG、PG、BP之间的数量关系即可．(3)首先根据△AOG≌△ADG，判断出∠AGO=∠AGD；然后根据∠1+∠AGO=90°，∠2+∠PGC=90°，判断出当∠1=∠2时，∠AGO=∠AGD=∠PGC，而∠AGO+∠AGD+∠PGC=180°，求出∠1=∠2=30°；最后确定出P、G两点坐标，即可判断出直线PE的解析式．(4)根据题意，分两种情况：①当点M在x轴的负半轴上时；②当点M在EP的延长线上时；根据以M、A、G为顶点的三角形是等腰三角形，求出M点坐标是多少即可．试题解析：(1)在Rt△AOG和Rt△ADG中，（HL）∴△AOG≌△ADG．(2)在Rt△ADP和Rt△ABP中，∴△ADP≌△ABP，则∠DAP=∠BAP；∵△AOG≌△ADG，∴∠1=∠DAG；又∵∠1+∠DAG+∠DAP+∠BAP=90°，∴2∠DAG+2∠DAP=90°，∴∠DAG+∠DAP=45°，∵∠PAG=∠DAG+∠DAP，∴∠PAG=45°；∵△AOG≌△ADG，∴DG=OG，∵△ADP≌△ABP，∴DP=BP，∴PG=DG+DP=OG+BP．(3)解：∵△AOG≌△ADG，∴∠AGO=∠AGD，又∵∠1+∠AGO=90°，∠2+∠PGC=90°，∠1=∠2，∴∠AGO=∠PGC，又∵∠AGO=∠AGD，∴∠AGO=∠AGD=∠PGC，又∵∠AGO+∠AGD+∠PGC=180°，∴∠AGO=∠AGD=∠PGC=180°÷3=60°，∴∠1=∠2=90°﹣60°=30°；在Rt△AOG中，∵AO=3，∴OG=AOtan30°=3×=，∴G点坐标为（，0），CG=3﹣，在Rt△PCG中，PC===3（﹣1），∴P点坐标为：（3，3﹣3 ），设直线PE的解析式为：y=kx+b，则，解得：，∴直线PE的解析式为y=x﹣3．(4)①如图1，当点M在x轴的负半轴上时，，∵AG=MG，点A坐标为（0，3），∴点M坐标为（0，﹣3）．②如图2，当点M在EP的延长线上时，，由（3），可得∠AGO=∠PGC=60°，∴EP与AB的交点M，满足AG=MG，∵A点的横坐标是0，G点横坐标为，∴M的横坐标是2，纵坐标是3，∴点M坐标为（2，3）．综上，可得点M坐标为（0，﹣3）或（2，3）．考点：几何变换综合题．。