反比例函数的图象和性质导学案

17.1.2反比例函数的图像和性质一．学习目标1．会用描点法画反比例函数的图象2.结合图象分析并掌握反比例函数的性质3．积极展示，挑战自我。

学习重点：理解并掌握反比例函数的图象和性质学习难点：正确画出图象，通过观察、分析，归纳出反比例函数的性质二．学法指导：自主学习课本第41--- 43页，用红笔划出重要知识，完成导学案，并记熟基础知识，用红笔做好疑难标记。

三．基础知识一、探究研讨：问题：我们已知道，一次函数y=kx+b（k≠0）的图象是一条直线，•那么反比例函数y=kx（k为常数且k≠0）的图象是什么样呢？【活动1】尝试用描点法来画出反比例函数的图象．画出反比例函数y=6x和y=-6x的图象．描点，以表中各对应值为坐标，在直角坐标系中描出各点．连线，用平滑的曲线把所描的点依次连接起来．思考：反比例函数y=kx（k≠0）的图象在哪些象限由什么因素决定？•在每一个象限内，y随x 的变化情况如何？它可能与坐标轴相交吗？归纳：（1）反比例函数y=kx（k为常数，k≠0）的图象是双曲线．（2）当k>0时，双曲线的两支分别位于第__________象限，在每个象限内，y•值随x值的增大而．____________（3）当k<0时，双曲线的两支分别位于第__________四象限，在每个象限内，y•值随x 值的增大而____________．四．拓展提升：（教材42页练习）五．整理导学案六．达标测评下列图象中，是反比例函数的图象的是（）七、归纳总结八、我的收获池北二中八年级数学学科导学案编号：14时间：年月日星期：班级：小组：姓名：设计人：姜春华课型：综合课备课组长：教研组长：装订线1。

17．1．2反比例函数的图象和性质（1）执教人：新疆石河子五中谢红英执教班级：8（6）班学习目标：1．会用描点法画反比例函数的图象；2．结合函数图象分析、归纳反比例函数的性质，并能正确运用；3．在学习过程中领会感悟数形结合的思想方法。

学习重点：理解并掌握反比例函数的图象和性质学习难点：正确画出图象，通过观察、分析，归纳出反比例函数的性质学习准备：1．举出反比例函数实例2．用描点法画图象的步骤是__________、__________、__________3．一次函数y=kx+b（k≠0）的图象是__________,那么反比例函数y=kx（k为常数且k≠0）的图象是什么样呢？尝试用描点法来画出反比例函数y=6x和y=-6x的图象．（在坐标纸上完成，在不同的坐标系内）学习过程：【活动1】小组就准备活动完成的情况交流讨论，用描点法画反比例函数的图象应注意哪些问题？【活动2】在同一个平面直角坐标系中画出反比例函数y=3x和y=-3x的图象．【活动3】观察分析：y=6x和y=-6x的图象及y=3x和y=-3x的图象探究：（1）它们有什么共同特征和不同点？（2）每个函数的图象分别位于哪几个象限？（3）在每一个象限内，y随x的变化而如何变化？它可能与坐标轴相交吗？（4）我们还发现了……猜想：反比例函数y=kx（k≠0）的图象在哪些象限由什么因素决定？•在每一个象限内，y随x的变化情况如何？归纳：（1）反比例函数y=kx（k为常数，k≠0）的图象是_________．（2）当k>0时，双曲线的两支分别位于第__________象限，在每个象限内．．．．．．，y•值随x值的增大而____________（3）当k<0时，双曲线的两支分别位于第__________象限，在每个象限内．．．．．．，y•值随x值的增大而____________．★在上述探究活动中，我们运用了哪些数学思想方法？我学我用（一）基础训练(基础题）1、请指出下面的图像中那一个是反比例函数的图像2、如图，这是下列四个函数中哪一个函数的图象（A ）y=5x （B ）y=2x+3 （C ）x y 4= （D ）xy 3-=3、仔细填一填：⑴函数 的图象在第________象限, 在每一象限内，y 随x 的增大而_________.⑵ 函数 的图象在第________象限, 在每一象限内，y 随x 的增大而_________.⑶函数 , 当x>0时,图象在第____象限,y 随x 的增大而_________.（二）变式训练（中档题）1、已知反比例函数(1) 若函数的图象位于第一、三象限， 则k______; (2) 若在每一象限内，y 随x 增大而增大， 则k______.2、（江苏南京）反比例函数 （K 为常数）图象位于（ ）Ａ．第一、二象限 Ｂ．第一、三象限 Ｃ．第二、四象限 Ｄ．第三、四象限 3、（2012菏泽）反比例函数xy 4=图象上的两点为),(),,(2211y x y x 且21x x ，则下列关系成立的是（） Ａ．1y ＞2y Ｂ．1y ＜2y Ｃ．1y =2y Ｄ．不能确定4、反比例函数xy 2-=，当x ＝－2时，y ＝ ；当x ＜－2时；y 的取值范围是 5、已知反比例函数52)1(--=a x a y ，当x >0时，y 随x 的增大而增大，求函数关系式。

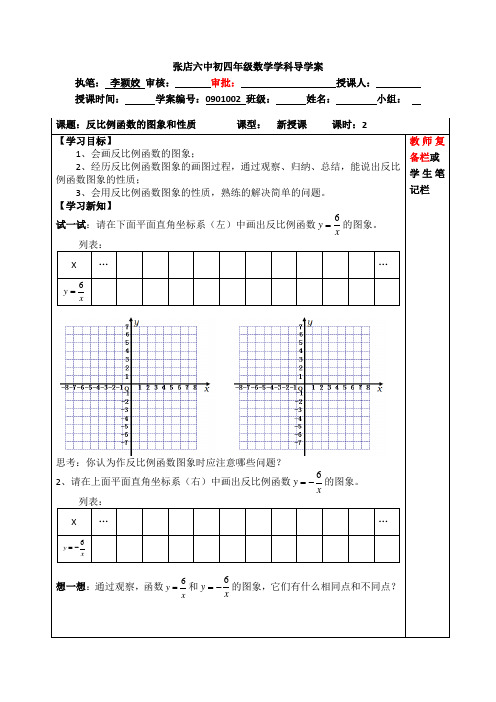
5.2 反比例函数的图象与性质（一）学习目标1．会作反比例函数的图象。

2．能从函数图象中获取信息，指导反比例函数的主要性质。

回顾交流1、请举一个一次函数的例子 正比例函数的例子2、一次函数的图象是 作函数图像的一般步骤是3、下列关系是反比例函数的是 （1）圆的周长C 与圆的半径R ； （2）圆的面积S 与圆的半径R ；（3）汽车从A 地到B 地所需的时间t 与平均速度v ； （4）当电池的电压一定时，电阻R 与电流强度I 。

4、请举一个反比例函数的例子 反比例函数的图像是直线吗？ 它会不会和坐标轴相交呢？为什么？ 自学探究你能画出xy 4-=的图象吗？x -8 -4 -3 -2 -1 -0.5 0.5 1 2 3 4 8xy 4-=议一议（1）你认为作反比例函数图象时应注意哪些问题？（2）在连线时必须用 连接各点。

曲线的发展趋势是（3）观察x y 4=和xy 4-=的图象，它们有什么相同点和不同点？ 总结：反比例函数图像的性质：反比例函数y = xk的图象是(1) 当 k>0 时，两支曲线分别位于第___、___象限， (2) 当 k<0 时，两支曲线分别位于第___、___象限. 练习巩固1.己知函数 的图象是双曲线,且y 随x 的增大而增大,则m=______;2.若M(2,2)和N(b,－1－n2)是反比例函数 图象上两点,则此函数的图象在第__________象限. 3.如果反比例函数xmy 41-=的图象位于第二、四象限，那么m 的范围为 . 4.所受压力为F (F 为常数且F ≠ 0) 的物体，所受压强P 与所受面积S 的图象大致为( )5．反比例函数 2k y x= (0≠k )的图象位于 （ ）（A ） 第一、二象限 （B ） 第一、三象限 （C ） 第二、四象限 （D ） 第一、四象限 回顾总结本节课主要内容是反比例函数的图像，你能说出它的图像的特点吗？()2212--=m x m y x ky =反馈练习 1．反比例函数xy 4=的图象是________，过点(2-，____)，其图象分布在_ __象限； 2．已知y 与x 成反比例，当1=y 时，4=x ，则当2=x 时，_____=y ；3．反比例函数和正比例函数的图象都经过点A(1-，2-)，则这两个函数的解析式分别是_________和_________；4．某厂有煤1500吨，这些煤能用的天数y 与每天用煤的吨数x 之间的函数关系式为_______ 5．下列等式中，哪个等式表示y 是x 的反比例函数 （ ） （A ） k y x =（B ） 23y x = （C ） 121y x =+ （D ） 21xy -= 6．已知反比例函数的图象经过点(1，2)，则它的图象也一定经过 （ ） （A ） (1-，2-) （B ） (1-，2) （C ） (1，2-) （D ） (2-，1)7．反比例函数 2k y x= (0≠k )的图象位于 （ ）（A ） 第一、二象限 （B ） 第一、三象限 （C ） 第二、四象限 （D ） 第一、四象限 8．如图，反比例函数ky x=的图象经过点A ，则k 的值是 （ ） （A ） 2 （B ） 1.5 （C ） 3- （D ） 32-9．点A 为反比例函数图象上一点，它到原点的距离为5，到x 轴的距离为3，若点A 在第二象限内，则这个反比例函数的解析式为 （ ） （A ） 12y x =（B ）12y x =- （C ） 112y x = （D ） 112y x=- 10．反比例函数my x=的图象分布在第二、四象限，则点(m ，2-m )在 （ ） （A ） 第一象限 （B ） 第二象限 （C ） 第三象限 （D ） 第四象限 11．若函数21(31)n n y n x --=-是反比例函数，且它的图象在二、四象限内，则n 的值是（ ）（A ）0 （B ） 1 （C ） 0或1 （D ） 非上述答案 12．已知12y y y =+，其中1y 与1x成反比例且比例系数为1k ，2y 与2x 成正比例且比系数为2k ，若1-=x 时，0=y ，则1k 与2k 的关系为 （ ） （A ） 12k k =- （B ） 12k k ≠ （C ） 121k k =- （D ） 12k k = 提升能力已知正比例函数y kx =与反比例函数3y x=的图象都过A(m ，1)点．求: (1)正比例函数的解析式；(2)正比例函数与反比例函数的另一个交点的坐标．。

y = x
1 反比例函数的图像与性质（一）
学习目标：
1、进一步熟悉作函数图象的主要步骤，会作反比例函数的图象；
2、观察反比例函数图象的特征从中得到反比例函数的简单性质
3、在自主探究反比例函数性质的过程中，感知反比例函数图象的对称性 过程：
一、复习回顾，引入新知
1. 下列函数中哪些是反比例函数？ ① y = 3x -1 ②y = 2x ③ ④
⑤ ⑥ ⑦ ⑧
二、动手画画，认识图象 画出反比例函数 x
y 4
= 的函数图象
2、 描点
3、 连线
通过刚刚的画图，你认为，画图时应注意哪些问题？ 三、观察图象，揭示函数 1、 画出反比例函数
y 4
-
=的函数图象。

观察：函数x
y =
和x y -= 的图象有什么相同点和不同点？
四、运用新知，巧妙解答
3、反比例函数 经过点（1， ）。

选作：5、若点 在函数 （x ＜0）的图象上，且 ，则它的图象大致是（ ）(2008年江西中考题）
五、自我反思，自我收获 1、 知识收获 2、合作收获 六、作业 必做： 选作：
自留作业：根据今天画 和 两个 函数图象，请你继续探索，反比例函数还存在什么性质？
),(00y x x
k y =200-=y x。

反比例函数的图像和性质（1）导学案学习目标1．会画反比例函数图象，理解反比例函数的图象和性质．2．感悟“数形结合”、“变化与对应”和“转化”的数学思想，并能应用数形结合和转化思想根据反比例函数的图象探究其性质．学习重点：1、反比函数的图像画法2、反比例函数的性质。

学习难学习难点：反比例函数的性质。

一、知识链接：（忆一忆）（注意：这里第1、2题要学生在上课前写在黑板上，可以多写几组，上课时，老师要稍微点一下。

为下面探究反比例函数的性质做一个铺垫。

3、4题问一下就可以了。

）1、函数做图的步骤是___________、_______________、____________。

2、正比例函数的性质填写下表：3、正比例函数的图像和性质是怎么得到的？是如何研究的？（经过哪几个步骤）4、反比例函数的表达式 ___________________________解析式中自变量x的取值能为0吗？为什么______________________、二、合作探究、展示交流1、做一做（展示）问题：反比例函数的图像是什么样的？画出下列函数图像①y=10/x y=8/x y=6/x（注意每两个小组做一个）做图应该注意的几点：（注意这里是学生在做图时思考的问题，教师在讲解时也要让学生进行口答）（1）列表时取值应注意什么？x的取值能为零吗？为什么？（2）连线时应该注意什么？（3）反比例函数图像还是直线吗？是什么？（4）图像和坐标轴有交点吗？为什么？（这里需要小组合作探究一下，从图像中和解析式中一起来考虑）2、议一议（这是小组合作的部分，要求小组成员合作完成）问题一：（1）观察前三个函数的解析式有什么共同点：（2）观察前三个函数图像有什么共同点：有哪些特征？你能填写下表吗？3）当取不同大于0的值时，上述结论是否适用于所有的反比例函数？（注意：这里需要教师用几何画板演示，还有要学生从解析式来分析所有的函数都符合这一规律）问题二：做出下列反比例函数的图像：④y=－6/x ⑤y=－8/x ⑥y=－10/x （注意每两个小组做一个）（4）观察后三个函数解析式有什么共同点：（5）观察后三个函数的图像有什么共同点：你能填写下表吗？（6）当取不同小于0的值时，上述结论是否适用于所有的反比例函数？问题三：（7）前三个函数解析式和后三个函数解析式有什么不同？（k的取值范围不同）前三个函数图象和后三个函数图象有什么不同？由什么决定的?（8）你能总结出反比例函数图像的性质吗？在新课改的形式下，如何激发教师的教研热情，提升教师的教研能力和学校整体的教研实效，是摆在每一个学校面前的一项重要的“校本工程”。

城关九年制学校“五问五学”模式导学案
城关九年制学校“五问五学”模式导学案五、拓展延伸
1．若反比例函数y＝k
x(k＜0)的函数图象过点P(2，m)，Q(1，n)，则m与n的大小关系是：m____n (填
“＞”“＝”或“＜”)．
2．已知一次函数y＝x－b与反比例函数y＝2
x的图象，
有一个交点的纵坐标是2，则b的值为________．3.当k>0时，下列图像中哪个可能是y=kx与k
y
x
=（k ≠0）在同一坐标系中的图像（）
：4.已知反比例函数的图像经过点A（2，6）。

5.如图，它是反比例函数
5
m
y
x
-
=的图像的一支，
根据图像，回答下列问题：
⑴图像的另一支在哪个象限？常数m的取值范
围是什么？
⑵在这人函数的图像的某一支上任取点
()
11
,
A x y和点()
22
,
B x y，如果
12
x x
>，那么1y和2y
有怎样的大小关系？
这些问题需要同学帮我解决这些问题需要老师帮我解决
组次小组长
展演卡
组次展演人选主持人
3．反比例函数y＝
k2＋1
x的图象大致是()。

反比例函数的图象和性质导学案一、新课导入 1.课题导入：我们都知道一次函数的图象是一条直线，二次函数的图象是抛物线，那么反比例函数的图象是什么样的呢？这节课我们一起来画反比例函数的图象. 2.学习目标：（1）会用描点法画反比例函数的图象. （2）根据反比例函数的图象探究其性质. 3.学习重难点：反比例函数的图象和性质. 二、分层学习：第一层次学习1.自学指导（1）自学內容：P4例2至P5练习前. （2）自学时间：10分钟.（3）自学方法：学生观察、分析及归纳，通过对比理解和掌握所学的内容. （4）自学参考提纲： ①画出反比例函数y =x6与y =x12的图象. 列表：描点连线：②观察反比例函数y =x 6和y =x12的图象. ○a 两个函数的图象分别位于哪些象限？ ○b 在每一个象限内，随着x 的增大，y 如何变化？你能有它们的解析式说明理由吗？ ③k>0⇔函数xky =的图象分别位于第 象限⇔在每个象限内y 都随x 的增大而 . 2.自学：学生可结合自学指导进行自学.3.助学：（1）师助生：①明了学情：了解学生是否会列表，是否理解表中的数据的意义以及画图中存在的问题.②差异指导：根据学情分类指导.（2）生助生：同桌之间、小组内交流、研讨.4.强化：k>0⇔函数的图象分别位于第一、三象限⇔在每一象限内，y 都随x 的增大而减小.第二层次学习1.自学指导：（1）自学内容：课本P5页探究. （2）自学时间：6分钟. （3）自学方法：完成探究提纲. （4）探究提纲：○1在平面直角坐标系中画出反比例函数y =-x3的图象.○a 函数的图象位于哪些象限？ ○b 在每一一象限内，随着x 的增大，y 如何变化？你能有它们的解析式说明理由吗？ ○2k<0⇔函数xky =的图象分别位于第 象限⇔在每个象限内y 都随x 的增大而 . ③总结反比例函数xky =的图象和性质. 2.自学：学生可结合自学指导进行自学.3.助学：（1）师助生：①明了学情：了解学生是否会列表，是否理解表中的数据的意义以及画图中存在的问题. ②差异指导：根据学情分类指导.（2）生助生：同桌之间、小组内交流、研讨. 4.强化：总结反比例函数的图象和性质. 三、评价：1.学生自我评价.2.教师对学生的评价：（1）表现性评价；（2）纸笔评价（评价检测）.3.教师的自我评价（教学反思）.。

17．1．2反比例函数的图象和性质（1）导学案学习目标：1．会用描点法画反比例函数的图象2．结合图象分析并掌握反比例函数的性质学习重点：理解并掌握反比例函数的图象和性质学习难点：正确画出图象，通过观察、分析，归纳出反比例函数的性质学习过程：一、课前准备：1.正比例函数y ＝kx （k ≠0）的图象是什么？其性质有哪些？一次函数呢？2.画函数图象的一般步骤有哪些？应注意什么？二、课堂学习画出反比例函数xy6和xy6的图象.(可分组完成)解:列表表示几组x 与y 的对应值(填表)x -6-5-4-3-2-1123456x y 6xy6描点连线:注意：（1）列表取值时，x ≠0，因为x ＝0函数无意义，为了使描出的点具有代表性，可以“0”为中心，向两边对称式取值，即正、负数各一半，且互为相反数，这样也便于求y 值（2）由于函数图象的特征还不清楚，所以要尽量多取一些数值，多描一些点，这样便于连线，使画出的图象更精确（3）连线时要用平滑的曲线按照自变量从小到大的顺序连接，切忌画成折线（4）x ≠0，k ≠0，所以y ≠0，函数图象永远不会与x 轴、y 轴相交，只是无限靠近两坐标轴。

思考反比例函数xy6和xy6的图象有什么共同特征？它们有什么关系？归纳总结反比例函数图像特点和性质反比例函数xky（k 为常数，0k ）图像是_____________图像性质当k >0当k <0注意：描述函数值的增减情况时，必须指出“在函数图像所在的哪个象限内”三、随堂练习1．点)6,1(在双曲线xk y 上，则k=______________.2．已知反比例函数xy6的图象经过点),2(a P ，则a=__________. 3．函数y a xa ()226，当x0时，y 随x 的增大而增大，则函数关系式为__________4. 做出下列反比例函数的图像：y=－8/x y=－10/x17．1．2反比例函数的图象和性质（2）导学案学习目标：1．结合图象分析并掌握反比例函数的性质。