常见隶属函数小结
- 格式:doc
- 大小:51.50 KB
- 文档页数:2

隶属函数的定义-概述说明以及解释1.引言1.1 概述引言部分的内容可以从以下几个方面展开:1. 隶属函数的概念:隶属函数是模糊逻辑和模糊集理论中的重要概念之一。
它用来描述事物或概念在某种属性上的模糊程度或隶属程度。
不同于传统的二值逻辑,隶属函数允许事物或概念具有部分属于某个集合的特性,使得模糊集理论能够更好地处理不确定性和模糊性问题。
2. 隶属函数的应用领域:隶属函数在许多领域中都有着广泛的应用,如模糊控制、模糊推理、模糊决策等。
它们能够帮助我们处理复杂的现实问题,尤其是在面对不确定性和模糊性较高的情况下,更能展现出其优势。
3. 隶属函数的研究意义:隶属函数的研究不仅仅是为了解决现实问题,更重要的是为了揭示事物或概念的模糊性本质和不确定性特点。
通过对隶属函数的研究,我们可以深入了解模糊逻辑的基本原理和运算规则,为进一步发展模糊逻辑和模糊集理论奠定基础。
总之,本文将重点介绍隶属函数的定义及其在实际应用中的作用,希望通过对隶属函数的深入研究,能够更好地理解和应用模糊逻辑,为解决复杂问题提供一种有效的方法。
1.2文章结构文章结构部分的内容可以包括以下内容:文章结构的设计是为了更好地组织和呈现文章的内容,使读者能够更好地理解和领会作者的观点和论述。
在本文中,我们将按照以下结构展开探讨隶属函数的定义。
首先,在引言部分,我们会对整篇文章进行一个简要的介绍,包括概述、文章结构和目的。
概述部分会对隶属函数的定义进行简要的概括说明,引导读者进入主题。
然后,我们会介绍文章的结构,包括各个章节的内容和次序,以及章节之间的逻辑关系。
最后,我们会明确文章的目的,即为了什么样的读者群体撰写本文,以及我们希望读者通过阅读本文能够获得哪些知识和见解。
接下来,在正文部分,我们将对隶属函数的基本概念进行详细阐述。
首先,我们将介绍隶属函数的概念以及其与其他相关概念的关系,如模糊集合和模糊逻辑等。
然后,我们将对隶属函数的数学定义进行深入剖析,详细说明其数学表达形式和数学性质。

隶属函数正确地确定隶属函数,是运用模糊集合理论解决实际问题的基础。
隶属函数是对模糊概念的定量描述。
我们遇到的模糊概念不胜枚举,然而准确地反映模糊概念的模糊集合的隶属函数,却无法找到统一的模式。
隶属函数的确定过程,本质上说应该是客观的,但每个人对于同一个模糊概念的认识理解又有差异,因此,隶属函数的确定又带有主观性。
一般是根据经验或统计进行确定,也可由专家、权威给出。
例如体操裁判的评分,尽管带有一定的主观性,但却是反映裁判员们大量丰富实际经验的综合结果。
对于同一个模糊概念,不同的人会建立不完全相同的隶属函数,尽管形式不完全相同,只要能反映同一模糊概念,在解决和处理实际模糊信息的问题中仍然殊途同归。
事实上,也不可能存在对任何问题对任何人都适用的确定隶属函数的统一方法,因为模糊集合实质上是依赖于主观来描述客观事物的概念外延的模糊性。
可以设想,如果有对每个人都适用的确定隶属函数的方法,那么所谓的“模糊性”也就根本不存在了。
2.5.1 隶属函数的几种确定方法这里仅介绍几种常用的方法,不同的方法结果会不同,但检验隶属函数建立是否合适的标准,看其是否符合实际及在实际应用中检验其效果。
1.模糊统计法在有些情况下,隶属函数可以通过模糊统计试验的方法来确定。
这里以张南组等人进行的模糊统计工作为例,简单地介绍这种方法。
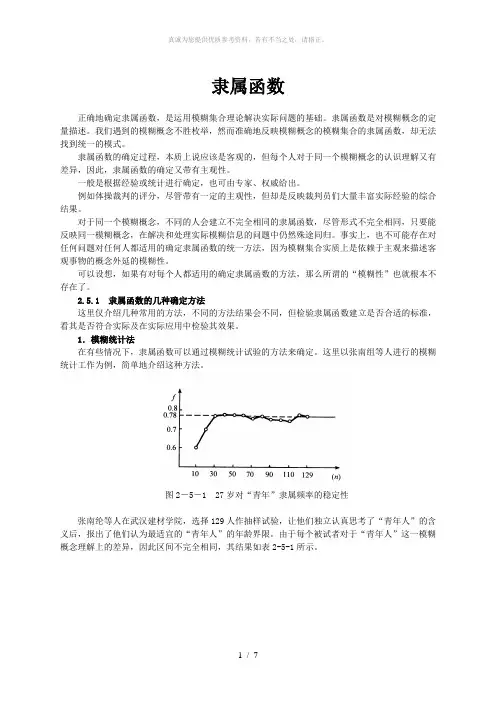
图2-5-1 27岁对“青年”隶属频率的稳定性张南纶等人在武汉建材学院,选择129人作抽样试验,让他们独立认真思考了“青年人”的含义后,报出了他们认为最适宜的“青年人”的年龄界限。
由于每个被试者对于“青年人”这一模糊概念理解上的差异,因此区间不完全相同,其结果如表2-5-1所示。
现选取0u =27岁,对“青年人”的隶属频率为)调查人数()岁的区间数(隶属次数包含n 27=μ (2-5-1)用μ作为27岁对“青年人”的隶属度的近似值,计算结果见表2-5-2。
78.027)=(青年人μ按这种方法计算出15~36岁对“青年人”的隶属频率,从中确定隶属度。

梯形隶属度函数1. 定义梯形隶属度函数(Trapezoidal Membership Function)是一种用于模糊逻辑中的隶属度函数,它定义了一个变量的值对于一个特定的模糊集合的隶属程度。
梯形隶属度函数具有四个参数,分别表示梯形的四个边界。
这些参数可以用来调整梯形的形状和位置,以适应不同的模糊集合。
在梯形隶属度函数中,变量的值落在梯形的上升边界和下降边界之间时,其隶属度为1。
变量的值在梯形顶部和边界之间时,其隶属度在0到1之间平滑过渡。
变量的值小于上升边界或大于下降边界时,其隶属度为0。
因此,梯形隶属度函数可以用来表示模糊规则的条件或输出的隶属度。
2. 用途梯形隶属度函数在模糊逻辑系统中广泛应用于建模和控制,用于表示模糊变量的隶属度。
模糊逻辑系统使用模糊集合和模糊规则来处理不确定性和模糊性,使得系统能够处理不确定和模糊的输入和输出。
梯形隶属度函数可以用于表示模糊集合的隶属度,例如温度的冷、温和、热等模糊集合。
通过调整梯形的参数,可以调节隶属度函数的形状和位置,以适应实际应用中的不同情况。
梯形隶属度函数还可以用于构建模糊规则,用于模糊推理和控制。
模糊规则是一种条件-输出语句,它根据输入的模糊变量的隶属度和规则的权重计算输出的模糊变量的隶属度。
梯形隶属度函数可用于指定模糊规则中的条件的隶属度。
3. 工作方式梯形隶属度函数的工作方式可以分为以下几个步骤:1.定义梯形的四个边界参数:上升边界、顶部、下降边界和底部。
这些参数用于调节梯形的形状和位置。
2.计算输入变量的值与梯形边界的相对位置。
3.根据相对位置计算输入变量的隶属度。
如果输入变量的值小于上升边界或大于下降边界,则隶属度为0;如果输入变量的值在上升边界和下降边界之间,则隶属度为1;如果输入变量的值在顶部和边界之间,则根据相对位置计算隶属度。
4.输出输入变量的隶属度。
梯形隶属度函数的形状和位置可以通过调整边界参数来进行灵活的调节,从而适应不同的模糊集合和模糊规则。

模糊函数python 隶属度函数模糊函数是一种基于模糊逻辑理论的函数,用于描述模糊概念,它可以将模糊输入转化为模糊输出,使一系列复杂的决策问题更加简单化,是目前很多智能系统、控制系统中广泛应用的一种技术手段。
而对于模糊函数的应用,隶属度函数起着至关重要的作用,本文将从隶属度函数入手,详细介绍如何使用python编写模糊函数的隶属度函数。
第一步:理解隶属度函数的含义隶属度函数是模糊函数中的一种关键概念,它用于描述模糊集合中元素(即模糊变量)与该模糊集合的隶属程度。
例如,一个人的身高可以被认为是“高”或“矮”,但是这些概念都是模糊的,不能用确定性值来刻画。
为了描述这种不确定程度,我们需要引入隶属度函数,将身高与“高”、“矮”的隶属程度映射到[0, 1]区间内的某一个值。
第二步:掌握隶属度函数的常见类型常见的隶属度函数类型有三角形隶属度函数、梯形隶属度函数、高斯隶属度函数等等,其中三角形隶属度函数是最为常见的一种类型。
三角形隶属度函数的公式如下:def triangular(x,a,b,c):if x<=a or x>=c:return 0elif a<x and x<=b:return (x-a)/(b-a)else:return (c-x)/(c-b)该函数接收四个参数:x为输入值,a和c分别为三角形左右两端点的位置,b为三角形高度(也叫峰值)的位置。
函数返回x对应的隶属度值,如图所示:第三步:使用python实现隶属度函数在python中,可以用函数的方式实现隶属度函数。
以三角形隶属度函数为例,实现该函数的python代码如下:def triangular(x,a,b,c):if x<=a or x>=c:return 0elif a<x and x<=b:return (x-a)/(b-a)else:return (c-x)/(c-b)其中x为输入值,a、b、c分别为三角形隶属度函数的三个参数,返回一个0到1之间的隶属程度值。

隶属度函数----------------------------精品word文档值得下载值得拥有----------------------------------------------美国加利福尼亚大学控制论教授扎得(L、A、Zadeh)经过多年的琢磨,终于在1965年首先发表了题为《模糊集》的论文。
指出:若对论域(研究的范围)U中的任一元素x,都有一个数A(x)?[0,1]与之对应,则称A为U上的模糊集,A(x )称为x对A的隶属度。
当x在U中变动时,A( x)就是一个函数,称为A的隶属函数。
隶属度A(x)越接近于1,表示x属于A的程度越高,A(x)越接近于0表示x属于A的程度越低。
用取值于区间[0,1]的隶属函数A(x)表征x 属于A的程度高低,这样描述模糊性问题比起经典集合论更为合理。
隶属度属于模糊评价函数里的概念:模糊综合评价是对受多种因素影响的事物做出全面评价的一种十分有效的多因素决策方法,其特点是评价结果不是绝对地肯定或否定,而是以一个模糊集合来表示。
隶属度函数及其确定方法分类隶属度函数是模糊控制的应用基础,正确构造隶属度函数是能否用好模糊控制的关键之一。
隶属度函数的确定过程,本质上说应该是客观的,但每个人对于同一个模糊概念的认识理解又有差异,因此,隶属度函数的确定又带有主观性。
隶属度函数的确立目前还没有一套成熟有效的方法,大多数系统的确立方法还停留在经验和实验的基础上。
对于同一个模糊概念,不同的人会建立不完全相同的隶属度函数,尽管形式不完全相同,只要能反映同一模糊概念,在解决和处理实际模糊信息的问题中仍然殊途同归。
下面介绍几种常用的方法。
(1)模糊统计法:模糊统计法的基本思想是对论域U上的一个确定元素vo是否属于论域上的一个可变动的清晰集合A3作出清晰的判断。
对于不同的试验者,清晰集合 A3可以有不同的边界,但它们都对应于同一个模糊集A。
模糊统计法的计算步骤是:在每次统计中, vo是固定的,A3的值是可变的,作 n次试验,其模糊统计可按下式进行计算v0对 A 的隶属频率 = v0?A 的次数 / 试验总次数 n随着 n的增大,隶属频率也会趋向稳定,这个稳定值就是 vo对A 的隶属度值。

隶属函数正确地确定隶属函数,是运用模糊集合理论解决实际问题的基础。
隶属函数是对模糊概念的定量描述。
我们遇到的模糊概念不胜枚举,然而准确地反映模糊概念的模糊集合的隶属函数,却无法找到统一的模式。
隶属函数的确定过程,本质上说应该是客观的,但每个人对于同一个模糊概念的认识理解又有差异,因此,隶属函数的确定又带有主观性。
一般是根据经验或统计进行确定,也可由专家、权威给出。
例如体操裁判的评分,尽管带有一定的主观性,但却是反映裁判员们大量丰富实际经验的综合结果。
对于同一个模糊概念,不同的人会建立不完全相同的隶属函数,尽管形式不完全相同,只要能反映同一模糊概念,在解决和处理实际模糊信息的问题中仍然殊途同归。
事实上,也不可能存在对任何问题对任何人都适用的确定隶属函数的统一方法,因为模糊集合实质上是依赖于主观来描述客观事物的概念外延的模糊性。
可以设想,如果有对每个人都适用的确定隶属函数的方法,那么所谓的“模糊性”也就根本不存在了。
2.5.1 隶属函数的几种确定方法这里仅介绍几种常用的方法,不同的方法结果会不同,但检验隶属函数建立是否合适的标准,看其是否符合实际及在实际应用中检验其效果。
1.模糊统计法在有些情况下,隶属函数可以通过模糊统计试验的方法来确定。
这里以张南组等人进行的模糊统计工作为例,简单地介绍这种方法。
图2-5-1 27岁对“青年”隶属频率的稳定性张南纶等人在武汉建材学院,选择129人作抽样试验,让他们独立认真思考了“青年人”的含义后,报出了他们认为最适宜的“青年人”的年龄界限。
由于每个被试者对于“青年人”这一模糊概念理解上的差异,因此区间不完全相同,其结果如表2-5-1所示。
现选取0u=27岁,对“青年人”的隶属频率为)调查人数()岁的区间数(隶属次数包含n 27=μ (2-5-1) 用μ作为27岁对“青年人”的隶属度的近似值,计算结果见表2-5-2。
78.027)=(青年人μ按这种方法计算出15~36岁对“青年人”的隶属频率,从中确定隶属度。

常见隶属函数小结1、比a 大得多的隶属函数:20;1();1()u a A u u a u a λ⎧≤⎪⎪=>⎨⎪+⎪-⎩其中λ为经验参数。
(如:取100λ=)2、老年人的隶属函数:20;01();2001()u A u u u λλαλ⎧≤≤⎪⎪=⎨<≤⎪+⎪-⎩其中;αλ为经验参数。
(如:取550αλ=⎧⎨=⎩)3、年轻人的隶属函数:21;01();2001()u A u u u λλλα⎧≤≤⎪⎪=⎨<≤-⎪+⎪⎩其中;αλ为经验参数。
(如:取525αλ=⎧⎨=⎩)4、正态模糊数:(接近a 的数)22()()u a a u eσ--= 其中:σ为经验参数。
构造隶属函数的几个方法1、三分法例:建立矮个子1()A u 、中等个子2()A u 、高个子3()A u 的隶属函数。
设:x ,y 分别是矮个子与中等个子,中等个子与高个子的分界线。
通过实验或调查,得到x 与y 的概率密度函数。
则有:1()()xuA u p x dx +∞=⎰ 3()()uyA u p y dy -∞=⎰ 213()1()()A u A u A u =-- (证明过程书中没有介绍。
)一般地,x 与y 可以取正态分布。
2、根据事物的特征来确定函数形式:如:正态模糊数 是更具离数a越远,隶属度越小;且具有对称性的特点给出的。
原则:1、隶属函数的值域比在[0,1]内。
2、隶属函数的趋势与实际相符。
3、参数可由经验给出,也可用统计方法估计。

隶属函数确定问题standalone; self-contained; independent; self-governed;autocephalous; indie; absolute; unattached; substantive隶属函数确定问题一、隶属函数的确定原则1、表示隶属度函数的模糊集合必须是凸模糊集合;即:在一定范围内或者一定条件下,模糊概念的隶属度具有一定的稳定性;从最大的隶属度函点出发向两边延伸时,其隶属度是单调递减的,而不许有波浪性,呈单峰;一般用三角形和梯形作为隶属度函数曲线。
2、变量所取隶属度函数通常是对称和平衡的模糊变量的标值选择一般取3-9个为宜,通常取奇数(平衡),在“零”“适中”等集合的两边语言值通常取对称。
3、隶属度函数要避免不恰当的重复在相同的论域上使用的具有语意顺序的若干标称的模糊集合,应该合力排序。
4、论语中的每个点应该至少属于一个隶属度函数的区域,同时它一般应该属于之多不超过两个隶属度函数的区域。
5、对于同一输入,没有两个隶属度函数会同时有最大隶属度6、对两个隶属度函数重叠时,重叠部分对于两个隶属度函数的最大隶属度不应该有交叉。
二、隶属度函数确定的方法1、模糊统计法模糊统计法的基本思想是对论域U上的一个确定元素v是否属于论域上的一个可变的清晰集的判断。
(清晰集、模糊集)模糊统计法计算步骤:Step1 确定论域Step2形成调查表Step3统计成频数分布表Step4建立隶属函数Step5隶属度(由频数分布表或者隶属函数可得)所谓模糊统计实验包含以下四个要素:假设做n次模糊统计试验,则可计算出:实际上,当n不断增大时,隶属频率趋于稳定,其频率的稳定值称为0x 对A的隶属度,即2、例证法例证法由已知的有限个隶属度函数的值,来估计论域U上的模糊子集A的隶属函数。
3、专家经验法是根据专家的实际经验给出模糊信息的处理算式或者相应的权系数值隶属函数的一种方法。
4、二元对比排序法5、群体决策法6、指派方法(待定来自算法大全第22章模糊数学模型)指派方法是一种主观的方法,它主要依据人们的实践经验来确定某些模糊集隶属函数的一种方法。


隶属函数法综合评价隶属函数法综合评价________________________隶属函数法是一种常用的多属性决策综合评价方法,它是基于属性取值的线性模糊集成,是模糊集理论在决策分析中的重要应用。
隶属函数法综合评价可以较好地解决多目标决策问题,是一种灵活的评价方法。
一、什么是隶属函数法隶属函数法是一种通过对决策属性取值进行模糊化来处理多目标决策问题的有效方法。
它把决策属性的取值转化为模糊集,利用隶属函数的形式来描述模糊集。
隶属函数的特性使得它可以反映出专家对决策对象的评价过程,对于决策者而言,隶属函数可以提供一个有利于理解的评价模型,使得多目标决策问题变得更加容易。
二、隶属函数法的原理隶属函数法是一种基于属性取值的模糊集合来实现的,它的原理是利用隶属函数的形式来描述模糊集。
即根据决策者的定义,对决策属性取值进行模糊化,然后将所有的决策属性取值用隶属函数表达式来表示,最后使用隶属函数进行评价,从而得到最优决策。
三、隶属函数法的优势1、它具有较强的弹性,可以根据不同的决策问题需要,在输入、输出、隶属函数形式上作出相应的调整;2、它具有较好的可操作性,即在计算过程中,可以使用多种数学工具来完成;3、它能够充分体现专家对决策对象的评价过程,对于决策者而言,也提供了一个有利于理解的评价模型;4、它能够反映决策者对不同属性及不同取值的重要性,在评价过程中充分体现决策者自身的主观意见;5、它能够有效地避免因不同评价者而引起的主观差异;6、它具有很好的适应性,能够适应各种不同形式的决策问题。
四、隶属函数法的应用隶属函数法在多目标决策中得到了广泛应用,其中包括四个主要方面:一是多目标优化问题;二是多目标决策问题;三是多目标冲突分析问题;四是多目标协调分析问题。
隶属函数法可以适用于各个领域,如工业企业生产、市场营销、金融投资、信息处理、医学诊断、文化事业、交通运输、能源开发、水利工程、土地开发、保护生态、气象预测、水文测量等。
模糊数学中的模糊集合与隶属度函数模糊数学是一门研究现实中模糊信息和不完全信息的数学理论。
在模糊数学中,模糊集合和隶属度函数是其核心概念之一。
一、模糊集合模糊集合是对现实世界中模糊或不确定概念的数学抽象。
与传统的集合理论不同,模糊集合并不要求元素的成员关系是确定的,而是通过隶属度函数来描述元素与集合的隶属关系。
一个元素可以同时隶属于多个模糊集合,并且隶属程度可以是连续的。
在模糊集合中,隶属度函数是描述元素与集合之间的隶属关系的数学函数。
它将元素映射到[0,1]的隶属度区间,表示元素与集合的隶属程度。
例如,对于一个模糊集合A来说,元素x的隶属度可以表示为μA(x),其中μA(x)的取值范围为[0,1]。
二、隶属度函数隶属度函数是描述元素与模糊集合之间隶属关系的数学函数。
它是模糊集合理论中的重要工具,常用于描述概念的模糊性和不确定性。
常见的隶属度函数包括三角形隶属度函数、梯形隶属度函数、高斯隶属度函数等。
三角形隶属度函数通过一个三角形的边界来表示元素的隶属度,具有对称性和简单性。
梯形隶属度函数通过一个梯形的边界来表示元素的隶属度,可以更精确地描述元素的隶属度。
高斯隶属度函数使用高斯曲线来表示元素的隶属度,具有光滑性和非对称性。
隶属度函数的选择需要根据具体情况来确定,可以根据实际需求和数学模型来选择最合适的隶属度函数。
三、模糊集合与隶属度函数的应用模糊集合与隶属度函数在实际应用中具有广泛的应用价值。
它们被广泛应用于模糊控制、人工智能、模式识别、决策分析等领域。
在模糊控制中,模糊集合与隶属度函数用于描述输入与输出之间的模糊关系,通过定义模糊规则和模糊推理来实现对系统的控制。
在人工智能中,模糊集合与隶属度函数用于处理模糊和不完全信息,进行模糊推理和模糊分类。
在模式识别中,模糊集合与隶属度函数用于进行特征提取和模式匹配,提高系统对不确定性和噪声的适应能力。
在决策分析中,模糊集合与隶属度函数用于处理决策变量的不确定性和模糊性,提供决策的支持和评估。
python 隶属函数隶属函数是Python编程语言中非常重要的概念之一。
在本文中,我们将探讨隶属函数的定义、作用以及如何在Python中使用隶属函数。
隶属函数是模糊逻辑中的一个概念,用于描述一个变量在一个特定的范围内的隶属程度。
隶属函数通常用来建模模糊变量的模糊集。
模糊集是由一系列隶属函数组成的,每个隶属函数都表示了变量在某个特定范围内的隶属程度。
在Python中,我们可以使用模糊逻辑库来定义和使用隶属函数。
一个常用的模糊逻辑库是scikit-fuzzy。
首先,我们需要导入scikit-fuzzy库:```pythonimport skfuzzy as fuzz```然后,我们可以定义一个隶属函数。
例如,我们可以定义一个三角形隶属函数,它在[0, 10]范围内的隶属度从0逐渐增加到1,然后再逐渐减少到0:```pythonx = np.arange(0, 10, 0.1)mfx = fuzz.trimf(x, [0, 5, 10])```在这个例子中,我们使用了trimf函数来定义一个三角形隶属函数。
trimf函数接受两个参数,一个是变量的范围,另一个是隶属函数的形状。
在这个例子中,我们定义了一个在[0, 5, 10]范围内的三角形隶属函数。
一旦我们定义了隶属函数,我们就可以使用它来计算变量的隶属度。
例如,假设我们有一个输入变量x,它的值为3。
我们可以使用隶属函数来计算x的隶属度:```pythonfuzz.interp_membership(x, mfx, 3)```在这个例子中,我们使用了interp_membership函数来计算变量x 的隶属度。
interp_membership函数接受三个参数,一个是变量的范围,一个是隶属函数,另一个是变量的值。
在这个例子中,我们计算了变量x=3的隶属度。
除了计算隶属度,我们还可以使用隶属函数进行模糊推理。
模糊推理是一种基于模糊逻辑的推理方法,它可以处理不确定性和模糊性的问题。
梯形隶属度函数
梯形隶属度函数是一种在模糊逻辑中常用的隶属度函数,其形状类似于一个梯形。
梯形隶属度函数的定义域是一个实数区间,其取值范围是[0,1]。
梯形隶属度函数通常用来描述一些非精确性的概念,比如“大约是60岁左右的人”、“大约有2000美元的收入”等。
这些概念很难用精确的数值来描述,因此需要使用模糊逻辑中的隶属度函数来表示。
梯形隶属度函数的形状可以通过四个参数来控制,分别是左边界、左斜率、右斜率和右边界。
其中左边界和右边界分别表示梯形左边和右边的水平位置,左斜率和右斜率表示梯形左边和右边的斜率。
这四个参数可以通过实际问题的需求来确定。
梯形隶属度函数是模糊逻辑领域中一个非常重要的概念,它被广泛应用于模糊控制、模糊决策等领域。
在实际应用中,需要根据问题的具体情况来选择适当的隶属度函数,以便更好地描述问题。
- 1 -。
生理指标隶属函数公式
定义:
若对论域(研究的范围)U中的任一元素x,都有一个数A(x)∈[0,1]与之对应,则称A为U上的模糊集,A(x)称为x对A的隶属度。
当x在U中变动时,A(x)就是一个函数,称为A的隶属函数。
参数说明:
隶属度A(x)越接近于1,表示x属于A的程度越高,A(x)越接近于0表示x属于A的程度越低。
用取值于区间(0,1)的隶属函数A(x)表征x属于A的程度高低。
相关知识说明
隶属度属于模糊评价函数里的概念:模糊综合评价是对受多种因素影响的事物做出全面评价的一种十分有效的多因素决策方法,其特点是评价结果不是绝对地肯定或否定,而是以一个模糊集合来表示。
隶属度函数的确定:
隶属度函数的确立还没有一套成熟有效的方法,大多数系统的确立方法还停留在经验和实验的基础上。
对于同一个模糊概念,不同的人会建立不完全相同的隶属度函数,尽管形式不完全相同,只要能反映同一模糊概念,在解决和处理实际模糊信息的问题中仍然殊途同归。
评分隶属度函数
评分隶属度函数是一种用于确定某个事物或情况在某一特定属性上的评分的数学工具。
它通常用于模糊逻辑和模糊控制中,可以帮助人们更好地理解和处理不确定性的问题。
在评分隶属度函数中,评分的取值范围通常是0到1之间,表示事物或情况在某一属性上的程度或程度。
值为0表示完全不符合该属性,值为1表示完全符合该属性,值在0和1之间表示部分符合该属性。
评分隶属度函数的形式可以有多种,常见的形式包括三角形隶属度函数、梯形隶属度函数和高斯隶属度函数。
三角形隶属度函数通常用于表示某个事物或情况在某一属性上的评分呈三角形分布的情况,梯形隶属度函数通常用于表示评分呈梯形分布的情况,而高斯隶属度函数通常用于表示评分呈正态分布的情况。
评分隶属度函数的选择取决于具体的应用场景和需求。
在实际应用中,人们可以根据自己的经验和知识选择合适的评分隶属度函数,或者通过数据分析和建模来确定合适的评分隶属度函数。
评分隶属度函数在许多领域都有广泛的应用,例如模糊控制、模糊决策、模糊搜索等。
它可以帮助人们更好地处理不确定性的问题,提高决策和控制的质量和效果。
评分隶属度函数是一种用于确定某个事物或情况在某一属性上的评
分的数学工具,在模糊逻辑和模糊控制中有广泛的应用。
它可以帮助人们更好地理解和处理不确定性的问题,提高决策和控制的质量和效果。
常见隶属函数小结
1、比a 大得多的隶属函数:
20;1();1()u a A u u a u a λ⎧≤⎪⎪=>⎨⎪+⎪-⎩
其中λ为经验参数。
(如:取100λ=)
2、老年人的隶属函数:
2
0;01();2001()u A u u u λλαλ⎧≤≤⎪⎪=⎨<≤⎪+⎪-⎩
其中;αλ为经验参数。
(如:取550αλ=⎧⎨=⎩)
3、年轻人的隶属函数:
2
1;01();2001()u A u u u λλλα⎧≤≤⎪⎪=⎨<≤-⎪+⎪⎩
其中;αλ为经验参数。
(如:取525αλ=⎧⎨=⎩)
4、正态模糊数:(接近a 的数)
22()()u a a u e
σ--= 其中:σ为经验参数。
构造隶属函数的几个方法
1、三分法
例:建立矮个子1()A u 、中等个子2()A u 、高个子3()A u 的隶属函数。
设:x ,y 分别是矮个子与中等个子,中等个子与高个子的分界线。
通过实验或调查,得到x 与y 的概率密度函数。
则有:
1()()x
u
A u p x dx +∞
=⎰ 3()()u
y
A u p y dy -∞=
⎰ 213()1()()A u A u A u =-- (证明过程书中没有介绍。
)
一般地,x 与y 可以取正态分布。
2、根据事物的特征来确定函数形式:
如:正态模糊数 是更具离数a越远,隶属度越小;且具有对称性的特点给出的。
原则:
1、隶属函数的值域比在[0,1]内。
2、隶属函数的趋势与实际相符。
3、参数可由经验给出,也可用统计方法估计。