正弦电流电路的分析
- 格式:ppt
- 大小:3.39 MB
- 文档页数:54


第4章 正弦稳态电路分析--例题√【例4.1】已知两个同频正弦电流分别为()A 3314cos 2101π+=t i ,()A 65314cos 2222π-=t i 。
求(1)21i i +;(2)dt di 1;(3)⎰dt i 2。
【解】 (1)设()i t I i i i ψω+=+=cos 221,其相量为i I I ψ∠=∙(待求),可得:()()()()A54.170314cos 224.14A54.17014.24A 34.205.14 A1105.19A j8.665 A15022A 601021︒-=︒-∠=--=--++=︒-∠+︒∠=+=∙∙t i j j I I I(2)求dtdi 1可直接用时域形式求解,也可以用相量求解()()︒+︒+=︒+⨯-=9060314cos 23140 60314sin 3142101t t dt di用相量形式求解,设dt di 1的相量为K K ψ∠,则有 )9060(31406010314K 1K ︒+︒∠=︒∠⨯==∠∙j I j ωψ两者结果相同。
(3)⎰dt i 2的相量为︒∠=︒∠︒-∠=∙12007.0903********ωj I【例4.2】 图4-9所示电路中的仪表为交流电流表,其仪表所指示的读数为电流的有效值,其中电流表A 1的读数为5 A ,电流表A 2的读数为20 A ,电流表A 3的读数为25 A 。
求电流表A 和A 4的读数。
图4-9 例4.2图【解】 图中各交流电流表的读数就是仪表所在支路的电流相量的模(有效值)。
显然,如果选择并联支路的电压相量为参考相量,即令V 0︒∠=∙S S U U ,根据元件的VCR 就能很方便地确定这些并联支路中电流的相量。
它们分别为:A 25 ,A 20 ,A 05321j I j I I =-=︒∠= 根据KCL ,有:()A095A 5A 457.07A 55324321︒∠==+=︒∠=+=++=j I I I j I I I I 所求电流表的读数为:表A :7.07 A ;表A 4:5 A【例4.3】 RLC 串联电路如图4-12所示,其中R =15Ω,L =12mH ,C =5μF ,端电压u =1002cos (5000t )V 。


二单元正弦交流电路引言正弦交流电的产生:正弦交流电路:含有正弦电源而且电路各部分所产生的电压和电流均按正弦规律变化的电路。
因为交流电可以利用变压器方便地改变电压、便于输送、分配和使用。
所以,在生产和生活中普遍应用正弦交流电。
着重讨论和分析交流电路的基本概念、基本规律和基本分析方法。
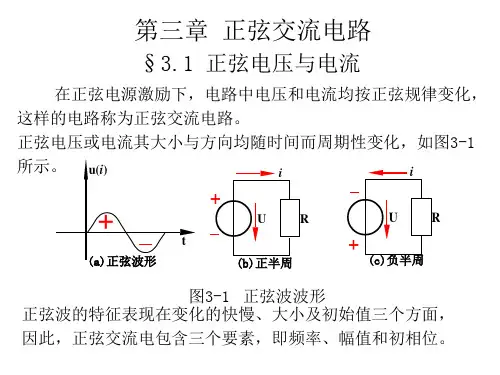
随时间按正弦规律变化的交流电压、电流、电动势称为正弦电压、电流、电动势。
正弦量:正弦电压、电流、电动势统称为正弦量。
Riab)sin(m i t I i ψω+=规定电流参考方向如图:iωtiψ正半周:电流实际方向与参考方向相同负半周:电流实际方向与参考方向相反+-最大值角频率初相角正弦量的三要素课题1正弦交流电的基本概念一、正弦量的三要素表达式:波形:用带有下标m 的大写字母表示:I m 、U m 、E m有效值:一个交流电流的做功能力相当于某一数值的直流电流的做功能力,这个直流电流的数值就叫该交流电流的有效值。
用大写字母表示:I 、U 、 E1. 最大值描述正弦量变化范围的参数。
tiT最大值I m⎰=Tdti TI 021正弦量最大值与有效值的关系EE m 2=II m 2=UU m 2=2. 角频率ω描述正弦量变化快慢的参数。
单位:rad/s周期(T ): 变化一个循环所需要的时间,单位(s)。
频率( f ): 单位时间内的周期数单位(Hz)。
三者间的关系示为:=2π/T =2πfωTωt 2ππtiTT/2我国和大多数国家采用50Hz 作为电力工业标准频率(简称工频),少数国家采用60Hz 。
iωt)sin(i m t I i ψω+=iψt =0 时的相位角称为初相角或初相位。
i ψ同频率正弦量的相位角之差,用ϕ表示。
二、相位差:180±取值范围:相位差可反映同频率正弦量超前滞后关系。
180±相位差的取值范围:3. 初相iψ影响初相得因素:项前负号(±180°)Cos (90 °))sin(1m ψtωU u +=如:)()(21ψωψωϕ+-+=t t 21ψψ-=若21>-=ψψϕ电压超前电流ϕ或电流滞后电压ϕuiu iϕωtO)2ψ+=t ωI i sin(m电流超前电压︒-=-=9021ψψϕ︒90电压与电流同相021=-=ψψϕ电流超前电压ϕ021<-=ψψϕ电压与电流反相︒=-=18021ψψϕu iωt ui ϕOu iωtui 90°O u i ωtui Oωtui u i O一、复数1. 复数的表示形式A = a + j b1)代数形式:为虚数单位1j -=ϕcos A a =ϕsin A b =22ba A +=ab=ϕtan aAb+1+jϕA实部虚部ϕA A =2)极坐标形式:模幅角2. 两种形式的互换代数极坐标代数极坐标课题2正弦量的相量表示法3. 复数运算(熟记公式)111j b a A +=222j b a A +=1)加减运算(用代数形式):则()()212121j b b a a A A ±+±=±设则222ϕA A =111ϕA A =212121ϕϕ+=⋅A A A A 212121ϕϕ-=A A A A 设2)乘除运算(用极坐标形式):1A 2A 3A 321A A A ++思考如何用作图的方法得到复数的差?3)复数的相等111j b a A +=222j b a A +=21a a =如果21b b =则21A A =222ϕA A =111ϕA A =如果21A A =21ϕϕ=则21A A =4. 旋转因子(模为1,辐角为的复数)ϕ一个复数乘以ϕj e等于把其逆时针旋转角。

正弦交流电路知识点总结一、正弦交流电路的基本概念正弦交流电路是指由正弦波形状的电压或电流组成的电路。
在正弦交流电路中,电压或电流随时间呈周期性变化,其波形为正弦曲线。
正弦交流电路中,频率、振幅、相位等是重要的参数。
二、正弦交流电路中的元件1. 交流源:提供正弦波形状的电压或电流。
2. 电阻:阻碍电流通过的元件。
3. 电感:储存磁能量并抵抗变化的元件。
4. 电容:储存电能量并抵抗变化的元件。
三、正弦交流电路中的基本定律1. 欧姆定律:U=IR,其中U为电压,I为电流,R为阻值。
2. 基尔霍夫定律:任意一个节点上所有进入该节点和离开该节点的支路所构成的代数和等于零。
3. 诺依曼定理:在任意一个闭合回路中,沿着这个回路方向绕一圈所得到所有增加量之和等于所有减少量之和。
四、串联和并联1. 串联:将多个电阻、电感、电容依次连接在一起,即为串联。
串联后的总阻值为各元件阻值之和。
2. 并联:将多个电阻、电感、电容同时连接在一起,即为并联。
并联后的总阻值等于各元件倒数之和的倒数。
五、交流电路中的功率交流电路中的功率分为有功功率和无功功率两部分:1. 有功功率:指交流电路中被转化成有用能量的功率。
2. 无功功率:指交流电路中被转化成储存于元件中的能量或者从元件中释放出来但不能做有用工作的能量。
六、交流电路中的相位相位是指两个正弦波形状的信号之间时间上的差异。
在正弦交流电路中,相位是一个重要参数。
不同元件间存在着不同相位差,而且相位差随频率变化。
七、滤波器滤波器是指通过对信号进行滤波,去除不需要或者干扰信号来得到所需信号的设备。
根据滤波器对信号处理方式不同,可以将其分为低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
八、交流电路中的共振共振是指在交流电路中,当电容和电感与外部信号频率相等时,电路中的阻抗达到最小值。
在共振状态下,电路中的能量传输效率最高。
九、交流电路中的谐波谐波是指在交流电路中,除了基频信号之外产生的频率为整数倍于基频信号频率的信号。





第九章正弦稳态电路的分析本章内容1.阻抗和导纳的概念2.阻抗的串并联及电路的相量图3.正弦稳态电路的分析4.瞬时功率、有功功率、无功功率、视在功率、复功率及最大输出功率5.串联和并联谐振本章重点:正弦量的向量正表示; 正弦电路中的阻抗和导纳;正弦电路的分析串联谐振的谐振条件及特征; 并联谐振的谐振条件及特征本章重点:正弦电路参数的分析及最大功率输出的分析§9-1 阻抗和导纳阻抗和导纳是正弦电流电路分析的重要内容一、阻抗在无源的线性网络中,端口的电压相量与电流相量的比值定义为该一端口的阻抗(复阻抗),用Z表示。
式中:•U=U∠ϕu•I=I∠ϕI阻抗的模:Z= U/I,阻抗角:ϕZ= ϕu-ϕi 阻抗的代数式: Z=R+jX式中:R—电阻 X—电抗1.若网络N 0内只含单一元件,则单一元件的复阻抗(1)电阻的复阻抗:Z R =R(2)电感的复阻抗:Z L =ωj L=jX L X L =ωL —感抗 (3)电容的复阻抗:Z C =cj ω1=c jω1-=jX C X C =cω1-—容抗 2.若网络N 0内为RLC 串联,则阻抗为(1)阻抗:Z=•U /•I = R+ωj L+cj ω1=R+j(ωL-Cω1)=R+jx=Z ϕ∠Z可见:阻抗Z 的实部为电阻R (R=Z cos ϕZ ),阻抗Z 的虚部为电抗X (X= R=Z sin ϕZ ),三者构成阻抗三角形 (2) 阻抗的模:Z =22)(C L X X R -+=22X R +=U/I (3)阻抗角:ϕZ =arctanR X X C L -=RX=ϕu -ϕi X 〉0 ωL>C ω1电路呈电感性 X<0 ωL<Cω1电路呈电容性X=0 电路呈电阻性一、 导纳:复阻抗的倒数定义为复导纳(电流相量与对应端口的电流相量的比值),用Y 表示 Y=Z 1=••UI =)(u i U Iϕϕ-∠=Y Y ϕ∠导纳的模: Y =U I导纳角: Y ϕ=u i ϕϕ- 导纳的代数式: Y=G+JB式中:G —电导 B —电纳1.若网络N 0内只含单一元件,则单一元件的复阻抗 (1) 电阻的复导纳:Y R =G=1/R (2) 电感的复导纳:Y L =Lj ω1=L jω1- =jB L B L =Lω1-—感纳 (3)电容的复导纳:Z C ==ωj C =jB C B C =ωC —容纳2.若网络N 0内为RLC 并联,则导纳为(1)导纳Y=••UI基尔霍夫电流定律的相量形式:∑•I =0•I =•I R +•I L +•I C =⎥⎦⎤⎢⎣⎡-+)1(1L C j R ωω•U =G+j(B C +B L )•UY=R 1+L j ω1+ωj C=R1+)1(L C j ωω-=G+jB可见:导纳Y 的实部为电导G (G=Y cos ϕY ),导纳Y 的虚部为电纳B (B= Y sin ϕY ),三者构成导纳三角形 (2)导纳的模:Y =22)(L C B B G -+=22B G +=I/U (3)阻抗角:ϕY =arctanG B B L C -=GB=ϕi -ϕu B 〉0 ωC>L ω1电路呈电容性 B<0 ωC<Lω1电路呈电感性B=0 电路呈电阻性二、阻抗和导纳相互转换(自学)§9-2 阻抗(导纳)串联和并联阻抗的串并联与电阻的串并联的计算规则相同,只是要把电阻换成阻抗。
第五章 正弦稳态电路分析习题解答5-1 已知正弦电流)60314cos(20 +=t i A ,电压)30314sin(210-=t u V 。
试分别画出它们的波形图,求出它们的有效值、频率及相位差。
解 电压u 可改写为)120314cos(210)30314sin(210 -=-=t t u Vi 、u 波形图如图所示。
其有效值为V 10142.14220=A==U I i 、u 的频率为Hz 5014.32314π2=⨯==ωfu 、i 的相位差为18060120-=--=-= ψψϕi u5-2 己知)3πcos(m +=t Ιi ω,当s 5001=t 时,第一次出现零值,求电流频率f 。
解 按题意有题5-1图0)3π500cos(m =+=ωI 2π3π500=+ω 得)3π2π(500-=ωHz 667.41)3π2π(2π500π2=-==ωf5-3 在图示相量图中,己知A 101=I ,A 52=I ,V 110=U ,Hz 50=f ,试分别写出它们的相量表达式和瞬时值表达式。
解 相量表达式为V0110A 455A 301021 ∠=∠=-∠=∙∙∙U I I瞬时值表达式为A )30314cos(2101 -=t i A )45314cos(252 +=t iV )314cos(2110t u =5-4 己知某正弦电压V )π100sin(10ψ+=t u ,当s 3001=t 时,V 5)(3001=u ,题5-3图 ∙U ∙则该正弦电压的有效值相量=∙U?解 按题意有5)300π100sin(10=+ψ求出6π300π100)105arcsin(-=-=ψ 故V 6π256π210-∠=-∠=∙U5-5 实际电感线圈可以用R 、L 串联电路等效,现有一线圈接在56V 直流电源上时,电流为7A ;将它改接于50Hz 、220V 的交流电源上时,电流为22A 。
试求线圈的电阻和电感。