小学数学圆的面积推导演示

所以圆面积＝（ πr）×（ r ）＝（ πr²） 如果用S表示圆的面积，那么圆的面积计算公式就是 ： S＝πr²
把圆平均分的份数越多，拼成的图形就越接近于长方 形，体现了极限思想。所谓极限思想是指用极限的概念分 析和解决问题的一种数学思想。
探究点 2 已知圆的半径（直径）求圆的面积
圆形草坪的直径是20 m，每平方米草皮8元，
圆所占平面的大小叫做圆的面积。
平行四边形的面积公 式是怎样得到的呢？
这个方法叫做 “割补法”
推导过程：长方形的面积=长×宽 平形四边形的面积=底×高
想一想： 圆的面积公式能不能通过 “割补法” 转化成我们已学
过的图形来推导出来呢？ 你想把圆转化成什么图形呢？
利用手中的学具，小组内合作学习完成。
四 等 分
铺满草坪需要多少钱？ 要求铺满草坪需要
2从0÷题2目＝中1你0（都m知）
多少钱，先要求出
3道.1了4×什1么0？²＝314（m²） 圆形草坪的面积是
314×8＝2512（元） 多少平方米。
答：铺满草皮需要2512元。
归纳总结：
圆的面积计算公式的应用：
1.已知圆的直径，求圆的面积：先根据r＝d÷2求出半
先求出半径，再
3.14×0.5²＝0.785（m²） 求圆的面积。
答：它的面积是0.785 m²。
2.根据下面所给的条件，求圆的面积。 （1）半径2 dm
3.14×22=3.14×4=12.56（dm2） （2）直径10 cm
3.14×（10÷2）2=3.14×25=78.5（cm2）
夯实基础 （选题源于《典中点》经典题库）
易错辨析 （选题源于《典中点》经典题库）
“半径2厘米的圆，它的周长和面积相等”这句话对 吗？为什么？ 不对，周长和面积不能比。 辨析：没有真正理解圆的周长与面积的意义，一个 是长度单位，一个是面积单位，没有相同不相 同的说法，但是可以说数值相同。

圆的面积多种推导方法
圆的面积是数学中的一个重要概念，下面我们介绍几种推导圆面积的方法。

方法一：积分法
我们先把圆分成n个等份，每个小部分的面积为∆S，现将∆S看成一个矩形，它的高为 r，宽为∆θ。

显然，对于圆形，n 越多，∆θ 越小，每个小面积越接近一个微元 dS，把所有小矩形的面积加起来就得到了圆的面积。

若用θ 表示两点 A、B 的夹角，则∆θ = θ/n。

当 n 趋近于无限大时，小矩形的面积就趋近于微元 dS，即：
S = ∫(0, 2π) rdθ
方法二：几何法
我们将圆平分成无数个极小的扇形，每个扇形的面积可以表示为：
S = 1/2 r²θ
其中，θ为扇形的角度。

因此，将所有扇形的面积相加，就得到圆的面积：
S = ∑(0, 2π) 1/2 r²θ
方法三：代数法
考虑一个单位圆的情形，其方程为 x²+y²=1，现在求它的面积。

我们可以化简方程得到：
y = √(1-x²)
对 y 在 [-1, 1] 范围内积分，得到圆的面积：
S = 2 ∫(-1, 1) √(1-x²) dx
以上是三种常见的推导圆面积的方法，它们虽然方法不同，但得出的结果都是相同的。

6种方法推导圆的面积公式1.通过矩形与圆的关系式推导：设圆周长为C,直径为d，由圆周长公式可得d=C/π,故若将圆截取矩形，则矩形面积为S=(d/2)x(C/π)=(C^2)/4π ,即圆的面积S = πr^2 =πd^2/4.2.通过极径弧长关系式推导：设圆的半径为r,圆心角为α，弧长关系式为l= α r，若将圆分成n段，即α= 2π/n，设单段弧长为L，则L=2π/n x r=2πr/n,再求出圆的面积S，即S=nL^2/4π=r^2n^2/4π,由变形得S=πr^23.通过三角形和圆的关系式推导：设圆的半径为r,圆周长为C，将圆分成n段，每段画斜边与两条弧之间的射线连接，构成三角形，其面积S1等于n个三角形的面积和：S1=r^2(n-1π/2)，由圆周长公式可求出圆的面积S2：S2=C^2/4π，设二者相等：令 S1=S2，由此得圆的面积S=π r^2.4.通过半径弦长关系式推导：设圆心角为α,半径为r，弦长关系式为l=2rsin (α/2)，若将圆分成n段，即α=2π/n，设单段弧长为L，则L=2rsin (π/n),再求出圆的面积S，即S=n[2rsin(π/n)]^2/4πr^2=n^2sin^2 (π/n)/2π,由变形得S=πr^2.5.通过正方形和圆的关系式推导：设圆的半径为r，正方形的边长为D，将圆分成四段，由圆周长公式可得D=2πr/4，设正方形的面积为S1，则S1=[2πr/4]^2，由正方形和四个圆形区域的面积和关系得圆的面积：S=S1+4S2=4S2=[2πr/4]^2+4S2=[2πr/4]^2+4πr^2/4=πr^26.通过台形和圆的关系式推导：设圆的半径为r，将圆分成n段同心圆，令半径比等于1:n,即r1:rn，由圆的内接外接台形面积关系可求出圆的面积:S= n(r^2 -r1^2)/2=πr^2。

1．把一张圆形纸片分成若干(偶数)等份，拼成一个近似 的长方形。如下图。
拼成的长方形的长相当于圆( 周长的一半 )，长方形的宽 相当于圆的( 半径 )，因为长方形的面积＝( 长×宽 )， 所以圆的面积公式用字母表示是( S＝πr2 )。
知识点 2 圆的面积公式的应用
2．根据公式计算圆的面积。
S＝πr2 ≈3.14×32 ＝28.26(dm2)
易错辨析
4．判断。(对的画“√”，错的画“×”) (1)半径为 2 cm 的圆的周长和面积相等。( )
辨析：忽视了周长和面积意义不同。
(2)圆的半径扩大到原来的 2 倍，圆的周长和面积都扩大 到原来的 2 倍。( ) 辨析：圆的面积公式是 S＝πr2，所以面积应扩大到 原来的 4 倍。
提升点 1 寻找隐含条件求圆的面积
四 等 分
八 等 分
十 六 等 分
三 十 二 等 分
以拼成的近似平行四边形为例： 圆面8等分时： 圆面16等分时： 圆面32等分时：
分的份数越多，拼成的图形越接近长方形。 从上图中可以看出圆的半径是r，
长方形的宽近似（ 圆的半)径，长 近似于( 圆周长的一半)。
因为长方形的面积＝（ 长）×（ 宽 ）
5圆
3.圆的面积 第1课时 圆的面积公式的推导与应用
RJ 六年级上册
平行四边形的面积公 式是怎样得到的呢？
这个方法叫做 “割补法”
推导过程：长方形的面积=长×宽
平形四边形的面积=底×高
探究点 1 圆的面积计算公式的推导
圆的面积怎样算呢？ 圆的面积公式能不能通过 “割 补法” 转化成我们已学过的图 形来推导出来呢？
5．如图，正方形的面积是 18 cm2，这个圆的面积是多
少平方厘米？ 3.14×18＝56.52(cm2)

( ×)
( √) ( ×)
3.如下图，求阴影部分的面积。
10×10-3.14×（10÷2）2=21.5（cm2） 答：阴影部分的面积是21.5 cm2。
1.圆的面积计算公式：S=πr2 ；
2.已知直径d，求面积S，先用d÷2=r，再用公式
S=πr2求出圆的面积。即：S
d 2
2
。
3.已知圆的周长求面积，先利用周长公式求出半
所以圆面积＝（ πr ）×（ r ）＝（ πr² ） 用S表示圆的面积，圆的面积计算公式就是： S＝πr²
2.根据下面所给的条件，求圆的面积。 （1）半径2 dm
3.14×22=3.14×4=12.56（dm2）
（2）直径10 cm 3.14×（10÷2）2=3.14×25=78.5（cm2）
小试牛刀
径或直径。计算公式：S
C 2
2
。
4.圆环的面积计算公式是S=πR2-πr2或S=π（R-r）2 。
1. 一个圆形茶几桌面的直径是1 m，它的面积是多少平方米？
1÷2＝0.5（m） 3.14×0.5²＝0.785（m²） 答：它的面积是0.785 m²。
探究点 2 已知圆的半径（直径）求圆的面积
圆形草坪的直径是20 m，每平方米草皮8元，铺满草坪需要
多少钱？
从题目中你都
知道了什么？
20÷2＝10（m）
圆
第屯市文化小学 谷艳秀
探究点 1 圆的面积计算公式的推导
什么是面积？ 圆的面积是指哪一部分的大小？ 圆所占平面的大小叫做圆的面积。
想一想： 圆的面积公式能不能通过 “割补法” 转化
成我们已学过的图形来推导出来呢？ 你想把圆转化成什么图形呢？
探究新知

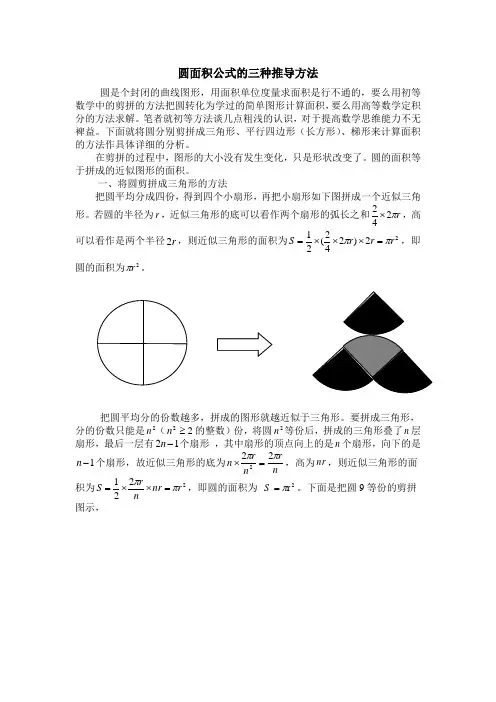
圆面积公式的三种推导方法圆是个封闭的曲线图形，用面积单位度量求面积是行不通的，要么用初等数学中的剪拼的方法把圆转化为学过的简单图形计算面积，要么用高等数学定积分的方法求解。

笔者就初等方法谈几点粗浅的认识，对于提高数学思维能力不无裨益。

下面就将圆分别剪拼成三角形、平行四边形（长方形）、梯形来计算面积的方法作具体详细的分析。

在剪拼的过程中，图形的大小没有发生变化，只是形状改变了。

圆的面积等于拼成的近似图形的面积。

一、将圆剪拼成三角形的方法把圆平均分成四份，得到四个小扇形，再把小扇形如下图拼成一个近似三角形。

若圆的半径为r ，近似三角形的底可以看作两个扇形的弧长之和r π242⨯，高可以看作是两个半径r 2，则近似三角形的面积为22)242(21r r r S ππ=⨯⨯⨯=，即圆的面积为2r π。

把圆平均分的份数越多，拼成的图形就越近似于三角形。

要拼成三角形，分的份数只能是2n （22≥n 的整数）份，将圆2n 等份后，拼成的三角形叠了n 层扇形，最后一层有12-n 个扇形 ，其中扇形的顶点向上的是n 个扇形，向下的是1-n 个扇形，故近似三角形的底为n r nr n ππ222=⨯，高为nr ，则近似三角形的面积为2221r nr nr S ππ=⨯⨯=，即圆的面积为 2r π= S 。

下面是把圆9等份的剪拼图示，二、将圆剪拼成平行四边形的方法把圆平均分成四份，得到四个小扇形，再把小扇形如图拼成一个近似平行四边形。

同样，圆的半径为r ，近似平行四边形的底可以看作2个扇形并成的为r π242⨯，高可以看作是小扇形的半径r ，则近似平行四边形的面积为222r r r S ππ=⨯⨯=，即圆的面积为2r π= S 。

同样的把圆平均分的份数越多，拼出来的图形越接近平行四边形，当分的份数无限大时，拼出的图形也可以看作是长方形。

要拼成平行四边形，分的份数只能是n 2（2≥n 的自然数）份，将圆n 2等份后，拼成的平行四边形（叠了一层）的底为n r n 22π⨯，高为半径r ，则平行四边形的面积为222r r nr n S ππ=⨯⨯=，即圆的面积2r π= S 。

圆的面积推导公式过程
圆的面积公式推导过程基于积分学，但也可以通过几何方法进行直观说明。

以下是两种方式的简单解释：
1. 几何方法：
1)首先，将一个圆分成无数个相等的小扇形。

2)当这些小扇形越来越多、越来越细时，每个扇形就越来越接近一个等腰三角形，而这个等
腰三角形的顶点就是圆心，底边是圆的半径。

3)每个这样的小三角形面积可以计算出来，为（圆的半径）*（圆周率π/360 * 角度θ）的一
半，因为三角形的高就是半径，底角为θ。

4)当我们将所有的小三角形面积加起来时，随着角度θ趋于无限小，所有小三角形的总面积
就趋近于圆的面积。

5)当θ从0到360度变化时，所有小三角形面积之和即为πr²。

2. 积分方法（微积分）：
1)设圆的半径为r，考虑圆盘在极坐标下的表示，任取一点P(ρ,θ)，其中ρ≤r。

2)在0到r的区间上对ρ进行积分，并考虑到θ从0到2π的变化，单个微元面积
dA=ρ*dρ*dθ。

3)整个圆的面积A就是所有微元面积的累加，即 A = ∫∫_D dA = ∫_0^2π ∫_0^r
ρ*dρ*dθ = ∫_0^2π [ρ²/2]_0^r dθ = πr²。

所以，无论采用几何分割法还是积分法，都可以得到圆的面积公式：A = πr²。

圆的面积的推导过程圆的面积是一个重要的几何概念，它是我们在日常生活中常常遇到的形状之一。

在这篇文章中，我将向您介绍圆的面积的推导过程。

我们需要明确圆的定义。

圆是一个由一条曲线组成的平面图形，其所有点到圆心的距离都相等。

圆的面积是指圆内部的所有点所覆盖的平面区域。

接下来，我们来推导圆的面积。

为了简化推导过程，我们假设圆的半径为r，圆心为O。

我们将圆分成无数个扇形，每个扇形的圆心角为θ。

由于圆的定义，每个扇形的弧长都相等，而弧长可以表示为弧度制下圆心角的值乘以半径，即L = θr。

我们可以将圆分成n个扇形，每个扇形的圆心角为θ。

此时，整个圆的弧长L可以表示为L = nθr。

接下来，我们将每个扇形展开，并将其变成一个三角形。

由于三角形的面积可以通过底边乘以高除以2来计算，我们可以得到每个三角形的面积为 S = (r/2) * r = r^2 / 2。

接着，我们将所有的三角形的面积相加，得到整个圆的面积。

由于圆由无数个扇形组成，所以我们可以将n趋近于无穷大，即n → ∞。

此时，整个圆的面积可以表示为 S = (r^2 / 2) * n。

我们使用极限的思想来计算整个圆的面积。

当n趋近于无穷大时，我们可以将整个圆的面积表示为S = lim (n → ∞) (r^2 / 2) * n。

通过数学推导，我们可以得到圆的面积公式为S = πr^2。

其中，π是一个无理数，近似值为3.14159。

圆的面积公式为S = πr^2。

这个公式不仅仅是数学上的一个结论，它也在工程、建筑、科学等领域中有着广泛的应用。

通过理解和运用这个公式，我们可以更好地理解和计算圆的面积，从而在实际问题中得到准确的结果。

希望通过本文的介绍，您对圆的面积的推导过程有了更深入的了解。

圆是几何学中的重要概念，其面积的推导过程也是数学思维的体现。

通过学习和理解这个过程，我们可以更好地掌握几何学的基本原理，并应用于实际问题的求解中。

圆的面积公式推导圆是数学中的一个基本几何形状，由一个固定点（圆心）到平面上所有距离等于该固定距离的点组成。

圆的面积是指圆所包含的平面上的所有点构成的区域的大小。

圆的面积公式可以通过几何和代数的方法推导得出。

几何推导：1.假设圆的半径为r，则圆的直径为2r。

2.将圆按照直径进行折叠，可以得到一个正方形。

3.正方形的边长为2r，面积为(2r)²=4r²。

4.圆的面积应该小于等于正方形的面积，所以圆的面积应该小于等于4r²。

5.将正方形一分为二，可以得到一个长方形，宽为r，长度为2r，面积为2r²。

6.将长方形旋转90度，可以得到一个与圆刚好内、外接的矩形。

7.矩形的面积应该大于圆的面积，所以圆的面积应该大于等于2r²。

8.根据步骤4和步骤7，得到不等式：2r²≤圆的面积≤4r²。

代数推导：1.圆的面积可以表示为A，半径可以表示为r。

2.将圆按照半径进行分割，可以得到n个等腰三角形，每个三角形的底边长度为2r，高为r。

3.由于圆的面积是由n个三角形组成的，所以圆的面积可以表示为A=n*(1/2)*2r*r。

4.简化公式得到A=n*r²。

5.当n趋近于无穷大时，圆被无限个等腰三角形所逼近，所以可以近似认为n无限大。

6.即当n无限大时，圆的面积可以表示为A=π*r²，其中π是一个无理数，约等于3.147.根据步骤6的结论，得到圆的面积公式：A=π*r²。

综合几何和代数推导，得到圆的面积公式：A=π*r²，其中A表示圆的面积，r表示圆的半径。

这个公式表明，圆的面积与其半径的平方成正比，且比例常数为π。

需要注意的是，圆的面积公式仅适用于均匀、完美无缺的圆形。

当圆存在缺陷或不规则时，可以通过近似方法或数值计算来估算圆的面积。

1圆
第5课时 圆的面积(一)》圆的面积公式的推导
BS六年级上册
提示：点击 进入习题
1
2
3
4
5
6
7
知识点1 数方格求圆的面积
1.数方格估算下面圆的面积。
28
50
知识点 2 圆的面积公式的推导
2.如图，将一张半径为r的圆形纸片16等分，拼成一个 近似的平行四边形。
等分的份数越多，每一份就会越小，拼成的图形就会越
7.将一个圆剪拼成一个近似的长方形(如图)，已知这 个长方形的周长是33.12dm，求圆的面积。
解：设圆的半径为rdm。 (3.14r＋r)×2＝33.12 r＝4 3.14×42＝50.24(dm2)
接近一个(
)。
平行四边形
(1)这个平行四边形的底相当于圆的( 周长的一半)，
平行四边形的高相当于圆的( 半径 )，拼成的平
行四边形的面积等于圆的(
)。
(2)因为平行四边形的面积＝底面×积高，相当于圆的
(
)×(
)，所以圆的面积公式用
字周母长表的示一是半S＝( 半)×径(
)＝(
)。
πr r
πr2
知识点 3 应用圆的面积公式计算圆的面积 3.根据公式计算下图中圆的面积。
圆的半径：6.28÷3.14÷2＝1(m) 圆(长方形)的面积：3.14×12＝3.14(m2) 长方形的长：3.14÷1＝3.14(m) 长方形的周长：(3.14＋1)×2＝8.28(m) 答：长方形的周长是8.28m。
提升点2 用“等量代换法”求圆的面积
6.如图，正方形的面积是18cm2，这个圆的面积是多 少平方厘米？ 3.14×18＝56.52(cm2) 答：这个圆的面积是56.52cm2。

近似梯形
近似三角形
三、以近似平行四边形为例：
等分的分数越多，其面积越接近圆的面积。
圆面8等分时：
圆面16等分时： 圆面32等分时：
23 4
5
6 7
1
8
16
9
151413 12
10 11
1234 5678
11 22 33 44 55 66 77 88 1234 5678 11661155 1144113311221111 1100 99 11661155 1144113311221111 1100 99
复习面积概念
长方形所占平面的大小叫做长方形的面积。
圆所占平面的大小叫做圆的面积。
有关直边形面积的计算
S = a 2 S = ab
S = ah
S = ah÷2
S = (a+b)h÷2
圆面积公式的推导 一、将圆分成若干等分。
34 56
2
7
1
8
16
9
15
10
14 13 12 11
二、用等分后的小块组成不同的形状 近似平行四边形
删掉哦，当然包括最后一页，最后祝 择一人深爱，陪一人到老。一路相扶相持，一路心手相牵，一路笑对风雨。在平凡的世界，不求爱的轰轰烈烈；不求誓
言多么美丽；唯愿简单的相处，真心地付出，平淡地相守，才不负最美的人生；不负善良的自己。 人海茫茫，不求人人都能刻骨铭心，但求对人对己问心无愧，无怨无悔足矣。大千世界，与万千人中遇见，只是相识的
一路走来，愿相亲相爱的人，相濡以沫，同甘共苦，百年好合。愿有情有意的人，不离不弃，相惜相守，共度人生的每 一个朝夕……直到老得哪也去不了，依然是彼此手心里的宝，感恩一路有你！
S=π r2