流体力学课后习题第四章作业答案

第一章习题答案选择题（单选题）1.1 按连续介质的概念，流体质点是指：（d ）（a ）流体的分子；（b ）流体内的固体颗粒；（c ）几何的点；（d ）几何尺寸同流动空间相比是极小量，又含有大量分子的微元体。

1.2 作用于流体的质量力包括：（c ）（a ）压力；（b ）摩擦阻力；（c ）重力；（d ）表面张力。

1.3 单位质量力的国际单位是：（d ）（a ）N ；（b ）Pa ；（c ）kg N /；（d ）2/s m 。

1.4 与牛顿内摩擦定律直接有关的因素是：（b ）（a ）剪应力和压强；（b ）剪应力和剪应变率；（c ）剪应力和剪应变；（d ）剪应力和流速。

1.5 水的动力黏度μ随温度的升高：（b ）（a ）增大；（b ）减小；（c ）不变；（d ）不定。

1.6 流体运动黏度ν的国际单位是：（a ）（a ）2/s m ；（b ）2/m N ；（c ）m kg /；（d ）2/m s N ⋅。

1.7 无黏性流体的特征是：（c ）（a ）黏度是常数；（b ）不可压缩；（c ）无黏性；（d ）符合RT p=ρ。

1.8 当水的压强增加1个大气压时，水的密度增大约为：（a ）（a ）1/20000；（b ）1/10000；（c ）1/4000；（d ）1/2000。

1.9 水的密度为10003kg/m ，2L 水的质量和重量是多少？ 解： 10000.002m V ρ==⨯=（kg ） 29.80719.614G mg ==⨯=（N ）答：2L 水的质量是2 kg ，重量是19.614N 。

1.10 体积为0.53m 的油料，重量为4410N ，试求该油料的密度是多少？ 解： 44109.807899.3580.5m G g V V ρ====（kg/m 3） 答：该油料的密度是899.358 kg/m 3。

1.11 某液体的动力黏度为0.005Pa s ⋅，其密度为8503/kg m ，试求其运动黏度。

第四章作业参考答案6．求下列流场的涡量场及涡线：（1）流体质点的速度与质点到Ox 轴的距离成正比，并与Ox 平行，即0,u v w c ===常数;（2）给定流场,;v xyzr r xi yj zk ==++（3）如果流体绕固定轴象刚体一样作旋转运动。

解：（1）涡量V j Ω=∇⨯=j =ydy zdz =⇒=，i.e.,22y z const +=。

（2） ()()()222222222i j kV xz xy i xy yz j zy zx k x y zx yz xy z xyz ∂∂∂Ω=∇⨯==-+-+-∂∂∂ 涡线为()()()222222dx dy dz x z y y x z z y x ==--- （3）在柱坐标系下，V re θω= ，所以涡量为2V k ω∇⨯=涡线为平行于z 轴的直线为常数。

7．速度场为2,2,2u y z v z x w x y =+=+=+（1）求涡量及涡线；（2）求在1x y z ++=平面上横截面为20.0001dS =米的涡管强度；（3）求在0z =平面上20.0001dS =米的面积上的涡通量。

解：（1）涡量222ij k V i j k xy z y z z x x y∂∂∂Ω=∇⨯==++∂∂∂+++ 涡线为dx dy dz == 积分得12x y c y z c -=⎧⎨-=⎩，因而涡线是两平面族的交线族。

(1) 涡管强度即涡通量。

令1F x y z =++-可得该平面法向为333F n F ⎛∇== ∇⎝⎭， 于是有()1,1,1J dS ndS n S S δδ=Ω⋅=Ω⋅=Ω⋅=⋅⎝⎭⎰⎰⎰⎰410S -==（3）又已知得平面的法向为()0,0,1 同理410J dS ndS n S δ-=Ω⋅=Ω⋅=Ω⋅=⎰⎰⎰⎰16．证明在理想不可压缩流体的平面运动中，若质量力有势，则沿轨迹有0d dtΩ= ，而且在 定常运动中，沿流线涡量Ω 保持常植。

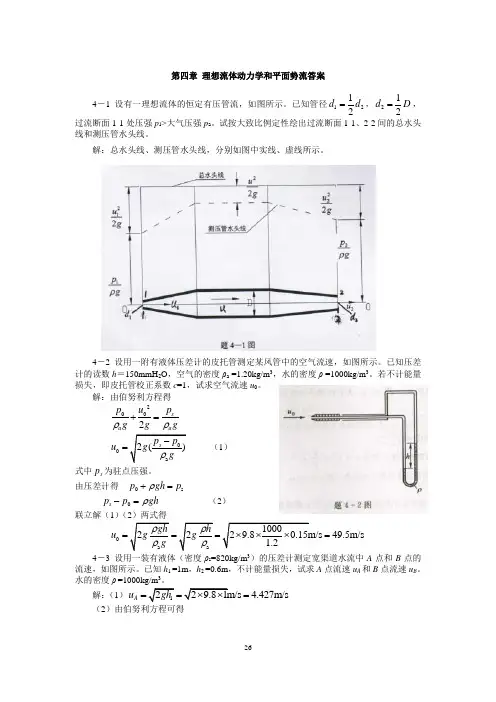
第四章 理想流体动力学和平面势流答案4－1 设有一理想流体的恒定有压管流，如图所示。

已知管径1212d d =，212d D =，过流断面1-1处压强p 1>大气压强p a 。

试按大致比例定性绘出过流断面1-1、2-2间的总水头线和测压管水头线。

解：总水头线、测压管水头线，分别如图中实线、虚线所示。

4－2 设用一附有液体压差计的皮托管测定某风管中的空气流速，如图所示。

已知压差计的读数h ＝150mmH 2O ，空气的密度ρa =1.20kg/m 3，水的密度ρ =1000kg/m 3。

若不计能量损失，即皮托管校正系数c =1，试求空气流速u 0。

解：由伯努利方程得2002s a a p u p g g gρρ+= 00a 2()s p p u g gρ-=（1） 式中s p 为驻点压强。

由压差计得 0s p gh p ρ+=0s p p gh ρ-= （2）联立解（1）（2）两式得0a a 10002229.80.15m/s 49.5m/s 1.2gh h u gg g ρρρρ===⨯⨯⨯= 4－3 设用一装有液体（密度ρs =820kg/m 3）的压差计测定宽渠道水流中A 点和B 点的流速，如图所示。

已知h 1 =1m ，h 2 =0.6m ，不计能量损失，试求A 点流速u A 和B 点流速u B 。

水的密度ρ =1000kg/m 3。

解：（1）1229.81m/s 4.427m/s A u gh ==⨯⨯= （2）由伯努利方程可得22A AA u p h g gρ+= （1）22B BB u p h g gρ+= （2）式中A h 、A p 和B h 、B p 分别为A 点和B 点处的水深和驻点压强。

由（1）、（2）式可得2222A B A BA B p p u u h h g g gρ-=+-- （3） 由压差计得，22ρρρρ--++=A A s B B p gh gh gh gh p ，所以220.82A BA B p p h h h h gρ-=+-- (4) 由（3）式、（4）式得2222 4.427(10.82)0.6(10.82)0.8922229.8B A u u h g g =--=--=⨯ 29.80.892m/s 4.18m/s B u =⨯⨯=。

第四章习题答案选择题（单选题）4.1等直径水管，A-A 为过流断面，B-B 为水平面，1、2、3、4为面上各点，各点的流动参数有以下关系：（c ）（a ）1p =2p ；（b ）3p =4p ；（c ）1z +1p g ρ=2z +2p g ρ；（d ）3z +3p g ρ=4z +4pgρ。

4.2伯努利方程中z +p g ρ+22v gα表示：（a ）（a ）单位重量流体具有的机械能；（b ）单位质量流体具有的机械能；（c ）单位体积流体具有的机械能；（d ）通过过流断面流体的总机械能。

4.3水平放置的渐扩管，如忽略水头损失，断面形心点的压强，有以下关系：（c ）p p 2（a ）1p >2p ；（b ）1p =2p ；（c ）1p <2p ；（d ）不定。

4.4黏性流体总水头线沿程的变化是：（a ） （a ）沿程下降；（b ）沿程上升；（c ）保持水平；（d ）前三种情况都有可能。

4.5黏性流体测压管水头线的沿程变化是：（d ） （a ）沿程下降；（b ）沿程上升；（c ）保持水平；（d ）前三种情况都有可能。

4.6平面流动具有流函数的条件是：（d ）无黏性流体；（b ）无旋流动；（c ）具有速度势；（d ）满足连续性。

4.7一变直径的管段AB ，直径A d =0.2m ，B d =0.4m ，高差h ∆=1.5m ，今测得A p =302/m kN ，B p =402/m kN ， B 处断面平均流速B v =1.5s m /.。

试判断水在管中的流动方向。

解： 以过A 的水平面为基准面，则A 、B 点单位重量断面平均总机械能为：42323010 1.0 1.50.40 4.89210009.80729.8070.2A A A A A p v H z g g αρ⨯⨯⎛⎫=++=++⨯= ⎪⨯⨯⎝⎭（m ）2324010 1.0 1.51.5 5.69210009.80729.807B B B B B p v H z g g αρ⨯⨯=++=++=⨯⨯（m ）∴水流从B 点向A 点流动。

流体力学习题及答案-第四章第四章 流体动力学基本定理及其应用4-1 欧拉运动微分方程和伯努利方程的前提条件是什么，其中每一项代表什么意义？答：（1）欧拉运动微分方程是牛顿第二定律在理想流体中的具体应用，其矢量表达式为：()p f v v t v ∇-=∇⋅+∂∂ρ1ρρρρ 其物理意义为：从左至右，方程每一项分别表示单位质量理想流体的局部惯性力、迁移惯性力、质量力和压力表面力。

（2）伯努利方程的应用前提条件是：理想流体的定常运动，质量力有势，正压流体，沿流线积分。

单位质量理想流体的伯努利方程的表达式为：C gz p =++ρ2V 2，从左至右方程每项分别表示单位质量理想流体的动能、压力能和位能，方程右端常数称流线常数，因此方程表示沿流线流体质点的机械能守恒。

4-2 设进入汽化器的空气体积流量为s m /15.0Q 3=，进气管最狭窄断面直径D=40mm ，喷油嘴直径d=10mm 。

试确定汽化器的真空度。

又若喷油嘴内径d=6mm ，汽油液面距喷油嘴高度为50cm ，试计算喷油量。

汽油的重度3/7355m N =γ。

答：（1）求A 点处空气的速度：设进气管最狭窄处的空气速度为1v ，压力为1p ，则根据流管的连续方程可以得到：()Q v d D =-12241π，因此：()2214d D Q v -=π。

（2）求真空度v p选一条流线，流线上一点在无穷远处F ，一点为A 点；并且：在F 点：0F p p =，0F =v ；在A 点：?1A ==p p ，1A v v =。

将以上述条件代入到伯努利方程中，可以得到：g v p p 202110+=+γγ 因此真空度为：()()222222221101842121d D Q d D Q v p p p v -⋅=⎥⎦⎤⎢⎣⎡-==-=πρπρρ 若取空气的密度为3/226.1m kg =ρ，那么计算得到：()Pa p v 3222221095.901.004.0114.315.0226.18⨯=-⨯⨯⨯=。

李玉柱流体力学课后题答案第四章第四章流体动力学基础4-1 设固定平行平板间液体得断面流速分布为,总流得动能修正系数为何值?解:因为所以172233821.0 1.01 1.0572BBA AB y u v d dy B A v B α--- ??? ?≈+=+?-= ? ? ??? ?????4-2 如图示一股水流自狭长得缝中水平射出,其厚度,平均流速V 0＝8m/s,假设此射流受重力作用而向下弯曲,但其水平分速保持不变。

试求(1)在倾斜角处得平均流速V ;(2)该处得水股厚度。

解:(1)由题意可知:在45度水流处,其水平分速度仍为8m/s,由勾股定理可得:V==11、31m/s(2)水股厚度由流量守恒可得:,由于缝狭长,所以两处厚度近似相等,所以m 。

4-3 如图所示管路,出口接一收缩管嘴,水流射人大气得速度V 2=20m/s,管径d 1＝0、1m,管嘴出口直径d 2＝0、05m,压力表断面至出口断面高差H ＝5m,两断面间得水头损失为。

试求此时压力表得读数。

解:取压力表处截面为截面1-1,收缩管嘴处截面为截面2-2,选择两截面包围得空间为控制体,由实际流体得恒定总流能量方程得: ,由连续性方程可得1-1断面流速,由上述两个方程可得压力表得读数(相对压强):,上式计算结果为:2、48at 。

所以,压力表得读数为2、48at 。

4-4 水轮机得圆锥形尾水管如图示。

已知A —A 断面得直径d A =0、6m,流速V A ＝6m ／s,B —B 断面得直径d B ＝0、9m,由A 到B 水头损失。

求(1)当z ＝5m 时A —A 断面处得真空度;(2)当A —A断面处得允许真空度为5m 水柱高度时,A —A 断面得最高位置。

解:(1)取A-A 与B-B 包围得空间为控制体,对其列伯努利方程:可得A-A 断面处得真空度,由连续性方程可得B-B 断面流速=2、67m/s,所以A-A 断面处真空度为6、42m 。

第一章习题答案选择题（单选题）1.1 按连续介质的概念，流体质点是指：（d ）（a ）流体的分子；（b ）流体内的固体颗粒；（c ）几何的点；（d ）几何尺寸同流动空间相比是极小量，又含有大量分子的微元体。

1.2 作用于流体的质量力包括：（c ）（a ）压力；（b ）摩擦阻力；（c ）重力；（d ）表面张力。

1.3 单位质量力的国际单位是：（d ）（a ）N ；（b ）Pa ；（c ）kg N /；（d ）2/s m 。

1.4 与牛顿内摩擦定律直接有关的因素是：（b ）（a ）剪应力和压强；（b ）剪应力和剪应变率；（c ）剪应力和剪应变；（d ）剪应力和流速。

1.5 水的动力黏度μ随温度的升高：（b ）（a ）增大；（b ）减小；（c ）不变；（d ）不定。

1.6 流体运动黏度ν的国际单位是：（a ）（a ）2/s m ；（b ）2/m N ；（c ）m kg /；（d ）2/m s N ⋅。

1.7 无黏性流体的特征是：（c ）（a ）黏度是常数；（b ）不可压缩；（c ）无黏性；（d ）符合RT p=ρ。

1.8 当水的压强增加1个大气压时，水的密度增大约为：（a ）（a ）1/20000；（b ）1/10000；（c ）1/4000；（d ）1/2000。

1.9 水的密度为10003kg/m ，2L 水的质量和重量是多少？ 解： 10000.0022m V ρ==⨯=（kg ）29.80719.614G mg ==⨯=（N ）答：2L 水的质量是2 kg ，重量是19.614N 。

1.10 体积为0.53m 的油料，重量为4410N ，试求该油料的密度是多少？ 解： 44109.807899.3580.5m G g V V ρ====（kg/m 3） 答：该油料的密度是899.358 kg/m 3。

1.11 某液体的动力黏度为0.005Pa s ⋅，其密度为8503/kg m ，试求其运动黏度。

第四章 习题解答 4-1 用直径为100mm的管道输送流量为10kg/s的水，如水温为5℃，试确定管内水的流态。如用这管道输送同样质量流量的石油，已知石油密度为3/850mkg=ρ

运动粘滞系数为

scm/14.12，试确定石油的流态。

解：水温为5℃时，其密度为3/1000mkg=ρ，运动粘滞系数为sm/10519.126−×=γ

因此，水在管道中流动的体积流量为： smmkgskgQ/01.0/1000/1033==

流速为： smmmsmAQ/27.1)1000100(14.341/01.023=××==υ

雷诺数为： 83863/10519.11000100/27.1Re26=××=−sm

mmsm

为紊流

当输送石油时： smmkgskgQ/012.0/850/1033==

流速为： smmmsmAQ/5.1)1000100(14.341/012.023=××==υ

雷诺数为： 1316/1014.11000100/5.1Re24=××=−sm

mmsm

为层流

4-2 一圆形风道，管径为300mm，输送的空气温度为20℃，求气流保持层流时的最大流量。若输送的空气量为200kg/h，气流是层流还是紊流？ 解：空气温度为20℃时，运动粘滞系数sm/107.1526-×=γ

，根据题意有：

6107.1510003002000−××=mmυ 解方程得：sm/105.0=υ 气体流量为：

smsmmmQ/0074.0/105.0)1000300(14.34132=×××=

质量流量为：

hkgskgmkgsmQ/29/0081.0/093.1/0074.033==×=

若输送的空气量为200kg/h，因此，空气在管道中流动的体积流量为： smmkghkgQ/051.03600/093.1

/2003

3=×=

󰀁

流速为： smmmsmAQ/72.0)1000300(14.34

1

/051.023

=××==υ

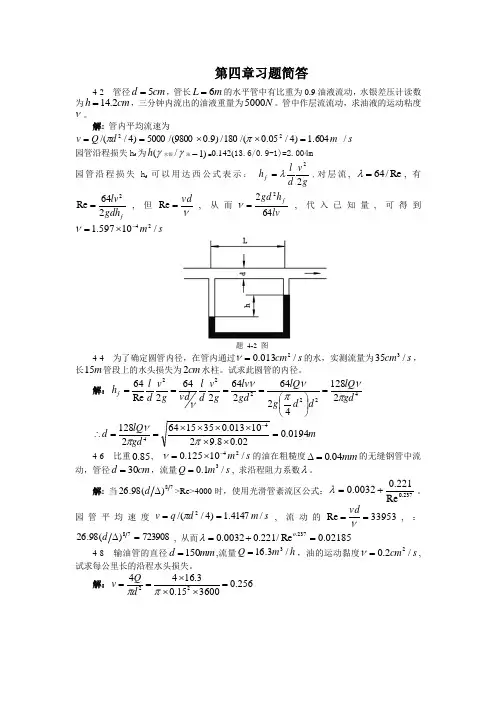
第四章习题简答4-2 管径cm d 5=，管长m L 6=的水平管中有比重为0.9油液流动，水银差压计读数为cm h 2.14=，三分钟内流出的油液重量为N 5000。

管中作层流流动，求油液的运动粘度ν。

解: 管内平均流速为s m d Q v /604.1)4/05.0/(180/)9.09800/(5000)4//(22=⨯⨯==ππ 园管沿程损失h f 为γ(h 水银γ/油)1-=0.142(13.6/0.9-1)=2.004m园管沿程损失h f 可以用达西公式表示： g v d l h f 22λ=,对层流, Re /64=λ, 有fgdh lv 264Re 2=, 但νvd =Re , 从而lv h gd f 6422=ν, 代入已知量, 可得到s m /10597.124-⨯=ν题 4-2 图4-4 为了确定圆管内径，在管内通过s cm /013.02=ν的水，实测流量为s cm /353，长m 15管段上的水头损失为cm 2水柱。

试求此圆管的内径。

解：422222212842642642642Re 64gd lQ d d g lQ gd lv g v d l vd g v d l h f πνπννν=⎪⎭⎫ ⎝⎛==== m gd lQ d 0194.002.08.9210013.0351********4=⨯⨯⨯⨯⨯⨯==∴-ππν 4-6 比重85.0, s m /10125.024-⨯=ν的油在粗糙度mm 04.0=∆的无缝钢管中流动，管径cm d 30=，流量s m Q /1.03=, 求沿程阻力系数λ。

解: 当78)(98.26∆d >Re>4000时，使用光滑管紊流区公式：237.0Re221.00032.0+=λ。

园管平均速度s m d q v /4147.1)4//(2==π, 流动的33953Re ==νvd , ： 723908)(98.2678=∆d , 从而02185.0Re /221.00032.0237.=+=o λ4-8 输油管的直径mm d 150=,流量h m Q /3.163=，油的运动黏度s cm /2.02=ν,试求每公里长的沿程水头损失。

流体力学第四章练习题答案流体力学第四章练习题答案流体力学是研究流体运动和力学性质的学科，它在工程领域中有着广泛的应用。

在学习流体力学的过程中，练习题是非常重要的一部分，通过解答练习题可以加深对理论知识的理解和应用能力的培养。

本文将给出流体力学第四章练习题的详细答案，帮助读者更好地掌握流体力学的相关内容。

1. 问题描述：一个圆柱形容器内装有水，容器的高度为H，底面半径为R。

求当容器底面上有一个小孔时，水从小孔流出的速度。

解答：根据伯努利方程，可以得到以下关系式：P1 + 1/2ρv1^2 + ρgh1 = P2 + 1/2ρv2^2 + ρgh2其中，P1和P2分别为容器内外的压力，v1和v2分别为水流出小孔前后的速度，h1和h2分别为小孔前后的高度。

由于小孔处的压力与容器内外的压力相等，即P1 = P2，且小孔前后的高度差h1 - h2可以近似为H，因此上述方程可以简化为：1/2ρv1^2 + ρgH = 1/2ρv2^2解上述方程可以得到v2 = √(2gH + v1^2/2)2. 问题描述：一个水箱内装有水，水箱的高度为H，底面积为A。

在水箱的底部有一个小孔，小孔的面积为a。

求水从小孔流出的速度。

解答：根据质量守恒定律，可以得到以下关系式：A√(2gH) = a√(2gh)其中，g为重力加速度，h为水箱底部水位的高度。

解上述方程可以得到h = (A/a)^2H因此，水从小孔流出的速度为v = √(2gh) = √(2g(A/a)^2H)3. 问题描述：一个喷嘴的出口直径为d，喷嘴内的水流速度为v，水的密度为ρ。

求喷嘴出口处的压力。

解答：根据质量守恒定律，可以得到以下关系式：Av = π(d/2)^2v = 喷嘴出口处的流量根据伯努利方程，可以得到以下关系式：P1 + 1/2ρv1^2 = P2 + 1/2ρv2^2其中，P1为喷嘴入口处的压力，P2为喷嘴出口处的压力，v1为喷嘴入口处的速度，v2为喷嘴出口处的速度。

第四章流体动力学基础 u f B / 2 — v 4-1设固定平行平板间液体的断面流速分布为一=盅

总流的动能修正系数为何值？

V0 = 8m/s,假设此射流受重力作用而向下弯曲， 但其水平分速保持不变。试求(1) 在倾斜角v -45处的平均流速V; (2)该处的水股厚度-o 解：(1)由题意可知：在45度水流处，其水平分速度仍为8m/s,由勾股定理 8 可得：V=—8 =11.31m/s sin 45

(2)水股厚度由流量守恒可得： TV0D0 -：VD，由于缝狭长，所以两处厚

度近似相等，所以：二泄 二0^8 =0.021 mo V 11.31 4-3如图所示管路，出口接一收缩管嘴，水流射人大气的速度V2=20m/s，管 径d1 = 0.1m，管嘴出口直径d2= 0.05m，压力表断面至出口断面高差 H = 5m，两

断面间的水头损失为0.5M2/2g)。试求此时压力表的读数

1 解：* 2d

1 -y

B2 .7

U maxdy Umax

8

(Au 1.0+—【A.— dA 也u =u —V所以

:1.0 - A • dA =1.0 - dy =1.05

4-2如图示一股水流自狭长的缝中水平射出，其厚度 「•0 = 0.03m，平均流

速

1/7 I ，y^0

Umax S 4-1 闭 魁47圈 2g g ‘ 2g g ? -Z2 hw

由连续性方程 7 二A2V可得1-1断面流速V =5m s, 由上述两个方程可得压力表的 乜2 -Vj ） —-——+Z2 —乙+h； gP，

< 2g 丿

读数（相 对压强）：

上式计算结果为：2.48at。所以，压力表的读数为2.48at。 4-4水轮机的圆锥形尾水管如图示。已知 A— A断面的直径

VA = 6m/s, B—B断面的直径dB = 0.9m，由A到B水头损失 厲 dA=0.6m，流速

= 0.15(V：求⑴当Z= 水柱高度时, 5m时A—A断面处的真空度；（2）当A—A断面处的允许真空度为5m

第四章 流体阻力与水头损失计算习题一、填空题1．雷诺数Re 是反映流体流动状态的准数，它反映了流体流动时 粘性力 与 惯性力 的对比关系，雷诺数Re 越大，说明液流的惯性力越大；雷诺数Re 越小，说明液流的粘滞力越大；2. 流体在管道中流动时，流动阻力包括 沿程阻力 和 局部阻力 ；3．流体流动阻力产生的根本原因是流体本身的 惯性 与 粘性 ，其中 粘性 是流动阻力的根本原因。

4．由紊流转变为层流的临界流速k v 小于 由层流转变为紊流的临界流速kv '， 其中kv '称为 上临界速度 ，k v 称为 下临界速度 ； 5.达西公式的表达式为 22f L v h d g λ= ，计算局部水头损失的通用公式是22j v h gξ= ; 7、对圆管来说，临界雷诺数值=k Re 2000 。

8、雷诺数的表达公式为 vd vd Re ρμν==，当Re ≤2000,则液体的流动状态为层流，当Re ＞2000,则液体的流动状态为紊流；9、通过雷诺实验，可知，流体的流动状态分为层流与紊流；其中，质点以平行于管轴方向呈直线运动而无横向运动的流动状态，称为层流状态。

液体质点的互相撞击和掺混，有横向位移，称为紊流状态。

层流到紊流的过渡，称为临界状态。

10、紊流由紊流核心、层流边层和过渡层三部分组成。

11、我们把在管壁附近作层流运动的液层称为层流边界层，其厚度用“δ”，表示。

12、壁面的粗糙度有两种表示方法：绝对粗糙度和相对粗糙度。

13、绝对粗糙度△是壁面粗糙突出的平均高度。

14、紊流的三种类型有水力光滑管、水力粗糙管、混合摩擦管 。

二、选择题1、雷诺数的物理意义表示：（c ）A 、粘滞力与重力之比；B 、重力与惯性力之比；C 、惯性力与粘滞力之比；D 、压力与粘滞力之比。

2、圆管紊流粗糙区的沿程摩阻系数λ D ；A 、与雷诺数Re 有关B 、与和管长l 有关C 、与Re 和d∆有关 D 、与管壁相对粗糙度d D 有关 3、在圆管流动中，层流的断面速度分布符合 C ； A 、均匀规律 B 、直线变化规律 C 、抛物线变化规律 D 、对数曲线规律4、流体在管内作层流流动时，其沿程损失h f 值与断面平均流速v 的 A 次方成正比。

第四章流体动力学基础总流的动能修正系数为何值？o = 8m/s,假设此射流受重力作用而向下弯曲， 但其水平分速保持不变。

试求（1） V在倾斜角0=45C处的平均流速V ； （2）该处的水股厚度o5 解：（1）由题意可知：在45度水流处，其水平分速度仍为8m/s,由勾股定理Q可得：V= -------- & = 11.31m/ssin 45（2）水股厚度由流量守恒可得： S oVo D ,由于缝狭长，所以两处厚度近似相等，所以6 J°V° =0.0? 8= --------------- =0.021m 。

V 11.314・3如图所示管路，出口接一收缩管嘴，水流射人大气的速度 V2=20m/s ,管 径di-0.1m,管嘴出口直径d2= 0.05m,压力表断面至出口断面高差H = 5m,两 断面间的水头损失为0.5（Vi 2/2g ）。

试求此时压力表的读数。

4-1设固定平行平板间液体的断面流速分布为—UmaxB/2-y ' I B/21/7因为a «= l ・0 +—| A’ -所以V31"一 f AA4・2如图示一股水流自狭长的缝中水平射出，其厚度平均流速 解：v =— f Aud AA .7 Umax ay = — Umax83 BdA =1.0 +— jjeV xB 2-1 dy =1.05题4-2圈解：取压力表处截面为截面1・1,收缩管嘴处截面为截面2・2,选择两截面包围 的空间为控制体，由实际流体的恒定总流能量方程得：由连续性方程AiVi = A2V2可得1・1断面流速Vi =5nV"s, 由上述两个方程可得压力表的读数(相对压强):v 22 - V12.)pi -P2 = ------------- +z2 _Z1+ hwl 炉，I 2g 丿上式计算结果为：2.48ato 所以，压力表的读数为2.48ato 4・4水轮机的圆锥形尾水管如图示。

第四章流体动力学基本定理及其应用4-1欧拉运动微分方程和伯努利方程的前提条件是什么，其中每一项代表什么意义？答：（1）欧拉运动微分方程是牛顿第二定律在理想流体中的具体应用，其矢量表达式为:.:t其物理意义为：从左至右，方程每一项分别表示单位质量理想流体的局部惯性力、迁移惯性力、质量力和压力表面力。

（2）伯努利方程的应用前提条件是：理想流体的定常运动，质量力有势，正压流体，沿流2线积分。

单位质量理想流体的伯努利方程的表达式为：- p g^ C，从左至右方程2 P每项分别表示单位质量理想流体的动能、压力能和位能，方程右端常数称流线常数，因此方程表示沿流线流体质点的机械能守恒。

4-2设进入汽化器的空气体积流量为Q = 0.15m3 / S,进气管最狭窄断面直径D=40mm，喷油嘴直径d=10mm。

试确定汽化器的真空度。

又若喷油嘴内径d=6mm，汽油液面距喷油嘴高度为50cm，试计算喷油量。

汽油的重度=7355N/m3。

答：（1）求A点处空气的速度：设进气管最狭窄处的空气速度为V i，压力为p i，则根据流管的连续方程可以得到:丄二D2_d2V i =Q，44Q因此：v14Q 厂。

江（D2-d2）（2 ）求真空度p v选一条流线，流线上一点在无穷远处F，—点为A点；并且:在F点：P F二P o ，V F = 0 ；在A点：P A二P1 二？，V A二W。

将以上述条件代入到伯努利方程中，可以得到:2也.0. v_02g-—；v f ， v A = v 2 = ?， z A = h = 50cm = 0.5m ；2在 B 点：P B = p 0， V B = 0，Z B = 0 ； 代入到伯努利方程中，可以得到:Ip 0才v 22rh 』0 0；整理得到:v ；二」V 12 -2gh ；2因此汽油喷出速度为:1V 2 -2gh ；其中空气重度1 = Sg =1.226 9.81 =12N/m 3 ； V 1缪 龙，并注意到喷油嘴的 兀(D -d )直径是6mm ，而不是原来的10mm ，则计算得到:因此汽油流量为:12 _43 3因此真空度为:P v 二 P o - P i4Q冷心2] D2—d 28 322 JI(D 2 —d 2 2若取空气的密度为3::=1.226kg/m ，那么计算得到:8 1.226 0.152pv3.1421 32 =9.95 103Pa 。