下载文档原格式
一、填空题1．离散系统输出响应的Z 变换为：()2320.3680.2642 1.6320.632z z C z z z z +=-+-则系统输出在前两个采样时刻的值为______，______。
[重庆大学()C nT ()0C =()C T =2006年研]【答案】0；0.3682．零阶保持器的传递函数是______，加入零阶保持器______会影响采样系统的稳定性。
[北京交通大学2009年研]【答案】；不1e Ts s--二、问答题1．如何判断离散系统的稳定性。
并图示说明之。
[东北大学研]答：由于Z 变换与拉普拉斯变换之间的映射关系为，其中T 为采样周期，在s平面内当系统稳定时所有特征根位于左半平面，映射到Z 平面中则是单位圆内，对应的映射关系如图8-1所示。
图8-1于是判断离散系统的稳定性时，只需判断其特征方程的根的模是否大于1，当其模大于1时，系统不稳定；模等于1时，系统临界稳定；当其模小于1时，系统稳定，为了能位于右半平面；位于左半平面；对应的映射关系如图8-2所示。
所示得到关于ω的特征方程，使用劳斯判据进行判断。
图8-22．线性定常离散系统的稳定性除了与系统结构参数有关之外，还与哪些因素有关？[南京航空航天大学2008年研]答：线性定常离散系统的稳定性除了与系统结构参数有关之外，还与采样周期T有关，当系统开环增益一定时，T越小，稳定性越好。
三、计算题1．先用Z变换法求解下面的微分方程，再求其终值e（∞）。
e（k＋2）＋3e（k＋1）＋2e（k）＝0，已知e（0）＝0，e（1）＝1。
[浙江大学研]解：将善分方程两沩讲行Z变换可以得到：将e（0）＝0，e（1）＝1代入整理可以得到：2．已知z变换求离散时间函数z（k）和采样函数[清华大学研]解：由对照典型函数的z 变换表可以得到即其中T为采样周期，为单位脉冲。
3．某离散系统如图8-3所示，试求其闭环脉冲传递函数[四川大学研]图8-3解：由题意，可以得到如下方程整理得到对式（3）两边进行z变换得到：（4）由两边进行Z 变换得到：（5）联立式（4），式（5），消去中间变量可以得到4．线性定常离散系统如图8-4所示，写出闭环系统的脉冲传递函数。
词汇第一章自动控制 ( Automatic Control) ：是指在没有人直接参与的条件下，利用控制装置使被控对象的某些物理量（或状态）自动地按照预定的规律去运行。
开环控制 ( open loop control )：开环控制是最简单的一种控制方式。
它的特点是，按照控制信息传递的路径，控制量与被控制量之间只有前向通路而没有反馈通路。
也就是说，控制作用的传递路径不是闭合的，故称为开环。
闭环控制 ( closed loop control) ：凡是将系统的输出量反送至输入端，对系统的控制作用产生直接的影响，都称为闭环控制系统或反馈控制 Feedback Control 系统。
这种自成循环的控制作用，使信息的传递路径形成了一个闭合的环路，故称为闭环。
复合控制 ( compound control ）：是开、闭环控制相结合的一种控制方式。
被控对象：指需要给以控制的机器、设备或生产过程。
被控对象是控制系统的主体，例如火箭、锅炉、机器人、电冰箱等。
控制装置则指对被控对象起控制作用的设备总体，有测量变换部件、放大部件和执行装置。
被控量 (controlled variable ) ：指被控对象中要求保持给定值、要按给定规律变化的物理量。
被控量又称输出量、输出信号。
给定值 (set value ) ：是作用于自动控制系统的输入端并作为控制依据的物理量。
给定值又称输入信号、输入指令、参考输入。
干扰 (disturbance) ：除给定值之外，凡能引起被控量变化的因素，都是干扰。
干扰又称扰动。
第二章数学模型 (mathematical model) ：是描述系统内部物理量（或变量）之间动态关系的数学表达式。
传递函数 ( transfer function) ：线性定常系统在零初始条件下，输出量的拉氏变换与输入量的拉氏变换之比，称为传递函数。
零点极点 (z ero and pole) ：分子多项式的零点（分子多项式的根）称为传递函数的零点；分母多项式的零点（分母多项式的根）称为传递函数的极点。
离散系统闭环脉冲传递函数的极点，则动态响应为（已知，则有的拉氏变换为，则判断题图中系统是否稳定非线性系统的及的轨迹如下图所示，试问）已知非线性系统的微分方程是,两输入，两输出的系统，其模拟结构图如图所示，其状态空间表达式为：（）B.C.已知系统传递函数,则系统的约旦标准型的实现为∙B.∙C.D.∙A.∙B.∙C.∙D.正确答案：B19已知系统：已知，下列有关该系统稳定性说法正确的是（）闭环脉冲传递函数分别为，输出为已知计算机控制系统如下图所示，采用数字比例控制，其中，,系统的闭环脉冲传递函数为的取值范围是系统的开环脉冲传递函数为的取值范围是已知，，。
符合系统描述的系统稳定系统稳定系统的闭环脉冲传递函数设离散系统如图所示，设，时，若要求其稳态误差,，该系统的闭环脉冲传递函数为该系统的开环脉冲传递函数为对于响应斜坡输入信号统（取F(z)=1），下列选项正确的是（）变换为数字控制器的脉冲传递函数为变换为变换为非线性系统的及的轨迹如下图所示，以下说法正确的是求下图中以电压为输入量，以电感中的电流和电容上的电压作为状态变量的状态方程为___，以电阻上的电压作为输出量的输出方程为___。
（）∙A.∙B.∙C.D.现用进行状态变换B.C.D.已知系统的传递函数为B. C.对线性系统作状态反馈 , A.某离散控制系统（单位反馈该系统稳态误差为代表时域中的延迟算子系统状态空间表达式中，若离散控制系统（单位反馈，则动态响应为的拉氏变换为，A.C.下图所示为某一闭环离散系统，则该系统的脉冲传递函数为（）离散系统闭环脉冲传递函数的极点,的的拉氏变换为，则。
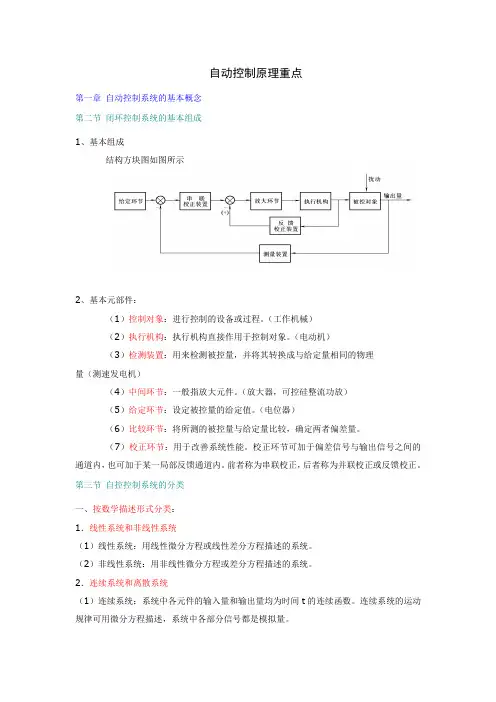
自动控制原理重点第一章自动控制系统的基本概念第二节闭环控制系统的基本组成1、基本组成结构方块图如图所示2、基本元部件：（1）控制对象：进行控制的设备或过程。
（工作机械）（2）执行机构：执行机构直接作用于控制对象。
（电动机）（3）检测装置：用来检测被控量，并将其转换成与给定量相同的物理量（测速发电机）（4）中间环节：一般指放大元件。
（放大器，可控硅整流功放）（5）给定环节：设定被控量的给定值。
（电位器）（6）比较环节：将所测的被控量与给定量比较，确定两者偏差量。
（7）校正环节：用于改善系统性能。
校正环节可加于偏差信号与输出信号之间的通道内，也可加于某一局部反馈通道内。
前者称为串联校正，后者称为并联校正或反馈校正。
第三节自控控制系统的分类一、按数学描述形式分类：1．线性系统和非线性系统（1）线性系统：用线性微分方程或线性差分方程描述的系统。
（2）非线性系统：用非线性微分方程或差分方程描述的系统。
2．连续系统和离散系统（1）连续系统：系统中各元件的输入量和输出量均为时间t的连续函数。
连续系统的运动规律可用微分方程描述，系统中各部分信号都是模拟量。
（2）离散系统：系统中某一处或几处的信号是以脉冲系列或数码的形式传递的系统。
离散系统的运动规律可以用差分方程来描述。
计算机控制系统就是典型的离散系统。
二、按给定信号分类（1）恒值控制系统：给定值不变，要求系统输出量以一定的精度接近给定希望值的系统。
如生产过程中的温度、压力、流量、液位高度、电动机转速等自动控制系统属于恒值系统。
（2）随动控制系统：给定值按未知时间函数变化，要求输出跟随给定值的变化。
如跟随卫星的雷达天线系统。
（3）程序控制系统：给定值按一定时间函数变化。
如程控机床。
第四节对控制系统的基本要求对控制系统的基本要求归纳为稳定性、动态特性和稳态特性三个方面1、系统的暂态过程2、稳定性3、动态特性4、稳态特性值得注意的是，对于同一个系统体现稳定性、动态特性和稳态特性的稳、快、准这三个要求是相互制约的。
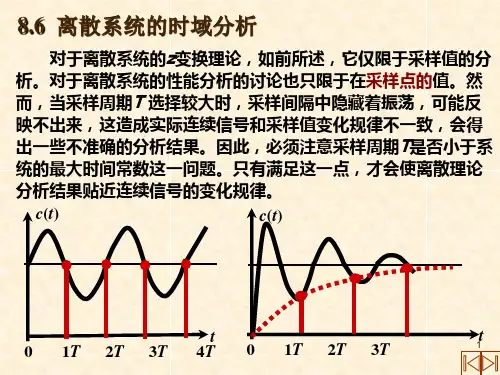
第八章线性离散控制系统8.1 概述8.2 信号采样与保持8.3 离散系统的数学模型8.4 离散控制系统的稳定性8.5 离散控制系统的动态性能分析8.6离散控制系统的稳态误差分析8.7 离散控制系统的最少拍校正8.8利用MATLAB辅助离散控制系统的分析与校正8.9 小结8.1概述本章知识体系离散控制系统的稳定性离散控制系统基本概念信号的采样与保持离散控制系统的数学模型离散控制系统的动态性能分析离散控制系统的稳态误差分析最少拍校正利用MATLAB辅助离散控制系统的分析与校正描述系统分析系统仿真分析、校正系统8.1概述时间上不连续的信号在现实系统中大量存在。
例如许多化工生产过程无法在线连续测量产品的质量指标而是通过定期采样化验就能保证产品质量的稳定。
系统内有一处或多处的信号仅存在于孤立的时间序列点上这类控制系统称为离散时间控制系统简称离散控制系统。
与此相对各处信号均为连续时间函数的控制系统称为连续时间控制系统简称连续控制系统。
8.1概述时间上离散的信号其幅值可能是连续的亦可能是离散的。
将时间上、幅值上都连续的模拟信号转换成时间上离散、但幅值上仍然连续的离散模拟序列信号的过程而这一过程就称为采样又称为波形的离散化过程相应的控制系统则称为采样控制系统。
若由数字计算机实现控制受计算机字长限制还需要进一步将幅值连续的理想化序列信号量化为数字序列信号进一步得到时间和幅值上都是离散的数字序列信号相应的控制系统则称为数字控制系统。
8.1 概述8.1.1 离散控制系统的基本概念 1.采样控制系统大惯性、大滞后控制系统出现的问题采样系统较早出现与某些大惯性、大滞后对象的控制系统中如炉温控制系统。
这类对象的相位滞后非常明显为保证系统的相位裕度开环传递系数一般取很小值难以有很高的稳定精度.提高稳态精度的一个方法在偏差信号和执行电机之间安装一个开关使其每隔较长时间才闭合一次且闭合时间很短。
当开关闭合时系统根据偏差闭环控制电机当开环断开时电机停止等待炉温变化。
209第8章 离散控制系统的分析和综合本章讲述离散控制系统的分析和综合.首先介绍离散控制系统的组成、研究方法、采样过程、采样定理、z 变换、脉冲传递函数和差分方程；在此基础上，介绍了离散控制系统的稳定性、稳态误差和动态性能的分析等有关问题；介绍了数字控制器的脉冲传递函数以及最少拍系统的设计；最后介绍应用MATLAB 对离散控制系统的分析。
习教材习题同步解析8。
1 设时间函数的拉氏变换为()X s ，采样周期T s =1秒,利用部分分式展开求对应时间函数的z 变换()X z .（1） (3)()(1)(2)s X s s s s +=++ （2） (1)(2)()(3)(4)s s X s s s ++=++（3） 227()(2)(413)X s s s s =+++ （4） 210()(2)(1261)X s s s s s =+++ 解 （1）将()X s 展成部分分式1.520.5()12X s s s s -=++++ 则其z 变换为()()()121.520.5(0.8310.011)()110.3680.135z z z z z X z z z e z e z z z ----=++=------ (2）将()X s 展成部分分式26()134X s s s =+-++ 则其z 变换为23422630.1960.001()10.0680.001z z z z X z z e z e z z ---++=+-=---+210（3）将()X s 展成部分分式22233633(2)()24132(2)3s s X s s s s s s ++=-=-++++++ 则其z 变换为22222433(cos3)()2cos3z z ze X z z e z ze e -----=---+（4）将()X s 展开为部分分式2210059010515125012501()(2)(1261)614121261s X s s s s s s s s s +==⋅-⋅+++++++ 22225151100625614122501(6)52501(6)5s s s s s +=⋅-⋅+⋅-⋅+++++ 则其z 变换为26622612261255100cos52sin 5()6114125012cos525012cos5z z z ze ze X z z z e z ze e z ze e --------=⋅-⋅+⋅-⋅---+-+8。
