数列 章末总结

数列知识点归纳总结一、定义数列是由一列有限或无限多个数按照一定的规律排列而成的集合。

其中，每个数称作数列的项，每项之间的间隔称作公差。

二、等差数列1. 定义等差数列是指数列中相邻两项之差相等的数列。

2. 性质（1）首项 a1，公差 d（2）第 n 项 an = a1 + (n-1)d（3）前 n 项和Sn = (a1 + an) × n ÷ 2 = n[a1 + a(n-1)/2]3. 求和（1）连续求和法若已知数列的首项、尾项及项数，则可以使用连续求和法求和。

公式如下：S = (a1 + an)× n ÷ 2（2）差数求和法若已知数列的首项、公差及项数，则可以使用差数求和法求和。

公式如下：S = n[a1 + a(n-1)/2]4. 应用（1）找公差通过两个连续的数的差来求得公差。

（2）求某一项通过公式 an = a1 + (n-1)d 来求某一项。

（3）求和通过公式 Sn = n[a1 + a(n-1)/2] 来求和。

三、等比数列1. 定义等比数列是指数列中相邻两项之比相等的数列。

2. 性质（1）首项 a1，公比 q（2）第 n 项an = a1 × q^(n-1)（3）前 n 项和 Sn = a1 (q^n - 1) ÷ (q - 1)3. 求和（1）分步求和法将等比数列分为两个等差数列求和。

将等比数列的第一项乘上公比 q，得到一个新的等比数列，其首项为a1 × q，公比为 q，使用等差数列求和公式求和。

两次求和结果相加即为等比数列的和。

（2）直接求和法使用公式 Sn = a1 (q^n - 1) ÷ (q - 1) 直接求和。

四、通项公式1. 概念通项公式是指数列中任意一项的计算公式。

通过通项公式，可以方便地计算数列中的任何一项。

2. 求法根据已知条件，列出数列的一般式或递推式，然后解出通项公式。

五、等差数列与等比数列的比较1. 不同点（1）等差数列中相邻两项的差相等，等比数列中相邻两项的比相等。

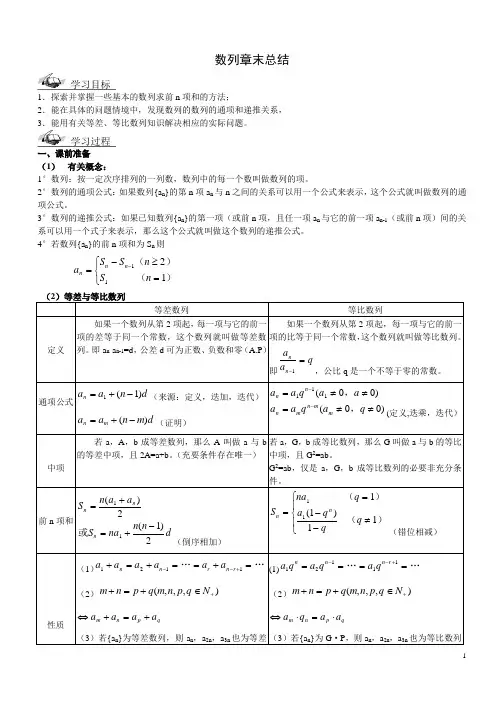
数列章末总结1．探索并掌握一些基本的数列求前n项和的方法；2．能在具体的问题情境中，发现数列的数列的通项和递推关系，一、课前准备（1）有关概念：1°数列：按一定次序排列的一列数，数列中的每一个数叫做数列的项。

2°数列的通项公式：如果数列{a n}的第n项a n与n之间的关系可以用一个公式来表示，这个公式就叫做数列的通项公式。

3°数列的递推公式：如果已知数列{a n}的第一项（或前n项，且任一项a n与它的前一项a n-1（或前n项）间的关系可以用一个式子来表示，那么这个公式就叫做这个数列的递推公式。

4°若数列{a n}的前n项和为S n则aS S nS nnn n=-≥=⎧⎨⎩-1121（）（）※数列通项公式的求法数列的通项公式是数列的核心内容之一。

它如同函数中的解析式一样，对研究数列的性质起着重要的作用。

围绕数列的通项公式，不仅可以判断数列的类型，研究数列的项的变化规律与趋势，而且还便于研究数列的前n 项和，因此求数列的通项公式往往是解决数列问题的突破口，在解题时，根据题目所给条件的不同，可以采用不同的方法求数列的通项公式，常见方法如下： 1.叠加法（累加法）对于形如a n+1-a n =f(n)型的，用叠加法例1：已知数列{a n }中，a 1=1，且a n+1-a n =3n-n ，求数列{a n }的通项公式。

变式：已知数列{}n a 满足211=a ，nn a a n n ++=+211，求n a 。

2.叠乘法（累乘法）对于形如1()n na f n a +=)型的，用叠加法 例2:已知数列{}n a 满足321=a ，n n a n na 11+=+，求n a 。

变式：已知31=a ，n n a n n a 23131+-=+ )1(≥n ，求n a 。

3.构造法其他的，已知数列递推公式求an ，用构造法（构造等差或等比数列） 例3：数列{}n a 中11=a ，)2(1211≥+=-n a a n n ，求该数列的通项公式n a 。

数列是数学中的一个重要概念，它是由一系列按照一定规律排列的数组成的。

数列知识点归纳总结如下：一、数列的定义1. 数列是由有限个或无限个数字组成的序列。

2. 数列中的数字按照一定的顺序排列。

3. 数列中的每个数字都有一个对应的位置或项数。

二、数列的分类1. 按项数分类：有限数列和无限数列。

2. 按项的性质分类：整数数列、实数数列、复数数列等。

3. 按项的规律分类：等差数列、等比数列、斐波那契数列等。

三、等差数列1. 等差数列是指从第二项起，每一项与它的前一项的差都相等的数列。

2. 等差数列的通项公式为：an = a1 + (n-1)d，其中an表示第n项，a1表示第一项，d表示公差。

3. 等差数列的求和公式为：Sn = n/2 * (a1 + an)，其中Sn表示前n项和。

四、等比数列1. 等比数列是指从第二项起，每一项与它的前一项的比都相等的数列。

2. 等比数列的通项公式为：an = a1 * r^(n-1)，其中an表示第n项，a1表示第一项，r表示公比。

3. 等比数列的求和公式为：Sn = a1 * (1 - r^n) / (1 - r)，其中Sn表示前n项和。

五、斐波那契数列1. 斐波那契数列是指从第三项起，每一项都是前两项之和的数列。

2. 斐波那契数列的前几项为：1, 1, 2, 3, 5, 8, 13, ...3. 斐波那契数列没有通项公式，但可以用递归或循环的方式生成。

六、递推关系与通项公式1. 递推关系是指数列中相邻两项之间的关系。

2. 递推关系可以用来推导出数列的通项公式。

3. 通项公式是用来表示数列中任意一项的公式。

4. 通项公式可以通过递推关系、图形法、矩阵法等方式推导得出。

七、数列的应用1. 数列在数学中有广泛的应用，如级数求和、概率计算、线性方程组求解等。

2. 数列在自然科学、经济学、计算机科学等领域也有重要的应用。

八、数列的极限1. 数列的极限是指当项数趋向无穷大时，数列的项趋向于一个确定的数值。

数列知识点及经典结论总结1、数列的概念：数列是按一定次序排成的一列数。

数列中的每一个数都叫做这个数列的项。

数列是一个定义域为正整数集N*（或它的有限子集｛1,2，3，…，n ｝）的特殊函数，如果数列{}a n 的第n 项a n 与n 之间的关系可以用一个公式来表示，则这个公式就叫做这个数列的通项公式。

数列的通项公式也就是相应函数的解析式。

递推关系式：已知数列{}a n 的第一项（或前几项），且任何一项a n 与它的前一项a n 1-（前n项）间的关系可以用一个式子来表示，则这个式子就叫数列的递推关系式。

数列的分类：①按项数多少，分为有穷数列、无穷数列；②按项的增减，分为递增数列、递减数列、摆动数列、常数列。

③按项有无界限，分为有界数列、无界数列。

数列的前n 项和： a a a a s n n ++++=...321. 已知s n 求a n 的方法（只有一种）：即利用公式a n =⎪⎩⎪⎨⎧≥=--)2(,)1(,11n n s s s n n注意：一定不要忘记对n 取值的讨论！最后，还应检验当n=1的情况是否符合当n ≥2的关系式，从而决定能否将其合并。

2.等差数列的有关概念：1、 等差数列的定义：如果数列{}a n 从第二项起每一项与它的前一项的差等于同一个常数，那么这个数列叫做等差数列，这个常数叫等差数列的公差。

即)2,*(1≥∈=--n N n d a a n n 且.(或)*(1N n d a a n n ∈=-+). （1） 等差数列的判断方法：a 定义法：)(1常数d a a n n =-+⇔{}a n 为等差数列。

b 中项法： a a a n n n 212+++=⇔{}a n为等差数列。

c 通项公式法：b an a n +=（a,b 为常数）⇔{}a n 为等差数列。

d 前n 项和公式法：Bn n A s n +=2（A,B 为常数）⇔{}a n 为等差数列。

（2） 等差数列的通项：1(1)n a a n d =+-或()n m a a n m d =+-。

必修五第二章数列归纳总结一、数列1. 数列的定义数列是按一定次序排成的一列数, 从函数观点看, 数列是定义域为正整数集(或它的有限子集)的函数f(n), 当自变量n 从1开始依次取正整数时所对应的一列函数值f(1), f(2), …, f(n), ….通常用an 代替f(n)．于是数列的一般形式为a1, a2, …, an, …, 简记为{an}．一、数列1. 数列的定义数列是按一定次序排成的一列数, 从函数观点看, 数列是定义域为正整数集(或它的有限子集)的函数f(n), 当自变量n 从1开始依次取正整数时所对应的一列函数值f(1), f(2), …, f(n), ….通常用an 代替f(n)．于是数列的一般形式为a1, a2, …, an, …, 简记为{an}．3. an 与Sn 的关系设Sn ＝a1＋a2＋a3＋…＋an,则a n ＝⎩⎪⎨⎪⎧S 1 (n ＝1)，S n －S n －1(n ≥2). 二、等差数列1. 等差数列的定义如果一个数列从第二项起, 每一项与它的前一项的差都等于同一个常数, 这样的数列叫做等差数列．2. 等差中项如果三数a 、A.b 成等差数列, 则A 叫做a 和b 的等差中项, ∴A ＝ .3. (1)通项公式a n ＝a 1＋(n －1)d .推导方法: 累加法an ＝(an －an －1)＋(an －1－an －2)＋…＋(a2－a1)＋a1.(2)前n 项和公式S n ＝n (a 1＋a n )2＝na 1＋n (n －1)2d . 推导方法: 倒序相加法.4. 用函数观点认识等差数列(1)an ＝nd ＋(a1－d)是n 的一次函数.(2)Sn ＝ n2＋(a1－ )n, 是关于n 的常数项为零的二次函数．5. 等差数列的判定方法(1)定义法: an ＋1－an ＝d(常数)(n ∈N*)⇔{an}是等差数列；(2)中项公式法: 2an ＋1＝an ＋an ＋2(n ∈N*)⇔{an}是等差数列；(3)通项公式法: an ＝kn ＋b(k, b 是常数)(n ∈N*)⇔{an}是等差数列；(4)前n 项和公式法：Sn ＝An2＋Bn(A 、B 是常数)(n ∈N*)⇔{an}是等差数列.(5){a n }是等差数列⇔{S n n}是等差数列 6. 等差数列的性质(1)下标和与项的和的关系在等差数列中, 若p ＋q ＝m ＋n, 则有ap ＋aq ＝am ＋an ；若2m ＝p ＋q, 则有2am ＝ap ＋aq, (p, q, m, n ∈N*).(2)任意两项的关系在等差数列{an}中, m 、n ∈N*, 则am －an ＝(m －n)d 或am ＝an ＋(m －n)d 或 ＝d.(3)在等差数列中, 等距离取出若干项也构成一个等差数列, 即an, an ＋m, an ＋2m, …为等差数列, 公差为md.等差数列的依次n项的和也构成一个等差数列, 即Sn, S2n－Sn, S3n－S2n, ……为等差数列, 公差为n2d.即下标成等差的项成等差数列, 下标和成等差的具有相同构成规律的项的和成等差数列.(4)设等差数列{an}的公差为d, 那么d>0⇔{an}是递增数列；d<0⇔{an}是递减数列；d＝0⇔{an}是常数数列.(5)①数列{λan＋b}仍为等差数列, 公差为λd.若{bn}, {an}都是等差数列, 则{an±bn}仍为等差数列, {λ1an＋λ2bn}(λ1, λ2为常数)也是等差数列.②项数为n的等差数列中, n为奇数时, 设m＝ , 则S奇－S偶＝am, ＝ , Sn＝na 中＝nam.n为偶数时, S偶－S奇＝ d.③若{an}与{bn}为等差数列, 且前n项和分别为Sn与S′n, 则＝ .④等差数列{an}中, 若an＝m, am＝n(m≠n), 则am＋n＝0.⑤若数列{an}的前p项和为Sp＝q, 前q项和为Sq＝p(p≠q), 则Sp＋q＝－(p＋q).⑥若数列{an}的前n项和为Sn, Sp＝Sq(p≠q), 则Sp＋q＝0.三、等比数列1. 等比数列的定义一般地, 如果一个数列从第2项起, 每一项与它的前一项的比等于同一个常数, 这个数列就叫做等比数列．2. 等比中项如果三个数a、G、b成等比数列, 那么G叫做a和b的等比中项, 即G2＝ab.3. 等比数列的通项公式an＝a1·qn－1(n∈N*).推导方法: 累乘法: ·……·＝qn－1.4. 等比数列的前n项和当q＝1时, Sn＝na1,当q≠1时. Sn＝＝.推导方法: 乘公比、错位相减法.5. 等比数列的判定方法(1)an＋1＝anq(q是不为0的常数, n∈N*, an≠0)⇔{an}是等比数列.(2)an＝cqn－1(c, q均是不为0的常数, n∈N*)⇔{an}是等比数列.(3)an＋12＝an·an＋2(an≠0, n∈N*)⇔{an}是等比数列.(4)Sn＝A·qn－A(A.q为常数且A≠0, q≠0,1)⇔{an}是公比不为1的等比数列．6. 等比数列的主要性质(1)下标和与项的积的关系在等比数列{an}中, 若m、n、p、q∈N*且m＋n＝p＋q, 则am·an＝ap·aq.特别地, 若2m＝p＋q, 则ap·aq＝am2；a1an＝a2an－1＝a3an－2＝….(2)任意两项的关系若{an}为等比数列, 则＝qm－n或am＝an·qm－n(m、n∈N*).(3)等间隔的k项和(或积)仍成等比数列.例如: {an}是等比数列, 则①a1, a3, a5, …, a2n－1；②a1＋a2, a2＋a3, a3＋a4, …；③a1a2, a2a3, a3a4, …；④a1＋a2, a3＋a4, a5＋a6……均成等比数列．(4)等比数列{a n}的单调性当, 或时, {an}为递增数列；当或时, {an}为递减数列.(5)①{an}是等比数列⇒{c·an}是等比数列(c≠0).②{an}、{bn}均为等比数列⇒{an·bn}、{ }仍是等比数列.③若{an}是等比数列, 则{an2}、{ }(an>0)、{ }、{|an|}均为等比数列.④非零常数列既是等差数列, 也是等比数列.⑤若{an}是等差数列, 则{ban}是等比数列.若{an}是正项等比数列, 则{lgan}是等差数列．误区警示1. 数列与数集应予区别, 数列中的数排列有序, 数集中的元素无序；数列中的数可重复出现, 数集中的元素互异.2. 并不是每一个数列都有通项公式, 给出前n项时, 写出的通项公式可以不止一个.3．已知{an}的前n项和Sn求an时,用an＝求解应注意分类讨论.an＝Sn－Sn－1是在n≥2条件下求出的, 应检验a1是否适合. 如果适合, 则合写在一块, 如果不适合, 则分段表示. 千万注意用an＝Sn－Sn－1判断数列{an}是否为等差(或等比)数列时, 不要忘记验证a1是否满足.如: Sn＝n2＋n时, {an}是等差数列.Sn＝n2＋n＋1时, {an}不是等差数列.Sn＝2n－1时, {an}是等比数列.Sn＝2n＋1时, {an}不是等比数列.4. 在讨论等差数列{an}的前n项和Sn的最值时, 不要忽视n是整数的条件及含0项的情形.如: 在等差数列{an}中, 已知a1＝20, 前n项和为Sn, 且如S10＝S15, 求当n取何值时, Sn有最大值, 并求出它的最大值．取最大值的应为S12和S13.5. G是a、b的等比中项 G＝.6. 在应用等比数列的前n项和公式时, 一定要对q＝1与q≠1进行分类讨论.7．等比数列中隐含着各项不为零、公比不为零, 项与公比的符号有着密切的联系, 解题时应特别注意．。

数列所有知识点归纳总结数列在数学中是一个重要的概念，它是由一系列按特定规律排列的数所组成的序列。

在数列的学习中，我们需要了解其基本概念、性质和常见的分类种类。

本文将对数列的各个知识点进行归纳总结，帮助读者更好地理解和掌握这一部分的数学知识。

一、数列的基本概念1. 数列的定义：数列是由一系列按照一定规律排列的数所组成的序列。

2. 项与序号：数列中的每个数称为项，用a₁，a₂，a₃，...表示；项所对应的位置称为序号，用n表示。

3. 数列的通项公式：数列中每一项与其序号之间存在着一定的关系，可以用一个公式表示，称为数列的通项公式。

二、数列的性质1. 数列的有界性：数列可能是有界的（存在上界或下界），也可能是无界的（既没有上界也没有下界）。

2. 数列的单调性：数列可以是递增的或递减的，也可以是常数列（即所有项相等）。

3. 数列的有限性：数列可以是有限的（只有有限个项），也可以是无限的（有无穷个项）。

4. 数列的周期性：部分数列具有周期性，即从某一项开始，每隔一定项都重复出现相同的数列。

三、常见数列的分类1. 等差数列：数列中每一项与前一项之差都相等的数列，通项公式为an = a₁ + (n-1)d，其中a₁为首项，d为公差。

2. 等比数列：数列中每一项与前一项之比都相等的数列，通项公式为an = a₁ * r^(n-1)，其中a₁为首项，r为公比。

3. 斐波那契数列：数列中每一项是前两项之和的数列，通项公式为an = a(n-1) + a(n-2)，其中a₁ = 1，a₂ = 1。

4. 幂次数列：数列中每一项都是一定的幂的数列，通项公式为an = a₁ * (n^p)，其中a₁为首项，p为幂次。

四、数列求和1. 等差数列的求和：对于公差为d的等差数列，其前n项和为Sn = (n/2)(a₁ + an) = (n/2)(2a₁ + (n-1)d)。

2. 等比数列的求和：对于公比为r的等比数列（r≠1），其前n项和为Sn = a₁(1 - r^n) / (1 - r)。

数列知识点及经典结论总结1、数列的概念：数列是按一定次序排成的一列数。

数列中的每一个数都叫做这个数列的项。

数列是一个定义域为正整数集N*（或它的有限子集｛1,2，3，…，n ｝）的特殊函数，如果数列{}a n 的第n 项a n 与n 之间的关系可以用一个公式来表示，则这个公式就叫做这个数列的通项公式。

数列的通项公式也就是相应函数的解析式。

递推关系式：已知数列{}a n 的第一项（或前几项），且任何一项a n 与它的前一项a n 1-（前n项）间的关系可以用一个式子来表示，则这个式子就叫数列的递推关系式。

数列的分类：①按项数多少，分为有穷数列、无穷数列；②按项的增减，分为递增数列、递减数列、摆动数列、常数列。

③按项有无界限，分为有界数列、无界数列。

数列的前n 项和： a a a a s n n ++++=...321. 已知s n 求a n 的方法（只有一种）：即利用公式a n =⎪⎩⎪⎨⎧≥=--)2(,)1(,11n n s s s n n注意：一定不要忘记对n 取值的讨论！最后，还应检验当n=1的情况是否符合当n ≥2的关系式，从而决定能否将其合并。

2.等差数列的有关概念：1、 等差数列的定义：如果数列{}a n 从第二项起每一项与它的前一项的差等于同一个常数，那么这个数列叫做等差数列，这个常数叫等差数列的公差。

即)2,*(1≥∈=--n N n d a a n n 且.(或)*(1N n d a a n n ∈=-+). （1） 等差数列的判断方法：a 定义法：)(1常数d a a n n =-+⇔{}a n 为等差数列。

b 中项法： a a a n n n 212+++=⇔{}a n为等差数列。

c 通项公式法：b an a n +=（a,b 为常数）⇔{}a n 为等差数列。

d 前n 项和公式法：Bn n A s n +=2（A,B 为常数）⇔{}a n 为等差数列。

（2） 等差数列的通项：1(1)n a a n d =+-或()n m a a n m d =+-。

数列知识点总结及结论一、数列的概念及分类数列是按照一定的顺序排列的一组数的集合。

在数学中，数列是一个非常重要的概念，它被广泛应用在各个领域，如微积分、概率论、离散数学等。

数列有多种分类方式，根据数列的各个项之间的关系不同可以将数列分为等差数列、等比数列、递推数列等。

在日常生活中，数列也有着广泛的应用，如金融领域中的利息计算，物理学中的等速运动等。

二、等差数列等差数列是一种非常简单的数列，其特点是数列中每一项与前一项的差是一个常数。

等差数列的通项公式为An = A1 + (n-1)d。

其中An表示等差数列中第n项的值，A1表示等差数列的首项，d表示等差数列的公差。

例如，1，3，5，7，9就是一个公差为2的等差数列。

在等差数列中，我们可以根据已知的条件，求出数列的首项、公差、任意项的值，以及数列的前n项和等一系列问题。

三、等比数列等比数列是另一种常见的数列，其特点是数列中每一项与前一项的比是一个常数。

等比数列的通项公式为An = A1 * q^(n-1)。

其中An表示等比数列中第n项的值，A1表示等比数列的首项，q表示等比数列的公比。

例如，1，2，4，8，16就是一个公比为2的等比数列。

在等比数列中，也可以根据已知的条件，求出数列的首项、公比、任意项的值，以及数列的前n项和等一系列问题。

四、递推数列递推数列是一种通过前一项来定义后一项的数列。

其通项公式并不是一个固定的公式，而是通过给定的递推关系来确定。

例如，斐波那契数列就是一个著名的递推数列，其定义为F(1)=1, F(2)=1, F(n)=F(n-1)+F(n-2)。

通过这个递推关系，我们可以得到斐波那契数列的每一项的值。

递推数列在计算机科学中有着广泛的应用，如动态规划算法、图论算法等。

它们的特点是可以通过已知的前几项来求得后面的项，而不需要知道整个数列的所有项。

五、数列的运算数列的运算是数列学习中的重要内容之一。

在数列的运算中，主要包括数列的加法、减法、乘法、除法等。

必修5 第二章《 数 列 》期末复习制卷：王小凤 学生姓名【知识梳理】一．等差数列与等比数列二．数列通项公式的求法1．根据n S ，利用公式11(1)(1)n n n S n a S S n -=⎧⎪=⎨->⎪⎩求通项n a 。

注．已知n S 求n a ，应分1=n 及2≥n 两步，最后验证1a 是否满足后面的n a .2．根据数列的递推关系，叠加法、累乘法求通项n a ，其要点是： （1）121321()()()n n n a a a a a a a a -=+-+-++-L ；（2）321121(2)n n n a a a a a n a a a -=⋅⋅⋅⋅≥L 3．构造新的等差、等比数列，转化法求通项n a 。

三．数列求和1．利用等差、等比数列的公式求和； 2．分组求和法；3．错位相减求和，适用于由一个等差数列和一个等比数列对应项乘积组成的数列； 4．裂项相消求和，它的基本思想是设法将数列的每一项拆成两项（裂项），并使它们在相加时除了首尾各有一项或少数几项外，其余各项都能前后相消.常见裂项公式：（1）1111()()n n k k n n k =-++ （2）11()n k n kn k n =+-++5．倒序相加法求和。

四．n S 的最值问题：在等差数列{}n a 中,有关n S 的最值问题——常用邻项变号法求解：(1)当0,01<>d a 时，满足⎩⎨⎧≤≥+001m m a a 的项数m 使得mS 取最大值.(2)当 0,01><d a 时，满足⎩⎨⎧≥≤+001m m a a 的项数m 使得mS 取最小值。

【考点题型】考点一：通项公式、递推公式的基本应用1．下列四个数中，哪一个是数列{(1)n n +}中的一项( ) A ．380 B ．39 C ．35 D ．232．已知数列{}n a ，13a =，26a =，且21n n n a a a ++=-，则数列的第五项为( ) A ．6 B ．3- C ．12- D ．6-等差数列 等比数列定义1n n a a d --=（2n ≥）通项公式 d n a a n )1(1-+=，(),()n m a a n m d n m =+->， 中项如果,,a A b 成等差数列，那么A 叫做a 与b 的等差中项，且2a bA +=．三个数成等差数列的设法： ．如果,,a G b 成等比数列，那么G 叫做a 与b 的等比中项，且 三个数成等比数列的设法：aq，a ，aq 前n 项和 1()2n n n a a S +=或1(1)2n n n S na d -=+当1q =时：n S = 当1q ≠时：n S =性质若q p n m +=+，则 m n p q a a a a +=+；若2m p q =+，则 *(,,,)p q n m N ∈若q p n m +=+，则2*2,,(,,,)m p q m p q a a a p q n m N =+=⋅∈若则有n S 、2n n S S -、32n n S S -为等差数列n S 、2n n S S -、32n n S S -为等比数列 函数思想 看数列12221()()22n n a dn a d An B d ds n a n An Bn =+-=+=+-=+111(1)11nn n n n n a a q Aq qa as q A Aq q q q===-=-≠--判定方法（1）定义法：证明)(*1N n a a n n ∈-+为一个常数； （2）等差中项：证明*11(2N n a a a n n n∈+=+-，)2≥n（3）通项公式:(,n a kn b k b =+为常数)(*N∈n )（4）2ns An Bn =+(,A B 为常数)(∈*n N )（1）定义法：证明)(*1N n a a nn ∈+为一个常数（2）中项：证明21nn a a -=*1(,2)n a n N n +⋅∈≥ （3）通项公式：(,nn a cq c q =均是不为0常数）（4）n ns Aq =A -(,A q 为常数，≠≠A 0,q 0,1）考点二：等差、等比数列的基本运算3．若等差数列{}n a 的前三项依次为1a -、1a +、23a +，则2011是这个数列的( ) A ．第1006项B ．第1007项C ．第1008项D ．第1009项4．已知等差数列{}n a 满足244a a +=，3510a a +=，则它的前10项的和10S =( ) A ．138B ．135C ．95D ．235．在等比数列}{n a 中,,8,1641=-=a a 则=7a ( )A ．4-B ．4±C ．2-D ．2±6．已知,,,a b c d 是公比为2的等比数列，则dc ba ++22= ( ) A ．1 B ．21 C ．41 D ．817．在等比数列{}n a 中，485756=-=+a a a a ，则10S 等于( ) A ．1023 B ．1024 C ．511 D ．5128．等差数列{}n a 的公差不为零，首项1a ＝1，2a 是1a 和5a 的等比中项，则数列的前10项之和是( )A ．90B ．100C ．145D ．1909．在3和9之间插入两个正数，使前三个数成等比数列，后三个数成等差数列，则二数之和为( )A ．2113B ．1114C ．2110 D ．21910．已知某等差数列共有10项，其奇数项之和为15，偶数项之和为30，则其公差为（ ）A ．5B ．4C ．3D ． 2考点三：等差、等比数列的性质的应用11．已知{}n a 是等差数列，且2381148a a a a +++=，则67a a += ( ) A ．12 B ．16 C ．20 D ．2412．已知等差数列{}n a 满足1231010a a a a ++++=L ，则有（ ） A ．11010a a +> B ．21000a a +< C.3990a a += D ．5151a = 13．设{}n a 是公差为正数的等差数列，若12315a a a ++=，12380a a a =，则111213a a a ++=（ ） A ．120 B ．105 C ．90 D ．75 14．等差数列{}n a 中，1590S =，则8a = ( )A ．3B ．4C ．6D ．1215．若一等差数列前四项的和为124，后四项的和为156，又各项的和为350，则此数列共有 ( ) A ．10项 B ．11项 C ．12项 D ．13项16．等比数列{}n a 中,0n a >,965=a a ,则313233310log log log log a a a a +++⋅⋅⋅+=( ) A ．12 B ．10 C ．8 D ．32log 5+ 17．等差数列{}n a 中，121015a a a +++=L ，11122020a a a +++=L ，则212230a a a +++=L ( )A ．15B ．25C ．35D ．4518．已知等比数列前10项的和为10，前20项的和为30，那么前30项的和为( ) A ．60 B ．70 C ．90 D ．126考点四：等差、等比数列的实际应用19．夏季高山上温度从山脚起每升高100米，降低0.7℃，已知山顶的温度是14.1℃，山脚的温度是26℃，则山的相对高度是( )A ．1500B ． 1600C ．1700D ．180020．某种细菌培养过程中，每半小时分裂一次（一次分裂为两个），经过4小时，这种细菌由1个可繁殖成( )个．A ．64B ．128C ．256D ．51221．一套共7册的书计划每2年出一册，若各册书的出版年份数之和为13979，则出齐这套书的年份是( )A ．1997B ． 1999C ．2001D ．2003考点五：等差数列前n 项和的最值22．等差数列{n a }中，39||||,a a =公差0,d <那么使前n 项和n S 最大的n 值为（ ） A ．5 B ．6 C ．5 或6 D ．6或723．数列{a n }是首项为23，公差为整数的等差数列，且第六项为正，第七项为负． (1)求数列的公差d ； (2)求前n 项和S n 的最大值．考点六：数列的通项公式的求解24．已知数列{}n a 满足1n n a a n +=+，11=a ，求n a ．25．已知数列{}n a 的前n 项和n n S 23+=，求n a ．考点七：等差、等比数列的证明数列求和26．已知数列{a n }是首项为a 且公比不等于1的等比数列，S n 为其前n 项和，a 1，2a 7，3a 4成等差数列，求证：12S 3，S 6，S 12－S 6成等比数列.27．在数列{}n a 中，11a =，122n n n a a +=+． （Ⅰ）设12nn n a b -=．证明：数列{}n b 是等差数列； （提示：利用等差数列定义证明） （Ⅱ）求数列{}n a 的前n 项和n S ． （提示：错项相减求和）28．等差数列{}n a 的各项均为正数，13a =，前n 项和为n S ，{}n b 为等比数列, 11b =，且2264,b S = 33960b S =．(1)求n a 与n b ； (2)求和：12111nS S S +++L ．（提示：裂项相消求和） （注：将第26—28题解题过程写在试卷背面 ）。

数列全部知识点归纳总结数列是高中数学中的一个重要概念，广泛应用于数学和其他学科的问题中。

它是由一组按照特定规律排列的数所组成的序列。

在数列中，每一个数被称为序列的项，而序列中的规律则被称为递推公式。

本文将对数列的基本概念、常见数列类型、性质及应用进行全面的知识点归纳和总结。

一、基本概念数列是由一组按特定顺序排列的数所组成的序列。

数列的每个数被称为序列的项，通常用字母表示，如a1, a2, a3等。

数列中每个项的位置被称为项号，通常用下标表示，如a1, a2, a3的项号分别为1, 2, 3。

数列也可以用函数来表示，即f(n)，其中n表示项号。

二、常见数列类型1.等差数列：等差数列是指数列中相邻两项之差都相等的数列。

它的递推公式为an = a1 + (n-1)d，其中a1为首项，d为公差。

2.等比数列：等比数列是指数列中相邻两项之比都相等的数列。

它的递推公式为an = a1 * r^(n-1)，其中a1为首项，r为公比。

3.等差数列的前n项和：等差数列的前n项和可以用求和公式Sn = (n/2)(a1+an)来表示，其中n为项数，a1为首项，an为第n项。

4.等比数列的前n项和：等比数列的前n项和可以用求和公式Sn = (a1(r^n-1))/(r-1)来表示，其中n为项数，a1为首项，r为公比。

三、数列的性质1.有界性：数列可以是有界的，也可以是无界的。

有界数列是指数列的所有项都在一定范围内，无界数列则相反。

2.单调性：数列可以是单调递增的、单调递减的或者既不递增也不递减的。

3.周期性：有些数列具有周期性，即数列中的项按照一定的规律循环出现。

4.递推关系：数列中的每一项可以通过前一项和递推公式来推导得到。

四、数列的应用1.数学问题：数列广泛应用于数学问题的求解中，如求解等差数列、等差数列的前n项和等。

2.物理问题：数列也常常用于物理问题的建模与求解中，如描述物体运动的规律等。

3.计算机科学：数列在计算机科学中有着重要的应用，如算法设计、数据压缩等领域。