第七章 静电场
- 格式:ppt
- 大小:1.20 MB
- 文档页数:42

N⋅
⨯≈
m
9880c
10
/
通过曲面S 的总电通量 ⎰⎰⋅=Φ=ΦS S e e S d E d
S 为闭合曲面时 ⎰⋅=ΦS e S d E
无关,只与被球面所包围的电量q 有关
虚线表示等势面,实线表示电力线 二、场强与电势梯度的关系 电势与场强的积分关系:⎰⋅=零点
l d E U
,
求出场强分布后可由该式求得电势分布.
空腔内有带电体q时,空腔内表面感应电荷为-q,导体外表面感应电荷为静电屏蔽
)在导体内部有空腔时,空腔内的物体不受外电场的影响。
)接地的导体空腔,空腔内的带电物体的电场不影响外界。
三、有导体存在的静电场场强与电势的计算
有极分子电介质的极化:在外电场作用下分子偶极矩转向与外电场接近平行的方向,叫取向极化。
五、极化强度和极化电荷
极化强度P
)。

1第7章 静电场中的导体和电介质 习题及答案1. 半径分别为R 和r 的两个导体球,相距甚远。
用细导线连接两球并使它带电,电荷面密度分别为1s 和2s 。
忽略两个导体球的静电相互作用和细导线上电荷对导体球上电荷分布的影响。
试证明:Rr =21s s。
证明:因为两球相距甚远,半径为R 的导体球在半径为r 的导体球上产生的电势忽略不计,半径为r 的导体球在半径为R 的导体球上产生的电势忽略不计,所以的导体球上产生的电势忽略不计,所以半径为R 的导体球的电势为的导体球的电势为R R V 0211π4e p s =014e s R =半径为r 的导体球的电势为的导体球的电势为r r V 0222π4e p s =024e s r = 用细导线连接两球,有21V V =,所以,所以Rr=21s s 2. 证明:对于两个无限大的平行平面带电导体板来说,证明:对于两个无限大的平行平面带电导体板来说,(1)(1)(1)相向的两面上,电荷的面密度总是相向的两面上,电荷的面密度总是大小相等而符号相反;大小相等而符号相反;(2)(2)(2)相背的两面上,电荷的面密度总是大小相等而符号相同。
相背的两面上,电荷的面密度总是大小相等而符号相同。
相背的两面上,电荷的面密度总是大小相等而符号相同。
证明: 如图所示,设两导体A 、B 的四个平面均匀带电的电荷面密度依次为1s ,2s ,3s ,4s (1)取与平面垂直且底面分别在A 、B 内部的闭合圆柱面为高斯面,由高斯定理得内部的闭合圆柱面为高斯面,由高斯定理得S S d E SD +==×ò)(10320s s e故+2s 03=s上式说明相向两面上电荷面密度大小相等、符号相反。
上式说明相向两面上电荷面密度大小相等、符号相反。
(2)在A 内部任取一点P ,则其场强为零,并且它是由四个均匀带电平面产生的场强叠加而成的,即电平面产生的场强叠加而成的,即0222204030201=---e s e s e s e s又+2s 03=s 故 1s 4s =3. 半径为R 的金属球离地面很远,并用导线与地相联,在与球心相距为R d 3=处有一点电荷+q ,试求:金属球上的感应电荷的电量。
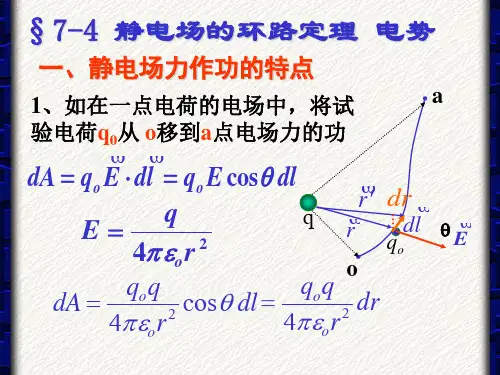



第七章、静 电 场一、大体概念 1、电场 (1)、电荷在周围空间激发电场,电荷之间的彼此作用是通过电场传递的。
电场对身处其中的电荷有力的作用(2)库伦定律 沿连线方向,同号相斥,异号相吸2、电场强度⑴、 实验电荷在电场中不同点所受电场力的大小、方向都可能不同;而在 同一点,电场力的大小与实验电荷电量成正比,若实验电荷异号,则所受电场力的方向相反。
咱们就用qF来表示电场中某点的电场强度,用E 表示,即qF E =⑵、点电荷的电场强度以点电荷Q 所在处为原点O,任取一点P(场点),点O 到点P 的位矢为r,把试验电荷q 放在P 点,有库仑定律可知,所受电场力为:r Qq F E 2041επ==⑶常见电场公式无穷大均匀带电板周围电场:εσ02=E3、电势⑴、电场中给定的电势能的大小除与电场本身的性质有关外,还与查验电荷有关,而比值qE pa 0则与电荷的大小和正负无关,它反映了静电场中某给定点的性质。
为此咱们用一个物理量-电势来反映那个性质。
即qE p V 0=⑶常见电势公式 点电荷电势散布:rq V επ04=半径为R 的均匀带点球面电势散布:Rq V επ04=()R r ≤≤0rq V επ04=()R r ≥221r qq k F =二、定理1、场强叠加定理点电荷系所激发的电场中某点处的电场强度等于各个点电荷单独存在时对 该点的电场强度的矢量和。
即E E E n E +++= (21)2、电势叠加定理V 1 、V 2 ...V n 别离为各点电荷单独存在时在P 点的电势点电荷系的电场中,某点的电势等于各点电荷单独 存在时在该点电势的代数和。
3、高斯定理在真空中的静电场内,通过任意封锁曲面的电通量等于该闭合曲面包围的所有电荷的代数和除以ε说明:①高斯定理是反映静电场性质的一条大体定理。
②通过任意闭合曲面的电通量只取决于它所包围的电荷的代数和。
③高斯定理中所说的闭合曲面,通常称为高斯面。
三、静电平衡1、静电平衡当一带电体系中的电荷静止不动,从而电场散布不随时刻转变时,带电 体系即达到了静电平衡。


第七章⎪⎪⎪静电场第39课时 电荷守恒定律和库仑定律(双基落实课)点点通(一) 电荷、电荷守恒定律 1.电荷(1)三种起电方式:摩擦起电、接触起电、感应起电。
(2)两种电荷:自然界中只存在两种电荷——正电荷和负电荷。
同种电荷相互排斥,异种电荷相互吸引。
2.对元电荷的理解(1)元电荷是自然界中最小的电荷量,用e 表示,通常取e =1.6×10-19C ,任何带电体的电荷量都是元电荷的整数倍。
(2)元电荷等于电子所带的电荷量,也等于质子所带的电荷量,但元电荷没有正负之分。
(3)元电荷不是点电荷,电子、质子等微粒也不是元电荷。
3.电荷守恒定律电荷既不会创生,也不会消灭,它只能从一个物体转移到另一个物体,或者从物体的一部分转移到另一部分;在转移过程中,电荷的总量保持不变。
4.电荷均分原理(1)适用于完全相同的导体球。
(2)两导体球接触一下再分开,如果两导体球带同种电荷,总电荷量直接平分;如果两导体球带异种电荷,则先中和再平分。
[小题练通]1.(鲁科教材原题)下列现象中,不属于摩擦起电的有()A.将被毛皮摩擦过的塑料棒靠近碎纸屑,纸屑被吸起B.在干燥的天气中脱毛线衣时,会听到轻微的噼啪声C.用干燥的毛刷刷毛料衣服时,毛刷上吸附有许多细微的脏物D.把钢针沿着磁铁摩擦几次,钢针就能吸引铁屑解析:选D A、B、C三个选项为摩擦起电,D选项为磁化现象,故D正确。
2.(多选)把两个相同的金属小球接触一下再分开一小段距离,发现两球之间相互排斥,则这两个金属小球原来的带电情况可能是()A.两球原来带有等量异种电荷B.两球原来带有同种电荷C.两球原来带有不等量异种电荷D.两球中原来只有一个带电解析:选BCD接触后再分开,两球相互排斥,说明分开后两球带同种电荷,两球原来可能带同种电荷、不等量的异种电荷或只有一个带电,故B、C、D正确。
3.(鲁科教材原题)将一物体跟一带正电的验电器的金属球接触时,验电器的金属箔先合拢然后又张开,从这一现象可知,接触金属球以前,物体()A.带正电荷B.带负电荷C.不带电荷D.都有可能解析:选B验电器的金属箔先合拢后张开,说明接触验电器金属球的物体和验电器金属球所带电荷的种类不同,即物体带负电荷。

第七章 静电场第1节 电场力的性质(1)任何带电体所带的电荷量都是元电荷的整数倍。
(√)(2)点电荷和电场线都是客观存在的。
(×)(3)根据F =k q 1q 2r 2,当r →0时,F →∞。
(×) (4)电场强度反映了电场力的性质,所以电场中某点的电场强度与试探电荷在该点所受的电场力成正比。
(×)(5)电场中某点的电场强度方向即为正电荷在该点所受的电场力的方向。
(√)(6)真空中点电荷的电场强度表达式E =kQ r 2中,Q 就是产生电场的点电荷。
(√) (7)在点电荷产生的电场中,以点电荷为球心的同一球面上各点的电场强度都相同。
(×)(8)电场线的方向即为带电粒子的运动方向。
(×)◎物理学史判断(1)法国物理学家牛顿利用扭秤实验发现了电荷之间的相互作用规律——库仑定律。
(×)(2)英国物理学家法拉第最早引入了电场概念,并提出用电场线表示电场。
(√)(3)美国物理学家密立根通过油滴实验精确测定了元电荷e 的电荷量,获得诺贝尔奖。
(√)1.在应用库仑定律时,应注意定律的适用条件,若带电物体不能看成点电荷,则不适用此公式。
2.注意电场强度三个表达式的适用条件,E =F q 适用于一切电场,E =k Q r2适用于真空中的点电荷,E =U d 适用于匀强电场。
3.在研究带电粒子的运动轨迹时,不要误认为运动轨迹与电场线一定重合,只有在特定的条件下,两者才重合。
4.三个自由点电荷,只在彼此间库仑力作用下而平衡,则“三点共线、两同夹异、两大夹小,近小远大”。
突破点(一) 库仑定律的理解及应用1.库仑定律适用于真空中静止点电荷间的相互作用。
2.对于两个均匀带电绝缘球体,可将其视为电荷集中在球心的点电荷,r 为球心间的距离。
3.对于两个带电金属球,要考虑表面电荷的重新分布,如图所示。
(1)同种电荷:F <k q 1q 2r2; (2)异种电荷:F >k q 1q 2r2。


静电场知识点总结一、几个关于电荷的概念1. 元电荷:电荷量为e= 的电荷叫做元电荷.质子和电子均带元电荷电荷量.2. 点电荷:形状和大小对研究问题的影响可的带电体称为点电荷.3. 场源电荷:电场是由电荷产生的,我们把产生的电荷叫做场源电荷.4. 试探电荷(检验电荷):研究电场的基本方法之一是放入一带电荷量很小的点电荷,考查其受力情况及能量况,这样的电荷称为试探电荷或检验电荷.二、库仑定律1.内容:在真空中静止的两个点电荷之间的作用力跟它们的电荷量的乘积成正比,跟它们之间的距离的平方成反比,作用力的方向在他们的连线上。
2.公式:3.适用条件:4.应用:三个自由点电荷的平衡规律:三个自由点电荷q1、q2、q3都平衡时,三个自由点电荷必共线.若q2位于q1、q3之间,与q1、q3间的距离分别为r1、r2,则中间电荷q2靠近电荷量较小的电荷,位置关系满足: ,库仑力关系满足: ,其中中间电荷q2的电荷量最小,电性为“ .”三、电场强度1. 定义:放入电场中的电荷受到的电场力F与它的电荷量q的比值,叫做该点的电场强度。
2.公式:单位:(决定因素:电场强度决定于电场本身,与q无关.)3.4. 方向:,(或与负电荷在电场中受到的电场力的方向相反)。
5. 叠加性:多个电荷在电场中某点的电场强度为各个电荷单独在该点产生的电场强度的矢量和,这种关系叫做电场强度的叠加,电场强度的叠加遵从。
四、电场线、匀强电场1.电场线:为了形象直观描述电场的强弱和方向,在电场中画出一系列的曲线,曲线上的各点的切线方向代表该点的电场强度的方向,曲线的疏密程度表示场强的大小。
2.电场线的特点⑴电场线是为了直观形象的描述电场而假想的、实际是不存在的理想化模型。
⑵始于,终于,静电场的电场线是不闭合曲线。
⑶任意两条电场线不相交。
⑷电场线的疏密表示,某点的切线方向表示,它不表示电荷在电场中的运动轨迹。
⑸沿着电场线的方向电势;电场线从高等势面(线)垂直指向低等势面(线)。