线面垂直的判定和性质定理习题课

教学过程在四棱锥P－ABCD中，P A⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，P A＝AB＝BC，E是PC的中点．证明：(1)CD⊥AE；(2)PD⊥平面ABE.规律方法证明线面垂直的方法：一是线面垂直的判定定理；二是利用面面垂直的性质定理；三是平行线法(若两条平行线中一条垂直于这个平面，则另一条也垂直于这个平面)．解题时，注意线线、线面与面面关系的相互转化；另外，在证明线线垂直时，要注意题中隐含的垂直关系，如等腰三角形的底边上的高、中线和顶角的角平分线三线合一、矩形的内角、直径所对的圆周角、菱形的对角线互相垂直、直角三角形(或给出线段长度，经计算满足勾股定理)、直角梯形等等.【训练1】(2013·江西卷改编)教学效果分析教学过程如图，直四棱柱ABCD－A1B1C1D1中，AB∥CD，AD⊥AB，AB＝2，AD＝2，AA1＝3，E为CD上一点，DE＝1，EC＝3.证明：BE⊥平面BB1C1C.考点二平面与平面垂直的判定与性质【例2】(2014·深圳一模)如图，在三棱柱ABC－A1B1C1中，AA1⊥平面ABC，AB＝BC＝AA1，且AC＝2BC，点D是AB的中点．证明：平面ABC1⊥平面B1CD.规律方法证明两个平面垂直，首先要考虑直线与平面的垂直，也教学效果分析教学过程可简单地记为“证面面垂直，找线面垂直”，是化归思想的体现，这种思想方法与空间中的平行关系的证明非常类似，这种转化方法是本讲内容的显著特征，掌握化归与转化思想方法是解决这类问题的关键．【训练2】如图，在长方体ABCDA1B1C1D1中，AB＝AD＝1，AA1＝2，M是棱CC1的中点．证明：平面ABM⊥平面A1B1M.考点三平行、垂直关系的综合问题教学效果分析教学过程【例3】(2013·山东卷)如图，在四棱锥P-ABCD中，AB⊥AC，AB⊥P A，AB∥CD，AB＝2CD，E，F，G，M，N分别为PB，AB，BC，PD，PC的中点．(1)求证：CE∥平面P AD；(2)求证：平面EFG⊥平面EMN.规律方法线面关系与面面关系的证明离不开判定定理和性质定理，而形成结论的“证据链”依然是通过挖掘题目已知条件来实现的，如图形固有的位置关系、中点形成的三角形的中位线等，都为论证提供了丰富的素材．【训练3】(2013·辽宁卷)如图，AB是圆O的直径，P A垂直圆O所在的平面，C是圆O上的点．(1)求证：BC⊥平面P AC；(2)设Q为P A的中点，G为△AOC的重心，求证：QG∥平面PBC.教学效果分析1．转化思想：垂直关系的转化2．在证明两平面垂直时一般先从现有的直线中寻找平面的垂线，若这样的直线图中不存在，则可通过作辅助线来解决．如有平面垂直时，一般要用性质定理，在一个平面内作交线的垂线，使之转化为线面垂直，然后进一步转化为线线垂直．故熟练掌握“线线垂直”、“面面垂直”间的转化条件是解决这类问题的关键．创新突破6——求解立体几何中的探索性问题【典例】(2012·北京卷)如图1，在Rt△ABC中，∠C＝90°，D，E分别为AC，AB的中点，点F为线段CD上的一点．将△ADE沿DE折起到△A1DE的位置，使A1F⊥CD，如图2.(1)求证：DE∥平面A1CB；(2)求证：A1F⊥BE；(3)线段A1B上是否存在点Q，使A1C⊥平面DEQ？说明理由．[反思感悟] (1)解决探索性问题一般先假设其存在，把这个假设作已知条件，和题目的其他已知条件一起进行推理论证和计算，在推理论证和计算无误的前提下，如果得到了一个合理的结论，则说明存在，如果得到了一个不合理的结论，则说明不存在．(2)在处理空间折叠问题中，要注意平面图形与空间图形在折叠前后的相互位置关系与长度关系等，关键是点、线、面位置关系的转化与平面几何知识的应用，注意平面几何与立体几何中相关知识点的异同，盲目套用容易导致错误．【自主体验】(2014·韶关模拟)如图1，在直角梯形ABCD中，∠ADC＝90°，CD∥AB，AD＝CD＝12AB＝2，点E为AC中点，将△ADC沿AC折起，使平面ADC⊥平面ABC，得到几何体D－ABC，如图2.(1)求证：DA⊥BC；(2)在CD上找一点F，使AD∥平面EFB.基础巩固题组(建议用时：40分钟)一、填空题1．设平面α与平面β相交于直线m，直线a在平面α内，直线b 在平面β内，且b⊥m，则“α⊥β”是“a⊥b”的________条件．2．(2014·绍兴调研)设α，β为不重合的平面，m，n为不重合的直线，则下列正确命题的序号是________．①若α⊥β，α∩β＝n，m⊥n，则m⊥α；②若m⊂α，n⊂β，m⊥n，则n⊥α；③若n⊥α，n⊥β，m⊥β，则m⊥α；④若m∥α，n∥β，m⊥n，则α⊥β.3.如图，AB是圆O的直径，P A垂直于圆O所在的平面，C是圆周上不同于A，B的任一点，则图形中有________对线面垂直．4．若M是线段AB的中点，A，B到平面α的距离分别是4 cm，6 cm，则M到平面α的距离为________．5．(2014·郑州模拟)已知平面α，β，γ和直线l，m，且l⊥m，α⊥γ，α∩γ＝m，β∩γ＝l，给出下列四个结论：①β⊥γ；②l⊥α；③m⊥β；④α⊥β.其中正确的是________．6.如图，在四棱锥P ABCD中，P A⊥底面ABCD，且底面各边都相等，M是PC上的一动点，当点M满足________时，平面MBD⊥平面PCD.(只要填写一个你认为正确的条件即可)7．设α，β是空间两个不同的平面，m，n是平面α及β外的两条不同直线．从“①m⊥n；②α⊥β；③n⊥β；④m⊥α”中选取三个作为条件，余下一个作为结论，写出你认为正确的一个命题：________(用代号表示)．8.如图，P A⊥圆O所在的平面，AB是圆O的直径，C是圆O上的一点，E，F分别是点A在PB，PC上的正投影，给出下列结论：①AF⊥PB；②EF⊥PB；③AF⊥BC；④AE⊥平面PBC.其中正确结论的序号是________．二、解答题9．(2013·北京卷)如图，在四棱锥P ABCD中，AB∥CD，AB⊥AD，CD＝2AB，平面P AD⊥底面ABCD，P A⊥AD.E和F分别是CD和PC的中点．求证：(1)P A⊥底面ABCD；(2)BE∥平面P AD；(3)平面BEF⊥平面PCD.10．(2013·泉州模拟)如图所示，在直四棱柱ABCD－A1B1C1D1中，DB＝BC，DB⊥AC，点M是棱BB1上一点．(1)求证：B1D1∥平面A1BD；(2)求证：MD⊥AC；(3)试确定点M的位置，使得平面DMC1⊥平面CC1D1D.能力提升题组(建议用时：25分钟)一、填空题1.如图，在斜三棱柱ABCA1B1C1中，∠BAC＝90°，BC1⊥AC，则C1在底面ABC上的射影H必在直线______上．2.如图，在四面体ABCD中，若截面PQMN是正方形，则在下列命题中，错误的为________．①AC⊥BD；②AC∥截面PQMN；③AC＝BD；④异面直线PM与BD所成的角为45°.3．(2013·南通二模)如图，已知六棱锥P ABCDEF的底面是正六边形，P A⊥平面ABC，P A＝2AB，则下列结论中：①PB⊥AE；②平面ABC⊥平面PBC；③直线BC∥平面P AE；④∠PDA＝45°.其中正确的有________(把所有正确的序号都填上)．二、解答题4．(2014·北京西城一模)。

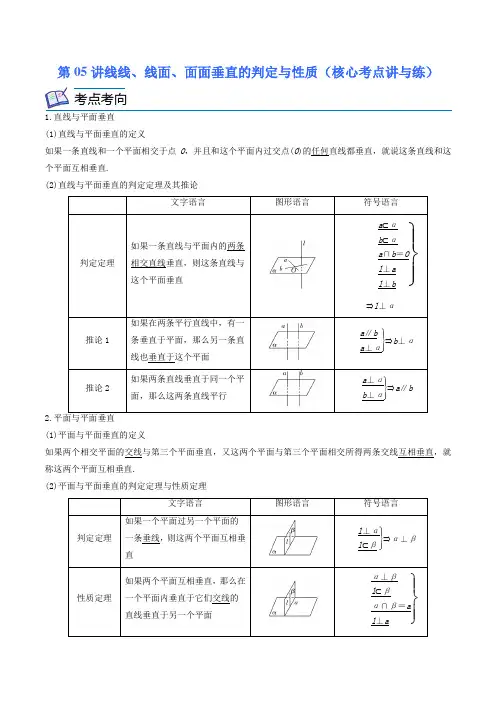
第05讲线线、线面、面面垂直的判定与性质（核心考点讲与练）1.直线与平面垂直(1)直线与平面垂直的定义如果一条直线和一个平面相交于点O，并且和这个平面内过交点(O)的任何直线都垂直，就说这条直线和这个平面互相垂直.(2)直线与平面垂直的判定定理及其推论文字语言图形语言符号语言判定定理如果一条直线与平面内的两条相交直线垂直，则这条直线与这个平面垂直⎭⎪⎬⎪⎫a⊂αb⊂αa∩b＝Ol⊥al⊥b⇒l⊥α推论1如果在两条平行直线中，有一条垂直于平面，那么另一条直线也垂直于这个平面⎭⎪⎬⎪⎫a∥ba⊥α⇒b⊥α推论2如果两条直线垂直于同一个平面，那么这两条直线平行⎭⎪⎬⎪⎫a⊥αb⊥α⇒a∥b2.平面与平面垂直(1)平面与平面垂直的定义如果两个相交平面的交线与第三个平面垂直，又这两个平面与第三个平面相交所得两条交线互相垂直，就称这两个平面互相垂直.(2)平面与平面垂直的判定定理与性质定理文字语言图形语言符号语言判定定理如果一个平面过另一个平面的一条垂线，则这两个平面互相垂直⎭⎪⎬⎪⎫l⊥αl⊂β⇒α⊥β性质定理如果两个平面互相垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面⎭⎪⎬⎪⎫α⊥βl⊂βα∩β＝al⊥a考点考向⇒l ⊥α1.证明直线和平面垂直的常用方法：①判定定理；②垂直于平面的传递性(a ∥b ，a ⊥α⇒b ⊥α)；③面面平行的性质(a ⊥α，α∥β⇒a ⊥β)；④面面垂直的性质．2.利用判定定理证明平面与平面垂直的一般方法先从现有的直线中寻找平面的垂线，若这样的垂线存在，则可通过线面垂直来证明面面垂直；若这样的垂线不存在，则需通过作辅助线来证明 3.证明面面垂直常用的方法： （1）面面垂直的定义； （2）面面垂直的判定定理.在证明面面垂直时，一般假设面面垂直成立，然后利用面面垂直转化为线面垂直，即为所证的线面垂直，组织论据证明即可题型一：线面垂直的判定 一、填空题1．（2021·上海浦东新·高二期中）直线与平面垂直的判定定理：如果一条直线与一个平面上的___________直线都垂直，那么此直线与该平面垂直.2．（2021·上海·高二专题练习）若E ，F 分别为四棱柱1111ABCD A B C D -的棱AB ，AD 的中点，则加上条件________，就可得结论：EF ⊥平面11DA C .（写出你认为正确的一个条件） 二、解答题3．（2021·上海市甘泉外国语中学高二期中）已知正方体ABCD ﹣A 1B 1C 1D 1.(1)求证：1//AD 平面C 1BD ；能力拓展方法技巧(2)求证：1AD ⊥平面A 1D C .4．（2021·上海市七宝中学高二期中）如图，在三棱锥P ABC -中，M 为AC 的中点，PA PC ⊥，AB BC ⊥，AB BC =，2PB =，2AC =，30PAC ∠=︒.(1)证明：BM ⊥平面PAC ；(2)求三棱锥P ABC -的体积.5．（2021·上海·高二专题练习）如图，在棱长为a 的正方体1111ABCD A B C D -中，E ，F ，M 分别是棱AB 、BC 和1DD 所在直线上的动点：（1）求1EB F ∠的取值范围：（2）若N 为面1EB F 内的一点，且45EBN ∠=︒，60FBN ∠=︒，求1B BN ∠的余弦值：（3）若E 、F 分别是所在正方形棱的中点，试问在棱1DD 上能否找到一点M ，使BM ⊥平面1EFB 若能，试确定点M 的位置，若不能，请说明理由. 题型二：线面垂直证明线线平行3．（2018·上海市宝山中学高二期中）,,a b c 表示直线，α表示平面，下列命题正确的是 A ．若//a b ，//a α，则//b α B ．若a ⊥b ， b ⊥α，则a ⊥α C ．若a ⊥c ，b ⊥c ，则//a b D ．若a ⊥α，b ⊥α，则//a b二、填空题4．（2021·上海·华师大二附中高二开学考试）如图，在正方体1111ABCD A B C D -中，,,M N P 分别为11B C ，1D D 和AB 的中点，则下列关系：①BM AB ⊥；②BM ∥平面11A PC ； ③1BM C P ⊥； ④1B N ⊥平面11A PC ，正确的编号为___________________. 题型三：线面垂直证明线线垂直 一、单选题1．（2022·上海·复旦附中高二期中）如图所示，一个灯笼由一根提竿PQ 和一个圆柱组成，提竿平行于圆柱的底面，在圆柱上下底面圆周上分别有两点A 、B ，AB 与圆柱的底面不垂直，则在圆柱绕着其旋转轴旋转一周的过程中，直线PQ 与直线AB 垂直的次数为（ ）A ．2B ．4C ．6D ．82．（2021·上海市嘉定区安亭高级中学高二阶段练习）已知点P 是△ABC 所在平面外一点，且P 到△ABC 三个顶点的距离相等，则P 点在平面ABC 上的射影是△ABC 的（ ） A ．重心 B ．垂心C ．内心D ．外心三、解答题5．（2021·上海市市西中学高二期中）如图，已知平行六面体ABCD —A 1B 1C 1D 1的底面ABCD 是菱形，且∠C 1CB＝∠C 1CD ＝∠BCD ＝60°(1)证明：C 1C ⊥BD ； (2)当1CDCC 的值为多少时，能使A 1C ⊥平面C 1BD ?请给出证明． 题型四：面面垂直的判定 一、单选题1．（2021·上海·复旦附中高二期中）在三棱锥A BCD -中，若AD BC ⊥，AD BD ⊥，那么必有（ ）A ．平面ADC ⊥平面BCDB ．平面ABC ⊥平面BCDC ．平面ABD ⊥平面ADC D ．平面ABD ⊥平面ABC二、填空题2．（2021·上海·华师大二附中高二阶段练习）如图所示，四棱锥P ABCD -的底面ABCD 是边长为a 的正方形，侧棱PA a =，2PB PD a ==，则它的5个面中，互相垂直的面有__________对.3．（2021·上海市七宝中学高二阶段练习）已知ABCD 是边长为a 的正方形，点P 在平面ABCD 外，侧棱PA a =，2PB PD a =，则该几何体P ABCD -的5个面中，互相垂直的面有______对三、解答题4．（2022·上海市杨浦高级中学高二期末）如图，三棱锥P ABC -中，,,PA PB PC 两两垂直，PA PB PC ==，且,M N 分别为线段,AB PC 的中点.(1)若点K 是线段PM 的中点，求证：直线//NK 平面ABC ；(2)求证：平面PCM ⊥平面ABC .5．（2021·上海·复旦附中高二期中）如图，已知四棱锥P ABCD -的底面ABCD 是边长为2的正方形，PD ⊥面,1ABCD PD =．(1)求证：面PAB ⊥面PAD ； (2)求四棱锥P ABCD -的侧面积． 题型五：面面垂直证线面垂直 一、单选题1．（2021·上海市南洋模范中学高二期中）已知点P 是正四棱锥的侧棱上异于点V 的一动点，则点P 在面上的射影落在（ ）A ．的外部B ．的内部C ．的一边上D ．以上皆有可能2．（2021·上海市延安中学高二期中）如图所示，在斜三棱柱111ABC A B C -中，90BAC ︒∠=，且1BC AC ，过1C 作1C H ⊥平面ABC ，垂足为H ，则点H 在（ ）A ．直线AC 上B ．直线AB 上C ．直线BC 上D ．ABC 内部3．（2021·上海市复兴高级中学高二期中）已知α，β是两个不同的平面，直线l α⊂，则“l β⊥”是“αβ⊥”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件二、填空题4．（2021·上海市松江二中高二期中）如图，在棱长均为23的正四面体ABCD 中，M 为AC 中点，E 为AB 中点，P 是DM 上的动点，Q 是平面ECD 上的动点，则AP PQ +的最小值是______.三、解答题5．（2021·上海·曹杨二中高二阶段练习）如图，在三棱锥P ABC -中，平面PAC ⊥平面,60,4ABC PAC BAC AC ∠∠===，3,2AB AP ==.(1)求PB 的长；(2)求点C 到平面PAB 的距离. 题型六：空间垂直的转化 一、单选题1．（2021·上海市奉贤区奉城高级中学高二期中）已知m 、n 为异面直线，m ⊥平面α，n ⊥平面β．平面α与β外的直线l 满足l m ⊥，l n ⊥，则（ ） A ．//αβ，且//l α B ．αβ⊥且l β⊥C ．α与β相交，且交线垂直于lD ．α与β相交，且交线平行于l二、填空题2．（2021·上海市七宝中学高二阶段练习）已知A ，B ，C ，D ，E 为空间不共面的五个点，顺次用线段连接这五个点构成空间五边形，则在此五边形中互相垂直的边最多有多少______对一、单选题1．（2021·上海·复旦附中高二期中）设m ､n 为两条直线，α､β为两个平面，则下列命题中假命题是（ ） A ．若m n ⊥，m α⊥，n β⊥，则αβ⊥巩固提升B ．若//m n ，m α⊥，//n β，则αβ⊥C ．若m n ⊥，//m α，//n β，则//αβD ．若//m n ，m α⊥，n β⊥，则//αβ2．（2021·上海市复兴高级中学高二期中）如图，点E 为正方形ABCD 边BC 上异于点B C 、的动点，将ABE△沿AE 翻折，得到如图所示的四棱锥B AECD -，且平面BAE ⊥平面AECD ，点F 为线段BD 上异于点B D 、的动点，则在四棱锥B AECD -中，下列说法： ①直线BE 与直线CF 必不在同一平面上； ②存在点E 使得直线BE ⊥平面DCE ； ③存在点F 使得直线CF 与平面BAE 平行； ④存在点E 使得直线BE 与直线CD 垂直. 以上叙述正确的是（ ）A ．①②B ．①③C ．①④D ．③④3．（2021·上海市金山中学高二期中）若a ，b 是异面直线，则下列命题中的假命题为（ ） A ．过直线a 有且仅有一个平面α与直线b 平行 B ．可能存在平面α与直线a ，b 都垂直 C ．唯一存在一个平面α与直线a ，b 等距 D ．过直线a 至多可以作一个平面α与直线b 垂直4．（2021·上海市宝山中学高二期中）已知直线,a b 和平面,M N ，且a M ⊥，那么（ ） A ．//b a b M ⊥⇒B ．//N M a N ⊥⇒C ．//b M b a ⇒⊥D ．//a N M N ⊂⇒5．（2021·上海市甘泉外国语中学高二期中）在三棱锥P ﹣ABC 中，顶点P 到AB 、AC 和BC 的距离都相等，P 在底面的投影为O 且在△ABC 内，则点O 是△ABC 的（ ） A ．内心B ．外心C ．重心D ．垂心6．（2021·上海·高二专题练习）如图，梯形ABCD 中，AD ∥BC ，AD ＝AB ＝1，AD ⊥AB ，∠BCD ＝45°，将△ABD 沿对角线BD 折起，设折起后点A 的位置为A ′，使二面角A ′—BD —C 为直二面角，给出下面四个命题：①A ′D ⊥BC ；②三棱锥A ′—BCD 2③CD ⊥平面A ′BD ；④平面A ′BC ⊥平面A ′D C ．其中正确命题的个数是（ ）A ．1B ．2C ．3D ．47．（2021·上海市宝山中学高二阶段练习）如图1，已知P ABC 是直角梯形，AB ∥PC ，AB ⊥BC ，D 在线段PC 上，AD ⊥PC ．将△P AD 沿AD 折起，使平面P AD ⊥平面ABCD ，连接PB ，PC ，设PB 的中点为N ，如图2．对于图2，下列选项错误的是（ ）A ．平面P AB ⊥平面PBC B ．BC ⊥平面PDCC ．PD ⊥AC D ．PB ＝2AN二、填空题8．（2021·上海市松江二中高二期中）“棱柱有相邻两个侧面是矩形”是“棱柱是直棱柱”的______________条件（填“充分不必要”、“必要不充分”、“充要”、“不充分不必要”）9．（2021·上海交大附中闵行分校高二阶段练习）设,,l m n 均为直线，其中,m n 在平面α内，“l α⊥”是“l m ⊥且l n ⊥”的___________条件.10．（2021·上海交大附中闵行分校高二阶段练习）已知Rt AH HEF ⊥△所在的平面，且HE EF ⊥，连接AE ，AF ，则图中直角三角形的个数是___________.11．（2021·上海·华东师大附属枫泾中学高二期中）如图，在长方体1111ABCD A B C D -中，11,2,3m AA cm AB cm BC c ===，则1A C 为___________cm .12．（2021·上海·高二专题练习）一条长为a 的线段夹在互相垂直的两个平面之间，它和这两个平面所成的角分别为45︒和30︒，由这条线段的两个端点向两个平面的交线引垂线，则垂足间的距离为________．13．（2021·上海外国语大学闵行外国语中学高二期中）《九章算术》中将底面为直角三角形且侧棱垂直于底面的三棱柱称为“堑堵”；底面为矩形，一条侧棱垂直于底面的四棱锥称之为“阳马”，四个面均为直角三角形的四面体称为“鳖臑”，如图在堑堵111ABC A B C -中，AC BC ⊥，且12AA AB ==.有下列命题：①四棱锥11B A ACC -为“阳马”；②四面体11AC CB 为“鳖臑”③四棱锥11B A ACC -体积最大为43；④过A 点分别作1AE A B ⊥于点E ，1AF A C ⊥于点F ，则1EF A B ⊥. 则正确命题是___________.14．（2021·上海市洋泾中学高二期中）如图，已知四棱锥P －ABCD ，底面ABCD 为正方形，P A ⊥平面ABCD ．给出下列命题：①PB ⊥AC ；②平面P AB 与平面PCD 的交线与AB 平行；③平面PBD ⊥平面P AC ；④△PCD为锐角三角形．其中正确命题的序号是________．15．（2021·上海市延安中学高二期中）如图，是一个正方体的平面展开图，在这个正方体中，①BM 与ED 是异面直线；②CN 与BE 平行；③CN 与BM 成60°角；④DM 与BN 垂直.请写出所有正确结论的序号____________.16．（2021·上海市松江二中高二期中）在正方体1111ABCD A B C D -中，6AB =，点P 在平面11AB D 内，132A P =，则点P 到1BC 距离的最大值为______________.17．（2021·上海市松江二中高二期中）如图，在三棱锥P ABC -中，能证明⊥AP BC 的条件是_______．①AP PB ⊥，AP PC ⊥；②AP PB ⊥，BC PB ⊥；③平面BCP ⊥平面PAC ，BC PC ⊥；④PB PC =，AB AC =.三、解答题18．（2021·上海·复旦附中高二期中）已知四棱柱1111ABCD A B C D -中，11111,AC D B F AC DB F ⋂=⋂=，(1)判断1A A 与1F F 是否平行？说明理由．(2)若面11A ACC ⊥面ABCD ，面11D DBB ⊥面ABCD ，且面11D DBB ⋂面1111A ACC FF =，判断1F F 与面ABCD 是否垂直？说明理由．19．（2021·上海市金山中学高二期末）圆锥的顶点为P ，底面圆心为O ，线段AB 是圆O 的直径，点C 是圆O 上异于A 、B 的点，PO 垂直于圆O 所在的平面，且1OB =，3OP =(1)若D 为线段AC 中点，求证：AC ⊥平面PDO ；(2)求圆锥的侧面积，并求三棱锥P ABC -体积的最大值；(3)当三棱锥P ABC -体积最大时，点C 沿圆锥表面运动到母线PB 中点1C ，求该点经过的路线的最小值. 20．（2021·上海·华东师范大学第三附属中学高二阶段练习）如图1，矩形ABCD ，1AB =，2BC =，点E 为AD 的中点，将ABE △沿直线BE 折起至平面PBE ⊥平面BCDE （如图2），点M 在线段PD 上，//PB 平面CEM .（1）求证：2MP DM =；（2）求证：平面PBE ⊥平面PEC ；（3）若在棱PB ，PE 分别取中点F ，G ，试判断点M 与平面CFG 的关系，并说明理由. 21．（2021·上海奉贤区致远高级中学高二期中）如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，底部ABCD 为菱形，E 为CD 的中点.（Ⅰ）求证：BD ⊥平面P AC ；（Ⅱ）若∠ABC =60°，求证：平面P AB ⊥平面P AE ；（Ⅲ）棱PB 上是否存在点F ，使得CF ∥平面P AE ？说明理由.22．（2022·上海·格致中学高二期末）在四面体ABCD 中，CB =CD ，AD BD ⊥，且E ，F 分别是AB ，BD 的中点，求证：（I ）直线EF ACD 面；（II ）EFC BCD ⊥面面．23．（2022·上海市控江中学高二期末）如图，在四棱锥P ABCD -中，四边形ABCD 为正方形，己知PD ⊥平面ABCD ，且PD AD =，E 为PC 中点．(1)证明：//PA 平面BDE ；(2)证明：平面PCD ⊥平面PBC ．24．（2021·上海市奉贤中学高二阶段练习）已知正方体1111ABCD A B C D -的棱长为a ，E ､F 分别为棱11C D ､11A D 的中点，P 为体对角线1BD 所在直线上一动点.(1)作出该正方体过点E ､F 且和直线1BD 垂直的截面，并证明该截面和直线1BD 垂直；(2)求出△EFP 绕直线EF 旋转而成的几何体体积的最小值；(3)若动点M 在直线EF 上运动，动点N 在平面11BCC B 上运动，求PM PN +的最小值.。

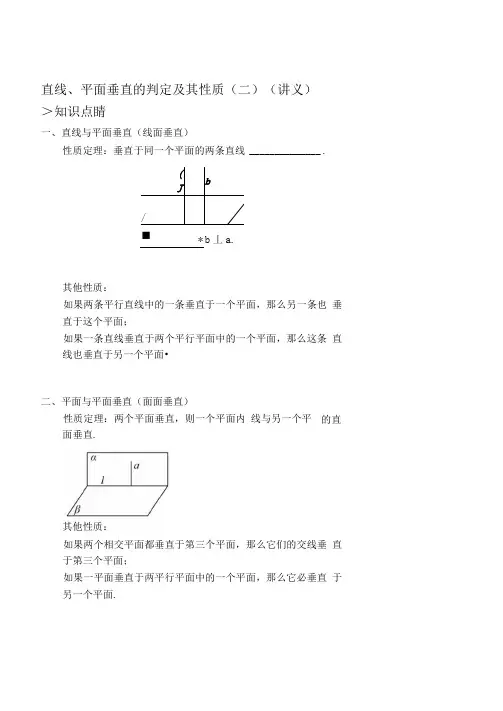
直线、平面垂直的判定及其性质（二）（讲义）＞知识点睛一、直线与平面垂直（线面垂直）性质定理：垂直于同一个平面的两条直线 ______________ .(Jb/ /■* b丄a.其他性质：如果两条平行直线中的一条垂直于一个平面，那么另一条也垂直于这个平面；如果一条直线垂直于两个平行平面中的一个平面，那么这条直线也垂直于另一个平面•二、平面与平面垂直（面面垂直）性质定理：两个平面垂直，则一个平面内线与另一个平面垂直.其他性质：如果两个相交平面都垂直于第三个平面，那么它们的交线垂直于第三个平面；如果一平面垂直于两平行平面中的一个平面，那么它必垂直于另一个平面.的直2 2精讲精练已知直线/垂直于直线AB 和AC.直线W 垂直于直线BC 和 AC.则直线/, /«的位置关系是（ ）A.平行B.异面 C •相交 m n 和平面6 0,能得出a 丄戶的一组条件是（ .in//a^n//Par\p=in^ rtuan 邛、inca> /»丄0, «丄戶若川，心/是互不重合的直线，g 緘7是互不重合的平面， 给出下列命题：① 若a 丄0, «门0二川，② 若ct 〃0, a n y=zz/»③ 若m 不垂直于<z,④ 若《门0二"f,加〃“，且"E Q , «妙，则n//a 且《〃0；⑤ 若《门0二加，n y=n » aPl 尸/,且ct 丄0, a 丄y, 0丄y,贝J w 丄川丄/, «丄人其中正确命题的序号是 _________________ •边长为a对于直线, A. in//n, B- 川丄心 C. m//D- m//川丄心则《丄《或《丄0：0n 尸小则加〃”； 则加不可能垂直于a 内的无数条直线;D ・垂直A. C 6C. --- a D ・aD的正方形ABCD沿对角线BD折成直二面角，则AC 的长为（如图，以等腰直角三角形ABC 斜边BC 上的高AD 为折痕， 把△ABD 和△ACD 折成互相垂直的两个平面后，某学生得出 下列四个结论：① BD 丄AC^② 是等边三角形；③ 三棱锥DMBC 是正三棱锥;④ 平面ADC 丄平面ABC.其中正确的是（如图，在斜三棱柱ABC-AiBiCi中， 则C,在底面ABC 上的射影H必在（）A.直线AB 上C.直线AC 上 已知直二面角0[-/-〃，点AEa. AC ■丄/,垂足为点C,点医0, BD 丄h 垂足为点D,若AB=2. AC=BD=i ,则CD 的长为3 CD. 1A.①②④B.①②③C.②③④ D-①③④ZBqC=90。

线面垂直的判定与性质练习题一．选择题（共16小题）1．（2014•甘肃二模）设m，n是两条不同直线，α，β是两个不同的平面，下列命题正确的是（）A．m∥α，n∥β且α∥β，则m∥n B．m⊥α，n⊥β且α⊥β，则m⊥nC．m⊥α，n⊂β，m⊥n，则α⊥βD．m⊂α，n⊂α，m∥β，n∥β，则α∥β2．（2014•上海模拟）已知m和n是两条不同的直线，α和β是两个不重合的平面，那么下面给出的条件中一定能推出m⊥β的是（）A．α⊥β，且m⊂αB．m∥n，且n⊥βC．α⊥β，且m∥αD．m⊥n，且n∥β3．（2014•宜昌三模）在三棱椎P﹣ABC中，PA⊥平面ABC，AC⊥BC，D为侧棱PC上的一点，它的正视图和侧视图如图所示，则下列命题正确的是（）A．A D⊥平面PBC且三棱椎D﹣ABC的体积为B．B D⊥平面PAC且三棱椎D﹣ABC的体积为C．A D⊥平面PBC且三棱椎D﹣ABC的体积为D．B D⊥平面PAC且三棱椎D﹣ABC的体积为4．（2014•甘肃二模）已知H是球O的直径AB上一点，AH：HB=1：2，AB⊥平面α，H为垂足，α截球O所得截面的面积为π，则球O的表面积为（）A ．B ． 4πC ．D ．5．（2013•甘肃三模）已知A ，B ，C ，D 是同一球面上的四个点，其中△ABC 是正三角形，AD ⊥平面ABC ，AD=2AB=6，则该球的表面积为（ ）A ． 16πB ． 24πC ． 32πD ． 48π 6．（2012•虹口区一模）正方体ABCD ﹣A 1B 1C 1D 1中，E 为线段B 1D 1上的一个动点，则下列结论中错误的是（ ） A ． A C ⊥BE B ． B 1E ∥平面ABCDC ． 三棱锥E ﹣ABC 的体积为定值D ． 直线B 1E ⊥直线BC 17．（2011•辽宁）如图，四棱锥S ﹣ABCD 的底面为正方形，SD ⊥底面ABCD ，则下列结论中不正确的是（）A ． A C ⊥SBB ． A B ∥平面SCDC ． S A 与平面SBD所成的角等于SC 与平面SBD所成的角D ． A B 与SC 所成的角等于DC 与SA 所成的角8．（2011•浙江）下列命题中错误的是（ ）A ． 如果平面α⊥平面β，那么平面α内一定存在直线平行于平面βB ． 如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面βC ． 如果平面α⊥平面γ，平面β⊥平面γ，α∩β=l ，那么l ⊥平面γD ． 如果平面α⊥平面β，那么平面α内所有直线都垂直于平面β9．（2010•辽宁）已知S，A，B，C是球O表面上的点，SA⊥平面ABC，AB⊥BC，SA=AB=1，，则球O的表面积等于（）A．4πB．3πC．2πD．π10．（2010•眉山二模）已知A，B，C，D在同一球面上，AB⊥平面BCD，BC⊥CD，若，则B，C两点间的球面距离是（）A．B．C．D．11．（2009•广东）给定下列四个命题：①若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行；②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直；③垂直于同一直线的两条直线相互平行；④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直．其中，为真命题的是（）A．①和②B．②和③C．③和④D．②和④12．（2005•北京）在正四面体P﹣ABC中，D，E，F分别是AB，BC，CA的中点，下面四个结论中不成立的是（）A．B C∥平面PDF B．D F⊥平面PAE C．平面PDF⊥平面ABC D．平面PAE⊥平面ABC13．如图，平面α⊥平面β，A∈α，B∈β，AB与两平面α、β所成的角分别为和．过A、B分别作两平面交线的垂线，垂足为A′、B′，则AB：A′B′=（）A．2：1 B．3：1 C．3：2 D．4：314．三棱锥P﹣ABC的高为PH，若三个侧面两两垂直，则H为△ABC的（）A．内心B．外心C．垂心D．重心15．如图所示，已知三棱柱ABC﹣A1B1C1的所有棱长均为1，且AA1⊥底面ABC，则三棱锥B1﹣ABC1的体积为（）A．B．C．D．16．在下列四个正方体中，能得出AB⊥CD的是（）A ．B ．C ．D ．二．填空题（共3小题）17．（2014•山西模拟）已知三棱锥P ﹣ABC 中，△ABC 是边长为6的正三角形，PA ⊥平面ABC ，且三棱锥外接球的表面积为64π，则PA= _________ ．18．（2013•兰州一模）如图，在四棱锥P ﹣ABCD 中，PA ⊥平面ABCD ，底面ABCD 是菱形，AB=2，∠BAD=60°． （Ⅰ）求证：BD ⊥平面PAC ；（Ⅱ）若PA=AB ，求棱锥C ﹣PBD 的高．19．如图SA ⊥平面ABC ，AB ⊥BC ，过A 做SB 的垂线，垂足为E ，过E 做SC 的垂线，垂足为F ，求证AF ⊥SC ．以下是证明过程：要证AF ⊥SC只需证 SC ⊥平面AEF 只需证 AE ⊥SC （因为EF ⊥SC ）只需证 AE ⊥平面SBC只需证 _________ （因为AE ⊥SB ）只需证 BC ⊥平面SAB只需证 _________ （因为AB ⊥BC ）由只需证 SA ⊥平面ABC 可知上式成立所以AF ⊥SC把证明过程补充完整① _________ ② _________ ．三．解答题（共11小题）20．（2014•福建）如图，三棱锥A ﹣BCD 中，AB ⊥平面BCD ，CD ⊥BD ．（Ⅰ）求证：CD ⊥平面ABD ；（Ⅱ）若AB=BD=CD=1，M 为AD 中点，求三棱锥A ﹣MBC 的体积．21．（2014•开封二模）如图，三棱柱ABC﹣A1B1C1中，CA=CB，AB=AA1，∠BAA1=60°（Ⅰ）证明：AB⊥A1C；（Ⅱ）若AB=CB=2，A1C=，求三棱柱ABC﹣A1B1C1的体积．22．（2014•江苏）如图，在三棱锥P﹣ABC中，D，E，F分别为棱PC，AC，AB的中点，已知PA⊥AC，PA=6，BC=8，DF=5．求证：（1）直线PA∥平面DEF；（2）平面BDE⊥平面ABC．23．（2014•北京）如图，在三棱柱ABC﹣A1B1C1中，侧棱垂直于底面，AB⊥BC，AA1=AC=2，BC=1，E，F分别是A1C1，BC的中点．（Ⅰ）求证：平面ABE⊥B1BCC1；（Ⅱ）求证：C1F∥平面ABE；（Ⅲ）求三棱锥E﹣ABC的体积．24．（2014•呼伦贝尔二模）如图，AB是圆O的直径，点C是弧AB的中点，点V是圆O所在平面外一点，D是AC的中点，已知AB=2，V A=VB=VC=2．（1）求证：OD∥平面VBC；（2）求证：AC⊥平面VOD；（3）求棱锥C﹣ABV的体积．25．（2014•梅州二模）已知四棱锥P﹣ABCD（图1）的三视图如图2所示，△PBC为正三角形，PA垂直底面ABCD，俯视图是直角梯形．（1）求正视图的面积；（2）求四棱锥P﹣ABCD的体积；（3）求证：AC⊥平面PAB．26．（2014•德州一模）已知四棱锥P﹣ABCD中，底面ABCD是直角梯形，AB∥CD，∠ABC=45°，DC=1，AB=2，PA⊥平面ABCD，M为PB中点．（Ⅰ）求证：MC∥平面PAD；（Ⅱ）求证：BC⊥平面PAC．27．（2014•河西区三模）如图，已知矩形ABCD中，AB=10，BC=6，将矩形沿对角线BD把△ABD折起，使A移到A1点，且A1在平面BCD上的射影O恰好在CD上．（1）求证：BC⊥A1D；（2）求证：平面A1BC⊥平面A1BD；（3）求三棱锥A1﹣BCD的体积．28．（2014•石景山区一模）已知四棱锥A﹣BCDE，其中AB=BC=AC=BE=1，CD=2，CD⊥面ABC，BE∥CD，F为AD的中点．（Ⅰ）求证：EF∥面ABC；（Ⅱ）求证：平面ADE⊥平面ACD；（Ⅲ）求四棱锥A﹣BCDE的体积．29．（2015•广东模拟）如图，四棱柱ABCD﹣A1B1C1D1的底面ABCD是平行四边形，且AB=1，BC=2，∠ABC=60°，E为BC的中点，AA1⊥平面ABCD．（1）证明：平面A1AE⊥平面A1DE；（2）若DE=A1E，试求异面直线AE与A1D所成角的余弦值．30．（2014•盐城三模）如图，四棱锥P﹣ABCD中，PA⊥底面ABCD，底面ABCD为菱形，点F为侧棱PC上一点．（1）若PF=FC，求证：PA∥平面BDF；（2）若BF⊥PC，求证：平面BDF⊥平面PBC．线面垂直的判定与性质练习题参考答案与试题解析一．选择题（共16小题）1．（2014•甘肃二模）设m，n是两条不同直线，α，β是两个不同的平面，下列命题正确的是（）A．m∥α，n∥β且α∥β，则m∥n B．m⊥α，n⊥β且α⊥β，则m⊥nC．m⊥α，n⊂β，m⊥n，则α⊥βD．m⊂α，n⊂α，m∥β，n∥β，则α∥β考点：平面与平面垂直的性质．专题：证明题；空间位置关系与距离．分析：对于A、由面面平行的判定定理，得A是假命题对于B、由m⊥α，n⊥β且α⊥β，可知m与n不平行，借助于直线平移先得到一个与m或n都平行的平面，则所得平面与α、β都相交，根据m与n所成角与二面角平面角互补的结论．对于C、通过直线与平面平行的判定定理以及平面与平面平行的性质定理，判断正误即可；对于D、利用平面与平面平行的判定定理推出结果即可．解答：解：对于A，若m∥α，n∥β且α∥β，说明m、n是分别在平行平面内的直线，它们的位置关系应该是平行或异面，故A错；对于B，由m⊥α，n⊥β且α⊥β，则m与n一定不平行，否则有α∥β，与已知α⊥β矛盾，通过平移使得m与n相交，且设m与n确定的平面为γ，则γ与α和β的交线所成的角即为α与β所成的角，因为α⊥β，所以m与n所成的角为90°，故命题B正确．对于C，根据面面垂直的性质，可知m⊥α，n⊂β，m⊥n，∴n∥α，∴α∥β也可能α∩β=l，也可能α⊥β，故C不正确；对于D，若“m⊂α，n⊂α，m∥β，n∥β”，则“α∥β”也可能α∩β=l，所以D不成立．故选B．点评：本题考查直线与平面平行与垂直，面面垂直的性质和判断的应用，考查逻辑推理能力，基本知识的应用题目．2．（2014•上海模拟）已知m和n是两条不同的直线，α和β是两个不重合的平面，那么下面给出的条件中一定能推出m⊥β的是（）A．α⊥β，且m⊂αB．m∥n，且n⊥βC．α⊥β，且m∥αD．m⊥n，且n∥β考点：直线与平面垂直的判定．专题：计算题；空间位置关系与距离．分析：根据A，B，C，D所给的条件，分别进行判断，能够得到正确结果．解答：解：α⊥β，且m⊂α⇒m⊂β，或m∥β，或m与β相交，故A不成立；m∥n，且n⊥β⇒m⊥β，故B成立；α⊥β，且m∥α⇒m⊂β，或m∥β，或m与β相交，故C不成立；由m⊥n，且n∥β，知m⊥β不成立，故D不正确．故选B．点评：本题考查直线与平面的位置关系的判断，是基础题，解题时要认真审题，仔细解答．3．（2014•宜昌三模）在三棱椎P﹣ABC中，PA⊥平面ABC，AC⊥BC，D为侧棱PC上的一点，它的正视图和侧视图如图所示，则下列命题正确的是（）A．A D⊥平面PBC且三棱椎D﹣ABC的体积为B．B D⊥平面PAC且三棱椎D﹣ABC的体积为C．A D⊥平面PBC且三棱椎D﹣ABC的体积为D．B D⊥平面PAC且三棱椎D﹣ABC的体积为考点：直线与平面垂直的判定；命题的真假判断与应用；简单空间图形的三视图．专题：空间位置关系与距离．分析：通过证明直线与平面内的两条相交直线垂直即可证明直线与平面垂直，求出几何体的体积即可．解答：解：∵PA⊥平面ABC，∴PA⊥BC，又AC⊥BC，PA∩AC=A，∴BC⊥平面PAC，∴BC⊥AD，又由三视图可得在△PAC中，PA=AC=4，D为PC的中点，∴AD⊥PC，∴AD⊥平面PBC．又BC=4，∠ADC=90°，BC⊥平面PAC．故．点评：本题考查直线与平面垂直的判断，几何体的体积的求法，考查命题的真假的判断与应用．4．（2014•甘肃二模）已知H是球O的直径AB上一点，AH：HB=1：2，AB⊥平面α，H为垂足，α截球O所得截面的面积为π，则球O的表面积为（）A．B．4πC．D．考点：直线与平面垂直的性质；球的体积和表面积．专题：球．分析：设球的半径为R，根据题意知由与球心距离为R的平面截球所得的截面圆的面积是π，我们易求出截面圆的半径为1，根据球心距、截面圆半径、球半径构成直角三角形，满足勾股定理，我们易求出该球的半径，进而求出球的表面积．解答：解：设球的半径为R，∵AH：HB=1：2，∴平面α与球心的距离为R，∵α截球O所得截面的面积为π，∴d=R时，r=1，故由R2=r2+d2得R2=12+（R）2，∴R2=∴球的表面积S=4πR2=．故选：C．点评：本题考查的知识点是球的表面积公式，若球的截面圆半径为r，球心距为d，球半径为R，则球心距、截面圆半径、球半径构成直角三角形，满足勾股定理．5．（2013•甘肃三模）已知A，B，C，D是同一球面上的四个点，其中△ABC是正三角形，AD⊥平面ABC，AD=2AB=6，则该球的表面积为（）A．16πB．24πC．32πD．48π考点：直线与平面垂直的性质；球的体积和表面积．专题：空间位置关系与距离．分析：由题意把A、B、C、D扩展为三棱柱如图，求出上下底面中心连线的中点与A的距离为球的半径，然后求出球的表面积．解答：解：由题意画出几何体的图形如图，把A、B、C、D扩展为三棱柱，上下底面中心连线的中点与A的距离为球的半径，AD=2AB=6，OE=3，△ABC是正三角形，所以AE==．AO==2 ．所求球的表面积为：4π（2）2=48π．故选D ．点评： 本题考查球的内接体与球的关系，考查空间想象能力，利用割补法结合球内接多面体的几何特征求出球的半径是解题的关键．6．（2012•虹口区一模）正方体ABCD ﹣A 1B 1C 1D 1中，E 为线段B 1D 1上的一个动点，则下列结论中错误的是（ ）A ． A C ⊥BEB ． B 1E ∥平面ABCDC ． 三棱锥E ﹣ABC 的体积为定值D ． 直线B 1E ⊥直线BC 1考点： 直线与平面垂直的性质；直线与平面垂直的判定．专题： 空间位置关系与距离．分析： 结合正方体的性质，利用线面平行和垂直的性质定理和判定定理分别进行判断证明．解答：解：A．∵在正方体中，AC⊥BD，AC⊥DD1，BD∩DD1=D，∴AC⊥面BB1D1D，∵BE⊂面BB1D1D，∴AC⊥BE，∴A正确．B．∵B1D1∥平面ABCD，∴B1E∥平面ABCD成立．即B正确．C．三棱锥E﹣ABC的底面△ABC为定值，锥体的高BB1为定值，∴锥体体积为定值，即C正确．D．∵D1C1⊥BC1D1，∴B1E⊥直线BC1错误．故选D．点评：本题主要考查空间直线和平面的位置关系的判断，要求熟练掌握相应的判定定理和性质定理．7．（2011•辽宁）如图，四棱锥S﹣ABCD的底面为正方形，SD⊥底面ABCD，则下列结论中不正确的是（）A．A C⊥SBB．A B∥平面SCDC．S A与平面SBD所成的角等于SC与平面SBD所成的角D．A B与SC所成的角等于DC与SA所成的角考点：直线与平面垂直的性质．专题：综合题；探究型．分析：根据SD⊥底面ABCD，底面ABCD为正方形，以及三垂线定理，易证AC⊥SB，根据线面平行的判定定理易证AB∥平面SCD，根据直线与平面所成角的定义，可以找出∠ASO是SA与平面SBD所成的角，∠CSO是SC与平面SBD所成的角，根据三角形全等，证得这两个角相等；异面直线所成的角，利用线线平行即可求得结果．解答：解：∵SD⊥底面ABCD，底面ABCD为正方形，∴连接BD，则BD⊥AC，根据三垂线定理，可得AC⊥SB，故A正确；∵AB∥CD，AB⊄平面SCD，CD⊂平面SCD，∴AB∥平面SCD，故B正确；∵SD⊥底面ABCD，∠ASO是SA与平面SBD所成的角，∠DSO是SC与平面SBD所成的，而△SAO≌△CSO，∴∠ASO=∠CSO，即SA与平面SBD所成的角等于SC与平面SBD所成的角，故C正确；∵AB∥CD，∴AB与SC所成的角是∠SCD，DC与SA所成的角是∠SAB，而这两个角显然不相等，故D不正确；故选D．点评：此题是个中档题．考查线面垂直的性质定理和线面平行的判定定理，以及直线与平面所成的角，异面直线所成的角等问题，综合性强．8．（2011•浙江）下列命题中错误的是（）A．如果平面α⊥平面β，那么平面α内一定存在直线平行于平面βB．如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面βC．如果平面α⊥平面γ，平面β⊥平面γ，α∩β=l，那么l⊥平面γD．如果平面α⊥平面β，那么平面α内所有直线都垂直于平面β考点：平面与平面垂直的性质．专题：常规题型．分析：本题考查的是平面与平面垂直的性质问题．在解答时：A注意线面平行的定义再结合实物即可获得解答；B反证法即可获得解答；C利用面面垂直的性质通过在一个面内作交线的垂线，然后用线面垂直的判定定理即可获得解答；D结合实物举反例即可．解答：解：由题意可知：A、结合实物：教室的门面与地面垂直，门面的上棱对应的直线就与地面平行，故此命题成立；B、假若平面α内存在直线垂直于平面β，根据面面垂直的判定定理可知两平面垂直．故此命题成立；C、结合面面垂直的性质可以分别在α、β内作异于l的直线垂直于交线，再由线面垂直的性质定理可知所作的垂线平行，进而得到线面平行再由线面平行的性质可知所作的直线与l平行，又∵两条平行线中的一条垂直于平面那么另一条也垂直于平面，故命题成立；D、举反例：教室内侧墙面与地面垂直，而侧墙面内有很多直线是不垂直与地面的．故此命题错误．故选D．点评：本题考查的是平面与平面垂直的性质问题．在解答的过程当中充分体现了面面垂直、线面垂直、线面平行的定义判定定理以及性质定理的应用．值得同学们体会和反思．9．（2010•辽宁）已知S，A，B，C是球O表面上的点，SA⊥平面ABC，AB⊥BC，SA=AB=1，，则球O的表面积等于（）A．4πB．3πC．2πD．π考点：直线与平面垂直的性质；球的体积和表面积．专题：压轴题．分析：先寻找球心，根据S，A，B，C是球O表面上的点，则OA=OB=OC=OS，根据直角三角形的性质可知O为SC的中点，则SC即为直径，根据球的面积公式求解即可．解答：解：∵已知S，A，B，C是球O表面上的点∴OA=OB=OC=OS=1又SA⊥平面ABC，AB⊥BC，SA=AB=1，，∴球O的直径为2R=SC=2，R=1，∴表面积为4πR2=4π．故选A．点评：本题主要考查了直线与平面垂直的性质，以及球的表面积等有关知识，考查空间想象能力、运算能力和推理论证能力，属于基础题．10．（2010•眉山二模）已知A，B，C，D在同一球面上，AB⊥平面BCD，BC⊥CD，若，则B，C两点间的球面距离是（）A．B．C．D．考点：直线与平面垂直的性质；余弦定理．分析：先寻找球心的可知AB的中点为球心，然后求出弦BC所对的球心角，再根据球面距离公式求解即可．解答：解：∵AB⊥平面BCD，BC⊥CD，取AD的中点为O∴OA=OB=OC=OD，即O为球心∵∴BC=4则OB=OC=BC=4，所以∠BOC=60°，半径为4∴d===，故选A点评：本题主要考查了直线与平面垂直的性质，以及球面距离等有关知识，考查空间想象能力、运算能力和推11．（2009•广东）给定下列四个命题：①若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行；②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直；③垂直于同一直线的两条直线相互平行；④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直．其中，为真命题的是（）A．①和②B．②和③C．③和④D．②和④考点：平面与平面垂直的判定；平面与平面平行的判定．专题：综合题．分析：从直线与平面平行与垂直，平面与平面平行与垂直的判定与性质，考虑选项中的情况，找出其它可能情形加以判断，推出正确结果．解答：解：①若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行；如果这两条直线平行，可能得到两个平面相交，所以不正确．②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直；这是判定定理，正确．③垂直于同一直线的两条直线相互平行；可能是异面直线．不正确．④若两个平面垂直，那么一个平面内与它们的平面也不垂直．正确．故选：D．点评：本题考查平面与平面垂直的判定，平面与平面平行的判定，是基础题．12．（2005•北京）在正四面体P﹣ABC中，D，E，F分别是AB，BC，CA的中点，下面四个结论中不成立的是（）A．B C∥平面PDF B．D F⊥平面PAE C．平面PDF⊥平面ABC D．平面PAE⊥平面ABC考点：平面与平面垂直的判定；直线与平面平行的判定；直线与平面垂直的判定．专题：计算题；压轴题．分析：正四面体P﹣ABC即正三棱锥P﹣ABC，所以其四个面都是正三角形，在正三角形中，联系选项B、C、D中有证明到垂直关系，应该联想到“三线合一”．D，E，F分别是AB，BC，CA的中点，由中位线定理可得BC∥DF，所以BC∥平面PDF，进而可得答案．解答：解：由DF∥BC可得BC∥平面PDF，故A正确．若PO⊥平面ABC，垂足为O，则O在AE上，则DF⊥PO，又DF⊥AEPAE，故B正确．由DF⊥平面PAE可得，平面PAE⊥平面ABC，故D正确．故选C．点评：本小题考查空间中的线面关系，正三角形中“三线合一”，中位线定理等基础知识，考查空间想象能力和思维能力．13．如图，平面α⊥平面β，A∈α，B∈β，AB与两平面α、β所成的角分别为和．过A、B分别作两平面交线的垂线，垂足为A′、B′，则AB：A′B′=（）A．2：1 B．3：1 C．3：2 D．4：3考点：平面与平面垂直的性质．专题：计算题．分析：设AB的长度为a用a表示出A'B'的长度，即可得到两线段的比值．解答：解：连接AB'和A'B，设AB=a，可得AB与平面α所成的角为，在Rt△BAB'中有AB'=，同理可得AB与平面β所成的角为所以，因此在Rt△AA'B'中A'B'=，所以AB：A'B'=，故选A．点评：本题主要考查直线与平面所成的角以及线面的垂直关系，要用到勾股定理及直角三角形中的边角关系．有一定的难度14．三棱锥P﹣ABC的高为PH，若三个侧面两两垂直，则H为△ABC的（）A．内心B．外心C．垂心D．重心考点：平面与平面垂直的性质；棱锥的结构特征．专题：常规题型．分析：先画出图形，三个侧面两两垂直，可看成正方体的一角，根据BC⊥面APH，而AH⊂面APH，推出AH⊥BC，同理可推出CH⊥AB，得到H为△ABC的垂心．解答：解：如图所示，三个侧面两两垂直，可看成正方体的一角，则AP⊥面PBC，PBC∴AP⊥BC而PH⊥面ABC，BC⊂面ABC∴PH⊥BC，又AP∩PH=P，∴BC⊥面APH，而AH⊂面APH∴AH⊥BC，同理可得CH⊥AB故H为△ABC的垂心故选：C点评：本题主要考查了平面与平面垂直的性质，以及棱锥的结构特征，考查空间想象能力、运算能力和推理论证能力，属于基础题．15．如图所示，已知三棱柱ABC﹣A1B1C1的所有棱长均为1，且AA1⊥底面ABC，则三棱锥B1﹣ABC1的体积为（）A．B．C．D．考点：直线与平面垂直的性质；棱柱、棱锥、棱台的体积．专题：计算题；空间位置关系与距离．分析：根据题意，三棱A1B1C1是棱长均为1的正三棱柱，算出它的体积V=．再根据锥体的体积公式得三棱锥A﹣A1B1C1、三棱锥C1﹣ABC的体积都等于三棱柱ABC﹣A1B1C1体积的，由此用三棱柱ABC﹣A1B1C1体积减去两个三棱锥的体积，即可算出三棱锥B1﹣ABC1的体积．解答：解：∵三棱柱ABC﹣A1B1C1的所有棱长均为1，∴底面△ABC为正三角形，面积S△ABC==又∵AA1⊥底面ABC，AA1=1∴三棱柱ABC﹣A1B1C1的体积V=S△ABC•AA1=∵三棱锥A﹣A1B1C1、三棱锥C1﹣ABC与三棱柱ABC﹣A1B1C1等底等高∴V=V=V=由此可得三棱锥B1﹣ABC1的体积V=V﹣V﹣V=故选：A点评：本题给出棱长均为1的正三棱柱，求其中的三棱锥B1﹣ABC1体积．着重考查了正三棱柱的性质、柱体和锥体的体积公式等知识，属于中档题．16．在下列四个正方体中，能得出AB⊥CD的是（）A．B．C．D．考点：直线与平面垂直的性质．专题：计算题；空间位置关系与距离．分析：在图A中作出经过AB的对角面，发现它与AB⊥CD成立；在图B中作出正方体过AB的等边三角形截面，可得CD、AB成60°的角；而在图C、D中，不难将直线CD进行平移，得到CD与AB所成角为锐角．由此可得正确答案．解答：解：对于A，作出过AB的对角面如图，可得直线CD与这个对角面垂直，根据线面垂直的性质，AB⊥CD成立；对于B，作出过AB的等边三角形截面如图，将CD平移至内侧面，可得CD与AB所成角等于60°；对于C、D，将CD平移至经过B点的侧棱处，可得AB、CD所成角都是锐角．故选A．点评：本题以正方体中的异面直线为例，要我们找直线，着重考查了空间两直线的位置关系和直线与平面垂直的判定与性质等知识，属于基础題．二．填空题（共3小题）17．（2014•山西模拟）已知三棱锥P﹣ABC中，△ABC是边长为6的正三角形，PA⊥平面ABC，且三棱锥外接球的表面积为64π，则PA=4．考点：直线与平面垂直的性质；球内接多面体．专题：空间位置关系与距离．分析：设球心O，球半径R，△ABC外接圆半径r，圆心H，由已知条件求出r==2，R=4，由PA=2能求出结果．解答：解：设球心O，球半径R，△ABC外接圆半径r，圆心H，r=HA=÷cos30°=÷=2，∵三棱锥外接球的表面积为64π，∴64π=4πR2，解得OP=OA=R=4．∴PA=2OH=2=2=2=4．故答案为：4．点评：本题考查线段长的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．18．（2013•兰州一模）如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD是菱形，AB=2，∠BAD=60°．（Ⅰ）求证：BD⊥平面PAC；（Ⅱ）若PA=AB，求棱锥C﹣PBD的高．考点：直线与平面垂直的判定；点、线、面间的距离计算．专题：空间位置关系与距离．分析：（Ⅰ）利用线面垂直的判定定理证明BD⊥平面PAC；（Ⅱ）利用等积法求棱锥C﹣PBD的高．解答：解：（Ⅰ）证明：因为四边形ABCD是菱形，所以AC⊥BD．又因为PA⊥平面ABCD，所以PA⊥BD．又PA∩AC=A，所以BD⊥平面PAC．…（6分）（Ⅱ）解：∵V C﹣PBD=V P﹣CBD，设棱锥C﹣PBD的高为h，∴…（8分）∵PA=AB，AB=2，∠BAD=60°，∴PB=PD=，BD=2∴，，…（10分）∴．即棱锥C﹣PBD的高为．…（12分）点评：本题主要考查空间线面垂直的判定以及空间距离的求法，利用相应的判定定理是解决本题的关键．19．如图SA⊥平面ABC，AB⊥BC，过A做SB的垂线，垂足为E，过E做SC的垂线，垂足为F，求证AF⊥SC．以下是证明过程：要证AF⊥SC只需证SC⊥平面AEF只需证AE⊥SC（因为EF⊥SC）只需证AE⊥平面SBC只需证①（因为AE⊥SB）只需证BC⊥平面SAB只需证②（因为AB⊥BC）由只需证SA⊥平面ABC可知上式成立所以AF⊥SC把证明过程补充完整①AE⊥BC②BC⊥SA．考点：直线与平面垂直的判定；空间中直线与直线之间的位置关系；直线与平面平行的判定．专题：证明题；空间位置关系与距离．分析：根据线面垂直的判定，只需证明直线垂直于平面内的两条相交直线，由此可得结论．解答：解：根据线面垂直的判定，要证明AE⊥平面SBC，因为AE⊥SB，所以只需证AE⊥BC，即①为AE⊥BC；要证BC⊥平面SAB，因为AB⊥BC，所以只需证BC⊥SA，即②为BC⊥SA故答案为AE⊥BC；BC⊥SA．点评：本题考查线面垂直，考查学生分析解决问题的能力，属于基础题．三．解答题（共11小题）20．（2014•福建）如图，三棱锥A﹣BCD中，AB⊥平面BCD，CD⊥BD．（Ⅰ）求证：CD⊥平面ABD；（Ⅱ）若AB=BD=CD=1，M为AD中点，求三棱锥A﹣MBC的体积．考点：直线与平面垂直的判定；棱柱、棱锥、棱台的体积．专题：综合题；空间位置关系与距离．分析：（Ⅰ）证明：CD⊥平面ABD，只需证明AB⊥CD；（Ⅱ）利用转换底面，V A﹣MBC=V C﹣ABM=S△ABM•CD，即可求出三棱锥A﹣MBC的体积．解答：（Ⅰ）证明：∵AB⊥平面BCD，CD⊂平面BCD，∴AB⊥CD，∵CD⊥BD，AB∩BD=B，∴CD⊥平面ABD；（Ⅱ）解：∵AB⊥平面BCD，BD⊂平面BCD，∴AB⊥BD．∵AB=BD=1，∴S△ABD=，∵M为AD中点，∴S△ABM=S△ABD=，∵CD⊥平面ABD，∴V A﹣MBC=V C﹣ABM=S△ABM•CD=．点评：本题考查线面垂直，考查三棱锥A﹣MBC的体积，正确运用线面垂直的判定定理是关键．21．（2014•开封二模）如图，三棱柱ABC﹣A1B1C1中，CA=CB，AB=AA1，∠BAA1=60°（Ⅰ）证明：AB⊥A1C；（Ⅱ）若AB=CB=2，A1C=，求三棱柱ABC﹣A1B1C1的体积．考点：直线与平面垂直的性质；棱柱、棱锥、棱台的体积．专题：空间位置关系与距离．分析：（Ⅰ）由题目给出的边的关系，可想到去AB中点O，连结OC，OA1，可通过证明AB⊥平面OA1C得要证的结论；（Ⅱ）在三角形OCA1中，由勾股定理得到OA1⊥OC，再根据OA1⊥AB，得到OA1为三棱柱ABC﹣A1B1C1的高，利用已知给出的边的长度，直接利用棱柱体积公式求体积．解答：（Ⅰ）证明：如图，取AB的中点O，连结OC，OA1，A1B．因为CA=CB，所以OC⊥AB．由于AB=AA1，，故△AA1B为等边三角形，所以OA1⊥AB．因为OC∩OA1=O，所以AB⊥平面OA1C．又A1C⊂平面OA1C，故AB⊥A1C；（Ⅱ）解：由题设知△ABC与△AA1B都是边长为2的等边三角形，所以．又，则，故OA1⊥OC．因为OC∩AB=O，所以OA1⊥平面ABC，OA1为三棱柱ABC﹣A1B1C1的高．又△ABC的面积，故三棱柱ABC﹣A1B1C1的体积．点评：题主要考查了直线与平面垂直的性质，考查了棱柱的体积，考查空间想象能力、运算能力和推理论证能力，属于中档题．22．（2014•江苏）如图，在三棱锥P﹣ABC中，D，E，F分别为棱PC，AC，AB的中点，已知PA⊥AC，PA=6，BC=8，DF=5．求证：（1）直线PA∥平面DEF；（2）平面BDE⊥平面ABC．考点：平面与平面垂直的判定；直线与平面垂直的判定．专题：证明题；空间位置关系与距离．分析：（1）由D、E为PC、AC的中点，得出DE∥PA，从而得出PA∥平面DEF；（2）要证平面BDE⊥平面ABC，只需证DE⊥平面ABC，即证DE⊥EF，且DE⊥AC即可．解答：证明：（1）∵D、E为PC、AC的中点，∴DE∥PA，又∵PA⊄平面DEF，DE⊂平面DEF，∴PA∥平面DEF；（2）∵D、E为PC、AC的中点，∴DE=PA=3；又∵E、F为AC、AB的中点，∴EF=BC=4；∴DE2+EF2=DF2，∴∠DEF=90°，∴DE⊥EF；∵DE∥PA，PA⊥AC，∴DE⊥AC；∵AC∩EF=E，∴DE⊥平面ABC；∵DE⊂平面BDE，∴平面BDE⊥平面ABC．点评：本题考查了空间中的平行与垂直问题，解题时应明确空间中的线线、线面、面面之间的垂直与平行的互相转化关系，是基础题目．23．（2014•北京）如图，在三棱柱ABC﹣A1B1C1中，侧棱垂直于底面，AB⊥BC，AA1=AC=2，BC=1，E，F分别是A1C1，BC的中点．。

直线、平面垂直的判定与性质【考纲说明】1、能够认识和理解空间中线面垂直的有关性质和判定定理。

2、能够运用公理、定理和已获得的结论证明一些空间图形的位置关系的简单命题。

【知识梳理】一、直线与平面垂直的判定与性质 1、直线与平面垂直（1）定义：如果直线l 与平面α内的任意一条直线都垂直，我们就说直线l 与平面α互相垂直，记作l ⊥α，直线l 叫做平面α的垂线，平面α叫做直线l 的垂面。

如图，直线与平面垂直时,它们唯一公共点P 叫做垂足。

（2）判定定理：一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直。

结论：如果两条平行直线中的一条垂直于一个平面，那么另一条也垂直于这个平面，记作.//a b b a αα⎫⇒⊥⎬⊥⎭（3）性质定理：垂直于同一个平面的两条直线平行。

即,//a b a b αα⊥⊥⇒.由定义知：直线垂直于平面内的任意直线。

2、直线与平面所成的角平面的一条斜线和它在平面上的射影所成的锐角叫做这条直线和这个平面所成的角。

一条直线垂直于平面，该直线与平面所成的角是直角；一条直线和平面平行，或在平面内，则此直线与平面所成的角是00的角。

3、二面角的平面角从一条直线出发的两个半平面所组成的图形叫做二面角，这条直线叫做二面角的棱，这两个半平面叫做二面角的面。

如果记棱为l ，那么两个面分别为αβ、的二面角记作l αβ--.在二面角的棱上任取一点，以该点为垂足，在两个半平面内分别作垂直于棱的射线，则两射线所构成的角叫做叫做二面角的平面角。

其作用是衡量二面角的大小；范围：000180θ<<.二、平面与平面垂直的判定与性质1、定义：一般地，两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面垂直.2、判定：一个平面过另一个平面的垂线，则这两个平面垂直。

简述为“线面垂直，则面面垂直”，记作l l βαβα⊥⎫⇒⊥⎬⊂⎭.3、性质：两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直，记作l m m m lαβαββα⊥⎫⎪=⎪⇒⊥⎬⊂⎪⎪⊥⎭I .【经典例题】【例1】（2012浙江文）设l 是直线,a,β是两个不同的平面 （ ） A ．若l ∥a,l ∥β,则a∥β B ．若l ∥a,l ⊥β,则a⊥β C ．若a⊥β,l ⊥a,则l ⊥β D ．若a⊥β,l ∥a,则l ⊥β 【答案】B【解析】利用排除法可得选项B 是正确的,∵l ∥a,l ⊥β,则a⊥β.如选项A:l ∥a,l ∥β时,a⊥β或a∥β;选项C:若a⊥β,l ⊥a,l ∥β或l β⊂;选项D:若若a⊥β,l ⊥a,l ∥β或l ⊥β.【例2】（2012四川文）下列命题正确的是 （ ）A ．若两条直线和同一个平面所成的角相等,则这两条直线平行B ．若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行C ．若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D ．若两个平面都垂直于第三个平面,则这两个平面平行 【答案】C【解析】若两条直线和同一平面所成角相等,这两条直线可能平行,也可能为异面直线,也可能相交,所以A 错;一个平面不在同一条直线的三点到另一个平面的距离相等,则这两个平面平行,故B 错;若两个平面垂直同一个平面两平面可以平行,也可以垂直;故D 错;故选项C 正确.【例3】（2012山东）已知直线m 、n 及平面α，其中m∥n ，那么在平面α内到两条直线m 、n 距离相等的点的集合可能是：①一条直线；②一个平面；③一个点；④空集．其中正确的是（ ）A ．①②③B ．①④C ．①②④D ．②④ 【答案】C【解析】如图1，当直线m 或直线n 在平面α内时有可能没有符合题意的点；如图2，直线m 、n 到已知平面α的距离相等且所在平面与已知平面α垂直，则已知平面α为符合题意的点；如图3，直线m 、n 所在平面与已知平面α平行，则符合题意的点为一条直线，从而选C.【例4】（2012四川理）如图，在正方体1111ABCD A B C D -中，M 、N 分别是CD 、1CC 的中点，则异面直线1A M 与DN 所成的角的大小是____________.【答案】90o【解析】方法一:连接D 1M,易得DN⊥A 1D 1,DN⊥D 1M,所以,DN⊥平面A 1MD 1,又A 1M ⊂平面A 1MD 1,所以,DN⊥A 1D 1,故夹角为90o方法二:以D 为原点,分别以DA,DC,DD 1为x,y,z 轴,建立空间直角坐标系D —xyz.设正方体边长为2,则D(0,0,0),N(0,2,1),M(0,1,0)A 1(2,0,2)故,），（），（2,121,2,01-== N MB 1A 1C 1D 1BD C所以,cos<|MA ||DN |111MA DN MA DN •=〉〈，=0,故DN⊥D 1M,所以夹角为90o【例5】（2012大纲理）三棱柱111ABC A B C -中,底面边长和侧棱长都相等,1160BAA CAA ∠=∠=︒,则异面直线1AB 与1BC 所成角的余弦值为_____________. 【答案】66【解析】设该三棱柱的边长为1,依题意有1111,AB AB AA BC AC AA AB =+=+-u u u r u u u r u u u r u u u u r u u u r u u u r u u u r,则22221111||()222cos603AB AB AA AB AB AA AA =+=+⋅+=+︒=u u u r u u u r u u u r u u u r u u u r u u u r u u u r而1111()()AB BC AB AA AC AA AB ⋅=+⋅+-u u u r u u u u r u u u r u u u r u u u r u u u r u u u r【例6】（2011·福建）如图，正方体ABCD －A 1B 1C 1D 1中，AB ＝2，点E 为AD 的中点，点F 在CD 上，若EF∥平面AB 1C ，则线段EF 的长度等于________． 【答案】【解析】∵EF∥面AB 1C ，∴EF∥AC .又E 是AD 的中点，∴F 是DC 的中点． ∴EF ＝AC ＝.【例7】（2012年山东文）如图,几何体E ABCD -是四棱锥,△ABD 为正三角形,,CB CD EC BD =⊥. （1）求证:BE DE =;（2）若∠120BCD =︒,M 为线段AE 的中点, 求证:DM ∥平面BEC .【解析】（1）设BD 中点为O ,连接OC ,OE ,则由BC CD =知CO BD ⊥,又已知CE BD ⊥,所以BD ⊥平面OCE .所以BD OE ⊥,即OE 是BD 的垂直平分线,所以BE DE =.（2）取AB 中点N ,连接,MN DN ,∵M 是AE 的中点,∴MN ∥BE , ∵△ABD 是等边三角形,∴DN AB ⊥.由∠BCD =120°知,∠CBD =30°, 所以∠ABC =60°+30°=90°,即BC AB ⊥,所以ND ∥BC ,所以平面MND ∥平面BEC ,又DM ⊂平面MND ,故DM ∥平面BEC . 另证:延长BC AD ,相交于点F ,连接EF.因为CB=CD,090=∠ABC . 因为△ABD 为正三角形,所以0090,60=∠=∠ABC BAD ,则030=∠AFB ,所以AF AB 21=,又AD AB =, 所以D 是线段AF 的中点,连接DM,又由点M 是线段AE 的中点知EF DM //,而⊄DM 平面BEC ,⊂EF 平面BEC ,故DM ∥平面BEC .【例8】（2011天津）如图，在四棱锥P －ABCD 中，底面ABCD 为平行四边形∠ADC ＝45°，AD ＝AC ＝1，O 为AC 的中点，PO ⊥平面ABCD ，PO ＝2，M 为PD 的中点． （1）证明：PB∥平面ACM ； （2）证明：AD ⊥平面PAC ；（3）求直线AM 与平面ABCD 所成角的正切值． 【解析】（1）证明：连接BD ，MO ，在平行四边形ABCD 中，因为O 为AC 的中点，所以O 为BD 的中点．又M 为PD 的中点，所以PB∥MO .因为PB ?平面ACM ，MO ?平面ACM ，所以PB∥平面ACM .（2）证明：因为∠ADC ＝45°，且AD ＝AC ＝1，所以∠DAC ＝90°，即AD ⊥AC ，又PO ⊥平面ABCD ，AD ?平面ABCD ，所以PO ⊥AD .而AC ∩PO ＝O ，所以AD ⊥平面PAC . （3）取DO 中点N ，连接MN ，AN .因为M 为PD 的中点，所以MN∥PO ，且MN ＝PO ＝1.由PO ⊥平面ABCD ，得MN ⊥平面ABCD ，所以∠MAN 是直线AM 与平面ABCD 所成的角，在Rt△DAO 中，AD ＝1，AO ＝，所以DO ＝，从而AN ＝DO ＝.在Rt△ANM 中，tan∠MAN ＝＝＝，即直线AM 与平面ABCD 所成角的正切值为.【例9】（2012湖南文）如图，在四棱锥P-ABCD 中,PA⊥平面ABCD,底面ABCD 是等腰梯形,AD∥BC,AC⊥BD. （1）证明:BD⊥PC;（2）若AD=4,BC=2,直线PD 与平面PAC 所成的角为30°,求四棱锥P-ABCD 的体积. 【解析】（1）因为,,.PA ABCD BD ABCD PA BD ⊥⊂⊥平面平面所以又,,AC BD PA AC ⊥是平面PAC 内的两条相较直线,所以BD ⊥平面PAC, 而PC ⊂平面PAC,所以BD PC ⊥.（2）设AC 和BD 相交于点O,连接PO,由(Ⅰ)知,BD ⊥平面PAC, 所以DPO ∠是直线PD 和平面PAC 所成的角,从而DPO ∠30=o . 由BD ⊥平面PAC,PO ⊂平面PAC,知BD PO ⊥. 在Rt POD V 中,由DPO ∠30=o ,得PD=2OD.因为四边形ABCD 为等腰梯形,AC BD ⊥,所以,AOD BOC V V 均为等腰直角三角形, 从而梯形ABCD 的高为111(42)3,222AD BC +=⨯+=于是梯形ABCD 面积 在等腰三角形AOD 中,2,22,2OD AD == 所以22242, 4.PD OD PA PD AD ===-=故四棱锥P ABCD -的体积为11941233V S PA =⨯⨯=⨯⨯=.【例10】（2012新课标理）如图,直三棱柱111ABC A B C -中,112AC BC AA ==,D 是棱1AA 的中点,BD DC ⊥1 （1）证明:BC DC ⊥1（2）求二面角11C BD A --的大小.【解析】（1）在Rt DAC ∆中,AD AC =得:45ADC ︒∠=同理:1114590A DC CDC ︒︒∠=⇒∠=得:111,DC DC DC BD DC ⊥⊥⇒⊥面1BCD DC BC ⇒⊥ （2）11,DC BC CC BC BC ⊥⊥⇒⊥面11ACC A BC AC ⇒⊥ 取11A B 的中点O ,过点O 作OH BD ⊥于点H ,连接11,C O C H1111111AC B C C O A B =⇒⊥,面111A B C ⊥面1A BD 1C O ⇒⊥面1A BD 1OH BD C H BD ⊥⇒⊥得:点H 与点D 重合且1C DO ∠是二面角11C BD A --的平面角设AC a =,则12C O =,111230C D C O C DO ︒==⇒∠= 既二面角11C BD A --的大小为30︒【课堂练习】．（2012浙江理）已知矩形ABCD ,AB =1,BC将∆ABD 沿矩形的对角线BD 所在的直线进行翻着，在翻着过程中（ ）A ．存在某个位置,使得直线AC 与直线BD 垂直B ．存在某个位置,使得直线AB 与直线CD 垂直C ．存在某个位置,使得直线AD 与直线BC 垂直D ．对任意位置,三直线“AC 与BD ”,“AB 与CD ”,“AD 与BC ”均不垂直 ．（2012四川理）下列命题正确的是 （ ）A ．若两条直线和同一个平面所成的角相等,则这两条直线平行B ．若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行C ．若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D ．若两个平面都垂直于第三个平面,则这两个平面平行3．（2011重庆）到两互相垂直的异面直线的距离相等的点( )A ．只有1个B ．恰有3个C ．恰有4个D ．有无穷多个4．（2012上海）已知空间三条直线l ，m ，n 若l 与m 异面,且l 与n 异面,则 （ ） A ．m 与n 异面. B ．m 与n 相交. C ．m 与n 平行. D ．m 与n 异面、相交、平行均有可能. 5．（2011烟台）已知m ，n 是两条不同的直线，α，β为两个不同的平面，有下列四个命题：①若m ⊥α，n ⊥β，m ⊥n ，则α⊥β；②若m∥α，n∥β，m ⊥n ，则α∥β；③若m ⊥α，n∥β，m ⊥n ，α•AB•β则α∥β；④若m ⊥α，n∥β，α∥β，则m ⊥n . 其中正确命题的个数为( ) A ．1 B ．2 C ．3 D ．4 6．（2011潍坊）已知m 、n 是两条不同的直线，α、β、γ是三个不同的平面，则下列命题正确的是( )A ．若α⊥γ，α⊥β，则γ∥βB ．若m∥n ，m ?α，n ?β，则α∥βC ．若m∥n ，m∥α，则n∥αD ．若n ⊥α，n ⊥β，则α∥β7.（2010全国卷文）直三棱柱111ABC A B C -中，若90BAC ∠=︒，1AB AC AA ==，则异面直线1BA 与1AC 所成的角等于（）A ．30°B．45°C．60°D．90°8.（2010全国卷）正方体ABCD-1111A B C D 中，B 1B 与平面AC1D 所成角的余弦值为（）AB．23D 9.（2010全国Ⅱ卷理）已知正四棱锥S ABCD -中，SA =，那么当该棱锥的体积最大时，它的高为（）A ．1B ．2D ．310.（2010全国Ⅰ卷）已知在半径为2的球面上有A ．B ．C ．D 四点，若AB=CD=2，则四面体ABCD 的体积的最大值为（）ABC．11.（2010江西理）过正方体1111ABCD A B C D -的顶点A 作直线L ，使L 与棱AB ，AD ，1AA 所成的角都相等，这样的直线L 可以作（） A ．1条B ．2条C ．3条D ．4条12.（2012大纲）已知正方形1111ABCD A B C D -中,,E F 分别为1BB ,1CC 的中点,那么异面直线AE 与1D F 所成角的余弦值为____.13.（2010上海文）已知四棱椎P ABCD -的底面是边长为6的正方形，侧棱PA ⊥底面ABCD ，且8PA =，则该四棱椎的体积是.14.（2010四川卷）如图，二面角l αβ--的大小是60°，线段AB α⊂.B l ∈，AB 与l 所成的角为30°.则AB 与平面β所成的角的正弦值是.15.（江西卷文）长方体1111ABCD A B C D -的顶点均在同一个球面上，11AB AA ==，2BC =，则A ，B 两点间的球面距离为16.（2010湖南理）如图所示，在正方体ABCD －A 1B 1C 1D 1中，E 是棱DD 1的中点。

线面面面垂直的判定和性质练习线面面面垂直的判定和性质练习线面&period;面面垂直的判定和性质练习低一班姓名：线、面间横向的认定与性质应用领域21.如图长方体中，ab ad23,cc12.例如图，四棱锥p—abcd的底面就是ab=2，bc=2的矩形，侧面pab就是等边三角形，且侧面pab⊥底面abcd。

（1）证明侧面pab⊥侧面pbc；（2）谋两端棱pc与底面abcd阿芒塔的角。

2，求二面角c1—bd—c的大小。

平面a1bc1；3.例如图，棱柱abc-a1b1c1的侧面bcc1b1就是菱形，b1c a1b。

证明：平面abc14.已知s是△abc所在平面外一点，sa⊥平面abc,平面sab⊥平面sbc,求证ab⊥bc。

5.例如图，在四棱锥p－abcd中，pa⊥底面abcd，ab⊥ad，ac⊥cd是pc的中点。

(1)求证：cd⊥ae；(2)求证：pd⊥面abe。

6.例如图，dc平面abc，eb//dc，ac bc eb2dc2，acb120，p,q分别为ae,ab的中点．（1）证明：pq//平面acd；（2）谋ad与平面abe所成角的正弦值。

高一班姓名：线、面间垂直的判定与性质应用11、未知a,b就是直线，,就是平面，以下观点恰当的就是（）a、,b，则bb、b，则b垂直于内的任意一条直线c、b垂直于内的无数条直线，则bd、b，则b与所成的角可以是锐角。

2、如图，四棱锥s-abcd的底面为正方形，sd⊥底面abcd,且sd=da=1，下列结论中错误的是()．．(a)sa与平面sbd阿芒塔的角等同于sc与平面sbd阿芒塔的角(b)ab与sc阿芒塔的角等同于dc与sa阿芒塔的角(c)ac⊥sb(d)ab∥平面scd3、例如图，空间四边形中，pb=pa，cb=ca，则pc与ab的关系就是_________________4、如图，在正方体abcd-a1b1c1d1中，直线a1b与平面a1b1cd阿芒塔的角为_________。

线面垂直的判定及其性质第1题. 已知直线a ，b 和平面α，且a b ⊥，a α⊥，则b 与α的位置关系是 ．答案：b α//或b α⊂．第2题. 已知两个平面垂直，下列命题①一个平面内已知直线必垂直于另一个平面内的任意一条直线． ②一个平面内的已知直线必垂直于另一个平面的无数条直线． ③一个平面内的任一条直线必垂直于另一个平面．④过一个平面内任意一点作交线的垂线，则此垂线必垂直于另一个平面．其中正确的个数是（ ） A ．３ Ｂ．２ Ｃ．１ Ｄ．０答案：Ｂ．第3题. 已知平面α，β，γ且αγ⊥，βγ//，求证αβ⊥．答案：证明：设l αγ=I ，在平面α内作直线a l ⊥． 因为αγ⊥，所以a γ⊥．过a 作一个平面δ与平面β相交于直线b ， 由αβ//，得a b //．又b β⊂，所以βγ⊥．因为a γ⊥，所以b γ⊥．第4题. 已知平面α，β，γ满足αγ⊥，βγ⊥，l αβ=I ，求证：l γ⊥．答案：在平面γ内做两条相交直线分别垂直于平面α，β与平面γ的交线，再利用面面垂直的性质定理证直线l γ⊥平面．第5题. 如图，已知平面α，β，直线a 满足αβ⊥，a β⊥，a α⊄，试判断直线a 与平面α的位置关系．答案：解：在α内作垂直于α与β交线的直线b ，因为αβ⊥，所以b β⊥． 因为a β⊥，所以a b //．又因为a α⊄，所以a α//．即直线a 与平面α平行．第6题. 如图所示，ABCD 为正方形，SA ⊥平面ABCD ，过A 且垂直于SC 的平面分别交SB ，SC ，SD 于E ，F ，G ． 求证：AE SB AG SD ⊥⊥，．αβbaS A B C FE D G答案：证明：∵SA ⊥平面ABCD ，SA BC ⊥∴． 又AB BC ⊥，∴BC SAB ⊥平面． AE SAB ⊂平面∵，BC AE ⊥∴，SC AEFG ⊥平面∵，SC AE AE SBC ⊥⊥平面，∴，AE SB ⊥∴． 同理AG SD ⊥．第7题. 已知直线l α⊥平面，有以下几个判断：①若m l ⊥，则m α//；②若m α⊥，则m l //；③若m α//，则m l ⊥；④若m l //，则m α⊥．上述判断中正确的是（ ） Ａ．①②③ Ｂ．②③④Ｃ．①③④Ｄ．①②④答案：Ｂ．第8题. αβ，是两个不同的平面，m n ，是平面α及β之外的两条不同的直线，给出四个论断：m n ⊥①；αβ⊥②；n β⊥③；m α⊥④．以其中三个论断作为条件，余下的一个论断作为结论，写出你认为正确的一个命题 ．答案：⇒⇒或②③④①①③④②．第9题. 如图所示，四棱锥P ABCD -的底面是正方形，PA ⊥底面ABCD ，AE PD ⊥，EF CD //，AM EF =．求证：MF 是异面直线AB 与PC 的公垂线． 答案：证明：PA ⊥∵底面，PA AB ⊥∴．已知AB AD ⊥，AB ⊥∴面PAD ．BA AE ⊥∴． 又AM CD EF ////，且AM EF =． AEFM ∴是矩形，AM MF ⊥∴．又AE PD ⊥∵，AE CD ⊥，AE ⊥∴平面PCD ． 又MF AE //，MF ⊥∴平面PCD ． MF PC ⊥∴．∴MF 是异面直线AB 与PC 的公垂线．BA PEFCDM第10题. 设O 为平行四边形ABCD 对角线的交点，P 为平面AC 外一点且有PA PC =，PB PD =，则PO 与平面ABCD 的关系是 ．答案：垂直第11题. 如图，直角ABC △所在平面外一点S ，且SA SB SC ==，点D 为斜边AC 的中点．（１） 求证：SD ⊥平面ABC ；（２） 若AB BC =，求证：BD ⊥面SAC ．答案：证明：（１）SA SC =∵，D 为AC 的中点，SD AC ⊥∴． 连结BD ．在ABC Rt △中，则AD DC BD ==． ADS BDS ∴△≌△，SD BD ⊥∴． 又AC BD D =I ，SD ⊥∴面ABC ．（２）BA BC =∵，D 为AC 的中点， BD AC ⊥∴．又由（１）知SD ⊥面ABC ， SD BD ⊥∴． 于是BD 垂直于平面SAC 内的两条相交直线． ∴BD ⊥面SAC ．第12题. 在三棱锥P ABC -中，侧面PAC 与面ABC 垂直，3PA PB PC ===． （１） 求证：AB BC ⊥；（２） 设23AB BC ==，求AC 与平面PBC 所成角的大小． 答案：证明：如图（１）所示，取AC 中点D ，连结BD ，PD ． PA PC =∵，PD AC ⊥∴．又平面PAC ⊥平面ABC ，PD ⊥∴面ABC ．ASCBDPA PB PC ==∵，DA DB DC ==∴． 可知 AC 为ABC △的外接圆直径． ∴AB BC ⊥．（２）解：如图（２），作CF PB ⊥于F ，连结AF ，DF ． PBC PBA ∵△≌△，AF PB ⊥∴，AF CF =． PB ⊥∴平面AFC ．∴面AFC ⊥面PBC ，交线为CF ．∴直线AC 在平面PBC 内的射影为直线CF ． ∴ACF ∠为AC 与平面PBC 所成的角．在ABC Rt △中，23AB BC ==，6BD =∴． 在PDC Rt △中，6DC =，3PD =．在PDB Rt △中，3623PD DB DF PB ⨯===g ． 在FDC Rt △中，23tan 36DF DCF DC ∠===． 30ACF ∠=∴þ．即AC 与平面PBC 所成角为30þ．AP D C B 图（１）APDCBF图（２）第13题. 在正方形ABCD 中，E ，F 分别是AB 及BC 的中点，M 是EF 的中点，沿DE ，DF 及EF 把DAE △，DFC △，EBF △折起使A ，B ，C 三点重合，重合后的点记作P ，那么在四面体P DEF -中必有（ ） Ａ．DP ⊥面PEF Ｂ．DM ⊥面PEF Ｃ．PM ⊥面DEF Ｄ．PF ⊥面DEF答案：Ａ．第14题. 直线a 不垂直于平面α，则α内与a 垂直的直线有（ ） Ａ．0条 Ｂ．1条 Ｃ．无数条Ｄ．α内所有直线答案：Ｃ．第15题. 已知三条直线m ，n ，l ，三个平面α，β，γ．下面四个命题中，正确的是（ ）Ａ．αγαββγ⊥⎫⇒⎬⊥⎭// Ｂ．m l l m ββ⎫⇒⊥⎬⊥⎭// Ｃ．m m n n γγ⎫⇒⎬⎭////// Ｄ．m m n n γγ⊥⎫⇒⎬⊥⎭//答案：Ｄ．第16题. 在空间四边形ABCD 中，若AB BC =，AD CD =，E 为对角线AC 的中点，下列判断正确的是（ ） Ａ．平面ABD ⊥平面BDC Ｂ．平面ABC ⊥平面ABD Ｃ．平面ABC ⊥平面ADC Ｄ．平面ABC ⊥平面BED答案：Ｄ．第17题. α，β，γ，ω是四个不同平面，若αγ⊥，βγ⊥，αω⊥，βω⊥，则（ ） Ａ．αβ//且γω//Ｂ．αβ//或γω//Ｃ．这四个平面中可能任意两个都不平行 Ｄ．这四个平面中至多有一对平面平行答案：Ｂ．第18题. 设a ，b 是异面直线，下列命题正确的是（ ）Ａ．过不在a ，b 上的一点P 一定可以作一条直线和a ，b 都相交 Ｂ．过不在a ，b 上的一点P 一定可以作一个平面和a ，b 垂直 Ｃ．过a 一定可以作一个平面与b 垂直 Ｄ．过a 一定可以作一个平面与b 平行答案：Ｄ．第19题. 已知a ，b 是异面直线，a α⊥，b β⊥，c αβ=I ，AB 是a ，b 的公垂线，求证：AB c //．答案：证明：过A 作b β⊥'，则b b '//．AB b ⊥∵，AB b ⊥∴'．又AB a ⊥∵，a b A =I '，设a ，b '确定平面γ，AB γ⊥∴． 又a α⊥，c α⊂，a c ⊥∴．同理b c ⊥'．c γ⊥∴．AB c ∴//．αacAB bβ 'b第20题. 下面四个命题：① 若直线a //平面α，则α内任何直线都与a 平行； ② 若直线a ⊥平面α，则α内任何直线都与a 垂直； ③ 若平面α//平面β，则β内任何直线都与α平行； ④ 若平面α⊥平面β，则β内任何直线都与α垂直． 其中正确的两个命题是（ ） Ａ．①与② Ｂ．②与③ Ｃ．③与④ Ｄ．②与④答案：Ｂ．第21题. 设平面α⊥平面β，且l αβ=I ，直线a α⊂，直线b β⊂，且a 不与l 垂直，b 不与l 垂直，那么a 与b （ ）Ａ．可能垂直，不可能平行 Ｂ．可能平行，不可能垂直 Ｃ．可能垂直，也可能平行 Ｄ．不可能垂直，也不能垂直答案：Ｂ．第22题. 已知：如图所示，平面α⊥平面β，l αβ=I ，在l 上取线段4AB =，AC ， BD 分别在平面α和平面β内，且AC AB ⊥，DB AB ⊥，3AC =，12BD =，求CD 长．答案：解：连结BC ．AC AB ⊥∵，AC β⊥∴，AC BD ⊥．βA CBDαlBD AB ⊥∵，BD α⊥∴，BD BC ⊥．CBD ∴△是直角三角形．在BAC Rt △中，22BC AC AB =+22345=+=，在CBD Rt △中，2251213CD =+=．CD ∴长为13．第23题. 在正三棱柱111ABC A B C -中，若11AB BC ⊥．求证：11AB A C ⊥．答案：证明：取AB 中点D ，11A B 中点1D ，连结1A D ，1BD ，CD ，11C D ，由正三棱柱性质知，CD AB ⊥，1111C D A B ⊥．又正三棱柱侧面与底面垂直，CD ⊥∴面11ABB A ，11C D ⊥面11ABB A ，1A D ∴，1BD 分别为1A C 与1BC 在面1ABB A 上的射影． 11AB BC ⊥∵，11AB BD ⊥∴．又11A D ∥ BD ，11A D BD ∴//．11A D AB ⊥∴． ∴11AB AC ⊥．βACB Dαl第24题. 设三棱锥P ABC -的顶点P 在底面ABC 内射影O （在ABC △内部，即过P 作PO ⊥底面ABC ，交于O ），且到三个侧面的距离相等，则O 是ABC △的（ ） Ａ．外心 Ｂ．垂心 Ｃ．内心 Ｄ．重心答案：Ｃ．第25题. 如图所示，AB 是圆O 的直径，C 是异于A ，B 两点的圆周上的任意一点，PA 垂直于圆O 所在的平面，则PAB △，PAC △，ABC △，PBC △中，直角三角形的个数是（ ）Ａ．1 Ｂ．2 Ｃ．3 Ｄ．4答案：Ｄ．第26题. 已知直线a ，b 和平面α，有以下四个命题：1C1A A1D1BCBDOP A BC① 若a α//，a b //，则b α//；② 若a α⊂，b A α=I ，则a 与b 异面； ③ 若a b //，b α⊥，则a α⊥； ④ 若a b ⊥，a α⊥，则b α//． 其中真命题的个数是（ ）Ａ．0 Ｂ．1 Ｃ．2 Ｄ．3答案：Ｂ．。

线面垂直的判定和性质定理（习题课）A组 1 C 2 B 3 D 4 D 5 C 6 ③ 7 ①② 8a或2a9 (2) d＝105. 10 (2) V＝ 3 (3)64B组 1 D 2 ①②③ 3 (2)433(3)32A组基础训练一、选择题1．已知平面α与平面β相交，直线m⊥α，则()A．β内必存在直线与m平行，且存在直线与m垂直B．β内不一定存在直线与m平行，不一定存在直线与m垂直C．β内不一定存在直线与m平行，但必存在直线与m垂直D．β内必存在直线与m平行，不一定存在直线与m垂直【解析】如图，在平面β内的直线若与α，β的交线a平行，则有m与之垂直．但却不一定在β内有与m平行的直线，只有当α⊥β时才存在．【答案】 C2．已知两个平面垂直，下列命题：①一个平面内已知直线必垂直于另一个平面内的任意一条直线．②一个平面内的已知直线必垂直于另一个平面的无数条直线．③一个平面内的任一条直线必垂直于另一个平面．④过一个平面内任意一点作交线的垂线，则此垂线必垂直于另一个平面．其中正确命题的个数是()A．3B．2C．1D．0【解析】根据面面垂直的性质定理知，命题④正确；两平面垂直，一个平面内的已知直线必垂直于另一个平面内与交线垂直的直线，故命题②正确，命题①③错误．【答案】 B3．(2013·广东高考)设m，n是两条不同的直线，α，β是两个不同的平面，下列命题中正确的是()A．若α⊥β，m⊂α，n⊂β，则m⊥nB．若α∥β，m⊂α，n⊂β，则m∥nC．若m⊥n，m⊂α，n⊂β，则α⊥βD．若m⊥α，m∥n，n∥β，则α⊥β【解析】如图，在长方体ABCD－A1B1C1D1中，平面BCC1B1⊥平面ABCD，BC1⊂平面BCC1B1，BC⊂平面ABCD，而BC1不垂直于BC，故A错误．平面A1B1C1D1∥平面ABCD，B1D1⊂平面A1B1C1D1，AC⊂平面ABCD，但B1D1和AC不平行，故B错误．AB⊥A1D1，AB⊂平面ABCD，A1D1⊂平面A1B1C1D1，但平面A1B1C1D1∥平面ABCD，故C错误．故选D.【答案】 D图7－5－104．(2014·大连模拟)如图7－5－10，四棱锥S－ABCD的底面为正方形，S D ⊥底面ABCD，则下列结论中不正确的是()A．AC⊥SBB．AB∥平面SCDC．SA与平面SBD所成的角等于S C与平面SBD所成的角D．AB与S C所成的角等于DC与SA所成的角【解析】∵四边形ABCD是正方形，∴AC⊥BD.又∵S D⊥底面ABCD，∴S D⊥AC.其中S D∩BD＝D，∴AC⊥面SDB，从而AC⊥S B.故A正确；易知B正确；设AC与DB交于O点，连结SO.则SA与平面SBD所成的角为∠ASO，S C与平面SBD所成的角为∠C SO，又OA＝OC，SA＝S C，∴∠ASO＝∠C SO.故C正确；由排除法可知选D.【答案】 D5．(2014·郑州模拟)设m，n是不同的直线，α，β是不同的平面，下列命题中正确的是()A．若m∥α，n⊥β，m⊥n，则α⊥βB．若m∥α，n⊥β，m⊥n，则α∥βC．若m∥α，n⊥β，m∥n，则α⊥βD．若m∥α，n⊥β，m∥n，则α∥β【解析】C中，当m∥α，m∥n时，有n∥α或n⊂α，当n⊥β时，有α⊥β，故C正确．【答案】 C二、填空题图7－5－116．如图7－5－11，在三棱锥D－ABC中，若AB＝CB，AD＝CD，E是AC 的中点，则下列命题中正确的有________(填序号)．①平面ABC⊥平面ABD；②平面ABD⊥平面BCD；③平面ABC⊥平面BDE，且平面ACD⊥平面BDE；④平面ABC⊥平面ACD，且平面ACD⊥平面BDE.【解析】由AB＝CB，AD＝CD知AC⊥DE，AC⊥BE，从而AC⊥平面BDE，故③正确．【答案】③图7－5－127．如图7－5－12，在直角梯形ABCD中，BC⊥DC，AE⊥DC，M，N分别是AD，BE的中点，将三角形ADE沿AE折起，下列说法正确的是________(填上所有正确的序号)．①不论D折至何位置(不在平面ABC内)都有MN∥平面DE C；②不论D折至何位置都有MN⊥AE；③不论D折至何位置(不在平面ABC内)都有MN∥A B.【解析】取AE的中点F，连接MF，N F，则MF∥DE，N F∥AB∥CE，从而平面MF N∥平面DE C，故MN∥平面DE C，①正确；又AE⊥MF，AE⊥N F，所以AE⊥平面MF N，从而AE⊥MN，②正确；又MN与AB是异面直线，则③错误．【答案】①②图7－5－138．如图7－5－13，在直三棱柱ABC－A1B1C1中，底面是∠ABC为直角的等腰直角三角形，AC＝2a，BB1＝3a，D是A1C1的中点，点F在线段AA1上，当AF＝________时，CF⊥平面B1DF.【解析】∵B1D⊥平面A1ACC1，∴CF⊥B1D，∴为了使CF⊥平面B1DF，只要使CF⊥DF(或CF⊥B1F)，设AF＝x，则CD2＝DF2＋F C2，∴x2－3ax＋2a2＝0，∴x＝a或x＝2a.【答案】a或2a三、解答题图7－5－149．(2013·江西高考)如图7－5－14，直四棱柱ABCD－A1B1C1D1中，AB∥CD，AD⊥AB，AB＝2，AD＝2，AA1＝3，E为CD上一点，DE＝1，E C＝3.(1)证明：BE⊥平面BB1C1C；(2)求点B1到平面EA1C1的距离．【解】(1)证明过点B作CD的垂线交CD于点F，则BF＝AD＝2，EF＝AB－DE＝1，F C＝2.在Rt△BFE中，BE＝ 3.在Rt△CFB中，BC＝ 6.在△BE C 中，因为BE 2＋BC 2＝9＝EC 2，故BE ⊥BC . 由BB 1⊥平面ABCD ，得BE ⊥BB 1， 所以BE ⊥平面BB 1C 1C.(2)连接B 1E ，则三棱锥E －A 1B 1C 1的体积V ＝13AA 1·S △A 1B 1C 1＝ 2.在Rt △A 1D 1C 1中，A 1C 1＝A 1D 21＋D 1C 21＝3 2. 同理，EC 1＝EC 2＋CC 21＝32， A 1E ＝A 1A 2＋AD 2＋DE 2＝23， 故S △A 1C 1E ＝3 5. 设点B 1到平面EA 1C 1的距离为d ， 则三棱锥B 1－EA 1C 1的体积V ＝13·d ·S △EA 1C 1＝5d ， 从而5d ＝2，d ＝105.图7－5－1510．(2014·青岛模拟)在如图7－5－15所示的多面体ABCDE 中，AB ⊥平面ACD，DE⊥平面ACD，且AC＝AD＝CD＝DE＝2，AB＝1.(1)请在线段CE上找到点F的位置，使得恰有直线BF∥平面ACD，并证明这一事实；(2)求多面体ABCDE的体积；(3)求直线E C与平面ABED所成角的正弦值．【解】(1)如图，由已知AB⊥平面ACD，DE⊥平面ACD，∴AB∥ED，设F为线段CE的中点，H是线段CD的中点，连接FH，则FH綊12ED，∴FH綊AB，∴四边形ABFH是平行四边形，∴BF∥AH，由BF⊄平面ACD内，AH⊂平面ACD，∴BF∥平面ACD；(2)取AD中点G，连接C G.AB⊥平面ACD，∴C G⊥AB又C G⊥AD，∴C G⊥平面ABED，即C G为四棱锥的高，C G ＝3，∴V C －ABED ＝13·（1＋2）2·2·3＝ 3. (3)连接EG ，由(2)有C G ⊥平面ABED ，∴∠CEG 即为直线CE 与平面ABED 所成的角．在Rt △CEG 中，sin ∠CEG ＝CG CE ＝322＝64. B 组 能力提升1．如图7－5－16所示，四边形ABCD 中，AD ∥BC ，AD ＝AB ，∠BCD ＝45°，∠BAD ＝90°.将△ADB 沿BD 折起，使平面ABD ⊥平面BCD ，构成三棱锥A —BCD .则在三棱锥A —BCD 中，下列命题正确的是( )图7－5－16A ．AD ⊥平面BCDB ．AB ⊥平面BCDC ．平面BCD ⊥平面ABC D ．平面ADC ⊥平面ABC【解析】 在四边形ABCD 中，AD ∥BC ，AD ＝AB ，∠BCD ＝45°，∠BAD ＝90°，∴BD ⊥CD ，又平面ABD ⊥平面BCD ，且平面ABD ∩平面BCD ＝BD ，∴CD⊥平面ABD，∴CD⊥AB，又AD⊥AB，故AB⊥平面ADC，从而平面ABC⊥平面ADC.【答案】 D图7－5－172．如图7－5－17所示，P A⊥圆O所在的平面，AB是圆O的直径，C是圆O上的一点，E、F分别是点A在PB、PC上的正投影，给出下列结论：①AF⊥PB；②EF⊥PB；③AF⊥BC；④AE⊥平面PBC.其中正确结论的序号是________．【解析】由题意知P A⊥平面ABC，∴P A⊥BC，又AC⊥BC，P A∩AC＝A，∴BC⊥平面P AC.∴BC⊥AF.∵AF⊥PC，BC∩PC＝C，∴AF⊥平面PBC，∴AF⊥PB，AF⊥BC.又AE⊥PB，AE∩AF＝A，∴PB⊥平面AEF.∴PB⊥EF.故①②③正确．【答案】①②③图7－5－183．(2013·浙江高考)如图7－5－18，在四棱锥P-ABCD中，P A⊥平面ABCD，AB＝BC＝2，AD＝CD＝7，P A＝3，∠ABC＝120°，G为线段PC上的点．(1)证明：BD⊥平面APC；(2)若G为PC的中点，求D G与平面APC所成的角的正切值；(3)若G满足PC⊥平面BG D，求PGGC的值．【解】(1)证明设点O为AC，BD的交点．由AB＝BC，AD＝CD，得BD是线段AC的中垂线，所以O为AC的中点，BD⊥AC.又因为P A ⊥平面ABCD ，BD ⊂平面ABCD ，所以P A ⊥BD .所以BD ⊥平面APC .(2)连接OG .由(1)可知，OD ⊥平面APC ，则D G 在平面APC 内的射影为OG ，所以∠OG D 是D G 与平面APC 所成的角．由题意得OG ＝12P A ＝32.在△ABC 中，AC ＝AB 2＋BC 2－2AB ·BC ·cos ∠ABC ＝4＋4－2×2×2×⎝ ⎛⎭⎪⎫－12＝23， 所以OC ＝12AC ＝ 3.在直角△OCD 中，OD ＝CD 2－OC 2＝7－3＝2. 在直角△OG D 中，tan ∠OG D ＝OD OG ＝433.所以D G 与平面APC 所成的角的正切值为433. (3)因为PC ⊥平面BG D ，OG ⊂平面BG D ，所以PC ⊥OG .在直角△P AC 中，PC ＝ P A 2＋AC 2＝3＋12＝15，所以G C ＝AC ·OC PC ＝23×315＝2155. 从而PG ＝3155，所以PG GC ＝32.。