谐振法测电感数据处理

并联
一、实验要求
设计一个能够测量电感参数的测量电路，该测量电路应具有如下功能
（1）电感L测量仪的量程范围如下：0.1mH—10mH
二、实验目的
培养电路设计能力
熟练掌握multisim仿真软件进行电路仿真和分析
培养对真实电路进行分析调试的能力
三、实验原理
如图所示为并联谐振法测电感的电路，其中C为标准电容，L为被测电感，Co为被测电感的分布电容。测量时，调节信号源频率，使电路谐振，即电压表指示最大，记下此时的信号源频率f，则
2
交流小信号分析最高点即为谐振点，读出f1=5.013kHz，则
=0.95uF
3
把Co代入L的表达式，即可得到被测电感的感量。
=1.061mH
六、实验步骤
1
按下图所示焊接电路
2
调节节信号发生器频率，使电路谐振，即示波器幅值最大，记下此时的信号源频率f
3
如图所示，不接标准电容C，调节信号源的频率，使电路自然谐振，即示波器幅值最大，记录此频率f1
由此可见，还需要测出分则
由上述两式可得
把Co代入L的表达式，即可得到被测电感的感量。
四、实验器材
信号发生器
示波器
电阻
电容若干或可变电容箱一只
待测电感
导线若干
五、实验仿真（以
1
交流小信号分析最高点即为谐振点，读出f=3.5kHz，则
4
5
将所得数据填入下表，改变标准电容C，多次测量去平均值
次数
数值
1
2
3
4
5
C
f
f1
C0
L
L平均值
七、误差分析
1.谐振频率测量不准确
2.实际电容值测量有误差

交流电路的谐振现象实验报告交流电路的谐振现象实验报告引言交流电路的谐振现象是电子学中的重要概念之一。

谐振是指当电路中的电感和电容元件达到特定的数值时，电路会发生共振现象，电流和电压的幅值会达到最大值。

本实验旨在通过搭建交流电路并观察其谐振现象，加深对谐振现象的理解。

实验材料和方法材料：电感线圈、电容器、电阻器、交流电源、示波器等。

方法：首先，我们按照实验要求搭建交流电路，将电感线圈、电容器和电阻器连接在一起，并接入交流电源。

然后，使用示波器测量电路中的电压和电流，并记录下来。

实验结果与分析在实验过程中，我们通过调节电感线圈和电容器的数值，观察到了电路的谐振现象。

当电感和电容的数值达到一定的比例时，电路中的电流和电压会达到最大值。

谐振频率的计算根据实验数据，我们可以计算出电路的谐振频率。

谐振频率的计算公式为：f=1/(2π√(LC))，其中f为谐振频率，L为电感的值，C为电容的值。

实验误差的分析在实验中，由于仪器的精度和实验条件的限制，可能会产生一定的误差。

例如，电感线圈和电容器的实际数值与标称数值可能存在一定的偏差，导致计算出的谐振频率与理论值有所差别。

谐振现象的应用谐振现象在电子学中有着广泛的应用。

例如，在无线通信中，天线的谐振频率与传输信号的频率相匹配，可以实现信号的传输和接收。

此外，谐振现象还应用于音响设备、电子滤波器等领域。

实验总结通过本次实验，我们深入了解了交流电路的谐振现象。

通过观察和测量实验数据，我们验证了谐振频率的计算公式，并分析了实验误差的来源。

谐振现象在电子学中有着重要的应用，对于我们理解和应用电路具有重要意义。

结语交流电路的谐振现象是电子学中的基础概念之一，通过本次实验，我们对谐振现象有了更深入的了解。

通过实验数据的分析和计算，我们验证了谐振频率的计算公式，并探讨了实验误差的来源。

谐振现象在电子学中有着广泛的应用，对于我们理解和应用电路具有重要意义。

通过本次实验，我们不仅提高了实验操作的能力，还加深了对交流电路谐振现象的理解。

RLC 串联谐振电路实验误差的分析及改进一、摘要：从RLC 串联谐振电路的方程分析出发，推导了电路在谐振状态下的谐振频率、品质因数和输入阻抗，并且基于Multisim仿真软件创建RLC 串联谐振电路，利用其虚拟仪表和仿真分析，分别用测量及仿真分析的方法验证它的理论根据。

其结果表明了仿真与理论分析的一致性，为仿真分析在电子电路设计中的运用提供了一种可行的研究方法。

二、关键词：RLC；串联；谐振电路；三、引言谐振现象是正弦稳态电路的一种特定的工作状态。

通常，谐振电路由电容、电感和电阻组成，按照其原件的连接形式可分为串联谐振电路、并联谐振电路和耦合谐振电路等。

由于谐振电路具有良好的选择性，在通信与电子技术中得到了广泛的应用。

比如，串联谐振时电感电压或电容电压大于激励电压的现象，在无线电通信技术领域获得了有效的应用，例如当无线电广播或电视接收机调谐在某个频率或频带上时，就可使该频率或频带内的信号特别增强，而把其他频率或频带内的信号滤去，这种性能即称为谐振电路的选择性。

所以研究串联谐振有重要的意义。

在含有电感L 、电容C 和电阻R 的串联谐振电路中，需要研究在不同频率正弦激励下响应随频率变化的情况，即频率特性。

Multisim 仿真软件可以实现原理图的捕获、电路分析、电路仿真、仿真仪器测试等方面的应用，其数量众多的元件数据库、标准化仿真仪器、直观界面、简洁明了的操作、强大的分析测试、可信的测试结果都为众多的电子工程设计人员提供了一种可靠的分析方法，同时也缩短了产品的研发时间。

四、正文（1）实验目的：1.加深对串联谐振电路条件及特性的理解。

2.掌握谐振频率的测量方法。

3.理解电路品质因数的物理意义和其测定方法。

4.测定RLC串联谐振电路的频率特性曲线。

(2)实验原理：RLC串联电路如图所示，改变电路参数L、C或电源频率时，都可能使电路发生谐振。

该电路的阻抗是电源角频率ω的函数：Z=R+j(ωL-1/ωC)当ωL-1/ωC=0时，电路中的电流与激励电压同相，电路处于谐振状态。

=1/2πfU=0.753/（2π ）=10nF
3、谐振法测量电容和电感：
=（T/2π）（T/2π） =1.103nF
4、电桥法测量电容：
+ =0.35+10=10.35nF
五、结论
实验表明，电容、电感作为在电路中起重要作用的电子元件，有多种方法可以达到测量目的，
测量结果与实际存在一定的误差，这是由于欧姆法有表前表后的测量误差问题。该方法同样适合测量电感。
图2
3、电容谐振法测量电路（图3）
谐振法测量电容和电感：如图3.操作过程如下：
1、连接电路，并设定L为已知值1mH
2、R1为阻尼电阻
3、启动仿真开关，合上开关J1再关闭，示波器上显示出LC阻尼振荡波形
利用公式测量电容为：
1、分压法测量电容和电感：电路如图1
正弦波信号源10V有效值，频率1kHz，Co为标准电容
Co和Cx所对应的Uo和Ux两个电压值不一定要相等，根据电容分压公式：
=
以上方法同样适合电感的测量。
图1
2、电容欧姆法测量电路（图2）
欧姆法测量电容和电感：电路如图2。R1起分压作用，要求不严格。
被测电容：
=1/2πfU
电容电阻电感的标法电容电感电感和电容的区别电容电感电路分析电感大小的测量电感与电容电容和电感电感测量电感怎么测量电感测量方法
、
电容、电感的测量仿真实验
一、实验题目：
电容、电感的测量仿真实验。
二、仿真电路：
（1）分压法原理电路
（2）欧姆法测量电路
（3）谐振法测量电路
（4）电桥法测量电路
三、仿真内容
1、分压法测电容、电感（图Hale Waihona Puke ）=（T/2π）（T/2π）

谐振法测介电常数原理
（最新版）
目录
1.谐振法测介电常数的基本原理
2.谐振法的测量设备和操作步骤
3.谐振法测介电常数的优缺点
4.实际应用案例
正文
一、谐振法测介电常数的基本原理
谐振法是一种广泛应用于测量介电常数的实验方法。

其基本原理是：通过改变电容器的电容量，使得电容器与电感器构成的谐振回路达到共振状态，进而计算出介电常数。

二、谐振法的测量设备和操作步骤
1.测量设备：主要包括电容器、电感器、信号发生器、示波器和数据处理系统。

2.操作步骤：
（1）将电容器与电感器连接成谐振回路；
（2）通过信号发生器向谐振回路施加一定频率的交流电压；
（3）观察示波器上的信号波形，找到谐振状态下的波形；
（4）根据谐振状态下的电容器和电感器的参数，计算出介电常数。

三、谐振法测介电常数的优缺点
1.优点：测量精度高、可靠性好、操作简便。

2.缺点：受温度、压力等因素影响较大，需要对环境条件进行严格控
制。

四、实际应用案例
谐振法测介电常数广泛应用于材料科学、电子元器件等领域。

例如，在研究新型陶瓷材料时，可通过谐振法测量其介电常数，以评估材料的性能。

综上所述，谐振法测介电常数具有原理清晰、操作简便、精度高等优点，是一种实用的测量方法。

最大，Z并两端电压有最大值。 R上电压UR与Z并上电压Uz并同相 在实验中可用适当的方法测出电路谐振时的频率 条件下，根据 可计算出电感 1
f0 = 2π LC
f 0 。在电容C已知的
1 (2πf 0 ) 2 C
L=
实验仪器
标准电容箱 待测电感（标准电感箱） 电阻箱 信号发生器 双踪示波器
实验要求
2 2 0
0
0
实验原理
2并联谐振
对图（b）所示的LC并联电路，可求得
Z= r 2 + (ωL) 2 (1 − ω 2 LC ) 2 + (ωCr ) 2
Z= L/C r 2 + (ωL − 1 2 ) ωC
接近谐振时，
ω 2 = ω02 =
当
1 LC,即
ω0 L =
1 ωC
时，Z并=L/rC，LC并联电路谐振。此时阻抗
（1）明确实验原理，拟定测量方案，画出实验电路图，作出数据 记录表。 （2）根据实验室提供的元器件，选择适当的测量参数。 （3）列出验步骤，进行测量与数据处理，得出实验结果。
(1)
利用幅值的四种方法 串联中1示波器并联到电感和电容一侧， 则当 时阻抗达最小示波器 1
ω0 L = ω0 C
峰值达最小时的频率是此时的谐振频率 2示波器并联到R两端，则当峰值达最大 时的频率为谐振频率 并联中 1示波器并联到电感和电容一侧，当示波 器上的峰值达最大时为谐振频率 2示波器并联到R两端时，峰值达最小时 为谐振频率
对上图的（a）所示的LC串联电路， 阻抗和相位关系可用矢量图表示如下 图（c） 由图可知
z = zr2 +(zL − zc )2 = r2 +(ωL− 1 2 ) ωC

基于C8051的谐振法测电容电感摘要：本系统以C8051F360单片机最小系统为核心，实现电容电感的自动测量与显示的功能。

输出信号是由AD9833产生频率范围为1Hz～1MHz可调的正弦波，输出信号通过AD637转换供单片机AD采样读取。

通过软件调节输出正弦波的频率，以达到自动测量的功能。

同时通过按键达到电容电感测量可切换。

电容测量范围为100pF～10000pF，电感的测量范围为100uH～10000uH，测量精度为±10%。

关键词：C8051F360；并联谐振；RMS；DDS1系统总体设计利用并联谐振法，基于DDS技术的高性能、高分辨率、高稳定度的信号源，能较好的解决频率稳定性的问题，通过合理的程序编写，能较好的解决测试时间长的问题，完全可以构成高性能RLC测量仪，故采用本方法。

系统总体原理框图如图（1）。

←→←→—→—→图1 系统总体结构2硬件电路设计2.1 DDS信号源采用AD9833产生正弦波，频率范围为1Hz～1MHz。

通过SPI串行接口与单片机相连，通过写28位频率字改变输出频率。

当外部参考时钟为25MHz时，输出信号可以达到小于0.1Hz的分辨率。

AD9833产生的信号通过两级放大，与电压跟随器，恒压输出到测试接口。

2.2 测试接口通过两个继电器的开合，使电路处于测电容状态和测电感状态，继电器的控制由单片机的一个I/O口控制。

当测量电容时，取2mH标准电感，电容的测量范围为100pF～10000pF，误差<10%。

当测量电感时，取313nF标准电容，电感的测量范围为100uH～10000uH，误差<10%。

2.3 AD637（RMS）AD637属于高准确度的单片真有效值/直流转换器。

输入电压有效值0～2V 时，最大非线性误差<0.02%。

它能计算任何复杂波形的有效值，并用分贝输出，量程为60dB，频带宽。

当输出信号有效值为1V时，其频率上限高达8MHz。

二、实验原理
1 RLC串联谐振电路：
RLC串联电路和向量计算如图(a)、(b)所示。
电路总阻抗
Z =
1 R + ωL − ωC
2
2
（1）
二、实验原理
电路电流
I = U = Z R U
2
（2）
2
1 + ωL − ωC
电流与信号源电压之间的相位差 ϕ = − arctan
ωL − 1 / ωC
R
（3）
对于所研究的电路，保持信号源输出电压幅度一定，以上各 参数都将随信号源频率ω的改变而变化。由式3不难看出，当信号源ห้องสมุดไป่ตู้的频ω满足 ωL =
1 条件时，电路总阻抗Z=R为最小值，而此时回路 ωC R
电流为最大值 I max = U ，相位差φ=0，即称电路谐振。
三、实验仪器
标准电容箱，待测电感（标准电感箱），电阻箱，信号发生器， 双踪示波器。
四、预习要求
每一位同学都要查阅相关参考资料。 在熟知RLC谐振电路基础上写出一份完整的设计性实验报告。 实验报告要求：明确实验原理，拟定实验测量方案，画出实验电路图， 列出实验步骤，作出实验数据记录表及数据处理方法。
五、评分标准
预习（40%），课堂操作（40%）报告（20%）
谐 振 法 测 电 感( 教
案)
一、实验目的
（1）研究RLC电路的交流谐振特性。 （2）利用RLC电路的谐振特性测电感。
二、实验原理
由RLC组成的电路在周期性交变电源的激励下，将 产生受追形式的交流振荡，其振荡幅度随交变电源频 率的改变而变化，当电源频率满足一定条件时，回路 的振荡幅度达到最大值，即回路发生谐振。谐振时， 电路的特性也因RLC电路的串联或并联的形式不同而展 现出不同的结果，分别讨论如下。

谐振法测电感实验报告
实验目的：
通过谐振法测量电感的大小。

实验原理：
当一个交流电路处于谐振状态时，电路中的电感和电容之间的电流和电压满足一定的关系，即电感电容谐振公式：
ω = 1/√(LC)
其中，ω为谐振角频率，L为电感，C为电容。

实验仪器：
1.信号发生器
2.电感L
3.电容C
4.示波器
5.电阻
6.电压表
7.电流表
实验步骤：
1.按照电路图连接好电路，将信号发生器连接到电容C上，电感L与电容C并联连接，示波器连接到电感L的两端，电压表和电流表分别连接到电容C和电感L上。

2.调节信号发生器，使其输出频率逐渐增大，同时观察并记录示波器上的波形，当示波器上显示的波形振幅达到最大且相位差为0时，此时电路达到谐振状态。

3.记录此时的频率f0，电流表和电压表的读数（电流表的读数
为电感L上的电流值，电压表的读数为电容C上的电压值）。

4.改变电容C或电感L的值，重新进行调节，得到新的谐振频率f1、电流表和电压表的读数。

5.依次改变电容C或电感L的值，重复步骤4，得到多组数据。

6.根据公式ω = 1/√(LC)，计算得到电感L的估计值。

实验结果：
根据实验数据计算得到的电感L的估计值为xxH。

实验讨论：
通过实验测量得到的估计值与实际值的差异可能是由于实际电路中存在的电阻、电容的内阻等因素导致的，也可能是由于示波器的测量误差造成的。

在实际操作中，还需要注意保持电路的稳定性，避免外界干扰对测量结果的影响。

实验1 RLC 稳态及谐振特性在RLC 电路中通正弦交流电，电流以及R 、L 、C 各元件上电压的大小是随电源频率变化而变化的，电流与电源电压间的相位差亦随电源频率的变化而变化。

一、基本教学要求1．研究交流信号在RLC 串联电路中的相频和幅频特性，了解RLC 电路的应用。

2．学习测量两个波形相位差的方法； 3.掌握RLC 电路的谐振特点； 二、实验原理1 RC 电路)1(CjR I U ω-=••； C j R Z ω1-=电阻R 两端的电压为:2)1(1CR UIR U R ω+==电容C 两端的电压为 2)(1C R U CI U Cωω+==电压相量•U 落后于电流相量•I 的相位差为 CR ωϕ1arctan =相频特性：在R ，C ，U 都保持不变的条件下，回路中的总电压与总电流间的相位差ϕ随ω的增加而趋于零，随ω的减少而趋于2/π-。

幅频特性：在R ，C ，U 都保持不变的条件下，电容电压和电阻电压的幅度C U 和R U 都将随ω的变化而变化，在低频时电源电压主要降落在电容C 上；在高频时，电源电压主要降落在电阻R 上。

2 RL 电路)(L j R I U ω+=•• , L j R Z ω+=由相量图可知电阻R 两端的电压为: 2)(1RLU IR U R ω+==电感两端的电压为:2)(1LRULIULωω+==电压相量•U超前于电流相量•I的相位差为:RLωϕarctan=相频特性:在R、L、U都保持不变的情况下，总电压与总电流之间的相位差ϕ随ω的增加而逐渐增大，趋于2/π，随ω的减小而趋于零。

幅频特性:在R，L，U都保持不变的情况下，电阻和电感上的电压RU和LU都随ω的变化而变化，当角频率ω增加时，回路电流i减小、电阻上压降RU将减小，而电感上压降LU将增大。

RL电路与RC电路的性质是相反的，这两类电路是一对对偶电路。

3.RLC串联电路)1(CjLjRIUωω-+=••，)1(CLjRZωω-+=回路电流22)1(CLRUIωω-+=电压相量•U与电流相量•I的相位差为：RCLωωϕ/1arctan-=相频特性：当CLωω1=时，0=ϕ，总电压•U与电流•I同相位，犹如电路中只有纯电阻元件，此时称电路发生了谐振，此频率称为谐振频率:LCfπ21=当CLωω1>时，0>ϕ，总电压•U超前于电流•I。

电路中的电感测量方法与误差分析在电路中，电感是一种常见的电子元件，用于存储和转换电磁能。

测量电感的方法和误差分析对于电路设计和故障排除都非常重要。

本文将介绍电路中常用的电感测量方法以及可能产生的误差分析。

一、电感测量方法1. 电桥法测量电感电桥法是一种常见的测量电感的方法。

它利用电桥平衡条件来判断待测电感与已知电阻和电容的电感之间的比例关系。

在测量过程中，通过调节电桥上的参数，使电桥两端的电压为零，从而得到电感的准确值。

2. LC谐振法测量电感LC谐振法是一种基于电路谐振的测量电感的方法。

通过连接待测电感与已知电容组成LC谐振电路，通过调节外加电压频率使该电路达到谐振状态，从而计算出电感的数值。

这种方法适用于测量较小的电感值。

3. 电流下降法测量电感电流下降法是一种利用电感自身的特性进行测量的方法。

通过将一个已知电阻与待测电感串联，加上一个脉冲电流，通过测量电流下降的时间来计算电感值。

这种方法对于测量较大的电感值非常有效。

二、误差分析1. 内部电阻误差在实际测量中，待测电感的内部电阻会对测量结果产生影响。

内部电阻会使得测量的电感值偏小，因此在测量过程中需要考虑并校正这一误差。

2. 磁性耦合误差当待测电感与其他电感或线圈紧密相连时，可能会产生磁性耦合效应，导致测量结果的偏差。

这种误差可以通过合理设计电路结构和减小电感之间的磁性耦合来减小。

3. 测量仪器误差测量仪器自身的误差也是影响测量结果准确性的因素之一。

在进行电感测量时，应选择合适的测量仪器，并对测量误差进行校正和补偿，以提高测量的精确度。

4. 外部干扰误差外部环境的干扰也会对电感测量结果产生误差。

例如，电磁场干扰、温度变化等都可能导致测量结果的偏差。

在测量过程中，应尽可能避免这些干扰因素，并采取相应的抗干扰措施。

总结：电路中的电感测量方法主要包括电桥法、LC谐振法和电流下降法。

在进行电感测量时，需要考虑内部电阻误差、磁性耦合误差、测量仪器误差和外部干扰误差等因素，并采取相应的校正和补偿措施，以保证测量结果的准确性和可靠性。

电感线圈参数的测量电感线圈是电力、通信、电子、天线等领域中常用的电气元件，其常用参数包括电感值、品质因数和自谐频。

由于电感线圈参数对于电路的性能和应用有重要影响，因此对其参数进行准确的测量和校正是十分必要的。

下面将详细介绍电感线圈参数的测量方法和注意事项。

一、电感值的测量1. 串联法串联法是一种常见的测量电感值的方法，其原理是通过测量线圈的总电压和总电流，计算出线圈的电感值。

具体步骤如下：（1）将待测线圈接入一定频率的电源中，记录电流值和电压值；（2）将标准电感器串联到待测线圈后，测量总电流和电压值；（3）通过计算，得到待测线圈的电感值：Lx = Ls × (Vx / Vs) × (Is / Ix)其中Ls是标准电感器的电感值，Vx和Is是待测线圈的电压值和电流值，Vs和Ix是总电压和总电流。

2. 平衡桥法（2）调节桥路中的电容器和可变电阻，使得桥路两端的电压差为零；（3）根据桥路中各元件的参数计算待测线圈的电感值。

3. 自感法（2）根据线圈的自感感应电压和电流，计算出线圈的电感值。

二、品质因数的测量品质因数是电感线圈的重要参数之一，其测量方法有许多种，下面仅介绍常用的两种方法。

（3）根据电压和电流计算品质因数：Q = 2πfL / R其中f是电路频率，L是电感值，R是线圈中的电阻。

2. 阻尼振荡法阻尼振荡法是通过观察电路中的振荡，测量品质因数的方法。

具体步骤如下：（1）将待测线圈和电容器接入边沿触发器中；（2）调整电容值和触发电压，使得电路从一个状态到另一个状态；（3）测量电路从一个状态到另一个状态所需要的时间，然后计算品质因数：Q = 1 / R × √(C / L)三、自谐频的测量自谐频是线圈自身的谐振频率，其测量方法可以通过网络分析仪或者通过频率扫描仪进行测量。

1. 网络分析仪网络分析仪可以直接测量线圈的自谐频，具体步骤如下：（1）将线圈接入网络分析仪中；（2）选择合适的频率范围，然后测量线圈的S参数曲线；（3）确定线圈的自谐频。

电力电子技术中的谐振变换器电感选型误差分析在电力电子技术的应用中，谐振变换器是一种常见的电力转换器，用于将电能从一种形式转换为另一种形式。

在谐振变换器的设计中，电感的选型是非常重要的一步，其误差可能对整个系统的性能产生影响。

本文将对电力电子技术中的谐振变换器电感选型误差进行分析，并提供准确的解决方案。

一、误差来源及其影响在谐振变换器电感选型中，误差主要来自于电感元件自身的制造和参数测量误差以及在电感选型过程中的近似假设。

1. 电感元件制造和参数测量误差电感元件的制造过程中存在一定的误差，如匝数、线径、绕线方式等都可能与设计要求存在一定的差异。

此外，电感元件参数的测量也存在一定的误差，包括电感值、内阻等。

这些误差会导致实际使用的电感元件的参数与设计值存在差异，进而影响到谐振变换器的性能。

例如，电感元件的电感值偏离设计值会导致谐振频率的偏移，电感元件的内阻偏离设计值会影响系统的效率等。

2. 近似假设误差在电感选型过程中，为了简化计算和设计，通常会做一些近似假设，这些假设在一定程度上会导致误差。

例如，在计算电感元件的等效电感时，常常假设电感元件的磁场分布均匀，而实际上由于边缘效应等因素的存在，磁场分布并不均匀。

这种近似假设误差会导致谐振变换器的性能下降。

二、解决方案为了减小电力电子技术中谐振变换器电感选型误差的影响，我们可以采取以下措施：1. 提高电感元件制造和参数测量的准确性在电感元件的制造过程中，可以加强质量控制，提高匝数、线径、绕线方式等的制造精度，从而减小制造误差。

同时，使用准确可靠的测试仪器对电感参数进行测量，避免测量误差的影响。

2. 优化近似假设与计算方法在电感选型中，可以优化近似假设的准确性，考虑更多实际因素的影响。

同时，使用更为精确的计算方法，如有限元分析等，来计算电感元件的等效电感和电磁场分布，从而减小近似假设误差。

3. 大量样本测试与灵活调整在实际应用中，可以通过大量样本测试的方式，对电感元件的参数进行统计与分析，从而了解电感元件参数的真实分布情况。

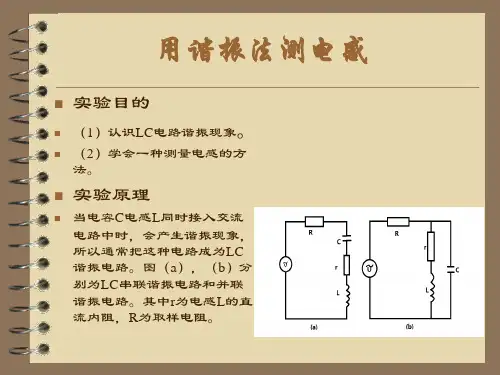
《电路分析》谐振法测量电感值实验一、实验目的1．理解RLC电路中谐振发生的条件，掌握合适的方法寻找RLC电路的谐振频率；2．学习信号发生器和示波器的使用方法。

3．熟练使用万用表测量交流电信号。

二、实验原理1．RLC串联电路的谐振图9-1根据相量法，串联回路的输入阻抗Z（jω）可表示为Z(jω)=1jωC +jωL+R=R+j(ωL−1ωC)（1）电感L和电容C来着的频率特性不仅相反，且电抗角差180°。

可以肯定一定存在一个角频率ω0使感抗和容抗相互完全抵消，即ω0L−1ω0C=0 .当端口电压和电流同相（电阻电压和输入电压同相）时，工程上将电路的这一特殊状态定义为谐振，发生谐振时的角频率ω0和f0为：ω0=√LCf0=2π√LC（2）2．RLC并联电路的谐振图9-2 并联谐振时，输入导纳Y(jω)最小Y(jω)=1jωL +jωC+G=G+j(ωC−1ωL)（3）3.串联谐振电路的品质因数Q用Q值表示U L(jω0)和U C(jω0)为：U Ｌ(jω)=U C(jω0)=QU s(jω0)（4）当Q＞1时，电感和电容两端将分别出现比U S(jω0)高Q倍的过电压，在高电压的电路系统中，这种过电压非常高，可能危及系统的安全，必须采取必要的防范措施。

但是在低电压的电路系统如无线收发系统（射频系统）中，则要利用谐振时出现的过电压来获取较大的输入信号。

Q=1R √LC（5）并联谐振的品质因数Q表达式为：Q=1G √CL（6）三、实验内容1．按图9-1接线，调节信号发生器频率时，用示波器观察信号源两端波形和电阻两端波形没有相位差时，得到谐振频率。

2．调节信号源频率，测量输入电压的有效值和电阻两端电压的有效值，计算增益的分贝值增益Gain（dB）=20log10Uo/Ui，绘制电路的伯德图，从示波器中读取信号相位差并记录下来。

谐振电路电感电流计算公式在电路中，谐振电路是一种特殊的电路，它能够在特定的频率下使电路中的电感和电容达到共振状态，从而使电路的电流和电压达到最大值。

谐振电路在电子设备中有着广泛的应用，因此对于谐振电路的分析和计算具有重要的意义。

在谐振电路中，电感电流是一个重要的参数，它能够帮助我们了解电路中的电流分布和能量传输情况。

本文将介绍谐振电路中电感电流的计算公式，并对其进行详细的推导和分析。

谐振电路是由电感和电容组成的串联或并联电路，它能够在特定的频率下使电路中的电感和电容达到共振状态。

在谐振状态下，电路中的电流和电压会达到最大值，这对于某些特定的应用非常重要。

在谐振电路中，电感电流是指通过电感器件的电流，它能够帮助我们了解电感器件的工作状态和性能。

因此，计算电感电流是谐振电路分析中的一个重要步骤。

在谐振电路中，电感电流可以通过以下公式进行计算：I = V / Xl。

其中，I表示电感电流，单位为安培（A）；V表示电路中的电压，单位为伏特（V）；Xl表示电感的阻抗，单位为欧姆（Ω）。

电感的阻抗Xl可以通过以下公式进行计算：Xl = 2πfL。

其中，f表示电路的频率，单位为赫兹（Hz）；L表示电感的电感值，单位为亨利（H）；π是一个常数，约等于3.14159。

通过以上公式，我们可以计算出谐振电路中电感电流的数值。

在实际的电路分析中，我们可以通过测量电路中的电压和电感的参数值，然后代入上述公式进行计算，从而得到电感电流的数值。

这对于谐振电路的设计和分析具有重要的意义。

在实际的电路设计和分析中，我们还需要考虑电路中的其他因素对电感电流的影响。

例如，电路中的电阻会对电感电流产生影响，我们需要将电路中的电阻考虑在内，从而得到更加准确的电感电流计算结果。

此外，电路中的电容也会对电感电流产生影响，我们需要综合考虑电感、电容和电阻等因素对电感电流的影响，从而得到全面的电路分析结果。

在谐振电路的实际应用中，电感电流的计算对于电路设计和性能分析具有重要的意义。

物理实验技术中的电感测量方法指南电感是研究电路中储存和传输能量的重要参数之一。

在物理实验中，准确测量电感是探索电磁现象和研究电路特性的关键步骤之一。

本文将介绍几种常见的电感测量方法，并讨论它们的原理、适用范围和注意事项。

1. 自感法测量电感自感法是最基本的测量电感方法之一。

它利用线圈自感现象来测量电感。

简单来说，当通过一根导线或线圈的电流改变时，它会产生一个自感电动势，并阻碍电流的改变。

根据自感电动势的大小可以推导出电感的数值。

实验中，我们可以通过以下步骤测量电感：（1）将待测电感连接到一个恒定的交流电源上。

（2）通过一根电阻限制电流大小。

（3）测量交流电源的电压和电流。

（4）利用欧姆定律和电感的定义，计算出电感的数值。

自感法测量电感的优点是简单易行，但需要注意使用合适的电源和测量设备，以确保测量结果的准确性。

2. 互感法测量电感互感法是通过测量两个线圈之间的互感现象来测量电感的方法。

它借助两个线圈之间的耦合作用，利用能量的传递和传输来测量电感。

实验中，我们可以按照以下步骤进行互感法的电感测量：（1）将待测电感和一个已知电感连接到两个线圈上。

（2）利用一个交流电源激励其中一个线圈，通过测量另一个线圈的电压来计算互感系数。

（3）根据已知电感和互感系数，计算出待测电感的数值。

互感法测量电感的优点是测量精度高，能够测量较小的电感。

但需要注意线圈之间的耦合系数，以及测量电压时的噪声和干扰。

3. 频谱法测量电感频谱法是一种较为细致的电感测量方法，可以通过电感元件所对应的电容和频率的关系进行测量。

它利用了电感和电容之间的共振现象，通过测量共振频率来计算电感。

实验中，我们可以按照以下步骤进行频谱法的电感测量：（1）将待测电感连接到一个电容上，形成一个谐振电路。

（2）通过改变电容的值，找到谐振频率。

（3）根据电容、频率和电感的关系，计算出待测电感的数值。

频谱法测量电感的优点是测量结果准确，适用于复杂电路中的电感测量。

用谐振法测电感实验报告
实验目的：应用谐振法测量电感的大小。

实验原理：
在一定频率下，电容与电感并联会形成一个谐振电路。

当谐振
电路中的电容和电感值确定时，有一定的工作电频。

此时，谐振
电路中的电感大小可以通过谐振频率的计算得到。

谐振频率的计算公式为：f=1/2π√(LC)
其中，f为谐振频率，L为电感值，C为电容值。

实验器材：电感、电容、信号源、万用表、示波器、万能电桥。

实验步骤：
1、将电感、电容并联起来，形成一个谐振电路。

2、用信号源产生一定的信号，并与谐振电路相连。

3、打开示波器，观察到电路呈现出振荡波形。

4、在示波器屏幕上测量得到谐振频率f。

5、通过谐振频率公式计算出电感L的值。

6、反复测量，取多次平均值，以提高数据的准确性。

实验结果：
在本次实验中，采用了0.1uF电容与220mH电感构成谐振电路。

通过实验测量得到的谐振频率为982Hz。

根据谐振频率公式，计
算出电感L的理论值为220.52mH。

在多次测量的结果中，平均得到的测量值为221.01mH，误差
为0.22%。

实验结果表明，本次实验所采用的谐振法确实能够测
量出电感的大小，且测量结果较为准确。

实验结论：
通过谐振法测量电感的大小的实验表明，该方法具有较高的实验精度，能够精确地测量出电感的大小。

本次实验所获得的结果与理论计算值的差异不大，误差较小，实验结果具有较高的可靠性。