1-1 描述运动的物理量 匀变速直线运动(新人教)

人教版物理必修1第一章运动的描述：匀变速直线运动（四）一、选择题。

1. 如图中高楼为上海中心大厦，建筑主体为118层，总高为632m．现假设外墙清洁工人在320m高处进行清洁时不慎掉落一瓶水，当他发现水瓶掉落时，水瓶已经下落了5s，此时他大声向下方行人发出警告．已知声速为340m/s，空气阻力忽略不计，g取10m/s2．下列说法正确的是（）A.正下方的行人先看见水瓶落地，再听见警告声，时间差超过2sB.正下方的行人先听见警告声，再看见水瓶落地，时间差超过2sC.正下方的行人先看见水瓶落地，再听见警告声，时间差不到1sD.正下方的行人先听见警告声，再看见水瓶落地，时间差不到1s2. 太空跳伞是一种挑战人类极限的运动，奥地利极限运动员鲍姆加特纳乘氦气球到达3.9万米高空后纵身跳下，在平流层接近真空的环境里自由落体持续了60秒，在距离地面2.1万米时才打开降落伞减速．关于鲍姆加特纳在这段自由落体运动时间里的位移或速度，以下说法正确的是（重力加速度g取10m/s2，且不随高度的变化而变化）（）A.自由落体运动的位移是3.9×104mB.自由落体运动的位移是2.1×104mC.自由落体运动的末速度是6.0×102m/sD.自由落体运动的平均速度是6.0×102m/s二、解答题。

气球下挂一重物，以v0=10m/s的速度匀速上升，当到达离地面高度ℎ=175m处时，悬挂重物的绳子突然断裂，那么重物经多长时间落到地面？落地时的速度多大？（空气阻力不计，取g取10m/s2）近几年大假期间，国家取消了7座及其以下的小车的收费公路的过路费，给自驾带来了很大的实惠，但车辆的增多也给交通道路的畅通增加了很大的压力，因此国家规定了免费车辆在通过收费站时在专用车道上可以不停车拿卡或交卡而直接减速通过．假设收费站的前、后都是平直大道，大假期间过站的车速要求不超过v t=21.6km/ℎ，事先小汽车未减速的车速均为v0=108km/ℎ，制动后小汽车的加速度的大小为a1=4m/s2．试问：（1）大假期间，驾驶员应在距收费站至少多远处开始制动？（2）假设车过站后驾驶员立即使车以a2=6m/s2的加速度加速至原来的速度，则从减速开始到最终恢复到原来速度的过程中，汽车运动的时间至少是多少？（3）在（1）（2）问题中，车因减速和加速过站而耽误的时间至少为多少？如图为某高速公路出口的ETC通道示意图．一汽车驶入ETC车道，到达O点的速度v0= 30m/s，此时开始减速，到达M时速度减至v=6m/s，并以6m/s的速度匀速通过MN 区．已知MN的长度d=36m，汽车减速运动的加速度大小a=3m/s2，求：（1）O、M间的距离x．（2）汽车从O点到N点所用的时间t．如图1所示，在成都天府大道某处安装了一台500万像素的固定雷达测速仪，可以准确抓拍超速车辆以及测量运动车辆的加速度．一辆汽车正从A点迎面驶向测速仪B，若测速仪与汽车相距355m，此时测速仪发出超声波，同时车由于紧急情况而急刹车，汽车运动到C处与超声波相遇，当测速仪接受到发射回来的超声波信号时，汽车恰好停止于D点，且此时汽车与测速仪相距335m，忽略测速仪安装高度的影响，可简化为如图2所示分析（已知超声波速度为340m/s）．（1）求汽车刹车过程中的加速度a；（2）此路段有80km/ℎ的限速标志，分析该汽车刹车时的行驶速度是否超速？参考答案与试题解析人教版物理必修1第一章运动的描述：匀变速直线运动（四）一、选择题。

匀变速直线运动1．匀变速直线运动基本公式0222001222t t tv v at x v t at ax v v v v x v t ⎧=+⎪⎪=+⎪⎨=-⎪⎪+⎪==⎩速度公式：位移公式：速度、位移公式：平均速度公式：在描述匀变速直线运动时，我们用到的基本物理量包括初速度0v 、末速度t v 、加速度a 、时间t 、位移x ，共5个。

上述4个基本公式中，只有2个是独立的（由任意两个公式可以推出另外两个），因此，对每个运动过程，必须知道其中的3个量才能求出另外2个量。

仔细观察上述基本公式可以发现：每个公式都只涉及4个物理量（有一个物理量不出现），知道其中的3个可以求出另外的1个。

因此，在解决问题时，应该分清哪些是已知量、哪些是所求量，选择合适的公式，可以减少运算量。

**************************************************************************************** 说明：每个公式中出现5个物理量中的4个，应该一共有5个公式。

上述4个基本公式中，第1个不出现x 、第2个不出现t v 、第3个不出现t 、第4个不出现a ，除此之外，还应该有一个不出现0v 的公式：212t x v t at =-，只不过这个公式我们一般不用而已。

****************************************************************************************知识点睛2．匀变速直线运动两个推论公式⑴ 某段时间的中间时刻的瞬时速度等于这段时间内的平均速度，即022tt v v v +=⑵ 在连续相等的时间间隔内的位移之差Δx 为恒定值，2Δx aT =。

拓展：2Δ()MN M N x x x M N aT =-=-（物体连续通过n 段位移，通过每段位移的时间均为T ，M x 为第M 段的位移长度，N x 为第N 段的位移长度）**************************************************************************************** 教师版说明：如果学生没有学过暑期课程或者不了解纸带实验，老师可以重新讲一下2Δx aT =这个公式。

匀速直线运动精华总结1、速度：物理学中将位移与发生位移所用的时间的比值定义为速度。

用公式表示为：V==2、瞬时速度：在某一时刻或某一位置的速度称为瞬时速度。

瞬时速度的大小称为瞬时速率，简称速率。

3、加速度：物理学中，用速度的改变量∆V与发生这一改变所用时间∆t的比值，定量地描述物体速度变化的快慢，并将这个比值定义为加速度。

α=单位：米每二次方秒；m/s2α即为加速度；即为一次函数图象的斜率；加速度的方向与斜率的正负一致。

速度与加速度的概念对比：速度：位移与发生位移所用的时间的比值加速度：速度的改变量与发生这一改变所用时间∆t的比值4、匀变速直线运动：在物理学中，速度随时间均匀变化，即加速度恒定的运动称为匀变速直线运动。

1)匀变速直线运动的速度公式：V t=V0+αt推导：α==速度改变量发生这一改变所用的时间2）匀变速直线运动的位移公式：S=V0t+2.(矩形和三角形的面积公式)推导：S=∙t (梯形面积公式) 如图：3）由速度公式和位移公式可以推导出的公式：⑴V t2-V02=2αS(由来：V t2-V02=(V0+αt)2 -V02=2αV0t +α2t2=2α(V0t+2)=2αS)⑵==(由来：V=V0+α====)⑶=(由来：因为：V t2-V02=2αS所以2-V02= α=α =)（2-V02=；2=V02=）⑷∆S=T2（做匀变速直线运动的物体，在任意两个连续相等的时间内的位移差为定值。

设加速度为α，连续相等的时间为T,位移差为∆S）证明：设第1个T 时间的位移为S 1；第2个T 时间的位移为S 2；第3个T 时间的位移为S 3 ..第n 个T 时间的位移即由：S =V 0t+2 得: S 1=V 0T+α 2S 2=V 02T+α 2-V 0T- α 2=V 0T+α 2 S 3=V 03T+α 2-V 02T-α 2=V 0T+α 2 S n= V 0nT+α 2-V 0(n-1)T-α 2∆S =S 2-S 1=S 3-S 2=(V 0T+ α 2)-(V 0T+ α 2)=(V 0T+ α 2)-(V 0T+α 2)= T 2 可以用来求加速度 =∆5、 初速度为零的匀加速直线运动的几个比例关系。

《匀变速直线运动的速度与时间的关系》知识全解【教学目标】1．根据实验得到的v-t 图像是一条倾斜的直线，建构匀变速直线运动的模型，了解匀变速直线运动的特点。

2．能根据v-t 图象得出匀变速直线运动的速度与时间的关系式v=v 0+at ，理解公式的含义。

3．能应用匀变速直线运动的速度和时间的关系式或图像分析和解决生产、生活中有关的实际问题。

【内容解析】1．匀变速直线运动速度与时间的关系物理量之间的函数关系可以用图象表示，也可以用公式表示。

用公式表示物理量之间的函数关系，往往显得更加简洁和精确。

那么，小车的速度图象——这条倾斜直线所表示的速度随时间变化的关系，怎样用公式来描述呢？对于匀变速直线运动来说，由于其速度图象是一条倾斜的直线，无论△t 大些还是小些，对应的速度变化量△v 与时间变化量△t 之比都是一样的。

设初始时刻（t =0）的速度为v 0，t 时刻的速度为v ，不妨取△t =t -0，则对应的△v =v -v 0。

从而，由：000v v v v v a t t t --∆===∆-，可得：0v v at =+。

这就是匀变速直线运动的速度公式。

2．对匀变速直线运动速度公式的理解匀变速直线运动速度公式表明，物体运动的速度是时间的一次函数，所以速度图象是一条倾斜的直线。

匀变速直线运动速度公式描述了物体运动的速度与时间的关系。

教材得出这一公式的逻辑推理过程，强化了从实验得出规律的一般性过程，让我们体验了科学推理的方法，练习了用图象分析问题的一般方法。

3．公式/2t v v =的再认识设物体做匀变速直线运动的初速度为v 0，加速度为a ，经时间t 后末速度为v ，并以/2t v 表示这段时间中间时刻的瞬时速度。

由：0v v at =+，/202t t v v a =+ 可得：0/22t v v v +=。

因为匀变速直线运动的速度随时间是均匀变化的，所以它在时间t 内的平均速度v 就等于时间t 内的初速度v 0和末速度v 的平均值，即0/22t v v v +=。

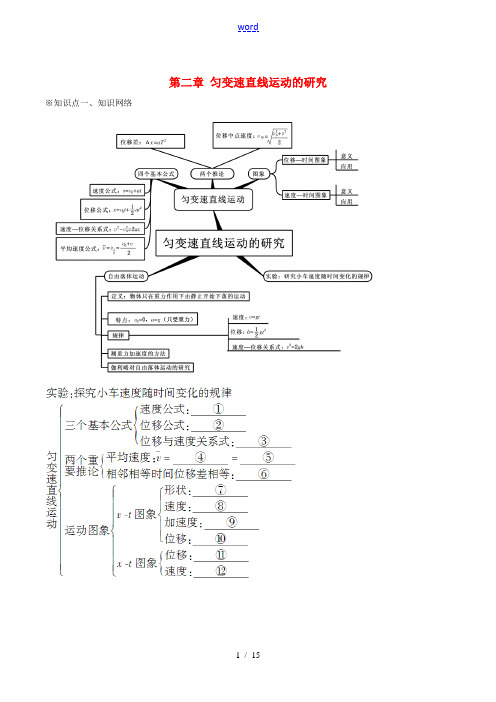
第二章匀变速直线运动的研究※知识点一、知识网络※知识点二、匀变速直线运动规律的理解与应用 1.公式中各量正负号的确定x 、a 、v 0、v 均为矢量，在应用公式时，一般以初速度方向为正方向(但不绝对，也可规定为负方向)，凡是与v 0方向相同的矢量为正值，相反的矢量为负值．当v 0＝0时，一般以a 的方向为正方向，这样就把公式中的矢量运算转换成了代数运算． 2．善用逆向思维法特别对于末速度为0的匀减速直线运动，倒过来可看成初速度为0的匀加速直线运动，这样公式可以简化⎝ ⎛⎭⎪⎫如v ＝at ，x ＝12at 2，初速度为0的比例式也可以应用．3．注意(1)解题时首先选择正方向，一般以v 0方向为正方向． (2)刹车类问题一般先求出刹车时间．(3)对于有往返的匀变速直线运动(全过程加速度a 恒定)，可对全过程应用公式v ＝v 0＋at 、x ＝v 0t ＋12at 2、……列式求解．(4)分析题意时要养成画运动过程示意图的习惯，特别是对多过程问题．对于多过程问题，要注意前后过程的联系——前段过程的末速度是后一过程的初速度；再要注意寻找位移关系、时间关系. 4．匀变速直线运动的常用解题方法【典型例题】【例题1】一个物体以v 0＝8m/s 的初速度沿光滑斜面向上滑，加速度的大小为2 m/s 2，冲上最高点之后，又以相同的加速度往回运动，下列说法错误的是( ) A ．1 s 末的速度大小为6 m/s B ．3 s 末的速度为零 C ．2 s 内的位移大小是12 m D ．5 s 内的位移大小是15 m【审题指导】分析题中已知条件选择合适的关系式求解． 【答案】 B【针对训练】在某地地震发生后的几天，通向灾区的公路非常难行，一辆救灾汽车由静止开始做匀变速直线运动，刚运动了8 s ，由于前方突然有巨石滚在路中央，所以又紧急刹车，经4 s 停在巨石前．则关于汽车的运动情况，下列说法正确的是 ( ) A ．加速、减速中的加速度大小之比a 1∶a 2＝1∶2 B ．加速、减速中的加速度大小之比a 1∶a 2＝2∶1 C ．加速、减速中的平均速度之比v －1∶v －2＝2∶1 D ．加速、减速中的位移之比x 1∶x 2＝1∶1 【答案】A 【解析】 由a ＝v －v 0t 可得a 1∶a 2＝1∶2，选项A 正确，B 错误；由v －＝v 0＋v 2可得v －∶v －2＝1∶1，选项C错误；又根据x ＝v －t ，x 1∶x 2＝2∶1，选项D 错误．※知识点三、x -t 图象和v -t 图象 ★x －t 图象和v －t 图象的比较2.在图象问题的学习与应用中首先要注意区分它们的类型，其次应从图象所表达的物理意义，图象的斜率、截距、交点、拐点、面积等方面的含义加以深刻理解．【典型例题】【例题2】在水平直轨道上距离A点右侧10 m处，一辆小车以4 m/s的速度匀速向右行驶，5 s末，小车的速度立即变为2 m/s匀速向左行驶．设小车做直线运动的位移和运动方向都以水平向左为正方向，(1)试作出小车在20 s内的v－t图象和x－t图象：(写出必要的计算过程，以小车出发点为位移坐标原点)；(如图所示)(2)根据图象确定小车在20 s末的位置．(用文字表达)【针对训练】一质点由静止开始做直线运动的v－t关系图象如图所示，则该质点的x－t关系图象可大致表示为下图中的( )【答案】 B※知识点四、纸带问题的处理方法纸带的分析与计算是近几年高考中考查的热点，因此应该掌握有关纸带问题的处理方法．1．判断物体的运动性质(1)根据匀速直线运动的位移公式x ＝vt 知，若纸带上各相邻的点的间隔相等，则可判定物体做匀速直线运动．(2)由匀变速直线运动的推论Δx ＝aT 2知，若所打的纸带上在任意两个相邻且相等的时间内物体的位移差相等，则说明物体做匀变速直线运动． 2．求瞬时速度根据在匀变速直线运动中，某段时间内的平均速度等于该段时间中间时刻的瞬时速度：v n ＝x n ＋x n ＋12T，即n 点的瞬时速度等于(n －1)点和(n ＋1)点间的平均速度． 3．求加速度 (1)逐差法虽然用a ＝ΔxT2可以根据纸带求加速度，但只利用一个Δx 时，偶然误差太大，为此应采取逐差法．如图所示，纸带上有六个连续相等的时间间隔T 内的位移x 1、x 2、x 3、x 4、x 5、x 6.由Δx ＝aT 2可得：x 4－x 1＝(x 4－x 3)＋(x 3－x 2)＋(x 2－x 1)＝3aT 2 x 5－x 2＝(x 5－x 4)＋(x 4－x 3)＋(x 3－x 2)＝3aT 2 x 6－x 3＝(x 6－x 5)＋(x 5－x 4)＋(x 4－x 3)＝3aT 2所以a ＝（x 6－x 3）＋（x 5－x 2）＋（x 4－x 1）9T 2＝（x 6＋x 5＋x 4）－（x 3＋x 2＋x 1）9T 2. (2)两段法将如图所示的纸带分为OC 和CF 两大段，每段时间间隔是3T ，可得：x 4＋x 5＋x 6－(x 1＋x 2＋x 3)＝a (3T )2，显然，求得的a 和用逐差法所得的结果是一样的，但该方法比逐差法简单多了． (3)v －t 图象法根据纸带，求出各时刻的瞬时速度，作出v －t 图象，求出该v －t 图象的斜率k ，则k ＝a . 这种方法的优点是可以舍掉一些偶然误差较大的测量值，有效地减少偶然误差． 【典型例题】【例题3】某兴趣小组利用自由落体运动测定重力加速度，实验装置如图所示．倾斜的球槽中放有若干个小铁球，闭合开关K ，电磁铁吸住第1个小球．手动敲击弹性金属片M ，M 与触头瞬间分开，第1个小球开始下落，M迅速恢复，电磁铁又吸住第2个小球．当第1个小球撞击M时，M与触头分开，第2个小球开始下落…….这样，就可测出多个小球下落的总时间．(1)在实验中，下列做法正确的是________．A．电路中的电源只能选用交流电源B．实验前应将M调整到电磁铁的正下方C．用直尺测量电磁铁下端到M的竖直距离作为小球下落的高度D．手动敲击M的同时按下秒表开始计时(2)实验测得小球下落的高度H＝1.980 m,10个小球下落的总时间T＝6.5 s．可求出重力加速度g＝________ m/s2.(结果保留两位有效数字)(3)某同学考虑到电磁铁在每次断电后需要时间△t磁性才消失，因此，每个小球的实际下落时间与它的测量时间相差△t，这导致实验误差．为此，他分别取高度H1和H2测量n个小球下落的总时间T1和T2.他是否可以利用这两组数据消除△t对实验结果的影响？________(填“是”或“否”)(4)在不增加实验器材的情况下，请提出减小实验误差的两个办法．①________________________________________________________________________；②________________________________________________________________________.【答案】(1)BD (2)9.4 (3)是(4)见解析(2)H ＝12gt 2＝12g ⎝ ⎛⎭⎪⎫T 102所以g ＝200H T 2＝200×1.980(6.5)2 m/s 2＝9.4 m/s 2(3)由H 1＝12g ⎝ ⎛⎭⎪⎫T 1n －Δt 2和H 2＝12g ⎝ ⎛⎭⎪⎫T 2n －Δt 2可得g ＝2n 2(H 1－H 2)2(T 1－T 2)2，因此可以消去Δt 的影响． (4)增加小球下落的高度或多次重复实验，取平均值做为最后的测量结果均能使实验误差减小【针对训练】 在做“探究小车速度随时间变化的规律”的实验中，取一段如图所示的纸带研究其运动情况．设O 点为计数的起始点，在四个连续的计数点中，相邻计数点间的时间间隔为0.1 s ，若物体做理想的匀加速直线运动，则计数点“A ”与起始点O 之间的距离x 1为________ cm ，打计数点“A ”时物体的瞬时速度为________ m/s ，物体的加速度为________ m/s 2.【答案】 4.00 0.50 2.00【解析】 设相邻相等时间内的位移之差为Δx ，则AB ＝x 1＋Δx ，BC ＝x 1＋2Δx ，OC ＝OA ＋AB ＋BC ＝3(x 1＋Δx )＝18.00 cm ，故AB ＝6.00 cm ，x 1＝4.00 cm ；由Δx ＝aT 2＝2.00 cm 可得a ＝2.00 m/s 2；A 点的速度v A ＝OA ＋AB2T＝0.50 m/s.※知识点五、追及相遇问题★追及问题的解题思路：(1)根据对两物体运动过程的分析，画出两物体运动的示意图．(2)根据两物体的运动性质，分别列出物体的位移方程，注意要将两物体运动时间的关系反映在方程中．(3)由运动示意图找出两物体位移间的关联方程，这是关键．(4)联立方程求解，并对结果进行简单分析．【典型例题】【例题4】A火车以v1=20m/s速度匀速行驶，司机发现前方同轨道上相距100m处有另一列火车B正以v2=10m/s 速度匀速行驶，A车立即做加速度大小为a的匀减速直线运动。

第2节 匀变速直线运动的规律一、匀变速直线运动的基本规律1．概念：沿一条直线且加速度不变的运动。

2．分类(1)匀加速直线运动：a 与v 方向相同。

(2)匀减速直线运动：a 与v 方向相反。

3．基本规律⎭⎪⎬⎪⎫1速度—时间关系：v ＝v 0＋at 2位移—时间关系：x ＝v 0t ＋12at 2――→初速度为零即v 0＝0⎩⎪⎨⎪⎧v ＝at x ＝12at2二、匀变速直线运动的重要关系式 1．两个导出式⎭⎪⎬⎪⎫1速度—位移关系：v 2－v 20＝2ax 2位移—平均速度关系：x ＝v －t ＝v 0＋v 2t――→初速为零v 0＝0⎩⎪⎨⎪⎧v 2＝2axx ＝v 2t2．三个重要推论(1)位移差公式：Δx ＝x 2－x 1＝x 3－x 2＝…＝x n －x n －1＝aT 2，即任意两个连续相等的时间间隔T 内的位移之差为一恒量。

可以推广到x m －x n ＝(m －n )aT 2。

(2)中间时刻速度v t2＝v ＝v 0＋v2，即物体在一段时间内的平均速度等于这段时间中间时刻的瞬时速度，还等于初、末时刻速度矢量和的一半。

(3)位移中点的速度v x2＝v20＋v22。

3．初速度为零的匀变速直线运动的四个常用推论(1)1T末、2T末、3T末…瞬时速度的比为v1∶v2∶v3∶…∶v n＝1∶2∶3∶…∶n。

(2)1T内、2T内、3T内…位移的比为xⅠ∶xⅡ∶xⅢ∶…∶x N＝12∶22∶32∶…∶n2。

(3)第一个T内、第二个T内、第三个T内…位移的比为x1∶x2∶x3∶…∶x n＝1∶3∶5∶…∶(2n－1)。

(4)从静止开始通过连续相等的位移所用时间的比为t1∶t2∶t3∶…∶t n＝1∶(2－1)∶(3－2)∶…∶(n－n－1)。

三、自由落体运动和竖直上抛运动自由落体运动运动条件(1)物体只受重力作用(2)由静止开始下落运动性质初速度为零的匀加速直线运动运动规律(1)速度公式：v＝gt(2)位移公式：h＝12gt2(3)速度—位移公式：v2＝2gh运动性质匀减速直线运动竖直上抛运动运动规律(1)速度公式：v＝v0－gt(2)位移公式：h＝v0t－12gt2(3)速度—位移关系式：v2－v20＝－2gh(4)上升的最大高度：H＝v202g(5)上升到最高点所用时间：t＝v0g一、思考辨析(正确的画“√”，错误的画“×”)1．匀变速直线运动是加速度均匀变化的直线运动。

第2节匀变速直线运动的规律,(1)匀变速直线运动是加速度均匀变化的运动。

(×)(2)匀加速直线运动是速度均匀变化的直线运动。

(√)(3)匀加速直线运动的位移是均匀增大的。

(×)(4)在匀变速直线运动中，中间时刻的速度一定小于该段时间内位移中点的速度。

(√)(5)物体由某高度由静止下落一定做自由落体运动。

(×)(6)做竖直上抛运动的物体，在上升过程中，速度的变化量的方向是向下的。

(√)(7)竖直上抛运动的速度为负值时，位移也为负值。

(×)意大利物理学家伽利略从理论和实验两个角度，证明了轻、重物体下落一样快，推翻了古希腊学者亚里士多德的“物体越重下落越快〞的错误观点。

突破点(一) 匀变速直线运动的根本规律1．解答运动学问题的根本思路画过程示意图→判断运动性质→选取正方向→选公式列方程→解方程并讨论2．运动学公式中正、负号的规定直线运动可以用正、负号表示矢量的方向，一般情况下，规定初速度v0的方向为正方向，与初速度同向的物理量取正值，反向的物理量取负值，当v0＝0时，一般以加速度a的方向为正方向。

3．多过程问题如果一个物体的运动包含几个阶段，就要分段分析，各段衔接处的速度往往是连接各段的纽带，应注意分析各段的运动性质。

[典例] (2017·孝感三中一模)如下列图，水平地面O点的正上方的装置M每隔相等的时间由静止释放一小球，当某小球离开M的同时，O点右侧一长为L＝1.2 m的平板车开始以a＝6.0 m/s2的恒定加速度从静止开始向左运动，该小球恰好落在平板车的左端，平板车上外表距离M的竖直高度为h＝0.45 m。

忽略空气阻力，重力加速度g取10 m/s2。

(1)求小车左端离O点的水平距离；(2)假设至少有2个小球落在平板车上，如此释放小球的时间间隔Δt应满足什么条件？[审题指导]第一步：抓关键点关键点获取信息由静止释放一小球小球做自由落体运动忽略空气阻力平板车以恒定加速度从静止开始向左运动小车做初速度为零的匀加速直线运动该小球恰好落在平板车的左端在小球自由落体的时间内，小车的左端恰好运动到O 点第二步：找突破口(1)小球下落的时间t 0可由h ＝12gt 02求得。