作业1静力学
- 格式:ppt
- 大小:526.00 KB
- 文档页数:30


1.[1,4,2,4,2,...,2,4,1]是()的辛氏乘数。
A.辛浦生第一法B.辛浦生第二法答案:A2.基平面与中线面的交线称为()。
A.基线B.水线C.纵剖线D.横剖线答案:A3.某船水线面按照船长分为4等分,等分间距l=0.5m,其等分点处半宽分别为3,4,5,4.5,3.5(单位m),用梯形法算水线面面积为多少平方米?()A.6B.10C.8.375D.16.75答案:D4.基平面与中线面的交线称之为()。
A.基线B.设计水线C.中纵剖线D.中横剖线答案:A5.推进器的研究属于()的研究。
A.船舶稳性B.船舶浮性C.船舶快速性D.船舶操纵性答案:C6.下列哪些需要在型线图的纵剖线图上画出的有?()A.龙骨线B.首尾轮廓线C.甲板边线D.舷墙顶线答案:ABCD7.属于操纵性研究对象的是()。
A.推进器B.船舶航行时所遭受的阻力C.保证操纵性的设备舵D.船舶本身对操纵性能的影响答案:CD8.干舷F的大小与下列哪些因素有关?()A.型深DB.吃水dC.船长LD.甲板及其敷料的厚度答案:ABD9.平均吃水=()+()/2。
应填入的选项为()。
A.设计吃水B.首吃水C.尾吃水D.干舷答案:BC10.下列哪些需要在型线图的纵剖线图上画出的有哪些?()A.龙骨线B.首尾轮廓线C.甲板边线D.舷墙顶线答案:ABCD11.军舰通常以通过尾轮廓和满载水线交点的垂线作为尾垂线。
()A.错误B.正确答案:A12.乞贝雪夫法可用于坐标不间距相等的情形。
()A.错误B.正确答案:B13.中横剖面系数表示水线面的肥瘦程度。
()A.错误B.正确答案:A14.乞贝雪夫法不可用于坐标不间距相等的情形。
()A.错误B.正确答案:A15.中站面是船体的对称面。
()A.错误B.正确答案:A16.在船舶静力学中,型线图和型值表是计算船体形状各项参数和静水力性能的主要依据。
()A.错误B.正确答案:B17.船舶尺度比与船舶性能、强度以及经济性等有密切关系。

静力学练习题及参考答案1. 问题描述:一根长度为L的均质杆以一端固定在墙上,另一端悬挂一重物。
重物造成的杆的弯曲应力最大为σ。
杆的质量可以忽略不计。
计算重物的质量m。
解答:根据静力学原理,杆的弯曲应力可以用公式计算:σ = M / S,其中M是杆的弯矩,S是杆的截面横截面积。
因为杆是均质杆,所以它的截面横截面积在整个杆上都是相等的。
设杆的截面横截面积为A。
杆的弯矩M可以通过杆的长度L和重物的力矩T计算得到:M = T * (L/2)。
代入上面的公式,我们可以得到:σ = (T * (L/2)) / A。
根据题目的描述,我们可以得到如下等式:σ = (m * g * (L/2)) / A,其中g是重力加速度。
我们可以将这个等式转换成求解未知质量m的方程。
将等式两边的A乘以m,并将等式两边的m乘以g,我们可以得到如下方程:m^2 = (2 * σ * A) / (g * L)解这个方程,我们可以求得未知质量m。
2. 问题描述:一根均质杆的长度为L,质量为M。
杆的一端固定在墙上,另一端悬挂一重物。
杆与地面的夹角为θ。
重物造成的杆的弯曲应力最大为σ。
求重物的质量m。
解答:在这个问题中,除了重物的力矩,还需要考虑到重力对杆的力矩。
由于杆是均质杆,其质量可以均匀分布在整个杆上。
假设杆上的每个微小质量元都受到与其距离一致的力矩。
重物造成的力矩可以用公式计算:M1 = m * g * (L/2) * sinθ,其中g 是重力加速度。
由于杆是均质杆,它的质心位于杆的中点。
因此重力对杆的力矩可以用公式计算:M2 = M * g * (L/2) * cosθ。
根据静力学的原理,杆的弯曲应力可以用公式计算:σ = M / S,其中M是杆的弯矩,S是杆的截面横截面积。
在这个问题中,我们可以将弯曲应力的计算公式推广到杆的中点(也就是质心):σ = (M1 + M2) / S代入上面的公式,我们可以得到:σ = ((m * g * (L/2) * sinθ) + (M *g * (L/2) * cosθ)) / S根据题目的描述,我们可以得到如下等式:σ = ((m * g * (L/2) * sinθ) + (M * g * (L/2) * cosθ)) / (A / 2),其中A是杆的横截面积。


静力学和动力学练习题(含答案)静力学和动力学练题 (含答案)静力学练题1. 一个质量为10kg的物体置于水平面上。
一个力F = 50N施加在物体上,使其保持静止。
求摩擦力的大小。
解答:根据静力学的条件,物体保持静止时,合力为零。
我们可以设置以下方程:ΣF = F - F_f = 0其中,ΣF为合力,F为施加在物体上的力,F_f为摩擦力。
代入已知数据,得到:50N - F_f = 0解方程得到 F_f = 50N,因此摩擦力的大小为50N。
2. 一个质量为5kg的物体沿斜面下滑,斜面的倾角为30度。
在不考虑摩擦的情况下,求物体的加速度。
解答:根据静力学的条件,物体在斜面上保持平衡时,合力沿着斜面的方向为零。
我们可以设置以下方程:ΣF = m * g * sinθ - m * g * cosθ = 0其中,ΣF为合力,m为物体的质量,g为重力加速度,θ为斜面的倾角。
代入已知数据,得到:5kg * 9.8m/s^2 * sin30° - 5kg * 9.8m/s^2 * cos30° = 0解方程得到加速度 a = 4.9m/s^2,因此物体的加速度为4.9m/s^2。
动力学练题1. 一个质量为2kg的物体以速度4m/s沿着水平方向运动。
一个恒力F = 6N施加在物体上,与运动方向垂直。
求物体在3秒后的速度。
解答:根据动力学的条件,物体在受到恒力作用时,速度的变化可以通过牛顿第二定律来计算。
我们可以使用以下公式:F = m * a其中,F为力的大小,m为物体的质量,a为物体的加速度。
根据题目已提供的数据,可以计算出物体的加速度:6N = 2kg * a解方程得到 a = 3m/s^2。
然后,我们可以使用以下公式来计算物体的速度变化:v = u + a * t其中,v为物体的最终速度,u为物体的初始速度,a为物体的加速度,t为时间间隔。
代入已知数据,计算得到:v = 4m/s + 3m/s^2 * 3s = 4m/s + 9m/s = 13m/s因此,物体在3秒后的速度为13m/s。


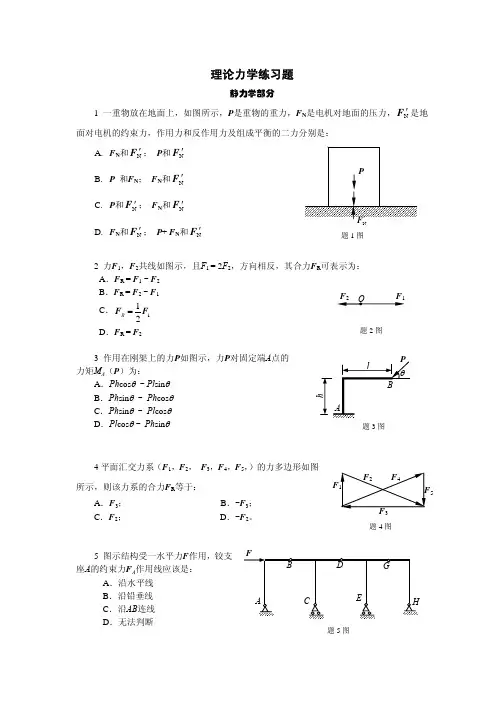
第1章 静力学基础
填空题
1、 欲使力F 沿x 、y 方向的分力的大小相等,则α=( 60 ),β=( 120)(任写一组);欲使力F 在x 、y 轴上的投影相等,则α=( 45 ),β=( 90 )。
x
题1
图 题3 图
2、 空间二力偶等效的条件是(力偶矩矢相等 )。
3、 图示长方形刚体,仅受二力偶作用,已知其力偶矩满足12M M =-,该长方体是否平衡?答:
( 等效 )。
4、 在平面约束中,由约束本身的性质就可以确定约束力方位的约束有(活动铰支座,二力杆件 ),可以确定约束力方向的约束有(光滑面接触,柔索 ),方向不能确定的约束有(固定铰支座,固定端约束 )(各写出两种约束)。
5、 力偶矩矢是一个矢量,它的大小为( 矢的长度 ),它的方向为(垂直力偶作用面)。

静力学补充练习1一、单选题(共0分)1.关于静摩擦力的说法,下列正确的是()A.静摩擦的方向总是与物体的相对运动的趋势方向相同B.静摩擦的方向总是与物体的相对运动的趋势方向相反C.两个相对静止的物体之间一定有静摩擦力的作用D.受静摩擦力作用的物体一定是静止的【答案】B【详解】AB.静摩擦力的方向总是与物体的相对运动的趋势方向相反,故A错误,B正确;C.两个相对静止的物体之间不一定有静摩擦力的作用,要满足静摩擦力产生的条件才会有静摩擦力,故C错误;D.运动的物体也可能受静摩擦力,比如在水平路面上,汽车启动时,车厢地板上的物体会受到静摩擦力的作用,故D错误。
故选B。
2.轮椅分为电动和手动轮椅,是用于伤员、病员、残疾人居家康复、周转运输、就诊、外出活动的重要移动工具。
如图是一款手动轮椅,该轮椅共有4个轮子,人用双手推动手轮圈,轮椅向前运动。
关于地面对4个轮子的摩擦力,下列说法正确的是()A.前轮、后轮受到的摩擦力都向前B.前轮、后轮受到的摩擦力都向后C.前轮受到的摩擦力向前,后轮受到的摩擦力向后D.前轮受到的摩擦力向后,后轮受到的摩擦力向前【答案】D【详解】因人在后轮用力,则后轮相对地面有向后滑动的趋势,可知后轮受到的摩擦力向前;前轮相对地面有向前运动的趋势,则前轮受到的摩擦力向后。
故选D。
3.如图所示,只有B物体左面是光滑的,其余各接触面都是粗糙的。
如果用水平力F将物体A和B压紧在竖直墙上不动,则物体A受到的摩擦力的情况是()A .左、右都受向上的摩擦力B .左侧受向上的摩擦力,右侧受向下的摩擦力C .左、右都受向下的摩擦力D .左侧受向下的摩擦力,右侧受向上的摩擦力【答案】D【详解】B 物体左面是光滑的,说明B 左侧只受水平力F 的作用,B 右侧受到向上的摩擦力,与其重力平衡,A 物体左侧受B 右侧施加的向下的摩擦力,A 还受到向下的重力,则A 物体右侧一定受向上的摩擦力,ABC 错误,D 正确。
1-3 试画出图示各结构中构件AB的受力图的受力图1-4 试画出两结构中构件ABCD的受力图的受力图1-5 试画出图a和b所示刚体系整体各个构件的受力图所示刚体系整体各个构件的受力图1-5a 1-5b 在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
为二力杆,受力方向分别沿着各杆端点连线的方向。
为二力杆,受力方向分别沿着各杆端点连线的方向。
6F 2 F BCF ABB45oy x F BCF CD C60o F 130ox y 力构成封闭的力多边形,如图所示。
力构成封闭的力多边形,如图所示。
为二力杆为二力杆((受力如图所示受力如图所示)),故曲杆10a F BC60o F 130o F 2 F BCAB45o 解:机构中AB杆为二力杆,点A,B出的约束力方向即可确定。
由力偶系作用下刚体的平衡条件,点O,C处的约束力方向也可确定,各杆的受力如图所示。
对BC杆有:0=åM30sin20=-××MCBFB对AB杆有:杆有:ABFF=对OA杆有:杆有: 0=åM01=×-AOFMA求解以上三式可得:mNM×=31,NFFFCOAB5===,方向如图所示。
,方向如图所示。
////2-6求最后简化结果。
解:解:2-6a2-6a坐标如图所示,各力可表示为坐标如图所示,各力可表示为: :j Fi FF23211+=,i FF=2,j Fi FF23213+-=先将力系向A点简化得(红色的):j Fi FFR3+=,kFaMA23=方向如左图所示。
由于AR MF^,可进一步简化为一个不过A点的力点的力((绿色的绿色的)),主矢不变,其作用线距A点的距离ad43=,位置如左图所示。
,位置如左图所示。
2-6b同理如右图所示,可将该力系简化为一个不过A点的力(绿色的),主矢为:,主矢为:i F F R2-= 其作用线距A 点的距离a d43=,位置如右图所示。
1 静力学内容讲解1静力学内容讲解1[静力学]内容讲解第一章静力学【竞赛知识要点】重心共点力作用下物体的平衡物体平衡的种类力矩刚体的平衡流体静力学(静止流体中的压强)【内容讲解】一.物体的战略重点1.常见物体的重心:质量均匀分布的三角板的重心在其三条中线的交点;质量均匀分布的半径r的半球体的重心在其对称轴上距球心3r/8处;质量均匀分布的高为h的圆锥体的重心在其对称轴上距顶点为3h/4处。
2.战略重点:在xyz三维坐标系中,将质量为m的物体分割为质点m1、m2、m3……mn.设重心坐标为(x0,y0,z0),各质点座标为(x1,y1,z1),(x2,y2,z2)……(xn,yn,zn).那么:mx0=∑miximy0=∑miyimz0=∑mizi【例题】1、(1)存有一质量均匀分布、厚度光滑的直角三角板abc,∠a=30°∠b=90°,该三角板水平置放,被a、b、c三点下方的三个支点提振着,三角板恒定时,a、b、c三点受到的支持力各就是na、nb、nc,则三力的大小关系就是.(2)半径为r的均匀球体,球心为o点,今在此球内挖去一半径为0.5r的小球,且小球恰与大球面内切,则挖去小球后的剩余部分的重心距o点距离为.2、如图所示,质量原产光滑、厚度光滑的梯形板abcd,cd=2ab,求该梯形的战略重点边线。
3、在质量分布均匀、厚度均匀的等腰直角三角形abc(角c为直角)上,切去一等腰三角形apb,如图所示。
如果剩余部分的重心恰在p点,试证明:△apb的腰长与底边长的比为4、(1)质量分别为m,2m,3m……nm的一系列小球(可以视作质点),用长均为l的细绳相连,用短也就是l的细绳立于天花板上,如图所示。
谋总战略重点的边线5、如图所示,质量均匀分布的三根细杆围成三角形abc,试用作图法作出其重心的位置。
6、如图所示,半径为r圆心角为θ的一段质量均匀分布的圆弧,谋其战略重点边线。
例题2-1 海水的比重为1.025,标准大气压为,试求以下各深度处的海水表压强和绝对压强。
海水密度310001000 1.0251025kg/m D ρ==⨯=; 海水重度310259.8110055N/m g γρ==⨯=解: 海水密度310001000 1.0251025kg/m D ρ==⨯=海水重度310259.8110055N/m g γρ==⨯= 由p h γ=可得 表压强:绝对压强:由于atm p p h γ=+,所以绝对压强就是在上述各项上再加上一个大气压例题2-2 潜艇内的水银气压计读数800mm a =,多管水银差压计读数500mm b =,海平面上水银气压计读数为760mm ,海水重度为10055N/m 3,试求潜艇在海面下的深度H 。
题2-2 图式中s γ为海水重度310055N/m s γ=;Hg γ为水银重度313.69810N/m Hg γ=⨯;解: 由潜艇中的水银气压计可以得出潜艇中的绝对压强为由多管水银差压计可知潜艇外面的绝对压强为这一潜艇外面绝对压强与海平面上的绝对压强a p 之差正反映了潜艇所在的水深H ,于是可得 ()2Hg aassa b p p p H γγγ+--==式中s γ为海水重度310055N/m s γ=;Hg γ为水银重度313.69810N/m Hg γ=⨯;760mmHg 0.76mHg 13.698100.76Pa a p ===⨯⨯。
将数据代入,有 [答]:13.8m H =例题2-3水在所示的管道内流动。
为测量流体压力,在管道某截面处连接一U 管压差计,指示液为水银,读数100mm,800mm R h ==。
为防止水银扩散至空气中,在水银液面上方充入少量水,其高度可忽略不计。
当地大气压力为101.3kPa ,试求管路中心处流体的压力。
题2-3 图解:过U 管右侧的水银面作水平面A A '-,那么根据流体静力学根本方程可得于是 w a Hg p p gh gR ρρ=-- 式中 101300Pa a p = 取3w 31000kg/m 13600kg/mHg ρρ==那么 10130010009.810.8136009.810.180140Pa p =-⨯⨯-⨯⨯=由计算结果可知,该处流体的绝对压力低于大气压力,故该处流体的真空度为。
大工14秋《船舶与海洋工程静力学》在线作业1
一,单选题
1. 船舶遭受海损事故而使舱室进水,但仍能保持一定的浮性和稳性而不致沉没或倾覆的能力。
指的是船舶的哪个性能?()
A. 快速性
B. 稳性
C. 抗沉性
D. 操纵性
?
正确答案:C
2. 辛浦生第一法适用条件为n一定是()。
A. 奇数
B. 偶数
?
正确答案:B
3. 船体外形一般都()双向曲面。
A. 是
B. 不是
?
正确答案:A
4. 船体计算常根据()用数值积分方法进行近似计算。
A. 结构图
B. 布置图
C. 横剖面图
D. 型线图
?
正确答案:D
5. 推进器的研究属于()的研究。
A. 船舶稳性
B. 船舶浮性
C. 船舶快速性
D. 船舶操纵性
?
正确答案:C
二,多选题
1. 在船体计算中,哪个数值积分法的原理是用抛物线代替曲线?()。