05五年级奥数——完全平方数

第八讲 完全平方数一个数如果是另一个整数的完全平方，那么我们就称这个数为完全平方数，也叫做平方数。

例如：0，1，4，9，16，25，36，49，64，81，100，121，144，169，196，225，256，289，324，361，400，441，484，……判断一个数是否为完全平方数，我们可以尝试能否将它分解为两个相同自然数的乘积，这就需要用到分解质因数的知识。

阅读小材料：毕达哥拉斯发现，当小石子的数目是1、4、9、16……等数时，小石子都能摆成正方形，他把这些数叫“正方形数”，如图所示：分别记各图所示的小石子个数为i a (i ＝1、2、3、……、n)不难发现： 1a ＝1＝212a ＝1＋3＝4＝223a ＝1＋3＋5＝9＝234a ＝1＋3＋5＋7＝16＝24………n a ＝1＋3＋5＋…＋(2n －1)＝[]2)1(1n n ⨯-+＝2n毕达哥拉斯通过直观图形把奇数和图形结合起来，得到一个定理：从1开始，任何连续个奇数之和都是完全平方数。

（注：这个和其实就是奇数个数的平方）【例一】 求自然数列前n 个奇数的和：1＋3＋5＋7＋……＋（2n －1）一讲一练：（04浙江五年级夏令营）袋子里共有415只小球，第一次从袋子里取出1只小球，第二次从袋子里取出3只小球，第三次从袋子里取出5只小球……依次地取球，如果剩下的球不够取，则将剩下的球留在袋中。

那么，最后袋中留下多少个球？【例二】 1234567654321×（1＋2＋……＋6＋7＋6＋……＋2＋1）是多少的平方？练习一：1×2×3×4×5×6×45×121是多少的平方？练习二：2A＝1008×B，其中A，B都是自然数，B的最小值是（）。

【例三】 36、49、60、64、72的约数各有多少个？约数个数是奇数的数有什么特征？一讲一练： 360、3969、7744各有多少个约数？【例四】（01ABC）少年宫游客厅内悬挂着200个彩色灯泡，这些灯泡或明或暗，十分有趣。

完全平方数知识框架一、完全平方数常用性质1.主要性质1.完全平方数的尾数只能是0，1，4，5，6，9。

不可能是2，3，7，8。

2.在两个连续正整数的平方数之间不存在完全平方数。

3.完全平方数的约数个数是奇数，约数的个数为奇数的自然数是完全平方数。

4.若质数p整除完全平方数2a，则p能被a整除。

2.性质性质1：完全平方数的末位数字只可能是0，1，4，5，6，9．性质2：完全平方数被3，4，5，8，16除的余数一定是完全平方数．性质3：自然数N为完全平方数⇔自然数N约数的个数为奇数．因为完全平方数的质因数分解中每个质-，因数出现的次数都是偶数次，所以，如果p是质数，n是自然数，N是完全平方数，且21|n p N则2|n p N．性质4：完全平方数的个位是6⇔它的十位是奇数．性质5：如果一个完全平方数的个位是0，则它后面连续的0的个数一定是偶数．如果一个完全平方数的个位是5，则其十位一定是2，且其百位一定是0，2，6中的一个．性质6：如果一个自然数介于两个连续的完全平方数之间，则它不是完全平方数．二、一些重要的推论1.任何偶数的平方一定能被4整除；任何奇数的平方被4（或8）除余1.即被4除余2或3的数一定不是完全平方数。

2.一个完全平方数被3除的余数是0或1.即被3除余2的数一定不是完全平方数。

3.自然数的平方末两位只有：00，01，21，41，61，81，04，24，44，64，84，25，09，29，49，69，89，16，36，56，76，96。

4.完全平方数个位数字是奇数（1，5，9）时，其十位上的数字必为偶数。

5.完全平方数个位数字是偶数（0，4）时，其十位上的数字必为偶数。

6.完全平方数的个位数字为6时，其十位数字必为奇数。

7.凡个位数字是5但末两位数字不是25的自然数不是完全平方数；末尾只有奇数个“0”的自然数不是完全平方数；个位数字为1，4，9而十位数字为奇数的自然数不是完全平方数。

三、重点公式回顾：平方差公式：22()()a b a b a b -=+-完全平方数是数论板块中一个比较精华的小分支，从知识特点上讲属于约数倍数和质数合数交叉的知识体系，其题目多为考察上述两块综合性知识，是杯赛和小升初试卷中的一个热点【例1】已知自然数n 满足：12!除以n 得到一个完全平方数，则n 的最小值是。

奥数：完全平方数1、把1—50这50个数的平方数从小到大排成一个多位数149162536……，请问这个多位数共有（）位数字。

分析与解答：1-3的平方只有一位数，共3个数字；4-9的平方有两位数字，共2×6=12个数字；10-31的平方有三位数字，共有3×22=66个数字；32-50的平方有四位数字，共有4×19=76个数字；合计：3+12+66+76=157个数字。

2、46305乘以一个自然数a，积是一个完全平方数，则最小的a是（）。

分析与解答：46305=5×3×3×3×7×7×7所以a最小是5×3×7=105。

3、祖孙三人，孙子和爷爷的年龄之积是1512，而爷爷，父亲，孙子三人的年龄之积是完全平方数，父亲的年龄是（）岁。

分析与解答：1512=3×3×3×2×2×2×7要使1521乘一个数的积是完全平方数，那么这个数最小是：3×2×7=42。

所以父亲的年龄是42岁。

4、把一个两位数的个位与十位数字交换后得到一个新数，它与原来的数字加起来恰好是某个自然数的平方，这个和数是（）。

分析与解答：我们设这个数原来为10a+b，那么现在是10b+a，它们的和为11×（a+b）是一个完全平方数，所以a+b必等于11，那么这个和数就为11×11=121。

5、已知n/2是完全平方数，n/3是立方数，则n的最小值为（）。

分析与解答：根据n/2是完全平方数，我们知道n里面有奇数个质因数2，而联系n/3是立方数，所以我们知道n里至少有3个质因数2；同样的道理我们知道n里至少有4个质因数3，那么n最小值为2×2×2×3×3×3×3=648。

6、已知一个自然数的平方的十位数是8，这个完全平方数的个位数字是（）。

奥数数论：完全平方数要点及解题技巧一、完全平方数的定义：一个数如果是另一个整数的完全平方，那么我们就称这个数为完全平方数，也叫做平方数。

二、完全平方数特征：1.末位数字只能是：0、1、4、5、6、9；反之不成立。

2.除以3余0或余1；反之不成立。

3.除以4余0或余1；反之不成立。

4.约数个数为奇数；反之成立。

5.奇数的平方的十位数字为偶数；反之不成立。

6.奇数平方个位数字是奇数；偶数平方个位数字是偶数。

7.两个相临整数的平方之间不可能再有平方数。

平方差公式：X2-Y2=（X-Y）（X+Y）完全平方和公式：（X+Y）2=X2+2XY+Y2完全平方差公式：（X-Y）2=X2-2XY+Y2三、完全平方数的性质：性质1：完全平方数的末位数只能是0,1,4,5,6,9。

性质2：奇数的平方的个位数字为奇数，十位数字为偶数。

性质3：如果完全平方数的十位数字是奇数，则它的个位数字一定是6；反之，如果完全平方数的个位数字是6，则它的十位数字一定是奇数。

性质4：偶数的平方是4的倍数；奇数的平方是4的倍数加1。

性质5：奇数的平方是8n+1型；偶数的平方为8n或8n+4型。

性质6：平方数的形式必为下列两种之一：3k,3k+1。

性质7：不能被5整除的数的平方为5k±1型，能被5整除的数的平方为5k型。

性质8：平方数的形式具有下列形式之一：16m,16m+1,16m+4,16m+9。

性质9：完全平方数的数字之和只能是0,1,4,7,9。

性质10：为完全平方数的充要条件是b为完全平方数。

性质11：如果质数p能整除a，但p的平方不能整除a，则a不是完全平方数。

性质12：在两个相邻的整数的平方数之间的所有整数都不是完全平方数，即若n^2<k^2<(n+1)^2，则k一定不是整数。

性质13：一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n本身)。

1. 學習完全平方數的性質；2. 整理完全平方數的一些推論及推論過程3. 掌握完全平方數的綜合運用。

一、完全平方數常用性質1.主要性質 1.完全平方數的尾數只能是0，1，4，5，6，9。

不可能是2，3，7，8。

2.在兩個連續正整數的平方數之間不存在完全平方數。

3.完全平方數的約數個數是奇數，約數的個數為奇數的自然數是完全平方數。

4.若質數p 整除完全平方數2a ，則p 能被a 整除。

2.性質性質1：完全平方數的末位數字只可能是0，1，4，5，6，9．性質2：完全平方數被3，4，5，8，16除的餘數一定是完全平方數．性質3：自然數N 為完全平方數⇔自然數N 約數的個數為奇數．因為完全平方數的質因數分解中每個質因數出現的次數都是偶數次，所以，如果p 是質數，n 是自然數，N 是完全平方數，且21|n p N -，則2|n p N ．性質4：完全平方數的個位是6⇔它的十位是奇數．性質5：如果一個完全平方數的個位是0，則它後面連續的0的個數一定是偶數．如果一個完全平方數的個位是5，則其十位一定是2，且其百位一定是0，2，6中的一個．性質6：如果一個自然數介於兩個連續的完全平方數之間，則它不是完全平方知識點撥教學目標5-4-5.完全平方數及應用（二）數．3.一些重要的推論1.任何偶數的平方一定能被4整除；任何奇數的平方被4（或8）除餘1.即被4除餘2或3的數一定不是完全平方數。

2.一個完全平方數被3除的餘數是0或1.即被3除餘2的數一定不是完全平方數。

3.自然數的平方末兩位只有：00，01，21，41，61，81，04，24，44，64，84，25，09，29，49，69，89，16，36，56，76，96。

4.完全平方數個位數字是奇數（1，5，9）時，其十位上的數字必為偶數。

5.完全平方數個位數字是偶數（0，4）時，其十位上的數字必為偶數。

6.完全平方數的個位數字為6時，其十位數字必為奇數。

7.凡個位數字是5但末兩位數字不是25的自然數不是完全平方數；末尾只有奇數個“0”的自然數不是完全平方數；個位數字為1，4，9而十位數字為奇數的自然數不是完全平方數。

一个自然数自乘所得的积称为完全平方数，100以内的完全平方数（又称平方数）是0、1、2x2=4、3x3=9,4x416,5x5=25,6x6=36,7x7=49,8x8=64,9x9=81共10个。

平方数有些特别的性质，可以解决一些有趣的问题：少年宫游戏厅内悬挂着200个彩色灯泡，这些灯泡或明或暗，闪烁不停。

这200个灯泡按1~200编号，它们每过1秒变化一下自己的明暗状态。

开始时，灯泡全部是暗的；第1秒，全部灯泡是亮着的；第2秒，凡编号为2的倍数的灯泡改变自己的明暗状态，即变暗。

第3秒，凡编号为3的倍数的灯泡改变自己的明暗状态：明的变暗，暗的变明，...,以此类推，第n秒钟，凡编号为n 的倍数的灯泡改变自己的明暗状态，每200秒钟为一周期，即到201秒时，全部灯泡大放光明，然后继续上述规则改变原来的状态。

问：第200秒时明亮的灯泡有多少？事实上，每个灯泡如果明暗改变次数为偶数次时，它还保持原来的明暗状态；如果变化次数为奇数次时，则明暗状态发生改变，原来明亮的灯泡将变暗，原来不亮的的灯泡将变明亮。

由于平方数的不同约数个数为奇数，从第2秒开始（此时偶数编号灯泡变暗，奇数编号灯泡变亮）起到200秒止，中间的平方数有4，9，16，25，36，49，64，81，100，121，144，169，196，在这些秒时，同样编号的灯泡由暗变明，加上1号灯泡始终是亮的，共14个灯泡是亮的。

下面举例来讨论平方数的一些问题。

从1~1989的自然数中，完全平方数共有个。

试一试在324，897，211，247，546中，哪些数是完全平方数。

46035乘以一个自然数a，是一个平方数，a最小是多少？试一试203500乘一个自然数a，是一个平方数，求a最小是多少？下面是一个算式：11x2+1x2x3+1x2x3x4+1x2x3x4x5+1x2x3x4x5x6.这个算式的得数能否是某个数的平方？请找出符合下列性质的所有四位数：（1）它是一个平方数（2）开始两位数的数字要相同（3）最末两位数的数字要相同试一试自然数N是一个两位数，它是一个完全平方数，而且N的个位数字与十位数字都是完全平方数，这样的自然数是自然数的平方按大小排成1，4，9，16，25，36，49，...,问第612个位置的数是几？下式中每个汉字表示1~9中的一个数字，不同的汉字代表不同的数字。

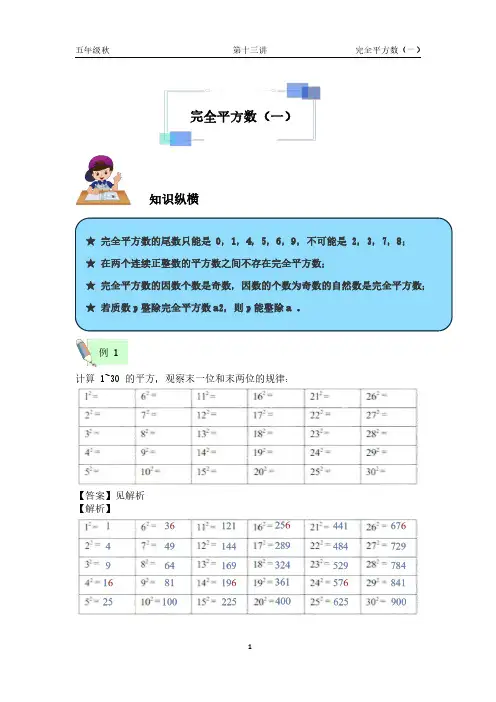
完全平方数（一）知识纵横★完全平方数的尾数只能是0，1，4，5，6，9，不可能是2，3，7，8；★在两个连续正整数的平方数之间不存在完全平方数；★完全平方数的因数个数是奇数，因数的个数为奇数的自然数是完全平方数；★若质数p 整除完全平方数a2，则p 能整除a 。

计算1~30的平方，观察末一位和末两位的规律：【答案】见解析【解析】例1（1）平方数的末尾可以是___________________________；一定不能是_____________________________________。

（2）当末尾是_________________时，十位必须是偶数，当十位是奇数时，个位只有____________________________。

（3）你还发现了哪些规律？【答案】见解析【解析】试判断下列各数是不是完全平方数，若不是请在横线上打“×”，并口述判断理由；若是请在横线上写出它是哪个数的平方。

（1）997：_______；（2）7613：______；（3）7840：______；（4）1275：______；（5）1199：______；（6）7886：______；（7）2304：______。

【答案】【解析】已知：12345654321×36是一个完全平方数，求它是几的平方?【答案】666666【解析】例2试一试11234567654321×(1+2+3+4+5+6+7+6+5+4+3+2+1)是_________的平方。

【答案】【解析】下面是一个算式：1+1×2+1×2×3+1×2×3×4+1×2×3×4×5+1×2×3×4×5×6，这个算式的得数能否是某个数的平方？【答案】不能【解析】小钱、小陆、小戴三人在猜一个1~99中的自然数，结果：小钱说：“它是一个完全平方数，且比5小。

完全平方数的性质和应用课前预习数字不重复的平方数观察只含两位数字的完全平方数：16＝42 25＝52 36＝62 49＝72 64＝82 81＝92 其中每个平方数都是两位数字互不相同。

含有三位数字的完全平方数，情况就不一样了。

例如： 100＝102 121＝112 144＝122这些平方数都已包含重复数字。

不过，也有许多三位平方数的各位数字互不相同，例如： 169＝132 196＝142 256＝162 62＝5252 含有四位数的完全平方数，包含重复数字的现象更为普遍。

1444＝382 不含重复数字的四位平方数也很多，例如1024＝322 2401＝492 1369＝372 1936＝442如果一个平方数有九位数字，每位数字各不相同，并且不含数字0，那么在这个数中，从1到9全都出现，全只出现一次。

其中最小的是：139854276＝118262，最大的是：923187456＝303842知识框架完全平方数常用性质1.性质性质1：完全平方数的末位数字只可能是0，1，4，5，6，9．不可能是2，3，7，8。

性质2：在两个连续正整数的平方数之间不存在完全平方数。

性质3：自然数N 为完全平方数自然数N 约数的个数为奇数．因为完全平方数的质因数分解中每个质因数出现的次数都是偶数次.性质4：若质数p 整除完全平方数，则p 能被整除。

2.一些重要的推论（1）任何偶数的平方一定能被4整除；任何奇数的平方被4（或8）除余1.即被4除余2或3的数一定不是完全平方数。

（2）一个完全平方数被3除的余数是0或1.即被3除余2的数一定不是完全平方数。

（3）自然数的平方末两位只有：00，01，21，41，61，81，04，24，44，64，84，25，09，29，49，69，89，16，36，56，76，96。

⇔⇔2a a（4）完全平方数个位数字是奇数（1，5，9）时，其十位上的数字必为偶数。

（5）完全平方数个位数字是偶数（0，4）时，其十位上的数字必为偶数。

第八讲 完全平方数一个数如果是另一个整数的完全平方，那么我们就称这个数为完全平方数，也叫做平方数。

例如：0，1，4，9，16，25，36，49，64，81，100，121，144，169，196，225，256，289，324，361，400，441，484，……判断一个数是否为完全平方数，我们可以尝试能否将它分解为两个相同自然数的乘积，这就需要用到分解质因数的知识。

阅读小材料：毕达哥拉斯发现，当小石子的数目是1、4、9、16……等数时，小石子都能摆成正方形，他把这些数叫“正方形数”，如图所示：分别记各图所示的小石子个数为i a (i ＝1、2、3、……、n)不难发现：1a ＝1＝212a ＝1＋3＝4＝223a ＝1＋3＋5＝9＝234a ＝1＋3＋5＋7＝16＝24………n a ＝1＋3＋5＋…＋(2n －1)＝[]2)1(1n n ⨯-+＝2n 毕达哥拉斯通过直观图形把奇数和图形结合起来，得到一个定理：从1开始，任何连续个奇数之和都是完全平方数。

（注：这个和其实就是奇数个数的平方）【例一】 求自然数列前n 个奇数的和：1＋3＋5＋7＋……＋（2n －1）一讲一练：（04浙江五年级夏令营）袋子里共有415只小球，第一次从袋子里取出1只小球，第二次从袋子里取出3只小球，第三次从袋子里取出5只小球……依次地取球，如果剩下的球不够取，则将剩下的球留在袋中。

那么，最后袋中留下多少个球？【例二】 1234567654321×（1＋2＋……＋6＋7＋6＋……＋2＋1）是多少的平方？练习一：1×2×3×4×5×6×45×121是多少的平方？A＝1008×B，其中A，B都是自然数，B的最小值是（）。

练习二：2【例三】 36、49、60、64、72的约数各有多少个？约数个数是奇数的数有什么特征？一讲一练： 360、3969、7744各有多少个约数？【例四】（01ABC）少年宫游客厅内悬挂着200个彩色灯泡，这些灯泡或明或暗，十分有趣。

五年级奥数完全平方数五年级奥数完全平方数：0，1，4，9，16，25，36，49，64，81，100，121，144，169，196，225，256，289，324，361，400，441，484，……判断一个数是否为完全平方数，我们可以尝试能否将它分解为两个相同自然数的乘积，这就需要用到分解质因数的知识。

阅读小材料：毕达哥拉斯发现，当小石子的数目是1、4、9、16……等数时，小石子都能摆成正方形，他把这些数叫“正方形数”，如图所示：分别记各图所示的小石子个数为i a (i ＝1、2、3、……、n)不难发现：1a ＝1＝212a ＝1＋3＝4＝223a ＝1＋3＋5＝9＝234a ＝1＋3＋5＋7＝16＝24………n a ＝1＋3＋5＋…＋(2n －1)＝[]2)1(1n n ⨯-+＝2n 毕达哥拉斯通过直观图形把奇数和图形结合起来，得到一个定理：从1开始，任何连续个奇数之和都是完全平方数。

（注：这个和其实就是奇数个数的平方）【例一】 求自然数列前n 个奇数的和：1＋3＋5＋7＋……＋（2n －1）一讲一练：（04浙江五年级夏令营）袋子里共有415只小球，第一次从袋子里取出1只小球，第二次从袋子里取出3只小球，第三次从袋子里取出5只小球……依次地取球，如果剩下的球不够取，则将剩下的球留在袋中。

那么，最后袋中留下多少个球？【例二】 1234567654321×（1＋2＋……＋6＋7＋6＋……＋2＋1）是多少的平方？练习一：1×2×3×4×5×6×45×121是多少的平方？A＝1008×B，其中A，B都是自然数，B的最小值是（）。

练习二：2【例三】 36、49、60、64、72的约数各有多少个？约数个数是奇数的数有什么特征？一讲一练： 360、3969、7744各有多少个约数？【例四】（01ABC）少年宫游客厅内悬挂着200个彩色灯泡，这些灯泡或明或暗，十分有趣。

第 1 页2019年小学奥数数论专题——完全平方数1．1234567654321(1234567654321)⨯++++++++++++是 的平方． 2． 112123123412345123456+⨯+⨯⨯+⨯⨯⨯+⨯⨯⨯⨯+⨯⨯⨯⨯⨯,这个算式的得数能否是某个数的平方？3．写出从360到630的自然数中有奇数个约数的数．4．一个数的完全平方有39个约数，求该数的约数个数是多少？5．从1到2019的所有自然数中,乘以72后是完全平方数的数共有多少个？6． 1016与正整数a 的乘积是一个完全平方数，则a 的最小值是________．7．已知3528a 恰是自然数b 的平方数，a 的最小值是 。

8．已知自然数n 满足：12!除以n 得到一个完全平方数，则n 的最小值是 。

9．考虑下列32个数:1!，2!，3!，……，32!,请你去掉其中的一个数，使得其余各数的乘积为一个完全平方数,划去的那个数是 ．10．一个数减去100是一个平方数,减去63也是一个平方数，问这个数是多少？11．能否找到这么一个数，它加上24，和减去30所得的两个数都是完全平方数?12．三个自然数，它们都是完全平方数，最大的数减去第二大的数的差为80，第二大的数减去最小的数的差为60，求这三个数．13．有5个连续自然数，它们的和为一个平方数,中间三数的和为立方数，则这五个数中最小数的最小值为 ．14．求一个最小的自然数，它乘以2后是完全平方数，乘以3后是完全立方数，乘以5后是5次方数．15．两个完全平方数的差为77,则这两个完全平方数的和最大是多少？最小是多少?16．有两个两位数，它们的差是14，将它们分别平方，得到的两个平方数的末两位数(个位数和十位数)相同,那么这两个两位数是 ．(请写出所有可能的答案）17．A 是一个两位数，它的6倍是一个三位数B ，如果把B 放在A 的左边或者右边得到两个不同的五位数，并且这两个五位数的差是一个完全平方数（整数的平方),那么A 的所有可能取值之和为 ．18．已知ABCA 是一个四位数，若两位数AB 是一个质数,BC 是一个完全平方数，CA 是一个质数与一个不为1的完全平方数之积，则满足条件的所有四位数是________．19．一个自然数与自身相乘的结果称为完全平方数．已知一个完全平方数是四位数，且各位数字均小于7．如果把组成它的数字都加上3,便得到另外一个完全平方数，求原来的四位数．20．有一个正整数的平方，它的最后三位数字相同但不为0，试求满足上述条件的最小的正整数．21．能够找到这样的四个正整数，使得它们中任意两个数的积与2002的和都是完全平方数吗?若能够，请举出一例;若不能够，请说明理由．22．证明：形如11，111，1111，11111，…的数中没有完全平方数。

第11讲完全平方数一、知识要点1.完全平方数的定义：一个自然数与自身相乘的乘积叫做完全平方数或平方数.2.完全平方数表：3.完全平方数的常用性质：完全平方数乘完全平方数是完全平方数。

二、例题精选【例1】计算：215，225，235，245，255，并说明规律。

【巩固1】计算：162,262,362,462,562，并说明规律。

【例2】试判断下列数是否是完全平方数，若不是请在横线上简述判断理由；若是请在横线上写出它是哪个数的平方。

997：____________________；6983：____________________；5112：____________________；6478：____________________；【巩固2】试判断下列数是否是完全平方数，若不是请在横线上简述判断理由；若是请在横线上写出它是哪个数的平方。

1199：____________________；7886：____________________；1834：____________________；1275：____________________；【例3】A 是由2017个“9”组成的多位数，即920179999个 ，A 是不是某个自然数B 的平方？如果是，写出B ；如果不是，请说明理由．【巩固3】A 是由2018个“56”组成的多位数，即 5620185656...5656个，A 是不是某个自然数B 的平方？如果是，写出B；如果不是，请说明理由．【例4】1016与正整数a的乘积是正整数b的平方，则a的最小值是多少？b的最小值是多少？【巩固4】已知3528a恰是自然数b的平方数，a的最小值是多少？b的最小值是多少？【例5】因为快乐学校的孩子都很喜欢平方数，所以将年份数是平方数的年份定义为“快乐年”。

如公元900年，900=302，所以公元900年是快乐年。

那么从1000年到今年（2018年），有多少个“快乐年”？【巩固5】黑暗世界的小朋友不喜欢年份数是平方数的年份，因为这些年份总会遭遇困恼，其他年份则不会。

完全平方数的性质和应用课前预习数字不重复的平方数观察只含两位数字的完全平方数：16＝4225＝5236＝6249＝7264＝8281＝92其中每个平方数都是两位数字互不相同。

含有三位数字的完全平方数，情况就不一样了。

例如：100＝102121＝112144＝122这些平方数都已包含重复数字。

不过，也有许多三位平方数的各位数字互不相同，例如：169＝132196＝142256＝162 62＝5252含有四位数的完全平方数，包含重复数字的现象更为普遍。

1444＝382不含重复数字的四位平方数也很多，例如1024＝322 2401＝4921369＝3721936＝442如果一个平方数有九位数字，每位数字各不相同，并且不含数字0，那么在这个数中，从1到9全都出现，全只出现一次。

其中最小的是：139854276＝118262，最大的是：923187456＝303842知识框架完全平方数常用性质1.性质性质1：完全平方数的末位数字只可能是0，1，4，5，6，9．不可能是2，3，7，8。

性质2：在两个连续正整数的平方数之间不存在完全平方数。

性质3：自然数N为完全平方数⇔自然数N约数的个数为奇数⇔．因为完全平方数的质因数分解中每个质因数出现的次数都是偶数次.性质4：若质数p整除完全平方数2a，则p能被a整除。

2.一些重要的推论（1）任何偶数的平方一定能被4整除；任何奇数的平方被4（或8）除余1.即被4除余2或3的数一定不是完全平方数。

（2）一个完全平方数被3除的余数是0或1.即被3除余2的数一定不是完全平方数。

（3）自然数的平方末两位只有：00，01，21，41，61，81，04，24，44，64，84，25，09，29，49，69，89，16，36，56，76，96。

（4）完全平方数个位数字是奇数（1，5，9）时，其十位上的数字必为偶数。

（5）完全平方数个位数字是偶数（0，4）时，其十位上的数字必为偶数。

（6）完全平方数的个位数字为6时，其十位数字必为奇数。

【五年级数学思维拓展】趣味入门—勇闯智慧岛（二）——完全平方数⑴认识完全平方数1.认识完全平方数2.完全平方数的性质3.完全平方数的解题技巧1. 1＋1×2＋1×2×3＋1×2×3×4＋1×2×3×4×5这个算式的得数能否是某个数的平方？2. 我们知道：121＝112，12321＝1112，1234321＝11112…都是完全平方数。

那么，121＋12321＋1234321＋…＋12345678987654321是不是完全平方数？3. 判断下面哪个是完全平方数？⑴ 108 ⑵ 224 ⑶ 625 ⑷ 1033（即是该课程的课后测试）1. 简答题：什么是完全平方数？2. 写出从360到630的自然数中有奇数个约数的数3. 一个数的完全平方有39个约数，求该数的约数个数是多少？4. 从1到2008的所有自然数中，乘以72后是完全平方数的数共有多少个？5. 1016与正整数a 的乘积是一个完全平方数，则a 的最小值是________．1. 答案：把一个自然数平方所得到的数叫做完全平方数或叫做平方数。

2. 一个合数的约数的个数是在严格分解质因数之后,将每个质因数的指数(次数)加1后所得的乘积.如:1400严格分解质因数后为23×52×7,所以它的约数有(3+1)×(2+1)×(1+1)=4×3×2=24个.(包括1和它自身)如果某个自然数有奇数个约数,那么这个数的所有质因子的个数均为偶数个.这样它们加1后均是奇数,所得的乘积才能是奇数.而所有质因数的个数均是偶数个的数为完全平方数.即完全平方数(除0外)有奇数个约数,反过来,有奇数个约数的数一定是完全平方数．由以上分析知,我们所求的为360～630之间有多少个完全平方数?18×18=324,19×19=361,25×25=625,26×26=676,所以在360～630之间的完全平方数为192,202,212,222,232,242,252．即360到630的自然数中有奇数个约数的数为361,400,441,484,529,576,625．3. 设该数为1212n a a a n p p p ⨯⨯⨯L ，那么它的平方就是1222212n a a a n p p p ⨯⨯⨯L ， 因此()()()1221212139n a a a +⨯+⨯⨯+=L ．由于39139313=⨯=⨯，⑴所以，1213a +=，22113a +=，可得11a =，26a =；故该数的约数个数为()()116114+⨯+=个；⑵或者，12139a +=，可得119a =，那么该数的约数个数为19120+=个． 所以这个数的约数个数为14个或者20个．4完全平方数，其所有质因数必定成对出现．而327223266=⨯=⨯⨯，所以满足条件的数必为某个完全平方数的2倍，由于2313119222008232322048⨯⨯=<<⨯⨯=，所以221⨯、222⨯、……、2231⨯都满足题意，即所求的满足条件的数共有31个．5. 先将1016分解质因数：310162127=⨯，由于1016a ⨯是一个完全平方数，所以至少为422127⨯，故a 最小为2127254⨯=。

小升初奥数数论完全平方数知识点【篇一】一、完全平方数的定义：一个数如果是另一个整数的完全平方，那么我们就称这个数为完全平方数，也叫做平方数。

二、完全平方数特征：1.末位数字只能是：0、1、4、5、6、9;反之不成立。

2.除以3余0或余1;反之不成立。

3.除以4余0或余1;反之不成立。

4.约数个数为奇数;反之成立。

5.奇数的平方的十位数字为偶数;反之不成立。

6.奇数平方个位数字是奇数;偶数平方个位数字是偶数。

7.两个相临整数的平方之间不可能再有平方数。

平方差公式：X2-Y2=(X-Y)(X+Y)完全平方和公式：(X+Y)2=X2+2XY+Y2完全平方差公式：(X-Y)2=X2-2XY+Y2三、完全平方数的性质：性质1：完全平方数的末位数只能是0,1,4,5,6,9。

性质2：奇数的平方的个位数字为奇数，十位数字为偶数。

【篇二】例题例1、一个自然数减去45及加上44都仍是完全平方数，求此数。

解：设此自然数为x，依题意可得x-45=m^2 (1)x+44=n^2................(2)(m,n为自然数)(2)-(1)可得n^2-m^2=89,(n+m)(n-m)=89但89为质数，它的正因子只能是1与89，于是。

解之，得n=45。

代入(2)得。

故所求的自然数是1981。

例2、求证：四个连续的整数的积加上1，等于一个奇数的平方。

分析：设四个连续的整数为n,(n+1),(n+2),(n+3)，其中n为整数。

欲证n(n+1)(n+2)(n+3)+1是一奇数的平方，只需将它通过因式分解而变成一个奇数的平方即可。

证明：设这四个整数之积加上1为m，则m=n(n+1)(n+2)(n+3)+1=(n^2+3n+1)^2=[n(n+1)+(2n+1)]^2而n(n+1)是两个连续整数的积，所以是偶数;又因为2n+1是奇数，因而n(n+1)+2n+1是奇数。

这就证明了m是一个奇数的平方。

【篇三】练习题1、祖孙三人，孙子和爷爷的年龄的乘积是1512，而爷爷、父亲、孙子三人的年龄之积是完全平方数，则父亲的年龄是()岁。

完全平方数一、完全平方数常用的三条性质1．完全平方数的末位数字必须是：0，1，4，5，6，9。

2．完全平方数分解质因数后每个质因子都必须有偶数个。

推论：完全平方数的约数一定有奇数个；有奇数个约数的数一定是完全平方数。

3．完全平方数除以3的余数只可能为为0或1；偶数的平方是4的倍数，奇数的平方除以4余1。

二、基本公式平方差公式:a2-b2=（a+b）（a-b）三、两个特殊的完全平方数7744（四位数中唯一一个前两位数字相同，后两位数字也相同）；1444（后三位数字相同的数中最小的）。

【例 1】下面是一个算式：1+1⨯2+1⨯2⨯3+1⨯2⨯3⨯4+1⨯2⨯3⨯4⨯5+1⨯2⨯3⨯4⨯5⨯6。

这个算式的得数能否是某个数的平方。

【巩固】8，88，888，8888…中有完全平方数吗？【例 2】已知3528 a恰是自然数b的平方数，a的最小值是。

【巩固】已知m，n都是自然数，且n2=126m，则n的最小值为。

【例 3】12+22+32+…+20012+20022除以4的余数是。

【巩固】A是由2002个“4”组成的多位数，即4444，A是不是某个自然数B的平方？如果是，写2002个4出B；如果不是，请说明理由。

【例 4】一个数减去100是一个平方数，减去63也是一个平方数，问这个数是多少？【巩固】能否找到这么一个数，它加上24，和减去30所得的两个数都是完全平方数？【例 5】两数乘积为2800，而且已知其中一数的约数个数比另一数的约数个数多1，那么这两个数分别是 、 。

【巩固】两数乘积为1080，而且已知其中一数的约数个数比另一数的约数个数多1，那么这两个数分别是 、 。

〖答案〗【例 1】 不能【巩固】 无【例 2】 2【巩固】 42【例 3】 1【巩固】 A =2002个44444=22⨯2002个11111，如果A 是完全平方数，需要2002个11111也是完全平方数，而2002个11111除以4余3；所以A 不是某个自然数的平方【例 4】 424【巩固】 不能【例 5】 24，52⨯7【巩固】 36，30。

五年级奥数-平方数22=4，32＝9，52＝25…，像4、9、25…这样的数，推及一般情况，我们把一个自然数平方所得到的数叫做完全平方数或叫做平方数。

如.12=1，22＝4，32＝9，42=16，…，112=121，122=144，…其中1，4，9，16，…，121，144，…都叫做完全平方数.下面让我们观察一下，把一个完全平方数分解质因数后，各质因数的指数有什么特征。

例如：把下列各完全平方数分解质因数：9，36，144，1600，275625。

解：9=32 36=22×32144=32×241600=26×52 275625=32×54×72可见，一个完全平方数分解质因数后，各质因数的指数均是偶数。

反之，如果把一个自然数分解质因数之后，各个质因数的指数都是偶数，那么这个自然数一定是完全平方数。

如36＝62，144=122，1600=402，275625=5252。

例4、已知2×2×3×A的积是一个平方数，那么A最小是，这个积是的平方。

练习1、已知2×2×3×5×A的积是B的平方，那么A最小是，B 是。

练习2、已知12×A的积是B的平方，那么A最小是，B是。

练习3、已知36×A的积是B的平方，那么A最小是，B是。

练习4、一个整数a与1080的乘积是一个完全平方数，求a的最小值与这个平方数。

练习6、一个自然数A与2100的积是B的平方，A最小是都是？这时B是多少？练习7、1176×a=b2，a、b都是自然数，求a的最小值，此时b是多少？6、13500除以一个最小的数使商成为一个完全平方数，这个最小的数是。

8、AABB表示一个完全平方数，符合条件的四位数是。

AB8是一个完全平方数，这个完全平方数是。

已知五位数BA10、把360表示成两个自然数的平方差有许多组，请尽可能多有写出来。