专训4用线段成比例法解几何问题的几种常见类型

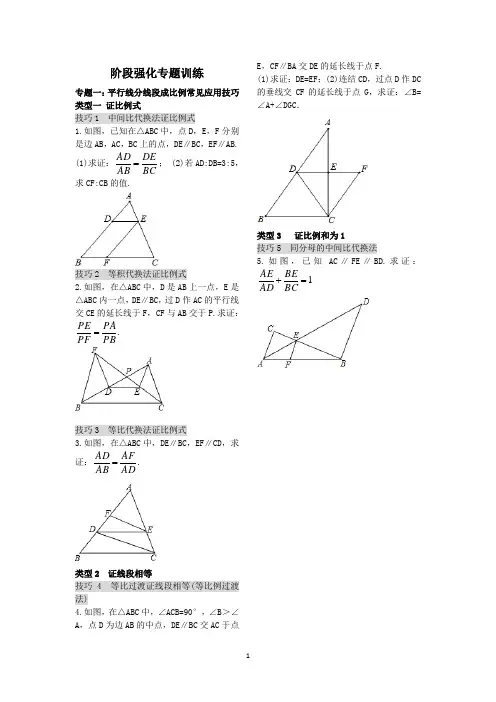
阶段强化专题训练专题一：平行线分线段成比例常见应用技巧 类型一 证比例式技巧1 中间比代换法证比例式1.如图，已知在△ABC 中，点D ，E ，F 分别是边AB ，AC ，BC 上的点，DE ∥BC ，EF ∥AB. (1)求证：BCDEAB AD =； (2)若AD:DB=3:5，求CF:CB 的值.技巧2 等积代换法证比例式2.如图，在△ABC 中，D 是AB 上一点，E 是△ABC 内一点，DE ∥BC ，过D 作AC 的平行线交CE 的延长线于F ，CF 与AB 交于P.求证：PBPAPF PE =.技巧3 等比代换法证比例式3.如图，在△ABC 中，DE ∥BC ，EF ∥CD ，求证：ADAFAB AD =.类型2 证线段相等技巧 4 等比过渡证线段相等(等比例过渡法)4.如图，在△ABC 中，∠ACB=90°，∠B ＞∠A ，点D 为边AB 的中点，DE ∥BC 交AC 于点E ，CF ∥BA 交DE 的延长线于点F.(1)求证：DE=EF ；(2)连结CD ，过点D 作DC 的垂线交CF 的延长线于点G ，求证：∠B=∠A+∠DGC ．类型3 证比例和为1技巧5 同分母的中间比代换法5.如图，已知AC ∥FE ∥BD.求证：1=+BCBEAD AE专题二：证明相似三角形的方法名师点金要找三角形相似的条件，关键抓住以下几点：(1)已知角相等时，找两对对应角相等，若只能找到一对对应角相等，判断夹相等的角的两边是否对应成比例；(2)无法找到角相等时，判断三边是否对应成比例；(3)除此之外，也可考虑平行线分线段成比例定理及相似三角形的“传递性．．．”.方法1 利用边或角的关系判定两直角三角形相似1.下面关于直角三角形相似叙述错误的是( )A.有一锐角对应相等的两个直角三角形相似B.两直角边对应成比例的两个直角三角形相似C.有一条直角边相等的两个直角三角形相似D.两个等腰直角三角形相似2.如图，BC⊥AD，垂足为C，AD=6.4，CD=1.6，BC=9.3，CE=3.1.求证：△ABC∽△DEC.方法2 利用角判定两三角形相似3.如图，△ABC是等边三角形，CE是外角平分线，点D在AC上，连接BD并延长，与CE 交于点 E. (1)求证：△ABD∽△CED； (2)若AB＝6，AD＝2CD，求BE的长．方法3 利用边角判定两三角形相似4.如图，AB＝3AC，BD＝3AE，又BD∥AC，点B，A，E在同一条直线上．求证：△ABD∽△CAE. 方法4 利用三边判定两三角形相似5.如图，AD是△ABC的高，E，F分别是AB，AC的中点．求证：△DEF∽△ABC.专训三巧作平行线构造相似三角形名师点金：解题时，往往会遇到要证的问题与相似三角形联系不上或者说图中根本不存在相似三角形的情况，添加辅助线构造相似三角形是这类几何证明题的一种重要方法．常作的辅助线有以下几种：(1)由比例式作平行线；(2)有中点时，作中位线；(3)根据比例式，构造相似三角形．训练角度1 巧连线段的中点构造相似三角形1.如图，在△ABC中，E，F是边BC上的两个三等分点，D是AC的中点，BD分别交AE，AF于点P，Q，求BP:PQ:QD.训练角度 2 过顶点作平行线构造相似三角形2.如图，在△ABC中，AC＝BC，F为底边AB 上一点，BF:AF＝3:2，取CF的中点D，连接AD并延长交BC于点E，求BE:EC的值．3.如图，过△ABC的顶点C任作一直线，与边AB及中线AD分别交于点F和点E.求证：AE:ED＝2AF:FB.训练角度 3 过一边上的点作平行线构造相似三角形4.如图，在△ABC中，AB＞AC，在边AB上取一点D，在AC上取一点E，使AD＝AE，直线DE和BC的延长线交于点P.求证: BP:CP=BD:EC.训练角度 4 过一点作平行线构造相似三角形5.如图，在△ABC中，点M为AC边的中点，点E为AB上一点，且AE=41AB，连接EM并延长交BC的延长线于点D.求证：BC＝2CD. 作辅助线的方法一：作辅助线的方法二：作辅助线的方法三：作辅助线的方法四：全章整合提升密码专训一：证比例式或等积式的技巧 名师点金证比例式或等积式，若遇问题中无平行线或相似三角形时，则需构造平行线或相似三角形，得到等比例线段；若比例式或等积式中的线段分布在两个三角形或不在两个三角形中，可尝试证这两个三角形相似或先将它们转化到两个三角形中再证两三角形相似，若在两个明显不相似的三角形中，可运用中间比代换．技巧1 构造平行线法1.如图，在△ABC 中，D 为AB 的中点，DF 交AC 于点E ，交BC 的延长线于点F ， 求证：AE ·CF ＝BF ·EC.2.如图，已知△ABC 的边AB 上有一点D ，边BC 的延长线上有一点E ，且AD ＝CE ，DE 交AC 于点F ，试证明：AB ·DF ＝BC ·EF.技巧2 三点找三角形相似法3.如图，在▱ABCD 中，E 是AB 延长线上的一点，DE 交BC 于F. 求证：DC AE ＝CF AD.4.如图，在△ABC 中，∠BAC ＝90°，M 为BC 的中点，DM ⊥BC 交CA 的延长线于D ，交AB于E.求证：AM 2＝MD ·ME.技巧3 构造相似三角形法5.如图，在等边三角形ABC 中，点P 是BC 边上任意一点，AP 的垂直平分线分别交AB ，AC 于点M ，N. 求证：BP ·CP ＝BM ·CN.技巧4 等比过渡法6.如图，在△ABC 中，AB ＝AC ，DE ∥BC ，点F 在边AC 上，DF 与BE 相交于点G ，且∠EDF ＝∠ABE. 求证：(1)△DEF ∽△BDE ；(2)DG ·DF ＝DB ·EF.7.如图，CE 是Rt △ABC 斜边上的高，在EC 的延长线上任取一点P ，连接AP ，作BG ⊥AP于点G ，交CE 于点D. 求证：CE 2＝DE ·PE.技巧5 两次相似法8.如图，在Rt △ABC 中，AD 是斜边BC 上的高，∠ABC 的平分线BE 交AC 于E ，交AD 于F. 求证：BF BE ＝ABBC.9.如图，在▱ABCD 中，AM ⊥BC ，AN ⊥CD ，垂足分别为M ，N.求证：(1)△AMB ∽△AND ；(2)AM AB ＝MNAC.技巧6 等积代换法10.如图，在△ABC 中，AD ⊥BC 于D ，DE ⊥AB 于E ，DF ⊥AC 于F.求证：AE AF ＝ACAB.技巧7 等线段代换法11.如图，等腰△ABC 中，AB ＝AC ，AD ⊥BC 于点D ，点P 是AD 上一点，CF ∥AB ，延长BP 交AC 于点E ，交CF 于点F ，求证：BP 2＝PE ·PF.12.已知：如图，AD 平分∠BAC ，AD 的垂直平分线EP 交BC 的延长线于点P.求证：PD 2＝PB ·PC.专训二 巧用“基本图形”探索相似条件 名师点金：几何图形大多数由基本图形复合而成，因此熟悉三角形相似的基本图形，有助于快速、准确地识别相似三角形，从而顺利找到解题思路和方法．相似三角形的四类结构图： 1.平行线型2.相交线型3.子母型4.旋转型训练角度1 平行线型1.如图，在△ABC 中，BE 平分∠ABC 交AC 于点E ，过点E 作ED ∥BC 交AB 于点D.(1)求证：AE ·BC ＝BD ·AC ； (2)如果S △ADE ＝3，S △BDE ＝2，DE ＝6，求BC 的长．训练角度2 相交线型2.如图，点D ，E 分别为△ABC 的边AC ，AB 上的点，BD ，CE 交于点O ，且EO BO ＝DOCO ，试问△ADE 与△ABC 相似吗？请说明理由．训练角度3 子母型3.如图，在△ABC 中，∠BAC ＝90°，AD ⊥BC 于点D ，E 为AC 的中点，ED 的延长线交AB 的延长线于点F.求证：AB AC ＝DFAF.训练角度4 旋转型 4.如图，已知∠DAB ＝∠EAC ，∠ADE ＝∠ABC.求证：(1)△ADE ∽△ABC ；(2)AD AE ＝BD CE.专训三 利用相似三角形巧证线段的数量和位置关系 名师点金：判断两线段之间的数量和位置关系是几何中的基本题型之一．由角的关系推出“平行或垂直”是判断位置关系的常用方法，由相似三角形推出“相等”是判断数量关系的常用方法．训练角度1 证明两线段的数量关系 类型1： 证明两线段的相等关系1.如图，已知在△ABC 中，DE ∥BC ，BE 与CD 交于点O ，直线AO 与BC 边交于点M ，与DE 交于点N. 求证：BM ＝MC.2.如图，一直线和△ABC 的边AB ，AC 分别交于点D ，E ，和BC 的延长线交于点F ，且AE:CE ＝BF:CF. 求证：AD ＝DB.类型2 证明两线段的倍分关系3.如图，在△ABC 中，BD ⊥AC 于点D ，CE ⊥AB 于点E ，∠A ＝60°，求证：DE ＝12BC.4.如图，AM 为△ABC 的角平分线，D 为AB 的中点，CE ∥AB ，CE 交DM 的延长线于E. 求证：AC ＝2CE.训练角度2 证明两线段的位置关系 类型1：证明两线段平行 5.如图，已知点D 为等腰直角三角形ABC 的斜边AB 上一点，连接CD ，DE ⊥CD ，DE ＝CD ，连接CE ，AE.求证：AE ∥BC.6.在△ABC 中，D ，E ，F 分别为BC ，AB ，AC 上的点，EF ∥BC ，DF ∥AB ，连接CE 和AD ，分别交DF ，EF 于点N ，M.(1)如图①，若E 为AB 的中点，图中与MN 平行的直线有哪几条？请证明你的结论； (2)如图②，若E 不为AB 的中点，写出与MN 平行的直线，并证明．类型2 证明两线垂直7.如图，在△ABC 中，D 是AB 上一点，且AC2＝AB ·AD ，BC 2＝BA ·BD ，求证：CD ⊥AB.8.如图，已知矩形ABCD ，AD ＝13AB ，点E ，F把AB 三等分，DF 交AC 于点G ，求证：EG ⊥DF.专训四巧用位似解三角形中的内接多边形问题名师点金位似图形是特殊位置的相似图形，它具有相似图形的所有性质，位似图形必须具备三个条件：(1)两个图形相似；(2)对应点的连线相交于一点；(3)对应边互相平行或在同一直线上.类型1 三角形的内接正三角形问题1.如图,用下面的方法可以画△AOB的内接等边三角形,阅读后证明相应问题.画法:①在△AOB内画等边三角形CDE,使点C在OA上,点D在OB上；②连接OE并延长,交AB于点E′,过点E′作E′C′∥EC,交OA于点C′,作E′D′∥ED,交OB于点D′；③连接C′D′,则△C′D′E′是△AOB的内接等边三角形.求证:△C′D′E′是等边三角形.类型2 三角形的内接矩形问题2.求作:内接于已知△ABC的矩形DEFG,使它的边EF在BC上,顶点D,G分别在AB,AC上,并且有DE∶EF=1∶2.类型 3 三角形的内接正形问题(方程思想)3.如图,△ABC 是一块锐角三角形余料,边BC=120mm ,高AD=80mm ,要把它加工成正方形零件,使正方形的一边QM 在BC上,其余两个顶点P ,N 分别在AB,AC上,则这个正方形零件的边长是多少?4.(1)如图①,在△ABC 中,点D ,E ,Q 分别在AB ,AC ,BC 上,且DE ∥BC ,AQ交DE 于点P.求证:DP：BQ=PE：QC.(2)在△ABC 中,∠BAC =90°,正方形DEFG 的四个顶点在△ABC 的边上,连接AG ,AF ,分别交DE 于M ,N 两点.①如图②,若AB=AC=1,直接写出MN的长；②如图③,求证:MN²=DM·EN.专训五： 图形的相似中的五种热门考点 名师点金：相似是初中数学的重要内容，也是中考重点考查内容之一，而对于成比例线段、相似三角形的判定与性质、位似图形等都是命题的热点．考点一： 比例线段及性质1.下列各组长度的线段，成比例线段的是( )A. 2 cm ，4 cm ，4 cm ，8 cmB. 2 cm ，4 cm ，6 cm ，8 cmC. 1 cm ，2 cm ，3 cm ，4 cmD. 2.1 cm ，3.1 cm ，4.3 cm ，5.2 cm2．若a 2＝b 3＝c 4＝d 7≠0，则a ＋b ＋c ＋d c ＝________.3．如图，乐器上的一根弦AB ＝80 cm ，两个端点A ，B 固定在乐器板面上，支撑点C 是靠近点B 的黄金分割点，则支撑点C 到端点A 的距离约为________．(5≈2.236，结果精确到0.01)考点二： 平行线分线段成比例4.如图，若AB ∥CD ∥EF ，则下列结论中，与AD AF 相等的是( ) A.AB EF B.CD EF C.BO OE D.BC BE5.如图，在Rt △ABC 中，∠ACB ＝90°，∠ABC ＝60°，以AC 为边向三角形外作正方形ACDE ，连接BE 交AC 于F ，若BF ＝ 3 cm ，则EF ＝________.6.如图，在△ABC 中，AM ∶MD ＝4∶1，BD ∶DC ＝2∶3，求AE ∶EC 的值．考点三 相似三角形的性质与判定7.已知△ABC ∽△DEF ，若△ABC 与△DEF 的相似比为3∶4，则△ABC 与△DEF 的面积之比为( ) A.4:3 B.3:4 C.16:9 D.9:168.在平行四边形ABCD 中，点E 在AD 上，且AE ∶ED ＝3∶1，CE 的延长线与BA 的延长线交于点F ，则S △AEF ∶S 四边形ABCE 为( ) A.3∶4 B.4∶3 C.7∶9 D.9∶79.若两个相似多边形的面积之比为1∶4，周长之差为6，则这两个相似多边形的周长分别是________．10.如图，△ABC 是直角三角形，∠ACB ＝90°，CD ⊥AB 于D ，E 是AC 的中点，ED 的延长线与CB 的延长线交于点F.(1)求证：FD 2＝FB ·FC ； (2)若FB ＝5，BC ＝4，求FD 的长．11.如图，四边形ABCD 是正方形，BD 是对角线，BE 平分∠DBC 交DC 于点E ，点F 是BC 的延长线上一点，且CE ＝CF ，BE 的延长线交DF 于点M.(1)求证：BM ⊥DF ； (2)若正方形ABCD 的边长为2，求ME ·MB.考点四相似三角形的应用12.一天晚上，李明和张龙利用灯光下的影子长来测量一路灯的高度CD.如图，当李明走到点A处时，张龙测得李明直立时身高AM 与影子长AE正好相等；接着李明沿AC方向继续向前走，走到点B处时，李明直立时身高BN的影子恰好是线段AB，并测得AB＝1.25 m，已知李明直立时的身高为1.75 m，求路灯的高度CD.(结果精确到0.1 m)13.某高中学校为高一新生设计的学生板凳的正面视图如图所示，其中BA＝CD，BC＝20 cm，BC，EF平行于地面AD且到地面AD的距离分别为40 cm，8 cm.为使板凳两腿底端A，D之间的距离为50 cm，那么横梁EF的长应为多少？(材质及其厚度等暂忽略不计)考点五图形的位似14.如图，已知正方形ABCD，以点A为位似中心，把正方形ABCD的各边缩小为原来的一半，得正方形A′B′C′D′，则点C′的坐标为________．15.如图，在6×8的网格图中，每个小正方形的边长均为1，点O和△ABC的顶点均在小正方形的顶点上．(1)以O为位似中心，在网格图中作△A′B′C′和△ABC位似，且相似比为1∶2；(2)连接(1)中的AA′，求四边形AA′C′C 的周长．(结果保留根号)专训六全章热门考点整合应用名师点金：本章主要内容为：平行线分线段成比例，相似三角形的判定及性质，位似图形及其画法等，涉及考点、考法较多，是中考的高频考点．其主要考点可概括为：3个概念、2个性质、1个判定、2个应用、1个作图、1个技巧．考点一：3个概念概念1：成比例线段1.下列各组线段，是成比例线段的是( )A.3cm，6cm，7cm，9cmB.2cm，5cm，0.6dm，8cmC.3cm，9cm，1.8dm，6cmD.1cm，2cm，3cm，4cm2.有一块三角形的草地，它的一条边长为25m，在图纸上，这条边的长为5cm，其他两条边的长都为4cm，则其他两边的实际长度都是________m.概念2：相似多边形3.如图，已知∠1′＝∠1，∠2′＝∠2，∠3′＝∠3，∠4′＝∠4，∠D′＝∠D，试判断四边形A′B′C′D′与四边形ABCD是否相似，并说明理由．概念3：位似图形4.如图，在△ABC中，A，B两个顶点在x轴的上方，点C的坐标是(－1，0)．以点C为位似中心，在x轴的下方作△ABC的位似图形，并把△ABC的边放大到原来的2倍，记所得的像是△A′B′C.设点B的对应点B′的坐标是(a，b)，求点B的坐标．考点二： 2个性质性质1：平行线分线段成比例的性质5.如图，在Rt△ABC中，∠A＝90°，AB＝8，AC＝6.若动点D从点B出发，沿线段BA运动到点A为止，运动速度为每秒2个单位长度．过点D作DE∥BC交AC于点E，设动点D运动的时间为x秒，AE的长为y.(1)求出y关于x的函数解析式，并写出自变量x的取值范围；(2)当x为何值时，△BDE的面积有最大值，最大值为多少？性质2：相似三角形的性质6.如图，已知D是BC边上的中点，且AD＝AC，DE⊥BC，DE与BA相交于点E，EC 与AD相交于点F.(1)求证：△ABC∽△FCD；(2)若S△FCD＝5，BC＝10，求DE的长．考点三： 1个判定——相似三角形的判定7.如图，△ACB为等腰直角三角形，点D为斜边AB上一点，连接CD，DE⊥CD，DE＝CD，连接AE，过C作CO⊥AB于O.求证：△ACE ∽△OCD.8.如图，在⊙O的内接△ABC中，∠ACB＝90°，AC＝2BC，过点C作AB的垂线l交⊙O 于另一点D，垂足为点E.设P是上异于点A，C的一个动点，射线AP交l于点F，连接PC 与PD，PD交AB于点G. (1)求证：△PAC∽△PDF； (2)若AB＝5，弧AP＝弧BP，求PD 的长．考点四： 2个应用应用1：测高的应用9.如图，在离某建筑物CE 4 m处有一棵树AB，在某时刻，1.2 m的竹竿FG垂直地面放置，影子GH长为2 m，此时树的影子有一部分落在地面上，还有一部分落在建筑物的墙上，墙上的影子CD高为2 m，那么这棵树的高度是多少？应用2：测宽的应用10.如图，一条小河的两岸有一段是平行的，在河的一岸每隔6 m有一棵树，在河的对岸每隔60 m有一根电线杆，在有树的一岸离岸边30 m处可看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住，并且在这两棵树之间还有三棵树，求河的宽度．考点五： 1个作图——作一个图形的位似图形11.如图，在方格纸中(每个小方格的边长都是1个单位长度)有一点O和△ABC.请以点O 为位似中心，把△ABC缩小为原来的一半(不改变方向)，画出△ABC的位似图形．考点六： 1个技巧——证明四条线段成比例的技巧12.如图，已知△ABC，∠BAC的平分线与∠DAC的平分线分别交BC及BC的延长线于点P，Q. (1)求∠PAQ的度数； (2)若点M为PQ的中点，求证：PM2＝CM·BM.。

高考解析几何中线段比值问题
在高考解析几何中，线段比值问题是比较常见的一类问题。

这类问题通常涉及到直线、圆、椭圆、双曲线等几何图形，以及点、线段之间的位置关系和长度计算。

以下是一些解决线段比值问题的方法和思路：
1. 利用坐标表示线段长度：在解析几何中，可以通过坐标来表示点的位置，进而计算线段的长度。

对于线段比值问题，可以将线段的两个端点坐标求出，然后利用两点间距离公式计算出线段长度，再进行比值计算。

2. 利用几何性质：解析几何中的几何图形具有一些特殊的性质，例如圆的性质、椭圆的性质、双曲线的性质等。

在解决线段比值问题时，可以利用这些性质来简化计算，例如利用圆的切线性质、椭圆的定义等。

3. 建立函数关系式：对于一些复杂的线段比值问题，可以通过建立函数关系式来解决。

例如，可以设出线段长度的变量，然后根据题目条件列出方程，进而求出线段比值。

4. 利用三角形相似或全等：在一些情况下，可以通过判断线段所在的三角形是否相似或全等来解决线段比值问题。

如果两个三角形相似或全等，则它们对应边的比值相等。

5. 数形结合：在解决线段比值问题时，要注重数形结合，将几何图形与代数计算相结合，通过画图、观察等方法帮助理解和解决问题。

需要注意的是，具体的解题方法会因题目不同而有所差异，需要根据具体情况选择合适的方法。

同时，在解题过程中要注意对题目的条件和要求进行仔细分析，避免出现错误。

期末提分练案 ∴△COD≌△COB(SAS)．∴∠CDO＝∠CBO＝90°. 又∵点 D 在⊙O 上，∴CD 是⊙O 的切线，故①正确． ∵△COD≌△COB，∴CD＝CB. ∵CD，CB 是⊙O 的切线，∴CO 平分∠DCB. ∴CO⊥DB，故②正确． ∵CD 为⊙O 的切线，AB 为⊙O 的直径， ∴∠EDO＝∠ADB＝90°.
人教版 九年级下
期末提分练案
第3讲 相似图形的判定及性质
第6课时 综合训练
用线段成比例法解几何问题的三种常
见类型
习题链接
提示：点击 进入习题
1B 2 ①③④
3 见习题 4A 5 见习题
ห้องสมุดไป่ตู้
答案显示
期末提分练案 1．(2019·安徽)如图，在 Rt△ABC 中，∠ACB＝90°，AC＝6，
BC＝12，点 D 在边 BC 上，点 E 在线段 AD 上，EF⊥AC 于 点 F，EG⊥EF 交 AB 于点 G.若 EF＝EG，则 CD 的长为( ) A．3.6 B．4 C．4.8 D．5
期末提分练案 【点拨】如图，连接 OD. ∵AB 为⊙O 的直径，BC 为⊙O 的切线，∴∠CBO＝90°. ∵AD∥OC，∴∠DAO＝∠COB，∠ADO＝∠COD. 又∵OA＝OD，∴∠DAO＝∠ADO. ∴∠COD＝∠COB.
CO＝CO， 在△COD 和△COB 中，∠COD＝∠COB，
OD＝OB，
期末提分练案 ∴32＋OCOC＝PPBB＋ ＋323PPBB＝58. ∴OC＝52，∴AB＝5. ∵△PBC∽△PCA，∴PPBC＝BACC＝12. ∴AC＝2BC. 在 Rt△ABC 中，AC2＋BC2＝AB2， ∴(2BC)2＋BC2＝52，解得 BC＝ 5. ∴AC＝2 5. ∴S△ABC＝12AC·BC＝5.

比 例 线 段◆比例线段1．相似形：在数学上，具有相同形状的图形称为相似形2．比例线段：在四条线段中，如果其中两条线段的比等于另外两条线段的比，那么这四条线段叫做成比例线段，简称比例线段3. 比例的项：已知四条线段a 、b 、c 、d ，如果a ∶b ＝c ∶d ，那么a 、b 、c 、d 叫做组成比例的项，线段a 、d 叫做比例的外项，线段b 、c 叫做比例的内项，线段d 叫做a 、b 、c 的第四比例项；比例中项：如果比例内项是两条相同的线段a ∶b ＝b ∶c ，即，那么线段b 叫做线段a 和c 的比例中项。

4. 比例的性质（1）基本性质:bc ad dc b a =⇔=， a ∶b ＝b ∶c ⇔b 2=ac 例1：6∶x = (5 +x )∶2 中的x = ；2∶3 = ( 5x -)∶x 中的x = 例2：若，则＝________（2）合、分比性质:dd c b b a d c b a d d c b b a d c b a -=-⇒=+=+⇒=或 注意:此性质是分子加（减）分母比分母,不变的是分母.想想是否可以拓展呢？即分母加（减）分子，不变的是分子例1：若43=-b b a ，则ba =_________ 例2：如果，则＝________（3）等比性质:若)0(≠+⋅⋅⋅+++=⋅⋅⋅===n f d b n m f e d c b a 则ba n f db m ec a =+⋅⋅⋅++++⋅⋅⋅+++. 例1：若9810z y x ==, 则 ______=+++z y z y x 例2：已知：，则＝________；如果，那么＝________例3:若a b+c =b c+a =c a+b=k ，求k 的值.（4）比例中项:若c a b c a b cb b a ,,2是则即⋅==的比例中项. 例1：已知：线段，若线段b 是线段a,c 的比例中项，则c ＝________例2： 2:)3(-a = )3(-a :8,则a ＝【练一练】1、 若a ∶3 =b ∶4 =c ∶5 , 且6=-+c b a , ___________,____,===c b a ；2、 已知x ∶y ∶z = 3∶4∶5 , 且12=++z y x , 那么_________,____,===z y x ；3、已知dc b a =＝f e ＝2 （b ＋d ＋f ≠0），求：（1）f d be c a ++++；（2）f d b e c a +-+-； （3）f d b ec a 3232+-+-；（4）f b ea 55--．4、 已知x ∶4 =y ∶5 = z ∶6 , 则 ①x ∶y ∶z = , ② )(y x +∶____)(=+z y ；5、 若322=-y y x , 则_____=yx ； 6、若345x y z ==，则x y z z ++＝ ．若x:y:z=2:3:4，则=+-+y x z y x 232 ．7、如果 ，则 ，。

线段成比例一、成比例线段 （一）知识点梳理1.把ba 的值叫做线段b a ,的比，若d cb a =，则称线段dc b a ,,,成比例线段。

2.bc ad d c b a dcb a =⇔=⇔=::，其中dc b a ,,,分别叫第一、第二、第三、第四比例项，d a ,称为外项， （a 称为前项，b 称为后项）c b ,称为内项；外项的积等于内项的积。

3.比例性质：①基本性质：bc ad dc b a =⇔=，如果ad=bc （a ，b ，c ，d 都不等于0，那么d cb a =）； ②反比性质：c da b d c b a =⇔=；③更比性质：a c a b b d c d =⇔=； ④合比性质：a c a b c db d b d±±=⇔=； ⑤等比性质：n n b a b a b a b a === 332211，则112121b a b b b a a a n n =+++++ 4.比例中项：若ac b =2，则称b 是ac 的比例中项5.若点P 分线段AB 得到较长线段是较短线段和整条线段的比例中项，则称点P 是线段AB 的黄金分割点；215,215--==较长线段较短线段整条线段较长线段叫做黄金比值。

（试证明） （二）题型讲解例1.下列各组中的四条线段成比例的是( )A.a=2，b=3，c=2，d=3B.a=4，b=6，c=5，d=10C.a=2，b=5，c=23，d=15D.a=2，b=3，c=4，d=1例2.已知线段a 、b 、c 、d 满足ab=cd ，把它改写成比例式，错误的是( ) A.a:d=c:b B.a:b=c:d C.d:a=b:c D.a:c=d:b 例3.若a=2，b=3，c=33，则a 、b 、c 的第四比例项d 为 例4.若ac=bd ，则下列各式一定成立的是( )A.d c b a =B.c c b d d a +=+C.c d b a =22D.dacd ab =例5.已知dcb a =,则下列式子中正确的是（ ） A.a:b=c 2:d 2B.a:d=c:bC.a:b=(a+c):(b+d)D.a:b=(a －d):(b －d) 例6.已知5:4:2::=c b a ，且632=+-a b a ，求c b a 23-+的值。

线段的比例问题线段的比例问题是数学中常见的一个概念，它涉及到了线段之间的相对长度关系。

在解决线段的比例问题时，可以利用几何知识和代数方法来求解。

本文将通过实例和步骤详细阐述解决线段的比例问题的方法和技巧。

1. 线段的比例定义在线段AB上，取一个点C分割成两个部分AC和CB，如果AC与CB之间的长度关系为a:b，可以表示为AC/CB=a/b（a和b为正数），则称线段AC与线段CB的比为a比b，也可以写作AC:CB=a:b。

2. 比例问题的解决步骤解决线段的比例问题的一般步骤如下：步骤一：了解题意首先，我们需要仔细阅读题目，理解题意，明确所给出的线段和要求的比例关系。

在理解题意的基础上，寻找线索和关键信息。

步骤二：画出示意图根据题目所给的线段和比例关系，在纸上画出示意图，标记出所给的线段和比例关系，为后续求解提供便利。

步骤三：设未知量根据题目要求，假设未知量，通常用字母表示。

例如，如果题目要求求解线段CD与线段EF的比例关系，可以设CD:EF=x:y，其中x和y为待求的未知量。

步骤四：利用等式求解根据已知条件和设定的未知量，利用等式求解未知量。

根据几何知识或代数方法，运用线段分割定理、相似三角形性质、等角关系等来推导和求解未知量。

同时，注意化简和整理结果，确保中间步骤的准确性和清晰性。

步骤五：验证结果在求解完未知量后，需要将结果代入题目中检验，验证结果的正确性。

确认结果是否满足题目所给的线段比例关系，若满足，则解题过程正确；若不满足，则需要重新检查求解过程，并找出错误之处。

3. 解题实例现举一个实例来说明线段的比例问题的求解过程。

例题：在线段AB上，点C将线段AB分为三等分，求线段AC和线段BC的比例关系。

解题步骤：步骤一：了解题意题目要求求解线段AC与线段BC之间的比例关系。

步骤二：画出示意图在纸上画出线段AB，并将线段AB等分为三等分，标记出点C。

C|------A------|||B步骤三：设未知量假设线段AC:CB=x:y，其中x和y为所求的未知量。

成比例线段知识点
成比例线段是初中数学中重要的概念之一，它涉及到线段的比例关系和相似三
角形的性质。

在学习成比例线段的过程中，我们需要掌握以下几个知识点：
1. 成比例线段的定义
成比例线段是指在两个线段中，它们的比等于另外两个线段的比。

即如果线段AB和线段CD成比例，那么就有AB/CD = AC/BD。

这个比例关系在几何学中非常
重要，它可以帮助我们解决许多与线段长度有关的问题。

2. 成比例线段的性质
成比例线段具有一些重要的性质，比如说如果两个线段成比例，那么它们的长
度比是唯一确定的，即使线段长度发生变化，它们的比例关系仍然成立。

此外，成比例线段的比例也可以用比例的倒数来表示，比如说如果AB/CD = 2/3，那么
CD/AB = 3/2。

3. 成比例线段的应用
成比例线段的应用非常广泛，它可以帮助我们解决许多实际问题，比如说测量
不规则图形的边长、比较不同尺寸的物体、计算地图的比例尺等。

在实际生活中，我们经常会用到成比例线段的知识，因此掌握好这个知识点对我们的日常生活和学习都非常有帮助。

总的来说，成比例线段是初中数学中的重要知识点，它涉及到线段的比例关系
和相似三角形的性质。

通过学习成比例线段，我们可以更好地理解线段的比例关系，解决实际问题，提高数学的应用能力。

希望同学们能够认真学习成比例线段的知识，掌握好相关的概念和性质，从而在数学学习中取得更好的成绩。

证明线段成比例问题的常用方法（1）方法一、三点定形法利用分析的方法，由欲证的比例式或等积式转化为比例式．寻找相似三角形，这是证明线段成比例问题最基本的方法之一，一般是找到以四条成比例线段为边的两个三角形，再证明这两个三角形相似．每一个三角形都是由三个不同的点所组成的，并且用三个不同的字母表示。

反过来想，由三个不同的字母必定可以确定一个三角形，如果四条成比例线段出自于一对相似三角形，我们必能从其比例式中看出是哪两个三角形相似。

【例1】如图，CD 、BE 是△ABC 的两条高，求证： ①AC AE AB AD ⋅=⋅ ②∠AED ＝∠ABC ③FE FB FC FD ⋅=⋅分析：①欲证AC AE AB AD ⋅=⋅即证ABACAE AD =I ．横看法：II ．竖找法：F ⑩DE ABC~AEB ∆⇒∆ADC ⇒∆AEBADC⇒∆ADE ⇒∆∆ACB ~ADE⇒∆⇒∆ADE试验：（射影定理）如图Rt △ABC 中，CD 是斜边AB 上的高， 求证： ①AB AD AC ⋅=2②BA BD BC ⋅=2③DB DA CD ⋅=2请用“三点定形法”尝试下面问题的可行性，看有何发现？ 1、已知：如图，△ABC 中，EF ∥BC ，AD 交EF 于G.求证： CDFGBD EG =；2、R t △ABC 中，∠C =90°，四边形DENM 为正方形， 求证：NB AM MN ⋅=2DCBAGABCF EDBCDEMNDCBADCBA证明线段成比例问题的常用方法（2）方法二、等量代换法当需要证明的比例式不能构成相似三角形时，往往需要进行等量代换，包括： 1.等比代换； 2.等线段代换； 3.等积代换．【例1】]已知：如图，AC 是□ABCD 的对角线，G 是AD 延长线上的一点，BG 交AC 于F ，交CD 于E ．求证：BFFEFG BF =。

归纳：这是利用中间比进行代换的典型例题，这种代换往往出现于平行截比定理以及相似三角形的综合应用．【例2】R t △ABC 中，∠C =90°，四边形DENM 为正方形， 求证：NB AM MN ⋅=2归纳：这是利用线段进行等量代换的典型例题，不难看出，这种代换方法往往需要含有等ABCDEMN腰三角形、平行四边形、正三角形、正方形、线段中点等已知条件或隐含条件．【例3】R t △ABC 中，∠BAC =90°， D 为AC 上一点，AE ⊥BD ①若DCB DEC ∠=∠，求证：D 为AC 的中点；②若AF ⊥BC 于F ，连EF ，求证：△BEF ∽△BCD归纳：此例为等积代换的典型例题，这种代换方法往往需要含有射影定理和另外一对相似三角形同时出现．【练习】△ABC 中，AD ⊥BC ，AB =AC ，E 为DA 上任意一点，CM ∥AB 交BE 于M ，BM 交AC 于F . 求证：EM EF BE ⋅=2ABCDEFABCDEABCEFM证明线段成比例问题的常用方法（3）方法三、辅助平行线法利用辅助平行线来转移比例是证明线段成比例的有效方法，这种方法经常通过平行线截比定理和平行相似定理来实现．【例1】如图，在△ABC 中，D 是AC 上一点，延长CB 到E ，使BE =AD ，ED 交AB 于F ．求证：ACBCEF DF．【例2】已知在△ABC 中，点D 为边BC 上一点，点E 为边AC 上的中点，AD 与BE 交于P ． （1）如图1，当BD ＝CD 时，PBPE＝ ；（2）如图2，当CD ＝2BD 时，求证：PE ＝PB ．DFABCEABC PE图1D图2ABC D PEFE DCB AFEDCB A【例3】如图，已知等腰Rt △ABC ，∠ACB ＝90°，AC ＝BC ，D 为BC 边上一动点，BC ＝nDC ，CE ⊥AD 于点E ，延长BE 交AC 于点F ． （1）若n ＝3，则=DE CE ，=DEAE（2）若n ＝2，求证：AF ＝2FC ；（3）当n ＝ ，F 为AC 的中点（直接填出结果，不要求证明）【练习】△ABC 中，D 是BC 中点，E 是AC 上一点，AD 、BE 交于F 。

初中二年级几何学习技巧如何解决线段比例与面积比例的问题在初中二年级的几何学习中，线段比例与面积比例是一个重要的知识点。

正确理解和应用线段比例与面积比例的技巧，对于解决相关问题非常关键。

本文将介绍一些有效的技巧，帮助同学们更好地掌握解决线段比例与面积比例的问题。

一、线段比例解决技巧1. 比例的定义和性质首先，我们需要理解比例的定义和性质。

比例是两个具有相同单位的量之间的对应关系。

在线段比例问题中，我们需要比较两个线段的长度，并确认它们是否成比例。

具体公式为：如果线段AB与线段CD 成比例，则有AB/CD = AC/BD。

掌握了比例的定义和性质后，我们就可以更好地解决线段比例的问题了。

2. 图形的放缩和相似线段比例与图形的放缩和相似有密切关系。

当两个图形相似时，它们的相应线段也成比例。

因此，我们可以利用图形的放缩和相似的特性，解决线段比例问题。

具体方法是通过计算两个图形的对应线段长度比例，来确定线段是否成比例。

3. 利用比例关系求解在实际问题中，有时候我们无法直接测量线段的长度，但可以根据线段的比例关系来求解。

例如，如果我们知道两个线段的比例为2:3，其中一个线段的长度为6cm，那么我们可以通过比例的性质计算出另一个线段的长度为9cm。

因此，利用比例关系可以方便地求解线段比例的问题。

二、面积比例解决技巧1. 面积比例的概念对于面积比例的问题，我们需要理解面积比例的概念。

面积比例是指两个图形的面积之间的对应关系。

具体公式为：如果图形A的面积为S1，图形B的面积为S2，那么它们的面积比例为S1:S2。

掌握了面积比例的概念后，我们就可以更好地解决面积比例的问题了。

2. 利用相似图形的性质与线段比例一样，面积比例与相似图形也有紧密的联系。

当两个图形相似时，它们的面积比例等于两个图形边长的比例的平方。

因此，我们可以利用相似图形的性质来解决面积比例的问题。

具体方法是通过计算图形边长的比例，然后将该比例的平方作为面积比例。

成比例线段的八种形式成比例线段是指两个线段的比值相等。

在几何学中，成比例线段有八种形式，分别是：1. 相等线段：当两个线段的长度相等时，它们是成比例线段的一种形式。

例如，AB和CD两个线段的长度相等，即AB = CD。

2. 同向线段：当两个线段的方向相同，并且它们的长度之比相等时，它们是成比例线段的一种形式。

例如，AB和CD两个线段的方向相同，并且它们的长度之比为k，即AB/CD = k。

3. 反向线段：当两个线段的方向相反，并且它们的长度之比相等时，它们是成比例线段的一种形式。

例如，AB和CD两个线段的方向相反，并且它们的长度之比为k，即AB/CD = k。

4. 互补线段：当两个线段的长度之和为常数，并且它们的长度之比相等时，它们是成比例线段的一种形式。

例如，AB和CD两个线段的长度之和为常数m，且它们的长度之比为k，即AB/(m-AB) = CD/(m-CD) = k。

5. 互逆线段：当两个线段的长度之积为常数，并且它们的长度之比相等时，它们是成比例线段的一种形式。

例如，AB和CD两个线段的长度之积为常数n，且它们的长度之比为k，即AB/CD = n/k。

6. 平方线段：当两个线段的长度之比等于它们的平方之比时，它们是成比例线段的一种形式。

例如，AB和CD两个线段的长度之比为k，且它们的平方之比为k^2，即AB^2/CD^2 = k^2。

7. 立方线段：当两个线段的长度之比等于它们的立方之比时，它们是成比例线段的一种形式。

例如，AB和CD两个线段的长度之比为k，且它们的立方之比为k^3，即AB^3/CD^3 = k^3。

8. 平方根线段：当两个线段的长度之比等于它们的平方根之比时，它们是成比例线段的一种形式。

例如，AB和CD两个线段的长度之比为k，且它们的平方根之比为√k，即√(AB/CD) = √k。

这八种形式的成比例线段在几何学中具有重要的应用价值，可以用于解决各种与线段长度相关的问题。

初一数学线段比例解题技巧
线段比例是初中数学中一个重要的知识点，它涉及到线段的长度和比例关系。

掌握线段比例的解题技巧对于解决这类问题至关重要。

解题步骤：
1. 确定已知条件：首先明确题目中给出的已知条件，如线段的长度或比例关系。

2. 画出图形：根据题意，画出相应的图形，以便更直观地理解问题。

3. 推导比例关系：根据已知条件和图形，推导出各线段之间的比例关系。

4. 求解未知量：利用比例关系，求解题目中要求的未知量。

5. 验证答案：最后，验证所得答案是否符合题意，确保解题过程无误。

注意事项：
1. 理解比例的基本性质：比例的基本性质是解决线段比例问题的关键，要熟练掌握。

2. 灵活运用相似三角形的性质：在解决线段比例问题时，常常需要利用相似三角形的性质进行推导。

3. 注意单位的一致性：在解题过程中，要确保所有涉及的长度单位一致，避免出现单位换算错误。

4. 细心审题：在解题前要仔细审题，明确题目要求和已知条件，避免因理解错误而导致解题错误。

通过以上步骤和注意事项，可以更好地掌握线段比例的解题技巧，提高解题效率和准确性。

初中数学“成比例线段”知识点全解析一、引言成比例线段是初中数学中的一个重要概念，它是研究比例关系的基础。

理解并掌握成比例线段的概念和性质，对于提高学生分析问题和解决问题的能力具有重要意义。

本文将详细解析成比例线段的概念、性质、判定方法以及应用，帮助学生更好地理解和掌握这一知识点。

二、成比例线段的概念1.定义：如果四条线段a, b, c, d满足a/b = c/d，那么我们就说这四条线段是成比例的，记作a:b = c:d。

2.术语解析：在a:b = c:d中，a和d称为比例的外项，b和c称为比例的内项。

三、成比例线段的性质1.等比性质：若a:b = c:d，则(a+b)/b = (c+d)/d。

这一性质表明，成比例线段的对应项之和与原线段的比例关系相同。

2.合比性质：若a:b = c:d，则(a-b)/b = (c-d)/d。

这一性质表明，成比例线段的对应项之差与原线段的比例关系相同。

3.更比性质：若a:b = c:d，则a/c = b/d。

这一性质表明，成比例线段的交叉项之比相等。

4.反比性质：若a:b = c:d，且b和d均不为0，则a/b = d/c。

这一性质表明，成比例线段的交叉项之积相等。

四、成比例线段的判定方法1.直接判定法：根据定义直接判断四条线段是否满足a/b = c/d。

2.等比中项法：如果两条线段的平方等于另外两条线段的乘积，那么这四条线段是成比例的。

即如果a² = bc，那么a, b, c以及另一条与它们成比例的线段d构成成比例线段。

3.相似三角形法：在相似三角形中，对应边之间的比例是相等的。

因此，可以通过证明两个三角形相似来判定四条线段是否成比例。

五、成比例线段的应用1.几何图形中的应用：在几何图形中，常常利用成比例线段的性质来解决一些问题，如证明两直线平行、证明两角相等、计算线段的长度等。

2.实际生活中的应用：在实际生活中，许多现象都与成比例线段密切相关。

例如，建筑设计师在设计建筑物时需要考虑不同部分之间的比例关系；摄影师在拍摄照片时需要运用成比例线段的原理来构图等。

专题05图形的相似重难点题型专训（6大题型）【题型目录】题型一比例的性质题型二线段的比题型三成比例线段题型四由平行判断成比例的线段题型五由平行截线求相关线段的长或比值题型六黄金分割【知识梳理】知识点一、线段的比与成比例线段线段的比两条线段长度的比叫做两条线段的比.注意：求两条线段的比时必须统一单位）．成比例线段四条线段a、b、c、d中，如果dcba，那么这四条线段a、b、c、d叫做成比例线段，简称比例线段．知识点二、比例的性质知识点三、黄金分割黄金分割若线段AB上一点C把线段AB分成两条线段AC与BC（AC>BC），如果ACBCABAC，这时称点C是AB的黄金分割点，这个比值称为黄金比，它的值为618.0215．知识点四、相似图形相似图形在数学上，我们把形状相同的图形称为相似图形(similar figures).要点诠释：(1)相似图形就是指形状相同，但大小不一定相同的图形；(2)“全等”是“相似”的一种特殊情况，即当“形状相同”且“大小相同”时，两个图形是全等；相似多边形如果两个多边形的对应角相等，对应边的比相等，我们就说它们是相似多边形．要点诠释：（1）相似多边形的定义既是判定方法，又是它的性质．（2）相似多边形对应边的比称为相似比．知识点五、平行线分线段成比例定理【经典例题一比例的性质】约分即可求解．【经典例题二线段的比】第二次裁剪所得矩形的长为第三次裁剪所得矩形的长为第四次裁剪所得矩形的长为第五次裁剪所得剩下的图形恰好是正方形，AC【答案】34/0.75为线段我们可以这样作图找到已知线段的黄金分割点：如图且12EF OE ，连接OF ；以F 为圆心，EF 交OE 于点P ．根据材料回答下列问题：(1)根据作图，写出图中相等的线段：________(2)求OP 的长；(3)求证：点P 是线段OE 的黄金分割点．【答案】(1)EF FH ，OH OP (2)51OP (3)见解析【分析】（1）由题意知，EF FH ，OH （2）由勾股定理得225OF OE EF （3）由51OP ，可得2251OP235625OE PE ，则2OP OE 【详解】（1）解：由题意知，EF FH ，OH 故答案为：EF FH ，OH OP ；（2）解：∵EF OE ，∴90OEF ∵2OE ，【经典例题三成比例线段】是线段【经典例题四由平行判断成比例的线段】九年级四川省成都市七中育才学校校考阶段练习）如图，直线A．103B．152【答案】D【分析】根据平行线分线段成比例定理列出比例式，求出【详解】解：∵a b c∥∥，∴AB DEAC DF，A．BH AGBC ADB．EG AGCD AD【答案】D【分析】根据平行线分线段成比例定理、中点定义及相似三角形对应边成比例逐项判断即可得到答案．【答案】54【分析】根据平行线分线段成比例定理得出比例式，解答即可．【详解】解：∵直线123l l l ∥∥45AD BC DF CE ，5CE【答案】6【分析】根据角平分线的定义和平行线的性质可得后根据平行线分线段成比例定理，可得【详解】解：∵AD平分，∴EAD CAD(1)求证：AG CG ；(2)求证：2CGE BDN (3)若4BD DG ，GP 【答案】(1)见解析(2)见解析(3)3AG a【分析】（1）证明ABG （2）先证明DAF GPD NDC DCP BDN BDC NDC （3）证明PM PC ，得出【经典例题五由平行截线求相关线段的长或比值】A．14B【答案】A【分析】根据a b∥可得BGA．3 20【答案】A【分析】过点F作FG∥由FG BN∥,得BF NG【答案】5:3:2【分析】首先过点M作MK点，根据平行线分线段成比例定理，即可求得【详解】解：过点M作MK∵M是AC的中点，∴MN NK AN AMEC EF AE AC∵E、F为BC的三等分点，，∴BE EF FC【答案】16【分析】过点D 作DG ::BD CD EG CG 的值．∵:1:3AF FD ，BD ∴::AF FD AE EG ∴3EG AE ，EG ∴3EC EG CG(1)如果4AB ，8BC ，(2)如果:2:3DE EF ，AB 【答案】(1)6(2)15【分析】（1）由平行线分线段成比例定理得到（2）由平行线分线段成比例定理得到392BC AB ，即可得到【详解】（1）解：如图，∵123l l l ∥∥，∴AB DE BC EF，∵4AB ，8BC ，EF【经典例题六黄金分割】【点睛】本题考查了黄金分割点的意义，正确理解黄金分割的定义是解题的关键．上找一点51 51【答案】8516【分析】设AC m ，BD n ，根据【答案】1555【分析】根据黄金分割的定义，得2PA BP AB ，构建方程计算求解．【详解】解：根据题意，2PA BP AB ；∴2(10)10BP BP【点睛】本题考查黄金分割的定义，一元二次方程的求解；掌握黄金分割的定义是解题的关键．5．（2023秋·全国·九年级专题练习）综合与实践综合与实践课上，老师让同学们以(1)【操作判断】根据以上操作，直接写出图3中AGGB的值：______；(2)【问题解决】请判断图3中四边形BG MG的形状，并说明理由．(3)【拓展应用】我们知道：将一条线段AB分割成长、短两条线段AP 割点．在以上探究过程中，已知矩形纸片ABCD的宽AB为【重难点训练】A ．5B 【答案】D 【分析】本题考查的是平行线分线段成比例定理，根据平行线分线段成比例定理列出比例式，计算即可．【详解】解：∵a b ∥∥A． 454【答案】A【分析】本题考查黄金分割比求线段长，熟记黄金分割比答案，熟记黄金分割比是解决问题的关键．【详解】解：由黄金分割比，根据题意可得AB∵，8cm5AP AB故选：A．3．（2022上·山西运城形蕴藏着丰富的美学价值，我们可以用这样的方法画出黄金矩形；作正方形接EF，以FD为半径画弧，A．1个B．2个BG A ．259B ．27【答案】A【分析】本题考查了平行线分线段成比例，正方形的性质，掌握平行线分线段成比例是解题的关键．作FH BC ∥交CD 于H ，则DH HC 根据勾股定理得25AE ，所以【详解】解：如图，作FH ∥则45DH DF HC FG ，E ∵为CD 边中点，19HE ED ，FH AD ∵∥，19FE HE AE DE ，224225AE ∵，259FE ．故选：A ．5．（2023上·浙江·九年级周测）如图，点D ，与BC 的垂线CE 相交于点A ．3:2B ．5:3【答案】A 【分析】本题主要考查了平行线分线段成比例，4FC BC BF ，再根据DF ∥【详解】∵BE 平分ABC ，∴ABD FBD ，∵DF BC ，90A ，∴90DFB A ，【分析】本题考查的是三角形的重心的概念和性质、坐标与图形性质等知识点，根据三角形的重心的概念8．（2023上·浙江金华，，上，连结AB BC CACF三角形的中位线的判定及性质的综合应用，∵点B 和点F 关于直线DE ∴BD DF BF DE ，，∵AD DF ，∴AD BD DF ，∴,DBF DFB DAF 又DBF DFB DAF ∴ 2180DFB DFA ∴90,DFB DFA 即∴DE AC ∥，∴BD BE AD CE，∵AD BD ，∴BE CE ，∴132BE BC ，在Rt ABF 与Rt CBF △，由勾股定理可得：2222BF AB AF FB CB ，∴2222AB AF CB CF ∵56AB AC BC ，，【答案】3【分析】本题考查了平行四边形的性质，平行线分线段成比例，设行四边形的性质可得AD ∥【详解】解：设FD x ，由2AF FD ，则2AF x ，∵四边形ABCD 是平行四边形，AD BC ∥，AB CD ∥，2233AE AF x EC BC x ，23BE AE EG EC ，∵2BE ，223EG ，3EG ，故答案为：3．10．（2023上·安徽合肥·九年级校考期中）如图，矩形形ABNM 和矩形CDMN ．（1）若矩形CDMN 与矩形的长是，如图所示．请你借助这张纸片，设法折出一个设正方形ABCD 的边长为在Rt BCF 中，BF 则2QF BF BQ 设AP PQ x ，则PD 在Rt QPF 和Rt DGF 有222FQ PQ DF 解得512x ，即点P 是AD 的黄金分割点（2）方法如图所示:第一步：对折矩形纸片第二步：再一次折叠纸片，使点14．（2023上·四川内江·九年级统考期中）巴台农神庙的设计代表了古希腊建筑艺术上的最高水平，它的平面图可看作宽与长的比是黄金矩形ABCD 的宽1AB (1)黄金矩形ABCD 的长BC ；(2)如图②，将图①中的黄金矩形裁剪掉一个以AB 为边的正方形ABEF ，得到新的矩形DCEF 是否为黄金矩形，并证明你的结论；(3)在图②中，连接AE ，求点D 到线段AE 的距离．【答案】(1)512(2)矩形DCEF 为黄金矩形，理由见解析(3)点D 到线段AE 的距离为1024【分析】本题考查了黄金分割，理解题目所给“黄金矩形”的定义是解题的关键．（1）根据512AB BC ，AB ，即可求解；（2）先求出512FD EC AD ，再求出DF EF 的值，即可得出结论；（3）连接AE ，DE ，过D DG AE 于点G ，根据1AB EF ，512AD，得出再根据12AED G S AD EF AE D ，即可求解．∵1AB EF ，AD∴22112AE ，在AED △中，12AED S 即AD EF AE DG ，则51122DG ，解得1024DG ，∴点D 到线段AE 的距离为15．（2022上·山西运城·九年级统考期中）阅读与思考请仔细阅读下列材料，并完成相应的任务．下面是小宇同学运用面积的思想对进行了证明．证明：如图，分别连接EB DC ，．设点E 到AB 的距离为1h ，点D 到AC 的距离为2h ，ADE BDE S S 111212AD h BD h AD BD ，ADE DEC S S …任务：(1)请补全以上证明过程．(2)应用以上结论解答问题：如图，在ABC 中，DG EC ∥，【答案】(1)见解析(2)见解析【分析】本题主要考查平行线分线段成比例定理的证明与应用：（1）根据两条平行线之间的距离处处相等，可得（2）直接利用平行线分线段成比例定理即可证明．【详解】（1）证明：如图，分别连接设点E 到AB 的距离为1h 则111212ADE BDE AD h S AD S DB BD h 221212ADE DEC AE h S AE S EC EC h ，设点B 到直线DE 的距离为∵DE BC ∥，点C 到直线DE 的距离与点∴12BDE DEC S S DE m ∴ADE BDE S S ADE DECS S ，∴ADDB AE EC．（2）证明：∵DG EC ∥∴AD AG DE GC，。

∴PD·PC＝PE·PBP. F
PD .
PC PA
∵DF∥AC，∴
∴PD·PC＝PF·PA.
PE PA . PF PB
∴PE·PB＝PF·PA. ∴
技巧3 等比代换法证比例式 3. 如图，在△ABC中，DE∥BC，EF∥CD.
AD AF .
证明：∵求E证F：∥CADB， AD
∴ AF AE .
同理
1 2
∵EG是ACGAB的HA中EC 点 ，14 .∴AE＝ DC.
∴
技巧2 等积代换法证比例式
2. 如图，在△ABC中，D是AB上一点，E是△ABC内
一点，DE∥BC，过D作AC的平行线交CE的延长线
PE
于F，CF与AB交于P，求证： PF
PA .
PB
证明：∵DE∥BC，∴
PD PE . PB PC
第四章 图形的相似
平行线分线段成比例
第2课时
利用平行线证比例式或等积式的方法： 当比例式或等积式中线段不在平行线上，若平行
线为一组(两条以上)时，可直接利用平行线分线段成 比例的基本事实证明；若平行线只有两条时，则利用 平行线分线段成比例的基本事实的推论证明；当比例 式或等积式中的线段不是对应线段时，则利用转化思 想，用等线段、等比例、等积替换进行论证．
类型 1 证比例式
技巧1 中间比代换法证比例式
1. 如图，▱ABCD中，点E是AB的中点，在AD上截 取2AF＝FD，EF交AC于点G，延长EF与CD的 延长线交于点H，
AG
求 GC 的值．
解：∵四边形ABCD是平行四边形，
∴△DAFFE∽H△D DF2H. .
FA
∴
AE AG AE .
HC HC

线段的比例与相似形教学方法在数学教学中，线段的比例与相似形是一个重要的概念，它们不仅在几何学中有着广泛的应用，而且在实际生活中也有很多实际意义。

如何有效地教授线段的比例与相似形，培养学生的数学思维和解决问题的能力，是每位数学教师都需要面对的挑战。

本文将介绍一些教学方法，以帮助教师更好地教授线段的比例与相似形。

首先，引入真实生活中的例子是一个很好的教学方法。

教师可以通过展示一些实际生活中的比例问题，如建筑物的比例模型、地图的比例尺等，来引起学生的兴趣和好奇心。

通过这些例子，学生可以更直观地理解线段的比例概念，并将其应用到实际问题中。

例如，教师可以让学生计算一栋建筑物的比例模型的尺寸，或者使用地图的比例尺来测量两个城市之间的距离。

通过这样的实际例子，学生可以更好地理解线段的比例与相似形的概念，并将其应用到实际生活中。

其次，通过图形的变换来教授线段的比例与相似形也是一个有效的教学方法。

教师可以使用平移、旋转、缩放等图形变换的方法，来帮助学生理解线段的比例与相似形的概念。

例如，教师可以让学生使用尺子在纸上画出一个线段，然后通过平移、旋转、缩放等变换方法，将该线段变换成不同的形状。

学生可以观察到线段在变换过程中的比例关系，并通过观察和实践来理解线段的比例与相似形的概念。

通过这样的图形变换方法，学生可以更深入地理解线段的比例与相似形，并培养他们的空间想象力和几何思维能力。

此外，教师还可以通过数学游戏和竞赛来教授线段的比例与相似形。

数学游戏和竞赛可以激发学生的兴趣和积极性，培养他们的团队合作精神和解决问题的能力。

例如，教师可以组织学生进行线段比例的测量比赛，要求学生在规定的时间内测量给定线段的比例，并比较结果的准确性。

通过这样的游戏和竞赛，学生可以在轻松愉快的氛围中学习线段的比例与相似形，并提高他们的测量和计算能力。

最后，教师可以通过举一反三的方法，将线段的比例与相似形与其他数学概念进行联系。

例如，教师可以引导学生思考线段的比例与相似形与三角形的相似性之间的关系。

专训4用线段成比例法解几何问题的几种常见类型名师点金：线段成比例法在三角形、四边形、圆中有着广泛的应用，是近几年中考命题的必考内容，题型既有选择题、填空题，也有解答题，有时也以压轴题的形式出现．与三角形有关的问题1．【2017·杭州】如图，在锐角三角形ABC中，点D，E分别在边AC，AB上，AG⊥BC于点G，AF⊥DE于点F，∠EAF＝∠GAC.(1)求证：△ADE∽△ABC；(2)若AD＝3，AB＝5，求AFAG的值．(第1题)与四边形有关的问题2．【2017·泰安】如图，四边形ABCD中，AB＝AC＝AD，AC平分∠BAD，点P是AC延长线上一点，且PD⊥AD.(1)求证：∠BDC＝∠PDC；(2)若AC与BD相交于点E，AB＝1，CE∶CP＝2∶3，求AE的长．(第2题)与圆有关的问题3．【2017·滨州】如图，点E是△ABC的内心，AE的延长线交BC于点F，交△ABC的外接圆⊙O于点D，连接BD，过点D作直线DM，使∠BDM＝∠DAC.(1)求证：直线DM是⊙O的切线；(2)求证：DE2＝DF·DA.(第3题)4．【中考·襄阳】如图，AB是⊙O的直径，点C为⊙O上一点，AE和过点C的切线互相垂直，垂足为E，AE交⊙O于点D，直线EC交AB的延长线于点P，连接AC，BC，PB PC＝1 2.(1)求证：AC平分∠BAD；(2)探究线段PB，AB之间的数量关系，并说明理由；(3)若AD＝3，求△ABC的面积．(第4题)答案1．(1)证明：∵AG ⊥BC ，AF ⊥DE ， ∴∠AFE ＝∠AGC ＝90°. ∵∠EAF ＝∠GAC ， ∴∠AED ＝∠ACB. 又∵∠EAD ＝∠CAB ， ∴△ADE ∽△ABC.(2)解：由(1)可知：△ADE ∽△ABC ， ∴AD AB ＝AE AC ＝35. 由(1)可知：∠AFE ＝∠AGC ＝90°， ∵∠EAF ＝∠CAG ，∴△EAF ∽△CAG . ∴AF AG ＝AE AC .∴AF AG ＝AD AB ＝35. 2．(1)证明：∵AB ＝AD ，AC 平分∠BAD ， ∴AC ⊥BD ，∴∠ACD ＋∠BDC ＝90°. ∵AC ＝AD ，∴∠ACD ＝∠ADC. ∴∠ADC ＋∠BDC ＝90°.又∵PD ⊥AD ，∴∠ADC ＋∠PDC ＝90°. ∴∠BDC ＝∠PDC.(2)解：如图，过点C 作CM ⊥PD 于点M.(第2题)∵∠BDC ＝∠PDC ，CM ⊥PD ，AC ⊥BD ， ∴CE ＝CM.∵∠CMP ＝∠ADP ＝90°，∠P ＝∠P ， ∴△CPM ∽△APD. ∴CM AD ＝PC PA. 设CM ＝CE ＝x ，∵CE ∶CP ＝2∶3， ∴PC ＝32x.∵AB ＝AD ＝AC ＝1，∴x 1＝32x 32x ＋1. 解得x ＝13，即CE ＝13.经检验，x ＝13是方程的解且符合题意．故AE ＝AC －CE ＝1－13＝23.3．证明：(1)如图，连接OD. ∵点E 是△ABC 的内心， ∴∠BAD ＝∠CAD. ∴BD ︵＝CD ︵.∴OD ⊥BC.又∵∠BDM ＝∠DAC ，∠DAC ＝∠DBC ， ∴∠BDM ＝∠DBC. ∴BC ∥DM.∴OD ⊥DM. ∴直线DM 是⊙O 的切线． (2)如图，连接BE. ∵点E 是△ABC 的内心，∴∠BAE ＝∠CAE ＝∠CBD ，∠ABE ＝∠CBE. ∴∠BAE ＋∠ABE ＝∠CBD ＋∠CBE ， 即∠BED ＝∠EBD.∴DB ＝DE. ∵∠DBF ＝∠DAB ，∠BDF ＝∠ADB ， ∴△DBF ∽△DAB. ∴DF DB ＝DBDA，即DB 2＝DF·DA. ∴DE 2＝DF·DA.(第3题)(第4题)4．(1)证明：如图，连接OC.∵PE 与⊙O 相切，∴OC ⊥PE. ∵AE ⊥PE ，∴OC ∥AE.∴∠CAD ＝∠OCA.∵OA ＝OC ，∴∠OCA ＝∠OAC.∴∠CAD ＝∠OAC.∴AC 平分∠BAD. (2)解：PB ，AB 之间的数量关系为AB ＝3PB. 理由如下：∵AB 为⊙O 的直径，∴∠ACB ＝90°. ∴∠BAC ＋∠ABC ＝90°.∵OB ＝OC ， ∴∠OCB ＝∠ABC.∵∠PCB ＋∠OCB ＝90°， ∴∠PCB ＝∠PAC.∵∠P ＝∠P ，∴△PCA ∽△PBC. ∴PC PB ＝PAPC.∴PC 2＝PB·PA.∵PB PC ＝12， ∴PC ＝2PB.∴PA ＝4PB.∴AB ＝3PB.(3)解：过点O 作OH ⊥AD 于点H ，如图，则AH ＝12AD ＝32，四边形OCEH 是矩形．∴OC ＝HE.∴AE ＝32＋OC.∵OC ∥AE ，∴△PCO ∽△PEA.∴OC AE ＝PO PA .∵AB ＝3PB ，AB ＝2OB ，∴OB ＝32PB.∴OC 32＋OC ＝PB ＋32PBPB ＋3PB ＝58，∴OC ＝52，∴AB ＝5.∵△PBC ∽△PCA ，∴PB PC ＝BC AC ＝12，∴AC ＝2BC.在Rt △ABC 中，AC 2＋BC 2＝AB 2，∴(2BC)2＋BC 2＝52，∴BC ＝5，∴AC ＝2 5. ∴S △ABC ＝12AC·BC ＝5，即△ABC 的面积为5.。