离散系统的Simulink仿真

离散控制系统中的仿真与实验验证离散控制系统是一种基于样本信号的控制系统，它将连续时间的信号转化为离散时间的信号，并利用离散时间信号进行控制和调节。

仿真和实验验证是离散控制系统设计和调试过程中非常重要的一部分，本文将针对离散控制系统中的仿真与实验验证进行探讨。

一、离散控制系统的仿真在离散控制系统中，仿真是一种重要的工具，用于模拟和评估系统的性能。

通过仿真，我们可以在电脑上构建一个离散控制系统的模型，并根据不同的输入信号，预测系统的动态响应。

1.1 离散控制系统的建模离散控制系统的仿真首先需要建立系统的数学模型。

通常，我们可以通过离散系统差分方程来描述系统的动态特性。

差分方程可以将系统的输入信号和输出响应相联系，从而实现系统性能的仿真。

例如，对于一个离散时间系统，差分方程可以表示为：y(k) = a1*x(k) + a2*x(k-1) + b1*u(k) + b2*u(k-1)其中，y(k)表示系统的输出信号，x(k)表示系统的状态变量，u(k)表示输入信号，a1、a2、b1、b2分别为系统的系数。

通过将差分方程转化为状态空间模型，我们可以更加方便地进行仿真分析。

状态空间模型可以用矩阵形式表示为：x(k+1) = F*x(k) + G*u(k)y(k) = H*x(k) + I*u(k)其中，F、G、H、I为状态空间模型的系数矩阵。

1.2 离散控制系统的仿真工具为了进行离散控制系统的仿真，我们通常会借助一些专门的仿真软件或工具。

例如MATLAB/Simulink等工具提供了丰富的离散控制系统仿真模块，可以方便地进行系统建模、仿真和参数调试。

通过在仿真软件中构建离散控制系统的模型，并设置各种参数和输入信号，我们可以获取系统的动态响应曲线和性能指标。

二、离散控制系统的实验验证仿真虽然可以提供对离散控制系统性能的预测，但最终的验证还需要通过实验来完成。

实验验证可以帮助我们检验仿真模型的准确性，并对系统的实际性能进行评估。

1.变步长(Variable—Step)求解器可以选择的变步长求解器有：ode45，ode23，ode113，odel5s，ode23s和discret．缺省情况下，具有状态的系统用的是ode45；没有状态的系统用的是discrete．1)ode45基于显式Runge—Kutta(4，5)公式，Dormand—Prince对．它是—个单步求解器(solver)。

也就是说它在计算y(tn)时，仅仅利用前一步的计算结果y(tn-1)．对于大多数问题．在第一次仿真时、可用ode45试一下．2)ode23是基于显式Runge—Kutta(2，3)．Bogackt和Shampine对．对于宽误差容限和存在轻微刚性的系统、它比ode45更有效一些．ode23也是单步求解器．3)odell3是变阶Adams-Bashforth—Moulton PECE求解器．在误差容限比较严时，它比ode45更有效．odell3是一个多步求解器，即为了计算当前的结果y(tn），不仅要知道前一步结果y(tn-1)，还要知道前几步的结果y(tn-2)，y(tn-3)，…；4)odel5s是基于数值微分公式(NDFs)的变阶求解器．它与后向微分公式BDFs(也叫Gear方法)有联系．但比它更有效．ode15s是一个多步求解器，如果认为一个问题是刚性的，或者在用ode45s时仿真失败或不够有效时，可以试试odel5s。

odel5s是基于一到五阶的NDF公式的求解器．尽管公式的阶数越高结果越精确，但稳定性会差一些．如果模型是刚性的，并且要求有比较好的稳定性，应将最大的阶数减小到2．选择odel5s求解器时，对话框中会显示这一参数．可以用ode23求解器代替。

del5s，ode23是定步长、低阶求解器．5)ode23s是基于一个2阶改进的Rosenbrock公式．因为它是一个单步求解器，所以对于宽误差容限，它比odel5s更有效．对于一些用odel5s不是很有效的刚性问题，可以用它解决．6)ode23t是使用“自由”内插式梯形规则来实现的．如果问题是适度刚性，而且需要没有数字阻尼的结果，可采用该求解器．7)ode23tb是使用TR—BDF2来实现的，即基于隐式Runge—Kutta公式，其第一级是梯形规则步长和第二级是二阶反向微分公式．两级计算使用相同的迭代矩阵．与ode23s相似，对于宽误差容限，它比odtl5s更有效．8)discrete(变步长)是simulink在检测到模型中没有连续状态时所选择的一种求解器．2.定步长(Flxed—Step)求解器可以选择的定步长求解器有：ode5，ode4，ode3，ode2，ode1和discrete．1)ode5是ode45的一个定步长版本，基于Dormand—Prince公式．2）ode4是RK4，基于四阶Runge—Kutta公式．3) ode3是ode23的定步长版本，基于Bogacki-Sbampine公式．4) ode2是Heun方法，也叫作改进Euler公式．5) odel是Euler方法．6) discrete(定步长)是不执行积分的定步长求解器．它适用于没有状态的模型，以及对过零点检测和误差控制不重要的模型．3.诊断页（Diagnostics)可以通过选择Simulation Parameters对话框的Diagnostics标签来指明在仿真期间遇到一些事件或者条件时希望执行的动作．对于每一事件类型，可以选择是否需要提示消息，是警告消息还是错误消息．警告消息不会终止仿真，而错误消息则会中止仿真的运行．（1）一致性检查一致性检查是一个调试工具．用它可以验证Simulink的0DE 求解器所做的某些假设．它的主要用途是确保s函数遵循Simulink内建模块所遵循的规则．因为一致性检查会导致性能的大幅度下阵(高达40％)，所以一般应将它设为关的状态．使用一致性检查可以验证s函数，并有助于确定导致意外仿真结果的原因．为了执行高效的积分运算，Simulink保存一些时间步的结果，并提供给下一时间步使用．例如，某一时间步结束的导数通常可以放下一时间步开始时再使用．求解器利用这一点可以防止多余的导数运算．一致性检查的另一个目的是保证当模块被以一个给定的t(时间)值调用时．它产生一常量输出．这对于刚性求解器(ode23s和odel5s)非常重要，因为当计算Jacobi行列式时．模块的输出函数可能会被以相同的t值调用多次．如果选择了一致性检查，Simulink置新计算某些值，并将它们与保存在内存中的值进行比较，如果这些值有不相同的，将会产生一致性错误．Simulink比较下列量的计算值： 1）输出； 2）过零点 3）导数； 4）状态．（2）关闭过零点检测可以关闭一个仿真的过零点检测．对于一个有过零点的模型，关闭过零点检测会加快仿真的速度，但是可能影响仿真结果的精度．这一选项关闭那些本来就有过零点检测的模块的过零点检测．它不能关闭Hir crossing 模块的过零点检测．（3）关闭优化I/O存储选择该选项，将导致Simulink为每个模块约I／()值分配单独的缓存，而不是重新利用援存．这样可以充分增加大模型仿真所需内存的数量．只有需要调试模型时才选择该选项．在下列情况下，应当关闭缓存再利用； 1)调试一个C-MEX S-函数； 2)使用浮点scope或display模块来察看调试模型中的信号．如果缓存再利用打开，并且试图使用浮点scope或display模块来显示缓存已被再利用的信号，将会打开一个错误对话框．（4）放松逻辑类型检验选择该选项，可使要求逻辑类型输入的模块接受双精度类型输入．这样可保证与Simulink 3版本之前的模型的兼容性．4.提高仿真性能和精度仿值性能相精度由多种因素决定，包括模型的设计和仿真参数的选择．求解器使用它们的缺省参数值可以使大多数模型的仿真比较精确有效，然而，对于一些模型如果调整求解器相仿真参数将会产生更好的结果．而且，如果对模型的性能比较熟悉，并且将这些信息提供给求解器，得到的仿真效果将会提高。

Simulink动态系统仿真入门Simulink是基于MA TLAB的图形化仿真设计环境，是MATLAB 提供的进行动态系统建模、仿真和综合分析的集成软件包。

它使用图形化的系统模块对动态系统进行描述，并在此基础上采用MATLAB 的计算引擎对动态系统在时域内进行求解。

它可以处理的系统包括：线性、非线性、离散、连续及混合、单任务、多任务离散事件等。

在MATLAB7.X版本中，可以直接在Simulink环境中运作的工具箱和模型库很多，已经覆盖了航天、航空、通信、控制、信号处理等等诸多领域，涉及内容专业性很强。

1、Simulink系统的启动由于Simulink和MATLAB是高度集成在一起的，因此启动Simulink必须先启动MA TLAB。

在MA TLAB启动Simulink可以通过在命令窗口输入Simulink，或者点击MATLAB工具栏的Simulink 快速启动图标。

启动Simulink后，出现Simulink的主窗口，选择主菜单File中的New\model，即可以打开系统模型编辑器。

下图依次是MATLAB 主窗口、Simulink主窗口和系统模型编辑窗口，图中的箭头表示了操作顺序。

在打开一个新的系统模型文件以后，用户可以从Simulink模块库中选择适合的系统模块或自定义模块来建立系统模型。

我们通过一个简单的例子来分步说明Simulink建模和仿真的能力。

1）在MATLAB 窗口运行Simulink。

打开Simulink模块库浏览器。

2）点击Source子库前的“+”展开库，可以看到各种信源模块。

3）点击新建图标，打开一个空白型的模型窗口。

4）用鼠标选中需要的信源模块，把它拖入新建的空白模型编辑窗口，生成一个正弦波的复制品。

5）同样将信宿库Sinks中的示波器Scope拷贝到模型窗口。

6）利用鼠标完成两个模块的连线操作，完成一个简单的模型。

7）为进行仿真，双击示波器模块，打开示波器显示屏。

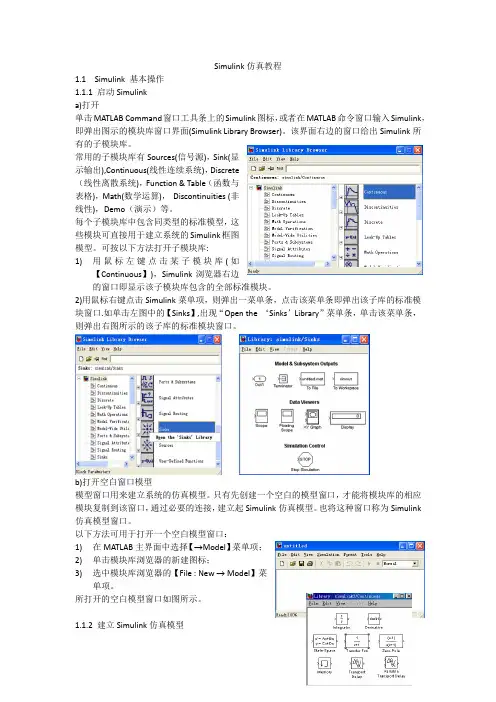
Simulink仿真教程1.1 Simulink 基本操作1.1.1 启动Simulinka)打开单击MATLAB Command窗口工具条上的Simulink图标，或者在MATLAB命令窗口输入Simulink，即弹出图示的模块库窗口界面(Simulink Library Browser)。

该界面右边的窗口给出Simulink所有的子模块库。

常用的子模块库有Sources(信号源)，Sink(显示输出),Continuous(线性连续系统)，Discrete（线性离散系统)，Function & Table（函数与表格)，Math(数学运算)，Discontinuities (非线性)，Demo（演示）等。

每个子模块库中包含同类型的标准模型，这些模块可直接用于建立系统的Simulink框图模型。

可按以下方法打开子模块库:1)用鼠标左键点击某子模块库(如【Continuous】)，Simulink浏览器右边的窗口即显示该子模块库包含的全部标准模块。

2)用鼠标右键点击Simulink菜单项，则弹出一菜单条，点击该菜单条即弹出该子库的标准模块窗口.如单击左图中的【Sinks】,出现“Open the ‘Sinks’Library”菜单条，单击该菜单条，则弹出右图所示的该子库的标准模块窗口。

b)打开空白窗口模型模型窗口用来建立系统的仿真模型。

只有先创建一个空白的模型窗口，才能将模块库的相应模块复制到该窗口，通过必要的连接，建立起Simulink仿真模型。

也将这种窗口称为Simulink 仿真模型窗口。

以下方法可用于打开一个空白模型窗口：1)在MATLAB主界面中选择【→Model】菜单项；2)单击模块库浏览器的新建图标；3)选中模块库浏览器的【File : New → Model】菜单项。

所打开的空白模型窗口如图所示。

1.1.2 建立Simulink仿真模型a)打开Simulink模型窗口(Untitled)b)选取模块或模块组在Simulink模型或模块库窗口内，用鼠标左键单击所需模块图标，图标四角出现黑色小方点，表明该模块已经选中。

SIMULINK的仿真算法在SIMULINK的仿真过程中选择合适的算法是很重要的，仿真算法是求常微分方程、传递函数、状态方程解的数值计算方法，这些方法主要有欧拉法(Euler)、阿达姆斯法(Adams)、龙格·库塔法(Rung-Kutta)，这些算法都主要建立在泰勒级数的基础上。

欧拉法是最早出现的一种数值计算方法，它是数值计算的基础，它用矩形面积来近似积分计算，欧拉法比较简单，但精度不高，现在已经较少使用。

阿达姆斯法是欧拉法的改进，它用梯形面积近似积分计算，所以也称梯形法，梯形法计算每步都需要经过多次迭代，计算量较大，采用预报-校正后只要迭代一次，计算量减少，但是计算时要用其他算法计算开始的几步。

龙格-库塔法是间接使用泰勒级数展开式的方法，它在积分区间内多预报几个点的斜率，然后进行加权平均，用作计算下一点的依据，从而构造了精度更高的数值积分计算方法。

如果取两个点的斜率就是二阶龙格-库塔法，取四个点的斜率就是四阶龙格-库塔法。

SIMULINK汇集了各种求解常微分方程数值解的方法，这些方法分为两大类，可变步长类算法和固定步长类算法。

7.1可变步长类算法可变步长(Variable-step)类算法是在解算模型(方程)时可以自动调整步长，并通过减小步长来提高计算的精度。

在SIMULINK的算法中可变步长类算法有如下几种:1.Ode45(Dormand-Prince)基于显式Rung-Kutla(4,5)和Dormand-Prince组合的算法，它是一种一步解法，即只要知道前一时间点的解y(tn-1)，就可以立即计算当前时间点的方程解y(tn)。

对大多数仿真模型来说，首先使用ode45来解算模型是最佳的选择，所以在SIMULINK的算法选择中将ode45设为默认的算法。

2.ode23(Bogacki-Shampine)基于显式Rung-Kutta(2,3)、Bogacki和Shampine相结合的算法，它也是一种一步算法。

色子科技大学学院学生卖验报告院别：电子传息学院课程名称：传号与糸统实验-、卖验目的1. 拿握富散糸统Simulink的建栈方冻。

2. 拿墟禽散糸统肘城响应、频城响应的Simulink仿真方出。

二、卖验原理富散糸统的Simulink建模、仿真方比匀连续糸统相似，其糸统橈型主要有z 城核型、传输函数栈空和状态咗间栈型等形无。

现采用图1的形无建立糸统仿真栈型，结合如下仿真的令令，可得到糸统的状态咗间变量、频率响应曲线J、单住阶趾响应和单伐冲激响应的沐形。

图1糸统响应Simulink仿真的综合棋型仿真令令：[ABC、叨二dlinmodC'棋型丈件名'丿％求状态空间矩阵，注意：'模黑丈件名不含护展名dimpulse(A,B,C,D) %求冲激响应dimpuke(A,B,C,D」,N]：N J %求k=N[~ N, £间(步长为U的冲激响应dimpulse（ABC,DJ,N]:△“：N2）%求冲激响应Ak=N[~ N2 g.间（步长NJ的部分祥■值dstep（A.BCD） %求阶跃响应dstep（A、BCD、1,N ] :Z\N:N Jdbode（A.B,C,D.T c）%求频率响应（频：“ = 0~上_,印0 = 0~兀丿。

为Ts取挥周期.一般去T$=1・dbode（A,B,C,D. T y ,i d ,w0: Aw:wJ % 求频率响应（频4 = ® ： 0 =w° ~ w「即&= （w（）~ W]丿T「Aw为频率步长丿；i“为糸疣输入夠D的偏号，糸统只冇一个输入端o肘取i“ =1.以上令令，可以逐条症MATLAB令令窗d输入.执行"也可偏写成M丈件并运行。

三、实验彖1.^＜糸统肘城柩图如国2所示。

建立Simulink核型，求其状态吨间矩阵.糸统函数.冲激响应.阶跃响应和频率特性。

3.^ ＜糸统差分方程为y伙）+ - y（k一1）一丄y（k一2） = /伙）+ 2 f（k一2）。

已知仿真条件为：G C(s)=k×(T3s+1)，其中T1=18，T2=0.035,T3=0.15s T1s+1(T2s+1)。

可得传递函数G c（s）=1500s+10000063s+1835s+100将S域的传递函数转换的Z域，打开matlab软件，创建一个m文件程序如下：%transfer functionsys=tf([15000 100000],[63 1835 1000]);%discretets=1;%²ÉÑùʱ¼ädsys=c2d(sys,ts,'z');%ת»¯Îª²î·Ö·½³Ì%extract[num,den]=tfdata(dsys,'v');运行dsys>> dsysTransfer function:46.36 z - 3.738--------------------------z^2 - 0.5738 z + 2.24e-013得到Z域的传递函数为：G c(z)=46.36z±3.738z2−0.5738z+2.24e−13打开matlab软件中的simulink模块，创建一个.mdl文件。

搭建离散化的仿真原理图如下：下面进行PID整定，常用PID整定方法有：⒈稳定边界法⒉4:1衰减法⒊鲁棒法⒋ISTE最优参数整定法。

边界稳定法和4：1衰减法调节时间快，上升时间短，鲁棒法和ISTE最优参数整定法超调量小，调节过程平衡，鲁棒性好。

4:1衰减法有一定局限性，鲁棒性差；iste法调节时间长，调节参数偏保守。

本文中采用稳定边界法来整定PID参数。

在闭环系统下首先将PIDcontrol 调节为纯P调节器，逐渐增大P参数，观察输出波形，记录此时波形。

利用simulink进行系统仿真张营湖北科技学院电子信息科学与技术，学号：133621024摘要：Simulink是MATLAB中的一种可视化仿真工具，是一种基于MATLAB的框图设计环境，是实现动态系统建模、仿真和分析的一个软件包，被广泛应用于线性系统、非线性系统、数字控制及数字信号处理的建模和仿真中。

Simulink可以用连续采样时间、离散采样时间或两种混合的采样时间进行建模，它也支持多速率系统，也就是系统中的不同部分具有不同的采样速率。

为了创建动态系统模型，Simulink提供了一个建立模型方块图的图形用户接口(GUI) ，这个创建过程只需单击和拖动鼠标操作就能完成，它提供了一种更快捷、直接明了的方式，而且用户可以立即看到系统的仿真结果。

【1】关键词：simulink；仿真；分析引言：Simulink是MATLAB的工具箱，MATLAB R2010a版使用的是simulink7.5,可以用来对动态系统进行建模、仿真和分析，支持连续的、离散的及线性的和非线性的系统，还支持具有多种采样速率的系统。

Simulink是面向框图的仿真软件，具有以下功能。

(1)用绘制方框图代替编写程序，结构和流程清晰。

(2)智能化地建立和运行仿真，仿真仔细，贴近实际。

自动建立各环节的方程，自动在给定精度要求时以最快速度进行系统仿真。

(3)适应面广，包括线性、非线性系统，连续、离散及混合系统，单任务、多任务离散事件系统。

【2】2391 Simulink概述Simulink是MATLAB最重要的组件之一，它提供一个动态系统建模、仿真和综合分析的集成环境。

【3】1.1 Simulink简介Simulink是MATLAB最重要的组件之一，它提供一个动态系统建模、仿真和综合分析的集成环境。

在该环境中，无需大量书写程序，而只需要通过简单直观的鼠标操作，就可构造出复杂的系统。

Simulink具有适应面广、结构和流程清晰及仿真精细、贴近实际、效率高、灵活等优点，并基于以上优点Simulink已被广泛应用于控制理论和数字信号处理的复杂仿真和设计。

电子科技大学学院学生实验报告院别：电子信息学院课程名称：信号与系统实验一、实验目的1.掌握离散系统Simulink的建模方法。

2.掌握离散系统时域响应、频域响应的Simulink仿真方法。

二、实验原理离散系统的Simulink建模、仿真方法与连续系统相似，其系统模型主要有z域模型、传输函数模型和状态空间模型等形式。

现采用图1的形式建立系统仿真模型，结合如下仿真的命令，可得到系统的状态空间变量、频率响应曲线、单位阶跃响应和单位冲激响应的波形。

图1 系统响应Simulink仿真的综合模型仿真命令：[A,B,C,D]=dlinmod〔‘模型文件名’〕%求状态空间矩阵，注意：‘模型文件名’不含扩展名dimpulse(A,B,C,D) %求冲激响应dimpulse(A,B,C,D,1,N1:N2) %求k=N1~N2区间〔步长为1〕的冲激响应dimpulse(A,B,C,D,1,N1:△N: N2) %求冲激响应在k=N1~N2区间〔步长为△N〕的局部样值dstep(A,B,C,D) %求阶跃响应dstep(A,B,C,D,1,N1:△N:N2)dbode(A,B,C,D,Ts ) %求频率响应〔频率围：Ts~πω=，即π~=〕。

Ts为取样周期，一般去Ts=1.dbode(A,B,C,D, Ts ,iu,w:△w:w1)%求频率响应〔频率=围：ω=w~w1，即θ=〔w0~w1〕Ts，△w为频率步长〕；iu为系统输入端口的编号，系统只有一个输入端口时取i u =1.以上命令，可以逐条在MATLAB 命令窗口输入、执行，也可编写成M 文件并运行。

三、实验容1.离散系统时域框图如图2所示。

建立Simulink 模型，求其状态空间矩阵、系统函数、冲激响应、阶跃响应和频率特性。

图2 图32.离散系统z 域框图如图3所示。

建立Simulink 模型，求其状态空间矩阵、系统函数、冲激响应、阶跃响应和频率特性。

3.离散系统差分方程为)2(2)()2(61)1(61)(-+=---+k f k f k y k y k y 。