高三复习专题

高三地理：摩擦力问题专题复习资料本文档将为您提供高三地理摩擦力问题的专题复资料。

1. 摩擦力基本概念摩擦力是物体之间接触时所产生的一种力，阻碍物体相对运动的趋势。

它与物体之间的接触面积、表面粗糙度以及物体间施加的压力有关。

2. 摩擦力的类型2.1 静摩擦力（Fs）：当物体间相对运动趋势为零时，两物体之间所产生的力。

2.2 动摩擦力（Fd）：当物体间相对运动时，两物体之间所产生的力，其方向与物体的相对运动方向相反。

3. 摩擦力的计算公式3.1 静摩擦力公式：Fs ≤ μ * N其中，Fs为静摩擦力，μ为摩擦因数，N为物体所受的压力。

3.2 动摩擦力公式：Fd = μ * N其中，Fd为动摩擦力，μ为摩擦因数，N为物体所受的压力。

4. 摩擦力的影响因素4.1 物体之间的接触面积接触面积越大，摩擦力越大。

4.2 物体表面的粗糙度表面越粗糙，摩擦力越大。

4.3 施加在物体上的压力施加的压力越大，摩擦力越大。

5. 摩擦力的应用摩擦力在生活中有着广泛应用，例如：- 阻止滑动：人们行走时，鞋底与地面之间的摩擦力阻止人滑倒。

- 刹车：车辆制动时，刹车片与刹车盘之间的摩擦力减慢车辆速度。

- 物体运输：人们用绳索拉动大型物体时，绳索与物体之间的摩擦力使物体移动。

6. 摩擦力问题的解决方法6.1 减小摩擦力：可以采取以下方法减小摩擦力：- 平滑物体表面- 使用润滑剂6.2 增大摩擦力：可以采取以下方法增大摩擦力：- 增加物体表面粗糙度- 增加施加在物体上的压力希望这份摩擦力问题专题复习资料能对您的学习有所帮助。

祝您学业进步！。

高三一轮复习专题一基本不等式及其应用【考点预测】 1.基本不等式如果00>>b a ，，那么2b a ab +≤，当且仅当b a =时，等号成立．其中，2ba +叫作b a ，的算术平均数，ab 叫作b a ，的几何平均数．即正数b a ，的算术平均数不小于它们的几何平均数．基本不等式1：若a b ∈，R ，则ab b a 222≥+，当且仅当b a =时取等号； 基本不等式2：若a b ∈，+R ，则ab ba ≥+2（或ab b a 2≥+），当且仅当b a =时取等号. 注意（1）基本不等式的前提是“一正”“二定”“三相等”；其中“一正”指正数，“二定”指求最值时和或积为定值，“三相等”指满足等号成立的条件.（2）连续使用不等式要注意取得一致. 【方法技巧与总结】 1.几个重要的不等式（1）()()()20,00,0.a a R a a a a R ≥∈≥≥≥∈ （2）基本不等式：如果,a b R +∈，则2a bab +≥(当且仅当“a b =”时取“”). 特例：10,2;2a ba a ab a>+≥+≥（,a b 同号）. （3）其他变形：①()2222a b a b ++≥(沟通两和a b +与两平方和22a b +的不等关系式)②222a b ab +≤(沟通两积ab 与两平方和22a b +的不等关系式)③22a b ab +⎛⎫≤ ⎪⎝⎭(沟通两积ab 与两和a b +的不等关系式)④重要不等式串：)222,1122a b a b ab a b R a b+++≤≤≤∈+即 调和平均值≤几何平均值≤算数平均值≤平方平均值(注意等号成立的条件). 2.均值定理 已知,x y R +∈.（1）如果x y S +=(定值)，则2224x y S xy +⎛⎫≤=⎪⎝⎭(当且仅当“x y =”时取“=”).即“和为定值，积有最大值”.（2）如果xy P =(定值)，则x y +≥=(当且仅当“x y =”时取“=”).即积为定值，和有最小值”. 3.常见求最值模型 模型一：)0,0(2>>≥+n m mn xnmx ，当且仅当m n x =时等号成立； 模型二：)0,0(2)(>>+≥+-+-=-+n m ma mn ma ax na x m a x n mx ，当且仅当m n a x =-时等号成立；模型三：)0,0(2112>>+≤++=++c a bac xc b ax c bx ax x ，当且仅当a cx =时等号成立； 模型四：)0,0,0(4)21)()(22mnx n m m n mx n mx m m mx n mx mx n x <<>>=-+⋅≤-=-（，当且仅当mnx 2=时等号成 立.【题型归纳目录】题型一：基本不等式及其应用 题型二：直接法求最值 题型三：常规凑配法求最值 题型四：消参法求最值 题型五：双换元求最值 题型六：“1”的代换求最值 题型七：齐次化求最值题型八：利用基本不等式解决实际问题【典例例题】题型一：基本不等式及其应用例1．（2022·江苏·高三专题练习）《几何原本》卷2的几何代数法（以几何方法研究代数问题）成了后世西方数学家处理问题的重要依据，通过这一原理，很多的代数的公理或定理都能够通过图形实现证明，也称之为无字证明．现有如图所示图形，点F 在半圆O 上，点C 在直径AB 上，且OF AB ⊥，设AC a =，BC b =，则该图形可以完成的无字证明为（ ）A ．0,0)2a ba b +≥>> B ．220,0)a b a b +≥>>C ．20,0)aba b a b ≤>>+ D ．0,0)2a b a b +>>【答案】D 【解析】 【分析】设,AC a BC b ==，得到2a br OF +==，2a b OC -=，在直角OCF △中，利用勾股定理，求得222=2a b FC +，结合FO FC ≤，即可求解.【详解】设,AC a BC b ==，可得圆O 的半径为122a br OF AB +===， 又由22a b a bOC OB BC b +-=-=-=， 在直角OCF △中，可得2222222()()222a b a b a b FC OC OF -++=+=+=，因为FO FC ≤，所以2a b +≤a b =时取等号． 故选：D.例2．（2022·黑龙江·哈尔滨三中高三阶段练习（文））下列不等式中一定成立的是（ ） A ．()2111x x >∈+R B ．()12,sin sin xx k x k π+>≠∈Z C ．21ln ln (0)4x x x ⎛⎫+>> ⎪⎝⎭D ．()212x x x +≥∈R【答案】D 【解析】 【分析】 由211x +≥得211x +的范围可判断A ；利用基本不等式求最值注意满足一正二定三相等可判断B ；作差比较214x +与x 的大小可判断C ；作差比较21x +与2x 的大小可判断D.【详解】因为x ∈R ，所以211x +≥，所以21011x <≤+，故A 错误； 1sin 2sin x x+≥只有在sin 0x >时才成立，故B 错误； 因为2211042x x x ⎛⎫-+=-≥ ⎪⎝⎭，所以214x x +≥，所以21ln ln 4x x ⎛⎫+≥ ⎪⎝⎭，故C 错误；因为()221210x x x +-=-≥，所以212x x +≥，故D 正确. 故选：D.（多选题）例3．（2022·全国·高三专题练习）下列函数中最小值为6的是（ ） A ．9ln ln y x x=+B ．36sin 2sin y x x=+C ．233xxy -=+ D ．2y =【答案】BC 【解析】 【分析】根据基本不等式成立的条件“一正二定三相等”，逐一验证可得选项. 【详解】解：对于A 选项，当()0,1x ∈时，ln 0x <，此时9ln 0ln x x+<，故A 不正确.对于B 选项，36sin 62sin y x x =+≥，当且仅当36sin 2sin x x =，即1sin 2x =时取“=”，故B 正确.对于C 选项，2336x x y -=+≥=，当且仅当233x x -=，即1x =时取“=”，故C 正确.对于D 选项，26y ≥=，=27x =-无解，故D 不正确.故选：BC.（多选题）例4．（2022·江苏·扬州中学高三开学考试）设0a >，0b >，下列结论中正确的是（ ）A ．()1229a b a b ⎛⎫++≥ ⎪⎝⎭B ．()2221a b a b +≥++C ．22b a a b a b+≥+D ．22a b a b+≥+【答案】ACD 【解析】 【分析】利用基本不等式可判断ACD 选项的正误，利用特殊值法可判断B 选项的正误. 【详解】对于A 选项，()12222559b a a b a b a b ⎛⎫++=++≥+= ⎪⎝⎭，当且仅当a b =时，等号成立，A 对；对于B 选项，取1a b ==，则()2221a b a b +<++，B 错；对于C 选项，22b a b a +≥=，22a b a b +≥=， 所以，2222b a a b a b a b +++≥+，即22b a a b a b+≥+，当且仅当a b =时，等号成立，C 对；对于D 选项，因为222a b ab +≥，则()()2222222a b a b ab a b +≥++=+，所以，()()22222a b a b a ba b a b +++≥=≥++a b =时，两个等号同时成立，D 对.故选：ACD. 【方法技巧与总结】熟记基本不等式成立的条件，合理选择基本不等式的形式解题，要注意对不等式等号是否成立进行验证.题型二：直接法求最值例5．（2022·河南河南·三模（理））已知二次函数()22f x ax x c =++（x ∈R ）的值域为[)0,∞+，则14c a+的最小值为（ ） A ．4- B ．4 C ．8 D ．8-【答案】B 【解析】 【分析】根据()f x 的值域求得1ac =，结合基本不等式求得14c a+的最小值.【详解】由于二次函数()22f x ax x c =++（x ∈R ）的值域为[)0,∞+，所以0Δ440a ac >⎧⎨=-=⎩，所以1,0ac c =>，所以144c a +≥=，当且仅当14c a =即12,2a c ==时等号成立.故选：B例6．（2022·湖北十堰·三模）函数()1111642x x x f x -=++的最小值为（ ） A ．4 B ．C ．3D ．【答案】A 【解析】 【分析】利用不等式性质以及基本不等式求解. 【详解】因为116224xx x +≥⨯，当且仅当1164x x =，即0x =时等号成立，1122222422x x x x -⨯+=⨯+≥=，当且仅当2222xx⨯=，即0x =时等号成立， 所以()f x 的最小值为4. 故选：A（多选题）例7．（2022·广东·汕头市潮阳区河溪中学高三阶段练习）已知a ，b 是两个正数，4是2a 与16b 的等比中项，则下列说法正确的是（ ） A ．ab 的最小值是1 B ．ab 的最大值是1 C ．11a b+的最小值是94D ．11a b +的最大值是92【答案】BC 【解析】 【分析】根据等比中项整理得44a b +=，直接由基本不等式可得ab 的最大值，可判断AB ；由111()(4)4a b a b +⋅+⋅展开后使用基本不等式可判断CD. 【详解】因为22164a b ⋅=，所以4422a b +=，所以4424a b ab +=，可得1ab ，当且仅当4a b =时等号成立， 所以ab 的最大值为1，故A 错误，B 正确．因为1111419()(4)(14)(524444b a a b a b a b +⋅+⋅=++++=， 故11a b +的最小值为94，无最大值，故C 正确，D 错误． 故选：BC【方法技巧与总结】直接利用基本不等式求解，注意取等条件.题型三：常规凑配法求最值例8．（2022·全国·高三专题练习（理））若11x -<< ，则22222x x y x -+=-有（ ）A ．最大值1-B ．最小值1-C ．最大值1D ．最小值1【答案】A 【解析】将给定函数化简变形，再利用均值不等式求解即得. 【详解】因11x -<<，则012x <-<，于是得21(1)1111[(1)]121212x y x x x -+=-⋅=--+≤-⋅---，当且仅当111x x-=-，即0x =时取“=”， 所以当0x =时，22222x x y x -+=-有最大值1-.故选：A例9．（2022·全国·高三专题练习）函数131y x x =+-(1)x >的最小值是（ ）A ．4B ．3C ．D ．3【答案】D 【解析】 由()13131y x x =-++-，利用基本不等式求最小值即可. 【详解】因为1x >，所以()131331y x x =-++≥-3=，当且仅当()1311x x -=-，即1x =+时等号成立.所以函数131y x x =+-(1)x >的最小值是3. 故选：D. 【点睛】本题考查利用基本不等式求最值，考查学生的计算求解能力，属于基础题. 例10．（2022·全国·高三专题练习）若0x >，0y >且x y xy +=，则211x yx y +--的最小值为（ ）A ．3B ．52C ．3D ．3+【答案】D 【解析】利用给定条件确定1,1x y >>，变形211x y x y +--并借助均值不等式求解即得. 【详解】因0x >，0y >且x y xy +=，则xy x y y =+>，即有1x >，同理1y >， 由x y xy +=得：(1)(1)1x y --=，于是得11222123()33111111x y x y x y x y +=+++=++≥+=+------当且仅当2111x y =--，即11x y =+=“=”，所以211x y x y +--的最小值为3+ 故选：D例11．（2022·上海·高三专题练习）若1x >，则函数211x x y x -+=-的最小值为___________.【答案】3 【解析】 【分析】由2111111x x y x x x -+==-++--，及1x >，利用基本不等式可求出最小值.【详解】由题意，()()()()222211111111111111x x x x x x x y x x x x x -++-+-+-+-+====-++----，因为1x >，所以111131y x x =-++≥=-，当且仅当111x x -=-，即2x =时等号成立.所以函数211x x y x -+=-的最小值为3.故答案为：3.例12．（2021·江苏·常州市北郊高级中学高一阶段练习）已知1xy =，且102y <<，则22416x yx y -+最大值为______．【解析】由1xy =且102y <<，可得1(2)y x x=>，可得40x y ->，再将22416x y x y -+化为18(4)4x y x y-+-后利用基本不等式求解即可． 【详解】解：由1xy =且102y <<，可得1(2)y x x =>，代入440x y x x-=->，又222441816(4)8(4)4x y x y x y x y xy x y x y--==≤=+-+-+-当且仅当844x y x y-=-，即4x y -= 又1xy =，可得x =y =时，不等式取等， 即22416x y x y -+，． 【方法技巧与总结】1．通过添项、拆项、变系数等方法凑成和为定值或积为定值的形式． 2．注意验证取得条件．题型四：消参法求最值例13．（2022·浙江绍兴·模拟预测）若直线30(0,0)ax by a b --=>>过点(1,1)-，则___________.【答案】【解析】 【分析】将点(1,1)-代入直线方程可得3a b +=. 【详解】直线30ax by --=过点(1,1)-，则3a b += 又0,0a b >>，设t =0t >2126t a b =++++=+由()()2121292a b a b +++⎛⎫++≤= ⎪⎝⎭，当且仅当12+=+a b ，即2,1a b ==时等号成立.所以2612t =+≤，即t ≤2,1a b ==时等号成立. 故答案为：例14．（2022·全国·高三专题练习）设正实数x ，y ，z 满足22340x xy y z -+-=，则当xy z取得最大值时，212x y z+-的最大值为（ ）A ．0B ．3C ．94D ．1【答案】D 【解析】 【分析】利用22340x xy y z -+-=可得143xy x y z y x=+-，根据基本不等式最值成立的条件可得22,2x y z y ==，代入212x y z++可得关于y 的二次函数，利用单调性求最值即可.【详解】由正实数x ，y ，z 满足22340x xy y z -+-=， 2234z x xy y ∴=-+．∴22111434432?xy xy x y z x xy y x y y x===-++-， 当且仅当20x y =>时取等号，此时22z y =．∴222122121(1)1122x y z y y y y+-=+-=--+，当且仅当1y =时取等号， 即212xyz+-的最大值是1． 故选：D 【点睛】本题主要考查了基本不等式的性质和二次函数的单调性，考查了最值取得时等号成立的条件，属于中档题.例15．（2022·全国·高三专题练习（理））已知正实数a ，b 满足220ab a +-=，则4a b +的最小值是（ ） A ．2 B．2 C．2 D ．6【答案】B 【解析】 【分析】根据220ab a +-=变形得22a b =+，进而转化为a b b b +=++842， 用凑配方式得出()b b ++-+8222，再利用基本不等式即可求解. 【详解】由220ab a +-=，得22a b =+，所以()a b b b b b b +=+=++-⋅=+++888422222222， 当且仅当,a b b b ==+++28222，即a b ==2取等号. 故选：B.例16．（2022·浙江·高三专题练习）若正实数a ，b 满足32+=b a ab ，则2+a bab 的最大值为______． 【答案】12【解析】 【分析】由已知得a ＝23b b -，代入2+a b ab ＝32323bb b b b +--＝222b b -+＝﹣2 （112b -）2+12，然后结合二次函数的性质可求． 【详解】因为正实数a ，b 满足b +3a ＝2ab ， 所以a ＝23bb -，则2+a b ab ＝32323bb b b b +--＝222b b -+＝﹣2 （112b -）2+12， 当112b =，即b ＝2 时取得最大值12．故答案为：12． 【点睛】思路点睛：b +3a ＝2ab ，可解出a ，采用二元化一元的方法减少变量，转化为1b的一元二次函数，利用一元二次函数的性质求最值.例17．（2022·全国·高三专题练习）若,x y R +∈，23()()-=x y xy ，则11x y+的最小值为___________. 【答案】2 【解析】 【分析】根据题中所给等式可化为211()xy y x-=，再通过平方关系将其与11x y +联系起来，运用基本不等式求解最小值即可. 【详解】因为23()()-=x y xy 且,x y R +∈，则两边同除以2()xy ，得211()xy y x-=，又因为224(111111()44)xy y y x xy xy x -+=+=+≥，当且仅当14xy xy =，即22x y ==211x y+.故答案为:2例18．（2022·浙江绍兴·模拟预测）若220,0,422>>+-=a b a b ab ，则12++ab a b的取值范围是_________．【答案】23⎡⎢⎣⎦【解析】 【分析】根据已知可得2(2)206a b ab +-=>，求得2a b +>2(2)26a b ab +=+结合基本不等式可求得02a b <+≤12++ab a b变形为14262a b a b ⎛⎫++ ⎪+⎝⎭，采用换元法，利用导数求得结果. 【详解】由题意220,0,422>>+-=a b a b ab 得：2(2)206a b ab +-=> ，则2a b +>，又222(2)26232+⎛⎫+=+≤+⨯ ⎪⎝⎭a b a b ab ，当且仅当2b a ==时取等号，故02a b <+≤2a b <+≤ 所以1142262ab a b a b a b +⎛⎫=++ ⎪++⎝⎭，令2,t a b t =+∈ ，则14()()6f t t t =+ ，222144()(1)66t f t t t -'=-=，2t << 时，()0f t '<，()f t 递减，当2t <≤时，()0f t '>，()f t 递增，故min 2()(2)3f t f ==，而f = ，f =，故2()[3f t ∈，即2[312ab a b ∈++，故答案为：23⎡⎢⎣⎦【方法技巧与总结】消参法就是对应不等式中的两元问题，用一个参数表示另一个参数，再利用基本不等式进行求解.解题过程中要注意“一正，二定，三相等”这三个条件缺一不可！题型五：双换元求最值例19．（2022·浙江省江山中学高三期中）设0a >，0b >，若221a b +=，则2ab -的最大值为（ ）A ．3B ．C ．1D ．2+【答案】D 【解析】【分析】法一：设c b =-，进而将问题转化为已知221a c +=，求ac 的最大值问题，再根据基本不等式求解即可；法二：由题知221()14a b +=进而根据三角换元得5cos ,(0)62sin a b πθθθθ⎧=⎪<<⎨=⎪⎩，再根据三角函数最值求解即可. 【详解】解：法一：（基本不等式）设c b =-2ab -=)a b ac -=，条件222211a b a c +=⇔+=，2212a c ac +=+≥，即2≤ac 故选：D.法二：（三角换元）由条件221()14a b +=，故可设cos sin 2a b θθ⎧=⎪⎪⎨⎪=⎪⎩，即cos ,2sin a b θθθ⎧=⎪⎨=⎪⎩， 由于0a >，0b >，故cos 02sin 0θθθ⎧>⎪⎨>⎪⎩，解得506πθ<<所以，5cos ,(0)62sin a b πθθθθ⎧=⎪<<⎨=⎪⎩，22sin 22ab θ-=≤+当且仅当4πθ=时取等号.故选：D.例20．（2022·天津南开·一模）若0a >，0b >，0c >，2a b c ++=，则4a ba b c+++的最小值为______．【答案】2+ 【解析】 【分析】令2,,(0,0)c m c n m n -==>> ，则2m n +=，由此可将4a b a b c+++变形为421m n +-，结合基本不等式，即可求得答案。

高三数学复习专题目录专题一、数列与不等式数列（1）数列（2）专题二、三角函数三角函数（1）三角函数（2）专题三、立体几何立体几何（1）立体几何（2）专题一、数列与不等式一.基础知识梳理数列：1. 了解数列的概念和几种简单的表示方法（列表、图像、通项公式）2.了解数列是自变量为正整数的一类函数.3.了解递推公式是给出数列的一种方法，能据递推公式写出前几项，同时求出通项公式.4,理解等差、等比数列的概念，掌握等差数列的通项公式与前n项公式，并能解决简单实际问题.5.体会等差数列、等比数列与一次函数，指数函数，二次函数的关系.不等式：（必修部分）1.一元二次不等式^2+^ + c>0（cz>0）与相应的函数y = ax2+bx+c（a>0\相应的方程ax2+bx +c = 0（«〉。

）之间的关系2.一元二次不等式恒成立情况小结：J G >0 [a<0 ax2 + bx + c>0（a/0）恒成立 o。

，ax2 +bx + c <0（a/0）恒成立o。

3.二元一次不等式表示的平面区域：直线I: ax + by + c = 0把直角坐标平面分成了三个部分：（1）直线/上的点（x, y）的坐标满足ax +by+ c = 0（2）直线Z一侧的平面区域内的点（x, y）^^ax + by + oO（3）直线Z另一侧的平面区域内的点（x,y）满足ox + /<y + c<0所以，只需要在直线Z的某一侧的平面区域内，任取一特殊点（将，光），从ax0+by0+c值的正负，即可判断不等式表示的平面区域。

4.线性规划：如果两个变量x,y满足一组一次不等式，求这两个变量的一个线性函数的最大值或最小值，称这个线性函数为目标函数，称一次不等式组为约束条件，像这样的问题叫作二元线性规划问题.其中，满足约束条件的解（x,y）称为可行解，由所有可行解组成的集合称为可行域，使目标函数取得最大值和最小值的可行解称为这个问题的最优解.5.基本不等式：⑴如果"eR,那么/+〃 2 2沥，（当且仅当“=。

高三文言文特殊句式专题复习(总5页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--高考题展1.古人欲知稼穑之艰难，斯盖贵谷务本之道也。

夫食为民天，民非食不生矣。

三日不粒，父之不能相存。

耕种之，锄之。

刈获之，载积之，打拂就无法生存。

三天不吃粮食，父亲和儿子就不能保全。

（3分）2.乡闾贫弱赖以不困。

洪武初，宁海及邻县饥，里中富人以麦贷贫乏者，每斗麦责谷二斗三升。

时贤母家有麦数廪，召诸子谓曰：“饥者众，而答案：村里有把麦子借给穷人的富人，每斗麦子要求归还二斗三升谷子。

3.汉五年，已并天下，诸候共尊汉王为皇帝于定陶。

高帝悉去秦苛仪法，为简易。

群臣饮酒争帝。

4.选出下列各组中不含定语后置的一项( )A.求人可使报秦者，未得。

B.客之美我者，欲有求于我也。

C.太子及宾客知其事者，皆白衣冠以送之。

D.石之铿然有声者，所在皆是也。

答案：B解析：ACD 是定语后置句；B 是状语后置句。

文言文常见的句式主要有:判断句、被动句、倒装句、省略句、疑问句。

一、判断句用名词或名词性短语断定人或事物是什么、属于什么的句子叫做判断句。

现代汉语一般是在主语和谓语之间用判断动词“是”来表示判断的。

但在古汉语里，“是”多作代词用，很少把它当作判断动词用。

因此，在绝大多数情况下借助语气词来表示判断。

（一）用“者”、“也”为标志表示判断。

可分为四种状况。

1、主语后面用“者”表示停顿，在谓语后面用“也”表示判断，构成“… …者， … …也。

”式。

①、廉颇者．，赵之良将也．。

《廉颇蔺相如列传》 ②、臣之所好者．，道也．。

《庖丁解牛》 2、“者也”在句尾连用，表示判断。

构成“……者也”式。

①城北徐公，齐国之美丽者也．．。

《邹忌讽齐王纳谏》② 莲，花之君子者也．．。

《爱莲说》 3、主语后面用“者”表示停顿，而谓语后面不用“也”，即“… …者， … …”式。

①粟者．，民之所种。

②天下者．，高祖天下。

句子连接
了解如何使用连接词和短语使句 子之间具有连贯性和衔接性。
语法运用
掌握பைடு நூலகம்作中的常见语法知识和错 误，避免写作中的语法问题。
专题六：短文改错
1
错误类型
了解短文改错中常见的错误类型，如时态、冠词和主谓一致等。
2
改错技巧
学习修改短文的技巧和方法，提高改错准确率。
3
模拟训练
通过大量的练习，熟悉短文改错题的考点和解题技巧。
专题七：模拟试题讲解
模拟试题挑战
针对高考英语试题进行讲解和解析，提供应对策略。
知识点巩固
总结模拟试题中的常见知识点，加深理解。
时间管理
教你如何在有限的时间内高效解答试题，提高答题速度。
提高策略
了解如何进行划线标记、摘要写 作等技巧，提高阅读理解能力。
专题四：听力技巧
预测内容
学习根据问题、选项等信息 预测听力材料的内容。
记笔记
掌握有效的记笔记技巧，有 助于听力理解和答题。
听力短文
通过听力短文训练，提高听 力水平，掌握听力技巧。
专题五：写作技巧
组织结构
学习如何合理组织文章结构，使 文章逻辑清晰。
专题二：词汇复习
1 单词记忆技巧
教你使用有效的记忆技巧 记忆单词，提升词汇量。
2 词义辨析
通过举例和对比，帮助你 理解和区分近义词和易混 淆词的意思。
3 词汇拓展
学习如何通过词根、前缀 和后缀等方式扩大词汇量。
专题三：阅读理解复习
技巧分享
掌握阅读理解技巧，如快速定位 信息、推断意义等。
文本类型
学习不同文本类型的特点和常见 考点，例如新闻报道、广告等。
高三英语专题复习课件

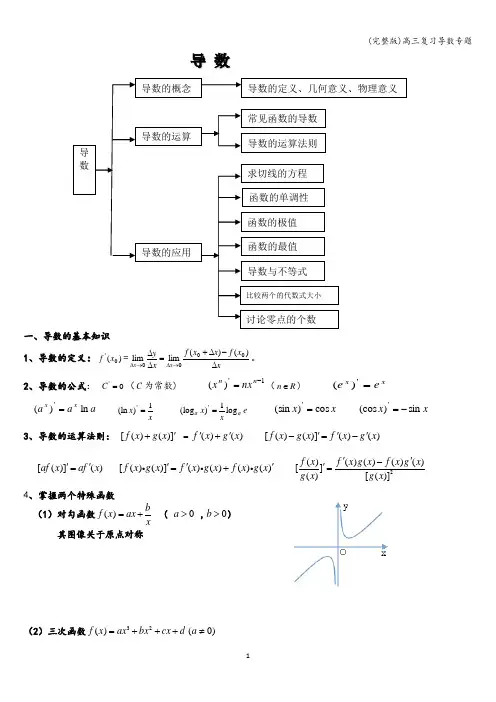
导 数一、导数的基本知识 1、导数的定义：)(0'x f =xx f x x f x yx x ∆-∆+=∆∆→∆→∆)()(limlim0000。

2、导数的公式： 0'=C （C 为常数) 1')(-=n n nx x （R n ∈) xx e e =')(a a a x x ln )('= xx 1)(ln '= exx a a log 1)(log '=x x cos )(sin '= x x sin )(cos '-=3、导数的运算法则： [()()]f x g x '+ =()()f x g x ''+ [()()]()()f x g x f x g x '''-=-[()]()af x af x ''= [()()]()()()()f x g x f x g x f x g x '''=+ 2()()()()()[]()[()]f x f x g x f x g x g x g x ''-'= 4、掌握两个特殊函数 （1）对勾函数()bf x ax x=+( 0a > ,0b >) 其图像关于原点对称（2）三次函数32()f x ax bx cx d =+++(0)a ≠导 数导数的概念 导数的运算导数的应用导数的定义、几何意义、物理意义 函数的单调性 函数的极值函数的最值 常见函数的导数导数的运算法则 比较两个的代数式大小导数与不等式讨论零点的个数求切线的方程导数的基本题型和方法1、、导数的意义：（1）导数的几何意义：0()k f x '= （2）导数的物理意义:()v s t '=2、、导数的单调性：（1）求函数的单调区间;()0()b]f x f x '≥⇔在[a,上递增 ()0()b]f x f x '≤⇔在[a,上递减（2）判断或证明函数的单调性; ()f x c ≠ （3)已知函数的单调性，求参数的取值范围。

2024届高三语文备考专题复习：语言文字运用专题练习（附答案解析）题组一（一）语言文字运用Ⅰ阅读下面的文字，完成问题。

中国食客们早已习惯了“中华美食甲天下”的尊荣，街边商厦的小吃店的墙上往往喜欢挂一段上逾千年的传说——虽然食客大多也不会把这些动辄与乾隆、诸葛亮、秦始皇甚至是黄帝、女娲的故事当真，但换个视角将华夏五千年历史视为五千年美食史，似乎也不算太夸张。

然而，历史真相往往令人感到意外。

中国历史虽然，但中华美食文化异常晚熟：“南食”“北食”直到唐宋时期才逐渐分野，土豆、玉米、番茄、辣椒等食材直到明代才传入中国，“四大菜系”直到清初才成型。

诸如大盘鸡、螺蛳粉等为人们所的小吃美食、菜肴菜式直到新中国成立之后才诞生，而“菜系”作为一个专有词条，直到1992年才被收录到《中国烹饪辞典》中，如今“八大菜系”的说法又被“34菜系”所取代。

中华美食荣光背后，是其发展的漫漫长路。

物质生活极大丰富的岁月里，“一粥一饭，当思来之不易”这句古训对食客们或许有更深的感动。

中华美食是美好的，华丽的，精致的，同时也是坚韧的，顽强的，隐忍的；中华美食文化是古老悠远的，同时也是厚积新成的。

五千年时光仿佛是一场漫长的蛰伏，为的只是在某一个时间，爆发出最绚烂的华章。

食客们在、推杯换盏之时其实不难发现，中国美食自古以来最不缺的，就是兼容并蓄的气度和能力。

1.依次填入文中横线上的词语，全都恰当的一项是（）A.林林总总源远流长津津乐道觥筹交错B.琳琅满目渊远流长津津有味杯盘狼籍C.林林总总源远流长津津有味杯盘狼籍D.琳琅满目渊远流长津津乐道觥筹交错2.文中画波浪线的句子有语病，下列修改最恰当的一项是（）A.物质生活极大丰富的岁月，“一粥一饭，当思来之不易”这句古训对食客们或许有更深的感悟。

B.物质生活极大丰富的岁月里，食客们或许对“一粥一饭，当思来之不易”这句古训有更深的感动。

C.在物质生活极大丰富的岁月里，食客们或许对“一粥一饭，当思来之不易”这句古训有更深的感悟。

高三语文专题复习文言文复习教案高三语文专题复习文言文复习教案为题，用中文写一篇3000字文章。

在高三语文备考中，文言文是一个重要的考点，掌握好文言文的阅读理解和写作能力对于取得好成绩十分关键。

为了帮助同学们更好地复习文言文，以下是一份文言文复习教案。

教案名称：文言文复习教案适用年级：高三主要内容：1. 文言文基础知识复习2. 文言文阅读理解技巧训练3. 文言文写作技巧训练一、文言文基础知识复习1. 字词的理解与运用：复习常用文言词汇、古文常用语法词汇、文言虚词等。

2. 句子的结构与翻译：复习文言句子结构，包括主谓宾结构、并列结构、状语结构等，并能准确翻译成现代汉语。

3. 文言文的修辞手法：复习并掌握常见的文言修辞手法，如夸张、比喻、拟人等，并能从文中找出相应的修辞手法进行解释。

二、文言文阅读理解技巧训练1. 理解古文篇章结构：通过多篇古文的阅读，培养对古文篇章结构的理解能力，包括开篇、承接、递进、高潮、结尾等部分。

2. 掌握古文重点句子分析：通过对古文中的关键句子进行分析，包括主谓宾结构、修饰成分、状语等，帮助理解整篇古文的意境。

3. 整体思维理解古文：通过阅读古文，培养对整体思维的运用能力，包括整体把握、推理分析等。

同时，注意借助上下文的提示，理解古文中的生僻词汇和句子。

三、文言文写作技巧训练1. 古文翻译训练：通过训练，掌握古文的翻译技巧，包括句子的翻译、句型的转换等。

2. 古文仿写训练：学习古文的写作技巧，进行古文仿写，模仿古文的表达方式和修辞手法，提高自己的写作水平。

3. 古文赏析和演讲：阅读分析古文，并能够进行赏析和演讲，深入理解古文背后的思想和文化。

四、综合练习和模拟考试1. 综合练习：进行一些综合性的文言文练习，包括阅读理解、翻译和写作等，帮助巩固所学知识。

2. 模拟考试：进行文言文的模拟考试，模拟真实的考试环境，提前适应考试的要求，并及时总结分析自己在文言文方面的不足，作针对性的复习和训练。

2．解析：(1)盖：承接上文，说明理由和原因， 表确定语气，相当于“本来是”“原来是”。 役：第一个“役”是名词，仆役；第二个“役” 是动词，役使，驱使。非：表否定判断。而已 也：三个语气词连用，表强调。 (2)向使：连词，假如，假使。佣：雇佣。若： 代词，你。直：通“值”，工钱。怠：怠慢。 货：财物。黜：贬退。罚：处罚。补齐省略成 分，即“（其）受若直……则（若）必甚怒而黜 罚之矣”。




【参考译文】

孟子说：“如今侍奉国君的人都说：‘我能为国君开拓土地， 充实府库。’——如今所说的好臣子，正是古代所说的残害百姓 的人。国君不向往道德，不立志行仁，却想法让他富有，这等于 是去让夏桀富有。（又说：）‘我能够替国君邀约盟国，每战一 定胜利。’——如今所说的好臣子，正是古代所说的残害百姓的 人。国君不向往道德，不立志行仁，却去想法让他武力强大，这 等于是去帮助夏桀。从如今这样的道路走下去，不改变如今的风 俗习气，即便把整个天下给他，也是一天都坐不稳的。”
(1) 太祖马鞍在库，而为鼠所啮，库吏惧必死，议欲面缚首罪， 犹惧不免

(2) 世俗以为鼠啮衣者，其主不吉。今单衣见啮，是以忧戚。 (3) 俄而库吏以啮鞍闻，太祖笑曰：“儿衣在侧，尚啮，况鞍 县柱乎？”一无所问
3．解析：(1)为„„所：表被动。 啮：咬。面缚：反绑双手，当面请罪。 首：自首。罪：用作动词，请罪。 “犹惧不免”是被动句。 (2)以：认为。为、见：均表被动。是 以：因此。戚：忧愁，悲哀。 (3)俄而：不久。以：介词。把。闻： 使动用法，使„„闻，报告。尚啮： 被动句。县：通“悬”。 答案：见“参考译文”。

(1) 远来相视，子令吾去，败义以求生，岂荀巨伯所行 邪！

不同物质溶液中同种离子浓度比较一. 不同盐溶液中同种离子浓度大小比较【例1】物质的量浓度相同的下列溶液中，NH4+浓度最大的是（）。

A．NH4Cl B．NH4HSO4C．NH3COONH4 D．NH4HCO3【答案】B【例2】物质的量浓度相同的下列溶液：① Na2CO3② NaHCO3 ③ H2CO3 ④ (NH4)2CO3 ⑤ NH4HCO3，按c（CO32-）由小到大排列的顺序是（）A．⑤＜④＜③＜②＜① B．③＜⑤＜②＜④＜①C．③＜②＜⑤＜④＜① D．③＜⑤＜④＜②＜①【答案】B【解析】不管是弱电解质的电离，还是盐的水解，在水溶液中大多以原来的微粒存在于溶液中，则：Na2CO3是易溶于水的盐，在水中完全电离，电离出的碳酸根离子部分水解，但水解微弱，所以，碳酸根离子浓度降低，碳酸根浓度接近0.1mol/L；NaHCO3是易溶于水的盐，在水中完全电离，电离出的碳酸氢根离子水解建立水解平衡，因碳酸氢钠溶液显碱性，所以，部分碳酸氢根离子的电离小于其水解，所以碳酸根浓度远远小于碳酸氢根浓度，及远远小于0.1mol/L；（NH4）2CO3是易溶于水的盐，在水中完全电离，电离出的铵根离子和碳酸根离子分别和水电离出的氢氧根离子和氢离子结合，水解相互促进，所以，碳酸根离子浓度比Na2CO3中碳酸根离子离子浓度小一些，碳酸根离子略小于0.1mol/L；H2CO3溶液是二元弱酸，且酸性很弱，电离时分两步电离，电离出的碳酸根离子浓度较小，但它是酸，溶液显酸性，所以，碳酸根浓度小于0.1mol/L，NH4HCO3溶液中电离出碳酸根离子只需碳酸氢根离子一步电离，而H2CO3溶液是二元弱酸，需两步电离，且第二步极其微弱，其碳酸根离子的浓度比NH4HCO3溶液中碳酸根离子浓度小；NH4HCO3是易溶于水的盐，在水中完全电离在水中完全电离，电离出的铵根离子和碳酸氢根离子分别和水电离出的氢氧根离子和氢离子结合，水解相互促进，所以，碳酸氢根离子电离出来的碳酸根离子的浓度非常小，比NaHCO3溶液中碳酸根离子浓度小；综上碳酸根离子浓度为：Na2CO3＞（NH4）2CO3＞NaHCO3＞NH4HCO3＞H2CO3，故选B。

（2） 河流利用： 防洪、发电、灌溉、养殖、航运、供水、生态效益
1.开发——水能
如何分析河流的水能资源？ 水量——气候、流域面积； 落差——地形 在等高线图上如何确定水电站的位置？
峡谷地带——工程量小； 上游有较大的集水面积，库容大； 尽量考虑集水后不淹没或少淹没村庄农田的位置；
思考：水能资源丰富的地方是否水电开发条件优？
（4）简述该图所示流域综合开发的主要方向，并说明理由。
思维导图解题法：
（4）简述该图所示流域综合开发的主要方向，并说明 理由。
在河流开发的基础上（1）结 合山地丘陵地形发展立体农业， 同时可延长特色农产品产业链， 发展特色加工业； （2）水量 大，落差大，可利用水能发电 （3 ）利用山水资源，发展旅 游业； （4）地处山区，注意 保护植被和湿地，防止水土流 失以及滑坡、泥石流，维护生 物多样性，并防治水污染。
高三一轮专题复习
——河流的开发与利用
【考点分析】
1.关注河流水能，探究流域内水能开发的条件 2.关注整体性，探究河流与其他各自然地理要素的关联 3.关注河流航运，突出对河流航运条件分析的考查 4.关注河流功能，考查城市在河流交通运输中的区位特点 5.关注人地矛盾，探寻河流综合整治的主要措施
河流
利用 改造
1.描述L河流域在乙地以上的自然地理环境特征？ 2.指出图中L河流域开发过程中可能出现的问题及治理措施？ 3.说出L河流在乙地以上和乙地以下不同的开发利用方向，并分析原因。
1.大部分地处热带，位于东南亚，自然资源 丰富，尤其是生物资源，地形为山河相间， 纵列分布，大部分为热带季风气候，植被 为热带季雨林，落差较大，流速较快，水 能资源丰富
工业 第三产业 人口 城市 经济发展水平
自然资源

高三高考语文复习专题《语序不当、搭配不当》试题汇编（附答案解析）【题组练】1.指出下列病句的病因,并做修改。

(1)强强联合制作的大戏,让人们不仅看到了中国戏曲的整体进步,而且看到了中国戏曲在现代化问题上迈出的可喜一步。

答案:语序不当(排查递进关系的复句,顺序颠倒了)。

应改为“让人们不仅看到了中国戏曲在现代化问题上迈出的可喜一步,而且看到了中国戏曲的整体进步”。

(2)近期卫生部表示,将继续密切关注重点省份以及全国流感疫情的形势,加强对流感疫情的分析、研判和监测,对重点省份的流感防控工作予以指导。

答案:并列短语语序不当(排查并列短语)。

应该是“监测、分析和研判”。

(3)虽然莫言获奖,不能说他已经参与了世界文明标准规则的建设,但至少可以说他开始影响西方文明,这就是文学的力量。

答案:语序不当(排查关联词位置,二、三分句是陈述“莫言获奖”的影响),“虽然”应放在“不能说”前面。

2.指出下列病句的病因,并做修改。

(1)为了使这项住房政策真正受惠于低收入家庭,政府制定了非常严格的申请程序,一旦发现诈骗,处罚极其严厉。

答案:语序不当(排查介词,误用介词“于”造成主客体颠倒),“这项住房政策”应与“低收入家庭”调换位置。

(2)凤凰传奇这个名字对中年人可能还有些陌生,可对青年人却是很熟悉的。

答案:语序不当(排查介词,误用“对”造成主客体颠倒),可在“中年人”“青年人”后面加“来说”。

(3)考古学家对两千六百年前在沂水纪王崮天上王城春秋大型古墓新出土的文物进行了多方面的研究,对墓主的级别有了进一步的了解。

答案:多项定语语序不当,应将“两千六百年前”移到“文物”之前,并在“文物”前加“的”。

(4)运动员的高超技能可以通过日常的刻苦训练获得,而良好的心理素质却要通过临场的无数竞技才能练就。

答案:多项定语语序不当(表数量的应在动词性短语前),“临场的无数竞技”应为“无数的临场竞技”。

3.指出下列病句的病因,并做修改。

(1)大学自主招生制度是对现有高考制度的一个有益补充,也为一些有创新潜质与学科特长的考生创设一个绿色通道,通过让他们自主招生的方式进入心仪的大学。

激素
（性腺） 调节激素的合成和分泌
（二）主要内分泌腺及功能
内分 泌腺
甲 状 腺
肾 上 腺
激素 名称
甲状腺激素
肾上 腺素
化学 性质
氨基 酸衍 生物
作用 部位
全身
全身
生理作用
备注
幼年过少： ①促进新陈代谢和生长 呆小症
发育
成年过少：
地方性
②提高神经系统的兴奋 甲状腺肿
性
成年过多：
甲亢
①升高血糖 ②加快代谢，增加产热
2.反馈调节
正反馈
负反馈
例如：排尿反射、血液凝固、 例如：体温调节、血糖平衡、
分娩过程等。
等大多数激素调节。
（三）水盐平衡的调节
“ ”神经调节 “ ”激素调节
饮水不足，体内失水过多或吃的食物过咸
“ ”反馈调节
细胞外液渗透压升高
（-）负反馈 细 胞
刺激 下丘脑渗透压感受器
传入
（-） 负反馈 细
胞
外
大脑皮层
专题十一
生命活动的调节（二）
激素调节及其与神经调节的关系
免
疫
调
节
主要内容
激素调节及与神经调节的关系
关注考纲
1.脊椎动物激素的调 节Ⅱ 2.体温调节、水盐调 节和血糖调节Ⅱ 3.神经-体液调节在 维持稳态中的作用Ⅱ 4.脊椎动物激素在生 产中的应用Ⅰ
近五年考情
2020卷ⅠT3，31 2020卷ⅡT31， 2020卷ⅢT30， 2019卷ⅠT4， 2019卷ⅡT4，30 2019卷ⅢT3， 2018卷ⅡT3,29 2018卷ⅠT31, 2017卷ⅠT4, 2017卷ⅡT5, 2017卷ⅢT31， 2016卷ⅡT3,30 2015卷ⅠT30， 2015卷ⅡT30，

高三语文专题复习（词类活用）教案教学设计高三语文专题复习（词类活用）教案教学设计「篇一」教学目标：1．了解扩展语句的类型。

2．掌握扩展语句的方法。

教学重点：掌握扩展语句的步骤和方法。

教学难点：加强扩展语句的能力。

教学方法：讲练结合课时安排：2课时第一课时教学内容：了解扩展语句的类型，掌握扩展语句的步骤和方法。

教学过程：一、导入新课1．请用“银河”、“树影”、“蛙声”等词语写一段情景交融的文字。

要求想象合理，语言连贯，不少于40个字。

（江苏卷）【参考答案】静谧的夏夜，银河横空，群星璀璨。

灿烂的星光隐隐映出村庄周围婆娑的树影。

微风掠过树梢，树叶沙沙作响，伴着四周稻田里传来的阵阵蛙声，宛如一曲动听的田园交响乐，令人陶醉。

（情景演绎式）2．按要求把下面的句子扩写成一段话。

（7分）这个冬季，天气异常寒冷。

要求：①正面描写与侧面描写相结合。

②至少运用两种不同的修辞方法。

③不少于80字。

【参考答案】正面：这是一个百年难遇的冬天，南方下起了大雪，大雪阻断了交通，使很多人陷入困境。

很多车被堵在路上，车连着车，犹如一条白色的长龙（比喻），这长龙在纷纷扬扬的大雪中颤抖着无奈的身躯（拟人）。

侧面：人们开始焦虑起来，疯狂起来。

（枝叶添加式）3．请以“和谐”为内容写三句话。

要求每句话都使用比喻，三句话构成排比。

（06全国卷Ⅰ）【参考答案】和谐是乐手演奏的动人旋律，和谐是画家创作的美丽画卷，和谐是设计师描绘的宏伟蓝图。

和谐是春风与细雨的默契，和谐是小桥与流水的融洽，和谐是蓝天和白云的辉映。

（中心阐发式）4．在下面一段话后续写。

要求：①先用一句话拟写出一种你自己不认同的看法，②然后写出自己的看法和充分的理由，③不超过100字。

（05北京卷）据报道，某位以独特的“搞笑”风格塑造了众多小人物的著名影星，被某大学聘为教授。

对于他能否胜任，人们有着不同的看法。

【参考答案】我坚决反对这种“圣者通吃”的荒唐做法。

教育界有教育界的尊严，不能说你在某一个领域干得好，就借此进入其他领域。

函数专题1、函数的基本性质复习提问：1、如何判断两个函数是否属于同一个函数。

2、如何求一个函数的定义域（特别是抽象函数的定义域问题）3、如何求一个函数的解析式。

（常见方法有哪些）4、如何求函数的值域。

（常见题型对应的常见方法）5、函数单调性的判断，证明和应用（单调性的应用中参数问题）6、函数的对称性（包括奇偶性）、周期性的应用7、利用函数的图像求函数中参数的范围等其他关于图像问题 知识分类一、函数的概念：函数的定义含有三个要素，即定义域A 、值域C 和对应法则f .当函数的定义域及从定义域到值域的对应法则确定之后，函数的值域也就随之确定.因此，定义域和对应法则为函数的两个基本条件，当且仅当两个函数的定义域和对应法则都分别相同时，这两个函数才是同一个函数. 1、试判断以下各组函数是否表示同一函数？（1）f （x ）=2x ，g （x ）=33x ；（2）f （x ）=x x ||，g （x ）=⎩⎨⎧<-≥;01,01x x（3）f （x ）=1212++n n x ，g （x ）=（12-n x ）2n －1（n ∈N *）；（4）f （x ）=x1+x ，g （x ）=x x +2；（5）f （x ）=x 2－2x －1，g （t ）=t 2－2t －1.二、函数的定义域（请牢记：凡是说定义域范围是多少，都是指等式中变量x 的范围） 1、求下列函数的定义域：(1)ｙ＝－221x ＋１(2)ｙ＝422--x x (3)x x y +=1 (4)ｙ＝241+-+-x x(5)ｙ＝3142-+-x x (8)ｙ＝3-ax （ａ为常数）2、（1）已知f (x )的定义域为 [ 1，2 ] ，求f (2x -1)的定义域； （2）已知f (2x -1)的定义域为 [ 1，2 ]，求f (x )的定义域；3、若函数)(x f y =的定义域为[ 1，1]，求函数)41(+=x f y )41(-⋅x f 的定义域 5、已知函数682-+-=k x kx y 的定义域为R ，求实数k 的取值范围。

如今在北方……那种久违的泥泞……仍然能使我……想起北 方的人民跋涉其中的艰难的背影，想起我们曾有过的苦难和 屈辱。
我们真应该感谢雪，……它诞生了单纯、美，也诞生了肮脏 和使人警醒给人力量的泥泞。
上善是最高的善。（总领） 离堆……玉垒山，因仰赖杜甫、陆游才名扬天下，而都江堰，
才真正是人类智慧的结晶。 （因为）都江堰，绝不危及生态；能防洪又能灌溉，是人类
每到这个季节，十一月上旬，我生上了炉 火，一直到明年四月初，将近半年的时光，我 进入静多动少的生活。每到安炉子和撤火的时 候，我的心里总有些感触，季候的变迁，情绪 的转换，打下了很鲜明、很深刻的印记… …
题目：第一段作者写了“秋去冬来 ‘的景色，这样写有什么作用？请简要 分析
[参考答案] 起铺垫作用（引出下文）。 写“秋去冬来”自然引出下文的“炉火”， 由自然环境变化写出了作者的感伤情绪， 为下文写“炉火”的意蕴预设了空间。
（2）文中运用的一些表现手法
如联想、想象、渲染、烘托、衬托（正 反）、对比、抑扬（先扬后抑或先抑后 扬） 、虚实、象征、铺垫等
（3）布局谋篇的技巧
承上启下 、统摄全篇、详略主次、 行文线索 、伏笔照应、卒章显志、画龙 点睛、设置悬念、点面结合、深化升华 主旨等
（4）修辞的技巧
比喻、夸张、拟人、排比、对偶、反复、 反问、设问共8种
第三类：议论性散文
哲理散文。这类散文以议论为主要表 达方式，但议论不是凭空而生，往往在 文章的开头交代议论的由头，或事，或 物，然后逐层递进式议论。主旨在物 （事）与理相通处。
典型写作思路：对现实的事、物有触 动（触发点）→类似事情相近或相反的 联想议论（联系点）→点出道理（感悟 点）→结合现实议论升华（升华点）
的神话。（上善之作） 伫立水边，我的心与晶莹和透明合而为一。(过渡） （然而）一想到黄河、长江、淮河（这些）赖以生息的湖泊

2,3,3,7,7－五甲基辛烷
原则5：小-----支链编号之和最小。
总结:烷烃系统命名法原则：
① 长-----选最长碳链为主链。
② 多-----遇等长碳链时,支链最多为主链。 ③ 近-----离支链最近一端编号。
④ 简-----两取代基距离主链两端等距离时， 从简单取代基开始编号。
⑤ 小-----支链编号之和最小。
答案：B
【解题方法漫谈三】
③新课标下可能出现的新题型
■现代光谱技术的应用
10．下图是一种分子式为C4H8O2的有机物的红外光谱 谱图,则该有机物的结构简式可能为： 。
三、有机物的命名
内容:烷、烯、炔、苯的同系物、 烃的衍生物的命名
有机物的命名
（一）、普通命名法（适用于简单化合物） 1~10个碳: 甲、乙、丙、丁、戊、己、庚、辛、壬、癸； 10个碳以上:十一、十二等。
碳架异构体:正、异、新。
CH3CH2CH2CH3
正丁烷
CH3CHCH3 CH3
异丁烷
（二）系统命名法（IUPAC命名法）
1、烷烃 步骤：
选主链 例 CH3 支链编号 CH3
书写名称
CH2 CH3 1 2 3 4 5 6 7 8 CH3-CH-CH2-CH2-CH—C-CH2-CH3 CH3 2，6，6 — 三 甲基 —5 —乙基 辛烷
★同分异构体的书写 分子式→官能团异构→碳链异构 →位置异构→立体异构
例1：写出分子式为C8H10O含有一个苯环的 所有物质的结构简式
C8H8O
例2：写出分子式为C4H8链状的有机物的结构简式 （考虑立体异构） 顺反异构判断：双键一侧的碳上连有不同的基团，
对映异构判断：手性分子 乳酸、葡萄糖等 （手性碳原子-----一个碳原子连接四个不同的基团） 例3：写出分子式为C4H8O2酯类有机物的结构简式 C5H10O2 分碳法 只须 R1—COOH中烃基 写 对应酸 酯 的同分异构体 写出