江苏省扬中市第二高级中学2015届高三数学午时30分钟训练23 Word版含答案
- 格式:doc
- 大小:359.50 KB
- 文档页数:1

高三数学午时30分钟训练17班级 姓名1.函数))(6cos()3sin(2R x x x y ∈+--=ππ的最小值等于 . 2. 已知函数()2sin sin sin 244f x x x x ππ⎛⎫⎛⎫=-⋅++ ⎪ ⎪⎝⎭⎝⎭,则函数()f x 的最小正周期是 3.把函数πϕωϕω<>+=||,0)((x f y )的图象向左平移6π个单位,再将图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到函数)(x f y =的图象,则,ωϕ== 4.函数x y sin =的定义域为[a ,b],值域为]21,1[-,则b-a 的最大值和最小值之和为5.函数1cos |sin |-=x x y 的最小正周期与最大值的和为 .6.函数y =cos 2(2x+3π)-sin 2(2x+3π)的最小正周期是 . 7.已知函数()sin()cos()f x x x 在3x 时取得最小值,则的一个值可 以是8.函数23cos 3cos sin 2-+=x x x y 的最小正周期为 . 9.已知函数θθθsin 2)sin()sin()(--++=x x x f ,⎪⎭⎫ ⎝⎛∈πθ23,0,且432tan -=θ,若对任意R x ∈,都有0)(≥x f 成立,则θcos 的值为 .10. 已知集合},23sin 22cos 21|{},2|3||{A x x a x y y B x x A ∈+--==≤-=集合ππ, 其中ππ≤≤a 6,设全集I=R ,欲使A B ⊆,求实数a 的取值范围.1. 1- )2. π3.3,2πϕω-== )4.π2 5.212-π 6.2π7. 4 8.π;9.解:依题意)1(cos sin 2sin 2cos sin 2)(-=-=x x x f θθθ01cos ≤-x 0sin ≤∴θ πθπ23<≤∴ 由432tan -=θ得3tan =θ 1010cos -=∴θ 10.集合}2225{|,sin 2sin 1(sin )166A x x y x a x x a a ππ=-≤≤=-+=-+-].1,21[sin ,-∈∴∈x A x ①若,451)21(,1,1622max 2min +=-+--=-=≤≤a a a y a y a 则π 欲使21,6,5546a B A a ππ⎧-≥-⎪⎪⊆⎨⎪+≤⎪⎩则 .16≤≤⇒a π ②若,,1.45,22,1max min φππ≠∴≤<+=-=≤<B a a y a y a 则 22,56{|22}.,55446a B y a y a B A a ππ⎧-≥-⎪⎪∴=-≤≤+⊆⎨⎪+≤⎪⎩要使则 .121π+≤⇒a 又.1211,1ππ+≤<∴≤<a a 综上述知a 的取值范围是.1216ππ+≤≤a}.451|{),(,162+≤≤-=∴≠∴≤≤a y a y B B B a φπ非空又。

高三数学午时30分钟训练15班级##1.函数y 2si n(2x)3π=-的单调递增区间是. 2.函数)42sin(log 21π+=x y 的单调减区间为. 3.若函数)2||,0)(sin()(πϕωϕω<>+=x x f 的部分图像如图所示,则=+ϕω4.把函数y=cos<x +34π >的图象向右平移φ个单位,所得到的图象正好是关于y 轴对称,则φ的最小正值是.5. 已知()sin()(0),()()363f x x f f πππωω=+>=,且()f x 在区间(,)63ππ有最小值,无最大值,则ω=6.当02x π<≤时,关于x 的方程2cos sin 0x x a -+=时有解,则a 的取值范围是7.方程sin x ax =〔a 为常数,0a ≠〕的所有根的和为8.已知()cos ()3n f n n N π+=∈,则(1)(2)(3)(2009)f f f f ++++的值为_____.9.已知函数y =2cosx<0≤x ≤2π>的图象和直线y =2围成一个封闭的平面图形,则其面积为__.10.下列说法正确的是〔填上你认为正确的所有命题的代号〕__。
①函数y =-sin<k π+x><k ∈Z>的奇函数;②函数y =sin<2x +3π>关于点< 12π ,0>对称; ③函数y =2sin<2x +3π>+sin<2x -3π>的最小正周期是π; ④△ABC 中,cosA >cosB 的充要条件是A <B ;⑤函数=cos 2x +sinx 的最小值是-11.511k,k1212ππ⎡⎤π+π+⎢⎥⎣⎦(k z)∈2、Zkkk∈+-],8,8(ππππ3、621π+ 4.3π5.14 36.(]1,1-;7.0 8.-1;由列举观察知,()f n的周期为6,200963345=⨯+,而一周期连续6数之和为0,前五项和为-1.___9.4π;10.①③④⑤.。

高三数学午时30分钟训练29班级 姓名1.设数列{}n a 的前n 项和为n S (N ∈n ). 关于数列{}n a 有下列三个命题:(1)若{}n a 既是等差数列又是等比数列,则)(1N ∈=+n a a n n ;(2)若()R ∈+=b a n b n a S n 、2,则{}n a 是等差数列; (3)若()nn S 11--=,则{}n a 是等比数列. 这些命题中,真命题的序号是 .2.在数列{}n a 中,已知前n 项的和2100781,n S n n a =-+=则 .3.数列{}n a 是项数为偶数的等差数列,它的奇数项之和为24,偶数项之和为30,若它的末项比首项大10.5,则数列的项数是 .4.三数成等比数列,若将第三数减去32,则成等差数列;若将该等差数列中项减去4,又成等比数列,则原三数为 .5.设等差数列112{}0,9,n k k a d a d a a a =的公差不为若是与的等比中项,则k 等于 .6.已知等差数列{}n a 的前n 项的和为n S ,若1200OB a OA a OC =+,且A ,B ,C 三点共线(该直线不过原点O ),则200S = . 7.已知数列{}n a 、{}n b 都是公差为1的等差数列,其首项分别为11a b 、,且115a b +=,11,.()n n b a b N c a n N **∈=∈设,则数列{}n c 的前10项和等于 .8.等差数列{}n a 的首项为a ,公差为1,n nn a a b +=1,若对+∈∀N n 都有8b b n ≥成 立,则实数a 的取值范围是 9.已知无穷数列0121555510,10,10,10,,n -探究:(1)这个数列是等比数列吗?(2)这个数列的任意两项的积还在这个数列中吗?1. (1)、(2)、(3)①不妨设数列}{n a 的前三项为d a a d a +-,,,则其又成等比数列,故222d a a -=,∴0=d ,即1+=n n a a ;②由n S 的公式,可求出b a n a n +-=)12(,故}{n a 是等差数列;③由n S 可求由1)1(2--=n n a ,故数列}{n a 是等比数列. 故选D .【总结点评】本题主要考查等差、等比数列的概念,n S 与n a 的关系,思维的灵活性.2.;3.8;4.;226338,,999;5.4;6.100;7.85;8.(8,7)--;9.(1)是,(2)在数列当中.。

高三数学午时30分钟训练19班级 姓名1.在ABC ∆中,已知2AC =,3BC =,5cos 13A =-,则sin B =_________ .2.满足30A ︒∠=,BC=10的ABC ∆恰好有不同两个,则边AB 的长的取值范围为 .3. 在△ABC 中,已知22,sin sin sin a b c A B C =+=,则△ABC 为 三角形. 4.已知ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c ,若1=a ,︒=45B ,ABC ∆的面积为2,则ABC ∆的外接圆直径等于 ;5.在ABC ∆中,如果A b a sin 23=,则=∠B .6. 在ABC ∆中,若22=b ,2=a ,且三角形有解,则A ∠的取值范围为 .7.在ABC ∆中,︒=10sin 4a ,︒=50sin 2b ,︒=70C ,则=∆ABC S .8.半径为1的圆内接三角形面积为41,设三角形的三边分别为a ,b ,c ,则=abc .9.在ABC ∆中,1=AB ,2=BC ,则C ∠的取值范围为 .10.在ABC ∆中, 2A C B +=,5,BC =且ABC ∆的面积为B = ;AB = .11.已知ABC ∆中,AC AB =,则A B cos cos +的最大值为 .12.在ABC ∆中,已知C BA sin 2tan=+,给出以下四个论断:①1cot tan =⋅B A②2sin sin 0≤+<B A ③1cos sin 22=+B A ④C B A 222sin cos cos =+其中正确的是 .13.在⊿ABC 中,角A 、B 、C 所对的边分别为a 、b 、c,且10103cos ,21tan ==B A(1)求tanC 的值; (2)若⊿ABC 最长的边为1,求b 。
1. 8132.(10, 20) 3. 等边 4.25; 5.︒︒12060或;6.]4,0(π;7.21. 8. 1;9.]6,0(π;10.3π,11. 8912.②④13、解:(1)cos 0,10B =>∴B 锐角,且sin 10B ==, sin 1tan cos 3B B B ∴==,[]11tan tan 23tan tan ()tan()1111tan tan 123A B C A B A B A B π++∴=-+=-+=-=-=--•-•(2)由(1)知C 为钝角, C 是最大角,最大边为c=1,tan 1,135,sin 2C C C =-∴=︒∴=,由正弦定理:sin sin b cB C =得1sin sin 52c Bb C===。

高三数学午时30分钟训练28班级 姓名1.若在所给的条件下,数列{an}的每一项的值都能唯一确定,则称该数列是“确定的”,在下列条件下,有哪些数列是“确定的”?请把对应的序号填在横线上 。
①{an}是等差数列,S1=a ,S2=b (这里的Sn 是{an }的前n 项的和,a,b 为常数,下同); ②{an}是等差数列,S1=a ,S10=b ; ③{an}是等比数列,S1=a ,S2=b ; ④{an}是等比数列,S1=a ,S3=b ; ⑤{an}满足a2n+2=a2n+a ,a2n+1=a2n-1+b, (n ∈N*), a1=c 2.已知数列{}n a 是等差数列,数列{}n b 是等比数列,其公比1≠q ,且0>ib( ,3,2,1=i ),若11b a =,1111b a =,则66b a(,<>用连接)3.已知数列{}n a 是公差为d 的等差数列,且0≠d ,数列{}n b 是公比为q 的等比数列,且31425121,,,1b a b a b a a ====,则=d , =q .4.已知数列}{n a 满足)(133,0*11N n a a a a n n n ∈+-==+,则20a = .5.在如图的表格中,每格填上一个数字后, 使每一横行成等差数列,每一纵行成等比数列, 则a +b +c 的值为 . 6.数列{}n a 满足122,1,a a ==并且1111(2)n n n n n n n n a a a a n a a a a -+-+--=≥⋅⋅.则数列的第100项为 . 7.在数列{an}中, a1=1, a2=2,且)( )1(12*+∈-+=-N n a a n n n ,则100S =__ __8.一个等差数列{an}中,a1=-5,它的前11项的平均值是5,若从中抽取一项,余下项的平均值是4,则抽取的是 .9.等差数列{}a n 中,a n ≠0,若a a a S m N m m m m -+--+==∈12121038,()*,则 m 的值等于 .10.把数列}12{+n 依次按第一个括号一个数,第二个括号两个数,第三个括号三个数,第四个括号四个数,第五个括号一个数,……,循环分为:(3),(5,7),(9,11,13),(15,17,19,21),(23),(25,27),(29,31,33),(35,37,39,41),(43),…,则第60个括号内各数之和为 .1. ①②③2.66b a > 3.2,3 4.3- 5.1 6.150 )7.26008.a119. 10)10.119212. 在等差数列{}n a 中,若46101290a a a a +++=,则101413a a -= 15。
高三数学午时30分钟训练23班级 姓名1.黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案:则第n 个图案中有白色地面砖___ _块.2.已知数列{an }中,8079--=n n a n ,(n ∈N+),则在数列{an }的前50项中最小项和最大项分别是3.已知数列{}n a 对任意的*p q ∈N ,满足p q p q a a a +=+,且26a =-,那么10a 等于 . 4.如果一个数列{}n a 满足1n n a a h -+=,其中h 为常数,*, 2.n N n ∈≥则称数列{}n a 为等和数列, h 为公和.已知等和数列{}n a 中a1=1,h=-3,则2006a =_____ ___.5.已知函数2()2log x f x x =+,数列{}n a 的通项公式是n a n 1.0=(N ∈n ),当|()2005|n f a -取得最小值时,n = .6.若()f n 为21n +的各位数字之和()n *∈N .如因为142+1=197,1+9+7=17,所以f(14)=17.记1()()f n f n =,21()(())f n f f n =,……,1()(())k k f n f f n +=,k *∈N ,则2005(8)f = .7.一次展览会上展出一套由宝石串联制成的工艺品,如图所示.若按照这种规律依次增加一定数量的宝石,则第n 件工艺品所用的宝石数为 颗 (结果用n 表示).8. 下图是用同样规格的黑、白两色正方形瓷砖铺设的若干图案,则按此规律第n 个图案中需用黑色瓷砖___________块.(用含n 的代数式表示)第1件 第2件 第3件 第4件17、下面是按照一定规律画出的一列“树型”图,设第n 个图有n a 个树枝,则1+n a 与(2)n a n ≥之间的关系是_1.42n +_2.a8, a9 ) 3.30- )4.-4;5.110 ;6.11;7.1322++n n 8.第(1)、(2)、(3)…个图案黑色瓷砖数依次为:15-3=12;24-8=16;35-15=20;…由此可猜测第(n )个图案黑色瓷砖数为:12+(n -1)×4=4n+88、121+=+n n a a .。
高三数学午时30分钟训练21班级##1.在ABC 中,CA a ,CB b ,M 是CB 的中点,N 是AB 的中点,且CN 、AM 交于点P ,用a 、b 表示AP 为.2.向量a =〔2,1〕在向量b =〔3,4〕上的射影是____________.3.若 a 、b 为单位向量, 若k k kk b a 则),0(4412>+=⋅= 4.已知向量1(1sin ,1),(,1sin ),2θθ=-=+a b 且//a b ,则锐角θ等于.5.若平面向量a a b a 则且的夹角是与,53||,180)2,1(=-= 等于.6.已知向量a =(1,2),向量b =(,2)x -,且a ⊥<a -b >,则实数x 等于.7.已知向量,a b 满足||1,||2==a b ,且()2•+=a a b ,则,a b 的夹角是__________。
8. 已知点(0,0)A ,B ,(0,1)C .设AD BC ⊥于D ,则有CD CB λ=,其中λ=________ .9.在ABC ∆中,c b a ,,分别为三个内角A 、B 、C 所对的边,设向量m (),,b c c a =-- n (),b c a =+,若向量m ⊥n ,则角A 的大小为.10.在ABC AB BC AB ABC ∆=+⋅∆则中,若,02是三角形11.在直角三角形ABC 中,2,4==CB CA ,M 为斜边AB 的中点,则MC AB ⋅的值为.12.已知向量(1,2)a =,(2,4)b =--,5||c =,若52()a b c +⋅=,则a 与c 的夹角为.13.已知Z k ∈, AB =()1,k , AC =()4,2,若|AB |若△ABC 是直角三角形,则=k .1. AP =13b 23a ;2. 2 3.12〔4. 45︒〕12.3π5.〔-3,6〕6. 9;8.14 9.3π〕10.直角三角形;11.6;12.120︒;13、-2,-1,36、已知ΔABC 的三个内角C B A 、、所对边的长分别为c b a 、、,向量()a b c a m -+=,,),(b c a n -=,若n m ⊥,则∠C 等于6、错误!。
高三数学午时30分钟训练5班级 姓名1.若()f x 的值域为()0,2,则()(2007)1g x f x =--的值域为 .2.二次函数f(x)=2x 2+bx+5,如实数p ≠q ,使f(p)=f(q),则f(p+q)= 。
3.已知()f x 是定义在[]2,2-上的偶函数,且在[]0,2上单调递增,()(1)f m f m <-,则m 的取值范围是: ;4.)(x f 是奇函数,当0>x 时,x x x f sin )(2+=,当0<x 时,)(x f 表达式为________;5.设奇函数()f x 在(0)+∞,上为增函数,且(1)0f =,则不等式()()0f x f x x --<的解集为 .6.已知()f x 为R 上的偶函数,且在(0,)+∞上是递减函数,则满足1()(1)f f x<的实数x 的取值范围是 . 7.设函数⎪⎩⎪⎨⎧<-=>=0,10,00,1)(x x x x f ,则方程)()12(1x f x x -=+的解为 8.已知函数()f x b 使得()f x 的定义域和值域相同,求非零实数a 的值。
1.()1,1-2. 5;3. 1[1,)2- 4. 2sin x x -_5.(10)(01)-,, 6.(10)(01)-,,8.解:(1)若0a >,对于正数b ,()f x 的定义域为(,][0,)bD a=-∞-+∞,但()f x 的值域[0,)A ⊆+∞,故D A ≠,不合要求.若0a <,对于正数b ,()f x 的定义域为[0,]b D a =-. 由于此时max [()]()2b f x f a =-=,故函数的值域A =. 由题意,有b a -=,由于0b >,所以4a =-.。
高三数学午时30分钟训练26班级 姓名1. 在数列{}n a 中,11a =,且对于任意正整数n ,都有1n n a a n +=+,则100a = ____. 2.已知n S 是}{n a 的前n 项和,且有12-=n n a S ,则数列}{n a 的通项=n a .3.已知等差数列{}n a 中,26a =,515a =,若2n n b a =,则数列{}n b 的前5项和等于 .4.在数列{}n a 中,12a =,11ln(1)n n a a n +=++,则n a = . 5.在数列{}n a 在中,542n a n =-,212n a a a an bn ++=+,*n N ∈,其中,a b 为常数,则ab =7.已知等比数列()n a 中21a =,则其前3项的和3S 的取值范围是 .8.已知{}n a 是等比数列,41252==a a ,,则13221++++n n a a a a a a = . 9.已知函数()2x f x =,等差数列{}x a 的公差为2.若246810()4f a a a a a ++++=,则212310log [()()()()]f a f a f a f a ⋅⋅⋅= .10.n S 为等差数列{}n a 的前n 项和,若24121n n a n a n -=-,则2n n S S = .11.已知数列}{n a 的前n 项和为)15(21-=n n S n ,+∈N n ,现从前m 项:1a ,2a ,…,m a 中抽出一项(不是1a ,也不是m a ),余下各项的算术平均数为37,则抽出的是 .12. 已知首项为正数的等差数列{an }满足:a2005+a2006>0,a2005·a2006<0,则使前项Sn>0成立的最大自然数n 是 .1. 4951;2.12-=n n a ,n 为正整数3.90 4.2ln n + 5. -17.(][),13,-∞-+∞ 8.332(n --41)9.-610.解析:答 由24121n n a n a n -=-,即 4121n na nd n a n +-=-,得121,22n n d a d a -==. 21()22n n n a a n d S +==,22(2)42n n n d S S ==.故2n n S S =4.11.第8项12. 4010 ,由题意知:等差数列中,从第1项到第2005项是正数,且从第2006项开始为负数,S4010=2005(a1+a4010)=2005(a2005+a2006)>0,S4011=4011(a1+a4011)2=4011a2006<0, 故n 的最大值为4010. 另解:由题意可得:等差数列中,从第1项到第2005项是正数,且从第2006项开始是负数,则所有的正项的和为Sn 的最大值,即当n=2005时,取得最大值,显然Sn 是关于n 的缺常数项的二次函数,且开口向下,所以第2005项离对称轴最近,故其对称轴介于2005到2005.5之间,又因为二次函数的图象与x 轴的一个交点是(0,0),则设另一个交点(x,0),x 应介于4010到4011之间.所以使Sn>0的最大自然数是4010,故选B.本小题结论可以推广成一般结论:等差数列中,a1>0,ak+ak+1>0,且akak+1<0,则使前n 项和Sn>0的最大自然数n 是2k..。
江苏省扬中市第二高级中学2015届高三数学午时30分钟训练13 Word版含答案
————————————————————————————————作者:————————————————————————————————日期:
2
3 高三数学午时30分钟训练13
班级 姓名
1.若点P 在
23π的终边上,且OP=2,则点P 的坐标 .
2. 角α的始边在x 轴正半轴、终边过点P (3,y ),且cosα=
12,则y 的值为 .
3. 已知角α的终边与函数)0(,0125≤=+x y x 决定的函数图象重合,则α
ααsin 1tan 1cos -+
的值为 4. 若角0600的终边上有一点()a ,4-,则a 的值是
5.若α是第四象限角,则πα-是 象限角.
6.已知锐角α终边上的一点P 坐标是(2sin 2,2cos2)-,则α= .
7.已知点P (ααcos ,tan )在第三象限,则角α在 象限.
8. 设扇形的半径长为8cm ,面积为24cm ,则扇形的圆心角的弧度数是
9.设角α是第二象限角,且2cos 2cos α
α
-=,则2
α角的终边在 象限 10.利用三角函数线,求满足下列条件的角x 的集合:
(1)2sin ,;2x x ≥∈(2)1cos ,;2
x x ≤-∈ (3)tan 1,;x x ≤-∈
(4)32sin cos ,;22x x x ≥->∈且
4 2.“3
4πα=”是“23sin -=α”的 ( A )A .充分而不必要条件
1.)3,1(-)2.±3 3. 7713- 4. 34- 5 第三象限角6.22π- 7.第二象限 8. 819 第三象限;。
1 高三数学午时30分钟训练23
班级 姓名
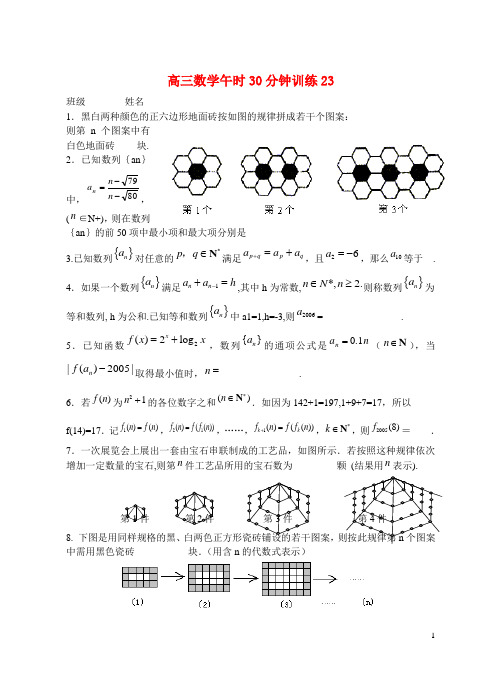
1.黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案:
则第n 个图案中有
白色地面砖___ _块.
2.已知数列{a n }中,8079
--=n n a n ,
(n ∈N +),则在数列
{a n }的前50项中
最小项和最大项分别是
3.已知数列{}n a 对任意的*p q ∈N ,满足p q p q a a a +=+,且26a =-,那么10a 等于 .
4.如果一个数列{}n a 满足1n n a a h -+=,其中h 为常数,*, 2.n N n ∈≥则称数列{}n a 为 等和数列, h 为公和.已知等和数列{}n a 中a 1=1,h=-3,则2006a =_____ ___.
5.已知函数2()2log x f x x =+,数列{}n a 的通项公式是n a n 1.0=(N ∈n ),当|()2005|n f a -取得最小值时,n = .
6.若()f n 为21n +的各位数字之和()n *∈N .如因为142+1=197,1+9+7=17,所以
f(14)=17.记1()()f n f n =,21()(())f n f f n =,……,1()(())k k f n f f n +=,k *∈N ,则2005(8)f = .
7.一次展览会上展出一套由宝石串联制成的工艺品,如图所示.若按照这种规律依次增加一定数量的宝石,则第n 件工艺品所用
8. 用黑色瓷砖___________块.(用含n
17、下面是按照一定规律画出的一列“树型”图,设第n 个图有n a 个树枝,则1+n a 与(2)n a n ≥之间的关系是
2.a 8, a 9 ) _1.42n +_
3.30
- )4.-4;5.110 ;6.11;
7.1322++n n 8.第(1)、(2)、(3)…个图案黑色瓷砖数依次为:15-3=12;24-8=16;35-15=20;…由此可猜测第(n )个图案黑色瓷砖数为:12+(n -1)×4=4n+8
8、 121+=+n n a a .。