江西省南昌市教研室命制2014届高三交流卷(十)数学(文)试题 Word版含答案

2014年江西省南昌市高考数学三模试卷（文科）一、选择题（共10小题，每小题5分，共50分）1．设集合A={x|﹣3≤2x ﹣1≤3}，集合B={x|x ﹣1＞0}；则A ∩B （）A ．（1，2）B ．[1，2]C ．[1，2）D ．（1，2]2．i 是虚数单位，的共轭复数为（）A ．﹣1+iB ．1+iC ．﹣1﹣iD ．1﹣i 3．常说“便宜没好货”，这句话的意思是：“不便宜”是“好货”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4．已知x ，y 的值如表所示：x2 3 4 y 5 4 6如果y 与x 呈线性相关且回归直线方程为，则b=（）A ．B ．C ．D ．5．在正四面体P ﹣ABC 中，D ，E ，F 分别是AB ，BC ，CA 的中点，下面四个结论中不成立的是（）A ．BC ∥平面PDFB ．DF ⊥平面PAEC ．平面PDF ⊥平面ABCD ．平面PAE ⊥平面ABC 6．程序框图表示求式子23×53×113×233×473×953的值，则判断框内可以填的条件为（）A ．i ≤90？B ．i ≤100？C ．i ≤200？D ．i ≤300？7．△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，a=80，b=100，A=30°，则此三角形（）A ．一定是锐角三角形B ．一定是直角三角形C ．一定是钝角三角形D ．可能是钝角三角形，也可能是锐角三角形8．设{a n }为等差数列，且a 3+a 7﹣a 10=2，a 11﹣a 4=7，则数列{a n }的前13项的和为S 13=（）A ．63B ．109C ．117D ．2109．设F 1、F 2分别为双曲线C ：﹣=1（a ＞0，b ＞0）的左、右焦点，A 为双曲线的左顶点，以F 1F 2为直径的圆交双曲线某条渐过线于M ，N 两点，且满足∠MAN=120°，则该双曲线的离心率为（）A ．B ．C ．D ．10．若函数f （x ）=（k ﹣1）a x ﹣a ﹣x （a ＞0，a ≠1）在R 上既是奇函数，又是减函数，则g （x ）=log a （x+k ）的图象是（）二、填空题（共5小题，每小题5分，共20分）11．函数f （x ）=sin （x+）+asin （x ﹣）的一条对称轴方程为x=，则a=_________．12．在四边形ABCD 中，AB ∥CD ，AB=2CD ，M ，N 分别为CD 、BC 的中点，若=λ+μ，则λ+μ=_________．13．已知函数f （x ）满足，且f （x ）是偶函数，当x ∈[0，1]时，f （x ）=x ，若在区间[﹣1，3]内，函数g （x ）=f （x ）﹣kx ﹣k 有4个零点，则实数k 的取值范围是_________．14．已知圆G ：x 2+y 2﹣2x ﹣2y=0经过椭圆+=1（a ＞b ＞0）的右焦点及上顶点．过椭圆外一点M （m ，0）（m ＞a ），倾斜角为π的直线l 交椭圆于C ，D 两点，若点N （3，0）在以线段CD 为直径的圆E 的外部，则m 的取值范围是_________．15．若关于x 的不等式|x ﹣1|﹣|x ﹣2|≥a 2+a+1（x ∈R ）的解集为空集，则实数a 的取值范围是_________．三、解答题（共6小题，共75分）16．（12分）近年来，我国许多省市雾霾天气频发，为增强市民的环境保护意识，某市面向全市征召N 名义务宣传志愿者，成立环境保护宣传组织．现把该组织的成员按年龄分成5组：第1组[20，25），第2组[25，30），第3组[30，35），第4组[35，40），第5组[40，45]，得到的频率分布直方图如图所示，已知第2组有35人．（1）求该组织的人数．（2）若从第3，4，5组中用分层抽样的方法抽取6名志愿者参加某社区的宣传活动，应从第3，4，5组各抽取多少名志愿者？（3）在（2）的条件下，该组织决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验，求第3组至少有一名志愿者被抽中的概率．17．（12分）已知A、B分别在射线CM、CN（不含端点C）上运动，∠MCN=π，在△ABC中，角A、B、C所对的边分别是a、b、c．（Ⅰ）若a、b、c依次成等差数列，且公差为2．求c的值；（Ⅱ）若c=，∠ABC=θ，试用θ表示△ABC的周长，并求周长的最大值．18．（12分）已知等差数列{a n}的公差d≠0，它的前n项和为S n，若S5=70，且a2，a7，a22成等比数列．（1）求数列{a n}的通项公式；（2）设数列的前n项和为T n，求证：．19．（12分）如图，四棱锥P﹣ABCD的底面ABCD为矩形，且PA=AD=1，AB=2，∠PAB=120°，∠PBC=90°．（1）求证：平面PAD与平面PAB垂直；（2）求直线PC与直线AB所成角的余弦值．20．（13分）已知函数在x=3处的切线方程为（2a﹣1）x﹣2y+3=0（1）若g（x）=f（x+1），求证：曲线g（x）上的任意一点处的切线与直线x=0和直线y=ax 围成的三角形面积为定值；（2）若f（3）=3，是否存在实数m，k，使得f（x）+f（m﹣x）=k对于定义域内的任意x 都成立；21．（14分）过椭圆=1（a＞b＞0）的左顶点A做斜率为2的直线，与椭圆的另一个交点为B，与y轴的交点为C，已知．（Ⅰ）求椭圆的离心率；（Ⅱ）设动直线y=kx+m与椭圆有且只有一个公共点，且与直线x=4相交于点Q，若x轴上存在一定点M（1，0），使得PM⊥QM，求椭圆的方程．。

江西省南昌市2014届高三二模考试数学（文科）试卷本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷1至2页，第Ⅱ卷3至4页，共150分． 考生注意：1.答题前，考生务必将自己的准考证号、姓名填写在答题卡上，考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致．2.第I 卷每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号．第Ⅱ卷用0.5毫米的黑色墨水签字笔在答题卡上作答．若在试题卷上作答，答案无效．3.考试结束，监考员将试题卷、答题卡一并收回．第Ⅰ卷一．选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．复数12i+在复平面内对应的点位于 A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限2．已知全集{}2,1,0,1,2,3U =--，{}1,0,1,3M =-，{}2,0,2,3N =-，则(∁U M )N 为 A ． {}1,1- B ．{}2- C ．{}2,2- D ．{}2,0,2- 3．下列说法正确的是A ．命题“存在x ∈R ，220130x x ++>”的否定是“任意x ∈R ，220130x x ++<” B ．两个三角形全等是这两个三角形面积相等的必要条件C ．函数1()f x x=在其定义域上是减函数 D ．给定命题p q 、，若“p 且q ”是真命题，则p ⌝是假命题4．已知函数x x f ωcos )(=)0,(>∈ωR x 的最小正周期为π，为了得到函数()=x g)4sin(πω+x 的图象，只要将()x f y =的图象A ．向左平移8π个单位长度 B ．向右平移8π个单位长度 C ．向左平移4π个单位长度 D ．向右平移4π个单位长度5．一几何体的三视图如图，该几何体的顶点都在球O的球面上， 球O 的表面积是A ．2πB ．4πC ．8πD ．16π6．方程22(20x y x +-=表示的曲线是A ．一个圆和一条直线B ．一个圆和一条射线C ．一个圆D ．一条直线7．已知函数()y f x =是周期为2的周期函数，且当[1,1]x ∈-时，||()21x f x =-，则函数()()|lg |F x f x x =-的零点个数是A ．9B ．10C ．11D ．128．已知函数()y f x =对任意的x ∈R 满足2'()2()ln 20x xf x f x ->（其中'()f x 是函数()f x 的导函数），则下列不等式成立的是2正(主)视图左(侧)视图俯视图A ．2(2)(1)f f -<-B ．2(1)(2)f f >C ．4(2)(0)f f ->D ．2(0)(1)f f >9．如图：正方体1111ABCD A BC D -的棱长为1，,E F 分别是棱11,A B CD 的中点，点M 是EF 的动点，FM x =，过点M 、直线AB 的平面将正方体分成上下两部分，记下面那部分的体积为()V x ，则函数()V x 的大致图像是10．过双曲线22221x y a b-=(0,0)a b >>的左焦点(,0)(0)F c c ->，作圆2224a x y +=的切线，切点为E ，延长FE 交双曲线右支于点P ，若2O P O E O F =-，则双曲线的离心率为 AB．5C ．2D文科数学 第Ⅱ卷注意事项：第Ⅱ卷共2页，须用黑色墨水签字笔在答题卡上书写作答，若在试题上作答，答案无效． 二、填空题：本大题共5小题，每小题5分，共25分11．若不等式2222x x a ++>-对于一切实数x 均成立，则实数a 的取值范围是______． 12．已知角α(0)πα-<<的终边与单位圆交点的横坐标是13，则cos()2πα+的值是___． 13．如果执行如图的程序框图，那么输出的值是__________．14AB C D13333235,37911,413151719,52123252729,=+=++=+++=++++，若类似上面各式方法将3m 分拆得到的等式右边最后一个数是109，则正整数m 等于____．15．如图放置的边长为1的正方形PABC 沿x 轴滚动,点B 恰好经过原点.设顶点(),P x y 的轨迹方程是()y f x =，则对函数()y f x =有下列判断：①函数()y f x =是偶函数；②对任意的x ∈R ，都有(2)(2)f x f x +=-；③函数()y f x =在区间[2,3]上单调递减；④函数()y f x =在区间[4,6]上是减函数.其中判断正确的序号是 .三、解答题：本大题共6个题，共75分．解答应写出文字说明、证明过程或演算步骤． 16. （本小题满分12分） 某公司生产产品A ，产品质量按测试指标分为：指标大于或等于90为一等品，大于或等于80小于90为二等品，小于80为三等品，生产一件一等品可盈利50元，生产一件二等品可盈利30元，生产一件三等品亏损10元．现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测，检测结果统计如下：们生产产品A 为一等品、二等品、三等品的概率．（1）计算甲生产一件产品A ，给工厂带来盈利不小于30元的概率；（2）若甲一天能生产20件产品A ，乙一天能生产15件产品A ，估计甲乙两人一天生产的35件产品A 中三等品的件数. 17．（本小题满分12分）已知公比不为1的等比数列{}na 的首项112a =，前n 项和为n S ，且445566,,a S a S a S +++成等差数列．（1）求等比数列{}n a 的通项公式；（2）对n +∈N ，在n a 与1n a +之间插入3n个数，使这32n+个数成等差数列，记插入的这3n个数的和为n b ，求数列{}n b 的前n 项和n T ． 18．（本小题满分12分）如图，已知正方形ABCD 的边长为6,点,E F 分别在边,AB AD 上,4AE AF ==,现将△AEF 沿线段EF 折起到△'A EF 位置，使得'A C =（1）求五棱锥'A BCDFE -的体积；（2）在线段'A C 上是否存在一点M ,使得//BM 平面'A EF ？若存在，求'A M ；若不存在，说明理由． 19．（本小题满分12分）如图已知ABC △中，1,2,120AB AC BAC ==∠=︒，点M 是边BC 上的动点，动点N 满足30MAN ∠=︒（点,,A M N 按逆时针方向排列）． （1）若2AN AC =，求BN 的长；（2）若3AM AN ⋅=，求△ABN 面积的最大值．ABCD F A 'ABCN20．（本小题满分13分）已知椭圆:C 22221(0)x y a b a b+=>>的左焦点为F ,左、右顶点分别为,A B ,过点F 且倾斜角为4π的直线l 交椭圆于,C D 两点,椭圆C AC AD BC BD ⋅-⋅=．（1）求椭圆C 的方程；（2）若12,P P 是椭圆上不同两点，12,P P x ⊥轴，圆R 过点12,P P ，且椭圆上任意一点都不在圆R 内，则称圆R 为该椭圆的内切圆．问椭圆C 是否存在过点F 的内切圆？若存在，求出点R 的坐标；若不存在，说明理由．21．（本小题满分14分）已知函数()sin cos f x x ax bx x =--(,)a b ∈∈R R . （1）若0b =，讨论函数()f x 在区间(0,)π上的单调性； （2）若2a b =且23a ≥，对任意的0x >，试比较()f x 与0的大小．参考答案二、填空题：本大题共4小题，每小题5分，共20分．11. (1,3) 12 13．32- 14． 10 15．①②④三、解答题：本大题共6个题，共75分．16．解：（1）甲生产一件产品A ，给工厂带来盈利不小于30元的概率为：11911010P =-=……………………………………………………………………………6分 （2）估计甲一天生产的20件产品A 中有120210⨯=件三等品，………………………8分 估计乙一天生产的15件产品A 中有215310⨯=件三等品，……………………………10分 所以估计甲乙两人一天生产的35件产品A 中共有5件三等品.………………………12分17．解：（1）因为445566,,a S a S a S +++成等差数列，所以55446655a S a S a S a S +--=+--，………………………………………………2分 即654230a a a -+=，所以22310q q -+=，因为1q ≠，所以12q =，……………4分 所以等比数列{}n a 的通项公式为12n na =；………………………………………………6分 （2）1333()242n nn n n a a b ++=⋅=，………………………………………………………9分133()39322[()1]344212n n n T +-==--．………………………………………………………12分18．解（1）连接AC ，设AC EF H ⋂=， 由ABCD 是正方形，4AE AF ==，得H 是EF 的中点，且,EF AH EF CH ⊥⊥，从而有',A H EF CH EF ⊥⊥， 所以EF ⊥平面'A HC ，从而平面'A HC ⊥平面ABCD ，…………………………… 2分 过点'A 作'A O 垂直HC 且与HC 相交于点O ，则'A O ⊥平面ABCD ………………3分 因为正方形ABCD 的边长为6，4AE AF ==，得到：'A H CH ==所以1cos '2A HC ∠==，所以'cos ''HO A H A HC A O =⋅∠==所以五棱锥'A BCDFE -的体积211(644)323v =⨯-⨯⨯=；………………6分 （2）线段'A C 上存在点M ，使得'//A M 平面'A EF，'2A M =．……………7分证明：'A M =1'4A C =，14HO HC =， 所以//'OM A H ，所以//OM 平面'A EF ，……………………………………………9分又//BD EF ，所以//BD 平面'A EF ，…………………………………………………10分 所以平面//MBD 平面'A EF ， …………………………………………………………11分 由BM 在平面MBD 内，所以//BM 平面'A EF .……………………………………12分 19．解：（1）由2AN AC =，得点N 在射线AC 上， 4AN =，2116214cos12021BN =+-⨯⨯⨯︒=，即BN =5分 （2）设B A M x ∠=，则120CAM x ∠=︒-，因为ABC △的面积等于△ABM 与△ACM面积的和，所以111sin sin(120)sin120222AB AM x AC AM x AB AC ⋅⋅⋅+⋅⋅⋅︒-=⋅⋅⋅︒，得：AM =，………………………………………………………7分又30,3MAN AM AN ∠=︒⋅=,所以cos303AM AN ⋅⋅︒=,即4sin AN x x =+，所以△ABN的面积1(4sin )sin(30)2S x x x =⋅+⋅+︒225sin cos 2x x x x =+即5sin 22)44444S x x x φ=-+=-+ ………………………10分 ABCD F A 'O H（其中：sin φφφ==为锐角）， 所以当290x φ-=︒时，△ABN12分 20．解：（12,a b c =， 所以椭圆方程可化为：222214x y b b+=，直线l的方程为y x =，………………2分由方程组222214x y b b y x ⎧+=⎪⎨⎪=+⎩，得：2224()4x x b +=,即22580x b ++=,…4分设1122(,),(,)C x y D x y，则125x x +=-，………………………………………5分 又1122112212(,)(,)(,)(,)2()AC AD BC BD x a y x a y x a y x a y a x x ⋅-⋅=+⋅+--⋅-=+，所以4()b ⋅=，所以1b =，椭圆方程是2214x y +=；………………7分 （2）由椭圆的对称性，可以设12(,),(,)P m n P m n -，点R 在x 轴上，设点(,0)R t ， 则圆R 的方程为2222:()()x t y m t n -+=-+，由内切圆定义知道，椭圆上的点到点R 距离的最小值是1||PR ， 设点(,)M x y 是椭圆C 上任意一点，则222223||()214MR x t y x tx t =-+=-++,…9分 当x m =时，2||MR 最小，所以24332t tm -=-=①……………………………………10分 又圆R 过点F，所以222()()t m t n =-+②……………………………………11分点1P 在椭圆上，所以2214m n =-③ ……………………………………………………12分由①②③解得：t =t =又t =时，2m =<-，不合，综上：椭圆C 存在符合条件的内切圆，点R的坐标是(．……………………13分 21.解：（1）0b =时，()sin f x x ax =-，则'()cos f x x a =-，……………………2分 当1a ≥时，'()0f x <，所以函数()f x 在区间(0,)π上单调递减；…………………3分 当1a ≤-时，'()0f x >，所以函数()f x 在区间(0,)π上单调递增；……………… 4分 当11a -<<时，存在(0,)φπ∈，使得cos a φ=，即()0f φ=，(0,)x φ∈时，'()0f x >，函数()f x 在区间(0,)φ上单调递增， ……………………5分 (,)x φπ∈时，'()0f x <，函数()f x 在区间(,)φπ上单调递减. ……………………6分（2）2a b =时，()sin (2cos )2af x x x x =-+，猜测()0f x <恒成立，……………7分 证明：()0f x <等价于sin 2cos 2x ax x <+， 记sin ()2cos 2x ag x x x =-+，则 222cos 1111'()3()(2cos )22cos 323x a a g x x x +=-=---+++，……………………………10分 当123a ≥，即23a ≥时，'()0g x ≤，()g x 在区间(0,)+∞上单调递减，……………12分 所以当0x >时，()(0)0g x g <=，即()0f x <恒成立；……………………………14分。

南昌市教研室命制2014届高三交流卷（九）数学（文）试题一、选择题（本题共10个小题，每题5分，共50分，每小题给出的四个选项中，只有一个是符合要求的）1若纯虚.数z 满足2(2i)4(1i)z b -=-+（其中i 是虚数单位，b 是实数），则b =（ ）A ．2-B ．2C ．-4D ．42．设集合33{|0},{|||},""""122x P x Q x x m P m Q x =≤=-≤∈∈-那么是的（ ） A ．充分不必要条件 B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件3．如图是函数y ＝sin(ωx ＋φ)(ω>0，0<φ<π)的图像的一部分，A ，B 是图像上的一个最高点和一个最低点，O 为坐标原点，则OA ·OB 的值为 A.12πB.19π2＋1C.19π2－1 D.13π2－1 4．设各项为正的等比数列}{n a 的公比1≠q ，且653,,a a a 成等差数列，则6453a a a a ++的值为 A ．215+ B.215- C.21 D.2 5．若一个底面是正三角形的三棱柱的正视图如图所示，其顶点都在一个球面上，则该球的表面积为( )A.163πB.193πC.1912πD.43π 6.已知奇函数)0,()(-∞在x f 上是单调减函数，且0)2(=f ，则不等式 0)1()1(>--x f x 的解集为:A ．}13|{-<<-x x B.}3111|{<<<<-x x x 或C ．}3103|{<<<<-x x x 或 D.}213|{><<-x x x 或7.已知1tan()42πα+=，且02πα-<<，则22sin sin 2cos()4ααπα+=-（ ）A.B.C.8．抛物线y 2＝2px (p ＞0)的焦点为F ，其准线经过双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的左顶点，点M 为这两条曲线的一个交点，且|MF |＝2p ，则双曲线的离心率为( )． A.102 B ．2 C. 5 D.529. 在R 上定义运算⊗：x ⊗y ＝x (1－y )，若不等式(x －a )⊗(x ＋a )＜1对任意实数x 成立，则( ).A ．－1＜a ＜1B ．0＜a ＜2C ．－12＜a ＜32D ．－32＜a ＜1210. 设函数f (x )＝1x，g (x )＝－x 2＋bx .若y ＝f (x )的图象与y ＝g (x )的图象有且仅有两个不同的公共点A (x 1，y 1)，B (x 2，y 2)，则下列判断正确的是( )A.x 1＋x 2>0，y 1＋y 2>0B.x 1＋x 2>0，y 1＋y 2<0C.x 1＋x 2<0，y 1＋y 2>0D.x 1＋x 2<0，y 1＋y 2<0二、填空题（本题共5个小题，每小题5分，共25分）11．已知向量a =(2,1),b =(x ,y ). 若x ∈{-1,0,1,2}，y ∈{-1,0,1}，求向量a ∥b 的概率为 .12．如图，正三角形ABC 的中线AF 与中位线DE 相交于点G ，已知△A ′ED 是△AED 绕DE 旋转过程中的一个图形，现给出下列四个命题：①动点A ′在平面ABC 上的射影在线段AF 上；②恒有平面A ′GF ⊥平面BCED ；③三棱锥A ′－FED 的体积有最大值；④直线A ′E 与BD 不可能垂直．其中正确的命题的序号是________．13．运行如右图所示的程序框图，若输出的y 值的范围是[0, 10]，则输入的x 的值的范围是 ．14. 已知函数⎩⎨⎧≤+>+=0),3(20,2log )(2x x f x x x f ，则=-)5(f 15.已知数列{a n }中，a 1＝1，且P (a n ，a n ＋1)(n ∈N *)在直线x －y ＋1＝0上，若函数f (n )＝1n ＋a 1＋1n ＋a 2＋1n ＋a 3＋…＋1n ＋a n(n ∈N *，且n ≥2)，函数f (n )的最小值是________．四、解答题（本题共6个小题，共75分，解答应写出文字说明、证明过程或演算步骤）.16．（本题满分12分）已知(cos sin )m x x x ωωω=+，()cos sin ,2sin n x x x ωωω=-，其中ω＞0．设函数f (x )＝m n ⋅，且函数f (x )的周期为π．(Ⅰ) 求ω的值；(Ⅱ)在△ABC中，a，b，c分别是角A，B，C的对边，且a，b，c成等差数列，当f(B)＝1时，判断△ABC的形状．17．(本小题满分12分)有一个3×4×5的长方体, 它的六个面上均涂上颜色. 现将这个长方体锯成60个1×1×1的小正方体，从这些小正方体中随机地任取1个.（1）求小正方体各面没有涂色的概率.（2）求小正方体有2面或3面涂色的概率.18.（本小题满分12分）如图，已知正三棱柱ABC—A1B1C1中，D是BC的中点，AA1=AB=1.（1）求证：平面AB1D⊥平面B1BCC1；（2）求证：A1C//平面AB1D；.19．（本小题满分12分）数列{a n}中，a1＝1，当n≥2时，其前n项和S n满足S2n＝a n(S n－1)．(1)求证：数列⎩⎨⎧⎭⎬⎫1S n 是等差数列；(2)设b n ＝log 2S n S n ＋2，数列{b n }的前n 项和为T n ，求满足T n ≥6的最小正整数n .20．（本小题满分13分）已知中心在原点的椭圆C ：x 2a 2＋y 2b 2＝1的一个焦点为F 1(0, 3)，M (x,4)(x ＞0)为椭圆C 上一点，△MOF 1的面积为32.(1)求椭圆C 的方程；(2)是否存在平行于OM 的直线l ，使得直线l 与椭圆C 相交于A ，B 两点，且以线段AB 为直径的圆恰好经过原点？若存在，求出直线l 的方程；若不存在，说明理由．答案17．(本题满分12分)(1)60个1×1×1的小正方体中，没有涂上颜色的有6个，61(0)6010P ξ===； (2) ）由（1）可知P =(2)P ξ=+(3)P ξ=2460=886015+=. 18.（本小题满分12分）解法一：证明：（1）因为B 1B ⊥平面ABC ，AD ⊂平面ABC ，所以AD ⊥B 1B （1分） 因为D 为正△ABC 中BC 的中点，所以AD ⊥BD （2分）又B 1B ∩BC=B ， 所以AD ⊥平面B 1BCC 1 （3分）又AD ⊂平面AB 1D ，故平面AB 1D ⊥平面B 1BCC 1 （4分）（2）连接A 1B ，交AB 1于E ，连DE （5分）因为点E 为矩形A 1ABB 1对角线的交点，所以E 为AB 1的中点 （6分）又D 为BC 的中点，所以DE 为△A 1BC 的中位线，所以DE//A 1C （7分）又DE ⊂平面AB 1D ，所以A 1C//平面AB 1D （8分）解法二：解：建立如图所示的直角坐标系，依题意有：111(((0,,0),(0,,1),221(0,,0),(0,0,0)(2)2A A B B C D --分 （1）证明：由13(,0,0),(0,1,0),(0,0,1)AD BC BB ===， 得110,,,0,AD BC AD BC AD BB AD BB ⎧⋅=⊥⎧⎪⎨⎨⊥⋅=⎩⎪⎩所以 又BC ∩⊥BB 1=B ，所以AD ⊥平面B 1BCC 1. （4分）又AD ⊂平面AB 1D ，所以平面AB 1D ⊥B 1BCC 1 （5分）（2）证明：连接A 1B ，交AB 1于E ，连DE ，因为点E 为正方形A 1ABB 1对角线的交点，所以E 为AB 1的中点，即11(,).42E - （6分） 11131131(,,),(,,1),4222,DE A C A C ED ==-=由得所以A C//ED.(7分)又DE ⊂平面AB 1D ，所以A 1C//平面AB 1D （8分）19. (1)证明：∵2n S ＝a n (S n －1)，∴2n S ＝(S n －S n －1)(S n －1)(n ≥2)．∴S n S n －1＝S n －1－S n ，即1S n －1S n －1＝1. ∴⎩⎨⎧⎭⎬⎫1S n 是以1为首项，1为公差的等差数列． (2)解：由(1)知S n ＝1n ，∴b n ＝log 2n ＋2n. ∴T n ＝log 2(31×42×53×64×…×n ＋2n )＝log 2(n ＋1)(n ＋2)2≥6. ∴(n ＋1)(n ＋2)≥128.∵n ∈N *，∴n ≥10.∴满足T n ≥6的最小正整数为10.20. 解：(1)因为椭圆C 的一个焦点为F 1(0,3)，所以b 2＝a 2＋9.则椭圆C 的方程为x 2a 2＋y 2a 2＋9＝1. 因为x ＞0，所以S △MOF 1＝12×3×x ＝32，解得x ＝1. 故点M 的坐标为(1,4)．因为M (1,4)在椭圆上，所以1a 2＋16a 2＋9＝1，得a 4－8a 2－9＝0，解得a 2＝9或a 2＝－1(不合题意，舍去)， 则b 2＝9＋9＝18，所以椭圆C 的方程为x 29＋y 218＝1. (2)假设存在符合题意的直线l 与椭圆C 相交于A (x 1，y 1)，B (x 2，y 2)两点，其方程为y ＝4x ＋m (因为直线OM 的斜率k ＝4)．由⎩⎪⎨⎪⎧y ＝4x ＋m ，x 29＋y 218＝1，消去y 化简得18x 2＋8mx ＋m 2－18＝0. 进而得到x 1＋x 2＝－8m 18，x 1x 2＝m 2－1818. 因为直线l 与椭圆C 相交于A ，B 两点，所以Δ＝(8m )2－4×18×(m 2－18)＞0，化简得m 2＜162，解得－92＜m ＜9 2.因为以线段AB 为直径的圆恰好经过原点，所以·＝0，所以x 1x 2＋y 1y 2＝0.又y 1y 2＝(4x 1＋m )(4x 2＋m )＝16x 1x 2＋4m (x 1＋x 2)＋m 2，x 1x 2＋y 1y 2＝17x 1x 2＋4m (x 1＋x 2)＋m 2＝17(m 2－18)18－32m 218＋m 2＝0. 解得m ＝±102.由于±102∈(－92，92)，所以符合题意的直线l 存在，且所求的直线l 的方程为y ＝4x ＋102或y ＝4x －102.21.【解析】（1）因为()22ln (0)a f x x a x x x=+->， 所以()()222222222()1x a x a a a x ax a f x x x x x +---'=--==． ①若0=a ，()x x f =，()x f 在()+∞,0上单调递增．②若0>a ，当()0,2x a ∈时，()0f x '<， ()x f 在()a 2,0上单调递减；当()2,x a ∈+∞时，()0f x '>，()x f 在()+∞,2a 上单调递增．③若0<a ，当()0,x a ∈-时，()0f x '<， ()x f 在()a -,0上单调递减；当(),x a ∈-+∞时，()0f x '>，()x f 在()+∞-,a 上单调递增．综上：①当0=a 时，()x f 在()+∞,0上单调递增．②当0>a 时，()x f 在()a 2,0上单调递减，()x f 在()+∞,2a 上单调递增．③当0<a 时，()x f 在()a -,0上单调递减，()x f 在()+∞-,a 上单调递增．（2）当1a =时，()()0ln 2>-+=x x xx x f ． 由（1）知，若1a =，当()0,2x ∈时，()0f x '<，()x f 单调递减，当()2,x ∈+∞时，()0f x '>，()x f 单调递增，所以()()2ln 32min -==f x f ．因为对任意的12,[1,e]x x ∈，都有12()()f x g x ≥成立，问题等价于对于任意[]1,e x ∈，()()min f x g x ≥恒成立，即23ln 224ln 2x bx --+-≥对于任意[]1,e x ∈恒成立， 即12b x x+≥对于任意[]1,e x ∈恒成立， 因为函数x x y 1+=的导数21'10y x =-≥在[]1,e 上恒成立， 所以函数x x y 1+=在[]1,e 上单调递增，所以max 11e e x x ⎛⎫+=+ ⎪⎝⎭， 所以12e e b +≥，所以e 122eb +≥．。

南昌一中、南昌十中2014届高三两校上学期联考数学（文）试题一、选择题（5×10=50分）1. 若数列｛a n ｝的前n 项和为S n ＝kq n －k (k ≠0)，则这个数列的特征是( ) (A )等比数列(B )等差数列(C )等比或等差数列 (D )非等差数列2. 已知1sin ,(,)322ππθθ=∈-，则3sin()sin()2πθπθ--的值为(A )922 (B )922-(C )91 (D )91-3. 数2()f x x =在点()2,(2)f 处的切线方程为（ ）(A )4y = (B )44y x =+ (C )42y x =+ (D )44y x =- 4. 设n S 是等差数列{}n a 的前n 项和，若65911a a =，则119SS ＝( ) (A )1 (B )－1 (C )2D.125.若变量,x y 满足约束条件30101x y x y y +-≤⎧⎪-+≥⎨⎪≥⎩，则24z x y =+-的最大值为(A )5 (B )4- (C )1- (D )1 6. 在∆A B C 中，a ，B ，c 分别是角A ，B ，C 的对边，若，B=A ． 45°或135°(B )45° (C )135°(D ) 以上答案都不对7. 已知等比数列{}n a 的前三项依次为1a -，1a +，4a +，则n a =（ ）(A )342n ⎛⎫⋅ ⎪⎝⎭ (B )1342n -⎛⎫⋅ ⎪⎝⎭(C )243n ⎛⎫⋅ ⎪⎝⎭ (D )1243n -⎛⎫⋅ ⎪⎝⎭8. 设b a 、是正实数，以下不等式恒成立的序号为 （ ） ①b a ab ab +>2，② b b a a -->，③ 22234b ab b a ->+，④ 22>+abab (A ) ②③ (B ) ①④ (C) ②④ (D ) ①③9. 若曲线1122(,)y x a a --=在点处的切线与两坐标轴围成的三角形的面积为9，则a =(A )16(B )8 (C )32 (D )6410. 已知向量()()ABC ∆︒︒=︒︒=则,45sin ,30cos ,120sin ,120cos 的形状为(A )直角三角形(B )等腰三角形 (C )钝角三角形 (D )锐角三角形二、填空题（5×5=25分）11. 在等比数列{}n a 中，n S 为其前n 项和，已知5423a S =+，6523a S =+，则此数列的公比q 为.12. 若数列{}n a 满足11a =，*12()nn n a n a a -=∈+N ，则它的通项n a =．（1）求A 的大小；（2）若sin sin 1B C +=，试判断ABC ∆的形状．17. （12分）在ABC ∆中，已知BC BA AC AB ⋅=⋅3． （1）求证：tanB=3tanA（2）若cos C =求A 的值．18．（12分）已知,)sin ,cos sin (),cos 32,cos sin (x x x x x x ωωωωωω+-=--=设函数f (x )=)(R x ∈+⋅λ的图像关于 对称,其中λ，ω为常数,且ω∈)1,21(（1）求函数f (x )的最小正周期T ；（2）函数过)0,4(π求函数在⎥⎦⎤⎢⎣⎡53,0π上取值范围。

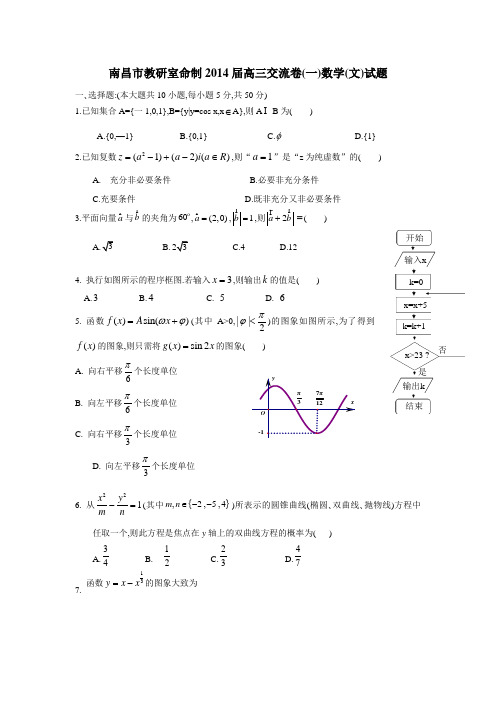
南昌市教研室命制2014届高三交流卷(一)数学(文)试题一､选择题:(本大题共10小题,每小题5分,共50分) 1.已知集合A={一1,0,1},B={y|y=cos x,x ∈A},则A B 为( ) A.{0,—1}B.{0,1}C.φD.{1}2.已知复数2(1)(2)()z a a i a R =-+-∈,则“1a =”是“z 为纯虚数”的( ) A. 充分非必要条件 B.必要非充分条件 C.充要条件 D.既非充分又非必要条件3.平面向量a 与b 的夹角为60,(2,0)a =,1b =,则2a b +=( )B.C.4D.124. 执行如图所示的程序框图.若输入3x =,则输出k 的值是( ) A.3 B.4C. 5D. 6 5. 函数()sin()f x A x ωϕ=+(其中A>0,2||πϕ<)的图象如图所示,为了得到()f x 的图象,则只需将()sin 2g x x =的图象( )A. 向右平移6π个长度单位B. 向左平移6π个长度单位C. 向右平移3π个长度单位 D. 向左平移3π个长度单位 6. 从221x y m n-=(其中{},2,5,4m n ∈--)所表示的圆锥曲线(椭圆､双曲线､抛物线)方程中任取一个,则此方程是焦点在y 轴上的双曲线方程的概率为( )A.34B. 12C.23D.477.函数13y x x =-的图象大致为是结束输出k 否x>23 ?k=k+1x=x+5k=0输入x 开始8. 四棱锥P ABCD -的顶点P 在底面ABCD 中的投影恰好是A ,其三视图如图所示,则四棱锥P ABCD -的表面积为 ( )A.222S a =B. 222S a =C. 224S a =D. 223S a =9.已知抛物线22(0)y p xp =>的焦点F 与椭圆22221(0)x ya b a b+=>>的一个焦点重合,它们在第一象限内的交点为T ,且T F 与x 轴垂直,则椭圆的离心率为( )A.212-1- C.13- D.213-10.如图,点P 从点O 出发,分别按逆时针方向沿周长均为12的正三角形､正方形运动一周,,O P 两点连线的距离y 与点P 走过的路程x 的函数关系分别记为(),()y f x y g x ==,定义函数()()()()()()()f x f x g x h x g x f x g x ⎧⎪=⎨>⎪⎩，≤，，．对于函数()y h x =,下列结论正确的个数是( )①(4)h = ;②函数()h x 的图象关于直线6x =对称; ③函数()h x值域为0⎡⎣ ;④函数()h x 增区间为05（，）. 第10题图 A.1B.2C.3D.4二､填空题(本大题共5小题,每小题5分,共25分. )11.已知数列1,,9a 是等比数列,数列121,,,9b b 是等差数列,则12a b b +的OPPO值为 .12.某校高三第一次模考中,对总分450分(含450分)以上的成绩进行统计,其频率分布直方图如图所示,若650~700分数段的人数为90,则500~550分数段的人数为_________人.13. 若关于x ,y 的不等式组10,10,10x y x ax y +-≥⎧⎪-≤⎨⎪-+≥⎩(a 为常数)所表示的平面区域的面积等于2,则a的值为 .14. 在直角三角形ABC 中,90ACB ∠=︒,2AC BC ==,点P 是斜边AB 上的一个三等分点,则CP CB CP CA ⋅+⋅= . 15. 给出下列四个命题:①ABC ∆中,A B >是sin sin A B >成立的充要条件; ②当01x x >≠且时,有1ln 2ln x x+≥; ③已知n S 是等差数列{}n a 的前n 项和,若75S S >,则93S S >; ④若函数)23(-=x f y 为R 上的奇函数,则函数)(x f y =的图象一定关于点)0,23(F 成中心对称.⑤函数)(cos sin cos )(23R x x x x x f ∈-+=有最大值为2,有最小值为0｡ 其中所有正确命题的序号为 .三､解答题:本大题共6小题,满分75分.解答须写出文字说明､证明过程和演算步骤. 16.(本小题满分12分) 设}2{Z ∈+≠=k k x x A ，ππ,已知)2s i n 2c o s 2(βαβα-+=，a ,)2sin 32(cos βαβα-+=，b ,其中A ∈βα、.(1)若32πβα=+,且b a 2=,求βα、的值;(2)若25=⋅b a ,求βαtan tan 的值.17.(本小题满分12分)一工厂生产甲, 乙, 丙三种样式的杯子,每种样式均有500ml 和700ml 两种型号,某天的产量如右表(单位:个):按样式分层抽样的方法在这个月生产的杯子中抽取100个,其中有甲样式杯子25个. （1） 求z 的值;（2） 用分层抽样的方法在甲样式杯子中抽取一个容量为5的样本,从这个样本中任取2个杯子,求至少有1个500ml 杯子的概率.18.(本小题满分12分)如图,已知AB ⊥平面ACD ,DE ∥AB ,2AD AC DE AB ====2,且F 是CD 的中点.AF=(Ⅰ)求证:AF ∥平面BCE ; (Ⅱ)求证:平面BCE ⊥平面CDE ; (III)求此多面体的体积.19.(本小题满分12分)已知数列{}n a 的前n 项和为n S ,且113n n S a +=)(*∈N n .(Ⅰ)求数列{}n a 的通项公式; (Ⅱ)设41log (1)n n b S +=-)(*∈N n ,12231111n n n T bb b b b b +=+++,求使10072016n T ≥成立的最小的正整数n 的值.20.(本小题满分13分)设椭圆222:1(0)2x y C a a +=>的左右焦点分别为1F ､2F ,A 是椭圆C 上的一点,2120AF F F ⋅=,坐标原点O 到直线1AF 的距离为113OF . (1)求椭圆C 的方程;(2)设Q 是椭圆C 上的一点,)0,1(-N ,连接QN 的直线交y 轴于点M ,=,求直线l 的斜率.21. (本小题满分14分)已知函数()ln()x f x e a =+(a 为常数)是实数集R 上的奇函数,函数()()sin g x f x x λ=+是区间[1,1]-上的减函数｡(1)求()g x 在[1,1]x ∈-上的最大值;(2)若2()1g x t t λ≤++对[1,1]x ∀∈-及(],1λ∈-∞-恒成立,求t 的取值范围; (3)讨论关于x 的方程2ln ()2x f x x ex m =-+的根的个数｡答案17.(本小题满分12分)解: (1).设该厂本月生产的乙样式的杯子为n 个,在丙样式的杯子中抽取x 个,由题意得,,8000500025x=,所以x=40. 则100-40-25=35,所以,,35500025n=n=7000, 故z=2500 6分 (2) 设所抽样本中有m 个500ml 杯子,因为用分层抽样的方法在甲样式杯子中抽取一个容量为5的样本, 所以,550002000m=,解得m=2 也就是抽取了2个500ml 杯子,3个700ml 杯子,分别记作S 1,S 2;B 1,B 2,B 3,则从中任取2个的所有基本事件为(S 1, B 1), (S 1, B 2) , (S 1, B 3) (S 2 ,B 1), (S 2 ,B 2), (S 2 ,B 3),( (S 1, S 2),(B 1 ,B 2), (B 2 ,B 3) ,(B 1 ,B 3) 共10个,其中至少有1个500ml 杯子的基本事件有7个基本事件:(S 1, B 1), (S 1, B 2) , (S 1, B 3) (S 2 ,B 1), (S 2 ,B 2), (S 2 ,B 3),( (S 1, S 2),所以从中任取2个, 至少有1个500ml 杯子的概率为710. 12分 18.(本小题满分12分)解:(Ⅰ)取CE 中点P ,连结FP ､BP , ∵F 为CD 的中点,∴FP ∥DE ,且FP =.21DE 又AB ∥DE ,且AB =.21DE∴AB ∥FP ,且AB =FP ,∴ABPF 为平行四边形,∴AF ∥BP . 又∵AF ⊄平面BCE ,BP ⊂平面BCE ,∴AF ∥平面BCE 4分(Ⅱ)∵2AF CD =,所以△ACD 为正三角形,∴AF ⊥CD ∵AB ⊥平面ACD ,DE //AB∴DE ⊥平面ACD 又AF ⊂平面ACD ∴DE ⊥AF又AF ⊥CD ,CD ∩DE=D∴AF ⊥平面CDE 又BP ∥AF ∴BP ⊥平面CDE 又∵BP ⊂平面BCE∴平面BCE ⊥平面CDE 8分 (III)此多面体是一个以C 为定点,以四边形ABED 为底边的四棱锥,(12)232ABED S +⨯==,ABDE ADC ⊥∴面面等边三角形AD 边上的高就是四棱锥的高 133C ABDEV -=⨯ 12分 19.(本小题满分12分)(1) 当1n =时,11a s =,由,11113134S a a +=⇒= ……………………1分当2n ≥时,11111113()01313n n n n n n n n S a S S a a S a ----⎧+=⎪⎪⇒-+-=⎨⎪+=⎪⎩114n n a a -⇒= ∴{}n a 是以34为首项,14为公比的等比数列. ……………………4分 故1311()3()444n n n a -== )(*∈N n ………………6分(2)由(1)知111111()34n n n S a +++-==, 14141l o g (1)l o g ()(1)4n n n b S n ++=-==-+ ………………8分 11111(1)(2)12n n b b n n n n +==-++++ 1223111111111111()()()23341222n n b b b b b b n n n +++⋅⋅⋅+=-+-+⋅⋅⋅+-=-+++1110072014222016n n -≥⇒≥+, 故使10072016n T ≥成立的最小的正整数n的值2014n =. ………………12分20.(本小题满分13分)解:(1)由题设知12(F F a >其中由于2120AF F F ⋅=,则有212AF F F ⊥,所以点A的坐标为2)a± 故1AF所在直线方程为1)y a=±+所以坐标原点O 到直线1AF又1OF =,= 解得:2a =所求椭圆的方程为22142x y += 6分 (2)由题意可知直线l 的斜率存在,设直线斜率为k 直线l 的方程为(1)y k x =+,则有(0,)M k 设11(,)Q x y ,由于Q ､N ､M 三点共线,=根据题意得1111(,)2(1,)x y k x y -=±+,解得112x y k =-⎧⎨=-⎩或11233x k y ⎧=-⎪⎪⎨⎪=⎪⎩又Q 在椭圆C 上,故22(2)()142k --+=或222()()33142k-+= 解得0,4k k ==±,综上,直线l 的斜率为0或4±. 13分21. (本小题满分14分)解:(1))ln()(a e x f x+=是奇函数, 则)ln()ln(a e a e x x +-=+-恒成立..1))((=++∴-a e a e x x.0,0)(,112=∴=++∴=+++--a a e e a a ae ae x x x x又)(x g 在[-1,1]上单调递减,,1sin )1()(max --=-=∴λg x g 4分 (2)2sin11t t λλ--≤++只需在(],1λ∈-∞-上恒成立,(]2(1)sin1101.t t λλ∴++++≥∈∞在－，－恒成立令),1(11sin )1()(2-≤++++=λλλt t h 则⎩⎨⎧≥+++--≤+,011sin 1012t t t221sin10,sin10t t t t t ≤-⎧∴-+≥⎨-+≥⎩而恒成立1-≤∴t . 9分(3)由(1)知,2ln ,)(2m ex x xxx x f +-=∴=方程为 令m ex x x f x xx f +-==2)(,ln )(221, 21ln 1)(x xx f -=' ,当],0()(,0)(,),0(11e x f x f e x 在时∴≥'∈上为增函数;),0[)(,0)(,),[11e x f x f e x 在时∴≤'+∞∈上为减函数,当e x =时,.1)()(1max 1ee f x f == 而222)()(e m e x x f -+-=,)(1x f 函数∴､)(2x f 在同一坐标系的大致图象如图所示,∴①当e e m e e m 1,122+>>-即时,方程无解. ②当e e m e e m 1,122+==-即时,方程有一个根.③当ee m e e m 1,122+<<-即时,方程有两个根. 14分。

12、“余额宝”作为一种网上百姓理财产品，自2013年底推出后便备受关注和热议。

由于利率比银行活期存款高出十几倍，短时间内便募集了大量资金。

对此，合理的解释是：A．“余额宝”及其它“宝宝”们的推出有利于推进利率市场化改革B．它不利于经济结构调整和金融稳定C．能促进商业银行之间的竞争从而提高商业银行的利润D．央行可顺其自然发展13、比特币，是一种由开源的P2P软件产生的电子货币，是一种网络虚拟货币。

比特币可以用来兑换成一些国家的货币。

使用者可以用比特币购买一些虚拟物品，也可以购买现实生活当中的物品。

下列关于比特币说法正确的是A.比特币在本质上是一般等价物B.意味着作为电子货币的比特币将取代纸币，使货币职能发生本质性的变化C.使用比特币可以节省流通中所需要的货币量，从而节约社会劳动D.比特币作为一种网络虚拟货币具有使用价值14、假定2013年某商品价值用人民币表示为1680元，人民币汇率为l美元=5元人民币。

如果2014年生产该商品的行业劳动生产率提高20％，且人民币对美元升值5％。

若其他条件不变。

该商品以美元标价应为A．336美元 B．294美元C．352.8美元 D．320美元15、2013年8月，国务院批准设立中国（上海）自由贸易试验区，通过负面清单和准入性国民待遇措施，使之成为中国主动开放市场，尤其是开放服务市场和资本市场的先行者。

此举措有利于①减少政府对经济的干预②加快我国企业拓展内销市场的速度③防范人民币升值过快带来的风险④促进我国服务业发展A.①② B．③④ C．①④ D．②③16、中央经济工作会议指出，未来我国的经济体制改革应从精简机构、减少审批，降低政府行政成本和市场交易成本；推进财税改革，特别是结构性减税；打破垄断，促进公平竞争，鼓励民营经济发展等方面入手：这要求我们的政府A.应坚持科学执政、依法行政B. 树立求真务实的工作作风C. 行使立法权、公正司法D.参政议政、民主监督17、为实现4％的教育经费投入，作为人大代表，可以A．行使司法权，完善有关财政教育经费投入的法律法规B．行使决定权，统筹规划各级政府的财政教育经费投入C．行使质询权，督促政府依法落实财政教育经费投入D．行使行政权，具体落实财政教育经费使用计划18、江西某地以十八届三中全会进一步加强新农村建设为契机，紧紧围绕农民最关心，反映最强烈的问题，抓好“新农合”．“村务公开”等事项。

20##普通高等学校招生全国统一考试〔##卷〕数学〔文科〕第Ⅰ卷〔选择题共40分〕一、选择题：本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项符合题目要求． 〔1〕[20####,文1,5分]若复数z 满足(1i)2i z +=〔i 为虚数单位〕,则||z =〔〕〔A 〕1〔B 〕2〔C D [答案]C[解析]解法一：∵若复数z 满足(1i)2i z +=,∴()()()21i 2i 1i 1i 1i 1i i z -===+++-,∴z ==故选C ． 解法二：设i z a b =+,则()()i 1i 2i a b ++=,()()i 2i a b a b -++=,0a b -=,2a b +=,解得1a =,1b =,1i z =+,1i z =+=故选C ．[点评]本题主要考查两个复数代数形式的乘除法,虚数单位i 的幂运算性质,求复数的模,属于基础题． 〔2〕[20####,文2,5分]设全集为R ,集合2{|90},{|15}A x x B x x =-<=-<≤,则()R A C B =〔〕〔A 〕(3,0)-〔B 〕(3,1)--〔C 〕(]3,1--〔D 〕(3,3)- [答案]C[解析]{|33},{|15}A x x B x x =-<<=-<≤,所以{}()31R A C B x x =-<<-,故选C ．[点评]本题主要考查集合的表示方法、集合的补集,两个集合的交集的定义和求法,属于基础题． 〔3〕[20####,文3,5分]掷两颗均匀的骰子,则点数之和为5的概率等于〔〕〔A 〕118〔B 〕19〔C 〕16〔D 〕112[答案]B[解析]点数之和为5的基本事件有：()1,4,()4,1,()2,3,()3,2,所以概率为41369=,故选B ．[点评]本题是一个古典概率模型问题,解题的关键是理解事件"抛掷两颗骰子,所得两颗骰子的点数之和为5〞,由列举法计算出事件所包含的基本事件数,判断出概率模型,理解求解公式nN是本题的重点,正确求出事件"抛掷两颗骰子,所得两颗骰子的点数之和为5〞所包含的基本事件数是本题的难点．〔4〕[20####,文4,5分]已知函数2,0()()2,0x xa x f x a R x -⎧⋅≥=∈⎨<⎩,若[(1)]1f f -=,则a =〔〕 〔A 〕14〔B 〕12〔C 〕1〔D 〕2 [答案]A[解析](1)2f -=,(2)4f a =,所以[(1)]41f f a -==,解得14a =,故选A ． [点评]本题主要考查了求函数值的问题,关键是分清需要代入到那一个解析式中,属于基础题．〔5〕[20####,文5,5分]在ABC ∆中,内角,,A B C 所对应的边分别为,,a b c ,若32a b =,则2222sin sin sin B AA-的值为〔〕〔A 〕19-〔B 〕13〔C 〕1〔D 〕72[答案]D[解析]222222222sin sin 2372121sin 22B A b a b A a a --⎛⎫⎛⎫==-=-= ⎪ ⎪⎝⎭⎝⎭,故选D ． [点评]本题主要考查正弦定理的应用,比较基础．〔6〕[20####,文6,5分]下列叙述中正确的是〔〕〔A 〕若,,a b c R ∈,则2"0"ax bx c ++≥的充分条件是2"40"b ac -≤〔B 〕若,,a b c R ∈,则22""ab cb >的充要条件是""a c >〔C 〕命题"对任意x R ∈,有20x ≥〞的否定是"存在x R ∈,有20x ≥〞 〔D 〕l 是一条直线,,αβ是两个不同的平面,若,l l αβ⊥⊥,则//αβ [答案]D[解析]〔1〕对于选项A ：若,,a b c R ∈,当2"0"ax bx c ++≥对于任意的x 恒成立时,则有：①当0a =时,0b =,0c ≥,此时240b ac -≤成立；②当0a >时,240b ac -≤．∴2"0"ax bx c ++≥ 是2"40"b ac -≤充分不必要条件,2"40"b ac -≤是2"0"ax bx c ++≥必要不充分条件．故A 不正确． 〔2〕对于选项B ：当22""ab cb >时,20b ≠,且a c >,∴22""ab cb >是""a c >的充分条件．反之,当a c >时,若0b =,则22ab cb =,不等式22ab cb >不成立．∴""a c >是22""ab cb >的必要不充分条件． 故B 不正确．〔3〕对于选项C ：结论要否定,注意考虑到全称量词"任意〞,命题"对任意x R ∈,有20x ≥〞的否定应该是"存在x R ∈,有20x <〞．故选项C 不正确．〔4〕对于选项D ：命题"l 是一条直线,,αβ是两个不同的平面,若,l l αβ⊥⊥,则//αβ．〞是两个平面平行的一个判定定理,故选D ．[点评]本题考查独立性检验的应用,考查学生的计算能力,属于中档题．〔7〕[20####,文7,5分]某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量之间的关系, 随机抽查52名中学生,得到统计数据如表1至表4,则与性别有关联的可能性最大的变量是〔〕 〔A 〕成绩〔B 〕视力〔C 〕智商〔D 〕阅读量 [答案]D[解析]表1：()225262210140.00916362032X ⨯⨯-⨯=≈⨯⨯⨯；表2：()22524201216 1.76916362032X ⨯⨯-⨯=≈⨯⨯⨯；表3：()2252824812 1.316362032X ⨯⨯-⨯=≈⨯⨯⨯；表4：()22521430616223.4816362032X ⨯⨯-⨯=≈⨯⨯⨯,∴阅读量与性别有关联的可能性最大,故选D ．[点评]本题考查独立性检验的应用,考查学生的计算能力,属于中档题．〔8〕[20####,文8,5分]阅读如下程序框图,运行相应的程序,则程序运行后输出的结果为〔〕〔A 〕7 〔B 〕9 〔C 〕10 〔D 〕11 [答案]B[解析]由程序框图知：135i 0lg lg lg lg 357i 2S =++++++的值,∵1371lg lg lg lg 13599S =+++=>-,而1391lg lg lg lg 1351111S =+++=<-,∴跳出循环的i 值为9,∴输出i 9=,故选B ．[点评]本题考查了循环结构的程序框图,根据框图的流程判断算法的功能是解题的关键．〔9〕[20####,文9,5分]过双曲线22221x y C a b-=：的右顶点作x 轴的垂线与C 的一条渐近线相交于A ．若以C 的右焦点为圆心、半径为4的圆经过A 、O 两点〔O 为坐标原点〕,则双曲线C 的方程为〔〕〔A 〕221412x y -=〔B 〕22179x y -=〔C 〕22188x y -=〔D 〕221124x y -=[答案]A[解析]以C 的右焦点为圆心、半径为4的圆经过坐标原点O ,则4c =．且4CA =．设右顶点为(),0B a ,(),C a b ,ABC ∆为Rt ∆222BA BC AC ∴+=,()22416a b ∴-+=,又22216a b c +==．得1680a -=,2a =,24a =,212b =,所以双曲线方程221412x y -=,故选A ．[点评]本题考查双曲线的方程与性质,考查学生的计算能力,属于基础题．〔10〕[20####,文10,5分]在同一直角坐标系中,函数22ay ax x =-+与()2322y a x ax x a a =-++∈R 的图像不可能的是〔〕〔A 〕〔B 〕〔C 〕〔D 〕[答案]B[解析]当0a =时,函数22ay ax x =-+的图象是第二,四象限的角平分线,而函数2322y a x ax x a =-++的图象是第一,三象限的角平分线,故D 符合要求；当0a ≠时,函数22a y ax x =-+图象的对称轴方程为直线12x a =,由2322y a x ax x a =-++可得：22341y a x ax '=-+,令0y '=,则113x a =,21x a=,即113x a =和21x a =为函数2322y a x ax x a =-++的两个极值点,对称轴12x a =介于113x a =和21x a =两个极值点之间,故A 、C 符合要求,B 不符合,故选B ．[点评]本题考查的知识点是函数的图象,其中熟练掌握二次函数的图象和性质,三次函数的极值点等知识点是解答的关键． 二、填空题：本大题共5小题,每小题5分,共25分．〔11〕[20####,文11,5分]若曲线ln y x x =上点P 处的切线平行于直线210x y -+=,则点P 的坐标是． [答案](),e e[解析]11ln ln 1y x x x x=⨯+⨯=+,切线斜率2k =,则0ln 12x +=,0ln 1x =,0x e ∴=()0f x e ∴=,所以(),P e e ． [点评]本题主要考查导数的几何意义,以与直线平行的性质,要求熟练掌握导数的几何意义．〔12〕[20####,文12,5分]已知单位向量12,e e 的夹角为α,且1cos 3α=,若向量1232a e e =-,则||a =．[答案]3[解析]()()()222221212123232129412cos 9a a e e e e e e α==-=+-⋅=+-=,解得3a =． [点评]本题主要考查两个向量的数量积的定义,求向量的模的方法,属于基础题． 〔13〕[20####,文13,5分]在等差数列{}n a 中,17a =,公差为d ,前n 项和为n S ,当且仅当8n =时n S 取最大值,则d 的取值X 围．[答案]71,8⎛⎫-- ⎪⎝⎭[解析]因为170a =>,当且仅当8n =时n S 取最大值,可知0d <且同时满足890,0a a ><,所以,89770780a d a d =+>⎧⎨=+<⎩,易得718d -<<-．[点评]本题主要考查等差数列的前n 项和公式,解不等式方程组,属于中档题．〔14〕[20####,文14,5分]设椭圆()2222:10x y Ca b a b+=>>的左右焦点为12F F ，,作2F 作x 轴的垂线与C 交于A B，两点,1F B 与y 轴交于点D ,若1AD F B ⊥,则椭圆C 的离心率等于．[答案 [解析]因为AB 为椭圆的通径,所以22b AB a=,则由椭圆的定义可知：212b AF a=-,又因为1AD F B ⊥,则1AF AB =,即2222b b a a a =-,得2223b a =,又离心率c e a=,结合222a b c =+,得到：e =． [点评]本题主要考查椭圆离心率的求解,根据条件求出对应点的坐标,利用直线垂直于斜率之间的关系是解决本题的关键,运算量较大．为了方便,可以先确定一个参数的值．〔15〕[20####,文15,5分],x y R ∈,若112x y x y ++-+-≤,则x y +的取值X 围为． [答案][]0,2[解析] 11x x +-≥,11y y +-≥,要使112x x y y +-++-≤,只能112x x y y +-++-=,11x x +-=,11y y +-=,∴01x ≤≤,01y ≤≤,∴02x y ≤+≤．[点评]本题主要考查绝对值的意义,绝对值不等式的解法,属于中档题．三、解答题：本大题共6题,共75分．解答应写出文字说明,演算步骤或证明过程．〔16〕[20####,文16,12分]已知函数()()()22cos cos 2f x a x x θ=++为奇函数,且04f π⎛⎫= ⎪⎝⎭,其中a ∈R ,()0,θπ∈．〔1〕求,a θ的值；〔2〕若245f α⎛⎫=- ⎪⎝⎭,,2παπ⎛⎫∈ ⎪⎝⎭,求sin 3πα⎛⎫+ ⎪⎝⎭的值．解：〔1〕()()1cos 1sin 042f a a ππθθ⎛⎫⎛⎫=++=-+= ⎪ ⎪⎝⎭⎝⎭()0θπ∈，,∴sin 0θ≠,∴10,1a a +=∴=-………2分函数()()()22cos cos 2f x a x x θ=++为奇函数()()02cos cos 0f a θθ∴=+==……………4分2πθ∴=．……………5分〔2〕有〔1〕得()()2112cos cos 2cos 2sin 2sin 422f x x x x x x π⎛⎫=-++=-=- ⎪⎝⎭……………7分 12sin425f αα⎛⎫=-=- ⎪⎝⎭∴4sin 5α=………8分2πθπ⎛⎫∈ ⎪⎝⎭，,3cos 5α∴=-……………10分413sin sin cos cos sin 333525πππααα⎛⎫∴+=+=⨯-= ⎪⎝⎭……………12分 [点评]本题主要考查了同角三角函数关系,三角函数恒等变换的应用,函数奇偶性问题．综合运用了所学知识解决问题的能力．〔17〕[20####,文17,12分]已知数列{}n a 的前n 项和232n n nS -=,*n N ∈． 〔1〕求数列{}n a 的通项公式；〔2〕证明：对任意1n >,都有*m N ∈,使得1a ,n a ,m a 成等比数列．解：〔1〕当1n =时111a S ==,当2n ≥时,()22131133222n n n n n n n a S S n ---+-=-=-=-检验,当1n =时11a =,32n a n ∴=-．〔2〕使1a ,n a ,m a 成等比数列．则21n m a a a =,()23232n m ∴--=,即满足()2233229126m n n n =-+=-+,所以2342m n n =-+,所以对任意1n >,都有m N *∈,使得1n m a a a ，，成等比数列． [点评]本题考查了递推式的意义、等差数列与等比数列的通项公式、二次函数的单调性等基础知识与基本技能方法,考查了恒成立问题的等价转化方法,考查了反证法,考查了推理能力和计算能力,属于难题．〔18〕[20####,文18,12分]已知函数22()(44f x x ax a =++其中0a <．〔1〕当4a =-时,求()f x 的单调递增区间；〔2〕若()f x 在区间[1,4]上的最小值为8,求a 的值．解：〔1〕当4a =-时,()()()222422f x x x =-=-()f x 的定义域为[)0,+∞,()(2'242x fx x-=-,令()'0f x >得20,25x x ≤<>,所以当4a =-时,()f x 的单调递增区间为()20,2+5⎡⎫∞⎪⎢⎣⎭和，．〔2〕()()22f x x a x =+,()()()()()2'22102222x a x a x a f x x a x xx+++=++=,令()'0f x =,得12,210a ax x =-=-,0a <,120x x ∴>>,所以,在区间,,,102a a ⎛⎫⎛⎫--+∞ ⎪ ⎪⎝⎭⎝⎭0上,()'0f x >,)(x f 的单调递增；在区间,102aa ⎛⎫-- ⎪⎝⎭上,()'0f x <,)(x f 的单调递减；又易知()()220f x x a x =+≥,且02a f ⎛⎫-= ⎪⎝⎭．①当12a-≤时,即20a -≤<时,)(x f 在区间]4,1[上的最小值为()1f ,由()21448f a a =++=,得222a =-±,均不符合题意．②当142a<-≤时,即82a -≤<-时,)(x f 在区间]4,1[上的最小值为02a f ⎛⎫-= ⎪⎝⎭,不符合题意．③当42a->时,即8a <-时,)(x f 在区间]4,1[上的最小值可能为1x =或4x =处取到,而()18f ≠,()242(6416)8f a a =++=,得10a =-或6a =-〔舍去〕,当10a =-时,()f x 在区间[1,4]上单调递减,()f x 在区间[1,4]上的最小值()48f =符合题意．综上,10a =-．[点评]本题考查的是导数知识,重点是利用导数判断函数的单调性,难点是分类讨论．对学生的能力要求较高,属于难题．〔19〕[20####,文19,12分]如图,三棱柱111ABC A B C -中,111,AA BC A B BB ⊥⊥．〔1〕求证：111AC CC ⊥；〔2〕若2,3,7AB AC BC ===,问1AA 为何值时,三棱柱111ABC A B C -体积最大,并求此最大值． 解：〔1〕三棱柱111ABC A B C -中,1AA BC ⊥,1BB BC ∴⊥,又11BB A B ⊥且1BC A B C =,11BB BCA ∴⊥面,11BB CC ∥11CC BCA ∴⊥面,又11AC BCA ∴⊂面,11AC CC ⊥．〔4分〕〔2〕设1AA x =,在Rt △11Rt A BB ∆中,22111=-=4AB A B BB x -,同理,2221111C=3A AC CC x -=-,在1ABC ∆中 1cos BAC ∠=22221122112(4)(3)A B A C BC x A B A C x x +-=---，2122127sin (4)(3)x BA C x x -∠=--,〔6分〕 所以121111127sin BA C 22A BCx S A B AC -=∠=△,〔7分〕从而三棱柱111ABC A B C -的体积 1211272A BC x x V S l S AA -=⋅=⋅=△〔8分〕,因22422636127127777x x x x x -=-=--+（）〔10分〕故当42=7x 时,即142AA =7时,体积V 取到最大值377． [点评]本题考查空间直线与平面垂直的判定与应用,几何体的体积的最值的求法,考查转化思想以与空间想象能力．〔20〕[20####,文20,13分]如图,已知抛物线2:4C x y =,过点(0,2)M 任作一直线与C 相交于,A B两点,过点B 作y 轴的平行线与直线AO 相交于点D 〔O 为坐标原点〕． 〔1〕证明：动点D 在定直线上；〔2〕作C 的任意一条切线l 〔不含x 轴〕与直线2y =相交于点1N ,与〔1〕中的定直线相交于点2N ,证明：2221||||MN MN -为定值,并求此定值解：〔1〕根据题意可设AB 方程为2y kx =+,代入2=4x y ,得()242x kx =+,即2480x kx --=,设()11,A x y ,()22,B x y ,则有：128x x =-,〔2分〕直线AO 的方程为11y y x x =；BD 的方程为2x x =,解得交点D 的 坐标为2121x x y x y x =⎧⎪⎨=⎪⎩〔4分〕,注意到128x x =-与211=4x y ,则有1121211824y x x y y x y -===-,〔5分〕 因此D 点在定直线y=-2上〔2x ≠〕〔6分〕．〔2〕依据题设,切线l 的斜率存在且不等于0,设切线l 的方程为()0y ax b a =+≠,代入2=4x y 得2=4+x ax b （）,即2440x ax b --=,由0∆=得216160a b +=,化简整理得2b a =-〔8分〕 故切线l 的可写为2y ax a =-．令2y =、2y =-得12,N N 坐标为12(,2)N a a +,22(,2)N a a-+-〔11分〕则222222122()4()8MN MN a a a a-=-+-+=,即2221MN MN -为定值8．〔13分〕[点评]本题考查抛物线的方程与性质、直线与圆锥曲线的位置关系等基础知识,考查抽象概括能力、推理论证能力、运算求解能力,考查特殊与一般思想、数形结合思想、函数与方程思想,属于难题．〔21〕[20####,文21,14分]将连续正整数1,2,,(*)n n N ∈从小到大排列构成一个数123n ,()F n 为这个数的位数〔如12n =时,此数为123456789101112,共有15个数字,(12)15f =〕,现从这个数中随机取一个数字,()p n 为恰好取到0的概率． 〔1〕求(100)p ；〔2〕当2014n ≤时,求()F n 的表达式．〔3〕令()g n 为这个数字0的个数,()f n 为这个数中数字9的个数,()()()h n f n g n =-,{|()1,100,*}S n h n n n N ==≤∈,求当n S ∈时()p n 的最大值．解：〔1〕当100n =时,这个数中总共有192个数字,其中数字0的个数为11,所以恰好取到0的概率为()11100192p =．〔2分〕 〔2〕当19n ≤≤时,这个数有1位数组成,()9F n =,当1099n ≤≤时,这个数有9个1位数组成,9n -个两位数组成,则()29F n n =-,当100999n ≤≤时,这个数有9个1位数组成,90个两位数组成,99n -个三位数组成,()3108F n n =-, 当10002014n ≤≤时,这个数有9个1位数组成,90个两位数组成,900个三位数组成,999n -个四位数组成,()41107F n n =-,所以,1929,1099()3108,10099941107,10002014n n n n F n n n n n ≤≤⎧⎪-≤≤⎪=⎨-≤≤⎪⎪-≤≤⎩〔5分〕〔3〕当n b =〔+19N b b ≤≤∈，〕,()0g n =；当()1019,09,,n k b k b k N b N +=+≤≤≤≤∈∈时,()g n k =；100n =时()11g n =,即,0,19,(),n 10,19,09,,11,n 100n g n k k b k b k N b N +⎧≤≤⎪==+≤≤≤≤∈∈⎨⎪=⎩〔8分〕同理有,0,18,,n 10,19,09,,()80,8998,20,n 99,100n k k b k b k N b N f n n n +≤≤⎧⎪=+≤≤≤≤∈∈⎪=⎨-≤≤⎪⎪=⎩〔10分〕由()()()1h n f n g n =-=h,可知9,19,29,49,59,69,79,89,90n =,所以当n 100≤时,}{9,19,29,39,49,59,69,79,89,90S =〔11分〕当9n =时,()90p =,当90n =,()()()901909019g p F ==,当()10918,n k k k N +=+≤≤∈时, ()()()29209g n k k p n F n n k ===-+〔13分〕由209ky k =+关于k 单调递增,故当109n k =+〔18k ≤≤,k N +∈〕时,()p n 的最大值为()889169p =,又8116919<,所以最大植为119．〔14分〕 [点评]本题为信息题,也是本卷的压轴题,考查学生认识问题、分析问题、解决问题的能力,本题的命题新颖,对学生能力要求较高,难度较大,解决本题的关键首先在于审清题意,搞清楚()F n 、()p n 的含义,这样就可以解决前两问,同时为第三问做好铺垫,第三问在前两问的基础上再加以深入,考查学生综合分 析问题的能力．本题由易到难,层层深入,是一道难得的好题．。

南昌市教研室命制2014届高三交流卷（二）数学（文）试题第I 卷（选择题 共60分）一、选择题:本大题共12个小题，每小题5分，共60分.每小题给出的四个选项中只有一项是符合题目要求的.1．已知全集R U =，集合{}21x A x =>，{}2340B x x x =-->，则A B ⋂=（ ）A ．{}0x x >B ．{}10x x x <->或 C ．{}4x x > D ．{}14x x -≤≤2．已知复数 231ii --（i 是虚数单位），它的实部和虚部的和是（ ）A ．4B ．6C ．2D ．3 3．下列命题中是假命题的是 （ ）A ．,)1()(,342是幂函数使+-⋅-=∈∃m m x m x f m R ),0(+∞且在上递减 B ．有零点函数a x x x f a -+=>∀ln ln )(,02 C ．βαβαβαsin cos )cos(,,+=+∈∃使R ; D ．,()sin(2)f x x ϕϕ∀∈=+R 函数都不是偶函数4．已知实数y x ,满足1218y y x x y ≥⎧⎪≤-⎨⎪+≤⎩，则目标函数y x z-=的最小值为（ ）A ．5B ．2-C ．6D ．7 5． “1a =”是“函数ax x f -=)(在区间[2,)+∞上为增函数”的（ ） A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件6．设振幅、相位、初相为方程sin()(0)y A x b A ωϕ=++>的基本量，则方程3sin(21)+4y x =- 的基本量之和为 （ ） A ．4 B ．23x + C ．8D ．21x +7．已知正四面体的俯视图如图所示，其中四边形ABCD 是边长为2的正方形， 则这个正四面体的主视图的面积为 （ ） A ．22 B ．2 C ．23 D ．38．F1，F2是双曲线2222:1(,0)x y C a b b a b -=>>的左、右焦点，过左焦点F1的直线l 与双曲线C 的左、右两支分别交于A ，B 两点，若22||:||:||3:4:5AB BF AF =，则双曲线的离心率是（ ）A ．3B ．15C ．2D ．139．设函数()12+-=ax x x f 在区间⎪⎭⎫⎝⎛321，上有零点，则实数a 的取值范围为（ ） A. ()∞+，2 B. [)∞+，2 C. ⎪⎭⎫⎢⎣⎡252， D. ⎪⎭⎫⎢⎣⎡3102， 10．已知()f x 是R 上的偶函数，当0x ≥时，12()22xf x x =-，又a 是函数2()ln(1)g x x x =+-的正零点，则(2)f -，()f a ，(1.5)f 的大小关系是 （ ） A ．(1.5)()(2)f f a f <<-B ．(2)(1.5)()f f f a -<<C ．()(1.5)(2)f a f f <<-D ．(1.5)(2)()f f f a <-<第Ⅱ卷（非选择题 共90分）二、填空题：本大题共4个小题，每小题4分，共16分.11．右边茎叶图表示的是甲、乙两人在5次综合测评中的成绩，其中有一个数字被污损，则甲的平均成绩超过乙的平均成绩的概率是____________．12．如图，已知||1,||3OA OB ==，OA 与OB 的夹角为56π，点C 是AOB ∆的外接圆上优孤AB 上的一个动点，则OA OC ⋅的最大值为 .13．右图是一个算法的程序框图，最后输出的W =________.14. n n .13S =++=，210S =++++=，321S =++++++=，那么5S =.15.若对于2||||,2≥-+-∈∀a x a x R x 恒成立，则实数a 的取值范围三、解答题:本大题共6小题，共74分. 16． (本题满分12分)已知θ为向量a 与b 的夹角，||2=a ，||1=b ，关于x 的一元二次方程2x -||a x 0+⋅=a b 有实根.（Ⅰ）求θ的取值范围；（Ⅱ）在（Ⅰ）的条件下，求函数2()sin cos f θθθθ=的最值.17．已知正方形ABCD 的边长为2，E 、F 、G 、H 分别是边AB 、BC 、CD 、DA 的中点．（1）从C 、D 、E 、F 、G 、H 这六个点中，随机选取两个点，记这两个点之间的距离的平方为m ， 求概率P （m ≤ 4）．（2）在正方形ABCD 内部随机取一点P ，求满足｜PE ｜＜2的概率．已知数列{}n a 的前n 项和为n S ，且满足22n n S aa a =-- （a 是常数且0a >,2a ≠）, 21n n n S b a =+．（1）求数列{}n a 的通项公式；（2）若数列{}n b 为等比数列，求{}n b 的通项公式；（3）在（2）的条件下，记31323log log log n n c b b b =+++()n N +∈，是否存在正整数m ，使111113n m c c c +++≥都成立？若存在，求出m 的值；若不存在，请说明理由．19．（本小题满分12分）如图，在斜三棱柱ABC-A1B1C1中，O 是AC 的中点，A1O ⊥平面ABC ，∠BCA=90°，AA1=AC=BC. （I ）求证： AC1⊥平面A1BC;（II ）若AA1=2，求三棱锥C-A1AB 的高的大小．如图，设F 是椭圆C :22221(0)x y a b a b +=>>的左焦点，MN 为椭圆的长轴，P 为椭圆C 上一点，且||[2,6]PF ∈．（Ⅰ）求椭圆C 的方程； （Ⅱ）设点(8,0)Q -，①求证：对于任意的割线QAB ，恒有AFM BFN ∠=∠；②求三角形ABF ∆面积的最大值．21.（本小题满分14分）设函数2()ln ()2af x x x a =+--，a R ∈.（1）若函数()f x 在1[, 2]2上单调递增，求实数a 的取值范围；（2）求函数)(x f 的极值点.（3）设x m =为函数()f x 的极小值点，()f x 的图象与x 轴交于1212(,0),(,0)()A x B x x x <两点,且120x x m<<<，AB 中点为0(,0)C x ，比较)('x f 与0的大小.答案第I 卷（选择题 共60分）一、选择题:本大题共12个小题，每小题5分，共60分.每小题给出的四个选项中只有一项是符合题目要求的.1．已知全集R U =，集合{}21x A x =>，{}2340B x x x =-->，则A B ⋂=（ ）A ．{}0x x >B ．{}10x x x <->或 C ．{}4x x > D ．{}14x x -≤≤2．已知复数 231ii --（i 是虚数单位），它的实部和虚部的和是（ ）A ．4B ．6C ．2D ．3 3．下列命题中是假命题的是 （ ） A ．,)1()(,342是幂函数使+-⋅-=∈∃m m xm x f m R ),0(+∞且在上递减B ．有零点函数a x x x f a -+=>∀ln ln )(,02C ．βαβαβαsin cos )cos(,,+=+∈∃使R ;D ．,()sin(2)f x x ϕϕ∀∈=+R 函数都不是偶函数4．已知实数y x ,满足1218y y x x y ≥⎧⎪≤-⎨⎪+≤⎩，则目标函数y x z -=的最小值为（ ）A ．5B ．2-C ．6D ．7 5． “1a =”是“函数ax x f -=)(在区间[2,)+∞上为增函数”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件6．设振幅、相位、初相为方程sin()(0)y A x b A ωϕ=++>的基本量，则方程3sin(21)+4y x =- 的基本量之和为 （ ） A ．4 B ．23x + C ．8D ．21x +7．已知正四面体的俯视图如图所示，其中四边形ABCD 是边长为2的正方形， 则这个正四面体的主视图的面积为 （ ） A ．22 B ．2 C ．23 D ．38．F1，F2是双曲线2222:1(,0)x y C a b b a b -=>>的左、右焦点，过左焦点F1的直线l 与双曲线C 的左、右两支分别交于A ，B 两点，若22||:||:||3:4:5AB BF AF =，则双曲线的离心率是（ ）A 3B 15C ．2D 139．设函数()12+-=ax x x f 在区间⎪⎭⎫⎝⎛321，上有零点，则实数a 的取值范围为（ ） A. ()∞+，2 B. [)∞+，2 C. ⎪⎭⎫⎢⎣⎡252， D. ⎪⎭⎫⎢⎣⎡3102， 10．已知()f x 是R 上的偶函数，当0x ≥时，12()22xf x x =-，又a 是函数2()ln(1)g x x x =+-的正零点，则(2)f -， ()f a ，(1.5)f 的大小关系是 （ ） A ．(1.5)()(2)f f a f <<-B ．(2)(1.5)()f f f a -<<C ．()(1.5)(2)f a f f <<-D ．(1.5)(2)()f f f a <-<第Ⅱ卷（非选择题 共90分）二、填空题：本大题共4个小题，每小题4分，共16分.11．右边茎叶图表示的是甲、乙两人在5次综合测评中的成绩，其中有一个数字被污损，则甲的平均成绩超过乙的平均成绩的概率是____________．答案：11012．如图，已知||1,||3OA OB ==，OA 与OB 的夹角为56π，点C 是AOB ∆的外接圆上优孤AB 上的一个动点，则OA OC ⋅的最大值为 . 17213．右图是一个算法的程序框图，最后输出的W =_____22___.14. n n . 11233S ⎡⎡⎡=++=⎣⎣⎣，24567810S ⎡⎡⎡⎤⎡=++++=⎣⎣⎣⎦⎣，3910111213141521S ⎡⎡⎡⎡⎡⎤⎡⎡⎤=++++++=⎣⎣⎣⎣⎣⎦⎣⎣⎦，那么5S =.5515.若对于2||||,2≥-+-∈∀a x a x R x 恒成立，则实数a 的取值范围 ),2[]1,(+∞--∞三、解答题:本大题共6小题，共74分.⋅CBAO17．已知正方形ABCD 的边长为2，E 、F 、G 、H 分别是边AB 、BC 、CD 、DA 的中点．（1）从C 、D 、E 、F 、G 、H 这六个点中，随机选取两个点，记这两个点之间的距离的平方为m ， 求概率P （m ≤ 4）．（2）在正方形ABCD 内部随机取一点P ，求满足｜PE ｜＜2的概率．解：（1）P=1115………………………6分(2)这是一个几何概型．所有点P 构成的平面区域是正方形ABCD 的内部，其面积是224⨯=．满足2<PE 的点P 构成的平面区域是以E 为圆心，2为半径的圆的内部与正方形ABCD 内部的公共部分，它可以看作是由一个以E 为圆心、2为半径、圆心角为3π的扇形的内部与两个直角边分别为1和3的直角三角形内部构成.其面积是3323121223212+=⨯⨯⨯+⨯⨯ππ．所以满足2<PE 的概率为.4364332+=+ππ…………………………12分18． (本题满分12分)已知数列{}n a 的前n 项和为n S ，且满足22n n S aa a =-- （a 是常数且0a >,2a ≠）, 21n n n S b a =+．（1）求数列{}n a 的通项公式；（2）若数列{}n b 为等比数列，求{}n b 的通项公式；（3）在（2）的条件下，记31323log log log n n c b b b =+++()n N +∈，是否存在正整数m ，使111113n m c c c +++≥都成立？若存在，求出m 的值；若不存在，请说明理由．解：(1)由22n n S aa a =--得：(2)2n n aS a a =--∴111(2)2aS a a a ==--，1a a =当n ≥2时，11(2)(2)2222n n n n n a a a a a a a a a a a a a --=---=----- 1(2)n n n a a aa aa --=-，∴12n n a aa -=∴数列{}n a 是首项为a ，公比为2a的等比数列 ∴1()2()22n nn a a a a -== (2)解：([1()]22()22212n nn a aa a a S a a --==--44()2(23)()12223221()2(2)22()(2)()22nnn n n naaa a a a a ab a a aa a a a -+--=⨯+==⨯+----若数列{}n b 为等比数列，则230a -=，23a =，此时，3nn b =(3)证：12313233123(1)log log log log log 32nn n n n n c b b b b b b ++++=+++===∴12112()(1)1n c n n n n ==-++121111111112[(1)()()]2(1)22311n c c c n n n +++=-+-++-=-++由121113n mc c c +++≥∀n ∈N*都成立得：12(1)13m n -+≥即661m n -+≤∀n ∈N*都成立 ∵m 是正整数，∴m 的值为1、2、3．19．（本小题满分12分）如图，在斜三棱柱ABC-A1B1C1中，O 是AC 的中点，A1O ⊥平面ABC ，∠BCA=90°，AA1=AC=BC. （I ）求证： AC1⊥平面A1BC;（II ）若AA1=2，求三棱锥C-A1AB 的高的大小． 解：（Ⅰ）因为A1O ⊥平面ABC ，所以A1O ⊥BC ．又BC ⊥AC ，所以BC ⊥平面A1ACC1，所以AC1⊥BC ． …2分 因为AA1＝AC ，所以四边形A1ACC1是菱形，所以AC1⊥A1C ．所以AC1⊥平面A1BC ． …6分 （Ⅱ）设三棱锥C-A1AB 的高为h ．由（Ⅰ）可知，三棱锥A-A1BC 的高为 12AC1＝3．因为VC-A1AB ＝VA-A1BC ，即1 3S △A1ABh ＝ 13S △A1BC ·3． 在△A1AB 中，AB ＝A1B ＝22，AA1＝2，所以S △A1AB ＝7． …10分在△A1BC 中，BC ＝A1C ＝2，∠BCA1＝90︒，所以S △A1BC ＝ 12BC ·A1C ＝2．所以h ＝2217．…12分20．(本题满分13分)如图，设F 是椭圆C :22221(0)x y a b a b +=>>的左焦点，MN 且||[2,6]PF ∈． （Ⅰ）求椭圆C 的方程； （Ⅱ）设点(8,0)Q -，①求证：对于任意的割线QAB ，恒有AFM BFN ∠=∠；②求三角形ABF ∆面积的最大值．解：（Ⅰ）2211612x y +=；（Ⅱ）①易知直线AB 斜率存在． 当AB 的斜率为0时，显然0AFM BFN ∠=∠=，满足题意，当AB 的斜率不为0时，设ABl : 8(0)x my m =-≠，11(,)A x y ，22(,)A x y ，由 22228(34)48144011612x my m y my x y =-⎧⎪⇒+-+=⎨+=⎪⎩．∴222222248412(34)24(4)04m m m m ∆=-⨯+=->⇒>， 1224834m y y m +=+，12214434y y m =+．则121222AF BF y y k k x x +=+++1212211212(6)(6)66(6)(6)y y y my y my my my my my -+-=+=----12121226()(6)(6)my y y y my my -+=--，又1212221444826()2603434mmy y y y m m m -+=⋅-⋅=++，∴0AF BF k k +=，从而AFM BFN ∠=∠．综合可知：对于任意的割线QAB ，恒有AFMBFN ∠=∠．②由①，211||||2ABF QBF QAFS S S QF y y ∆∆∆=-=⋅-=，272163(4)16m ==≤=-+，当且仅当=，即3m =±（此时适合于0>∆的条件）时取等号．∴ 三角形ABF ∆面积的最大值是33．(0)t t =>，则27272163163t t t t ==≤=++．21.（本小题满分14分）设函数2()ln ()2af x x x a =+--，a R ∈.（1）若函数()f x 在1[, 2]2上单调递增，求实数a 的取值范围；（2）求函数)(x f 的极值点.（3）设x m =为函数()f x 的极小值点，()f x 的图象与x 轴交于1212(,0),(,0)()A x B x x x <两点,且120x x m<<<，AB 中点为0(,0)C x ，比较)('x f 与0的大小.解：（1） 21221()2()x ax f x x a x x -+'=+-=依题意得，在区间1[, 2]2上不等式22210x ax -+≥恒成立.又因为0x >，所以12(2)a x x ≤+.所以2a ≤a ≤所以实数a的取值范围是(,-∞.（2）2221()x ax f x x -+'=，令2()221h x x ax =-+①显然，当0a ≤时，在(0,)+∞上()0h x >恒成立，这时()0f x '>，此时，函数()f x 没有极值点； …………………………………6分 ②当0a >时，（ⅰ）当0∆≤，即0a <时，在(0,)+∞上()0h x ≥恒成立，这时()0f x '≥，此时，函数()f x 没有极值点； （ⅱ）当0∆>，即a >易知，当22a a x +<<时，()0h x <，这时()0f x '<；当02a x -<<或2a x >时，()0h x >，这时()0f x '>；所以，当a >x 是函数()f x的极大值点；x =是函数()f x 的极小值点.综上，当a ≤()f x 没有极值点；当a >x =是函数()f x 的极大值点；x =是函数()f x 的极小值点. ………9分（3）由已知得2211122222()ln ()02()ln ()02a f x x x a a f x x x a ⎧=+--=⎪⎪⎨⎪=+--=⎪⎩两式相减，得：()112122ln ()2x x x x x a x +-+-……①由'1()2()f x x a x =+-，得'0001()2()f x x a x =+-…………② 得①代入②，得'001201212()2()(2)f x x a x x a x x x =+-=++-+=221222*********(1)211ln ln ()()1x x x x x x x x x x x x x x ⎡⎤-⎢⎥⎢⎥-=-+--⎢⎥+⎢⎥⎣⎦令12(0,1),x t x =∈且2222(1)()ln (01),()0,1(1)t t t t t t t t t ϕϕ--'=-<<=-<++()t ϕ∴在(0,1)上递减，()(1)0t ϕϕ∴>= 120,()0x x f x '<∴<。

一、选择题：本大题共10个小题,每小题5分,共50分.在每小题给出的四 个选项中，只有一项是符合题目要求的.1 .若复数z 满足(1i)i(i )z +=为虚数单位，则z 为（ ） A .1i 2+ B .21-i C .1i - D .1i - 2.已知集合A={}2|1,x x x R ≥∈，B={}2|log 2,x x x R <∈ 则R C A B ⋂= A .[]1,0 B .()1,0 C .()1,3- D .[]1,3-3已知函数2(0)()0)xx f x x ⎧≥⎪=< 则1x = 是()2f x = 成立的 （ ）A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.已知1sin 3α=，则2cos ()24απ+= A . 16 B .23 C . 13 D .125 .为了解高中生平均每周上网玩微信，刷微博，打游戏享受智能手机带来的娱乐生活体验，从高三年级学生中抽取部分同学进行调查，将所得的数据整理如下，画出频率分布直方图（如图），其中频率分布直方图从左至右前3个小组的频率之比为1：3：5 ,第二组的频数为150，则被调查的人数应为 （ ）A .600B .400C .700D .5006．已知变量y x ,满足约束条件⎪⎩⎪⎨⎧≥-≤+-≤-+0101205x y x y x ,则222z x y =++的最大值( )A ．15B ．17C ．18D ．197. 某几何体的三视图如右图（其中侧视图中的圆弧是半圆），则该几何体的表面积为（ ） A .9214π+ B .8214π+C .9224π+D .8224π+8.已知m 是区间[]0,4内任取的一个数，那么函数3221()233f x x x m x =-++ 在x R ∈上是增函数的概率是（ ）A ．14B ．13C ．12D ．239 .过椭圆)0(12222>>=+b a b y a x 右焦点F 斜率为1的直线交椭圆于A ，B 两点，向量31OA OB α+=-与向量（，） 共线，则该椭圆的离心率为 （ ）ABCD．310 .如图正方形ABCD 边长为4cm ，E 为BC 的中点，现用一条垂直于AE 的直线l 以0.4m/s 的速度从1l 平行移动到2l ，则在t 秒时直线l 扫过的正方形ABCD 的面积记为2()()F t m ，则()F t 的函数图像大概是 （ ）第II 卷（非选择题）二、填空题（本大题共5小题，每小题5分，共25分。

2014年普通高等学校招生全国统一考试（江西卷）数学（文科）一．选择题：本大题共10小题，每小题5分，共50分. 在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 若复数z 满足(1)2z i i +=（i 为虚数单位），则||z =（ ）.1A .2B C D 【答案】C【解析】：设Z=a+bi 则(a+bi)( 1+i)=2i ¦ (a-b)( a+b)i=2i a-b=0 a+b=2 解得 a=1 b=1Z=1+1i Z =i 11+=22.设全集为R ，集合2{|90},{|15}A x x B x x =-<=-<≤，则()R AC B =( ).(3,0)A - .(3,1)B -- .(3,1]C -- .(3,3)D -【答案】C【解析】 {|33},{|15}A x x B x x =-<<=-<≤，所以{}()31R A C B x x =-<<-3．掷两颗均匀的骰子，则点数之和为5的概率等于（ ）1.18A 1.9B 1.6C 1.12D 【答案】B【解析】点数之和为5的基本事件有：（1,4）（4,1）（2,3）（3,2），所以概率为364=914. 已知函数2,0()()2,0x x a x f x a R x -⎧⋅≥=∈⎨<⎩，若[(1)]1f f -=，则=a （ ）1.4A 1.2B .1C .2D【答案】A【解析】(1)2f -=，(2)4f a =，所以[(1)]41f f a -==解得14a =5. 在ABC ∆中，内角A,B,C 所对应的边分别为,,,c b a ，若32a b =，则2222sin sin sin B AA-的值为（ ）1.9A -1.3B .1C 7.2D 【答案】D【解析】222222222sin sin 2372121sin 22B A b a b A a a --⎛⎫⎛⎫==-=-= ⎪ ⎪⎝⎭⎝⎭6.下列叙述中正确的是（ ）.A 若,,a b c R ∈，则2"0"ax bx c ++≥的充分条件是2"40"b ac -≤ .B 若,,a b c R ∈，则22""ab cb >的充要条件是""a c >.C 命题“对任意x R ∈，有20x ≥”的否定是“存在x R ∈，有20x ≥” .D l 是一条直线，,αβ是两个不同的平面，若,l l αβ⊥⊥，则//αβ【答案】D【解析】当0a ≠时，A 是正确的；当0b =时，B 是错误的；命题“对任意x R ∈，有20x ≥”的否定是“存在x R ∈，有20x <”，所以C 是错误的。