信号时频分析作业
- 格式:doc
- 大小:193.50 KB
- 文档页数:11

线性调频信号的时频分析研究随着通信技术的发展,线性调频信号(Linear Frequency Modulation,LFM)在通信系统中得到了广泛的应用。
线性调频信号是一种在一段时间内频率线性变化的信号,其具有宽带、抗多径衰落、抗高噪声等特点,因此适用于高分辨率雷达、超声定位、地震勘探等领域。
为了更好地理解和设计线性调频信号的应用系统,对其进行时频分析研究是非常重要的。
时频分析是一种将信号在时间和频率域上进行联合分析的方法,可以提供关于信号特性的更详细的信息。
对于线性调频信号而言,时频分析可以帮助我们获得信号的调频特性和调制参数。
下面将介绍几种常见的时频分析方法,以及它们在线性调频信号研究中的应用。
STFT是一种将信号在时间和频率上进行分析的方法,它通过将信号分成多个小时间窗口,并对每个窗口进行傅里叶变换,得到该窗口内信号的频谱信息。
STFT可以提供线性调频信号的瞬时频率信息,帮助我们理解信号的调频特性。
2. Wigner-Ville分布(Wigner-Ville Distribution,WVD)WVD是一种采用时频联合分析的方法,它通过计算信号的瞬时相位和瞬时幅度,得到信号在时频上的分布。
WVD可以提供线性调频信号的瞬时频率和瞬时频谱信息,有助于我们研究信号的调频参数和调频性质。
3. 希尔伯特-黄变换(Hilbert-Huang Transform,HHT)此外,还有一些其他的时频分析方法,如连续小波变换(Continuous Wavelet Transform,CWT)、自适应滤波器(Adaptive Filter),它们在线性调频信号研究中也有一定的应用。
通过将这些方法相互结合,可以更好地理解线性调频信号的时频特性和调制参数。
在线性调频信号的时频分析研究中,我们可以分析信号的频谱特性、瞬时频率变化、调制参数等。
通过这些分析,我们可以了解信号是否具有带宽限制特性、频率变化规律,以及在特定调制参数下,信号的传输性能如何。



信号处理中的时频分析方法研究一、引言在信号处理领域,时频分析是一种重要的分析方法,它可以展示信号在时间和频率两个维度上的变化规律。
时频分析方法可以被广泛应用于许多领域,例如通信、医学、音乐和地震学等领域。
本文将介绍一些常见的时频分析方法,并探讨它们的应用与优缺点。
二、短时傅里叶变换(STFT)短时傅里叶变换是时频分析中最常见的一种方法。
它可以通过将信号分解成不同时间窗口内的频率成分来获得时域和频域分布。
在STFT中,信号被乘以一个窗口函数,然后在每个时间点上窗口的长度和形状都保持不变。
然后,使用快速傅里叶变换在每个时间窗口内计算频域分量。
由于不同的时间窗口可以为其提供不同的频率分辨率,因此可以选择窗口长度以平衡时间和频率分辨率之间的折衷。
STFT的优点是可以清晰地看到信号随时间和频率的变化。
它在信号处理和地震学分析方面得到了广泛的应用。
但它也有一些局限性,例如窗口函数的选择对分析结果有很大的影响,一般情况下只能得到离散的时频信息,无法获得连续的时频特性。
三、连续小波分析(CWT)连续小波分析是一种时变滤波器的应用,是一种常用的时频分析方法。
它采用一组母小波(通常称为分析小波),在不同的时刻对输入信号进行滤波。
这些分析小波可以缩放和平移,以便提供不同的频率和时间精度,并且可以在尺度和时间轴上提供常规分析不能提供的信息。
相较于STFT,CWT可以获得更连续的时频信息,而且由于可以根据需要改变小波的尺度和位置,因此比STFT更加灵活。
然而,CWT计算时需要进行大量的计算,处理大量的数据将导致算法效率较低。
四、峭度尺度分析(KSA)峭度尺度分析是一种基于二阶统计的非参数时频分析方法。
它利用峭度作为指标来计算信号在不同尺度下的频率分解表达。
KSA通过计算每个尺度下信号的二阶矩来确定信号的局部频率,因此不需要进行时域和频域的分析。
此外,KSA可以提供高频率分辨率和极低频的有效处理,因此可以获得有关信号的更广泛的信息。

短时傅里叶变换(STFT)算法研究与仿真实现学号:姓名:短时傅里叶变换(STFT)算法研究与仿真实现摘要:本文首先介绍了时频分析的发展,然后主要介绍了一种时频变换技术——短时傅里叶变换(STFT)的基本原理和特点,并应用短时傅里叶变换的方法对仿真信号进行了时频分析。
最后,介绍了时频变换在雷达方面的具体应用。
关键词:时频分析,STFT1引言傅里叶变换是应用最广泛的信号分析工具之一,其基本观点是一个任意信号总是可以分解成一组不同频率的正弦信号,即实质上是将信号投影为一组基函数的过程,每一个基函数是频率固定的正弦波,投影的结果形成了原始信号的傅里叶变换,它在一个特定频率的值是信号与该频率正弦基相似性的度量,因此,信号的频率特性可以通过傅里叶变换表现出来。
现实世界中许多信号的频率是随时间变换的,在这种情况下,利用简单的正弦波作为基函数并且通过频谱来描述信号不总是最好的办法,时频变换就是为了描述信号的时变频率分量而发展起来的。
时间信号的时频表示开始于Gabor,称为短时傅里叶变换(STFT)。
它是一个移动窗口傅里叶变换,通过移动时间窗口来分析信号频率分量,这样得到一个二维的时频分布,称为谱图,谱图包含了信号在不同时间的频率信息。
时频变换主要分为两类:线性时频变换和双线性变换。
本文主要讨论的STFT 是线性时频变换,而双线性变换的典型算法是Wigner-Ville分布(WVD)。
本文主要研究了短时傅里叶变换(STFT)的基本原理和特点,并应用短时傅里叶变换的方法对仿真信号进行了时频分析。
最后,介绍了时频分析在雷达方面的具体应用。
2短时傅里叶变换(STFT)2.1 连续信号的STFT分析时变频率分量信号的一种标准方法是把时间信号分成许多段,然后对每傅里叶变换,即为STFT 操作,信号()x t 的短时傅里叶变换定义如下:()()(),j x t x t e d STFT ττττηΩ∞*Ω=-⎰-∞ (0-1)短时傅里叶变换与傅里叶变换唯一的区别就是给定了一个窗函数()t η去截取()x t ,对截下来的局部信号做傅里叶变换,即可得到t 时刻的该段信号的傅里叶变换。
基于STFT 的语音信号时频分析摘要:视频分析是近年来信号处理的新热点。
本文首先介绍了语音信号STFT 的相关知识,随后利用MATLAB 将采集到的语音信号进行处理,并进行了信号时域和频域的相关分析。
关键词:语音信号 STFT 时频分析语音信号的短时傅里叶变换傅里叶变换是一种信号的整体变换,要么完全在时域,要么完全在频域进行分析处理,无法给出信号的频谱如何随时间变化的规律。
而有些信号,例如语音信号,它具有很强的时变性,在一段时间内呈现出周期性信号的特点,而在另一段时间内呈现出随机信号的特点,或者呈现出两个混合的特性。
对于频谱随时间变化的确定性信号以及非平稳随机信号,利用傅里叶变换分析方法有很大的局限性,或者说是不合适的。
傅里叶变换无法针对性的分析相应时间区域内信号的频率特征。
可以用一个窗函数与时间信号相乘积,当该窗函数的时宽足够窄,使取出的信号可以被看成是平稳信号时,就可以对乘积信号进行傅里叶变换,从而反映该时宽中的信号频谱变化规律。
早在1946年,Gabor 就提出了短时傅立叶变换(Short Time Fourier Transform ,STFT )的概念,用以测量声音信号的频率定位[64]。
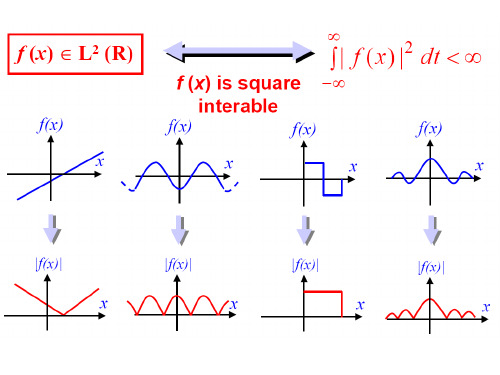
给定一信号)()(2R L t x ∈,其STFT 定义为 式中 τττΩΩ-=j t e t g g )()(,及 1||)(||=τg ,1||)(||,=Ωτt g并且窗函数)(τg 应取对称函数。
STFT 的含义可解释如下:在时域用窗函数)(τg 去截)(τx (注:将)(t x ,)(t g 的时间变量换成τ),对截下来的局部信号作傅立叶变换,即得在t 时刻得该段信号得傅立叶变换。
不断地移动t ,也即不断地移动窗函数)(τg 的中心位置,即可得到不同时刻的傅立叶变换。
这些傅立叶变换的集合,即是),(Ωt STFT x ,如图1所示。
显然,),(Ωt STFT x 是变量),(Ωt 的二维函数。
北京航空航天大学传感器技术与测试系统实验报告实验一信号的时频域分析及处理院系:宇航学院探测制导与控制技术班级:1 2 1 5 1 4学号:12151059姓名:张立新应用MATLAB软件:(1).产生不同的周期信号,包括正弦信号、方波信号、锯齿波,在时域分析这些波形特征(幅值、频率(周期));以下为MATLAB产生波形:正弦信号:y=sin(2*pi*10*t); 幅值A=1,频率f=10Hz方波信号:y=square(2*pi*10*t);幅值A=1,频率f=10Hz锯齿波:y=sawtooth(2*pi*10*t);锯齿波信号幅值A=1,频率f=10Hz(2).在matlab中产生随机噪声;随机噪声:y=randn(size(t))(3).对产生的信号进行Fourier变换,从频率域分析信号的特征,并说明方波信号和锯齿波信号的信号带宽;正弦信号的Fourier变换:方波信号的Fourier变换:锯齿波信号的Fourier变换:结果分析:可以看出信号的的频率为10Hz在频域图中,找到对应幅值0.707倍的两个交点,差值即为所求信号带宽。
计算得方波信号带宽为10.8-8.8=2Hz锯齿波信号带宽为11.25-8.25=3Hz(4).产生复合信号:由三个不同频率、幅值的正弦信号叠加的信号,从图形上判断信号的特征;y=sin(2*pi*20*t)+sin(2*pi*30*t)+sin(2*pi*40*t);产生由正弦信号和随机信号叠加的混合信号,从图形上判断信号的特征;y=sin(2*pi*10*t)+randn(size(t));产生由正弦信号和方波叠加的信号,从图形上判断信号的特征;y=sin(2*pi*10*t)+square(2*pi*20*t);对三个不同频率和幅值叠加的正弦信号,从图上可以看出叠加信号的幅值为 2.5,频率为10Hz;对正弦信号和随机信号叠加,从时域图上可以看出叠加信号的频率为10Hz对正弦信号和方波叠加的信号,从时域图上可以看出叠加信号的频率为10Hz(5).对步骤四中的三种复合信号进行FFT计算,从图形上判断信号的特征y=sin(2*pi*20*t)+sin(2*pi*30*t)+sin(2*pi*40*t);y=sin(2*pi*10*t)+square(2*pi*20*t);y=sin(2*pi*10*t)+square(2*pi*20*t);实验思考问题:(1)、信号的时频域转换的方法及其发展过程。
短时傅里叶变换(STFT)算法研究与仿真实现学号:姓名:短时傅里叶变换(STFT)算法研究与仿真实现摘要:本文首先介绍了时频分析的发展,然后主要介绍了一种时频变换技术——短时傅里叶变换(STFT)的基本原理和特点,并应用短时傅里叶变换的方法对仿真信号进行了时频分析。
最后,介绍了时频变换在雷达方面的具体应用。
关键词:时频分析,STFT1引言傅里叶变换是应用最广泛的信号分析工具之一,其基本观点是一个任意信号总是可以分解成一组不同频率的正弦信号,即实质上是将信号投影为一组基函数的过程,每一个基函数是频率固定的正弦波,投影的结果形成了原始信号的傅里叶变换,它在一个特定频率的值是信号与该频率正弦基相似性的度量,因此,信号的频率特性可以通过傅里叶变换表现出来。
现实世界中许多信号的频率是随时间变换的,在这种情况下,利用简单的正弦波作为基函数并且通过频谱来描述信号不总是最好的办法,时频变换就是为了描述信号的时变频率分量而发展起来的。
时间信号的时频表示开始于Gabor,称为短时傅里叶变换(STFT)。
它是一个移动窗口傅里叶变换,通过移动时间窗口来分析信号频率分量,这样得到一个二维的时频分布,称为谱图,谱图包含了信号在不同时间的频率信息。
时频变换主要分为两类:线性时频变换和双线性变换。
本文主要讨论的STFT 是线性时频变换,而双线性变换的典型算法是Wigner-Ville分布(WVD)。
本文主要研究了短时傅里叶变换(STFT)的基本原理和特点,并应用短时傅里叶变换的方法对仿真信号进行了时频分析。
最后,介绍了时频分析在雷达方面的具体应用。
2短时傅里叶变换(STFT)2.1 连续信号的STFT分析时变频率分量信号的一种标准方法是把时间信号分成许多段,然后对每傅里叶变换,即为STFT 操作,信号()x t 的短时傅里叶变换定义如下:()()(),j x t x t e d STFT ττττηΩ∞*Ω=-⎰-∞ (0-1)短时傅里叶变换与傅里叶变换唯一的区别就是给定了一个窗函数()t η去截取()x t ,对截下来的局部信号做傅里叶变换,即可得到t 时刻的该段信号的傅里叶变换。
由于窗函数()t η的存在使短时傅里叶变换具有了局部特性,它既是时间的函数,又是频率的函数。
对给定的时间t ,(),x t STFT Ω可以看作是该时刻的频谱。
为了提高短时傅里叶变换的时间分辨率,需要选择尽可能短的窗函数()t η;另一方面要得到高的频率分辨率,要求选择的时间的窗函数()t η的时间宽度尽可能的长,因此与时间分辨率的提高相矛盾。
对于非平稳信号,利用短时傅里叶变换方法很难找到一个合适的时间窗口来适应不同的时间段,这是它最大的不足之处。
与其它的时频分布(如Wigner 分布)的方法相比,基于短时傅里叶变换的微多普勒有速度快、算法简单、易实现等特点。
2.2 离散信号的STFT实际应用中要实现一个信号的STFT ,必须对该信号进行离散化,且为有限长。
设采样后的信号为()n x ,0,1,,1n L =- ,对应式((0-1)有()()()()(),,j j nj n x nm e x n n mN ex n g n mN e STFT g ωωω*-=-=-∑ (0-2) 式子中N 是在时间窗函数移动的步长;s T ω=Ω是圆周频率,s T 为由()x t 得到()n x 的采样间隔。
式(0-2)对应傅里叶变换中的DTFT ,即时间是离散的,频率是连续的。
为了在工程中实现,还应将ω离散化,令2k k Mπω=,则()()()2,jkn Mx k nm x n n mN eSTFT g πω-*=-∑ (0-3)上式将频率域的一个周期2π分成了M 个点,显然,它是一个M 个点的DFT 。
若函数()g n 的宽度正好也是M 点,那么上式可以写成()()()10,M nkx M n m k n mN STFT W x n g -*==-∑ , 0,1,,1k M =- (0-4)若()g n 的宽度小于M ,那么可以将其补零,使之变为M ;若()g n 的宽度大于M ,则应增大M 使之等于窗函数的宽度。
总之,上式为一标准的DFT ,时域、频域的长度都是M 。
上式中,N 的大小决定了窗函数沿时间轴移动的间距,N 越小,m 的取值越多,得到的时频曲线越密。
若1N =,即窗函数在()n x 的方向上每个一个点移动一次,这样按照上式共做L N 个M 点的DFT 。
上式的反变换是()()11n ,M nk Mm k x STFT m k WM--==∑∑ (0-5)式中,m 的求和取值范围取决于数据的长度L 及窗函数移动的步长N 。
3仿真实现以线性调频信号和正弦调频信号为例,仿真结果如下所示。
3.1 线性调频(LFM )信号 3.1.1 单个信号分量信号的参数为:调频斜率K=500Hz/s ,时长1s ,带宽500Hz ,中心频率200Hz ,采样频率1600HZ-800-600-400-2000200400600800-10-50510152025303540d Bfrequency (Hz)Spectrum of Signal图 0-1 单个LFM 信号的频谱其STFT 时频分布图如下:time (s)f r e q u e n c y (H z )STFT of the Signal00.10.20.30.40.50.60.70.80.9-800-600-400-2000200400600图 0-2 单个LFM 信号的STFT 时频分布3.1.2 多个信号分量设信号包含两个LFM 信号,信号参数如下:信号1:调频斜率500Hz/s ,时长1s ,带宽500Hz ,中心频率200Hz ; 信号2:调频斜率500Hz/s ,时长1s ,带宽500Hz ,中心频率300Hz ; 采样频率1800HZ 。
-1000-800-600-400-20002004006008001000-1001020304050d Bfrequency (Hz)Spectrum of Signal图 0-3 多个LFM 信号混合的频谱其STFT 时频分布图如下:time (s)f r e q u e n c y (H z )0.10.20.30.40.50.60.70.80.9-800-600-400-2000200400600800图 0-4 多个LFM 信号混合的STFT 时频分布3.2 正弦调频信号 3.2.1 单个信号分量信号参数:调制频率2Hz ,带宽160Hz ,信号时长1s ,载频200Hz 。
-600-400-200200400600-300-250-200-150-100-5050d Bfrequency (Hz)图 0-5 单个正弦调频信号的实部其STFT 时频分布图如下:time (s)f r e q u e n c y (H z )STFT of the Signal00.10.20.30.40.50.60.70.80.9-600-400-200200400图 0-6 单个正弦调频信号的STFT 时频分布3.2.2 多个信号分量设信号包含两个正弦信号分量,其参数如下信号1:调制频率2Hz ,带宽160Hz ,信号时长1s ,载频200Hz ; 信号2:调制频率1Hz ,带宽50Hz ,信号时长1s ,载频200Hz 。
-600-400-200200400600-300-250-200-150-100-50050100d Bfrequency (Hz)Spectrum of Signal图 0-7 两个正弦调频混合信号的频谱该信号的STFT 时频分布结果如下。
time (s)f r e q u e n c y (H z )STFT of the Signal00.10.20.30.40.50.60.70.80.9-600-400-200200400图 0-8 两个正弦调频混合信号的STFT 时频分布3.3 结果分析由各个时频分析结果看出,不论对于LFM 信号,还是对于正弦调频信号,STFT 的时间—频率分辨率较差,两个LFM 信号的频率直线无法分辨,图 0-两个分量的时频曲线几乎重叠在一起;对于某时刻,频率主瓣较宽,频率很难定位。
但是在时间—频率分辨率要求不高的情况下STFT 实现较为方便。
4 时频变换在雷达方面的应用傅里叶变换在雷达信号和图像处理领域已被广泛应用,当雷达信号呈现时变特性时,在时频域中表示强度或能量分布的变换,即时频变换才是最理想的变换。
如今,时频变换对于噪声中微弱信号检测、雷达后向散射分析、机动目标图像聚焦、运动补偿、微多普勒分析等方面,是很有用的工具。
参考文献[1] 雷达成像与信号分析时频变换.Victor C. Chen , Hao Ling著.种劲松,余颖译.海洋出版社.2008.8[2] 雷达系统设计MATLAB仿真.Bassem R. Mahafaza , Atef Z. Elsherbeni著.朱国富黎向阳等译.电子工业出版社.2009.10[3] 葛哲学,陈仲生.Matlab时频分析技术及其应用.2006.11。