电阻电路补充问题讲解
- 格式:doc
- 大小:4.70 MB
- 文档页数:13

高中物理电阻题解题技巧电阻是物理学中的重要概念,也是高中物理中常见的考点之一。
在解题过程中,理解电阻的概念和特性,掌握一些解题技巧是非常重要的。
本文将介绍一些高中物理电阻题解题技巧,并通过具体的题目进行解析,帮助高中学生和他们的父母更好地理解和应用这些技巧。
一、串联电阻的计算在串联电路中,电流依次通过多个电阻,电阻值相加即可得到总电阻。
例如,有一个由三个电阻串联而成的电路,电阻分别为R1、R2、R3,求总电阻R。
解题思路:总电阻R = R1 + R2 + R3举一反三:如果电路中有更多的电阻串联,只需将各个电阻的电阻值相加即可得到总电阻。
二、并联电阻的计算在并联电路中,电流分别通过多个电阻,总电流等于各个电阻分流之和。
例如,有一个由三个电阻并联而成的电路,电阻分别为R1、R2、R3,求总电阻R。
解题思路:1/R = 1/R1 + 1/R2 + 1/R3举一反三:如果电路中有更多的电阻并联,只需将各个电阻的倒数相加,再取倒数即可得到总电阻。
三、电阻的等效在一些复杂的电路中,可以将多个电阻进行等效,简化计算。
例如,有一个由两个电阻并联而成的电路,电阻分别为R1、R2,求等效电阻Re。
解题思路:1/Re = 1/R1 + 1/R2举一反三:如果电路中有更多的电阻进行等效,只需将各个电阻的倒数相加,再取倒数即可得到等效电阻。
四、电阻与电流的关系根据欧姆定律,电阻与电流呈线性关系。
例如,有一个电阻为R的电路,电流为I,求电压U。
解题思路:U = R × I举一反三:如果已知电阻和电压,可以通过欧姆定律计算电流。
五、电阻与功率的关系根据功率公式,电阻与功率呈平方反比关系。
例如,有一个电阻为R的电路,电流为I,求功率P。
解题思路:P = I² × R举一反三:如果已知电阻和功率,可以通过功率公式计算电流。
通过以上解题技巧的学习和应用,希望能够帮助高中学生和他们的父母更好地解决电阻题。

第三章电阻电路的一般分析习题一、填空题。
1、对于n个节点b条支路的连通图,其树支数为.二、计算题。
1.求图1所示电路的电压U和受控源发出的功率。
解:独立回路的选择以及回路绕行方向如图2所示,列回路电流方程为:/“=4A,/2=2A(6+3+3)∕11+3×∕zi+3×∕z2=3,单连支回路数为解:用结点法求出U=32V,1=1.6ΛEA"人心一、+、,50-15/U—151 ..受控源的电流为-------- + -------- =4A10 4受控源发出的功率为-151X4=96W2.用回路法求图2所示电路的电流I。
6QI1 ----- 1—即有I=I 13=-1.25A(2+2+2)/—2×5—2x4=—u ∣ M 1=2×(5-7)1 1 1∖l , 11. 11. , ti. ------- +一÷—)v.—v>—匕=/<——-R i +R2 R. ---------- R 1l R.2R 13 5 R 1V+(—+—+—)⅛-—½=0R3叫&-R5 --v 1--v,+(—+—+—)½=e+以RJ1.&&R 凡K求得:I 13—=-1.25A123.图3所示电路,用回路法求I 。
图3ς-=i∩ςτ+z n-'n-'m=i n-z rκ+l nι-【=力-力-力£⅛+oι=⅛t+z∕-7-⅛-ι=f∕-z∕ε+7-o=t z-1+7-=力z z-,zε5Ω图9I l=lΛ-2∕,+10∕2-∕3=5(∕X-2∕1-∕2+3∕3=-10U x=I(I3-I2)z1 1 1、〃1rr w s∙1(R+R+y+0)U川—v U“2=⅛+-7-_/u ZH+(,+,)U〃2=仇KI KAκ5补充方程,=-上」R∖+R?14 .列出图14所示电路的结点电压方程(其中④为参考结点)(RR+丁+B)Unl-KU la=i si+ι∖∣+0Kyι∖∣∕∖4^⅛^+⅛+⅛^2=^R∣+R215 .电路如图15所示,求:(1)以4为参考结点,列写结点1、2、3的结点方程。


1-1 说明图(a ),(b )中, (1),u i 的参考方向是否关联? (2)ui 乘积表示什么功率?(3)如果在图(a )中u>0, i<0;图(b )中u>0, i>0,元件实际发出还是吸收功率?解:(1)(a )图参考方向是关联的(b )图参考方向为非关联。
(2) (a )图中的ui 乘积表示元件吸收的功率(b )图中的ui 乘积表示元件发出的功率。
(3) (a )图中当0,0<>i u ,有0<=ui p ,表示元件实际发出功率。
(b )图中当0,0>>i u ,有p=-ui<0,表示元件实际发出功率。
1—2在题1—2图(a)与(b)中,试问对于N A 与N B ,“u 、i 的参考方向是否关联?此时乘积ui 对N A 与N B 分别意味着什么功率?解:图(a)中,u 、i 的方向对N A 是非关联的,对N B 则是关联的; 因此,P a = -ui ,N a 发出功率, P B = ui ,N B 吸收的功率。
图(b)中,u 、i 的方向对N A 是关联的,对N B 是非关联的; 因此,P A = ui ,N a 吸收的功率。
P B = -ui ,N B 发出功率,1-4 在指定的电压u 和电流i 参考方向下,写出各元件u 和i 的约束方程(元件的组成关系)。
10K+ u -10+ u -+10V-- 5V +(b)(a)(c)(d)(e)(f)解:(a ) (b )i i R u 31010⨯-=-= V (c) u=10V (d )V u 5-= (e )i=10mA1-8 试求图中各电路的电压U ,并讨论其功率平衡。
解:用KCL 先计算电阻电流R I ,再根据欧姆定律计算电阻电压,从而得出端电压U ,最后计算功率。
(a )图中 A I R 862=+=V I U U R R 16822=⨯=⨯==P u =UI=16×2=32WP Is =-6U=-6×16=-96WW I P R R 12882222=⨯=⨯=P u +P Is =P R即输入电路的功率和电源发出的功率都被电阻消耗了。
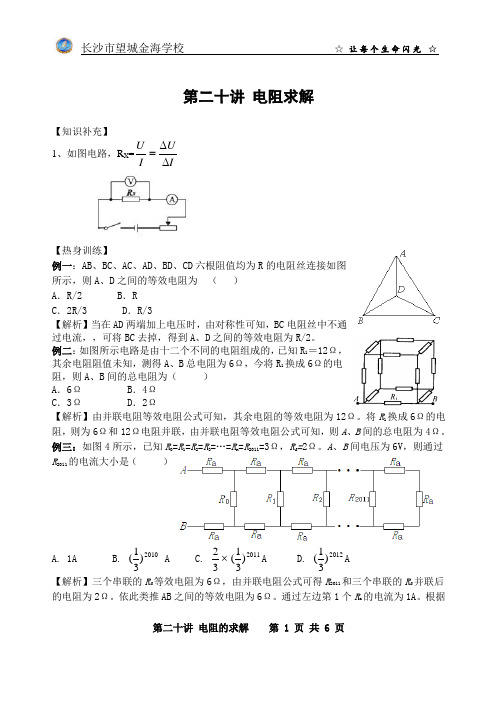
第二十讲 电阻的求解 第 1 页 共 6 页第二十讲 电阻求解【知识补充】1、如图电路,R X =IU I U ∆∆=【热身训练】例一:AB 、BC 、AC 、AD 、BD 、CD 六根阻值均为R 的电阻丝连接如图所示,则A 、D 之间的等效电阻为 ( )A .R/2B .RC .2R/3D .R/3【解析】当在AD 两端加上电压时,由对称性可知,BC 电阻丝中不通过电流,,可将BC 去掉,得到A 、D 之间的等效电阻为R/2。
例二:如图所示电路是由十二个不同的电阻组成的,已知R 1=12Ω,其余电阻阻值未知,测得A 、B 总电阻为6Ω,今将R 1换成6Ω的电阻,则A 、B 间的总电阻为( )A .6ΩB .4ΩC .3ΩD .2Ω【解析】由并联电阻等效电阻公式可知,其余电阻的等效电阻为12Ω。
将R 1换成6Ω的电阻,则为6Ω和12Ω电阻并联,由并联电阻等效电阻公式可知,则A 、B 间的总电阻为4Ω。
例三:如图4所示,已知R 0=R 1=R 2=R 3=…=R n =R 2011=3Ω,R a =2Ω。
A 、B 间电压为6V ,则通过R 2011的电流大小是( )A. 1AB. 2010)31( A C. ⨯322011)31( A D. 2012)31( A 【解析】三个串联的R a 等效电阻为6Ω,由并联电阻公式可得R 2011和三个串联的R a 并联后的电阻为2Ω。
依此类推AB 之间的等效电阻为6Ω。
通过左边第1个R a 的电流为1A 。
根据并联电阻分流原理,通过R0的电流为23A,通过左边第2个R a的电流为13A。
同理,通过R1的电流为23×13A,通过左边第3个R a的电流为13×13A。
通过R2的电流为23×(13)2A,通过左边第4个R a的电流为13×13×13A。
···。
依此类推,通过R2011的电流为322011)31( A ,选项C正确。

【中考物理】2023届第一轮复习分类专题—电流、电压、电阻(基础篇)1.小明利用图甲所示的电路探究“通过导体的电流与电阻的关系”,根据实验的数据绘出了1I﹣图像,如图乙所示。
分析图像可知,当导体的电阻为___Ω时,通过它的电流为R0.2A;当电流分别为0.25A和0.5A时,接入电路的导体的电阻之比为______;实验过程中,小明控制导体两端的电压为____V.2.某同学在“探究通过导体的电流与电阻的关系”时,他用图甲所示的电路进行实验,实验中R 2.5V电阻两端的电压始终保持不变,电路中仪表均完好无损。
a(1)某同学将最后一根导线接入滑动变阻器的A接线柱后就完成电路的连接,该同学连接过程中存在的问题是___________;P(2)连接好电路后闭合开关,移动滑动变阻器的滑片,电压表有示数,电流表无示数,则电路故障的原因可能是___________;(3)排除故障后,某同学将不同阻值的电阻接入电路进行实验,某次实验时电流表的示数如RΩ图乙所示,此时电阻的阻值为___________;R10Ω15Ω(4)在实验过程中,当把电阻由更换为时,滑动变阻器接入电路中的电阻应___________(选填“变大”“变小”或“不变”)。
3.用如图所示电路探究电流与电阻的关系,电源电压不变,电阻有5Ω、10Ω、15Ω、20Ω。
连接电路闭合开关,发现电流表无示数,电压表示数接近电源电压为了找出故障,把导线M的一端从接线柱a移开,分别连到接线柱b和c上,发现两表指针位置均和之前一样,进一步检查发现电流表完好,则电路的故障是___________排除故障后,将不同阻值的电阻分别接入电路,移动滑片记录的数据如下表:实验次数1234电阻/Ω5101520电流/A0.400.200.130.10分析表中数据,实验中电阻两端的电压为___________V,实验得出的结论是___________。
4.在探究“电流与电阻的关系”实验中,如图甲所示。
图2 电阻测量实验题归类例析伏安法测电阻是欧姆定律的重要应用,也是中考考查的重点,命题内容主要有:实验原理,仪器、器材的选择,电压表和电流表的用法及读数,滑动变阻器的连接和作用,电路图及实物图的连接,操作步骤,记录、分析数据等。
笔者对2007年各省、市中考物理试题分析发现,根据电路图或具体要求连接实物图,电压表或电流表的读数,实验过程中电路故障的排除等都是命题频率较高的知识点,而且考查的综合性很强,往往一道题同时覆盖以上多个考查点。
下面,笔者对各个考查点进行归类例析,希望广大师生在学习加以注意。
一、连接电路1.把电路图(或实物图)补充完整例1:在用“伏安法”测量小灯泡工作时的电阻Rx 的实验中,使用下列器材进行实验: A .电流表一个(量程0~0.6A ,0~3A); B .电压表一个(量程0~3V ,0~15V); C .串联的干电池三节;D .滑动变阻器R(阻值为0~12Ω);E .待测小灯泡Rx ,(阻值约为6Ω);F .开关一个;导线若干。
则:(1)该实验依据的原理是 (用课本中的字母表示);并根据题意在右上边的图1虚线方框内画出所需要的实验电路图(其中部分已画好)。
将实物图(2)根据所画的电路图,用铅笔..画线代替导线(图2)连接完整(其中部分导线已连接好)。
解析:(1)“伏安法”是测量小灯泡电阻最基本的方法,它的原理是用电压表测出小灯泡两端的电压,用电流表测出小灯泡中的电流,根据欧姆定律计算出小灯泡的电阻值。
该题考查了学生用“伏安法”测电阻的基本技能,难度不大,须注意的是题中要求“用课本中的字母表示”,即IU R =。
题中给出了部分电路,在此基础上学生很容易画出完整的电路图。
(2)在连接实物之前,必须先确定电流表、电压表的量程。
由于电源是三节干电池串联,电压为4.5V ,许多同学可能会选择电压表0~15V 的量程,但是,当小灯泡两端电压为4.5V 时,电流表示数A75.06V 5.4RxU I =Ω==,即电流表须选择0~3A 量程,这样,电流表指针偏转的角度很小,误差较大,所以电压表选择0~15V 量程不是最佳选择。
第三章电阻电路的一般分析本章内容:1.电路的图及KCL和KVL独立方程数 2.支路分析法3.网孔分析法4.回路电流法5.结点分析法本章重点:主要学习电阻电路的方程建立及一般分析方法(支路分析法、网孔分析法、节点分析法、回路分析法。
其中,支路分析法是最基本的方法)。
本章难点:独立回路数的确定, 回路分析法及节点分析法.§3-1 电路的图本节介绍有关图论的初步知识,学习应用图的方法选择电路方程的独立变量一、电路的图(G)数学上的图:是边(支路)和顶点(结点)的集合,每一条边都连到相应的顶点上,边是抽象的线段,当移去边时,顶点保留,当移去顶点时,应将顶点所连的支路移走。
1.电路的图(连通图G):是将支路画成的抽象线段形成的节点和支路的集合,结点相对于数学图的顶点,支路相当于数学图中的边。
支路是实体。
KVL和KCL 与元件的性质无关,故可用图讨论其方程。
2.无向图:画出的没有方向的图为无向图3.有向图:画出的有方向的图为有向图4.连通图:任意两个结点之间至少有一条支路或路径时的图为连通图。
二、电路的图的画法(有几种,其中简便的画法)1.一般将电阻和电压源串联的组合,电阻和电流源并联的组合看成一条支路, 将流过同一个电流的每一个分支看成一条支路。
如(b)2.指定电流和电压的参考方向,一般选关联参考方向。
如图(c)(a) (b) (c)§3-2 KCL和KVL的独立方程数一、KCL的独立方程数(n个结点电路,KCL的独立方程是n-1个)将电路的有向图,结点和支路加以编号,如下图,对结点①②③④列写KCL 方程有由于每条支路与两个结点相联,其电流从一个节点流出,从另一个结点流入,一正,一负(从表达式可见),将上面4个方程相加,等式两边为0,说明4个方程不是独立的;将上面3个方程相加,等式两边不为0,说明3个方程是独立的。
可见,n个结点电路,n-1个结点的KCL方程是独立的一、KVL的独立方程数(b条支路,n个结点,KVL为b-(n-1)个)KVL的独立方程数等于独立回路数独立回路数等于基本回路数,回路与支路的方向无关,以无向图讨论。
电阻电路补充问题讲解一.等效电阻的计算1.串并联如何判断元件的串并联关系,是一项细致的工作,元件的串并联关系是依赖于端口的,必须从端口看进去才能判断,如下图中,从端口A B 看进去,其入端电阻 ()AB 12534////R R R R R R =++⎡⎤⎣⎦,然而,从端口C D 看进去,则入端电阻()CD 34512////R R R R R R =++⎡⎤⎣⎦。
判断元件的串并联,可以设想在端口处加电压,从端口看进去,若两元件的电流相同,则这两个元件是相串联的;若两元件的电压相同,则这两个元件是相并联的。
尔后,逐一化简,顺藤摸瓜,跟踪追击,最后可得到入端电阻的结果。
对于一些比较复杂的电路,在电路图中可能有一些短接线交织在一起,对于这样的电路图,一般宜将电路图中的节点和支路进行编号,重新画出能较清晰地反映电路元件串并联关系的电路图,而不要被一些短接线所迷惑。
例 求ab R 。
R⇒R显然:()1246753////////ab R R R R R R R R =++⎡⎤⎣⎦对左图分析观察,发现此八个电阻均连接于a 、b 节点间,恰为并联联接,所以:18ab R R=CD2.桥式电路的平衡等电位点如图所示的电路,对端口A B 而言,若12341423::(:)R R R R or R R R R ==则C D 两点是等电位点(C D 0u =)。
在求入端电阻A B R 时,C D 两点间的电阻,既可以断开,也可以短接。
对桥式电路的平衡等电位点的分析,还可以进一步扩展。
如下图所示的电路,对端口A B 而言,若123456::::R R R R R R =,则对图(a )来说,C 与D 及E 与F 分别是等电位点(CD EF 0,0u u ==),对图(b )来说,E F G、、是等电位点。
在求入端电阻A B R 时,其间的支路既可以开路,也可以短接。
应该指出,关于电桥的概念,是有赖于端口的,离开了端口,也就谈不上它的“桥”。
在电路分析中,如果能判断出某两点的电压为零,则可以将这两点短接;如果能判断出某条支路的电流为零,则可以将这条支路断开。
这样处理的结果,不会影响整个电路的工作状态。
然而,这两种处理的性质是不同的。
在求入端电阻时,对于无源的电阻支路,若能判断出该支路两端的电位为等电位点,则该支路的电流为零,所以,对于这样的支路是既可以作短接处理,也可以作开路处理的。
这样的等电位点,称为“自然等电位点”。
3.对称电路等电位点的分析与判断电路对端口的对称性有两种类型:(1)平衡对称 (2)传递对称 (1)平衡对称电路如果一个电路,用垂直平分端口的平面横切过去,可以将该端口切成上、下完全相等的两个部分,且上下两部分之间没有交叉联接的支路。
这样的电路就称为平衡对称电路。
这个横切面,就是该电路对端口的平衡对称面。
在平衡对称电路中,若在端口加激励,则落在平衡对称面的点都是等电位点。
(2)传递对称电路如果一个电路,用一个过端口的平面直劈过去,可以将该电路劈成左、右两半完全相等的部分,则这样的电路就称为传递对称电路。
这个直劈面,就是该电路的传递对称面。
在传递对称的电路中,与传递对称面对称的点,称为传递对称点。
若在端口加激励,则每一对传递对称点,分别是等电位点。
一般来说,平衡对称面只有唯一的一个,就像地球的赤道面只有一个一样,然而,传递对称面不一样,它可能不只一个,正如地球的子午圈不止一个一样。
例:求下图电路的等效电阻ab R 。
解:求ab R ,即为求R 与kb R 之串联电阻。
因此,关键是求kb R 。
求kb R 可有多种方法。
可用Y ∆-变换来求解,亦可过k 、b 取传递对称面,根据对称性可知:c 与d 的电位相等,g 与h 的电位相等,从而可将c 、d 支路与g 、h 支路断开。
同时可过e 、f 取平衡对称面,从而知e 、f 的电位相等,可将短接。
从而有:1282223ab R R R R R R R R ⋅⎡⎤=+⨯+=⎢⎥+⎣⎦4.其它例题:例:求下图(a)、(b)所示电路的总电阻12R 。
R解(a)图:此题易将上、下两部分看成∆形联接。
12(400400)(18001200)80020001600() 1.6()R k ++=+=Ω=Ω(b)图化简为:⇒⇒或者化简为:⇒⇒1218R ∴=Ω二 电路的系统分析法(1)列出下图所示电路的节点电压方程。
2解:先选取节点0为参考节点,各节点的自导分别为 节点1的自导 112367111G R R R R =+++(必须注意,电阻11s R i 与串联的支路,对其余部分的作用可以等效为一个电流源1s i 。
另外,67R R 和相串联的支路电导是电阻67R R 和串联后的倒数。
)节点2的自导 22345671111G R R R R R =++++节点1和2的互导 122136711G G R R R=-++=()从而,据(1)列出节点方程: 节点1: 6121323673676711111()s n n s u u u i i R R R R R R R R R β++-+=-++++()节点2: 6212336734567567111111()s n n u u u u i R R R R R R R R R R R μβ-+++++=+-+++()为了用节点电压来表示受控源的控制量32,i u 可列出方程:21123333n n n n u u u u i R R R -==-21n u u =将它们代入节点电压方程,经整理后得:61212336733676711111()s n n s u u u i R R R R R R R R R R R ββ+++-++=++++()61233567335676711111()s n n u u u R R R R R R R R R R R R βμβ-+++++++=-+++()(2) 节点法中另一需作特别处理的情况是:若电路中具有某些电压源支路,这些电压源没有电阻与之串联(从而该支路电导为∞),有二种方法可以处理:①采用混合变量,除节点电压外,还把电压源支路的电流作为变量,再补充一个该支路电压与相应节点电压的关系方程。
②设置广义节点例:列出下图所示电路的节点电压方程。
解:选取节点0为参考节点。
由于电路中存在特殊电压源支路,故假设两支路电流12,i i (如图)。
从而可以写出:节点1: 122122111()n n u u i R R R +-=(1)节点2: 123122331111()n n n u u u iR RRR-++-= (2)节点3: 232334111()n n u u iR RR-++=- (3)由支路电压和节点电压的关系,可列出两个辅助方程:21n s u u = (4) 312n n s u u u -= (5)这样,五个方程正好解五个未知量。
但是,因为已取节点O 为参考节点,节点2的电压21n s u u =是已知的,所以节点2的方程不需要列写,1i 也不需要作为未知量。
于是,由式(1)、(3)、(5)三个独立方程刚好可以解出231i u u n n 和、。
如果并不要求2i ,那么将式(3)代入(1)则得:1223122323111111()()0n n n n u u u u R R R R R R +--++=考虑到 21n s u u = 则上式成为:131123423111111()()()0n n s u u u R R R R R R +++-+=(6)这样,由式(5)和(6)就可以求出13n n u u 和。
式(6)是可以直接凭观察写出来的。
这只要将图3-5中虚线所示部分看作一个广义节点(复合节点)。
对这个广义节点直接列出节点电压方程,是不困难的。
一般来说,对于仅含一条电压源支路的电路,将此支路的一端选作参考点,则该支路另一端(节点)的节点电压值即为电压源的电压值,从而此节点的电压方程不需要列写,这样将使问题的分析更容易一些。
但当存在两个分离的电压源时,无论怎样选取参考点,都无法避免列出一个广义节点方程。
(3)列出下图所示电路的回路电流方程,并求x y u i 和。
21解:为了避免写出包含电流源两端电压为未知量的回路电流方程,选择右图中实线所示的树,以基本回路作为独立回路。
这样,在连支中的电流就是各回路电流。
由此,可以写出:回路1 19l i = (1) 回路2 22l x i u = (2) 回路3 2342329l l l i i i -+-=- (3) 回路4 1234222523l l l l l y i i i i i +-+=+ (4) 因为 234y l l l i i i i =-+- (5)142()x l l u i i =+ (6)通过上面6个方程,完全可以求出各未知量,由于只要求x y u i 和,将式(1)、(2)、(5)和(6)式代入式(3)和(4),经整理后得只有x y u i 和两个未知量的方程。
514x y u i =+6 322x y u i -=10由上两方程可求得:x u =4V1A y i =-从本例可以看出,如果要使所选回路电流就是电流源(或受控电流源)的电流值,只要将电流源(或受控电流源)所在的支路选为连支,以基本回路作为一组独立回路来列写方程是很方便的。
三 例题讲解例1:下图所示电路中,A 为一含独立电源的线性电路(讲完齐性定理后讲)。
已知:(1)当s u 和s i 均为零时,毫安表的读数为20mA ;(2)当5V,0s s u i ==时,毫安表的读数为70mA ;(3)当0,1A s s u i ==时,毫安表的读数为50mA ;求:当3V ,2A s s u i ==-时,毫安表的读数。
解:本题是应用叠加定理求解的另一类型问题,根据叠加定理,流经毫安表的电流的表达式可假设为:s s ci bu a i ++=式中a 为A 中的电源所产生的毫安表中的电流分量。
由于A 中的电源没有变化,所以a 是一个常数,其单位为m A ,b 是电流s u i 与的比例常数,单位为S ,c为s i i 和无单位的比例常数,从而可得到在任何组合的输入情况下的输出。
所以i 的一般表达式为:201030(m A )s s i u i =++当3V ,2A s s u i ==-时: 2010330210mi =+⨯-⨯=-例2. 左下图示电路,当1K 与2K 都断开时,电流表读书为1.2A ,当1K 闭合2K 断开时,电流表的读数为3A ,求1K 断开2K 闭合时电流表的读数。
i解:由题意有(等效电路图如右):(4020)1.212(20)3A 7(40)s i s i s i u R u R i u R i =++⨯⎫⎪=+⨯⇒=⎬⎪=+⨯⎭例3. 图示电路,求电表M 的读数:(1)当M 为一理想电压表时;(2)当M 为一理想电流表时。