高考物理备考之临界状态的假设解决物理试题压轴突破训练∶培优易错试卷篇含详细答案

备战高考物理临界状态的假设解决物理试题(大题培优易错试卷)一、临界状态的假设解决物理试题1．如图所示，在光滑的圆锥顶用长为L 的细线悬挂一质量为m 的小球，圆锥顶角为2θ，当圆锥和球一起以角速度ω匀速转动时，球压紧锥面．()1此时绳的张力是多少？()2若要小球离开锥面，则小球的角速度至少为多少？【答案】（1）()22cos sin T mg m l θωθ=+（2）cos gl ωθ=【解析】（1）小球此时受到竖直向下的重力mg ，绳子的拉力T ，锥面对小球的支持力N ，三个力作用，合力充当向心力，即合力2sin F m l ωθ= 在水平方向上有，sin cos T N ma F ma θθ-==，， 在竖直方向上：cos sin T N mg θθ+= 联立四个式子可得()22cos sin T mg m l θωθ=+（2）重力和拉力完全充当向心力时，小球对锥面的压力为零， 故有向心力tan F mg θ=，2sin F m l ωθ=，联立可得cos gl ωθ=，即小球的角速度至少为cos gl ωθ=；2．如图甲所示，小车B 紧靠平台的边缘静止在光滑水平面上，物体A （可视为质点）以初速度v 0从光滑的平台水平滑到与平台等高的小车上，物体和小车的v -t 图像如图乙所示，取重力加速度g =10m /s 2，求：(1)物体A 与小车上表面间的动摩擦因数； (2)物体A 与小车B 的质量之比； (3)小车的最小长度。

【答案】(1)0.3；(2)13；(3)2m 【解析】 【分析】 【详解】(1)根据v t -图像可知，A 在小车上做减速运动，加速度的大小21241m /s 3m /s 1v a t ==∆-∆=若物体A 的质量为m 与小车上表面间的动摩擦因数为μ，则1mg ma μ=联立可得0.3μ=(2)设小车B 的质量为M ，加速度大小为2a ，根据牛顿第二定律2mg Ma μ=得13m M = (3)设小车的最小长度为L ，整个过程系统损失的动能，全部转化为内能22011()22mgL mv M m v μ=-+解得L =2m3．如图甲，小球用不可伸长的轻绳连接绕定点O 在竖直面内圆周运动，小球经过最高点的速度大小为v ，此时绳子拉力大小为F ，拉力F 与速度的平方的关系如图乙所示，图象中的数据a 和b 以及重力加速度g 都为已知量，以下说法正确的是（ ）A．数据a与小球的质量有关B．数据b与小球的质量无关C．比值只与小球的质量有关，与圆周轨道半径无关D．利用数据a、b和g能够求出小球的质量和圆周轨道半径【答案】D【解析】【分析】【详解】A.当时，此时绳子的拉力为零，物体的重力提供向心力，则有：解得：解得：与物体的质量无关，A错误；B.当时，对物体受力分析，则有：解得：b=mg与小球的质量有关，B错误；C.根据AB可知：与小球的质量有关，与圆周轨道半径有关，C错误；D. 若F=0，由图知：，则有：解得：当时，则有：解得：D正确．4．一根细线一端系一小球（可视为质点），另一端固定在光滑圆锥顶上，如图所示，设小球在水平面内做匀速圆周运动的角速度为ω，细线的张力为F T，则F T随ω2变化的图象是（）A．B．C．D．【答案】C【解析】【分析】【详解】由题知小球未离开圆锥表面时细线与竖直方向的夹角为θ，用L表示细线长度，小球离开圆锥表面前，细线的张力为F T，圆锥对小球的支持力为F N，根据牛顿第二定律有F T sinθ－F N cosθ＝mω2L sinθF T cosθ＋F N sinθ＝mg联立解得F T＝mg cosθ＋ω2mL sin2θ小球离开圆锥表面后，设细线与竖直方向的夹角为α，根据牛顿第二定律有F T sinα＝mω2L sinα解得F T＝mLω2故C正确。

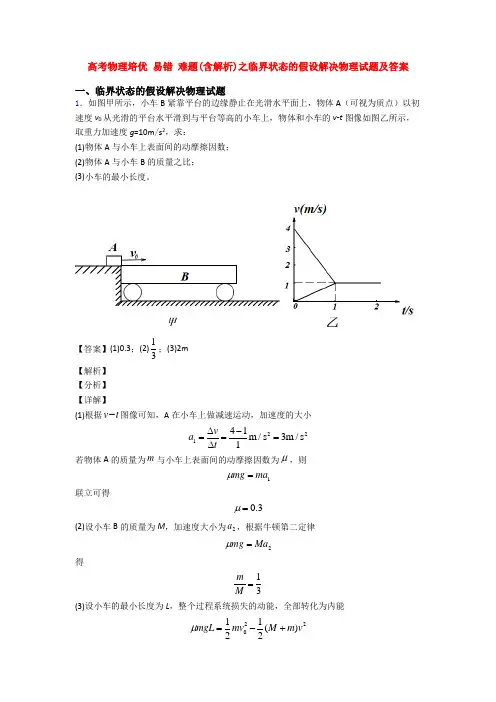
高考物理培优 易错 难题(含解析)之临界状态的假设解决物理试题及答案一、临界状态的假设解决物理试题1．如图甲所示，小车B 紧靠平台的边缘静止在光滑水平面上，物体A （可视为质点）以初速度v 0从光滑的平台水平滑到与平台等高的小车上，物体和小车的v -t 图像如图乙所示，取重力加速度g =10m /s 2，求：(1)物体A 与小车上表面间的动摩擦因数； (2)物体A 与小车B 的质量之比； (3)小车的最小长度。

【答案】(1)0.3；(2)13；(3)2m 【解析】 【分析】 【详解】(1)根据v t -图像可知，A 在小车上做减速运动，加速度的大小21241m /s 3m /s 1v a t ==∆-∆=若物体A 的质量为m 与小车上表面间的动摩擦因数为μ，则1mg ma μ=联立可得0.3μ=(2)设小车B 的质量为M ，加速度大小为2a ，根据牛顿第二定律2mg Ma μ=得13m M = (3)设小车的最小长度为L ，整个过程系统损失的动能，全部转化为内能22011()22mgL mv M m v μ=-+解得L =2m2．平面OM 和平面ON 之间的夹角为30°，其横截面（纸面）如图所示，平面OM 上方存在匀强磁场，磁感应强度大小为B ，方向垂直于纸面向外。

一带电粒子的质量为m ，电荷量为q （q >0）。

粒子沿纸面以大小为v 的速度从OM 的某点向左上方射入磁场，速度与OM 成30°角。

已知该粒子在磁场中的运动轨迹与ON 只有一个交点，并从OM 上另一点射出磁场。

不计粒子重力。

则粒子离开磁场的出射点到两平面交线O 的距离为A ．2mvqBB ．3mvqBC ．2mvqBD ．4mvqB【答案】D 【解析】 【详解】 、粒子进入磁场做顺时针方向的匀速圆周运动，轨迹如图所示，根据洛伦兹力提供向心力，有2v qvB m R=解得mv R qB =根据轨迹图知22mvPQ R qB==， ∠OPQ =60°则粒子离开磁场的出射点到两平面交线O 的距离为4 2mvOP PQqB==，则D正确，ABC错误。

高考物理 临界状态的假设解决物理试题 培优易错试卷练习(含答案)含答案一、临界状态的假设解决物理试题1．一带电量为＋q 、质量为m 的小球从倾角为θ的光滑的斜面上由静止开始下滑．斜面处于磁感应强度为B 的匀强磁场中，磁场方向如图所示，求小球在斜面上滑行的速度范围和滑行的最大距离．【答案】m gcosθ/Bq ， m 2gcos 2θ/(2B 2q 2sinθ) 【解析】 【分析】 【详解】带正电小球从光滑斜面下滑过程中受到重力m g 、斜面的支持力N 和洛伦兹力f 的作用于小球下滑速度越来越大，所受的洛伦兹力越来越大，斜面的支持力越来越小，当支持力为零时，小球运动达到临界状态，此时小球的速度最大，在斜面上滑行的距离最大 故cos mg qvB θ= 解得：cos mg v qBθ=，为小球在斜面上运动的最大速度 此时小球移动距离为：22222cos 2(2sin )v m g s a B q θθ==．2．小明同学站在水平地面上，手握不可伸长的轻绳一端，绳的另一端系有质量为m =0.3kg 的小球，甩动手腕，使球在竖直平面内做圆周运动.当球在某次运动到最低点时，绳恰好达到所能承受的最大拉力F 而断掉，球飞行水平距离s 后恰好无碰撞地落在临近的一倾角为α＝53°的光滑斜面上并沿斜面下滑，已知斜面顶端与平台的高度差h ＝0.8 m ．绳长r =0.3m(g 取10 m/s 2，sin 53°＝0.8，cos 53°＝0.6)求：(1)绳断时小球的速度大小v 1和小球在圆周最低点与平台边缘的水平距离s 是多少. (2)绳能承受的最大拉力F 的大小.【答案】（1）3m/s ，1.2m （2）12N【解析】 【详解】(1)由题意可知：小球落到斜面上并沿斜面下滑，说明此时小球速度方向与斜面平行，否则小球会弹起，所以有v y =v 0 tan53°又v y 2=2gh ，代入数据得：v y =4m/s ，v 0=3m/s故绳断时球的小球做平抛运动的水平速度为3m/s ； 由v y =gt 1得：10.4s y v t g==则s =v 0 t 1=3×0.4m=1.2m（2）由牛顿第二定律：21mv F mg r-= 解得：F =12N3．如图甲，小球用不可伸长的轻绳连接绕定点O 在竖直面内圆周运动，小球经过最高点的速度大小为v ，此时绳子拉力大小为F ，拉力F 与速度的平方的关系如图乙所示，图象中的数据a 和b 以及重力加速度g 都为已知量，以下说法正确的是（ ）A ．数据a 与小球的质量有关B ．数据b 与小球的质量无关C ．比值只与小球的质量有关，与圆周轨道半径无关D ．利用数据a 、b 和g 能够求出小球的质量和圆周轨道半径 【答案】D 【解析】 【分析】 【详解】 A.当时，此时绳子的拉力为零，物体的重力提供向心力，则有：解得：解得：与物体的质量无关，A错误；B.当时，对物体受力分析，则有：解得：b=mg与小球的质量有关，B错误；C.根据AB可知：与小球的质量有关，与圆周轨道半径有关，C错误；D. 若F=0，由图知：，则有：解得：当时，则有：解得：D正确．4．质量为m的光滑圆柱体A放在质量也为m的光滑“ V”型槽B上，如图，α=60°，另有质量为M的物体C通过跨过定滑轮的不可伸长的细绳与B相连，现将C自由释放，则下列说法正确的是( )A ．当M= m 时，A 和B 保持相对静止，共同加速度为0.5g B ．当M=2m 时，A 和B 保持相对静止，共同加速度为0.5gC ．当M=6m 时，A 和B 保持相对静止，共同加速度为0.75gD ．当M=5m 时，A 和B 之间的恰好发生相对滑动 【答案】B 【解析】 【分析】 【详解】D.当A 和B 之间的恰好发生相对滑动时，对A 受力分析如图根据牛顿运动定律有：cot 60mg ma ︒= 解得cot 603a g g =︒=B 与C 为绳子连接体，具有共同的运动情况，此时对于B 和C 有：()Mg M m a =+所以3M a g g M m ==+，即3MM m=+ 解得3 2.3713M m =≈-选项D 错误；C.当 2.37M m >，A 和B 将发生相对滑动，选项C 错误；A. 当 2.37M m <，A 和B 保持相对静止。

高考物理培优 易错 难题(含解析)之临界状态的假设解决物理试题附答案解析一、临界状态的假设解决物理试题1．如图所示，在光滑的圆锥顶用长为L 的细线悬挂一质量为m 的小球，圆锥顶角为2θ，当圆锥和球一起以角速度ω匀速转动时，球压紧锥面．()1此时绳的张力是多少？()2若要小球离开锥面，则小球的角速度至少为多少？【答案】（1）()22cos sin T mg m l θωθ=+（2）cos gl ωθ= 【解析】（1）小球此时受到竖直向下的重力mg ，绳子的拉力T ，锥面对小球的支持力N ，三个力作用，合力充当向心力，即合力2sin F m l ωθ= 在水平方向上有，sin cos T N ma F ma θθ-==，， 在竖直方向上：cos sin T N mg θθ+= 联立四个式子可得()22cos sin T mg m l θωθ=+（2）重力和拉力完全充当向心力时，小球对锥面的压力为零， 故有向心力tan F mg θ=，2sin F m l ωθ=，联立可得cos gl ωθ=，即小球的角速度至少为cos gl ωθ=；2．壁厚不计的圆筒形薄壁玻璃容器的侧视图如图所示。

圆形底面的直径为2R ，圆筒的高度为R 。

(1)若容器内盛满甲液体，在容器中心放置一个点光源，在侧壁以外所有位置均能看到该点光源，求甲液体的折射率；(2)若容器内装满乙液体，在容器下底面以外有若干个光源，却不能通过侧壁在筒外看到所有的光源，求乙液体的折射率。

【答案】(1)5n≥甲；(2)2n>乙【解析】【详解】(1)盛满甲液体，如图甲所示，P点刚好全反射时为最小折射率，有1sinnC=由几何关系知222sin2RCRR=⎛⎫+ ⎪⎝⎭解得5n=则甲液体的折射率应为5n≥甲(2)盛满乙液体，如图乙所示，与底边平行的光线刚好射入液体时对应液体的最小折射率，A点1sinnC='乙由几何关系得90Cα'=︒-B点恰好全反射有Cα'=解各式得2n=乙则乙液体的折射率应为2n>乙3．如图所示，圆心为O、半径为r的圆形区域外存在匀强磁场，磁场方向垂直于纸面向外，磁感应强度大小为B。

高考物理备考之临界状态的假设解决物理试题压轴突破训练∶培优易错试卷篇及答案解析(1)一、临界状态的假设解决物理试题1．一带电量为＋q 、质量为m 的小球从倾角为θ的光滑的斜面上由静止开始下滑．斜面处于磁感应强度为B 的匀强磁场中，磁场方向如图所示，求小球在斜面上滑行的速度范围和滑行的最大距离．【答案】m gcosθ/Bq ， m 2gcos 2θ/(2B 2q 2sinθ) 【解析】 【分析】 【详解】带正电小球从光滑斜面下滑过程中受到重力m g 、斜面的支持力N 和洛伦兹力f 的作用于小球下滑速度越来越大，所受的洛伦兹力越来越大，斜面的支持力越来越小，当支持力为零时，小球运动达到临界状态，此时小球的速度最大，在斜面上滑行的距离最大 故cos mg qvB θ= 解得：cos mg v qBθ=，为小球在斜面上运动的最大速度 此时小球移动距离为：22222cos 2(2sin )v m g s a B q θθ==．2．如图甲所示，小车B 紧靠平台的边缘静止在光滑水平面上，物体A （可视为质点）以初速度v 0从光滑的平台水平滑到与平台等高的小车上，物体和小车的v -t 图像如图乙所示，取重力加速度g =10m /s 2，求：(1)物体A 与小车上表面间的动摩擦因数； (2)物体A 与小车B 的质量之比； (3)小车的最小长度。

【答案】(1)0.3；(2)13；(3)2m 【解析】 【分析】 【详解】(1)根据v t -图像可知，A 在小车上做减速运动，加速度的大小21241m /s 3m /s 1v a t ==∆-∆=若物体A 的质量为m 与小车上表面间的动摩擦因数为μ，则1mg ma μ=联立可得0.3μ=(2)设小车B 的质量为M ，加速度大小为2a ，根据牛顿第二定律2mg Ma μ=得13m M = (3)设小车的最小长度为L ，整个过程系统损失的动能，全部转化为内能22011()22mgL mv M m v μ=-+解得L =2m3．壁厚不计的圆筒形薄壁玻璃容器的侧视图如图所示。

高考物理临界状态的假设解决物理试题(大题培优易错试卷)一、临界状态的假设解决物理试题1．如图所示，在光滑的圆锥顶用长为L 的细线悬挂一质量为m 的小球，圆锥顶角为2θ，当圆锥和球一起以角速度ω匀速转动时，球压紧锥面．()1此时绳的张力是多少？()2若要小球离开锥面，则小球的角速度至少为多少？【答案】（1）()22cos sin T mg m l θωθ=+（2）cos gl ωθ=【解析】（1）小球此时受到竖直向下的重力mg ，绳子的拉力T ，锥面对小球的支持力N ，三个力作用，合力充当向心力，即合力2sin F m l ωθ= 在水平方向上有，sin cos T N ma F ma θθ-==，， 在竖直方向上：cos sin T N mg θθ+= 联立四个式子可得()22cos sin T mg m l θωθ=+（2）重力和拉力完全充当向心力时，小球对锥面的压力为零， 故有向心力tan F mg θ=，2sin F m l ωθ=，联立可得cos gl ωθ=，即小球的角速度至少为cos gl ωθ=；2．如图所示，用长为L =0.8m 的轻质细绳将一质量为1kg 的小球悬挂在距离水平面高为H =2.05m 的O 点，将细绳拉直至水平状态无初速度释放小球，小球摆动至细绳处于竖直位置时细绳恰好断裂，小球落在距离O 点水平距离为2m 的水平面上的B 点，不计空气阻力，取g =10m/s 2求：(1)绳子断裂后小球落到地面所用的时间； (2)小球落地的速度的大小； (3)绳子能承受的最大拉力。

【答案】(1)0.5s(2)6.4m/s(3)30N 【解析】 【分析】 【详解】(1)细绳断裂后，小球做平抛运动，竖直方向自由落体运动，则竖直方向有212AB h gt =，解得2(2.050.8)s 0.5s 10t ⨯-==(2)水平方向匀速运动，则有02m/s 4m/s 0.5x v t === 竖直方向的速度为5m/s y v gt ==则2222045m/s=41m/s 6.4m/s y v v v =+=+≈(3)在A 点根据向心力公式得2v T mg m L-=代入数据解得24(1101)N=30N 0.8T =⨯+⨯3．用一根细线一端系一小球（可视为质点），另一端固定在一光滑锥顶上，如图所示。

高考物理临界状态的假设解决物理试题培优易错试卷练习(含答案)含答案解析一、临界状态的假设解决物理试题1．今年入冬以来，我国多地出现了雾霾天气，给交通安全带来了很大的危害．某地雾霾天气中高速公司上的能见度只有72m，要保证行驶前方突发紧急情况下汽车的安全，汽车行驶的速度不能太大．已知汽车刹车时的加速度大小为5m/s2．（1）若前方紧急情况出现的同时汽车开始制动，汽车行驶的速度不能超过多大？（结果可以带根号）（2）若驾驶员从感知前方紧急情况到汽车开始制动的反应时间为0.6s，汽车行驶的速度不能超过多大？【答案】（1）125m/s；（2）24m/s．【解析】试题分析：（1）根据速度位移公式求出求出汽车行驶的最大速度；（2）汽车在反应时间内的做匀速直线运动，结合匀速直线运动的位移和匀减速直线运动的位移之和等于72m，运用运动学公式求出汽车行驶的最大速度．解：（1）设汽车刹车的加速度a=﹣5m/s2，要在s=72m内停下，行驶的速度不超过v1，由运动学方程有：0﹣v12=﹣2as ①代入题中数据可得：v1=12m/s（2）设有汽车行驶的速度不超过v2，在驾驶员的反应时间t0内汽车作匀速运动的位移s1：s1=v2t0 ②刹车减速位移s2=③s=s1+s2 ④由②～④式并代入数据可得：v2=24m/s答：（1）汽车行驶的速度不能超过m/s；（2）汽车行驶的速度不能超过24m/s．【点评】解决本题的关键知道在反应时间内汽车做匀速直线运动，刹车后做匀减速直线运动，抓住总位移，结合运动学公式灵活求解．2．火车转弯时，如果铁路弯道内外轨一样高，外轨对轮绝（如图a所示）挤压的弹力F提供了火车转弯的向心力（如图b所示），但是靠这种办法得到向心力，铁轨和车轮极易受损．在修筑铁路时，弯道处的外轨会略高于内轨（如图c所示），当火车以规定的行驶速度转弯时，内、外轨均不会受到轮缘的挤压，设此时的速度小为，以下说法中正确的是A．该弯道的半径B．当火车质量改变时，规定的行驶速度也将改变C．当火车速率大于时，外轨将受到轮缘的挤压D．当火车速率小于时，外轨将受到轮缘的挤压【答案】C【解析】【详解】火车拐弯时不侧向挤压车轮轮缘，靠重力和支持力的合力提供向心力，设转弯处斜面的倾角为θ，根据牛顿第二定律得：mgtanθ=mv2/R，解得：R= v2/ g tanθ，故A错误；根据牛顿第二定律得：mgtanθ=mv2/R, 解得：v=gRtan ，与质量无关，故B错误；若速度大于规定速度，重力和支持力的合力不够提供，此时外轨对火车有侧压力，轮缘挤压外轨．故C 正确；若速度小于规定速度，重力和支持力的合力提供偏大，此时内轨对火车有侧压力，轮缘挤压内轨．故D错误．故选C.点睛：火车拐弯时以规定速度行驶，此时火车的重力和支持力的合力提供圆周运动所需的向心力．若速度大于规定速度，重力和支持力的合力不够提供，此时外轨对火车有侧压力；若速度小于规定速度，重力和支持力的合力提供偏大，此时内轨对火车有侧压力．3．质量为m的光滑圆柱体A放在质量也为m的光滑“ V”型槽B上，如图，α=60°，另有质量为M的物体C通过跨过定滑轮的不可伸长的细绳与B相连，现将C自由释放，则下列说法正确的是( )A．当M= m时，A和B保持相对静止，共同加速度为0.5gB．当M=2m时，A和B保持相对静止，共同加速度为0.5gC．当M=6m时，A和B保持相对静止，共同加速度为0.75gD．当M=5m时，A和B之间的恰好发生相对滑动【答案】B【解析】 【分析】 【详解】D.当A 和B 之间的恰好发生相对滑动时，对A 受力分析如图根据牛顿运动定律有：cot 60mg ma ︒= 解得cot 603a g g =︒=B 与C 为绳子连接体，具有共同的运动情况，此时对于B 和C 有：()Mg M m a =+所以3M a g g M m ==+，即3MM m=+ 解得3 2.3713M m =≈-选项D 错误；C.当 2.37M m >，A 和B 将发生相对滑动，选项C 错误；A. 当 2.37M m <，A 和B 保持相对静止。

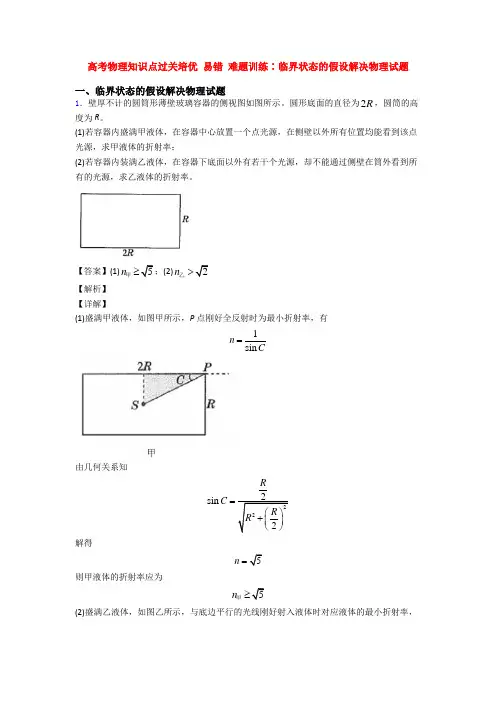
高考物理知识点过关培优 易错 难题训练∶临界状态的假设解决物理试题一、临界状态的假设解决物理试题1．壁厚不计的圆筒形薄壁玻璃容器的侧视图如图所示。

圆形底面的直径为2R ，圆筒的高度为R 。

(1)若容器内盛满甲液体，在容器中心放置一个点光源，在侧壁以外所有位置均能看到该点光源，求甲液体的折射率；(2)若容器内装满乙液体，在容器下底面以外有若干个光源，却不能通过侧壁在筒外看到所有的光源，求乙液体的折射率。

【答案】(1)5n≥甲；(2)2n >乙【解析】 【详解】(1)盛满甲液体，如图甲所示，P 点刚好全反射时为最小折射率，有1sin n C=由几何关系知222sin 2R C R R =⎛⎫+ ⎪⎝⎭解得5n =则甲液体的折射率应为5n ≥甲(2)盛满乙液体，如图乙所示，与底边平行的光线刚好射入液体时对应液体的最小折射率，A 点1sin n C ='乙 由几何关系得90C α'=︒-B 点恰好全反射有C α'=解各式得2n =乙则乙液体的折射率应为2n >乙2．如图所示，用长为L =0.8m 的轻质细绳将一质量为1kg 的小球悬挂在距离水平面高为H =2.05m 的O 点，将细绳拉直至水平状态无初速度释放小球，小球摆动至细绳处于竖直位置时细绳恰好断裂，小球落在距离O 点水平距离为2m 的水平面上的B 点，不计空气阻力，取g =10m/s 2求：(1)绳子断裂后小球落到地面所用的时间； (2)小球落地的速度的大小； (3)绳子能承受的最大拉力。

【答案】(1)0.5s(2)6.4m/s(3)30N 【解析】 【分析】 【详解】(1)细绳断裂后，小球做平抛运动，竖直方向自由落体运动，则竖直方向有212AB h gt =，解得2(2.050.8)s 0.5s 10t ⨯-==(2)水平方向匀速运动，则有02m/s 4m/s 0.5x v t === 竖直方向的速度为5m/s y v gt ==则2222045m/s=41m/s 6.4m/s y v v v =+=+≈(3)在A 点根据向心力公式得2v T mg m L-=代入数据解得24(1101)N=30N 0.8T =⨯+⨯3．中国已进入动车时代，在某轨道拐弯处，动车向右拐弯，左侧的路面比右侧的路面高一些，如图所示，动车的运动可看作是做半径为R 的圆周运动，设内外路面高度差为h ，路基的水平宽度为d ，路面的宽度为L ，已知重力加速度为g ，要使动车轮缘与内、外侧轨道无挤压，则动车拐弯时的速度应为（ ）A gRhLB gRhdC 2gR D gRdh【答案】B 【解析】 【详解】把路基看做斜面，设其倾角为θ，如图所示当动车轮缘与内、外侧轨道无挤压时，动车在斜面上受到自身重力mg和斜面支持力N，二者的合力提供向心力，即指向水平方向，根据几何关系可得合力F=mg tanθ，合力提供向心力，根据牛顿第二定律，有mg tanθ＝2 v mR计算得v＝tangR ，根据路基的高和水平宽度得tanθ＝h d带入解得v＝gRhd，即动车拐弯时的速度为gRhd时，动车轮缘与内、外侧轨道无挤压，故B正确，ACD错误。

高考物理培优 易错 难题(含解析)之临界状态的假设解决物理试题附答案一、临界状态的假设解决物理试题1．一带电量为＋q 、质量为m 的小球从倾角为θ的光滑的斜面上由静止开始下滑．斜面处于磁感应强度为B 的匀强磁场中，磁场方向如图所示，求小球在斜面上滑行的速度范围和滑行的最大距离．【答案】m gcosθ/Bq ， m 2gcos 2θ/(2B 2q 2sinθ) 【解析】 【分析】 【详解】带正电小球从光滑斜面下滑过程中受到重力m g 、斜面的支持力N 和洛伦兹力f 的作用于小球下滑速度越来越大，所受的洛伦兹力越来越大，斜面的支持力越来越小，当支持力为零时，小球运动达到临界状态，此时小球的速度最大，在斜面上滑行的距离最大 故cos mg qvB θ= 解得：cos mg v qBθ=，为小球在斜面上运动的最大速度 此时小球移动距离为：22222cos 2(2sin )v m g s a B q θθ==．2．水平传送带上A 、B 两端点间距L ＝4m ，半径R ＝1m 的光滑半圆形轨道固于竖直平面内，下端与传送带B 相切。

传送带以v 0＝4m/s 的速度沿图示方向匀速运动，m ＝lkg 的小滑块由静止放到传送带的A 端，经一段时间运动到B 端，滑块与传送带间的动摩擦因数μ＝0.5，g ＝10m/s 2。

(1)求滑块到达B 端的速度；(2)求滑块由A 运动到B 的过程中，滑块与传送带间摩擦产生的热量；(3)仅改变传送带的速度，其他条件不变，计算说明滑块能否通过圆轨道最高点C 。

【答案】(1)v B =4m/s ； (2)Q ＝8J ； (3)不能通过最高点 【解析】【分析】本题考查了动能定理和圆周运动。

【详解】⑴滑块在传送带上先向右做加速运动，设当速度v = v 0时已运动的距离为x 根据动能定理201-02mgx mv μ=得x=1.6m ＜L所以滑块到达B 端时的速度为4m/s 。

⑵设滑块与传送带发生相对运动的时间为t ，则0v gt μ=滑块与传送带之间产生的热量0()Q mg v t x μ=-解得Q = 8J⑶设滑块通过最高点C 的最小速度为C v 经过C 点，根据向心力公式2C mv mg R= 从B 到C 过程，根据动能定理2211222C B mg R mv mv -⋅=- 解得经过B 的速度B v =m/s从A 到B 过程，若滑块一直加速，根据动能定理2102m mgL mv μ=-解得m v =m/s由于速度v m ＜v B ，所以仅改变传送带的速度，滑块不能通过圆轨道最高点。

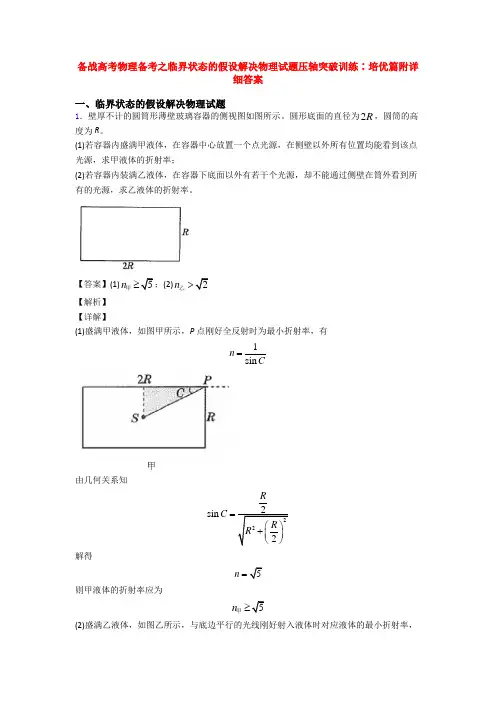
备战高考物理备考之临界状态的假设解决物理试题压轴突破训练∶培优篇附详细答案一、临界状态的假设解决物理试题1．壁厚不计的圆筒形薄壁玻璃容器的侧视图如图所示。

圆形底面的直径为2R ，圆筒的高度为R 。

(1)若容器内盛满甲液体，在容器中心放置一个点光源，在侧壁以外所有位置均能看到该点光源，求甲液体的折射率；(2)若容器内装满乙液体，在容器下底面以外有若干个光源，却不能通过侧壁在筒外看到所有的光源，求乙液体的折射率。

【答案】(1)5n≥甲；(2)2n >乙【解析】 【详解】(1)盛满甲液体，如图甲所示，P 点刚好全反射时为最小折射率，有1sin n C=由几何关系知222sin 2R C R R =⎛⎫+ ⎪⎝⎭解得5n =则甲液体的折射率应为5n ≥甲(2)盛满乙液体，如图乙所示，与底边平行的光线刚好射入液体时对应液体的最小折射率，A 点1sin n C ='乙 由几何关系得90C α'=︒-B 点恰好全反射有C α'=解各式得2n =乙则乙液体的折射率应为2n >乙2．如图甲，小球用不可伸长的轻绳连接绕定点O 在竖直面内圆周运动，小球经过最高点的速度大小为v ，此时绳子拉力大小为F ，拉力F 与速度的平方的关系如图乙所示，图象中的数据a 和b 以及重力加速度g 都为已知量，以下说法正确的是（ ）A ．数据a 与小球的质量有关B ．数据b 与小球的质量无关C ．比值只与小球的质量有关，与圆周轨道半径无关D ．利用数据a 、b 和g 能够求出小球的质量和圆周轨道半径 【答案】D 【解析】 【分析】 【详解】 A.当时，此时绳子的拉力为零，物体的重力提供向心力，则有：解得：解得：与物体的质量无关，A错误；B.当时，对物体受力分析，则有：解得：b=mg与小球的质量有关，B错误；C.根据AB可知：与小球的质量有关，与圆周轨道半径有关，C错误；D. 若F=0，由图知：，则有：解得：当时，则有：解得：D正确．3．质量为m的光滑圆柱体A放在质量也为m的光滑“ V”型槽B上，如图，α=60°，另有质量为M的物体C通过跨过定滑轮的不可伸长的细绳与B相连，现将C自由释放，则下列说法正确的是( )A ．当M= m 时，A 和B 保持相对静止，共同加速度为0.5g B ．当M=2m 时，A 和B 保持相对静止，共同加速度为0.5gC ．当M=6m 时，A 和B 保持相对静止，共同加速度为0.75gD ．当M=5m 时，A 和B 之间的恰好发生相对滑动 【答案】B 【解析】 【分析】 【详解】D.当A 和B 之间的恰好发生相对滑动时，对A 受力分析如图根据牛顿运动定律有：cot 60mg ma ︒= 解得cot 603a g g =︒=B 与C 为绳子连接体，具有共同的运动情况，此时对于B 和C 有：()Mg M m a =+所以3M a g g M m ==+，即3MM m=+ 解得3 2.3713M m =≈-选项D 错误；C.当 2.37M m >，A 和B 将发生相对滑动，选项C 错误；A. 当 2.37M m <，A 和B 保持相对静止。

备战高考物理备考之临界状态的假设解决物理试题压轴突破训练∶培优易错试卷篇含详细答案一、临界状态的假设解决物理试题1．一带电量为＋q 、质量为m 的小球从倾角为θ的光滑的斜面上由静止开始下滑．斜面处于磁感应强度为B 的匀强磁场中，磁场方向如图所示，求小球在斜面上滑行的速度范围和滑行的最大距离．【答案】m gcosθ/Bq ， m 2gcos 2θ/(2B 2q 2sinθ) 【解析】 【分析】 【详解】带正电小球从光滑斜面下滑过程中受到重力m g 、斜面的支持力N 和洛伦兹力f 的作用于小球下滑速度越来越大，所受的洛伦兹力越来越大，斜面的支持力越来越小，当支持力为零时，小球运动达到临界状态，此时小球的速度最大，在斜面上滑行的距离最大 故cos mg qvB θ= 解得：cos mg v qBθ=，为小球在斜面上运动的最大速度 此时小球移动距离为：22222cos 2(2sin )v m g s a B q θθ==．2．如图所示，在光滑的圆锥顶用长为L 的细线悬挂一质量为m 的小球，圆锥顶角为2θ，当圆锥和球一起以角速度ω匀速转动时，球压紧锥面．()1此时绳的张力是多少？()2若要小球离开锥面，则小球的角速度至少为多少？【答案】（1）()22cos sin T mg m l θωθ=+（2）cos gl ωθ=【解析】（1）小球此时受到竖直向下的重力mg ，绳子的拉力T ，锥面对小球的支持力N ，三个力作用，合力充当向心力，即合力2sin F m l ωθ= 在水平方向上有，sin cos T N ma F ma θθ-==，， 在竖直方向上：cos sin T N mg θθ+= 联立四个式子可得()22cos sin T mg m l θωθ=+（2）重力和拉力完全充当向心力时，小球对锥面的压力为零， 故有向心力tan F mg θ=，2sin F m l ωθ=，联立可得cos gl ωθ=，即小球的角速度至少为cos gl ωθ=；3．中国已进入动车时代，在某轨道拐弯处，动车向右拐弯，左侧的路面比右侧的路面高一些，如图所示，动车的运动可看作是做半径为R 的圆周运动，设内外路面高度差为h ，路基的水平宽度为d ，路面的宽度为L ，已知重力加速度为g ，要使动车轮缘与内、外侧轨道无挤压，则动车拐弯时的速度应为（ ）A ．gRhLB ．gRhdC ．2gR D ．gRdh【答案】B 【解析】 【详解】把路基看做斜面，设其倾角为θ，如图所示当动车轮缘与内、外侧轨道无挤压时，动车在斜面上受到自身重力mg 和斜面支持力N ，二者的合力提供向心力，即指向水平方向，根据几何关系可得合力F =mg tan θ，合力提供向心力，根据牛顿第二定律，有mg tanθ＝2 v mR计算得v＝tangRθ，根据路基的高和水平宽度得tanθ＝h d带入解得v＝gRhd，即动车拐弯时的速度为gRhd时，动车轮缘与内、外侧轨道无挤压，故B正确，ACD错误。

高考物理备考之临界状态的假设解决物理试题压轴突破训练∶培优易错试卷篇及详细答案一、临界状态的假设解决物理试题1．如图所示，圆心为O、半径为r的圆形区域外存在匀强磁场，磁场方向垂直于纸面向外，磁感应强度大小为B。

P是圆外一点，OP=3r，一质量为m、电荷量为q（q>0）的粒子从P点在纸面内沿着与OP成60°方向射出（不计重力），求：(1)若粒子运动轨迹经过圆心O，求粒子运动速度的大小；(2)若要求粒子不能进入圆形区域，求粒子运动速度应满足的条件。

【答案】(1)3Bqrm；(2)(332)vm≤+或(332)vm≥-【解析】【分析】【详解】(1)设粒子在磁场中做圆周运动的半径为R，圆心为O'，依图题意作出轨迹图如图所示：由几何知识可得：OO R'=()222(3)6sinOO R r rRθ'=+-解得3R r=根据牛顿第二定律可得2vBqv mR=解得3Bqrvm=(2)若速度较小，如图甲所示：根据余弦定理可得()22211196sin r R R r rR θ+=+-解得1332R =+若速度较大，如图乙所示：根据余弦定理可得()22222296sin R r R r rR θ-=+-解得2332R =-根据BqRv m=得1(332)v m =+，2(332)v m =-若要求粒子不能进入圆形区域，粒子运动速度应满足的条件是(332)v m ≤+或(332)v m≥-2．一根细线一端系一小球（可视为质点），另一端固定在光滑圆锥顶上，如图所示，设小球在水平面内做匀速圆周运动的角速度为ω，细线的张力为F T ，则F T 随ω2变化的图象是（ ）A．B．C．D．【答案】C【解析】【分析】【详解】由题知小球未离开圆锥表面时细线与竖直方向的夹角为θ，用L表示细线长度，小球离开圆锥表面前，细线的张力为F T，圆锥对小球的支持力为F N，根据牛顿第二定律有F T sinθ－F N cosθ＝mω2L sinθF T cosθ＋F N sinθ＝mg联立解得F T＝mg cosθ＋ω2mL sin2θ小球离开圆锥表面后，设细线与竖直方向的夹角为α，根据牛顿第二定律有F T sinα＝mω2L sinα解得F T＝mLω2故C正确。

高考物理培优易错试卷(含解析)之临界状态的假设解决物理试题附答案一、临界状态的假设解决物理试题1．如图所示，在光滑的圆锥顶用长为L 的细线悬挂一质量为m 的小球，圆锥顶角为2θ，当圆锥和球一起以角速度ω匀速转动时，球压紧锥面．()1此时绳的张力是多少？()2若要小球离开锥面，则小球的角速度至少为多少？【答案】（1）()22cos sin T mg m l θωθ=+（2）cos gl ωθ= 【解析】（1）小球此时受到竖直向下的重力mg ，绳子的拉力T ，锥面对小球的支持力N ，三个力作用，合力充当向心力，即合力2sin F m l ωθ= 在水平方向上有，sin cos T N ma F ma θθ-==，， 在竖直方向上：cos sin T N mg θθ+= 联立四个式子可得()22cos sin T mg m l θωθ=+（2）重力和拉力完全充当向心力时，小球对锥面的压力为零， 故有向心力tan F mg θ=，2sin F m l ωθ=，联立可得cos gl ωθ=，即小球的角速度至少为cos gl ωθ=；2．平面OM 和平面ON 之间的夹角为30°，其横截面（纸面）如图所示，平面OM 上方存在匀强磁场，磁感应强度大小为B ，方向垂直于纸面向外。

一带电粒子的质量为m ，电荷量为q （q >0）。

粒子沿纸面以大小为v 的速度从OM 的某点向左上方射入磁场，速度与OM 成30°角。

已知该粒子在磁场中的运动轨迹与ON 只有一个交点，并从OM 上另一点射出磁场。

不计粒子重力。

则粒子离开磁场的出射点到两平面交线O 的距离为A ．2mv qBB ．3mv qBC ．2mv qBD ．4mv qB【答案】D 【解析】 【详解】 、粒子进入磁场做顺时针方向的匀速圆周运动，轨迹如图所示，根据洛伦兹力提供向心力，有2v qvB m R=解得mv R qB =根据轨迹图知22mvPQ R qB==， ∠OPQ =60°则粒子离开磁场的出射点到两平面交线O 的距离为42mvOP PQ qB==， 则D 正确，ABC 错误。

高考物理备考之临界状态的假设解决物理试题压轴突破训练∶培优 易错 难题篇附答案(1)一、临界状态的假设解决物理试题1．如图所示，在光滑的圆锥顶用长为L 的细线悬挂一质量为m 的小球，圆锥顶角为2θ，当圆锥和球一起以角速度ω匀速转动时，球压紧锥面．()1此时绳的张力是多少？()2若要小球离开锥面，则小球的角速度至少为多少？【答案】（1）()22cos sin T mg m l θωθ=+（2）cos gl ωθ=【解析】（1）小球此时受到竖直向下的重力mg ，绳子的拉力T ，锥面对小球的支持力N ，三个力作用，合力充当向心力，即合力2sin F m l ωθ= 在水平方向上有，sin cos T N ma F ma θθ-==，， 在竖直方向上：cos sin T N mg θθ+= 联立四个式子可得()22cos sin T mg m l θωθ=+（2）重力和拉力完全充当向心力时，小球对锥面的压力为零， 故有向心力tan F mg θ=，2sin F m l ωθ=，联立可得cos gl ωθ=，即小球的角速度至少为cos gl ωθ=；2．平面OM 和平面ON 之间的夹角为30°，其横截面（纸面）如图所示，平面OM 上方存在匀强磁场，磁感应强度大小为B ，方向垂直于纸面向外。

一带电粒子的质量为m ，电荷量为q （q >0）。

粒子沿纸面以大小为v 的速度从OM 的某点向左上方射入磁场，速度与OM 成30°角。

已知该粒子在磁场中的运动轨迹与ON 只有一个交点，并从OM 上另一点射出磁场。

不计粒子重力。

则粒子离开磁场的出射点到两平面交线O 的距离为A ．2mv qBB ．3mv qBC ．2mv qBD ．4mv qB【答案】D 【解析】 【详解】 、粒子进入磁场做顺时针方向的匀速圆周运动，轨迹如图所示，根据洛伦兹力提供向心力，有2v qvB m R=解得mv R qB =根据轨迹图知22mvPQ R qB==， ∠OPQ =60°则粒子离开磁场的出射点到两平面交线O 的距离为42mvOP PQ qB==， 则D 正确，ABC 错误。

高考物理备考之临界状态的假设解决物理试题压轴突破训练∶培优篇含答案一、临界状态的假设解决物理试题1．如图所示，用长为L =0.8m 的轻质细绳将一质量为1kg 的小球悬挂在距离水平面高为H =2.05m 的O 点，将细绳拉直至水平状态无初速度释放小球，小球摆动至细绳处于竖直位置时细绳恰好断裂，小球落在距离O 点水平距离为2m 的水平面上的B 点，不计空气阻力，取g =10m/s 2求：(1)绳子断裂后小球落到地面所用的时间； (2)小球落地的速度的大小； (3)绳子能承受的最大拉力。

【答案】(1)0.5s(2)6.4m/s(3)30N 【解析】 【分析】 【详解】(1)细绳断裂后，小球做平抛运动，竖直方向自由落体运动，则竖直方向有212AB h gt =，解得2(2.050.8)s 0.5s 10t ⨯-==(2)水平方向匀速运动，则有02m/s 4m/s 0.5x v t === 竖直方向的速度为5m/s y v gt ==则2222045m/s=41m/s 6.4m/s y v v v =+=+≈(3)在A 点根据向心力公式得2v T mg m L-=代入数据解得24(1101)N=30N 0.8T =⨯+⨯2．如图所示，圆心为O、半径为r的圆形区域外存在匀强磁场，磁场方向垂直于纸面向外，磁感应强度大小为B。

P是圆外一点，OP=3r，一质量为m、电荷量为q（q>0）的粒子从P点在纸面内沿着与OP成60°方向射出（不计重力），求：(1)若粒子运动轨迹经过圆心O，求粒子运动速度的大小；(2)若要求粒子不能进入圆形区域，求粒子运动速度应满足的条件。

【答案】(1)3Bqr；(2)(332)vm≤+或(332)vm≥-【解析】【分析】【详解】(1)设粒子在磁场中做圆周运动的半径为R，圆心为O'，依图题意作出轨迹图如图所示：由几何知识可得：OO R'=()222(3)6sinOO R r rRθ'=+-解得3R r=根据牛顿第二定律可得2vBqv mR=解得3Bqrv=(2)若速度较小，如图甲所示：根据余弦定理可得()22211196sin r R R r rR θ+=+-解得1332R =+若速度较大，如图乙所示：根据余弦定理可得()22222296sin R r R r rR θ-=+-解得2332R =-根据BqRv m=得1(332)v m =+，2(332)v m =-若要求粒子不能进入圆形区域，粒子运动速度应满足的条件是(332)v m ≤+或(332)v m≥-3．如图所示，C ﹑D 两水平带电平行金属板间的电压为U ，A ﹑B 为一对竖直放置的带电平行金属板，B 板上有一个小孔，小孔在C ﹑D 两板间的中心线上，一质量为m ﹑带电量为＋q 的粒子（不计重力）在A 板边缘的P 点从静止开始运动，恰好从D 板下边缘离开，离开时速度度大小为v ０，则A ﹑B 两板间的电压为A ．20v 2m qU q-B ．2022mv qU q -C ．20mv qU q -D ．202mv qU q-【答案】A 【解析】 【分析】 【详解】在AB 两板间做直线加速，由动能定理得：2112AB qU mv =；而粒子在CD 间做类平抛运动，从中心线进入恰好从D 板下边缘离开，根据动能定理：220111222qU mv mv =-；联立两式可得：202AB mv qU U q-=；故选A.【点睛】根据题意分析清楚粒子运动过程是解题的前提与关键，应用动能定理、牛顿第二定律与运动学公式即可解题．4．如图所示，在竖直平面内的光滑管形圆轨道的半径为R （管径远小于R ），小球a 、b 大小相同，质量均为m ，直径均略小于管径，均能在管中无摩擦运动。

高考物理备考之临界状态的假设解决物理试题压轴突破训练∶培优 易错 难题篇附详细答案一、临界状态的假设解决物理试题1．如图所示，M 、N 为两块带等量异种电荷的平行金属板，两板间电压可取从零到某一最大值之间的各种数值。

静止的带电粒子带电荷量为＋q ，质量为m （不计重力），从点P 经电场加速后，从小孔Q 进入N 板右侧的匀强磁场区域，磁感应强度大小为B ，方向垂直于纸面向外，CD 为磁场边界上的一绝缘板，它与N 板的夹角θ＝45°，孔Q 到板的下端C 的距离为L ，当M 、N 两板间电压取最大值时，粒子恰垂直打在CD 板上，求：（1）两板间电压的最大值U m ；（2）CD 板上可能被粒子打中区域的长度s ； （3）粒子在磁场中运动的最长时间t m 。

【答案】（1）两板间电压的最大值m U 为222qB L m；（2）CD 板上可能被粒子打中的区域的长度x 为(22)L ； （3）粒子在磁场中运动的最长时间m t 为mqBπ。

【解析】 【分析】（1）粒子恰好垂直打在CD 板上，根据粒子的运动的轨迹，可以求得粒子运动的半径，由半径公式可以求得电压的大小；（2）当粒子的运动的轨迹恰好与CD 板相切时，这是粒子能达到的最下边的边缘，在由几何关系可以求得被粒子打中的区域的长度．（3）打在QE 间的粒子在磁场中运动的时间最长，均为半周期，根据周期公式即可求解。

【详解】（1）M 、N 两板间电压取最大值时，粒子恰垂直打在CD 板上，所以圆心在C 点，CH=QC=L ，故半径R 1=L ，又因211v qvB m R =2m 112qU mv =所以22m 2qB L U m=（2）设轨迹与CD 板相切于K 点，半径为R 2，在△AKC 中：22sin 45R R L ︒=- 所以2(21)R L =-即KC 长等于2(21)R L =-所以CD 板上可能被粒子打中的区域即为HK 的长度12(21)(22)x HK R R LL L -===-=﹣﹣ （3）打在QE 间的粒子在磁场中运动的时间最长，均为半周期：2mT qBπ=所以m 12m t T qBπ==【点睛】本题考查带电粒子在匀强磁场中的运动，要掌握住半径公式、周期公式，画出粒子的运动轨迹后，几何关系就比较明显了。

备战高考物理培优 易错 难题(含解析)之临界状态的假设解决物理试题及详细答案一、临界状态的假设解决物理试题1．如图所示，在光滑的圆锥顶用长为L 的细线悬挂一质量为m 的小球，圆锥顶角为2θ，当圆锥和球一起以角速度ω匀速转动时，球压紧锥面．()1此时绳的张力是多少？()2若要小球离开锥面，则小球的角速度至少为多少？【答案】（1）()22cos sin T mg m l θωθ=+（2）cos gl ωθ= 【解析】（1）小球此时受到竖直向下的重力mg ，绳子的拉力T ，锥面对小球的支持力N ，三个力作用，合力充当向心力，即合力2sin F m l ωθ= 在水平方向上有，sin cos T N ma F ma θθ-==，， 在竖直方向上：cos sin T N mg θθ+= 联立四个式子可得()22cos sin T mg m l θωθ=+（2）重力和拉力完全充当向心力时，小球对锥面的压力为零， 故有向心力tan F mg θ=，2sin F m l ωθ=，联立可得cos gl ωθ=，即小球的角速度至少为cos gl ωθ=；2．质量为m 2=2Kg 的长木板A 放在水平面上，与水平面之间的动摩擦系数为0.4；物块B （可看作质点）的质量为m 1=1Kg ，放在木板A 的左端，物块B 与木板A 之间的摩擦系数为0.2.现用一水平向右的拉力F 作用在木板A 的右端，让木板A 和物块B 一起向右做匀加速运动．当木板A 和物块B 的速度达到2 m/s 时，撤去拉力，物块B 恰好滑到木板A 的右端而停止滑动，最大静摩擦力等于动摩擦力，g=10m/s 2，求：（1）要使木板A 和物块B 不发生相对滑动，求拉力F 的最大值； （2）撤去拉力后木板A 的滑动时间； （3）木板A 的长度。

【答案】（1）18N （2）0.4s （3）0.6m 【解析】 【详解】（1）当木板A 和物块B 刚要发生相对滑动时，拉力达到最大 以B 为研究对象，由牛顿第二定律得1111m g m a μ=可得2112m/s a g μ==．再以整体为研究对象，由牛顿第二定律得212121 ))F m m g m m a μ-+=+（（ 故得最大拉力18F N =；（2）撤去F 后A 、B 均做匀减速运动，B 的加速度大小仍为1a ，A 的加速度大小为2a ，则 2121122)m m g m g m a μμ+-=（解得225m/s a =故A 滑动的时间220.45v t s s a === （3）撤去F 后A 滑动的距离22122m=0.4m 225v x a ==⨯B 滑动的距离22212m=1m 222v x a ==⨯故木板A 的长度210.6m L x x =-=．【点睛】解题的关键是正确对滑块和木板进行受力分析，清楚滑块和木板的运动情况，根据牛顿第二定律及运动学基本公式求解。

【物理】培优易错试卷临界状态的假设解决物理试题辅导专题训练含详细答案一、临界状态的假设解决物理试题1．如图所示，在光滑的圆锥顶用长为L 的细线悬挂一质量为m 的小球，圆锥顶角为2θ，当圆锥和球一起以角速度ω匀速转动时，球压紧锥面．()1此时绳的张力是多少？()2若要小球离开锥面，则小球的角速度至少为多少？【答案】（1）()22cos sin T mg m l θωθ=+（2）cos gl ωθ= 【解析】（1）小球此时受到竖直向下的重力mg ，绳子的拉力T ，锥面对小球的支持力N ，三个力作用，合力充当向心力，即合力2sin F m l ωθ= 在水平方向上有，sin cos T N ma F ma θθ-==，， 在竖直方向上：cos sin T N mg θθ+= 联立四个式子可得()22cos sin T mg m l θωθ=+（2）重力和拉力完全充当向心力时，小球对锥面的压力为零， 故有向心力tan F mg θ=，2sin F m l ωθ=，联立可得cos gl ωθ=，即小球的角速度至少为cos gl ωθ=；2．平面OM 和平面ON 之间的夹角为30°，其横截面（纸面）如图所示，平面OM 上方存在匀强磁场，磁感应强度大小为B ，方向垂直于纸面向外。

一带电粒子的质量为m ，电荷量为q （q >0）。

粒子沿纸面以大小为v 的速度从OM 的某点向左上方射入磁场，速度与OM 成30°角。

已知该粒子在磁场中的运动轨迹与ON 只有一个交点，并从OM 上另一点射出磁场。

不计粒子重力。

则粒子离开磁场的出射点到两平面交线O 的距离为A ．2mv qBB ．3mv qBC ．2mv qBD ．4mv qB【答案】D 【解析】 【详解】 、粒子进入磁场做顺时针方向的匀速圆周运动，轨迹如图所示，根据洛伦兹力提供向心力，有2v qvB m R=解得mv R qB =根据轨迹图知22mvPQ R qB==， ∠OPQ =60°则粒子离开磁场的出射点到两平面交线O 的距离为42mvOP PQ qB==， 则D 正确，ABC 错误。

培优 易错 难题临界状态的假设解决物理试题辅导专题训练含详细答案一、临界状态的假设解决物理试题1．如图所示，在光滑的圆锥顶用长为L 的细线悬挂一质量为m 的小球，圆锥顶角为2θ，当圆锥和球一起以角速度ω匀速转动时，球压紧锥面．()1此时绳的张力是多少？()2若要小球离开锥面，则小球的角速度至少为多少？【答案】（1）()22cos sin T mg m l θωθ=+（2）cos gl ωθ=【解析】（1）小球此时受到竖直向下的重力mg ，绳子的拉力T ，锥面对小球的支持力N ，三个力作用，合力充当向心力，即合力2sin F m l ωθ= 在水平方向上有，sin cos T N ma F ma θθ-==，， 在竖直方向上：cos sin T N mg θθ+= 联立四个式子可得()22cos sin T mg m l θωθ=+（2）重力和拉力完全充当向心力时，小球对锥面的压力为零， 故有向心力tan F mg θ=，2sin F m l ωθ=，联立可得cos gl ωθ=，即小球的角速度至少为cos gl ωθ=；2．如图所示，用长为L =0.8m 的轻质细绳将一质量为1kg 的小球悬挂在距离水平面高为H =2.05m 的O 点，将细绳拉直至水平状态无初速度释放小球，小球摆动至细绳处于竖直位置时细绳恰好断裂，小球落在距离O 点水平距离为2m 的水平面上的B 点，不计空气阻力，取g =10m/s 2求：(1)绳子断裂后小球落到地面所用的时间； (2)小球落地的速度的大小； (3)绳子能承受的最大拉力。

【答案】(1)0.5s(2)6.4m/s(3)30N 【解析】 【分析】 【详解】(1)细绳断裂后，小球做平抛运动，竖直方向自由落体运动，则竖直方向有212AB h gt =，解得2(2.050.8)s 0.5s 10t ⨯-==(2)水平方向匀速运动，则有02m/s 4m/s 0.5x v t === 竖直方向的速度为5m/s y v gt ==则2222045m/s=41m/s 6.4m/s y v v v =+=+≈(3)在A 点根据向心力公式得2v T mg m L-=代入数据解得24(1101)N=30N 0.8T =⨯+⨯3．平面OM 和平面ON 之间的夹角为30°，其横截面（纸面）如图所示，平面OM 上方存在匀强磁场，磁感应强度大小为B ，方向垂直于纸面向外。