苏教版七上2.6有理数的乘法与除法2
- 格式:ppt
- 大小:461.00 KB
- 文档页数:13

2.6 有理数的乘法与除法(课时2)【教学目标】知识与技能:(1)掌握有理数的除法法则,并熟练运用除法法则.(2)体会乘法与除法的辨证关系及化归思想.过程与方法:经历除法法则的归纳过程,培养学生的观察、归纳、概括和运算能力.情感态度与价值观:让学生感知数学知识具有普遍联系性、相互转化性.【重难点】重点:(1)理解有理数除法法则,能正确熟练的进行有理数的除法运算.(2)能熟练的进行有理数的乘除混合运算.难点:理解商的符号及其绝对值与被除数和除数的关系.【教学过程】活动一:复习回顾,导入新课1.前面我们学习了有理数的乘法,那么有理数有除法吗?如何进行有理数的除法运算呢?开门见山,直接引出本节知识的核心.投影显示:(-12)÷(-3)=?2.回忆小学里乘法与除法互为逆运算,并提问:被除数、除数、商之间的关系:学生回答:被除数=除数×商所以我们只需找到-12=(-3)×?就能找到商是多少.学生很容易知道-12=(-3)×4. 在学习过程中,一定要抓住被除数=除数×商,从而得到(-12)÷(-3)=4.活动二:实践探究,交流新知【探究1】有理数的除法法则教师提问:怎样计算(-70)÷7呢?学生小组讨论,教师提示:根据除法是乘法的逆运算,即求一个数,与7相乘得-70,因为(-10)×7=-70,所以(-70)÷7=-10.另一方面,()170=107⨯--,所以有()()1707=7010⎛⎫÷⨯ ⎪⎝⎭--- 教师提问:观察上面的式子,你能发现什么?学生思考,讨论交流,师生共同归纳:有理数的除法法则:除以一个数不等于0的数,等于乘这个数的倒数.例1 计算:(1)(-15)÷(-3);(2)12÷(-14);(3)(-0.75)÷(0.25).解:(1)(-15)÷(-3)=+(15÷3)=5;(2)12÷(-14)=-(12÷14)=-48; (3)(-0.75)÷(0.25)=-(0.75÷0.25)=-3.处理方式:学生自主完成,老师巡视.请3位学生板书.教师提问:有理数的除法运算中,怎样确定商的符号?学生思考,师生共同总结:注意先确定运算的符号.两数相除,同号得正,异号得负并把绝对值相除.0除以任何不等于0的数,都得0.【探究2】有理数的乘除混合运算例2 计算:(1)-2.5÷58×(-14);(2)(-47)÷(-314)×(-112). 解:(1)原式=-52×85×(-14)=52×85×14=1; (2)原式=(-47)×(-143)×(- 32)=-(47×143×32)=-4. 处理方式:教师板演,并总结:有理数的乘除混合运算,先把除法转化为乘法,再统一计算.【当堂反馈】1.如果,那么a 是().A.正数B.负数 C .非负数 D .非正数2.如果两个非零数互为相反数,那么下列说法中错误的是().A.它们的和一定为零B.它们的差一定是正数C.它们的积一定是负数 D .它们的商一定等于一l3.若0≠mn ,则 nn m m+的值不可能是( ). A.0 B.l C. 2 D .-24.计算:(1)(-12)÷(-3); (2)312 ÷(611-); (3))53(8543-÷÷-; (4)[()()(12787431-+--)] ÷(87-); (5)1(48)8(25)()5-÷÷-⨯-;(6)355(2)514÷-⨯.【课后小结】 本节课我们要注意在运用运算律进行简化计算时,要仔细审题,看看能否用运算律简便而准确地化简式子,可以将式子进行适当变形,也可用逆向分配律,学会运用技巧解决复杂的计算问题.【教学反思】。

课题: 2.6有理数的乘法与除法(2)【学习目标】1. 会使用乘法运算律实行有理数的乘法运算2.理解倒数的概念,会求非零有理数的倒数【重点难点】重点:有理数乘法运算律和倒数的概念难点:有理数乘法运算律的熟练使用【自主学习】读一读:阅读欣赏课本P 43-P 44想一想:1. 小学里学过的乘法有哪些运算律?2.在有理数范围内这些运算律是否还成立? _ _3.满足什么条件的两个数互为倒数?0有倒数吗? _练一练:1.(-6)×(-7)= (-7)×(-6)=2×(-9)= (-9)×2=2. [2×(-3)]×(-4)= ×(-4)=2×[(-3)×(-4)]= 2× =3.(-2)×[(-3)+5]= (-2)× =(-2)×(-3)+(-2)×5= + =4.31×3= (-37)×(-73)= 5.14-的倒数是 ; -8的倒数是 .6. 假如a ×b=1,且a=23-,那么b= .【新知归纳】1. 有理数乘法运算律:乘法交换律:乘法结合律:乘法分配律:2. 乘积为 的两个数互为倒数,其中一个数是另一个数的倒数.【例题教学】例 1 计算:(1)()713135.767⨯-⨯ (2)4×(-8.99)×(-2.5)(3)(21-65+127)×(-36) (4)()8161519-⨯例 2 计算:(1)(-7)×(-722)+19×(-722)-5×(-722)(2)(-10.8)×(-9.25)-(-0.75)×10.8【课堂检测】1.使用运算律填空.(1)-2×(-3)=(-3)×(_______)(2)[(-3)×2.5]×(-4)=(-3)×[(______)×(______)](3)(-5)×[(-2)+(-3)]=(-5)×(____)+(____)×(-3)2.211的倒数是__________,-2.5的倒数是__________,3--的倒数是___________. 3. 倒数等于本身数是___________.4.计算:(1)(−4)×5×(−0.25) (2)(79-56-718)×(-36)(3)(-4)×57 - 4×43 (4) 36727199⨯⎪⎭⎫ ⎝⎛-【课后巩固】1. 6的倒数是__________,322-的倒数是__________,5.2--的倒数是___________. 2. 5的相反数的倒数是__________,-4.3的绝对值的倒数是_________.3. 若干个不等于0的有理数相乘,积的符号( )A.由因数的个数决定B.由正因数的个数决定C.由负因数的个数决定D.由负因数和正因数的个数的差决定4.计算:(1)(-4)×(-18.36)×2.5 (2) 0.125×(-2)×(-8)(3)()()11360234--+⨯- (4)17(3)(0.125)0.125(4)88-⨯--⨯-(5) 111(5)(7)12(7)(7)(7)333-⨯++⨯-+-⨯+(6)54 ×(-135)-(-53)×(-135)-135×(-153)。


七年级数学上册第2章有理数2.6 有理数的乘法与除法第2课时有理数的乘法运算律同步练习(新版)苏科版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(七年级数学上册第2章有理数2.6 有理数的乘法与除法第2课时有理数的乘法运算律同步练习(新版)苏科版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为七年级数学上册第2章有理数2.6 有理数的乘法与除法第2课时有理数的乘法运算律同步练习(新版)苏科版的全部内容。
第2课时有理数乘法运算律知识点 1 有理数乘法运算律1.在算式-27×24+16×24-79×24=(-27+16-79)×24中运用了()A.加法交换律 B.加法结合律C.乘法结合律 D.乘法分配律2.计算-错误!×错误!×错误!的结果是( )A.1 B.-112C.1错误! D.4错误!3.2017·滨湖区期中计算(1-错误!+错误!+错误!)×(-12)时,运用哪种运算律可以避免通分( )A.乘法分配律 B.乘法结合律C.乘法交换律 D.乘法结合律和交换律4.下列计算正确的是( )A。
错误!×错误!=-8+6+1=-1B。
错误!×错误!=12+8+24=44C。
错误!×错误!=9D.-5×2×错误!=-205.在横线上写出下列变化中所运用的运算律:(1)3×(-2)×(-5)=3×[(-2)×(-5)]________;(2)48×(错误!-2错误!)=48×错误!-48×错误!________.6.填空:错误!×错误!=错误!×________+错误!×________=________+________=________.7.计算:(-4。

七年级数学上册第二章有理数 2.6 有理数的乘法与除法运用乘法交换律、结合律简化运算素材 (新版)苏科版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(七年级数学上册第二章有理数 2.6 有理数的乘法与除法运用乘法交换律、结合律简化运算素材(新版)苏科版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为七年级数学上册第二章有理数2.6 有理数的乘法与除法运用乘法交换律、结合律简化运算素材 (新版)苏科版的全部内容。
运用乘法交换律、结合律简化运算难易度:★★关键词:有理数答案:(1)乘法交换律:两个数相乘,交换因数的位置,积不变。
即ab=ba。
(2)乘法结合律:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积不变。
即(ab)c=a(bc)。
【举一反三】典例:计算思路导引:一般来说,此类问题应仔细观察题目中的数据,找到两两相结合的数据后交换位置。
,原式标准答案:—3以上就是本文的全部内容,可以编辑修改。
高尔基说过:“书是人类进步的阶梯。
”我希望各位朋友能借助这个阶梯不断进步。
物质生活极大丰富,科学技术飞速发展,这一切逐渐改变了人们的学习和休闲的方式。
很多人已经不再如饥似渴地追逐一篇文档了,但只要你依然有着这样一份小小的坚持,你就会不断成长进步,当纷繁复杂的世界牵引着我们疲于向外追逐的时候,阅读一文或者做一道题却让我们静下心来,回归自我。
用学习来激活我们的想象力和思维,建立我们的信仰,从而保有我们纯粹的精神世界,抵御外部世界的袭扰。
The above is the wholecontent of this article, Gorkysaid: "the bookis the ladder of human progress." I hopeyou can make progress with the help of this ladder.Material life is extremel y rich, science and technology are developing rapidly,all of which gradually change the way of people's study andleisure. Many people are no longer eager to pursue a document, b utas long as you still have such a small persistence, you willcontinueto grow and progress. When the complexworld leads us to chaseout, reading an article or doing aproblem makes us calm down andreturn to ourselves. Withlearning, we can activateour imagination and thinking,establish our belief, keep our pure spiritual worldandresist the attack of the external world.。

2.6有理数的乘法与除法(2)1.若四个有理数相乘,积为负数,则负因数的个数是( )A .1B .2C .3D .1或32.下列计算正确的是( )A .(-5)×(-4)×(-2)×(-2)=5×4×2×2=80 B .(-12)×(13-14-1)=-4+3+1=0 C .(-9)×5×(-4)×0=9×5×4=180 D .(-2)×5-2×(-1)-(-2)×2=(-2)×(5+1-2)=-83..在算式(57)2436247924(573679)24-⨯+⨯-⨯=-+-⨯中,这是应用了( ) A .加法交换律B .乘法交换律C .乘法结合律D .乘法分配律 4.算式可以化为( ) A . B . C . D .5.下列计算(-55)×99+(-44)×99-99正确的是( )A .原式=99×(-55-44)=-9801B .原式=99×(-55-44+1)=-9702C .原式=99×(-55-44-1)=-9900D .原式=99×(-55-44-99)=-19602 6.利用乘法运算律填空:(1)( 1.25)3(8)( 1.25)________3-⨯⨯-=-⨯⨯;(2)1[2(4)]2[________]4⎛⎫⨯-⨯+=⨯ ⎪⎝⎭; (3)1271________________9⎛⎫⨯-=+ ⎪⎝⎭.7.规定一种新运算:1a b ab a b ∆=--+,请比较(3)4-∆____4(3)∆-.(填“>”“<”或“=”) 8. 写出下面每一步计算根据的运算法则或运算律: (4)(8)( 2.5)(125)-⨯+⨯-⨯-48 2.5125=-⨯⨯⨯( )4 2.58125=-⨯⨯⨯( )(4 2.5)(8125)=-⨯⨯⨯()10100010000=-⨯=-9.运用简便方法计算:(1)157()(12)2612+-⨯-; (2)337()(4)0.751144⨯--⨯--⨯.(3)991718×(﹣9); (4)(﹣5)×(﹣367)+(﹣7)×(﹣367)+12×(﹣367)10.学习有理数的乘法后,老师给同学们这样一道题目:计算:492425×(-5),看谁算的又快又对,有两位同学的解法如下:聪聪;原式=-124925×5=-12495-24945;明明:原式=(49+2425)×(-5)=49×(-5)+2425×(-5)=-24945,(1)对于以上两种解法,你认为谁的解法较好?(2)上面的解法对你有何启发,你认为还有更好的方法吗?如果有,请把它写出来;(3)用你认为最合适的方法计算:391516×(-8).11.计算:,这一步用到的运算律是()A.乘法结合律B.乘法交换律C.分配律D.乘法交换律和乘法结合律12.(-758)×8可化为()A.-7×58×8 B.-7×8+58C.-7×8+58×8 D.-7×8-58×813.下列说法正确的是()A.负数没有倒数B.﹣1的倒数是﹣1C.任何有理数都有倒数D.正数的倒数比自身小14.在2-,3,4,5-这四个数中,任取两个数相乘,所得的乘积最小是.15. 计算:(-60)×(34+56)=________.16.写出下列运算中每一步所依据的运算律或法则:(-0.4)×(-0.8)×(-1.25)×2.5=-(0.4×0.8×1.25×2.5)(第一步)=-(0.4×2.5×0.8×1.25)(第二步)=-[(0.4×2.5)×(0.8×1.25)](第三步)=-(1×1)=-1.第一步:____________;第二步:____________;第三步:____________.17.已知||3x=,2y=且0xy<,则x y-=.18.计算:20199920202020⨯=.19.用简便方法计算:(1)7115187⎛⎫⎛⎫-⨯⨯-⎪ ⎪⎝⎭⎝⎭;(2)124105375⎛⎫-+-⨯⎪⎝⎭;(3)7833.51272⎛⎫⎛⎫-⨯⨯-⨯-⎪ ⎪⎝⎭⎝⎭;(4)25(128)2511425141⨯-+⨯-⨯;(5)179(19)19⨯-;(6)121|12|234⎛⎫-+-⨯-⎪⎝⎭.20.将2018减去它的12,再减去余下的13,再减去余下的14……以此类推,直至减去余下的12018,最后的得数是多少?21.已知有理数a,b,c满足||||||1a b ca b c++=,求||abcabc的值.22.把-1,+2,-3,+4,-5,+6,-7,+8,-9填入下面的方框内,使得每行.每列.每条对角线上的三个数都满足:(1)三数乘积都是负数;(2)三数绝对值的和都相等.。


苏教版七年级数学目录七年级数学教材的好坏决定了教学的质量,教材目录是什么呢?下面小编给大家分享一些苏教版七年级数学上下册目录,大家快来跟小编一起欣赏吧。
苏教版七年级数学上册目录第一章我们与数学同行1.1 生活数学1.2 活动思考第二章有理数2.1 比0小的数2.2 数轴2.3 绝对值与相反数2.4 有理数的加法与减法2.5 有理数的乘法与除法2.6 有理数的乘方2.7 有理数的混合运算第三章用字母表示数3.1 字母表示数3.2 代数式3.3 代数式的值3.4 合并同类项3.5 去括号第四章一元一次方程4.1 从问题到方程4.2 解一元一次方程4.3 用方程解决问题第五章走进图形世界5.1 丰富的图形世界5.2 图形的变化5.3 展开与折叠5.4 从三个方向看第六章平面图形的认识(一)6.1 线段射线直线6.2 角6.3 余角补角对顶角6.4 平行6.5 垂直苏教版七年级数学下册目录第七章平面图形的认识(二)7.1 探索直线平行的条件7.2 探索平行线的性质7.3 图形的平移7.4 认识三角形7.5 三角形的内角和第八章幂的运算8.1 同底数幂的乘法8.2 幂的乘方与积的乘方8.3 同底数幂的除法第九章从面积到乘法公式9.1 单项式乘单项式9.2 单项式乘多项式9.3 多项式乘多项式9.4 乘法公式9.5 单项式乘多项式法则的再认识------因式分解(一)9.6 乘法公式的再认识------因式分解(二)第十章二元一次方程10.1 二元一次方程10.2 二元一次方程组10.3 解二元一次方程组10.4 用方程组解决问题第十一章图形的全等11.1 全等图形11.2 全等三角形11.3 探索三角形全等的条件第十二章数据在我们身边12.1 普查与抽样调查12.2 统计图的选用12.3 频数分布表和频数分布图第十三章感受概率13.1 确定与不确13.2 可能性。

2.6 有理数的乘法与除法一.选择题(共10小题)1.计算:(﹣3)×5的结果是()A.﹣15B.15C.﹣2D.22.﹣2的倒数是()A.﹣B.C.2D.﹣23.下列各组数中互为倒数的是()A.﹣5和﹣B.﹣3和C.0.125和﹣8D.和﹣24.已知两个有理数a,b,如果ab<0且a+b>0,那么()A.a>0,b>0B.a<0,b>0C.a、b同号D.a、b异号,且正数的绝对值较大5.(﹣21)÷7的结果是()A.3B.﹣3C.D.6.﹣|﹣|的负倒数是()A.B.C.D.7.商店降价销售某种商品,每件降价5元,售出60件后,与原价销售同样数量的商品相比,销售额的变化情况算式表示为()A.(﹣5)×60B.5×60C.5×(﹣60)D.(﹣5)×(﹣60)8.若ab>0,a+b<0,则()A.a、b都为负数B.a、b都为正数C.a、b中一正一负D.以上都不对9.3x﹣12的值与互为倒数,则x的值为()A.3B.﹣3C.5D.﹣510.我们把2÷2÷2记作2③,(﹣4)÷(﹣4)记作(﹣4)②,那么计算9×(﹣3)④的结果为()A.1B.3C.D.二.填空题(共6小题)11.﹣2019的倒数是.12.在﹣3、4、﹣2、5四个数中,任意两个数之积的最小值为.13.若|a|=3,|b|=5,且a、b异号,则a•b=.14.下面是一种算法:输入任意一个数x,都是“先乘以2,再减去3”,进行第1次这样的运算,结果为y1,再对y1实施同样的运算,称为第2次运算,结果为y2,这样持续进行,要使第n次运算结果为0,即y n=0,则最初输入的数应该是.(用含有n的代数式表示).15.P为正整数,现规定P!=P(P﹣1)(P﹣2)…×2×1.若m!=24,则正整数m=.16.用f(n)表示组成n的数字中不是零的所有数字乘积,例如:f(5)=5,f(29)=18,f(207)=14.则f(1)+f(2)+……+f(200)=.三.解答题(共4小题)17.若a、b互为相反数,c、d互为倒数,m的绝对值为2.(1)直接写出a+b,cd,m的值;(2)求m+cd+的值.18.已知|a|=10,|b|=6,ab<0.求:(1)4a﹣2b的值;(2)ab的值.19.如图,A,B两点在数轴上对应的数分别为a,b,且点A在点B的左边,|a|=10,a+b =80,ab<0.(1)求出a,b的值;(2)现有一只电子蚂蚁P从点A出发,以3个单位长度/秒的速度向右运动,同时另一只电子蚂蚁Q从点B出发,以2个单位长度/秒的速度向左运动.①设两只电子蚂蚁在数轴上的点C相遇,求出点C对应的数是多少?②经过多长时间两只电子蚂蚁在数轴上相距20个单位长度?20.在1,﹣2,3,﹣4,﹣5中任取两个数相乘,最大的积是a,最小的积是b.(1)求ab的值;(2)若|x﹣a|+|y+b|=0,求(﹣x﹣y)•y的值.答案与解析一.选择题(共10小题)1.计算:(﹣3)×5的结果是()A.﹣15B.15C.﹣2D.2【分析】根据正数与负数相乘的法则得(﹣3)×5=﹣15;【解答】解:(﹣3)×5=﹣15;故选:A.【点评】本题考查有理数的乘法;熟练掌握正数与负数的乘法法则是解题的关键.2.﹣2的倒数是()A.﹣B.C.2D.﹣2【分析】根据乘积是1的两个数叫做互为倒数解答.【解答】解:∵(﹣2)×(﹣)=1,∴﹣2的倒数是﹣.故选:A.【点评】本题考查了倒数的定义,是基础题,熟记概念是解题的关键.3.下列各组数中互为倒数的是()A.﹣5和﹣B.﹣3和C.0.125和﹣8D.和﹣2【分析】直接利用互为倒数的定义分析得出答案.【解答】解:A、﹣5和﹣,两数之积为1,是互为倒数,故此选项正确;B、﹣3和,两数之积为﹣1,不是互为相反数,故此选项错误;C、0.125和﹣8,两数之积为﹣1,不是互为相反数,故此选项错误;D、和﹣2,两数之积为﹣1,不是互为相反数,故此选项错误;故选:A.【点评】此题主要考查了倒数,正确把握倒数的定义是解题关键.4.已知两个有理数a,b,如果ab<0且a+b>0,那么()A.a>0,b>0B.a<0,b>0C.a、b同号D.a、b异号,且正数的绝对值较大【分析】先由有理数的乘法法则,判断出a,b异号,再用有理数加法法则即可得出结论.【解答】解:∵ab<0,∴a,b异号,∵a+b>0,∴正数的绝对值较大,故选:D.【点评】此题主要考查了有理数的加法和乘法法则,熟记法则是解本题的关键.5.(﹣21)÷7的结果是()A.3B.﹣3C.D.【分析】根据有理数的除法法则计算即可.【解答】解:原式=﹣3,故选:B.【点评】本题考查有理数的除法法则,属于基础题.6.﹣|﹣|的负倒数是()A.B.C.D.【分析】根据相反数,倒数的定义,负倒数是相反数的倒数.【解答】解:﹣|﹣|=﹣,﹣的负倒数是.故选:B.【点评】主要考查相反数,倒数的概念.相反数的定义:只有符号不同的两个数互为相反数,0的相反数是0;倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数.7.商店降价销售某种商品,每件降价5元,售出60件后,与原价销售同样数量的商品相比,销售额的变化情况算式表示为()A.(﹣5)×60B.5×60C.5×(﹣60)D.(﹣5)×(﹣60)【分析】根据一件减少的销售额×件数=售出60件后销售额减少量,列式计算.【解答】解:依题意,每售出一件,销售额减少了5元,则售出60件后,与原价销售同样数量的商品相比,销售额的变化情况算式表示为(﹣5)×60.故选:A.【点评】本题考查了乘法在生活中的应用.熟知负数的意义是解答本题的关键.8.若ab>0,a+b<0,则()A.a、b都为负数B.a、b都为正数C.a、b中一正一负D.以上都不对【分析】根据有理数的加法,有理数的乘法,可得答案【解答】解:∵ab>0,∴a、b同时为正数或同时为负数,又∵a+b<0,∴a、b同时为同时为负数故选:A.【点评】本题考查了有理数的乘法,熟记法则并根据法则计算是解题关键.9.3x﹣12的值与互为倒数,则x的值为()A.3B.﹣3C.5D.﹣5【分析】由倒数的定义得到:(3x﹣12)×(﹣)=1,通过解该方程可以求得x的值.【解答】解:∵代数式3x﹣12的值与﹣互为倒数,∴(3x﹣12)×(﹣)=1,即﹣x+4=1,解得,x=3.故选:A.【点评】考查了倒数的定义:乘积是1的两数互为倒数.10.我们把2÷2÷2记作2③,(﹣4)÷(﹣4)记作(﹣4)②,那么计算9×(﹣3)④的结果为()A.1B.3C.D.【分析】根据新定义列出算式9×[(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)],再根据有理数的乘除运算法则计算可得.【解答】解:9×(﹣3)④=9×[(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)]=9×=1,故选:A.【点评】本题主要考查有理数的除法,解题的关键是理解并掌握新定义及有理数乘除运算法则.二.填空题(共6小题)11.﹣2019的倒数是.【分析】直接利用倒数的定义进而得出答案.【解答】解:﹣2019的倒数是.故答案为:.【点评】此题主要考查了倒数,正确把握倒数的定义是解题关键.12.在﹣3、4、﹣2、5四个数中,任意两个数之积的最小值为﹣15.【分析】首先求出任意两个数的积是多少,然后根据有理数的大小比较法则比较即可.【解答】解:(﹣3)×4=﹣12,(﹣3)×(﹣2)=6,(﹣3)×5=﹣15;4×(﹣2)=﹣8,4×5=20,(﹣2)×5=﹣10,∵﹣15<﹣12<﹣10<﹣8<6<20,∴在﹣3、4、﹣2、5四个数中,任意两个数之积的最小值为﹣15.故答案为:﹣15.【点评】此题主要考查了有理数的乘法的运算方法,要熟练掌握.13.若|a|=3,|b|=5,且a、b异号,则a•b=﹣15.【分析】根据绝对值的性质可知;a=±3,b=±5,由a、b异号确定出a、b的取值情况,然后可求得a•b的值.【解答】解:∵|a|=3,|b|=5,∴a=±3,b=±5.∵a、b异号,∴a=3,b=﹣5或a=﹣3,b=5.∴ab=﹣15.故答案为:﹣15.【点评】本题主要考查的是绝对值、有理数的乘法,根据题意确定出a、b的取值情况是解题的关键.14.下面是一种算法:输入任意一个数x,都是“先乘以2,再减去3”,进行第1次这样的运算,结果为y1,再对y1实施同样的运算,称为第2次运算,结果为y2,这样持续进行,要使第n次运算结果为0,即y n=0,则最初输入的数应该是3﹣.(用含有n的代数式表示).【分析】根据题意列出式子即可.【解答】解:根据题意得:最初输入的数应该是3﹣,故答案为:3﹣【点评】此题考查了有理数的乘法,减法,熟练掌握运算法则是解本题的关键.15.P为正整数,现规定P!=P(P﹣1)(P﹣2)…×2×1.若m!=24,则正整数m=4.【分析】根据规定p!是从1,开始连续p个整数的积,即可.【解答】解:∵P!=P(P﹣1)(P﹣2)…×2×1=1×2×3×4×…×(p﹣2)(p﹣1),∴m!=1×2×3×4×…×(m﹣1)m=24,∵1×2×3×4=24,∴m=4,故答案为:4.【点评】此题是有理数的乘法,主要考查了新定义的理解,理解新定义是解本题的关键.16.用f(n)表示组成n的数字中不是零的所有数字乘积,例如:f(5)=5,f(29)=18,f(207)=14.则f(1)+f(2)+……+f(200)=2116.【分析】根据题意可以得到规律:一位数结果为个位数,两位数结果为十位数×个位数,三位数为百位数×个位数.据此规律解决此题即可.【解答】解:f(1)+f(2)+f(3)+…+f(200)=(1+2+3…+9)+1×(1+2+3…+9)+2×(1+2+3…+9)+3×(1+2+3…+9)+…+9×(1+2+3…+9)+(1+2+3…+9+1)=(1+2+3…+9)×(1+1+2+3…+9)+46=45×46+46=2116.故答案为:2116.【点评】本题考查了数字变化类问题,解题的关键是仔细地观察题目并从中总结规律,利用总结的规律进行计算即可.三.解答题(共4小题)17.若a、b互为相反数,c、d互为倒数,m的绝对值为2.(1)直接写出a+b,cd,m的值;(2)求m+cd+的值.【分析】(1)根据互为相反数的和为0,互为倒数的积为1,绝对值的意义,即可解答;(2)分两种情况讨论,即可解答.【解答】解:(1)∵a、b互为相反数,c、d互为倒数,m的绝对值为2,∴a+b=0,cd=1,m=±2.(2)当m=2时,m+cd+=2+1+0=3;当m=﹣2时,m+cd+=﹣2+1+0=﹣1.【点评】本题考查了倒数、相反数、绝对值,解决本题的关键是熟记倒数、相反数、绝对值的意义.18.已知|a|=10,|b|=6,ab<0.求:(1)4a﹣2b的值;(2)ab的值.【分析】(1)先根据绝对值的性质得出a,b的值,再由ab<0知a,b异号,从而确定a,b的值,代入计算可得;(2)将以上所得a,b的值代入计算即可得.【解答】解:(1)∵|a|=10,|b|=6,∴a=±10,b=±6,又∵ab<0,∴a=10,b=﹣6或a=﹣10,b=6,当a=10,b=﹣6时,4a﹣2b=40+12=52;当a=﹣10,b=6时,4a﹣2b=﹣40﹣12=﹣52;综上,4a﹣2b的值为±52;(2)当a=10,b=﹣6时,ab=﹣60;当a=﹣10,b=6时,ab=﹣60;综上,ab=﹣60.【点评】本题主要考查有理数的乘法,解题的关键是掌握绝对值的性质与有理数的乘法法则.19.如图,A,B两点在数轴上对应的数分别为a,b,且点A在点B的左边,|a|=10,a+b =80,ab<0.(1)求出a,b的值;(2)现有一只电子蚂蚁P从点A出发,以3个单位长度/秒的速度向右运动,同时另一只电子蚂蚁Q从点B出发,以2个单位长度/秒的速度向左运动.①设两只电子蚂蚁在数轴上的点C相遇,求出点C对应的数是多少?②经过多长时间两只电子蚂蚁在数轴上相距20个单位长度?【分析】(1)根据题意可以a、b的符号相反、可得a=﹣10,根据a+b=80可得b的值,本题得以解决;(2)①根据题意可以求得两只电子蚂蚁在数轴上的点C相遇是点C对应的数值;②根据题意和分类讨论的数学思想可以解答本题.【解答】解:(1)∵A,B两点在数轴上对应的数分别为a,b,且点A在点B的左边,|a|=10,a+b=80,ab<0,∴a=﹣10,b=90,即a的值是﹣10,b的值是90;(2)①由题意可得,点C对应的数是:90﹣[90﹣(﹣10)]÷(3+2)×2=90﹣100÷5×2=90﹣40=50,即点C对应的数为:50;②设相遇前,经过m秒时间两只电子蚂蚁在数轴上相距20个单位长度,[90﹣(﹣10)﹣20]÷(3+2)=80÷5=16(秒),设相遇后,经过n秒时间两只电子蚂蚁在数轴上相距20个单位长度,[90﹣(﹣10)+20]÷(3+2)=120÷5=24(秒),由上可得,经过16秒或24秒的时间两只电子蚂蚁在数轴上相距20个单位长度.【点评】本题考查有理数的乘法、绝对值、数轴、有理数的加法,解答本题的关键是明确题意,找出所求问题需要的条件,利用分类讨论的数学思想解答.20.在1,﹣2,3,﹣4,﹣5中任取两个数相乘,最大的积是a,最小的积是b.(1)求ab的值;(2)若|x﹣a|+|y+b|=0,求(﹣x﹣y)•y的值.【分析】(1)根据有理数的乘法法则得出a,b的值,代入计算可得;(2)将a,b的值代入|x﹣a|+|y+b|=0,根据非负数的性质得出x,y的值,继而代入计算可得.【解答】解:(1)根据题意知a=(﹣4)×(﹣5)=20,b=3×(﹣5)=﹣15,所以ab=20×(﹣15)=﹣300;(2)由题意知|x﹣20|+|y﹣15|=0,则x﹣20=0且y﹣15=0,解得x=20,y=15,∴(﹣x﹣y)•y=(﹣20﹣15)×15=﹣35×15=﹣525.【点评】本题主要考查有理数的乘法,解题的关键是熟练掌握有理数的乘法法则和绝对值的性质.。

第二章有理数2.6有理数的乘法与除法(第一二课时)一、单选题1.计算:(−3)×9的结果等于()A.−27B.−6C.27D.6【详解】解:(−3)×9=-27故选A2.有理数a、b、c满足a+b+c>0,且abc<0,则a、b、c中正数有()个.A.0B.1C.2D.3【详解】∵有理数a、b、c满足a+b+c>0,且abc<0,∴a,b,c中负数有1个,正数有2个.故选C.3.有理数,在数轴上的位置如图所示,下面结论正确的是()A.−<0B.B>0C.+>0D.|U>|UA.1B.−1C.±1D.±1和0A.±3B.−3C.3D.±5【详解】解:∵|a|=1,|b|=4,∴a=±1,b=±4,∵ab<0,∴a+b=1-4=-3或a+b=-1+4=3,故选A.6.观察算式(−4)×17×(−25)×14,在解题过程中,能使运算变得简便的运算律是()A.乘法交换律B.乘法结合律C.乘法交换律和结合律D.乘法分配律4A.−14×43−38−112B.−14×43−38×43−112×43C.−1443841124D.−1443841124A.(3﹣412)×2=3﹣412×2B.﹣4×(﹣7)×(﹣125)=﹣(4×125×7)C.91819×16=(10﹣119)×16=160﹣1619D.[3×(﹣25)]×(﹣2)=3×[(﹣25)×(﹣2)]9.已知|U=5,|U=2,且+<0,则B的值是________.【详解】解:∵|a|=5,|b|=2,∴a=±5,b=±2,∵a+b<0,∴a=-5时,b=2或-2,ab=(-5)×2=-10,ab=(-5)×(-2)=10,a=5不符合.综上所述,ab的值为10或-10.故答案为10或-10.10.在数-5,-3,-1,2,4,6中任取三个相乘,所得的积中最大的是___.【详解】解:要想所得的积中最大,积必须为正而且所选数字绝对值较大,可选2,4,6相乘或-5,-3,6相乘,∵2×4×6=48,-5×(-3)×6=90,故答案为:90.三、解答题11.计算:78×(﹣3)+(﹣11)×(﹣3)+(﹣33)×3=_________.(1)(−2)×54×(−910)×(−23)(2)(-6)×5×(−76)×27;(3)(-4)×7×(-1)×(-0.25);(4)(−5831(4)(−524)×815×(−32)×14=524×815×32×14=124.提升篇一、单选题13.对有理数a,b,规定运算如下:a※b=a+ab,则-2※3的值为()A.-10B.-8C.-6D.-4【详解】解:由题可知-2※3=-2+(-2)×3=-2-6=-8故选B.14.六个整数的积⋅⋅⋅⋅⋅=−36,、、、、、互不相等,则++++ +=().A.0B.4C.6D.8【详解】解:∵-36=(-1)×1×(-2)×2×(-3)×3,∴这六个互不相等的整数是-1、1、-2、2、-3、3,∴a+b+c+d+e+f=(-1)+1+(-2)+2+(-3)+3=0.故选A.15.若2018×63=p,则2018×64的值可表示为()A.p+1B.p+63C.p+2018D.6364p【详解】∵2018×63=p,∴2018×64=2018×(63+1)=2018×63+2018=p+2018故选C.16.如果有4个不同的正整数a、b、c、d满足(2019﹣a)(2019﹣b)(2019﹣c)(2019﹣d)=9,那么a+b+c+d的值为()A.0B.9C.8048D.8076【详解】解:∵a、b、c、d是四个不同的正整数,∴四个括号内的值分别是:±1,±3,∴2019+1=2020,2019﹣1=2018,2019+3=2022,2019﹣3=2016,∴a+b+c+d=2020+2018+2022+2016=8076.故选D.二、填空题17.用h表示1×2×3×⋯×,例1995!=1×2×3×⋯×1995,那么1!+2!+3!+⋯+ 2020!的个位数字是_____________.【详解】1!=1,2!=1×2=2,3!=1×2×3=6,4!=1×2×3×4=24,5!=1×2×3×4×5=120,6!=1×2×3×4×5×6=5!×6=720,由此可知,5!,6!,⋯,h的个位数字都是0(其中,≥5且为整数),则1!+2!+3!+⋯+2020!的个位数字与1!+2!+3!+4!的个位数字相同,因为1!+2!+3!+4!=1+2+6+24=33,其个位数字是3,所以1!+2!+3!+⋯+2020!的个位数字是3,故答案为:3.三、解答题18.观察下列等式11×2=1﹣12,12×3=12﹣13,13×4=13﹣14,将以上三个等式两边分别相加得11×2+12×3+13×4=1﹣12+12﹣13+13﹣14=1﹣14=34.(1)猜想并写出1or1)=;(2)11×2+12×3+13×4+…+12016×2017=;(3)探究并计算:12×4+14×6+16×8+⋯+12016×2018;(4)计算:111111111.。
2.6有理数的乘法与除法【学习目标】1.会根据有理数的乘法法则进行乘法运算,并运用相关运算律进行简算;2.理解乘法与除法的逆运算关系,会进行有理数除法运算;3. 巩固倒数的概念,能进行简单有理数的加、减、乘、除混合运算;4. 培养观察、分析、归纳及运算能力.【要点梳理】要点一、有理数的乘法1.有理数的乘法法则:(1)两数相乘,同号得正,异号得负,并把绝对值相乘;(2)任何数同0相乘,都得0.要点诠释: (1) 不为0的两数相乘,先确定符号,再把绝对值相乘.(2)当因数中有负号时,必须用括号括起来,如-2与-3的乘积,应列为(-2)×(-3),不应该写成-2×-3.2. 有理数的乘法法则的推广:(1)几个不等于0的数相乘,积的符号由负因数的个数决定.当负因数有奇数个时,积为负;当负因数的个数有偶数个时,积为正;(2)几个数相乘,如果有一个因数为0,那么积就等于0.要点诠释:(1)在有理数的乘法中,每一个乘数都叫做一个因数.(2)几个不等于0的有理数相乘,先根据负因数的个数确定积的符号,然后把各因数的绝对值相乘.(3)几个数相乘,如果有一个因数为0,那么积就等于0.反之,如果积为0,那么至少有一个因数为0.3. 有理数的乘法运算律:(1)乘法交换律:两个数相乘,交换因数的位置,积相等,即:ab=ba.(2)乘法结合律:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积相等.即:abc=(ab)c=a(bc).(3)乘法分配律:一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.即:a(b+c)=ab+ac.要点诠释:(1)在交换因数的位置时,要连同符号一起交换.(2)乘法运算律可推广为:三个以上的有理数相乘,可以任意交换因数的位置,或者把其中的几个因数相乘.如abcd =d(ac)b .一个数同几个数的和相乘,等于把这个数分别同这几个数相乘,再把积相加.如a(b+c+d)=ab+ac+ad . (3)运用运算律的目的是“简化运算”,有时,根据需要可以把运算律“顺用”,也可以把运算律“逆用”. 要点二、有理数的除法1.倒数的意义: 乘积是1的两个数互为倒数.要点诠释:(1)“互为倒数”的两个数是互相依存的.如-2的倒数是,-2和是互相依存的; (2)0和任何数相乘都不等于1,因此0没有倒数;(3)倒数的结果必须化成最简形式,使分母中不含小数和分数; (4)互为倒数的两个数必定同号(同为正数或同为负数). 2. 有理数除法法则:法则一:除以一个不等于0的数,等于乘这个数的倒数,即. 法则二:两数相除,同号得正,异号得负,并把绝对值相除.0除以任何一个不等于0的数,都得0.要点诠释:(1)一般在不能整除的情况下应用法则一,在能整除时应用法则二方便些.(2)因为0没有倒数,所以0不能当除数.(3)法则二与有理数乘法法则相似,两数相除时先确定商的符号,再确定商的绝对值.要点三、有理数的乘除混合运算由于乘除是同一级运算,应按从左往右的顺序计算,一般先将除法化成乘法,然后确定积的符号,最后算出结果.12-12-1(0)a b ab b÷=≠要点四、有理数的加减乘除混合运算有理数的加减乘除混合运算,如无括号,则按照“先乘除,后加减”的顺序进行,如有括号,则先算括号里面的. 【典型例题】类型一、有理数的乘法运算例1.算式(﹣1)×(﹣3)×之值为何?( ) A .B .C .D .例2.(1); (2)(-5)×(-8.1)×3.14×0.【基础巩固】1.计算:()111513333⨯--⨯=⨯( )=_______. 2.计算:(-4)×125×(-25)×(-0.08)=_______.3.如果两个有理数在数轴上的对应点在原点的同侧,那么这两个有理数的积 ( )A .一定为正B .一定为负C .为零D .可能为正,也可能为负4.若a<0,b>0,则a b _______0;若a>0,b>0,则ab _______0; 若a =0,b<0,则a b _______0;若a>0,b<0,则ab _______0.54(3)1(0.25)65⎛⎫-⨯⨯-⨯- ⎪⎝⎭5.若干个不等于0的有理数相乘,积的符号( ) A .由因数的个数决定 B .由正因数的个数决定 C 由负因数的个数决定D .由负因数和正因数个数的差决定 6.下列运算结果为负值的是 ( )A .(-7)×(-6)B .(-6)+(-4)C .0×(-2)(-3)D .(-7)-(-15) 7.利用分配律计算981009999⎛⎫-⨯ ⎪⎝⎭时,正确的方法可以是( ) A .-981009999⎛⎫-+⨯ ⎪⎝⎭ B .-981009999⎛⎫--⨯ ⎪⎝⎭ C .981009999⎛⎫-⨯ ⎪⎝⎭ D .11019999⎛⎫--⨯ ⎪⎝⎭ 8.下列运算错误的是A .(-2)×(-3)=6B .()1632⎛⎫-⨯-= ⎪⎝⎭C .(-5)×(-2)×(-4)=-40D .(-3)×(-2)×(-4)=-24 9.下列说法错误的是 ( ) A .任何有理数都有倒数 B .互为倒数的两个数的积为1 C .互为倒数的两个数同号 D .1和-1互为负倒数 10.计算下列各题:(1)42575610⎛⎫⎛⎫⨯-⨯- ⎪ ⎪⎝⎭⎝⎭; (2)()511.249⎛⎫⨯-⨯- ⎪⎝⎭;(3)3416401373⎛⎫⎛⎫-⨯-⨯⨯ ⎪ ⎪⎝⎭⎝⎭; (4)-5×8×(-7)×(-0.25);(5)318772156⎛⎫⎛⎫⎛⎫⎛⎫-⨯-⨯-⨯+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.11.用简便方法计算:(1)(-25)×(-85)×(-4); (2)11116428⎛⎫--⨯ ⎪⎝⎭;(3)315606060777⨯-⨯+⨯; (4)()()()()7.3342.07 2.077.33-⨯+-⨯-;(5) 2415127754⎛⎫⎛⎫-÷-⨯⨯-÷ ⎪ ⎪⎝⎭⎝⎭;(7) 134118432-÷⨯⨯-;【拓展提优】12.倒数等于它本身的有理数是_______.13.算式411010.05810.0454⎛⎫-⨯-+=-+- ⎪⎝⎭.这个运算过程应用了 ( )A .加法结合律B .乘法结合律C .乘法交换律D .乘法分配律 14.一个数的相反数与这个数的倒数的和为0,则这个数的绝对值为 ( ) A .2 B .1 C .0.5 D .0 15.若ab ≠0,则a ba b+的取值不可能是 ( ) A .0 B .1 C .2 D .-2 16.下列说法正确的是 ( ) A .有理数m 的倒数是1mB .任何正数大于它的倒数C .小于1的数的倒数一定大于1D .若两数的商为正,则这两个数同号 17.已知230x y ++-=,求152423x y xy --+的值.18.若a 、b 互为相反数,c 、d 互为倒数,m 的绝对值是1,求(a +b)cd -2012m 的值.19.已知a、b互为相反数,c、d互为倒数,x的绝对值等于1,求x2+(a+b)x -(a+b-cd)的值.课后作业一、填空题1.运用运算律填空:(1)5×(-3)=(-3)×_______.(2)[(-3)×2]×5=(-3)×(_______×_______).(3)(-12)×[12+(-13)]=(-12)×_______+(-12)×_______.2.12的倒数是_______.3.计算:19.8×125-12.5×118=_______.4.114的相反数与114的倒数的积是_______.5.绝对值小于2011的所有整数的积是_______.二、选择题6.-13的倒数是( )A.-3 B.3 C.-13D.137.下列运算其中错误的有( )①2×(-4)=-4×2=-8;②3×(-14)=34;③4×3×(-13)=4×(-1)=-4;④10×(15-5)=10×15-10×5=2-50=48.A.1个B.2个C.3个D.4个8.利用运算律计算(-334×4)时,下列运算正确的是( )A.-3×4+34×4 B.-3×34×4 C.-3×4-34×4 D.-3×4-349.下列计算中正确的是( )A.-10÷10=1 B.(-10)÷(-1)=-10 C.1÷(-10)=-10 D.0÷(-10)=0 10.下列运算错误的是( )A.3÷(-13)=3×(-3) B.-5÷(-12)=-5×(-2)C.8÷(-2)=8+2 D.0÷3=011.如果1a a=-,那么a 是 ( )A .正数B .负数C .非负数D .非正数 12.两个不为0的有理数相除,如果交换被除数与除数的位置,它们的商不变,那么这两个数 ( )A .一定相等B .一定互为倒数C .一定互为相反数D .相等或互为相反数 三、解答题 13.计算:(1)(-4)×(+8.9)×(-0.25); (2)(13-14+25-56)×(-60); (3) (-0.25)×0.5×(-427)×4;(4)(-5)×(-367)+(-7)×(-367)-(-12)×(-367).(5)(-5)÷(217 )×45×(-214)÷7; (6) -8÷[(-38)×38]÷(-1023);预习:2.7有理数的乘方1.计算:234-⎛⎫⎪⎝⎭的值是( )A.一916B.916C.一169D.1692.下列各对数中,数值相等的是( )A.+32与+22B.-23与(-2)3C.-32与(-3)2D.3×22与(3×2)2 3.下列等式成立的是( )A.-3×23=-32×2 B.-32=(-3)2C.-23=(-2)3 D.-32=-23 4.对于式子(-3)6与-36,下列说法中,正确的是( ) A.它们的意义相同B.它们的结果相同C.它们的意义不同,结果相等D.它们的意义不同,结果也不相等5.下列叙述中:①正数与它的绝对值互为相反数;②非负数与它的绝对值的差为0;③-1的立方与它的平方互为相反数;④±1的倒数与它的平方相等.其中正确的个数有( )A.1 B.2 C.3 D.46.将3×3×3写成乘方的形式是;将-3×3×3写成乘方的形式是;将(-3)×(-3)×(-3)写成乘方的形式是.7.计算:-32+(-2)3的值是.8.在有理数-32,0,20,-1.25,314,-(-2),(-4)2中,正数有个.9.平方等于它本身的数是;立方等于它本身的数是.。
做含有带分数和小数的除法运算
难易度:★★
关键词:有理数
答案:
有理数除法的法则只有两点,但在具体运算中有一些含有带分数和假分数的除法,不加以变化,仅运用法则,较难解决
【举一反三】
典例:计算
思路导引:一般来说,此类问题运算过程中一般化为假分数,小数化为分数
标准答案:
尊敬的读者:
本文由我和我的同事在百忙中收集整编出来,本文稿在发布之前我们对内容进行仔细校对,但是难免会有不尽如人意之处,如有疏漏之处请指正,希望本文能为您解开疑惑,引发思考。
文中部分文字受到网友的关怀和支持,在此表示感谢!在往后的日子希望与大家共同进步,成长。
This article is collected and compiled by my colleagues and I in our busy schedule. We proofread the content carefully before the release of this article, but it is inevitable that there will be some unsatisfactory points. If there are omissions, please correct them. I hope this article can solve your doubts and arouse your thinking. Part of the text by the user's care and support, thank you here! I hope to make progress and grow with you in the future.。
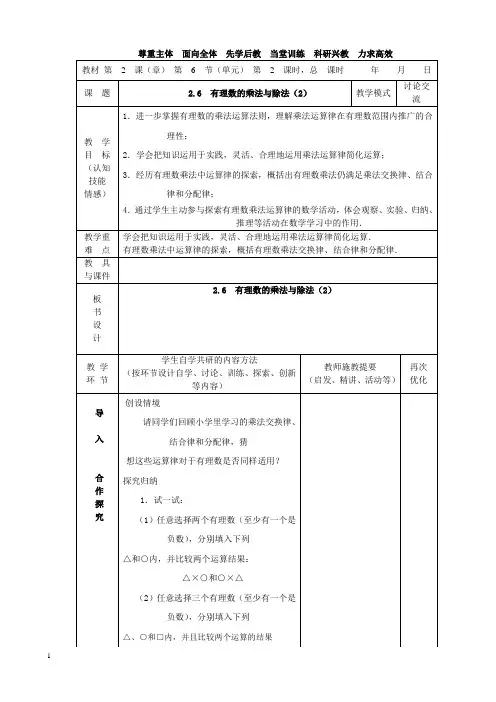
数学教学设计
教材:义务教育教科书·数学(七年级上册)
作者:赵莹莹(苏州市南环中学)
2.6 有理数的乘法与除法(2)
1.进一步掌握有理数的乘法运算法则,理解乘法运算律在有理数范围内推广的合理性;
2.学会把知识运用于实践,灵活、合理地运用乘法运算律简化运算;
3.经历有理数乘法中运算律的探索,概括出有理数乘法仍满足乘法交换律、结合律和分配律;
4.通过学生主动参与探索有理数乘法运算律的数学活动,体会观察、实验、归纳、推理等活动在数学学习中的作用学会把知识运用于实践,灵活、合理地运用乘法运算律简化运算.
有理数乘法中运算律的探索,概括有理数乘法交换律、结合律和分配律.
育评注(课堂设计理念,实际教学效果及改进设想):
学曾经学过的知识点,关键是对照学习!但是,又要找到和小学的不同,是小学知识的升华!让学生通过自己独立思需总结.。